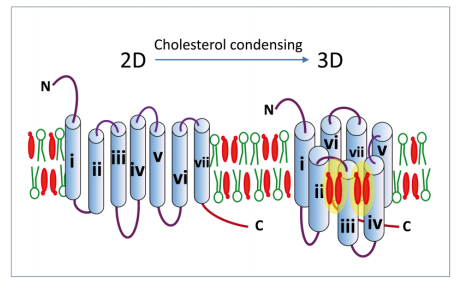
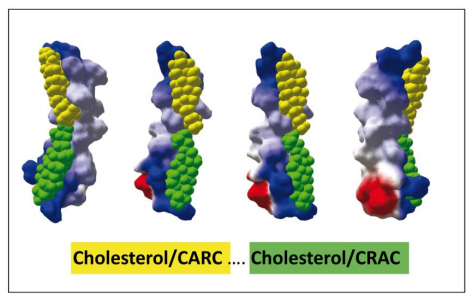
The cohabitation of lipids and proteins in the plasma membrane of mammalian cells is controlled by specific biochemical and biophysical rules. Lipids may be either constitutively tightly bound to cell-surface receptors (non-annular lipids) or less tightly attached to the external surface of the protein (annular lipids). The latter are exchangeable with surrounding bulk membrane lipids on a faster time scale than that of non-annular lipids. Not only do non-annular lipids bind to membrane proteins through stereoselective mechanisms, they can also help membrane receptors acquire (or maintain) a functional 3D structure. Cholesterol is the prototype of membrane lipids that finely controls the 3D structure and function of receptors. However, several other lipids such as sphingolipids may also modulate the function of membrane proteins though conformational adjustments. All these concepts are discussed in this review in the light of representative examples taken from the literature.
1.
Introduction
The Zika virus is spread by the same species of mosquito, namely Aedes aegypti (A. aegypti), as dengue. It is a member of the virus family Flaviviridae. The first discovery of the Zika virus was in 1947, however despite being around for a while, the Zika virus has not received much attention until recently when it has been discovered that it is associated with microcephaly which is a serious birth defect in newborns, caused if women are infected with Zika during pregnancy. Most importantly there is still no vaccine to prevent the Zika virus. Apart from causing severe birth defects to newborn babies, infected individuals can also experience fever, rash and joint pain. As a result, in this paper we will use an existing mathematical model for dengue to analyse the dynamical behaviour for the Zika virus, especially in Brazil, as well as obtaining the future expected number of cases of microcephaly due to Zika. Although the Zika virus and dengue are very similar and thus some parameter values would remain the same, parameters such as the transmission probabilities as well as the basic reproduction number may vary. Therefore in this paper we will also use some existing data values in Brazil to estimate those required parameter values. We will use four different approaches to estimate the expected number of cases of microcephaly in Brazil due to pregnant women exposed to the Zika virus.
This paper is arranged as follows: In Section 2, we will look at the first approach by working with a delayed dengue model without seasonality as well as defining the parameter values. We will then look at the results obtained by using the least squares estimation technique in R. The basic reproduction number for our model without seasonality is also calculated. In Section 3, we will look at the second approach where we will improve on our model by adding seasonality into the birth function of the A. aegypti mosquitoes. In Section 4, we will continue to work with the same model as in Section 2, but we will make the model more realistic, but also more complicated, by taking into account the age-structure of the human population. In Section 5, we will look at the last approach where we introduce seasonality into the more complicated age-structured model given in Section 4. Lastly in Section 6, we will summarise all our results. Numerical simulations are produced throughout the paper to illustrate our findings.
2.
The delayed Zika model without seasonality
Let us define $ S_H(t), I_H(t) $ and $ R_H(t) $ to respectively represent the susceptible, infected and recovered individuals for humans, while $ S_v(t), L_v(t) $ and $ I_v(t) $ respectively represent the susceptible, latent and infected mosquitoes. $ N_H = S_H+I_H+R_H $ denotes the total human population size and $ N_v = S_v+L_v+I_v $ represents the total A. aegypti population size where both populations are constant. The delayed mathematical model for dengue mentioned in [1] is as follows:
with initial conditions $ S_H(t_0), R_H(t_0), I_v(t_0), L_v(t_0), \{ I_H(\eta) : \eta \in [t_0-\tau, t_0] \} $ and $ \{ S_v(\eta) : \eta \in [t_0-\tau, t_0] \} $. The definitions of the parameter values used in Eq (2.1) and their corresponding values are given in Table 1.
Note that the model described by Eq (2.1) does not have an exposed class in humans. However, it is important to note that much work has already been done on the Zika virus without a human exposed class [2,3,4,5,6,7,8,9,10,11,12]. Therefore, we hope that the results mentioned in this paper will be able to contribute to this research area.
As we can see from Table 1, the two most crucial parameter values $ b $ and $ c $ can take values within the ranges given and thus one of the main aims in this project is to use the least squares estimation technique in R and the real Zika virus data (the weekly incidence cases of Zika) from Brazil given in [13] to estimate these two parameter values. In the next section, we will discuss in detail the idea behind the estimation technique.
2.1. Parameter estimation
The basic reproduction number is defined as the expected number of secondary cases caused when a newly infected individual enters a disease-free population at equilibrium. A secondary case is a case infected from the original infected case via only one mosquito. In the context of mosquito-borne disease such as Zika it can equally be defined as the expected number of secondary cases caused when a newly infected mosquito enters a disease-free population at equilibrium. All epidemics begin with a single infected host entering a disease-free population and the basic reproduction number $ R_0 $ exceeds one. Therefore in our case, it is reasonable to assume that a single Zika infected human enters the disease-free population at some time $ t_0 $, where $ t_0 < t_1 $ and $ t_1 $ is the time when we have available Zika data values in Brazil obtained from [13]. In this case $ t_1 $ represents the first week in 2015. Let us now assume a single infected human has entered the Brazilian population at some time before $ t_1 $, say $ t_0 $, where $ S_H(t_0) = 207,847,999, I_H(t_0) = 1, R_H(t_0) = 0, L_v(t_0) = 0, I_v(t_0) = 0, \{ I_H(\eta) = 0 $ for $ \eta \in [t_0-\tau, t_0] \} $ and $ \{ S_v(\eta) = 207,848,000 \times 1.5 $ for $ \eta \in [t_0-\tau, t_0] \}. $ Note that these initial values correspond to the time $ t_0 $ at which the first human case of Zika virus was first introduced into a disease-free population. The values of these variables at the later time $ t_1 $ will be different.
We used the least squares estimation technique in R (R version 3.0.2, Frisbee Sailing 2013 version) using the function $\mathtt{ nls.lm}$ and the library $\mathtt{ minpack.lm}$ to perform the least squares fitting. By comparing the least square minimised results with the real data values for Zika cases in Brazil given in [13], the estimated values for $ b, c $ and $ t_1-t_0 $ with different values of $ a $ are given in Table 2 where $ t_1-t_0 $ is in units of weeks. The corresponding 95% confidence intervals for the estimated values are given in Table 3. Clearly, all the values we obtained for both $ b $ and $ c $ lie within the appropriate ranges mentioned by Andraud et al. [14] and Chikak and Ishikama [15].
Note that in Eq (2.1) if we multiply $ a $ by a constant factor $ k $, divide both $ b $ and $ c $ by the same factor, and keep $ t_0 $ the same, then the output of the model does not change. Therefore, when we had found the optimal least squares fitted values $ b $ and $ c $ corresponding to $ a $ = 0.20 per day, we could then find the optimal values of $ b $ and $ c $ for the other values of $ a $ by dividing those values for $ a $ = 0.20 per day by the appropriate factor and keeping $ t_0 $ the same. As a result, we have chosen to illustrate only the results obtained for when $ a $ = 0.20 per day.
Note also that applying the procedure suggested above to $ a $ = 0.50 per day (namely dividing $ b $ and $ c $ from $ a $ = 0.20 per day by a factor of 2.5) gives resulting values of $ b $ and $ c $ which are outside the constraints for these model parameters suggested by the literature. As a result, we have decided to obtain an alternative set of optimal values for when $ a $ = 0.50 per day, where $ b $ and $ c $ are within the ranges suggested by literature. In this situation, these constraints force the least squares algorithm to fit to a later phase of the epidemic after most people have become infected (note the number of recovered humans in expressions (2.1) and (2.2)). Hence the model predictions with the least squares fitted parameters are virtually the same for $ a $ = 0.20 per day, $ a $ = 0.25 per day and $ a $ = 0.30 per day but different for $ a $ = 0.50 per day.
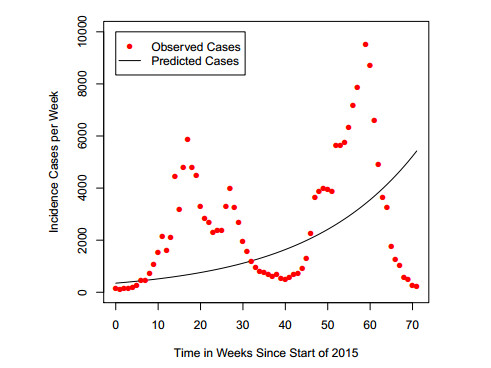
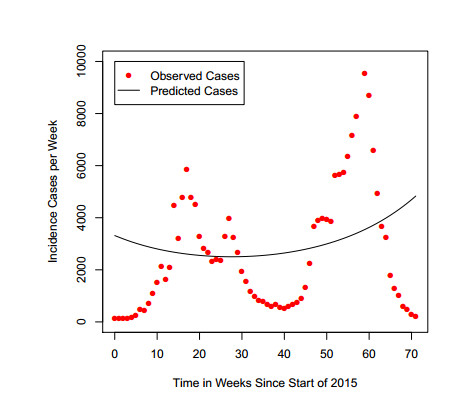
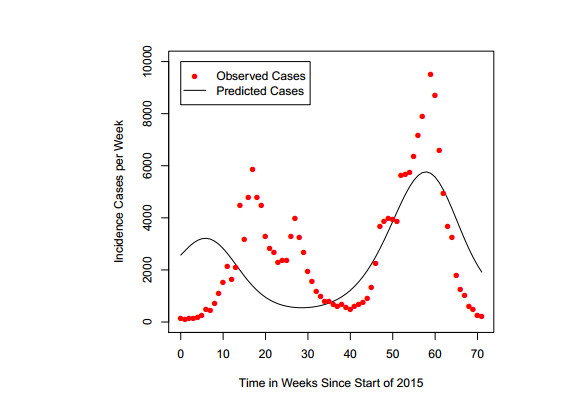
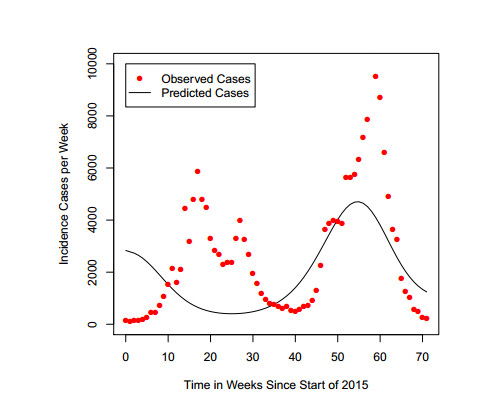
For the purpose of illustration, the data fitting against the real Zika data using Eq (2.1) for $ a = 0.20 $/day and $ a = 0.50 $/day are given in Figure 1 and Figure 2 respectively. The results shown in these figures are not a perfect fit and one of the main reasons could be that seasonality is not included in Eq (2.1). Motivated by this, later on in this paper, we will modify Eq (2.1) by including seasonality into the model to improve the data fitting and the accuracy of our estimation.
In addition, in order to allow us to make more estimates for the future expected number of cases of microcephaly, it is important that we have reasonable starting values for $ S_H, I_H, R_H, S_v, L_v $ and $ I_v $. As a result, by keeping the assumption that a single infected human enters a disease-free population at some point $ t_0 $, we also obtained estimated expected values at time $ t_1 $ corresponding to different biting rates given as follows. In each case the values of $ S_v(\eta) $ and $ I_H(\eta) $ for $ \eta \in [t_1-\tau, t_1] $ are given by the simulation using the estimated parameters.
● For $ a = 0.20 $/day and $ t_1 = t_0+180.5848 $ weeks, the values at time $ t_1 $ are
● For $ a = 0.50 $/day and $ t_1 = t_0+500 $ weeks, the values at time $ t_1 $ are
The values at time $ t_1 $ will be used as initial values for future simulations in Section 2.3.
Now that we have all the required parameter values and the initial values for each biting rate, we can estimate the future expected number of cases of microcephaly as a result of pregnant women infected with Zika during pregnancy. However before we do this, it is important for us to find another important epidemiological parameter value namely the basic reproduction number.
2.2. The basic reproduction number
The basic reproduction number, $ R_0 $, is a very important parameter value in infectious disease modelling as it often acts as a threshold which determines whether a particular epidemic will die out ($ R_0 < 1 $) or persist ($ R_0 > 1 $). In the context of our model the basic reproduction number is defined as the expected number of secondary cases of disease caused by a single newly infected individual entering a disease-free population at equilibrium. As a result, it is important for us to calculate this particular value. The basic reproduction number for our delayed Zika model given in [19] is defined as
All the parameter values are defined as in Table 1 where $ b $ and $ c $ are the least squares estimated values obtained in R given in Table 2 corresponding to different biting rates. By substituting all the required values, we have the basic reproduction number for each biting rate shown in Table 4 to 4 d.p.
Note that when performing data fitting using the least squares estimation technique mentioned in Section 2.1, we notice that there are two different cases in which we can achieve a best fit against the real Zika data given by Ferguson et al. [13]. The first case is demonstrated by biting rates of $ a = 0.20 $ per day where the epidemic is just starting and it has yet to reach its peak epidemic level. This scenario is highlighted by having a relatively low basic reproduction number given in Table 4. Another case is when the epidemic has already reached its maximum level and this is illustrated for when $ a = 0.50 $ per day which has a high basic reproduction number. This is also why we noticed a huge number of recovered individuals in this case as given by (2.2). Although the basic reproduction number given when $ a = 0.50 $ per day is relatively high compared to the other biting rates, this value is still reasonable as various papers have also estimated a relatively high $ R_0 $ for different dengue outbreaks [20,21].
In the next section, we will estimate the future number of cases of microcephaly due to Zika virus for different biting rates.
2.3. Estimated number of cases of microcephaly
In this section, we will focus on estimating the expected number of cases of microcephaly in Brazil due to the Zika virus both in the short-term and in the long-term. In this paper, we focus on analysing the effect of pregnant women infected with Zika virus during their first trimester as various reports (e.g. [22,23]) suggest that pregnant women who are infected with the Zika virus during the first trimester have a much higher risk of their babies developing microcephaly as opposed to those who are infected with Zika in their second or third trimesters. This makes sense biologically as during the first trimester, the brain of the baby is still developing and thus it is more susceptible to external factors. Note that the method used in this section can be easily extended and applied to other Zika time periods and to other countries in which Zika is present.
WHO [16] state that Brazil has a total population size of 207,847,000 of which according to the United Nations [24] around 28.2% (58,612,854) were women at the age of fertility (between 15–44 years old). Recall that $ t_1 $ represents the start of 2015. The unit of time is in weeks unless stated otherwise. For the purpose of illustration, we will show only the simulations which illustrate the dynamical behaviour of humans and mosquitoes both in the long- and in the short-term in the first example.
Note that the models and parameters contain a great deal of uncertainty. We are interested in short-term estimates as they can tell us what happens in the immediate future. However we expect that in the long-term the model will settle down to a unique endemic equilibrium. Hence it is valuable to do simulations over a long time so that we can predict what will happen after the short term transient effects of the disease invading a susceptible population have faded away and we can predict the long-term consequences of Zika too.
Example 1. ($ a = 0.20 $/day) Let us recall the estimated initial values starting from time $ t_1 $ obtained from parameter estimation:
with $ I_H(\eta) $ and $ S_v(\eta) $ given for $ \eta \in [t_1-\tau, t_1] $ by the simulation.
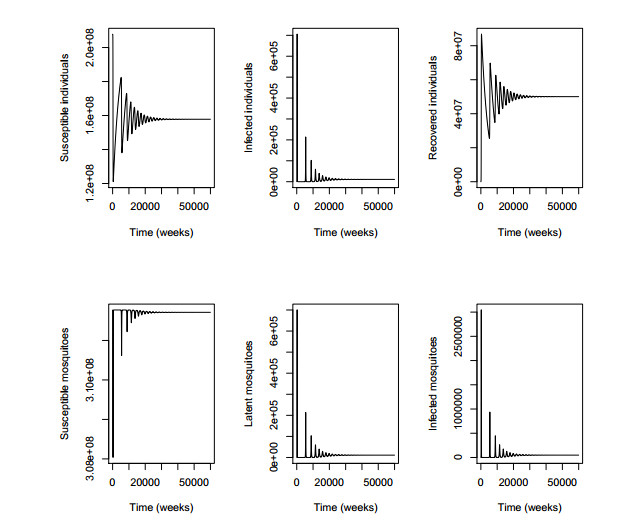
Let us now define the parameter values as given in Table 1 but with $ b = 0.2489 $ and $ c = 0.4513 $ (to 4 d.p). Then by using R to integrate the delayed differential equations given in Eq (2.1) the numerical simulations in the long-term are as shown in Figure 3. We can see that the number of infected individuals persists with an endemic equilibrium of 10,992.89.
From various reports (e.g. [22,23]), it is estimated that if a pregnant woman is infected with Zika during the first trimester, then the risk of her baby developing microcephaly ranges from $ 1\% $ to $ 13\% $. The majority of papers in the literature estimate this probability to be in this range. However Nishiura et al. [25] estimated a higher risk of up to $ 100\% $ using data from Brazil. Their estimates depend on the unknown fraction of Zika virus infections among seronegative dengue-like illness cases. Hence we also include estimates of the number of microcephaly cases when the risk of microcephaly following infection with Zika in the first trimester of preganancy is up to $ 100\% $. In order to enhance our understanding of the effect of having different risk percentages on the number of microcephaly cases, we will produce the results where the risk percentage is $ 1\%, 7\%, 13\%, 40\%, 70\% $ and $ 100\% $. Note that not all of those infected pregnant women are infected during the first trimester and since pregnancy is divided into three different trimesters, we will assume that the probability that an infected pregnant woman is in the first trimester is $ 1/3 $.
On average, each of the women currently giving birth now has been pregnant for 270 days of which the first 90 days is considered to be the first trimester in pregnancy. Recall that the average infectious period of the Zika virus is around 6 days. Let us define $ M_1(t) $ to be the expected future number of cases of microcephaly in newborns as a result of pregnant women infected with the Zika virus in the first trimester. We have that $ M_1 $ is given by
where $ P_1 $ represents the probability that a baby develops microcephaly given that the pregnant mother is infected in the first trimester which in this case is either $ 1\%, 7\%, 13\%, 40\%, 70\% $ or $ 100\% $, and $ 15I^{*} $ represents the number of different distinct infectious cohorts of women that will be infected during their first trimester of pregnancy. Note that $ I^{*} $ is the endemic equilibrium of the number of infected people which in this case is 10,992.89. Note also that the current model assumes that everyone in the population can give birth. If only women give birth we need to halve $ I^* $ but double $ \mu_H $ which gives the same answer.
By using Eq (2.5), we can estimate the future expected number of cases of microcephaly per year in the long-term at endemic equilibrium, provided that the women are infected with the Zika virus during their first trimester of pregnancy with different risk percentages. The results are given in Table 5.
Although it is interesting for us to see the estimated number of cases of microcephaly at equilibrium, it is more practical for us to find out what happens in the short-term. As a result, we will now focus on a shorter period, say 500 weeks. For a shorter period of time, it is not suitable to use Eq (2.5) as the number of infected individuals is fluctuating over time. As a result, we will introduce an additional differential equation namely $ dM(t)/dt $ which describes the number of microcephaly cases in a given time period.
where $ \bar\tau $ represents the midpoint of the first trimester which in this case will be around $ 32.1429 $ weeks (to 4 d.p) and $ P_1 $ is defined as before.
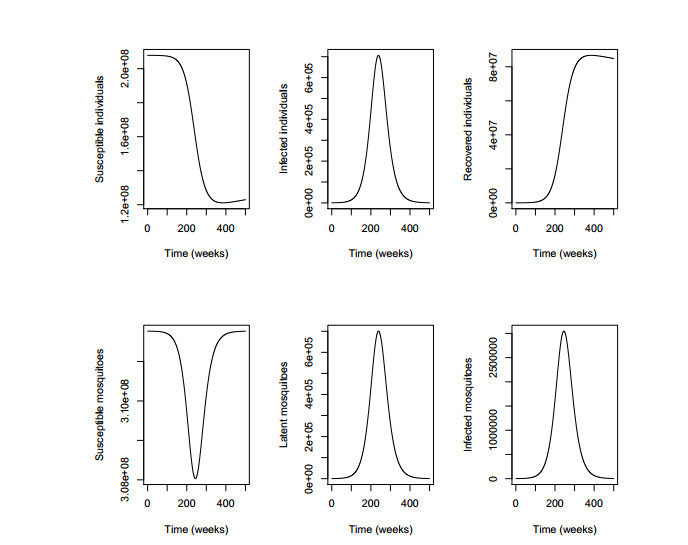
Similarly, by solving Eqs (2.1) and (2.6) in R, we have the numerical simulations which illustrate the behaviour of susceptible, infected and recovered individuals over a shorter period of time, namely 500 weeks. The result is shown in Figure 4. From Figure 4, we have the numerical simulation results but in the nearer future. By integrating the differential equation $ dM(t)/dt $, we have that the cumulative number of cases of microcephaly over the first 9.6 years (500 weeks) with different risk percentages are given in Table 6.
Example 2. ($ a = 0.50 $/day) Let us recall the estimated initial values starting from time $ t_1 $ obtained from parameter estimation for when $ a = 0.50/day $:
again the initial values for $ I_H(\eta) $ and $ S_v(\eta), \ \eta \in [t_1- \tau, t_1] $, are obtained from the simulation. By carrying out the same procedure as in Example 1, we have that the total number of infected individuals persists with an endemic equilibrium of approximately 43,818.92. The future expected number of microcephaly cases at endemic equilibrium per year caused by women who have been infected with the Zika virus in their first trimester of pregnancy with different risk percentages are given in Table 7. For over a shorter period of time, the total cumulative number of microcephaly cases over the first 9.6 years (500 weeks) with different risk percentages are given in Table 8.
3.
The delayed Zika model with seasonality
It is well-known that the life cycle of A. aegypti is influenced by many environmental factors such as rainfall and temperature (e.g. [26,27,28]). This might be the reason why the data fitting results shown in Figure 1 and Figure 2 are not ideal. As a result, in order to fully capture the behaviour of the A. aegypti under the influence of environmental factors and its effect on the number of microcephaly cases, in this section we decide to improve on our model by adding seasonality into the birth function of A. aegypti. Note that the unit of time is now in weeks. Thus, our delayed Zika model with seasonality becomes:
where all the parameter values are defined as before. $ \alpha $ is the amplitude of the seasonality function and $ \phi $ is the peak of the function.
Because we are already fitting a large number of parameters we choose to estimate $ \alpha $ heuristically and then fit the remaining parameters $ a, b, c, t_1-t_0 $ and $ \phi $. Heuristically we get the best result by taking $ \alpha = 1 $. By choosing $ \alpha $ to be 1 and making the same assumptions as we did in Section 2.1, we have obtained a new set of parameter values for $ b, c, t_1-t_0 $ and $ \phi $ corresponding to different biting rates which fitted the real data values for Zika in Brazil [13] much better than the ones we have obtained using Eq (2.1), which is exactly what we expected as environmental factors play an important role in the life cycle of A. aegypti. Recall that $ t_1 $ represents the first week of 2015 and $ t_1-t_0 $ is in units of weeks. The results are shown in Table 9 with their corresponding 95% confidence intervals given in Table 10.
Similarly to before, the estimated values of $ t_1-t_0 $ are the same for each value of the biting rate and the estimates for $ b $ and $ c $ for the values $ a $ = 0.25 per day, $ a $ = 0.30 per day and $ a $ = 0.50 per day can be obtained from the values for $ a $ = 0.20 per day by dividing by the corresponding ratio of $ a $-values. So for example for $ a $ = 0.25 per day the values of $ b $ and $ c $ for $ a $ = 0.20 per day could be divided by 1.25 to obtain the new $ b $ and $ c $ values. Note also that the values of $ b $ and $ c $ for $ a $ = 0.20 per day, $ a $ = 0.25 per day, and $ a $ = 0.30 per day are within the range of values suggested by the literature whilst for $ a $ = 0.50 per day they are lower than this range of values. Because this means that all sets of different fitted values will predict the same initial values and numbers of microcephaly cases we present the results only for one of them, $ a $ = 0.20 per day. As before we also illustrate the results for $ a $ = 0.5/day with alternative least squares parameter estimates for $ b $ and $ c $ which do lie within the ranges suggested by the literature.
The real Zika data in Brazil [13] from the beginning of 2015 are shown in Figure 5. The way in which we have introduced seasonality is used in many papers for mosquito-borne diseases [27,29,30,31,32,33,34]. Over a long period of time we expect the data to follow a regular seasonal pattern. However we had only 71 weeks data available and as can be seen in Figure 5 the data has two peaks, a lower one at 17 weeks after the start of 2015 and a higher one at 6 weeks after the start of 2016. However in the output of the model with a seasonal mosquito birth rate the plotted incidence will have peaks 52 weeks apart. Additionally the design of the least squares estimation assigns equal weights to all datapoints thus it effectively gives more weight to the larger peak as there are larger potential deviations there. So even the best fit simulation is not a perfect fit to the dataset. An example fit for $ a = 0.2 $/day is shown in Figure 5.
The data fitting against real Zika data for each biting rate is shown in Figures 5 and 6 where the unit of time is in weeks. Note that the real Zika data in Brazil from [13] represents the incidence case data of Zika, thus in the least squares fitting to fit the output from the model we have to integrate the incidence term
equivalently $ \lambda(t)S_H(t) $ where $ \lambda(t) = \frac{abI_v(t)}{N_H} $ is the per capita force of infection for humans, over a week to get the incidence data for that week.
The corresponding estimated initial values in Brazil at time $ t_1 $, the first week of 2015, to 4 d.p. for each biting rate, are given as follows:
● For $ a = 0.20 $/day, the values at time $ t_1 = t_0+600.4457 $ weeks are
● For $ a = 0.50 $/day, the values at time $ t_1 = t_0+595 $ weeks are
Again in (3.2) and (3.3), the initial values for $ I_H(\eta) $ and $ S_v(\eta), \ \eta \in [t_1- \tau, t_1) $, are given by the simulation using the estimated parameter values. Similarly to Section 2.3, we will now calculate the expected number of cases of microcephaly due to Zika virus both in the short-term and at endemic equilibrium. As the idea is similar to the ones that are presented in Section 2.3, in this section, we will illustrate the results only for when $ a = 0.20 $/day and for when $ a = 0.50 $/day, which represent the two cases we encountered in data fitting mentioned in Section 2.2.
Example 3. For $ a = 0.20 $/day, the number of infected humans has an endemic equilibrium value of around 15,417 rounded to the nearest whole number. Again by using Eq (2.5), we have that the endemic equilibrium number of cases of microcephaly per year are as given in Table 11.
For a shorter period of time, say 600 weeks in other words in about 11.5 years, the cumulative number of microcephaly cases for the first 11.5 years caused by women being infected with the Zika virus in the first trimester of their pregnancy with different risk percentages are given in Table 12.
Example 4. For $ a = 0.50 $/day, the number of infected humans has an endemic equilibrium value of around 43,236 rounded to the nearest whole number. Again by using Eq (2.5), we can estimate the expected number of microcephaly cases per year in the long-term at endemic equilibrium, are as given in Table 13.
For a shorter period of time, say 600 weeks in other words in about 11.5 years, the cumulative number of microcephaly cases for the first 11.5 years caused by women being infected with the Zika virus in the first trimester of their pregnancy with different risk percentages are given in Table 14.
4.
Age-structured model
Another way, in which we can calculate the expected number of cases of microcephaly is to introduce the age-structure of the human population into our delayed Zika model given in Eq (2.1). Note that the unit of time is now in days for the age-structured model. Let us now define the age-structured delayed Zika model as follows:
where $ S_H(0, t) = \mu_H N_H, R_H(0, t) = 0 $ for $ t \ge t_1, \ I_H(0, t) = 0 $ for $ t \ge t_1-\tau $ are the boundary conditions for susceptible, recovered and infected individuals respectively. In addition, $ S_H(\xi, t_1) = \mu_HN_H e^{-\mu_{H} \xi}, R_H(\xi, t_1) = 0 $ and $ I_H(\xi, \eta) = 0, \ \eta \in [t_1-\tau, t_1] $, are the initial values for susceptible, recovered and infected individuals respectively. All the other parameter values and the mosquito initial conditions are defined as before. Note that $ I_H(\xi, t) $ represents the density with respect to age of the number of infected individuals at time $ t $. Therefore, the number of infected individuals between two ages, say $ A_1 $ and $ A_2 $, at time $ t $ is given as
Similarly, in order for us to calculate the future expected number of cases of microcephaly, we would introduce an additional differential equation, $ dM(t)/dt $, into the Eq (4.1), and thus we have
where $ \bar\tau $ and $ P_1 $ are defined as before.
Example 5. ($ a = 0.20/day $) By using the parameter estimated values $ b, c $ and $ t_1-t_0 $ from Section 2.1 and other parameter values given in Table 1 with $ a $ = 0.20/day, we have obtained that for the next 800 days (around 2.19 years), the cumulative number of microcephaly cases is estimated to be around 595, 4,165 and 7,735 (to the nearest whole number) corresponding to having risk percentage of $ 1\%, 7\% $ and $ 13\% $ respectively. For risk percentages $ 40\% $, $ 70\% $ and $ 100\% $ these numbers are 23,800, 41,650 and 59,500 respectively.
Example 6. ($ a = 0.50/day $) By using the parameter estimated values $ b, c $ and $ t_1-t_0 $ from Section 2.1 and other parameter values given in Table 1 with $ a $ = 0.50/day, we have obtained that for the next 800 days (around 2.19 years), the cumulative number of microcephaly cases is estimated to be around 162, 1,135 and 2,106 (to the nearest whole number) corresponding to having risk percentage of $ 1\%, 7\% $ and $ 13\% $ respectively. For risk percentages $ 40\% $, $ 70\% $ and $ 100\% $ these numbers become respectively 6,480, 11,340 and 16,200.
Note that the computational time required to generate the results for this age-structured model is considerably longer than for the model given in Eq (2.1) and thus it is difficult to produce results for a longer period of time.
5.
The delayed age-structured Zika model with seasonality
In this section, we will continue to examine the effect of seasonality on the spread of the Zika virus by now introducing seasonality into the more complicated age-structured Zika model. As before, we would also need to introduce an additional differential equation $ dM(t)/dt $ which will allow us to calculate the expected future number of cases of microcephaly at a particular time period. Note that the unit of time is now in days for the age-structured model. Thus we have
where $ \bar\tau $ and $ P_1 $ are defined as before.
Example 7. ($ a = 0.20 $/day) Let us recall that for $ a = 0.20 $/day, in the non-age-structured seasonal model, $ \alpha = 1 $ and $ \phi = -0.2865 $ weeks. By solving the differential equations, including $ dM(t)/dt $, we have that in the next 900 days (around 2.47 years), the cumulative number of cases of microcephaly is around 702, 4,914 and 9,126 (to the nearest whole number) corresponding to having risk percentage of $ 1\% $, $ 7\% $ and $ 13\% $ respectively. For risk percentages $ 40\% $, $ 70\% $ and $ 100\% $ these numbers are 28,080, 49,140 and 70,200 respectively.
Example 8. ($ a = 0.50 $/day) Again recall that for $ a = 0.5 $/day, in the non-age-structured seasonal model, $ \alpha = 1 $ and $ \phi = -0.2865 $ weeks. Similarly, by solving the differential equations, including $ dM(t)/dt $, we have that in the next 900 days (around 2.47 years), the cumulative number of cases of microcephaly is around 189, 1,323 and 2,457 (to the nearest whole number) corresponding to having risk percentage of $ 1\% $, $ 7\% $ and $ 13\% $ respectively. For risk percentages $ 40\% $, $ 70\% $ and $ 100\% $ these numbers become respectively 7,560, 13,230 and 18,900.
Again due to the computational time required to generate the results for this age-structured model being considerably longer than for the model given in Eq (3.1) it is difficult to produce results for a longer period of time.
6.
Conclusion and discussion
Zika virus is transmitted by A. aegypti, the same mosquitoes that are responsible for the transmission of dengue. Although the Zika virus has been around for a while, it has not received much attention until now, when the connection between the Zika virus and microcephaly has recently been discovered. Microcephaly is a serious birth defect in newborns. Motivated by this, in this paper, we focused on using mathematical models and numerical simulations to calculate the future expected number of cases of microcephaly if pregnant women are exposed to Zika.
We used four different approaches to examine this. The first one is using an existing delayed dengue model mentioned in [1], the second one is introducing the age-structure of the human population. The third one is introducing seasonality into the birth function of the A. aegypti mosquitoes to monitor the effect that environmental factors such as rainfall and temperature would have on the spread of Zika between humans and mosquitoes. Lastly, we continue to investigate the effect of seasonality but now on the more complicated age-structured model.
We have used the least squares estimation technique to estimate the two crucial parameter values namely the transmission probabilities between humans and A. aegypti. We have also calculated the basic reproduction number which is a threshold that determines whether a disease will die out or persist over time. We have fitted our models against real Zika data in Brazil from Ferguson et al. [13]. The data fitting results for our seasonality model are as given in Figures 5–6. The method by which we incorporate the effect of seasonality into our model is a well-known method used in many papers (e.g. [27,29,30,31,32,33,34]). The estimated transmission probabilities obtained for Zika between A. aegypti mosquitoes and humans are within the ranges given by the literature.
For each approach, we then solve the ODEs and PDEs using the programming language R and produced results in the long- and short-term which will help us with future planning and control policies for Zika in relation to microcephaly. We have introduced an additional differential equation $ dM(t)/dt $ into our model where $ M(t) $ represents the total cumulative expected future number of cases of microcephaly from the start up to a given time. Numerical simulations are then produced throughout the paper to give our results. Note that the techniques we used in this paper can be applied to any countries that have Zika or even other mosquito-born diseases such as dengue, yellow fever and chikungunya which are all spread by A. aegypti mosquitoes or other mosquito-born diseases, for example malaria.
In Sections 4 and 5, we focussed on the age-structured Zika model with and without seasonality respectively. In both cases we have used the differential equation
where $ \bar \tau $ is the time from the midpoint of the first trimester to birth. This is based on the observation that the average duration of infection is 6 days and the first trimester of pregnancy lasts 90 days. So assuming as a simplification that each infection lasts exactly 6 days and the level of infection during the first trimester of individuals giving birth now was approximately constant at the midpoint of that 6-day interval a slightly more accurate but more complex version is given by
where $ \bar \tau_1 $ is three days into the first trimester, the midpoint of the first infectious period of pregnancy, $ \bar\tau_2 $ is nine days into the first trimester, $ \bar\tau_3 $ is fifteen days into the first trimester $\ldots$ and so on up to $ \bar\tau_{15} $ which is three days before the end of the first trimester.
However if the age-related fertility rate for Brazil is available then we can use an alternative approach in working out the expected number of cases of microcephaly. To be more specific the new differential equation for $ \frac{dM(t)}{dt} $ will become
Here $ f(\xi, t) $ represents the age-related fertility rates for different age-groups in Brazil, $ \tau_1 $ is 270 days which is the average length of a pregnancy and $ \bar\tau $ is 225 days which is the average length of time from the midpoint of the first trimester to delivery. $ P_1 $ is defined as before. Equation (6.3) is derived from Eq (6.1) by introducing the age-dependent fertility rate and dividing by two as only females reproduce. However if we decide to use this approach then the population size will vary with respect to time and thus we would also need to use age-related birth and death rates. As a result the age-structured model would become significantly more complicated.
As before we can make this model more accurate by dividing the first trimester up into fifteen distinct six day periods and using the midpoint of each instead of a single approximation at the midpoint of the first trimester to give
The first Zika case was first reported in Brazil in 2015. Since then there has been a rapid increase in the number of Zika cases all across the country. According to the report given by [35], the number of Zika cases in Brazil reached its peak in Week 6 of 2016 with around 17,800 suspected cases of which around 11,000 of them were confirmed. From the report given in [35], between 2016 and 2017, various states in the central-West region of Brazil have recorded high Zika incidence rates as shown in Table 15.
For the purposes of comparison of the figures obtained in this paper with actual data, at April 23, 2016, the number of confirmed and suspected cases of microcephaly was 4,908, just one case more than a week earlier. Of these the number of confirmed cases climbed to 1,198 from 1,168 a week earlier. Brazil had registered 91,387 likely cases of Zika infection in the period February until April 2, 2016 with the most diagnoses in Rio de Janeiro [36]. In addition from another report [37], for the period between August 2015 up to June 25th, 2016, there were 8,165 notified microcephaly cases in Brazil of which 1,638 were confirmed, 3,466 excluded and 3,061 under investigation.
We may ask which of our four models performs the best. We know that for other mosquito-borne diseases the mosquito population varies according to the time of year. Additionally by comparing the data fitting results from the Zika model against the results from the Zika model with seasonality, the ones with seasonality provide a better fit against the real Zika data in Brazil. Moreover as fertility rates vary with age we expect the age-structured models to be more accurate. Hence in general the age-structured seasonal model should give the best answer. Note that as we had data only for a relatively short timescale it was difficult to estimate parameters for the seasonal models. Also the age-structured models could predict the short-term incidence of microcephaly but because of the computing power needed they could not predict long-term endemic levels of microcephaly cases. Thus all of the models have different advantages and disadvantages.
One of the motivations behind this paper is the recent discovery of the connection between the Zika virus and microcephaly and other birth defects in newborns. It is important for us to understand how many of the microcephaly cases are directly caused by pregnant women being exposed to Zika and thus its impact on pregnant women travelling to countries infected with the Zika virus. Therefore, we have obtained simulations which allow us to calculate the expected future number of cases of microcephaly as a result of women being pregnant and thus infected with Zika during their first trimester of pregnancy. Furthermore, the technique used here can be applied to analysing the association between the Zika virus and other birth defects such as Guillain-Barré Syndrome. These results will be beneficial for policy makers in deciding the risk involved for pregnant women travelling to countries infected with Zika.
The models discussed in this paper assume that the transmission of Zika in Brazil occurs in a homogeneous fashion within a single population. Of course this assumption is not realistic as Brazil has a huge human population distributed over a large area. Thus transmission parameters will in practice vary throughout the country. Moreover climatic conditions and socio-economic variables such as urban or rural settings vary greatly through the country causing different population dynamics for vector populations. Therefore using a single parameter for mosquito populations may not be realistic even if assuming an average value. So ideally we should break down the population into smaller regions and use different parameters for each region. However such data are difficult to find.
In addition epidemic models commonly assume a homogeneously mixing population as an approximation. For example Agusto et al. [38] model malaria transmission using a host-vector model in different regions of Africa using a geographically homogeneous model. Some of the parameters are temperature dependent but there is no other spatial geographical variability. Koutou et al. [39] apply a homogeneous host-vector model for malaria transmission to model vector population growth and malaria virus transmission to humans. Coudeville and Garnett [40] applied a geographically heterogeneous host-vector model to estimate the potential impact of dengue vaccination in South Vietnam. Maier et al. [41] used a spatially geographically heterogeneous host-vector model to analyse the effect of the Sanofi Pasteur vaccine Dengvaxia in Brazil. Gao et al. [42] discuss a homogeneously mixing compartmental model for the transmission of Zika and apply it to data in Brazil, Colombia and El Salvador. This applies the same model parameters to the three countries and their model provides good fits to the observed data. Wang et al. [43] discuss modelling and control of Zika in Brazil using the Wolbachia parasite. They also use a spatially geographically homogeneous model.
Amaku et al. [44,45] deploy a similar geographically homogeneous disease transmission model to estimate the prevalence of undiagnosed hepatitis C virus (HCV) infections across the whole of Brazil. Similarly to Zika the actual disease transmission parameters, for example needle sharing rates for HCV, will vary throughout Brazil, but a spatially homogeneous model is used as an approximation.
The models discussed in this paper consider only transmission of Zika between humans and mosquitoes. Other potential transmission routes such as sexual transmission and vertical transmission from an infected human mother to her child have not been included. Vertical transmission of Zika can occur but is thought to be rare. Recent studies have shown that although sexual transmission of Zika can occur this is a very small component of disease transmission and also recent evidence suggests that the risk of sexual transmission of Zika may dissipate quickly [46,47]. There is also a good deal of uncertainty about the effect of sexual transmission [48].
Several previous models have been developed to model the spread of the Zika virus. Kucharski et al. [49] study a mathematical model for the 2013–2014 French Polynesia outbreak. This model focusses on human vector transmission which it says is the main transmission method. Funk et al. [50] compares three outbreaks of dengue and Zika virus in two different island settings in Micronesia, the Yap main island and Fais using a mathematical model. Again they focus on host-vector transmission and ignore the effects of sexual transmission.
Majumder et al. [51] also say that Zika virus is primarily transmitted by $ Aedes $ mosquitoes although evidence of vertical human to human and sexual transmission between humans exists. The basic reproduction number was estimated from data.
In their model Gao et al. [42] also include sexual transmission of Zika. They find that it plays a small part in Zika transmission, contributing about 3.04% to the $ R_0 $ value and 4.44% of the total transmission attack rate, although the confidence intervals for these percentages are quite large. Sexual transmission seems to be modelled crudely as a disease spread by direct contact rather than by dividing the population into males and females. Wang et al. [43] develop a model for using the Wolbachia bacteria to control Zika. They include sexual transmission between humans but again model it crudely as a disease spread by direct contact. Moreover again from their estimated parameter values it seems as though the effect of sexual transmission is small compared with the route between humans and vectors.
Hence although human to human vertical and sexual transmission of Zika exist their effect is small compared with spread between humans and mosquitoes and also computationally difficult to model accurately as this would increase the model complexity. Therefore we follow Kucharski et al. [49] and Funk et al. [50] and do not explicitly include either vertical or sexual human transmission in our model.
Acknowledgements
The authors are grateful to the EPSRC and the University of Strathclyde for support for this work under the EPSRC Global Challenges Research Fund Institutional Award 2016 (EPSRC grant reference number EP/P511055/1) and the British Council, Malaysia for funding from the Dengue Tech Challenge (Application Reference DTC 16022). DG is grateful to the Science Without Borders Program, Brazil, for a Special Visiting Fellowship (CNPq grant 30098/2014-7), with Professor E. Massad, Department of Legal Medicine, University of Sao Paulo, Sao Paulo, Brazil, and to the Leverhulme Trust for support from a Leverhulme Research Fellowship (RF-2015-88).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: