Citation: D Kelly, L Mackenzie, David A. Saint. Mechanoelectric feedback does not contribute to the Frank-Starling relation in the rat and guinea pig heart[J]. AIMS Biophysics, 2014, 1(1): 16-30. doi: 10.3934/biophy.2014.1.16
| [1] | Oltion Marko, Joana Gjipalaj, Dritan Profka, Neritan Shkodrani . Soil erosion estimation using Erosion Potential Method in the Vjosa River Basin, Albania. AIMS Environmental Science, 2023, 10(1): 191-205. doi: 10.3934/environsci.2023011 |
| [2] | Alma Sobrino-Figueroa, Sergio H. Álvarez Hernandez, Carlos Álvarez Silva C . Evaluation of the freshwater copepod Acanthocyclops americanus (Marsh, 1983) (Cyclopidae) response to Cd, Cr, Cu, Hg, Mn, Ni and Pb. AIMS Environmental Science, 2020, 7(6): 449-463. doi: 10.3934/environsci.2020029 |
| [3] | Raden Darmawan, Sri Rachmania Juliastuti, Nuniek Hendrianie, Orchidea Rachmaniah, Nadila Shafira Kusnadi, Ghassani Salsabila Ramadhani, Yawo Serge Marcel, Simpliste Dusabe, Masato Tominaga . Effect of electrode modification on the production of electrical energy and degradation of Cr (Ⅵ) waste using tubular microbial fuel cell. AIMS Environmental Science, 2022, 9(4): 505-525. doi: 10.3934/environsci.2022030 |
| [4] | Seiran Haghgoo, Jamil Amanollahi, Barzan Bahrami Kamangar, Shahryar Sorooshian . Decision models enhancing environmental flow sustainability: A strategic approach to water resource management. AIMS Environmental Science, 2024, 11(6): 900-917. doi: 10.3934/environsci.2024045 |
| [5] | M.A. Rahim, M.G. Mostafa . Impact of sugar mills effluent on environment around mills area. AIMS Environmental Science, 2021, 8(1): 86-99. doi: 10.3934/environsci.2021006 |
| [6] | Motharasan Manogaran, Mohd Izuan Effendi Halmi, Ahmad Razi Othman, Nur Adeela Yasid, Baskaran Gunasekaran, Mohd Yunus Abd Shukor . Decolorization of Reactive Red 120 by a novel bacterial consortium: Kinetics and heavy metal inhibition study. AIMS Environmental Science, 2023, 10(3): 424-445. doi: 10.3934/environsci.2023024 |
| [7] | Martina Grifoni, Francesca Pedron, Gianniantonio Petruzzelli, Irene Rosellini, Meri Barbafieri, Elisabetta Franchi, Roberto Bagatin . Assessment of repeated harvests on mercury and arsenic phytoextraction in a multi-contaminated industrial soil. AIMS Environmental Science, 2017, 4(2): 187-205. doi: 10.3934/environsci.2017.2.187 |
| [8] | Adrian Schmid-Breton . Transboundary flood risk management in the Rhine river basin. AIMS Environmental Science, 2016, 3(4): 871-888. doi: 10.3934/environsci.2016.4.871 |
| [9] | Jerry R. Miller . Potential ecological impacts of trace metals on aquatic biota within the Upper Little Tennessee River Basin, North Carolina. AIMS Environmental Science, 2016, 3(3): 305-325. doi: 10.3934/environsci.2016.3.305 |
| [10] | Maja Radziemska, Agnieszka Bęś, Zygmunt M. Gusiatin, Jerzy Jeznach, Zbigniew Mazur, Martin Brtnický . Novel combined amendments for sustainable remediation of the Pb-contaminated soil. AIMS Environmental Science, 2020, 7(1): 1-12. doi: 10.3934/environsci.2020001 |
Asopos River basin, in East-Central Greece is characterized by a recorded problem of hexavalent chromium contamination, exceeding in some cases the value of 100 μg L−1 as measured in groundwater samples collected from the area [1]. Geogenic and anthropogenic components have contributed to the recorded high levels of chromium contamination in the Asopos River Basin. The geological character of surrounding area of Asopos River basin mainly is Neogene lake-shallow marine sediments, clastic formations of continental origin and parts of ophiolite complexes [2]. The detection of elements, such as Cr and Ni in soils and waters, has often a strong lithogenic origin correlated to the existence of ophiolite outcrops composed by ultramafic rocks [3], but also Fe-Ni deposits [4,5]. Cases where occurrence of hexavalent chromium is primarily of geogenic origin have also been documented for California [6,7,8], New Caledonia [9], Zimbabwe [10], Italy [11], etc. The geogenic mobilization of Cr(Ⅵ) from highly insoluble Cr(Ⅲ) minerals, like chromite, takes place via a two-stage mechanism [10]. At first Cr(Ⅲ) in the matrix of chromite is hydrolyzed to Cr(OH)3. The following stage is the oxidation of Cr(Ⅲ) to Cr(Ⅵ) under the action of easily reducible Mn oxides (the mixed Mn(Ⅱ)/Mn(Ⅲ) oxide hausmannite (Mn3O4) or the Mn(Ⅲ) oxide manganite (MnOOH)). It is considered [10] that this natural process is probably continuous in concretionary subsoils subject to wetting-drying cycles.
Industrialization in the Asopos River Basin area started in the early 1960’s and today more than 400 installations exist in the area. Metal finishing and manufacturing plants, often using Cr-based chemicals in their processes were major chromium polluters in the area. All facilities were obliged to treat their effluents in-house in appropriate wastewater treatment units, but until 2008 the treated effluent was allowed to be discharged underground via disposal in absorption type sinks. As a result of this the anthropogenic factor, the observed Cr contamination in Asopos River basin cannot be neglected. University of Athens research [12] suggests that the Asopos river sediments are enriched with Cr and Ni by a factor of almost 2.5 compared to the local background values.
The objective of this work was to:
 investigate whether previous disposal practices in four (4) metal finishing facilities have led to potential contamination to the adjacent soils, and
investigate whether previous disposal practices in four (4) metal finishing facilities have led to potential contamination to the adjacent soils, and
 to compare the potential contaminated soil concentration values of the metal finishing facilities with
to compare the potential contaminated soil concentration values of the metal finishing facilities with
❖ greater area background metal concentration values
❖ Potentially polluted and newly investigated soil metal concentration values of the Inofyta Industrial Area (IIA).
The four investigated metal finishing industrial sites are Hellenic Aerospace Industry S.A. (designated as HAI), Europa Profile Aluminium S.A. (EU), Aluminco S.A. (AL) and Viometale S.A. (Ⅵ) [13,14,15,16]. The reason for selecting these metal finishing sites is:
 HAI, EU, AL are three of the larger installations in the area using Hexavalent Chromium
HAI, EU, AL are three of the larger installations in the area using Hexavalent Chromium
 In Ⅵ a discrete thin metal contamination layer on surface soils was found to the south of the area during a Prefecture Environmental Audit.
In Ⅵ a discrete thin metal contamination layer on surface soils was found to the south of the area during a Prefecture Environmental Audit.
 Prefecture of Sterea Ellada(relevant Environmental Authority) considers HAI, EU, AL and VI as priority potential polluters.
Prefecture of Sterea Ellada(relevant Environmental Authority) considers HAI, EU, AL and VI as priority potential polluters.
The study area is focusing on the four above mentioned metal finishing industrial sites HAI, EU, AL VI and the Inofyta Industrial Area (IIA). Sampling strategy involved the collection of three groups of soil samples and for comparison reasons the data collected from Inofyta industrial area by the research team of the EU funded project LIFE-CHARM “Chromium in Asopos groundwater system: Remediation technologies and Measures” [17] (data available at http://www.charm-life.gr/charm/index.php/en/documents) were also evaluated, called as fourth group (LGR-4) sampling. The first group (GR-1) assumed free of anthropogenic influence was intended to represent natural geochemical background values close to the industrial sites. Selected sampling points (depicted as HR, ER, AR and VR in Figure 1) were in the vicinity of the metal finishing and industrial sites but not affected from any potential polluting factors. The second group (GR-2), collected in the period 2011-2012 (campaigns by Sybilla Ltd), and consisted of samples from areas suspected of pollution from ongoing activities or historical disposal practices. Samples are either samples from soil shallow layers, i.e. 0-80 cm, or soil core samples from boreholes, up to a depth of 15 meters. The greater Asopos river Basin area Industrial Sites, and location of investigated surface soil sampling points of investigated metal finishing units of GR-1 (HR1-VR1-ER1-ER2-ER3-ER4-ER5-ER6, AR1.) and GR-2 (HB1-HB2-HB3, VB2-VB2, EB1-EB2-EB3-EB4, AB1-AB2-AB3-AB4, HR1-VR1-ER1-ER2-ER3-ER4-ER5-ER6, AR1) group campaigns are presented in Figure 1. GR-1, GR-2, GR-3 and LGR-4 sampling locations and the total number of analyzed samples per industrial site are presented in Tables 1-4.
The third group (GR-3) consisted of more than 10 samples collected in summer 2015 (campaigns by Sybilla ltd in the framework of EU IED Directive [18]) Baseline Site Investigation Study [19,20]) from areas suspected of pollution from ongoing activities or previous disposal practices. Samples are either soils collected from the shallow layers, i.e. 0-80 cm, or core samples from boreholes, drilled down to a depth of about 15 meters. The location of boreholes is shown in Figure 2.
For comparison reasons data collected from Inofyta industrial area by the research team of the EU funded project LIFE-CHARM “Chromium in Asopos groundwater system: Remediation technologies and Measures” [17] (data available at http://www.charm-life.gr/charm/index.php/en/documents) were also evaluated. This Life Project, fourth group campaign (LGR-4) of samples was collected at the period 2011-2012. A sampling program was carried out during which seven (7) new groundwater wells with a depth of approximately 30-50 m were drilled at Inofyta industrial area (N1, N2, N3, N4, N5, N6, N7), between January and February 2012. During the construction, drill core samples were collected from each borehole and relevant chemical analyses followed. Boreholes sampling was followed by a surface soil sampling where a series of 12 surface soil samples were also collected during this action in order to investigate the presence of Cr.The location of relevant boreholes is shown in Figure 3.
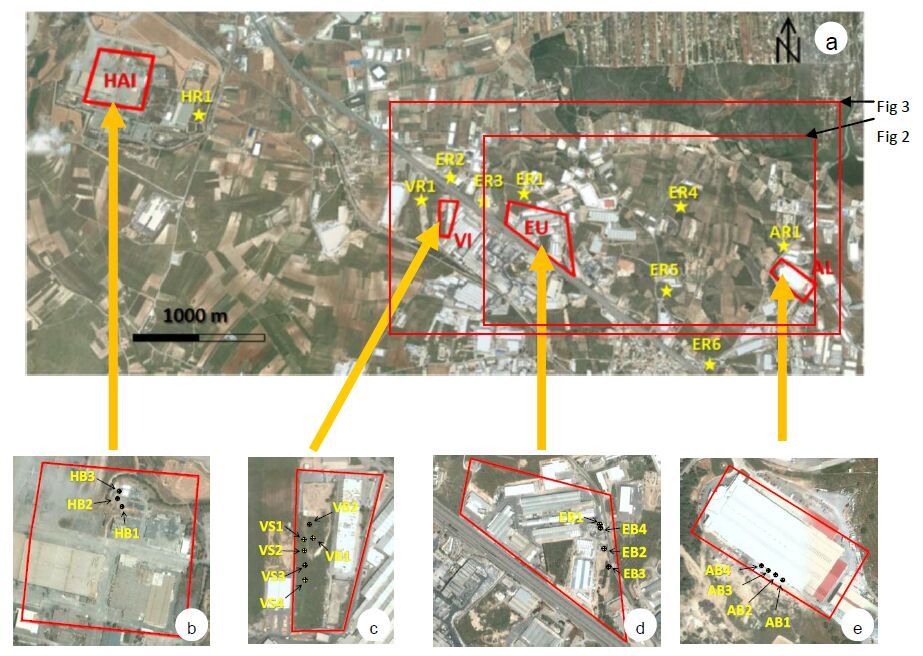 Figure 1. First (GR-1) and Second (GR-2) Group Campaigns. Investigated metal finishing installation sites (a-total sampling area, b- Hellenic Aerospace Industry S.A-HAI area, d-Europa S.A.-EU area, e-Aluminco S.A.-AL area and c-Viometale S.A.-VI area) and boreholes (GR-2 sampling points HB1-HB2-HB3, VB2-VB2, EB1-EB2-EB3-EB4, AB1-AB2-AB3-AB4) and surface soil sampling points (GR-1 and GR-2 sampling points HR1-VR1-ER1-ER2-ER3-ER4-ER5-ER6, AR1) are depicted
Figure 1. First (GR-1) and Second (GR-2) Group Campaigns. Investigated metal finishing installation sites (a-total sampling area, b- Hellenic Aerospace Industry S.A-HAI area, d-Europa S.A.-EU area, e-Aluminco S.A.-AL area and c-Viometale S.A.-VI area) and boreholes (GR-2 sampling points HB1-HB2-HB3, VB2-VB2, EB1-EB2-EB3-EB4, AB1-AB2-AB3-AB4) and surface soil sampling points (GR-1 and GR-2 sampling points HR1-VR1-ER1-ER2-ER3-ER4-ER5-ER6, AR1) are depicted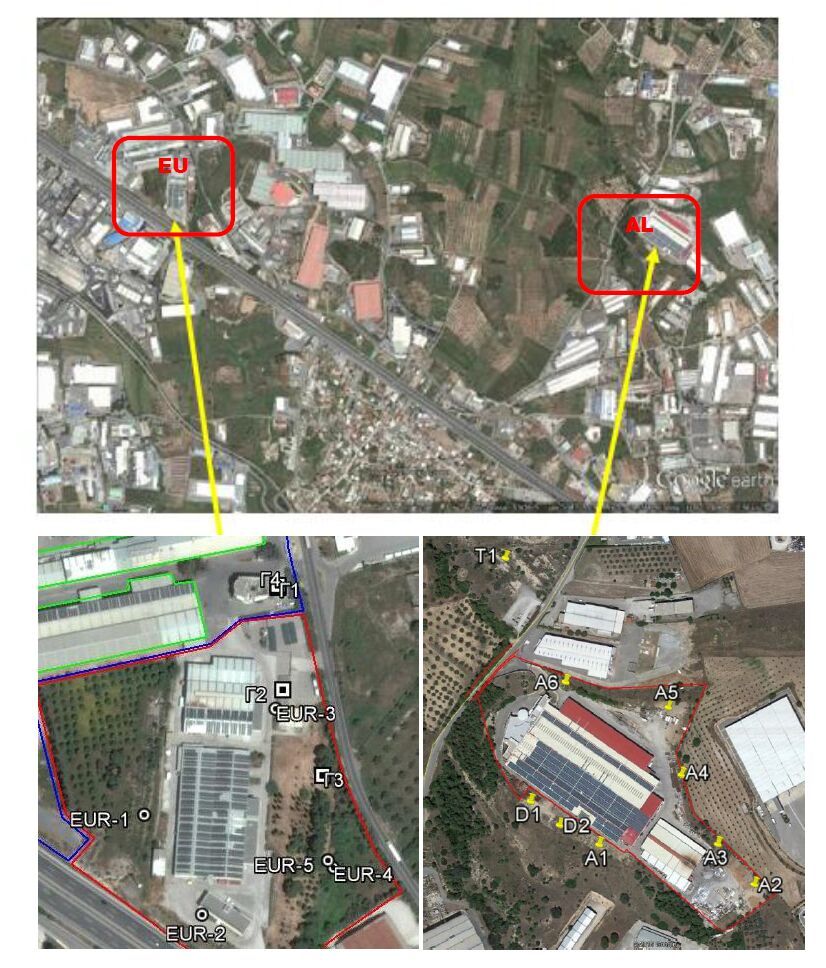 Figure 2. Location of investigated surface soil sampling points for the Europa SA. (EU) and Aluminco SA (AL). Sybilla 2015. Third Group (GR-3) campaign
Figure 2. Location of investigated surface soil sampling points for the Europa SA. (EU) and Aluminco SA (AL). Sybilla 2015. Third Group (GR-3) campaign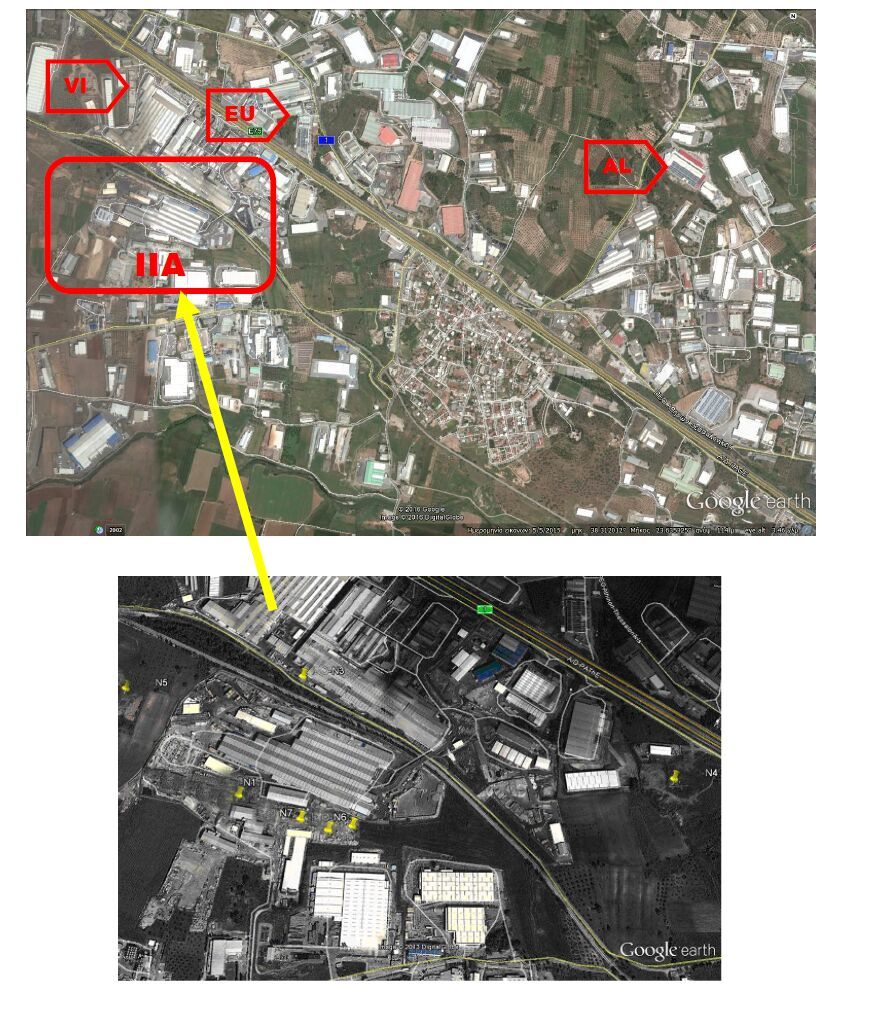 Figure 3. Location of investigated industrial sites and surface soil sampling points. LIFE-CHARM 2012. Fourth Group (LGR-4) Campaign
Figure 3. Location of investigated industrial sites and surface soil sampling points. LIFE-CHARM 2012. Fourth Group (LGR-4) CampaignLaboratories involved in the chemical analysis of the collected soil samples, the analytical methods used, and the parameters analyzed, are presented in Tables 1-4.
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) |
| HAI | 1 (1) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Europa | 6 (6) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Aluminco | 1 (1) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | ||
| Viometale | 1 (1) | Cr, Ni, Cu, Zn, etc.Cr(Ⅵ) | XRF(d), AR(a)Alkaline digestion(c) | LabMet |
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| HAI | 1 (7) | 3 (42) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Europa | 6 (13) | 4 (49) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Aluminco | 1 (6) | 4 (12) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | |||
| Viometale | 1 (4) | 6 (19) | Cr, Ni, Cu, Zn, etc. | XRF(d)AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| Europa | 2 | 3 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Aluminco | 1 | 5 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed |
Methods | Labs(*) | |
| Un-contaminated | Suspected for contamination | ||||
| Boreholes | - | 38 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| Surface Soil | - | 12 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| (a) Digestion with aqua regia followed by determination of metals in solution by AAS or ICP-MS (EN 13657) (b) Elution with water, determination of soluble Cr(Ⅵ) (DIN 38405-24: 05.87, AWWA-3500-Cr/B) (c) Alkaline digestion, determination of extracted Cr(Ⅵ) (USEPA, SW-846 Methods 3060A and 7196) (d) Determination of total elements concentration by X-ray fluorescence spectrometry (EN 15309) (*) Laboratories: (a) Andreou, K. Andreou. Ltd, Athens, (b) EuF: Eurofins Umwelt Ost GmbH, Jena, Germany, (c) LabMet: Laboratory of Metallurgy, NTUA, Athens. For the majority of samples, namely those collected from HAI, Europa and Aluminco, the elemental analysis was carried out following the digestion of samples with aqua regia (AR). The samples collected from Viometale were analyzed by X-ray fluorescence (XRF) spectrometry, (mainly due to time constraints - XRF analysis is much more rapid, as there is no need for any pretreatment steps, such as acid leaching or fusion). The LIFE-CHARM samples were also analyzed by XRF. | |||||
Analysis by XRF determines the total content of elements in the solid samples, which does not coincide with the amount extracted by aqua regia. As discussed in a previous paper [21], using GR-1 and GR-2 campaigns results and a dataset of 40 surface soil samples collected throughout the whole Greek territory in the framework of the Geochemical Atlas of Europe [22], the concentration of chromium determined by the method of aqua regia digestion, Cr (AR), is about 4 times less compared to the total content of Cr determined by XRF, Cr (XRF). This can be attributed to the fact that the highest percentage of chromium in Greek soils is incorporated into insoluble minerals, e.g. substituted aluminosilicates or spinel minerals like chromite, which are not affected by the AR digestion. On the contrary, the total amount of Ni in soils is soluble in AR. As a consequence, the concentration of Ni determined by the AR digestion method, Ni(AR), is very close to the total content, as determined by XRF, Ni (XRF).
For the assessment of Cr and Ni background concentration values in Asopos River Basin area soils, we quote data collected from various references consisting of various soil samples analyzed from locations which were assumed free of contamination from industrial activities. Total Cr, Ni and Cr (Ⅵ) concentrations are presented in the following Table 5.
| Area (Number of samples) |
Cr (mg/kg) |
Ni (mg/kg) |
Cr(Ⅵ) (mg/kg) |
Source | ||
| Range | Mean | Range | Mean | Range | ||
| Asopos (n = 30) |
60-410 | 220 | 91-1200 | 620 | >0.1-9.3 (a) | [21] |
| Oropos (n = 33) |
17-600 | 212 | -- | [3] | ||
| Thebes (n = 51) |
134-856 | 277 | 621-2639 | 1591 | -- | [23] |
| Atalante (n = 64) |
48-4200 | 453 | 44-2730 | 533 | -- | [24] |
| All Greece (n = 41) |
2-466 | 102 | 2-1812 | 171 | -- | [22] |
| (a) Cr(Ⅵ) detected in 3 among the 30 analyzed reference soils (5.5, 6.0 and 9.3 mg/kg). | ||||||
Chromium concentration values determined by aqua regia (AR) method are similar to the concentration levels determined at Oropos [3] and at Thebes [24], adjacent to the study area, with similar geological formations. As far as Cr (Ⅵ) is concerned, this species was detected only in three (3) among the 26 analyzed samples of Asopos Area, with concentrations 5.5, 6.0 and 9.3 mg/kg respectively. Ni concentrations determined by aqua regia (AR) method in the Asopos river Basin Area, were significantly higher.
Since Greece has not yet developed national soil quality guidelines for Cr and Ni, relevant guidelines from three European countries, namely Italy, Germany and Belgium (Wallonia), were used and are presented in Table 6 [25]. These values represent the upper allowed concentration levels of Cr and Ni in soils for residential and industrial land use. Cr(Ⅵ) threshold concentrations limits exist only in the regulations of Wallonia.
As seen in Table 5, the mean concentration of total Cr in Asopos soils (220 mg/kg), slightly exceeds the Italian threshold limit value for residential areas, but satisfies all other limit values. On the contrary, the mean concentration of Ni (620 mg/kg) exceeds the German limit for industrial areas. In Thebes’s soils, most samples of Ni were exceeding the threshold limits. An analysis of Table 6, ends up to the conclusion that the use of these soil quality guidelines when applied in metalliferous areas, like those encountered in many regions of Greece is questionable (since the geochemical background for at least Cr and Ni elements is often higher).
| Soil limit values (mg/kg) | ||||||
| Residential areas* | Industrial areas* | |||||
| IT | DE | BE(W) | IT | DE | BE(W) | |
| Cr | 150 | 400 | 520 | 800 | 1000 | 700 |
| Ni | 120 | 140 | 300 | 500 | 900 | 500 |
| Cr(Ⅵ) | -- | -- | 4.2 | -- | -- | -- |
| (*) Cr, Ni digestion of samples with aqua regia (AR). | ||||||
Figure 1b presents three boreholes that were drilled at HAI grounds, close to potentially polluting HAI sites, i.e. ponds that were used for the treatment of hazardous industrial wastewater, storage of physicochemically treated wastewater and for the storage and drying of industrial sludge. Total Cr concentration profiles are presented in Figure 4a. Total Chromium, Aqua regia (AR) Cr(AR), concentration values varied from 51 to 281 mg/kg with a mean value of 124 mg/kg. Total Ni aqua regia (AR) Ni (AR), concentration values varied from 132 to 618 mg/kg with a mean value of 262 mg/kg (Figure 5a). All these Cr(AR) and Ni(AR) soil concentration values are of the same order of magnitude with soil concentration values assumed free of anthropogenic contamination. Hexavalent Cr content was not detected in any of the soil samples examined.
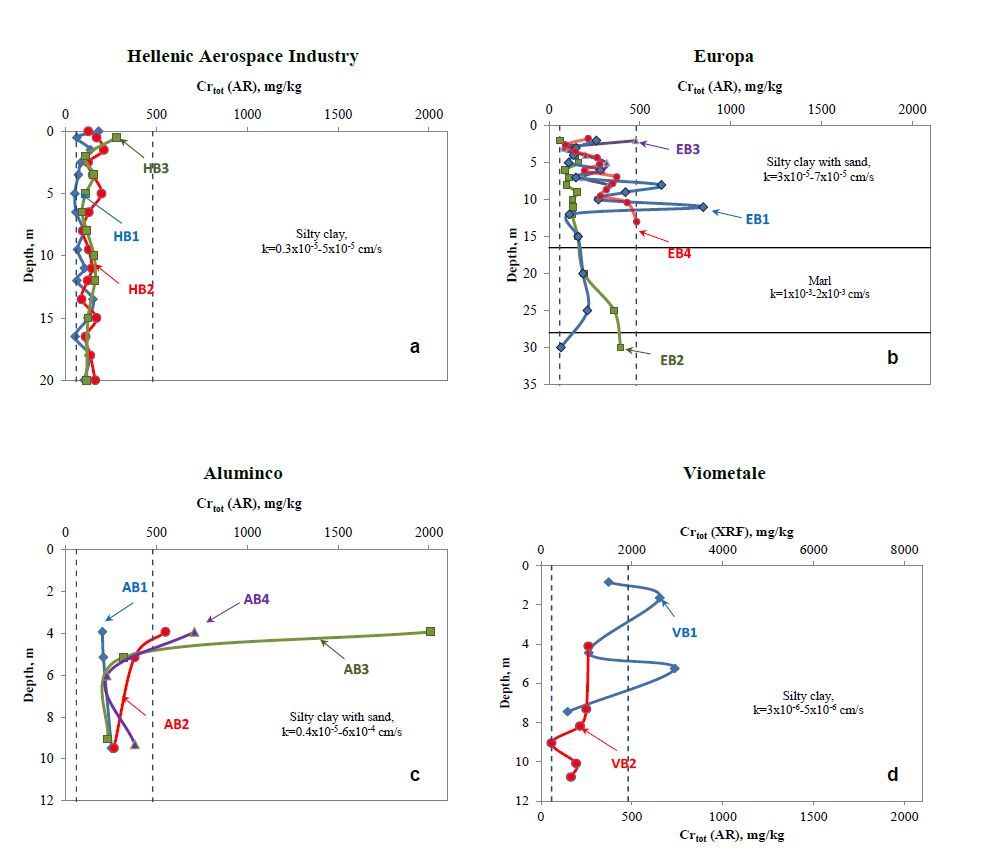 Figure 4. Total Cr (AR) (and Cr(XRF) at Viometal) concentration values and profiles in boreholes drilled in the metal finishing industrial sites of the (HAI) Hellenic Aerospace Industry, Europa, Aluminco and Viometale. Second Campaign GR-2 Group. Dashed lines indicate the range of concentration values measured in the reference soils. (k: soil hydraulic permeability)
Figure 4. Total Cr (AR) (and Cr(XRF) at Viometal) concentration values and profiles in boreholes drilled in the metal finishing industrial sites of the (HAI) Hellenic Aerospace Industry, Europa, Aluminco and Viometale. Second Campaign GR-2 Group. Dashed lines indicate the range of concentration values measured in the reference soils. (k: soil hydraulic permeability)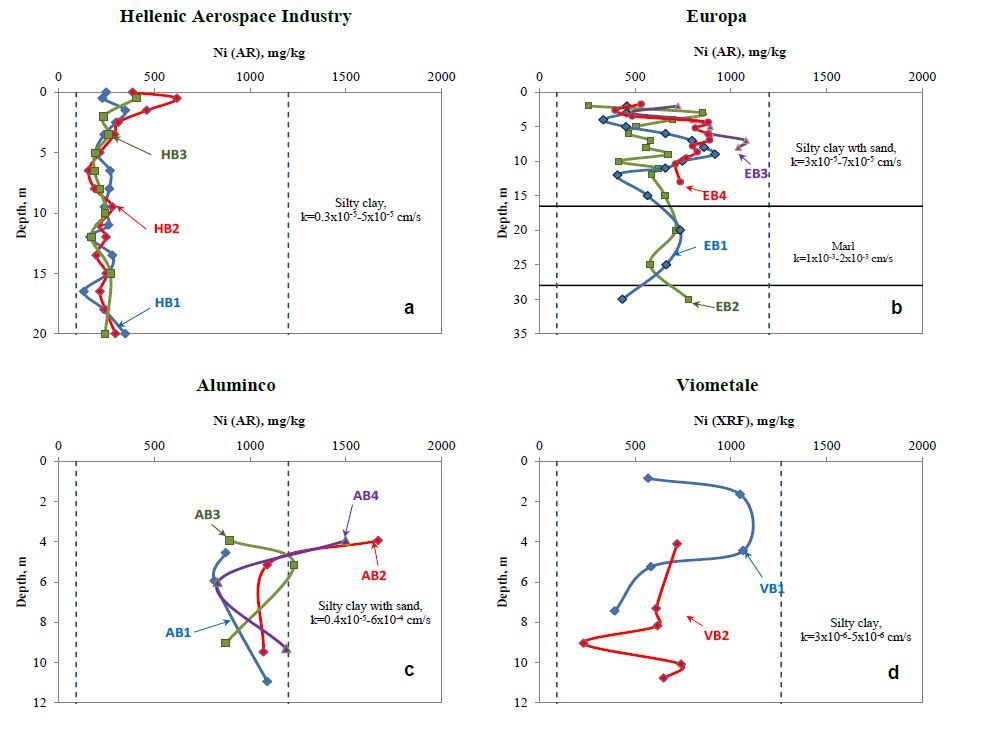 Figure 5. Ni concentration values and profiles in boreholes drilled in the sites of the metal finishing installations of (HAI) Helllenic Aerospace Industry, Europa, Aluminco and Viometale. Second Campaign GR-2 Group. Dashed lines indicate the range of concentration values measured in the reference soils. (k: soil hydraulic permeability)
Figure 5. Ni concentration values and profiles in boreholes drilled in the sites of the metal finishing installations of (HAI) Helllenic Aerospace Industry, Europa, Aluminco and Viometale. Second Campaign GR-2 Group. Dashed lines indicate the range of concentration values measured in the reference soils. (k: soil hydraulic permeability)For assessing the potential soil investigation in Europa grounds four boreholes were drilled at locations shown in Figure 1d. Borehole #1 (EB1) was drilled beneath the sink, where physicochemically treated wastewater from the electrostatic coating process was disposed for over two decades. For assessing the potentially contaminated soil directly beneath the sink, one inclined borehole was drilled with a 45o angle (EB4). A schematic drawing of the two above mentioned boreholes is given in Figure 6.
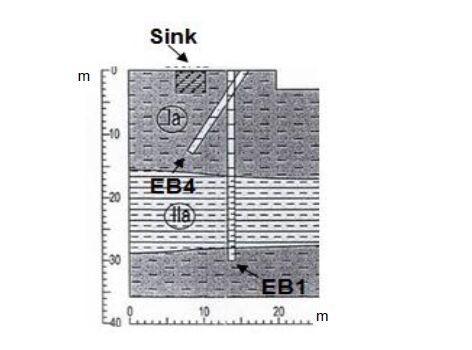 Figure 6. Boreholes at the metal finishing Europa (EB1 and EB4) beneath the sink of the installation (Ia: silty clay and Ⅱa: marl)
Figure 6. Boreholes at the metal finishing Europa (EB1 and EB4) beneath the sink of the installation (Ia: silty clay and Ⅱa: marl)Borehole EB3 was drilled at a location where a small stream enters the metal finishing Europa installation area whereas borehole EB2 was drilled 60 meters downstream of the treated wastewaters sink. Total Cr concentration values of Europa boreholes are within the background values of the area as presented within this article, except for two soil samples of EB1 (depths of 8 and 11 m), where Cr soil concentration values are 619 and 849 mg/kg respectively. Borehole EB4 (inclined borehole) close to EB1, presents a similar total Cr profile but the Cr soil concentration values at depths of 8 and 11 m lie within the background levels range. It must be noticed that at the bottom of the sink (depth of 4 m) a thin greenish solid layer no more than a few centimeters thickness was found. This layer was a Cr-rich sludge, i.e. Cr concentration value of about 80100 mg/kg of trivalent Cr. It is argued that the treated effluents containing some small amount of suspended sludge solids, had been filtered and retained inside the sink. It must be noticed though that the soil beneath the sink is relatively contamination free. Soil samples at 4, 5 and 6 meters under the sink (boreholes EB1 and EB4) have low Cr concentration values, ranging from 100 to 280 mg/kg. Ni soil concentration values varied between 257 and 1080 mg/kg and were close to Ni concentration values in reference soils (Figure 5b). Hexavalent chromium was found in 15 of the 49 samples, at a maximum soil concentration value of 10.1 mg/kg, close to reference soil samples.
Five surface soil samples were analyzed during the Fourth Group GR-4 campaign at Europa Profile Aluminium grounds, within the facility borders. Chromium concentration values are shown in Figure 7. Chromium, Cr (AR), concentration varied between 95 and 495 mg/kg with a mean value of 247 mg/kg. All these values but one are within the range of concentrations measured in the uncontaminated reference soils. Hexavalent Cr (Ⅳ) soil concentration values were below detection limit in any of these samples examined.
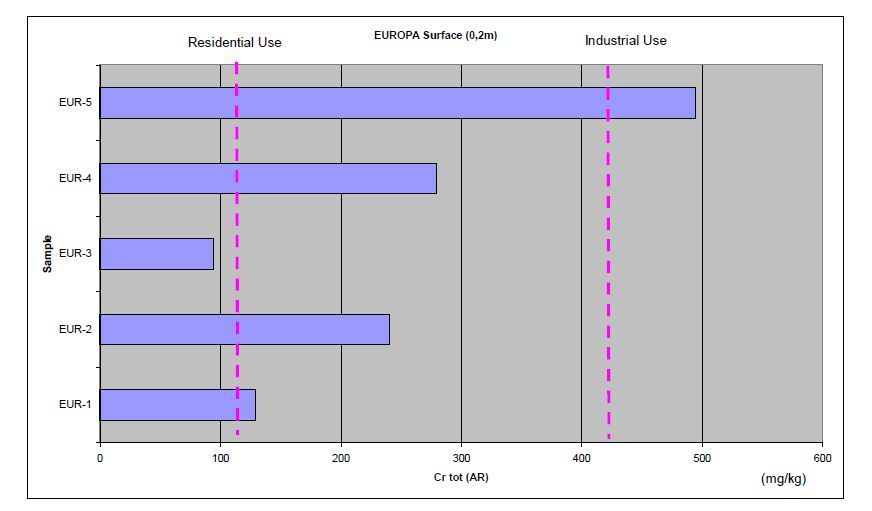 Figure 7. Total Cr concentration values in Sybilla 2015 Fourth Group GR-4 Campaign surface samples. Europa Profile Aluminium (Locations in Figure 2). Dashed lines indicate German Soil Threshold concentration values for different land uses
Figure 7. Total Cr concentration values in Sybilla 2015 Fourth Group GR-4 Campaign surface samples. Europa Profile Aluminium (Locations in Figure 2). Dashed lines indicate German Soil Threshold concentration values for different land usesThe metal finishing unit Aluminco disposed its physicochemicaly treated industrial wastewater in two parallel sinks, at a depth of 4 m, from 2003 until May 2008. For the assessment of potentially contaminated soil four boreholes, inclined with slopes 60o-75o, were drilled (two boreholes per sink), as shown in Figure 1e. There exists a thin layer of polluted soil just at the bottom of the sinks that seems to be affected due to the entrainment of suspended solids. Soil samples were collected below the sinks, from depths 4 m to about 10 m. Soil concentration values of total Cr profiles are shown in Figure 4c. At depth of 4 m, boreholes AB4 and AB3 soil samples have high total Cr (AR) concentration values between 710 mg/kg and 2010 mg/kg, while borehole AB2 Cr soil concentration value was slightly above the reference range. It appears that the treated effluents disposal has an impact on a limited depth soil layer below the sink since the samples of depths at 5, 6 and 9 meters had soil Cr concentration values from 200 to 380 mg/kg. Soil concentration values of Hexavalent chromium (analyzed with the alkaline digestion method) was found to be from 0.2 to 4 mg/kg. Soil concentration values of Ni, ranged from 830 to1650 mg/kg, as presented in Figure 5c. The two Ni highest soil concentration values 1500 and 1650 mg/kg exceed the range of soil concentration values measured in Asopos river Basin reference soils, while similar levels of Ni soil concentration values were measured in soils assumed free of contamination near Thebes and thus a geogenic origin cannot be excluded [23].
Ten surface soil samples were analyzed during Fourth Group (GR-4) campaign at Aluminco grounds, and their locations are presented in Figure 2, within the facility borders. Chromium soil concentration values are shown in Figure 8. Chromium, Cr (AR), concentration varied between 108 and 327 mg/kg with a mean value of 197 mg/kg. All these values are within the range of concentrations measured in the uncontaminated reference soils. Hexavalent Cr (Ⅳ) soil concentration values were below detection limit in any of these samples examined.
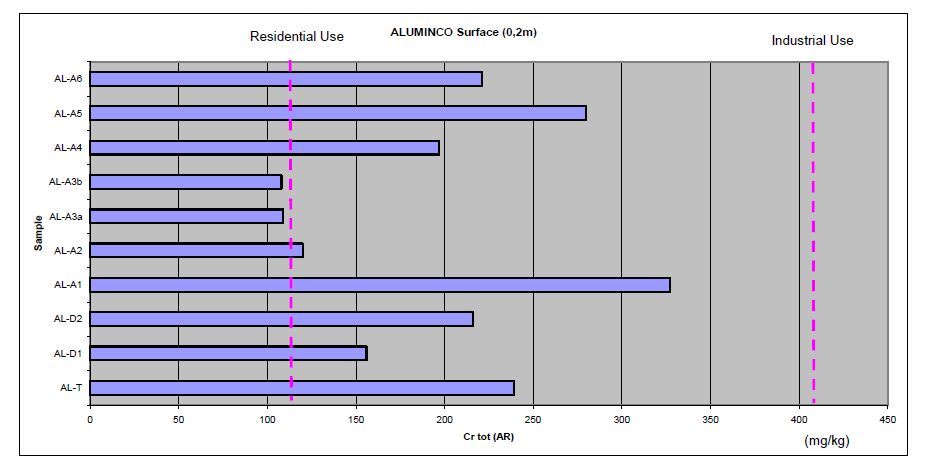 Figure 8. Cr concentration values in Sybilla 2015 Fourth Group Campaign surface samples. Aluminco (Locations in Figure 2). Dashed lines indicate German Soil Threshold concentration values for different land uses
Figure 8. Cr concentration values in Sybilla 2015 Fourth Group Campaign surface samples. Aluminco (Locations in Figure 2). Dashed lines indicate German Soil Threshold concentration values for different land usesAs mentioned before in Viometale site a discrete thin metal contamination layer on surface soils was found to the south of the area during a Prefecture Environmental Audit. Two boreholes were drilled in metal finishing unit Viometale grounds for assessing potentially contaminated soils. These boreholes, denoted as VB1 and VB2, were drilled near and beneath a sink and shown in Figure 1c. Figure 1c, depicts the surface (and low depth (0-0.8m)) soil samples noted as VS1, VS2, VS3 and VS4 samples. Samples VS1 to VS4 are assumed to be representative of incoming pollution located at a land point receiving runoff water from nearby fields, and the outlet of a duct, draining storm water situated to the north of the national road. Boreholes VB1 and VB2 soil Cr concentration values and profiles are depicted in Figure 4d. Since the metal finishing unit at Viometale does not use any trivalent or hexavalent Cr-based chemicals, Cr soil concentrations were measured for comparison reasons, while pollutant of concern (POC) related to these industrial operations is mainly Ni. Measured Cr(XRF) soil concentration values varied from 234 to 2950 mg/kg, equivalent to soil concentration values 58-738 mg/kg of Cr (AR), since Cr(XRF) soil concentration values are approximately 4 times higher to Cr(AR) values. Soil concentrations of Ni remained within the range of reference soils, as shown in Figure 5d and varied from 230 to 1064 mg/kg. Soil surface and low depth samples at points VS1, VS2, VS3 and VS4, end up to the conclusion that there exists high Ni soil contamination mainly in the upper 40 cm soil layer, measured Ni soil concentration values up to 10340 mg/kg.
As depicted in Figure 9, Inofyta Industrial Area (IIA) investigationcampaign consisted of samples collected at the period 2011-2012 (LGR-4 campaigns by EU funded project LIFE-CHARM) [17], where
 drill core samples were collected from seven boreholes (N1, N2, N3, N4, N5, N6, N7)
drill core samples were collected from seven boreholes (N1, N2, N3, N4, N5, N6, N7)
 a series of 12 surface soil samples were also collected
a series of 12 surface soil samples were also collected
and relevant chemical analyses followed in order to investigate the presence of Cr.
The relevant soil Cr (XRF)/Cr (AR) concentration values are presented at Figures 9 and 10. The elevated Cr concentrations demonstrate that the industrial site studied is contaminated. Chromium, Cr (AR), concentration values varied between 51 and 281 mg/kg with a mean value of 430 mg/kg which exceeds slightly the maximum background concentration. 26 of these values are within the range of concentrations measured in the uncontaminated reference soils while 12 exceed the range of background concentrations. Hexavalent Cr (Ⅳ) soil concentration values were below detection limit in of 37 (out of 38) samples examined. Potential sources of this contamination are either buried hazardous wastes or wastewater directly discharged into groundwater.
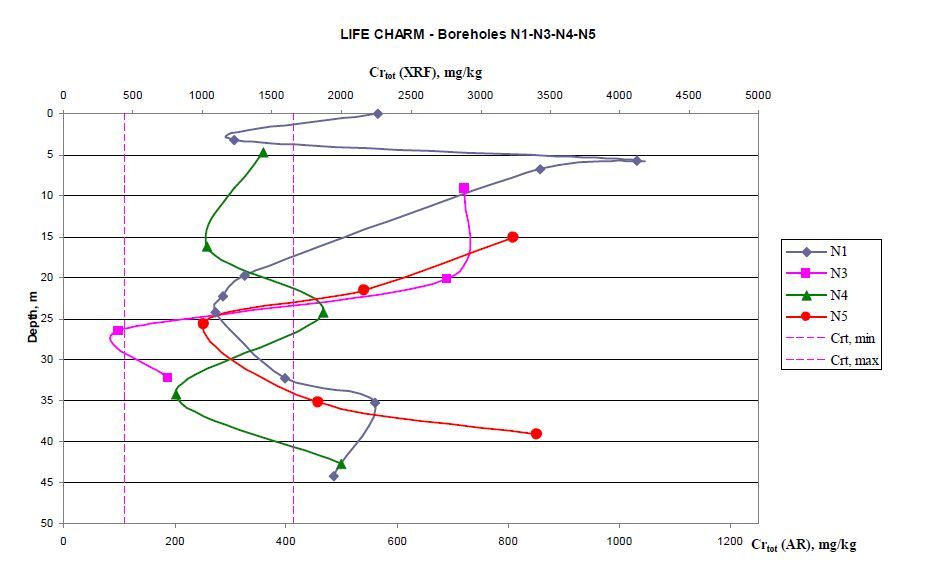 Figure 9. Cr profiles in LIFE-CHARM Campaign boreholes N1, N3, N4, N5 drilled in the Inofyta industrial area
Figure 9. Cr profiles in LIFE-CHARM Campaign boreholes N1, N3, N4, N5 drilled in the Inofyta industrial areaSoil samples collected close to the existing wastewater physicochemical treatment unit and the sludge storage facilities at the Hellenic AerospaceIndustry S.A. (HAI) do not seem to indicate soil contamination.
At the second metal finishing unit under investigation, Europa (EU), disposal of physicochemicaly treated effluents in absorption type sinks led to a thin layer of sludge solids in the bottom of the sink. However, the soil beneath the disposal sink was found to be rather contamination free, and the relevant contamination seems to be localized and not dispersed further.
Measured soil concentration values at Aluminco (AL) end up to the conclusion that there exists a thin layer of polluted soil just at the bottom of the sinks that seems to be affected due to the entrainment of suspended solids. At lower soil layers the soil concentration values of Cr and Ni varied within the range of reference soils concentration values. So the above mentioned contamination (polluted soil just at the bottom of the sinks), does not seem to have an impact on soil contamination beneath it.
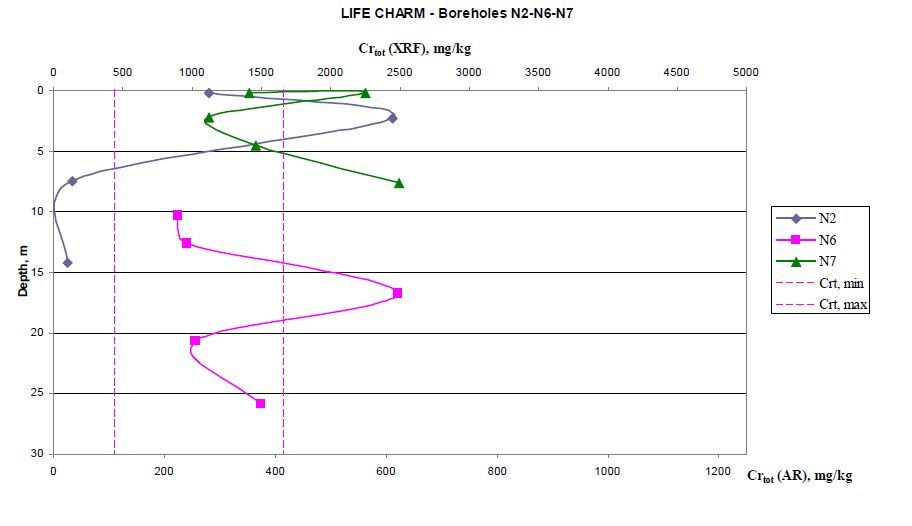 Figure 10. Cr profiles in LIFE-CHARM Campaign boreholes N2, N6, N7 drilled in the Inofyta industrial area
Figure 10. Cr profiles in LIFE-CHARM Campaign boreholes N2, N6, N7 drilled in the Inofyta industrial areaFinally, at the last unit analyzed for soil pollution, Viometale (Ⅵ), Ni contamination of surface soils was found to the south of the area. However, the soil near and beneath the sink used in the past for physicochemicaly treated effluents disposal, seems to be contamination free. So the above mentioned contamination (thin discrete layer on the surface soil), does not seem to have an impact on soil contamination beneath it.
Comparison of soil pollution measurement of the four above mentioned metal finishing units (HAI, EU, AL, VI) with a group of data collected in the framework of EU funded project LIFE-CHARM indicate that the Inofyta Industrial Area (IIA) soil seems to be contaminated. Mean Cr soil concentration values of the boreholes samples slightly exceed the maximum background concentration of the greater area while around 33% of the IIA Cr soil concentration values are well above the maximum background concentration by a number of two.
Comparison of obtained results allows to ascertain that previous disposal practices at the mentioned four (4) metal finishing facilities HAI, EU, AL and VI have not led to significant potential contamination to the adjacent soils and definitely these installation do not pose a general soil contamination threat to the study area. There was no indication of downstream migration from the land-based treated effluents disposal of the above mentioned facilities. Soil concentration values adjacent to these facilities were rather free of contamination.
The Cr and Ni soil concentration values in the lower soil layers of the above mentioned metal finishing facilities are of the same order of magnitude with greater area background metal concentration values and significantly lower of documented and newly investigated contaminated soil metal concentration values of the Inofyta Industrial Area (IIA).
At Inofyta Industrial Area (IIA) the detected soil contamination (measured high Cr soil concentration values) requires special attention for future environmental protection planning actions.
The authors declare there is no conflict of interest.
| [1] | Allen DG, Kentish JC (1985) The cellular basis of the length-tension relation in cardiac muscle. J Mol Cell Cardiol 17: 821–840. |
| [2] | Babu A, Sonnenblick E, Gulati J (1988) Molecular basis for the influence of muscle length on myocardial performance. Science 240: 74–76. |
| [3] | Bainbridge FA (1915) The influence of venous filling upon the rate of the heart. J Physiol 50:65–84. |
| [4] | Blinks JR (1956) Positive chronotropic effect of increasing right atrial pressure in the isolated mammalian heart. Am J Physiol 186: 299–303. |
| [5] | Bockenhauer D, Zilberberg N, Goldstein SA (2001) KCNK2: reversible conversion of a hippocampal potassium leak into a voltage-dependent channel. Nat Neurosci 4: 486–491. |
| [6] | Bustamante JO, Ruknudin A, Sachs F (1991) Stretch-activated channels in heart cells: relevance to cardiac hypertrophy. J Cardiovasc Pharmacol 17 Suppl 2: S110–113. |
| [7] | Calaghan SC, Belus A, White E (2003) Do stretch-induced changes in intracellular calcium modify the electrical activity of cardiac muscle? Prog Biophys Mol Biol 82: 81–95. |
| [8] | Calaghan SC, Le Guennec JY, White E (2004) Cytoskeletal modulation of electrical and mechanical activity in cardiac myocytes. Prog Biophys Mol Biol 84: 29–59. |
| [9] | Calkins H, Levine JH, Kass DA (1991) Electrophysiological effect of varied rate and extent of acute in vivo left ventricular load increase. Cardiovasc Res 25: 637–644. |
| [10] | Dean JW, Lab MJ (1990) Regional changes in ventricular excitability during load manipulation of the in situ pig heart. J Physiol 429: 387–400. |
| [11] | Franz MR (1996) Mechano-electrical feedback in ventricular myocardium. Cardiovasc Res 32:15–4. |
| [12] | Franz MR, Cima R, Wang D, et al. (1992) Electrophysiological effects of myocardial stretch and mechanical determinants of stretch-activated arrhythmias. Circulation 86: 968–978. |
| [13] | Fuchs F, Martyn DA (2005) Length-dependent Ca(2+) activation in cardiac muscle: some remaining questions. J Muscle Res Cell Motil 26: 199–212. |
| [14] | Hansen DE, Craig CS, Hondeghem LM (1990) Stretch-induced arrhythmias in the isolated canine ventricle. Evidence for the importance of mechanoelectrical feedback. Circulation 81:1094–1105. |
| [15] | Hennekes R, Kaufmann R, Lab M (1981) The dependence of cardiac membrane excitation and contractile ability on active muscle shortening (cat papillary muscle). Pflugers Arch 392: 22–28. |
| [16] | Hu H, Sachs F (1997) Stretch-activated ion channels in the heart. J Mol Cell Cardiol 29:1511–1523. |
| [17] | Kamkin A, Kiseleva I, Wagner KD, et al. (2000) Mechano-electric feedback in right atrium after left ventricular infarction in rats. J Mol Cell Cardiol 32: 465–477. |
| [18] | Kaufmann RL, Lab MJ, Hennekes R, et al. (1971) Feedback interaction of mechanical and electrical events in the isolated mammalian ventricular myocardium (cat papillary muscle). Pflugers Arch 324: 100–123. |
| [19] | Kelly D, Mackenzie L, Hunter P, et al. (2006) Gene expression of stretch-activated channels and mechanoelectric feedback in the heart. Clin Exp Pharmacol Physiol 33: 642–648. |
| [20] | Kiseleva I, Kamkin A, Wagner KD, et al. (2000) Mechanoelectric feedback after left ventricular infarction in rats. Cardiovasc Res 45: 370–378. |
| [21] | Kohl P, Bollensdorff C, Garny A (2006) Effects of mechanosensitive ion channels on ventricular electrophysiology: experimental and theoretical models. Exp Physiol 91: 307–321. |
| [22] | Lab MJ (1999) Mechanosensitivity as an integrative system in heart: an audit. Prog Biophys Mol Biol 71: 7–27. |
| [23] | Lab MJ, Allen DG, Orchard CH (1984) The effects of shortening on myoplasmic calcium concentration and on the action potential in mammalian ventricular muscle. Circ Res 55:825–829. |
| [24] | Lange G, Lu HH, Chang A, et al. (1966) Effect of stretch on the isolated cat sinoatrial node. Am J Physiol 211: 1192–1196. |
| [25] | Legrice IJ, Hunter PJ, Smaill BH (1997) Laminar structure of the heart: a mathematical model. Am J Physiol 272: H2466–2476. |
| [26] | Nazir SA, Lab MJ (1996) Mechanoelectric feedback in the atrium of the isolated guinea-pig heart. Cardiovasc Res 32: 112–119. |
| [27] | Nickerson D, Niederer S, Stevens C, et al. (2006) A computational model of cardiac electromechanics. Conf Proc IEEE Eng Med Biol Soc 1: 5311–5314. |
| [28] | Ravens U (2003) Mechano-electric feedback and arrhythmias. Prog Biophys Mol Biol 82:255–266. |
| [29] | Reiter MJ, Synhorst DP, Mann DE (1988) Electrophysiological effects of acute ventricular dilatation in the isolated rabbit heart. Circ Res 62: 554–562. |
| [30] | Riemer TL, Tung L (2003) Stretch-induced excitation and action potential changes of single cardiac cells. Prog Biophys Mol Biol 82: 97–110. |
| [31] | Rozenberg S, Tavernier B, Riou B, et al. (2006) Severe impairment of ventricular compliance accounts for advanced age-associated hemodynamic dysfunction in rats. Exp Gerontol 41:289–295. |
| [32] | Sackin H (1995) Mechanosensitive channels. Annu Rev Physiol 57: 333–353. |
| [33] | Stacy GP, Jr, Jobe RL, Taylor LK, et al. (1992) Stretch-induced depolarizations as a trigger of arrhythmias in isolated canine left ventricles. Am J Physiol 263: H613–621. |
| [34] | Stones R, Calaghan SC, Billeter R, et al. (2007) Transmural variations in gene expression of stretch-modulated proteins in the rat left ventricle. Pflugers Arch 454: 545–549. |
| [35] | Taggart P (1996) Mechano-electric feedback in the human heart. Cardiovasc Res 32: 38–43. |
| [36] | Tan JH, Liu W, Saint DA (2004) Differential expression of the mechanosensitive potassium channel TREK-1 in epicardial and endocardial myocytes in rat ventricle. Exp Physiol 89:237–242. |
| [37] | Tan JH, Liu W, Saint DA (2002) Trek-like potassium channels in rat cardiac ventricular myocytes are activated by intracellular ATP. J Membr Biol 185: 201–207. |
| [38] | Tavi P, Han C, Weckstrom M (1998) Mechanisms of stretch-induced changes in [Ca2+]i in rat atrial myocytes: role of increased troponin C affinity and stretch-activated ion channels. Circ Res83: 1165–1177. |
| [39] | Todaka K, Ogino K, Gu A, et al. (1998) Effect of ventricular stretch on contractile strength, calcium transient, and cAMP in intact canine hearts. Am J Physiol 274: H990–1000. |
| [40] | Volk T, Nguyen TH, Schultz JH, et al. (1999) Relationship between transient outward K+ current and Ca2+ influx in rat cardiac myocytes of endo- and epicardial origin. J Physiol 519 Pt 3:841–850. |
| [41] | White E, Boyett MR, Orchard CH (1995) The effects of mechanical loading and changes of length on single guinea-pig ventricular myocytes. J Physiol 482 ( Pt 1): 93–107. |
| [42] | Wilhelm J, Kondratev D, Christ A, et al. (2006) Stretch induced accumulation of total Ca and Na in cytosol and nucleus: a comparison between cardiac trabeculae and isolated myocytes. Can J Physiol Pharmacol 84: 487–498. |
| [43] | Zabel M, Koller BS, Sachs F, et al. (1996) Stretch-induced voltage changes in the isolated beating heart: importance of the timing of stretch and implications for stretch-activated ion channels. Cardiovasc Res 32: 120–130. |
| 1. | Ioannis Karaouzas, Natalia Kapetanaki, Angeliki Mentzafou, Theodore D. Kanellopoulos, Nikolaos Skoulikidis, Heavy metal contamination status in Greek surface waters: A review with application and evaluation of pollution indices, 2021, 263, 00456535, 128192, 10.1016/j.chemosphere.2020.128192 |
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) |
| HAI | 1 (1) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Europa | 6 (6) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Aluminco | 1 (1) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | ||
| Viometale | 1 (1) | Cr, Ni, Cu, Zn, etc.Cr(Ⅵ) | XRF(d), AR(a)Alkaline digestion(c) | LabMet |
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| HAI | 1 (7) | 3 (42) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Europa | 6 (13) | 4 (49) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Aluminco | 1 (6) | 4 (12) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | |||
| Viometale | 1 (4) | 6 (19) | Cr, Ni, Cu, Zn, etc. | XRF(d)AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| Europa | 2 | 3 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Aluminco | 1 | 5 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed |
Methods | Labs(*) | |
| Un-contaminated | Suspected for contamination | ||||
| Boreholes | - | 38 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| Surface Soil | - | 12 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| (a) Digestion with aqua regia followed by determination of metals in solution by AAS or ICP-MS (EN 13657) (b) Elution with water, determination of soluble Cr(Ⅵ) (DIN 38405-24: 05.87, AWWA-3500-Cr/B) (c) Alkaline digestion, determination of extracted Cr(Ⅵ) (USEPA, SW-846 Methods 3060A and 7196) (d) Determination of total elements concentration by X-ray fluorescence spectrometry (EN 15309) (*) Laboratories: (a) Andreou, K. Andreou. Ltd, Athens, (b) EuF: Eurofins Umwelt Ost GmbH, Jena, Germany, (c) LabMet: Laboratory of Metallurgy, NTUA, Athens. For the majority of samples, namely those collected from HAI, Europa and Aluminco, the elemental analysis was carried out following the digestion of samples with aqua regia (AR). The samples collected from Viometale were analyzed by X-ray fluorescence (XRF) spectrometry, (mainly due to time constraints - XRF analysis is much more rapid, as there is no need for any pretreatment steps, such as acid leaching or fusion). The LIFE-CHARM samples were also analyzed by XRF. | |||||
| Area (Number of samples) |
Cr (mg/kg) |
Ni (mg/kg) |
Cr(Ⅵ) (mg/kg) |
Source | ||
| Range | Mean | Range | Mean | Range | ||
| Asopos (n = 30) |
60-410 | 220 | 91-1200 | 620 | >0.1-9.3 (a) | [21] |
| Oropos (n = 33) |
17-600 | 212 | -- | [3] | ||
| Thebes (n = 51) |
134-856 | 277 | 621-2639 | 1591 | -- | [23] |
| Atalante (n = 64) |
48-4200 | 453 | 44-2730 | 533 | -- | [24] |
| All Greece (n = 41) |
2-466 | 102 | 2-1812 | 171 | -- | [22] |
| (a) Cr(Ⅵ) detected in 3 among the 30 analyzed reference soils (5.5, 6.0 and 9.3 mg/kg). | ||||||
| Soil limit values (mg/kg) | ||||||
| Residential areas* | Industrial areas* | |||||
| IT | DE | BE(W) | IT | DE | BE(W) | |
| Cr | 150 | 400 | 520 | 800 | 1000 | 700 |
| Ni | 120 | 140 | 300 | 500 | 900 | 500 |
| Cr(Ⅵ) | -- | -- | 4.2 | -- | -- | -- |
| (*) Cr, Ni digestion of samples with aqua regia (AR). | ||||||
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) |
| HAI | 1 (1) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Europa | 6 (6) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | |||
| Aluminco | 1 (1) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | ||
| Viometale | 1 (1) | Cr, Ni, Cu, Zn, etc.Cr(Ⅵ) | XRF(d), AR(a)Alkaline digestion(c) | LabMet |
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| HAI | 1 (7) | 3 (42) | Cr, Ni, Cu, Zn, Pb, Al | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Europa | 6 (13) | 4 (49) | Cr, Ni | Digestion with AR(a) | Andreou |
| Cr(Ⅵ) | Elution with water(b) | ||||
| Aluminco | 1 (6) | 4 (12) | Cr, Ni, Fe, Al | Digestion with AR(a)XRF(d) | EuF/LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | LabMet | |||
| Viometale | 1 (4) | 6 (19) | Cr, Ni, Cu, Zn, etc. | XRF(d)AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed | Methods | Labs (*) | |
| Un-contaminated | Suspected for contamination | ||||
| Europa | 2 | 3 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Aluminco | 1 | 5 | Cr, Ni, Fe, Al | Digestion with AR(a) | LabMet |
| Cr(Ⅵ) | Alkaline digestion(c) | ||||
| Site | No of sampling locations (no of samples) | Parameters analyzed |
Methods | Labs(*) | |
| Un-contaminated | Suspected for contamination | ||||
| Boreholes | - | 38 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| Surface Soil | - | 12 | Cr, Ni, Fe, Al | XRF(d) | LabMet |
| Cr(Ⅵ) | AR(a) | ||||
| (a) Digestion with aqua regia followed by determination of metals in solution by AAS or ICP-MS (EN 13657) (b) Elution with water, determination of soluble Cr(Ⅵ) (DIN 38405-24: 05.87, AWWA-3500-Cr/B) (c) Alkaline digestion, determination of extracted Cr(Ⅵ) (USEPA, SW-846 Methods 3060A and 7196) (d) Determination of total elements concentration by X-ray fluorescence spectrometry (EN 15309) (*) Laboratories: (a) Andreou, K. Andreou. Ltd, Athens, (b) EuF: Eurofins Umwelt Ost GmbH, Jena, Germany, (c) LabMet: Laboratory of Metallurgy, NTUA, Athens. For the majority of samples, namely those collected from HAI, Europa and Aluminco, the elemental analysis was carried out following the digestion of samples with aqua regia (AR). The samples collected from Viometale were analyzed by X-ray fluorescence (XRF) spectrometry, (mainly due to time constraints - XRF analysis is much more rapid, as there is no need for any pretreatment steps, such as acid leaching or fusion). The LIFE-CHARM samples were also analyzed by XRF. | |||||
| Area (Number of samples) |
Cr (mg/kg) |
Ni (mg/kg) |
Cr(Ⅵ) (mg/kg) |
Source | ||
| Range | Mean | Range | Mean | Range | ||
| Asopos (n = 30) |
60-410 | 220 | 91-1200 | 620 | >0.1-9.3 (a) | [21] |
| Oropos (n = 33) |
17-600 | 212 | -- | [3] | ||
| Thebes (n = 51) |
134-856 | 277 | 621-2639 | 1591 | -- | [23] |
| Atalante (n = 64) |
48-4200 | 453 | 44-2730 | 533 | -- | [24] |
| All Greece (n = 41) |
2-466 | 102 | 2-1812 | 171 | -- | [22] |
| (a) Cr(Ⅵ) detected in 3 among the 30 analyzed reference soils (5.5, 6.0 and 9.3 mg/kg). | ||||||
| Soil limit values (mg/kg) | ||||||
| Residential areas* | Industrial areas* | |||||
| IT | DE | BE(W) | IT | DE | BE(W) | |
| Cr | 150 | 400 | 520 | 800 | 1000 | 700 |
| Ni | 120 | 140 | 300 | 500 | 900 | 500 |
| Cr(Ⅵ) | -- | -- | 4.2 | -- | -- | -- |
| (*) Cr, Ni digestion of samples with aqua regia (AR). | ||||||