1.
Introduction
Hirschsprung disease (HSCR) is a congenital intestinal neuropathy that results in functional intestinal obstruction due to distal intestinal nerve derangement [1]. The disease occurs in approximately 1 in 5,000 live births [2]. HSCR has multifactorial causes, with RET [3] being the first gene identified to be involved in HSCR. The role of gene abnormalities, including EDNRB [4], EDN3 [5], ECE1 [6], SOX10 [7], PHOX2B [8] and other genes in the development of the disease, is gradually being explored. Clinical manifestations usually include delayed expulsion of meconium in newborns or severe constipation in older infants and children. The gold standard for the diagnosis of HSCR is the histological evaluation of tissue obtained from a deep rectal biopsy, showing a complete absence of submucosal (and intestinal muscle) ganglion cells [2]. Current treatment involves surgical removal of the intestine to eliminate the area where the enteric nervous system is missing [9]. Despite the removal of the diseased bowel segment, postoperative abnormalities in gastrointestinal function, such as constipation and bowel incontinence, are present [10]. Therefore, the search for treatment modalities to improve outcomes is of clinical importance.
Cistanche deserticola Y.C. Ma has long been used for medicinal purposes in China for a long time [11]. Ancient Chinese texts suggest that it can cure dryness and stagnation of the bowels in the elderly. One of these components, echinacoside (ECH), is gaining more and more attention as research progresses. Experimental studies strongly suggest that ECH exhibits a variety of beneficial pharmacological activities associated with anti-inflammatory, anti-endoplasmic reticulum stress, anti-apoptotic and neuroprotective effects [12]. ECH has been found to reverse myocardial remodeling and improve heart function [13]. In terms of nerve protection, ECH protects dopaminergic neurons by regulating the IL-6/JAK2/STAT3 pathway [14], and its metabolites may have neuroprotective activity and may directly complement neurotransmitter deficiencies [15]. Additionally, ECH attenuates lipopolysaccharide (LPS) induced inflammation and apoptosis in rat intestinal epithelial cells by inhibiting the mTOR/STAT3 pathway [16], and it can inhibit the NLRP3 inflammasome signaling pathway [17].
There are several challenges in managing HSCR, and identifying effective treatments is crucial for improving patient outcomes [18]. Stem cell therapy shows promise as a non-surgical alternative [19], but the limited proliferation and differentiation capacity of enteric neuronal stem cells presents a challenge [20]. Moreover, patients with HSCR often experience intestinal inflammation, which can lead to a poor long-term prognosis and the need for a reoperation [21,22]. What is more important to note is that children with HSCR are at risk of a potentially life-threatening inflammatory process [23]. Given its neuroprotective and anti-inflammatory properties, ECH may have potential as a treatment for HSCR. To explore this possibility, we conducted a network pharmacology analysis to assess the feasibility of using ECH in both clinical and experimental settings.
2.
Materials and methods
2.1. Identification of HSCR–associated genes
The HSCR-associated genes consist of two parts: the differential genes obtained through differential analysis of the normal and disease groups, respectively, and the other part collected through several databases. We downloaded microarray gene expression data from GSE96854, which included three normal and three disease samples from the Gene Expression Omnibus database (GEO, https://www.ncbi.nlm.nih.gov/geo/). We used the "limma" R package [24] (version 3.52.2) to identify differentially expressed genes (DEGs) between the disease and normal groups. Cut-off values for DEGs were set to |log2 (Fold Change) | > 1, with an adjusted P value < 0.05. The results are presented as volcano plots and heat maps. We collected the disease-associated genes from multiple databases. In the OMIM (https://omim.org/) database [25], we searched for "hirschsprung disease" and obtained 14 related genes. The disease code C0019569 was searched in the "DisGeNET" (https://www.disgenet.org/) database [26,27], and 55 related genes were obtained by using the screening criteria of Score_gda > 0.1. A search of the "Genecard" database [28] for HSCR yielded 983 results, which were further screened based on the criterion of score > 10, resulting in 385 genes. Finally, we searched the NCBI database (https://www.ncbi.nlm.nih.gov/) for "Hirschsprung's disease AND Homo sapiens" and obtained 96 genes.
2.2. Screening the targets of ECH
The structural model of ECH was obtained via a download from the PubChem database (https://pubchem.ncbi.nlm.nih.gov/). We used three different databases, including PharmMapper [29] (http://lilab-ecust.cn/pharmmapper/), Drugbank [30] (https://go.drugbank.com/) and TargetNet [31] (http://targetnet.scbdd.com/), to predict the targets of drug action. And, all targets were screened according to " Homo sapiens ". After combining the results from the three databases, we obtained 93 ECH targets.
2.3. Enrichment analysis
For the enrichment analysis of related genes, we used the "clusterProfiler" R package [32] (version 4.4.4) in the Gene Ontology (GO) [33] and Kyoto Encyclopedia of Genes and Genomes (KEGG) [34] databases. For the Gene Set Enrichment Analysis (GSEA) algorithm enrichment analysis, we selected results based on the following criteria: |NES| > 1, NOM P value < 0.05 and FDR (adjusted P value) < 0.25. Additionally, we applied a screening criterion of adjusted P value < 0.05 for the enrichment results. To visualize the results, we employed the enrichplot R package (version 1.16.2) and ggpubr R package (version 0.4.0).
2.4. Construction of protein-protein interaction network and ceRNA
The protein-protein interaction (PPI) networks were identified automatically by using Search Tool for the Retrieval of Interacting Genes/Proteins (version 11.5; https://string-db.org/). The setting parameters were as follows: "Homo sapiens", and the minimum required interaction score is "medium confidence (0.4)". The data for the construction of the ceRNA network map were obtained using the "multiMiR" R package [35] (version 1.18.0). And, we screened the validated miRNAs as the final results. Cytoscape software (version 3.9.1) was used for visualization.
2.5. Molecular docking
By taking intersections of HSCR-associated genes and targets from ECH, we obtained eight potential binding locations. First, we downloaded the structures of the eight targets in the PDB database [36] (https://www.rcsb.org/). Then, we used PyMOL software [37] to perform the pre-processing steps, such as separating single chains and removing water. We downloaded the 2D structure of ECH in sdf format from the PubChem database (https://pubchem.ncbi.nlm.nih.gov/compound/5281771), and then converted it to pdb format for pre-processinig with PyMOL. The gridbox parameters were obtained in the following two ways before docking. (1) The ligand is present in the receptor file, and the gridbox parameters are obtained by ligand expansion using PyMOL's plugin getbox. (2) No ligand in the receptor file or no viable docking site can be obtained by ligand expansion: in this case, we chose to include all receptor molecules in the gridbox for docking. Using the pre-processed ligands and receptors, we performed molecular docking according to the official AutoDock tutorial in AutoDock-GPU [38]. Result analysis was performed by using mgltools [39]. The visualization of the molecular docking results was implemented in PyMOL.
2.6. Gene mutation analysis and immunohistochemical staining analysis
Exploring and visualizing mutations in target genes from multiple types of cancer by the cBioPortal for Cancer Genomics [40] (http://www.cbioportal.org). Gene expression in tissues was analyzed by obtaining immunohistochemical results from the Human Protein Atlas [41] (https://www.proteinatlas.org/) database. The links to download the original images are as follows: CA1 (https://www.proteinatlas.org/ENSG00000133742-CA1/tissue/rectum#img), CA2 (https://www.proteinatlas.org/ENSG00000104267-CA2/tissue/colon#img), CA9 (https://www.proteinatlas.org/ENSG00000107159-CA9/tissue/small+intestine#img), CA12 (https://www.proteinatlas.org/ENSG00000074410-CA12/tissue/rectum#img), DNA methyltransferase 1 (DNMT1) (https://www.proteinatlas.org/ENSG00000130816-DNMT1/tissue/colon#img), regulating synaptic membrane exocytosis 2 (RIMS2) (https://www.proteinatlas.org/ENSG00000176406-RIMS2/tissue/colon#img), RPGRIP1L (https://www.proteinatlas.org/ENSG00000103494-RPGRIP1L/tissue/small+intestine#img) and zinc finger E-box-binding homeobox 2 (ZEB2) (https://www.proteinatlas.org/ENSG00000169554-ZEB2/tissue/cerebral+cortex#img).
2.7. Statistical analysis
All data processing and analysis were performed in R software (version 4.2.1) by RStudio. Statistical analysis was calculated using the built-in functions of the R package. The main statistical tests were P value and adjusted P value. All statistical P values were two-sided, and P < 0.05 was considered statistically significant.
2.8. Ethics approval of research
The study was based on open-source data from multiple databases. Ethical approval has been provided for the patients involved in these databases. Therefore, there are no ethical issues with this article.
3.
Results
3.1. Differentially expressed genes analysis between healthy and diseased individuals
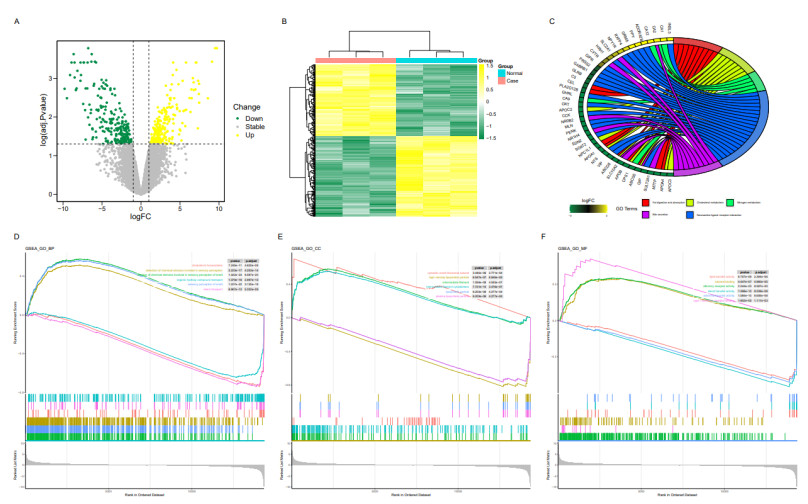
To investigate in depth the key genes causing HSCR, we obtained a total of 471 differential genes using the "limma" package in the expression matrix of GSE96854 data between healthy and diseased individuals. Of these, 223 were highly expressed genes in patients relative to the control group, and 248 were lowly expressed genes (Figure 1A). A heat map has been used to show the expression of differential genes in different groups, and the clustering results show that differential genes can distinguish well between diseased and normal individuals (Figure 1B). To better understand the mechanism of differential genes on disease development, we further explored the function of expressed genes by conducting enrichment analysis. The KEGG results showed that fat digestion and absorption, cholesterol metabolism, nitrogen metabolism, neuroactive ligand-receptor interaction and bile secretion were the significant pathways (Figure 1C). Through further analysis using the GSEA enrichment method, we could find that the pathways of Biological Process (BP) in highly expressed genes were associated with the detection of chemical stimuli involved in the sensory perception of smell, the sensory perception of smell and the detection of chemical stimuli involved in sensory perception. For the lowly expressed genes, the enrichment results showed that they were mainly involved in cholesterol homeostasis, sterol transport and organic hydroxy compound transport (Figure 1D). The top three terms of highly expressed genes of Cellular Component (CC) were intermediate filament, intermediate filament cytoskeleton and cytosolic small ribosomal subunit. Correspondingly, the lowly expressed genes were mainly concentrated in plasma lipoprotein particles, lipoprotein particles and high-density lipoprotein particles (Figure 1E). There were also significant differences in the Molecular Function (MF) pathways between the differentially expressed genes. Olfactory receptor activity, type I interferon receptor binding and odorant binding were mainly pathways concentrated in the diseased group. For the normal group, the top three enrichment results were lipid transfer activity, sterol transfer activity and sterol transporter activity (Figure 1F). The results of the enrichment analysis reveal possible mechanisms of intestinal dysfunction in disease states, which are closely related to clinical manifestations. We then constructed a PPI network using the STRING database to explore the interrelationships between proteins. The top 30 genes based on the degree algorithm were further demonstrated using the cytoHubba plug-in in Cytoscape (Supplemental Figure S1A). The complete protein network interaction map can be seen in the Supplemental Figure S1B.
3.2. Identification of a set of HSCR-associated genes
In addition to the previous differential analysis to obtain possible potential pathogenic genes, we further obtained 461 genes through GeneCards, OMIM, DisGeNET and NCBI database collections (Figure 2A). Based on the enrichment results from the database genes, we further understood the mechanism of the disease. The top five terms in Biological Process were axon development, gland development, axonogenesis, embryonic organ development and gliogenesis (Figure 2B). The results of Cellular Component were mainly involved in the neuronal cell body, MKS complex, ciliary transition zone, membrane raft and membrane microdomain (Figure 2C). Signaling receptor activator activity, receptor ligand activity, G protein-coupled receptor binding, DNA-binding transcription factor binding and growth factor activity were the top five terms for Molecular Function (Figure 2D). The KEGG enrichment results, on the other hand, revealed that these genes play important roles in multiple pathways. The first five pathways were microRNAs in cancer, breast cancer, EGFR tyrosine kinase inhibitor resistance, PI3K-Akt signaling pathway and signaling pathways regulating pluripotency of stem cells (Figure 2E). We also mapped PPI networks for these 461 genes through the STRING database (Supplemental Figure S2). We combined the differential genes obtained from the differential analysis and the genes from the database collection as HSCR-associated genes for subsequent analysis. The list of genes is provided in Supplementary Materials.
3.3. Identifying ECH targets
TargetNet, Drugbank and PharmMapper databases were used to determine the targets of ECH, and we obtained a total of 93 targets (Figure 3A). The interaction of these targets with each other was shown by the PPI networks (Figure 3B). We further used GO enrichment analysis to predict the possible molecular functions of the targets (Figure 3C). Carbonate dehydratase activity, with its upstream signaling pathway, was the most prominent signaling pathway among these targets, and nuclear receptor activity also played an important role. The results of KEGG enrichment showed that the main pathways involved in the targets were nitrogen metabolism, prostate cancer, proximal tubule bicarbonate reclamation, antifolate resistance and the apelin signaling pathway (Figure 3D). Based on the enrichment results, we can infer the pharmacological mechanism of ECH.
3.4. Binding of ECH to HSCR-intersecting potential target genes
By intersection analysis of ECH targets with HSCR-associated genes, we obtained eight potential action points (Supplemental Figure S3). They were RPGRIP1L, DNMT1, ZEB2, CA1, CA2, CA9, CA12 and RIMS2. The structural details of these targets for molecular docking are shown in the Table 1. Following the parameters in the methodology section, we performed molecular docking of the eight targets (Figure 4A–H). Information on the position and energy of molecular docking is shown in Table 2. These docking sites are the optimal results for multiple computational docking, predicting that, once the drug reaches the target site, it will bind to a specific target and perform a physiological function. The yellow dotted lines represent the hydrogen bonds in the drug receptor complex.
3.5. Validation of target expression in the tissue
Through molecular docking, we further identified potential therapeutic targets. To investigate the expression of the targets in the gastrointestinal tract, we obtained the immunohistochemistry results for eight targets in the Human Protein Atlas project database. Among them, CA1, CA2, CA9 and CA12 have obvious gastrointestinal tissue specificity. The other three targets, including DNMT1, RIMS2 and RPGRIP1L, although less tissue-specific, were also positive in the gastrointestinal tract. For CA1, it exhibited selective cytoplasmic and nuclear expression in the large intestine. From the staining results, the staining of nuclei in endocrine cells was high and the intensity was strong (Figure 5A). Meanwhile, CA2 staining in the nuclei of endocrine cells, enterocytes and goblet cells showed their high incidence of occurrence, and it also showed strong positivity in enterocyte microvilli (Figure 5B). CA9 expression was concentrated in cytoplasmic and membranous glandular cells (Figure 5C). The staining of CA12 in endocrine cells, enterocytes, goblet cells and peripheral nerves/ganglia in rectum tissue was high and the intensity was strong (Figure 5D). For DNMT1, although its staining in the nuclei of glandular cells was medium, the intensity was strong (Figure 5E). RIMS2 showed only low staining results in glandular cells in colon tissue (Figure 5F). The cytoplasmic/membranous staining of RPGRIP1L in glandular cells was medium and the intensity was moderate (Figure 5G). In the HPA database, the tissue specificity of ZEB2 was mainly expressed in the brain (Figure 5H).
3.6. Mutations, ceRNA networks and pathways of the core targets
Based on the previous enrichment results showing close association with cancer pathways, we further explored the mutation of eight genes in a variety of mutations in multiple cancers. In terms of mutations, RIMS2 had the highest mutation rate of 9% and amplification was the predominant mutation type for RIMS2. CA1, CA2, CA9, CA12, RPGRIP1L DNMT1and ZEB2 were more conservative, with all seven genes having a mutation rate of less than 5% (Figure 6A). To gain insight into the regulatory mechanisms of target genes, we assembled validated target miRNAs to construct a ceRNA network map (Figure 6B). Green, yellow and red indicate one evidence, two evidences and greater than or equal to three evidences of association between the miRNA and the target gene, respectively. And, detailed miRNA information is provided in the Supplementary Material. Eight core genes were analyzed for enrichment, and the enrichment results were visualized using Cytoscape (Figure 6C). The green color represents the BP enrichment results. Yellow represents the CC enrichment results, and blue represents MF enrichment result. The pathways with the most significant enrichment results for BP and MF are one-carbon metabolic processes and carbonate dehydratase activity. For CC enrichment, the results mainly include cytoskeletons of the presynaptic active zone, axonemal microtubules and presynaptic cytoskeletons.
4.
Discussion
The absence of enteric ganglion cells is responsible for the presence of HSCR, which is characterized by persistent contraction of the affected bowel segment, leading to intestinal obstruction and distension of the proximal bowel segment [42]. As research progresses, more pathogenic mechanisms are being revealed, including epigenetic mechanisms such as DNA methylation, histone modifications and other epigenetic mechanisms [43]. However, there has been no significant breakthrough in treatment modalities, and postoperative constipation and its associated complications remain a long-term concern following surgery [10]. Therefore, the search for drugs to improve intestinal function is of great clinical importance, and the multiple properties of ECH have great potential for therapeutic use [12]. Molecular docking is a method for assessing the preferred orientation of one molecule to another as they bind to each other to form stable complexes, and it is one of the most commonly used methods in structure-based drug design [44]. The main purpose of this study is to explore the potential mechanism of ECH in the treatment of HSCR.
We obtained HSCR-associated genes through database collection and gene analysis. By enrichment analysis of HSCR-related genes, the results reflect the diversity of HSCR pathogenesis, with multiple pathways being involved in disease occurrence and progression. These included pathways associated with axon development (BP), the neuronal cell body (CC) and signaling receptor activator activity (MF). The targets of ECH were also collected from three databases. We also collected the targets of ECH from three databases and identified eight potential targets through molecular docking and immunohistochemistry analysis. These targets include CA1, CA2, CA9, CA12, DNMT1, RIMS2, RPGRIP1L and ZEB2.
CA1, CA2, CA9 and CA12 are all carbonic anhydrases (CAs), which constitute a large family of zinc metalloenzymes. These enzymes can catalyze the reversible hydration of carbon dioxide, a crucial process for maintaining the body's internal environment homeostasis. Specifically, CAs balance the CO2 and HCO3 pools to regulate the pH and homeostasis in the blood and various tissues. Additionally, CAs are involved in other processesm such as water formation, cerebrospinal fluid secretion, gastric fluid formation, gluconeogenesis, lipogenesis, urea production and more [45]. Due to their diverse functions, CAs have potential as therapeutic targets for drugs. CA inhibitors could serve as novel anti-obesity, anti-cancer and anti-infective agents [46]. In the present study, ECH demonstrated a strong affinity for CAs in molecular docking.
DNMT1 can transfer methyl groups to cytosine nucleotides of genomic DNA. Maintaining optimal levels of DNMT1 is essential for normal growth and health [47]. DNMT1 is being explored as a therapeutic target in pancreatic cancer, triple-negative breast cancer and oral squamous cell carcinoma [48,49,50]. Meanwhile, DNMT1 has an important role in maintaining genomic stability during intestinal development [51]. In animal studies, LINC00346 has been found to regulate cell migration and proliferation through competitive binding to DNMT1 in HSCR [52]. DNMT1 deletion in neurons leads to the apoptosis of differentiated cells [47]. As more research is conducted, DNA methylation is shown to play a key role in the development of enteric nervous system and HSCR pathogenesis [43]. Therefore, the combination of ECH with DNMT1 has great potential in the treatment of HSCR.
RIMS2 encodes a presynaptic protein. Research on it has gradually increased in recent years. With the help of whole-exome sequencing, it was found that RIMS2 plays a key role in tardive dyskinesia [53]. And, RIMS2 is an important synaptic locus in the cognitive progression of Parkinson's disease [54]. All of these findings suggest that RIMS2 is closely associated with neurological disorders.
RPGRIP1L can stabilize epidermal keratinocyte adhesion by regulating the endocytosis of desmoglein [55]. It has been shown that overexpression of RPGRIP1L increases the number of POMC cells, and that RPGRIP1L is required for the development of hypothalamic arcuate neurons [56]. The results of immunohistochemistry showed that the gene is highly expressed in glandular cells, which could be a potential therapeutic target for the relief of intestinal obstruction. It is worth noting that all seven genes mentioned above are expressed in the epithelial layer of the intestine. This is consistent with the study that showed that ECH attenuated apoptosis and inflammatory responses in rat intestinal epithelial cells [16]. Therefore, the location of ECH action in the intestine may be in the epithelial layer.
ZEB2 is a transcription factor famous for its role in the epithelial to mesenchymal transition (EMT) [57]. The EMT is crucial in the development of the embryo [58]. Heterozygous mutations or deletions in ZEB2 cause Mowat-Wilson syndrome, a multiple congenital anomaly syndrome that includes HSCR [59]. Given that the core genes have been shown to be associated with HSCR in numerous studies, we performed an additional in-depth analysis of them. Network analysis of ceRNA revealed the regulatory mechanisms of eight core genes. The enrichment pathways most significant for BP and MF were those associated with one-carbon metabolic processes and carbonate dehydratase activity. The results for CC enrichment mainly included cytoskeletons of the presynaptic active zone, axonemal microtubules and presynaptic cytoskeletons.
It has been shown that DNMT1 is involved in the regulation of the JAK2/STAT3 signaling pathway [60,61]. ZEB2 is induced to be produced in the presence of intestinal inflammation [62]. Activation of mTOR complex 1 was increased in RPGRIP1L-negative mice [63]. Meanwhile, CA9 was associated with the mTOR pathway [64]. Combined with the effects of ECH, including IL-6/JAK2/mTOR/STAT3 pathways [14,16], ECH may exert anti-inflammatory and intestinal lubrication effects by influencing core genes in the intestinal epithelium to treat HSCR.
In summary, this study identified eight genes that showed good docking results through molecular docking, and the immunohistochemistry results indicated their expression in the gastrointestinal tract and cerebral cortex. These findings suggest that ECH has great potential for the treatment of HSCR. However, this study has some limitations. The collection of HSCR-associated genes and ECH targets was limited to databases, which may have excluded relevant genes and targets. Additionally, the use of bioinformatic methods for exploring the mechanism of action of ECH targets through enrichment analysis may not fully represent the efficacy of ECH. Furthermore, the limited number of studies available for these eight genes requires further validation through subsequent pharmacodynamic and molecular experiments. Despite these limitations, the potential targets and mechanisms identified in this study have significant research implications and scope for development to improve the treatment of HSCR.
5.
Conclusions
Based on bioinformatics and molecular docking techniques, this study investigated the mechanism of action of ECH targets and the signaling pathways involved in HSCR-related genes. The potential targets of ECH for the treatment of HSCR include CA1, CA2, CA9, CA12, DNMT1, RIMS2, RPGRIP1L and ZEB2. This study provides a reference for further research into the mechanisms of ECH and therapeutic approaches to HSCR.
Data Availability
The genetic data used in this study are available in the GEO database (https://www.ncbi.nlm.nih.gov/geo/). The following databases were used for target collection: the OMIM (https://omim.org/) database, the DisGeNET (https://www.disgenet.org/) database, Genecard (https://www.genecards.org/) database, NCBI (https://www.ncbi.nlm.nih.gov/) database, PharmMapper (http://lilab-ecust.cn/pharmmapper/) database, Drugbank (https://go.drugbank.com/) database and TargetNet (http://targetnet.scbdd.com/) database. Mutation information for the eight genes in multiple types of cancer were obtained from the cBioPortal for Cancer Genomics (http://www.cbioportal.org). We used the PubChem(https://pubchem.ncbi.nlm.nih.gov/)database to get the structure.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgment
We would like to acknowledge the public databases, including GEO, OMIM, DisGeNET, Genecard, NCBI, PharmMapper, Drugbank, TargetNet, PubChem, the cBioPortal and STRING, for their contributions to human medicine in which they share vast volumes of data. Thanks to the authors of the R package for their contribution to the advancement of bioinformatics. Thanks to all of the authors of the references for their hard work and contributions to the development of medicine. Finally, we would like to thank Professor BAO WG and his yeast model and molecular genetics laboratory for providing us with the computing platform. This research was funded by the Tianjin Health Science and technology project (ZC20014).
Conflict of interest
We declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary
Supplementary Materials include HSCR-associated genes, miRNA information and Supplemental Figure S1-S3.









 DownLoad:
DownLoad: