A dissipation model for concrete based on an enhanced Timoshenko beam

1.   Introduction

It is remarkable that despite its widespread use in civil engineering, concrete remains relatively unknown. Indeed, in technical practice, oversimplified models that ignore some essential aspects are used. From ancient times to the present day, human structures have been crafted from concrete, initially comprising rudimentary cement made by crushing and burning gypsum or limestone. Over the course of civil engineering history, concrete has evolved into a sophisticated composite material. Nowadays, concrete is a fundamental construction material that plays a pivotal role in shaping our built environment, providing stability, durability, and versatility in a wide range of construction projects. Ongoing research in concrete technology is crucial for advancing the construction industry, promoting sustainability, enhancing safety, and meeting the evolving demands of our built environment.

Among some of the most significant current research areas concerning concrete, we can summarize the following categories: ⅰ) supplementary cementitious materials (SCMs); ⅱ) nanotechnology; ⅲ) self-healing concrete; ⅳ) ultra-high-performance concrete (UHPC); ⅴ) digital tools in concrete design.

SCMs are materials like fly ash, slag, and silica fume that can be added to concrete in addition to Portland cement to improve its properties and reduce its carbon footprint ^[1,2,3]. By incorporating these SCMs into concrete mixtures, construction professionals can decrease the amount of Portland cement needed, a significant source of carbon emissions in concrete production. This substitution not only improves the technical properties of concrete but also contributes to more sustainable and environmentally friendly construction practices, making it an essential aspect of modern concrete research and construction ^[4].

Incorporating nanomaterials into concrete formulations represents a promising possibility for enhancing the mechanical properties and longevity of the material. This research area is continually evolving and has the potential to revolutionize the construction industry by producing stronger, more durable, and sustainable concrete structures. Potentially, the inclusions could be nanoparticles ^[5], fibers ^[6,7,8], and suitable complex microstructures enancing the performaces ^[9,10,11]. Nanotechnology applied to concrete can improve particle packing and reduce permeability. Nanoparticles are much smaller in size than traditional concrete materials. When incorporated into the concrete mix, they fill in the gaps between larger particles, improving particle packing. This denser packing enhances the concrete's overall strength and reduces porosity, increasing surface area. Nanomaterials, such as nano-silica or nanotubes, have a high surface area-to-volume ratio ^[12]. This increased surface area allows for better bonding with cement particles and enhances chemical reactions. Moreover, they can be employed to form additional cementitious compounds that contribute to increased strength and durability, increased flexural and compressive strength, and shifting of the mitigation of early-age cracking. Nanomaterials can help mitigate early-age cracking by reducing the heat of hydration, controlling the formation of microcracks, and improving the overall curing process.

Research on self-healing concrete focuses on developing innovative materials and techniques that allow it to repair its cracks autonomously ^[13]. This area of study is essential for improving the durability and longevity of concrete structures. The idea of self-healing originates from the aim to enhance the performance of building materials like concrete with extra features mimicking the behavior of biological tissues, such as bone (see, e.g., ^[14,15] to exploite mechanical properties, and ^{[16,17,18,19]} for biologocal processes that allow the healing of the tissue). Key aspects of research on self-healing concrete are self-healing mechanisms, healing agents, and microstructural changes. Self-healing concrete typically relies on several mechanisms, including autogenous and encapsulated healing. Autogenous healing occurs when unhydrated cement particles in the presence of water fill small cracks through continued hydration, sealing the crack ^[20]. Encapsulated healing involves the use of microcapsules containing healing agents embedded in the concrete. When a crack forms, these capsules rupture, releasing healing agents that react and seal the crack ^[21]. Various healing agents can be embedded in self-healing concrete, such as bacteria, polymers, or organic and inorganic materials. Bacteria-based systems use specially designed bacteria that produce calcium carbonate (CaCO$_3$) when exposed to moisture and oxygen. This CaCO$_3$ seals cracks by precipitating in them. Polymer-based systems rely on the expansion of polymers to seal cracks. These polymers can be embedded within the concrete mix or applied as an external layer. This field of research aims to understand how self-healing affects the microstructure of concrete, ensuring that the healing process does not compromise the overall strength and durability of the material. Techniques like scanning electron microscopy (SEM) and X-ray micro-computed tomography ($\mu$-CT) are used to analyze the effectiveness of self-healing mechanisms.

UHPC is a relatively recent development in the field of concrete technology ^[22]. It is characterized by its exceptional strength, durability, and unique properties that distinguish it from traditional concrete. UHPC typically comprises a precise blend of materials, including Portland cement, fine quartz or silica fume, very fine sand, high-range water-reducing admixtures, and sometimes steel fibers. The exact mix design can vary but is characterized by the use of outstanding materials and minimal water content.

Moreover, ultra high performance fiber-teinforced concrete (UHP FRC) is an advanced concrete variant that incorporates high-strength fibers to significantly enhance its mechanical and durability properties ^[23]. Characterized by a compressive strength greater than 150 MPa, UHP FRC surpasses conventional concrete, which typically ranges from 20 to 50 MPa. The inclusion of fibers like steel, glass, or synthetic materials boosts its tensile strength and ductility, enabling it to withstand greater tensile forces and deform more without cracking. UHP FRC features a dense matrix with very low porosity, making it highly resistant to water penetration and chemical attacks. This density is achieved through optimized particle packing and the use of fine powders such as silica fume, fly ash, and superplasticizers. The combination of a dense matrix and high fiber content results in exceptional durability, providing resistance to freeze-thaw cycles, abrasion, and aggressive environments. Typically self-consolidating, UHP FRC flows and fills complex molds without the need for mechanical vibration, facilitating the creation of intricate architectural elements. The components of UHP FRC include high-quality Portland cement as the primary binder, fine aggregates to ensure dense particle packing, silica fume to fill voids and increase strength, superplasticizers to enhance workability and fluidity without increasing water content, and high-strength fibers like steel, glass, polypropylene, or carbon to improve tensile strength and ductility. UHP FRC finds applications in bridges and infrastructure, architectural elements, repair and rehabilitation, and security and defense structures due to its high strength, durability, and impact resistance. Its advantages lie in its superior mechanical properties, exceptional durability, design flexibility, and potential contributions to sustainable construction through reduced material usage and longer lifespan. However, the production of UHP FRC is more costly than conventional concrete, requiring precise mix design, quality control, and specialized knowledge for design and construction. Despite these challenges, UHP FRC stands out as a cutting-edge material suitable for demanding applications in modern construction.

Computer simulations and modeling play a crucial role in designing and optimizing concrete structures. These tools provide technicians and engineers with valuable insights, enabling them to make informed decisions, improve designs, and enhance the overall performance of concrete structures. Computer simulations and modeling provide a comprehensive and detailed understanding of how concrete structures perform in real-world conditions. This knowledge allows for more efficient and sustainable designs, reduced construction costs, improved safety, and enhanced durability, ultimately leading to better-engineered concrete structures. For instance, potential applications of this method include 3D modeling of concrete ^[24,25], research focused on optimizing key aspects of concrete performance or its internal structure ^[26,27,28], and aided design techniques ^[29,30,31].

Fundamentally, it is the internal microstructure of concrete that defines its unique properties. Comprising components like Portland cement, sand, and gravel of various sizes and shapes, concrete is a highly heterogeneous material. Its strength is significantly influenced by factors such as the water-to-cement ratio and the incorporation of additives that chemically or mechanically alter its properties.

Describing the behavior of concrete poses numerous challenges from a modeling perspective. Among these challenges, the key is its nonlinear behavior both at the macro level of observation, in a standard context ^[32,33,34], as well as in porous materials ^[35], and at the microscopic level ^[36,37], even under small deformations. The dissipative effects stemming from its microstructure in both elastic and plastic regimes^[38] and the evolution of cracks within it ^[39] are also crucial.

At its core, the microstructure of concrete consists of a matrix formed by the solid phase of the cement paste, interspersed with pieces of inert material of varying sizes. Additionally, the microstructure is further complicated by factors such as chemical species and thermal cycles during curing, which naturally give rise to microcracks within the material. While these microcracks impact the macroscopic behavior of concrete, their effects remain subdued unless subjected to significant external loads ^[40].

Various models have been explored in the literature to predict concrete behavior. In addition to traditional models like the Cauchy model, alternative approaches within the framework of generalized continua have been investigated. Among them, we recall the second-gradient continua ^{[41,42,43,44]} or even of higher order ^[45], micromorphic continua ^[46,47,48], and functionally graded materials ^[49]. These include also Cosserat-type models to account for the presence of stiff aggregates and higher gradient continua to address the material strong heterogeneity (see, e.g., ^{[50,51,52,53,54]}).

Furthermore, concrete can be treated as a porous material due to voids formed during the curing process and microcracks ^[55,56]. These microcracks, in particular, affect concrete behavior by introducing asymmetry in its mechanical response due to compressive or tensile loads, and generating internal friction under cyclic compressive loads.

Modeling the dissipation in concrete presents a significant challenge. While viscous models are commonly used, they often offer a simplistic linearization of dissipative actions. Alternatively, Coulomb-type friction between microcrack surfaces is proposed as a more appropriate mechanism for dissipative behavior, which remains nearly independent of frequency. Rheological models and thermodynamic frameworks with diffusive internal variables are also employed to address dissipation in solid materials ^[57,58,59].

Finally, while this paper primarily focuses on dissipative effects in concrete under small deformations, it is important to acknowledge ongoing research efforts related to plasticity and damage evolution (see, e.g., ^{[60,61,62,63]}). Variational formulations are favored for their logical consistency and ability to minimize unnecessary assumptions (see, e.g., applications to damage formulation ^[64,65,66], buckling ^[67], internal friction in solid materials ^[68,69], and thermoelastic theory ^[70]). Recent studies explored the use of material particles akin to swarms of robots, offering promising computational efficiency ^[71].

In summary, this work aims to explore the Coulomb nature of dissipative effects in concrete due to the mechanics of microcracks through numerical simulations obtained for a 1D generalized model, which is an enhanced version of the Timoshenko beam, built upon a previously introduced 3D model ^[72]. The proposed Timoshenko-like beam is a very efficient and powerful tool for quickly assessing material behavior. This novel beam model shows an improved capability to analyze the behavior of materials under certain circumstances, subsequently providing significant advantages over traditional beam models. In comparison with traditional beam models, this Timoshenko-like beam is more effective in predicting the dissipation in materials that are subjected to cyclic loads, and, as in the standard case, it is capable of more accurately predicting the effects of shear deformation. As a result of these improvements, the Timoshenko-like beam model can provide engineers and researchers with greater insight into the behavior of materials and allow them to make more informed decisions when designing structures and mechanical components.

2.   The micromorphic beam model

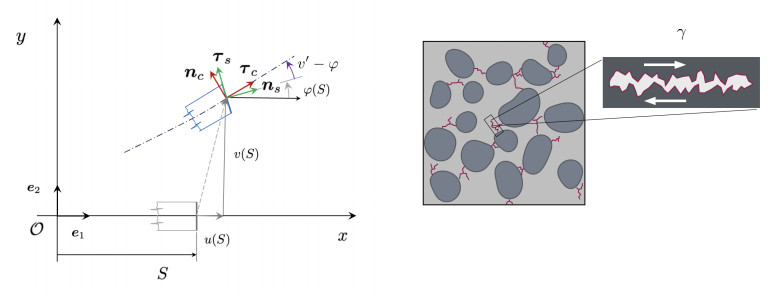
The present section concerns a planar 1D model of a cement-based beam that can be described primarily by a reference curve $\mathscr{C}^*$ in the plane $xy$, which lies on the $x$-axis in its undeformed configuration and whose length is $L$. The current configuration of the beam, $\mathscr{C}$, is represented by the map $\boldsymbol{\chi}$, which depends on a generic $S$-abscissa, as illustrated in Figure 1. To this end, we propose to enlarge the standard kinematical description used in the Timoshenko model with a further descriptor that is able to take into account, to some extent, the sliding effect of the opposite faces of microcracks within the cement matrix ^[38,72,73]. Since we consider the small displacement and small deformation regime, we assume that the density of microcracks remains the same throughout the tests; thus, no damage evolution occurs. The fundamental kinematic assumption in the Timoshenko model is that, although the conservation of plane cross-sections and their rigidity apply, the orthogonality between the axial beam line and the cross-section is not retained. This refers to the hypothesis in which the influence of shear distortion on the beam deformation is not neglected ^[74]. The complete kinematical description of the system configuration is specified by means of the kinematic variables: $u$, $v$, $\varphi$, and $\gamma$. Expressly, these kinematical descriptors represent the longitudinal and transverse displacement of the beam axis, the cross-section rotation, and an average inner relative sliding between the opposite faces of microcracks, respectively. The first three variables are characteristic of the classical Timoshenko model accounting for extension, while the novel-introduced variable is assumed to be a scalar field since, as a first approximation, we can postulate that no preferential direction characterizes the microcracks and a random distribution of their orientation is in place ^[72,75]. Thus, we define the map $\boldsymbol{\chi}$ as:

where the vector $\boldsymbol{r}$ specifies the position of the material particles lying on the axial line of the beam, and $\hat{\varphi}$ and $\hat{\gamma}$ are the characteristic features that describe the essential properties of the microstructure, i.e., the orientation of the cross-section and the sliding in the microcracks.

Figure 1.  Kinematic descriptors of the beam (on the left); scheme of the microcrack microstructure of the beam material (on the right). $\boldsymbol{\tau}_c$ and $\boldsymbol{n}_c$ are the tangent and normal unit vectors to the axial curve of the beam, while $\boldsymbol{\tau}_s$ and $\boldsymbol{n}_s$ are the tangent and normal unit vectors to the beam cross-section. The red lines on the concrete section represent the microcracks; thus, $\gamma$ can be interpreted as a descriptor of micro-slip accumulation within the material.

DownLoad: Full-Size Img PowerPoint

In order to characterize the behavior of the considered system, we employ an expanded version of the principle of virtual work (PVW). This principle states that, at equilibrium, the virtual work exerted by the external forces applied to the system, denoted by $\delta \mathcal{W}^{ext}$, must balance the virtual work performed by the internal contact forces, namely, $\delta \mathcal{W}^{el}$ for the conservative part associated with the elastic deformation, as well as any virtual work dissipated within the system, $\tilde{\delta} \mathcal{D}$, for the same virtual displacements; therefore, we consider the extended principle of virtual work as follows:

neglecting the inertial effects since we consider low-frequency applications of the materials. In this extended version of the variational principle, it is important to note that the dissipative contribution is not calculated as the first variation of $\mathcal{D}$. As a result, we use a different symbol, $\tilde{\delta}$, to account for the Rayleigh extension of Lagrangian formalism for dissipation.

The inner virtual work related to the elastic deformation is evaluated starting from a plausible expression of an elastic deformation energy based on the abovementioned kinematic variables:

where the material parameters $\text{k}_b$, $\text{k}_s$, $\text{k}_e$, $\text{k}_{m2}$, and $\text{k}_{m4}$ are stiffnesses, while $\alpha_b$, $\alpha_s$, and $\alpha_e$ are coupling coefficients; all these parameters have to be determined by a micro-macro identification and validated with experimental tests. This elastic energy represents the energy stored in a material due to deformation, therefore, it must be inherently positive because it represents the ability of the material to do work when it returns to its original shape. To ensure that the postulated energy $\mathcal{W}^{el}$ is positive definite, then, we can assume that the coefficients satisfy the following inequalities:

The first three contributions of the energy (2.3) represent the classical constitutive behavior of the extensible Timoshenko model. They are representative of the bending, the shear, and the elongation energy that can be stored in the beam. The other contributions newly introduced in (2.3), are linked to the energy associated with the microcracks. In particular, the terms quadratic and quartic in $\gamma$ are the amount of elastic energy that can be stored in the microcracks. The idea behind that is related to the specific morphology of the microcracks. From a geometric perspective, ideally, a microcrack can be visualized as a coin-shaped empty space. The microcrack consists of two faces or lips on opposite sides, which delimit the crack. Each lip of the microcrack exhibits asperities that may interact when the two lips on the opposite side of a crack come into contact (see Figure 1). When this occurs, these asperities can bend and, therefore, store a certain amount of elastic energy. We postulate a material nonlinearity with the quartic term on the ground that many experimental observations show a macroscopic nonlinear behavior in cement-based materials even at the small displacement and deformation regime ^[76]. The last three contributions of Eq (2.3) stand for the coupling energy exchanged between the macroscopic bending deformation and the microscopic asperity deformation within the microcracks, between the macroscopic shear distortion of the beam and the asperity deformation, as well as between the macroscopic elongation of the beam and the asperity deformation. Naturally, we can assume that a bending, a shear, or a change-of-length deformation of the beam could be responsible for the sliding of the microcrack lips. We have to remark, though, that the effect of such a sliding is noticeable only if the opposite faces of the microcracks are pushed against each other. This means that this effect becomes significant only in the case of compression. When bending and shear deformation are activated, only the part of the cross-section interested in compression is affected by such a phenomenon. On the contrary, the tensile part is free from this type of energy exchange. However, since the model is mono-dimensional, we cannot distinguish between the compressed and stretched parts of the cross-section, and thus, we have only to consider whether or not a compressed region exists. Consequently, whenever the beam bends, it produces a compressed region, and, hence, we can imagine that this phenomenon can be activated in this simple 1D context. The virtual work exerted by the inner forces is straightforwardly computed by the first variation of the elastic energy (2.3) as:

and, by performing an integration by parts, we can rearrange the contributions of the internal elastic energy as follows:

In order to model the process of dissipation, we take into account the virtual work carried out by the friction force applied at the microcrack face level, as follows:

The parameters $\zeta_b$ and $\zeta_c$ are related to the friction coefficient for the bending deformation and the compression, respectively. The appearance of the absolute value of the derivative of the angle of rotation $\vert \varphi' \vert$ in the first contribution of Eq (2.7) is due to the fact that when a cross-section undergoes a change in rotation, this can lead to a compression that closes the microcracks, at least in some parts of the cross-section. On the other hand, in the second integral, we consider the term $\vert u' \vert$, which represents a uniform compression within the cross-section that allows the microcracks to be closed. We have to remark that if the term $\vert u' \vert$ is originated by a tensile case, the dissipated energy associated with the second contribution must be erased from the model because there is no interaction between the microcrack asperities. For this reason, we introduce the boolean variable $\varsigma_C$ that assumes the value 1 for compression and 0 for traction. The concept of friction force could be accurately modeled with a Coulomb behavior. However, due to the non-Lipschitz continuity of the forcing term (a sign function), we lose the uniqueness of the solution. To overcome this challenge, a smoother version of the sign function, namely, the '$\tanh$'-term has been developed to mimic the Coulomb behavior while avoiding the issue mentioned above. This approach has proven to be effective in ensuring the accuracy of simulations and models in a variety of contexts. Moreover, it introduces a viscous behavior for small velocity $\dot{\gamma}$ which could be beneficial in some context, without mentioning that with the slope $\eta$, we can control the feature tuning of the mechanical response on the basis of experimental observations. Here, for the sake of simplicity, we consider the same value of $\eta$ for both contributions in Eq (2.7). For a comprehensive understanding of the formulation of the dissipative term, refer to ^[77,78,79].

The virtual work of external forces and torques can be expressed as:

where we admit distributed forces $b_x$ and $b_y$ in the $x$-direction and $y$-direction as well as torques $\mu$ per unit length, point forces $F_x$ and $F_y$ in the $x$-direction and $y$-direction, as well as torques $W$ applied at both ends, compatible with the energy (2.3).

By substituting the expressions (2.6)–(2.8) in the principle (2.2), the bulk equations are deduced as below:

alongside the essential boundary conditions related to the values of $u$, $v$, and $\varphi$ and the natural boundary conditions associated with the axial force, the shear force, and the bending moment:

respectively. We remark that from the deduction of the PVW, no boundary condition is provided for the variable $\gamma$ since, in the energy, this quantity does not appear with the spatial derivative. Naturally, in the actual concrete sample, we do not have access to the microcracks, so we cannot give any boundary conditions on that level.

3.   Numerical simulations

To evaluate the mechanical properties of cement-based materials, three-point flexural tests and compression tests are performed through numerical simulations to assess the predictive properties of the proposed model. The main advantage of these tests is the ease of specimen preparation and testing as well as widely available testing equipment. In the bending tests, a sample (in the shape of a parallelepiped of side $d$ $\times$ $d$ $\times$ $L$, namely, $25$ $\times$ $25$ $\times$ $87.5$ cm) is placed on two supports positioned at a distance of $\ell = 75$ cm from each other, and a force is applied at the center on the top. These setups create a scenario where the material is subjected to both tension and compression, allowing for the measurement of various mechanical properties. The compression tests are instead performed on a cylindrical sample with a diameter $\phi$ of 11.28 cm and a height $L$ of 22 cm. In particular, hereby, we are interested in evaluating the dissipative behavior of the specimen.

The numerical computations are carried out using the commercial software COMSOL Multiphysics^®, which enabled the direct use of Eq (2.2) with the weak form partial differential equation (PDE) package. Since a generalized continuum model of the first gradient in the kinematical descriptors is employed, we opted for the standard Lagrangian quadratic polynomials as the shape functions for the finite element interpolation. It is worth noting that said shape functions are particularly suited for such a formulation involving, at most, only the first derivative of the kinematical descriptors. For further details regarding the numerical implementation of similar problems, we refer the interested reader to ^[80,81] for the isogeometric analysis and ^{[82,83,84,85]} for lumped models.

Specifically, we assumed for the considered material a Young modulus, $Y_c$ = 31.45 GPa, and a Poisson ratio $\nu = 0.15$. Using the isotropic material symmetry the shear modulus is, thus, $G_c = Y_c/[2\, (1+\nu)]$. This information can be used to evaluate the classical stiffnesses for the bending $\text{k}_b = Y_c\, J$, being $J$ the second moment of area of the beam cross-section and for the shear stiffness $\text{k}_s = 5/6\, G_c\, d^2$ for the three-point bending test, while $\text{k}_s = G_c\, \pi\, (\phi/2)^2$ is the expression considered in the cylinder specimen. The stiffness due to the stretching/compression deformation $\text{k}_e = Y_c\, A_c$, where $A_c$ is the area of the cross-section. The slope characterizing the dissipative behavior in Eq (2.7) is set to be $\eta = 225$ s/m. To summarize, all values needed for the simulations are reported in Tables 1 and 2 for the bending and compression tests, respectively. The process of identifying all the necessary parameters that characterize the model can pose a significant challenge due to the complex mechanical responses that must be considered. However, it is pertinent to note that specific techniques commonly used for complex generalized materials, such as digital image correlation (DIC), energy methods, and neural networks, can also be applied in this context. These methods have proven to be effective tools in similar situations, as evidenced by their successful application in previous studies (see, for instance, references ^{[86,87,88,89,90,91,92,93,94,95]}). To analyze the dissipation, an external cyclic force with a sinusoidal trend is applied to the sample, as follows:

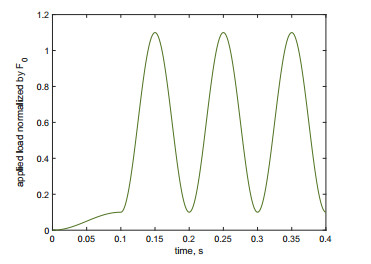
where the amplitude of oscillation is $F_0$, and $F_p$ is a small force set to ensure the adhesion and the closure of the microcracks with a pre-compression originated by the specific test (in the compression test, it is uniform, while in the bending test, it is related only to half part of the cross-section, where actually the dissipation occurs); in the numerical simulations, we set its value to $F_p = 0.1\, F_0$. The time $t_s = 0.1$ s defines the interval of application of the initial ramp of amplitude $F_p$ (see Figure 2). The value of $F_0$ has been meticulously selected to mitigate any potential growth of microcracks. The force magnitude applied during the two tests was appropriately small to ensure reliable and accurate results. Specifically, $F_0 = 100$ kN for the compression tests and $F_0 = 15$ kN for the three point bending tests. The frequency $f_q$ of the sinusoidally varying contribution is set to 10 Hz.

Table 1.  Values of the coefficients used as a reference in the three-point flexural tests for the prism specimen.

$\text{k}_b$	$\text{k}_s$	$\text{k}_e$	$\text{k}_{m2}$	$\text{k}_{m4}$
$1.023\times 10^7$ N m$^2$	$7.121\times 10^8$ N	$1.544\times 10^9$ N	$7.5\times 10^8$ N/m$^2$	$1.0\times 10^8$ N/m$^4$
$\alpha_b$	$\alpha_s$	$\alpha_e$	$\zeta_b$	$\zeta_c$
$2.764\times 10^7$ N	$2.5\times 10^6$ N/m	$1.25\times 10^8$ N/m	$3.68\times 10^8$ N	$2.212\times 10^8$ N/m

---

 | Show Table

DownLoad: CSV

Table 2.  Values of the coefficients used as a reference in the compression tests for the cylindrical specimen.

$\text{k}_b$	$\text{k}_s$	$\text{k}_e$	$\text{k}_{m2}$	$\text{k}_{m4}$
$2.499\times 10^5$ N m$^2$	$1.366\times 10^8$ N	$3.143\times 10^8$ N	$7.5\times 10^8$ N/m$^2$	$1.0\times 10^8$ N/m$^4$
$\alpha_b$	$\alpha_s$	$\alpha_e$	$\zeta_b$	$\zeta_c$
$9.48\times 10^6$ N	$2.5\times 10^6$ N/m	$1.25\times 10^8$ N/m	$3.68\times 10^6$ N	$2.212\times 10^8$ N/m

---

 | Show Table

DownLoad: CSV

Figure 2.  Normalized force applied to the samples for the cyclic tests.

DownLoad: Full-Size Img PowerPoint

4.   Results and Discussion

The mechanical responses obtained performing finite-element-method-based numerical simulations are collected and discussed in this section. To begin, we consider two tests, the three-point and the compression one, with assumed reference parameters (see Tables 1 and 2) that allow us to mimic with reasonable accuracy the known experimental behavior of a building beam made of plain concrete. In addition to these reference cases, here we explore the influence of some crucial parameters, especially concerning the dissipative behavior of the material.

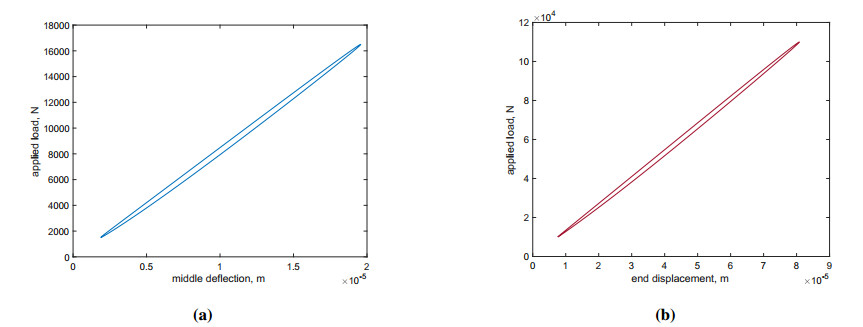
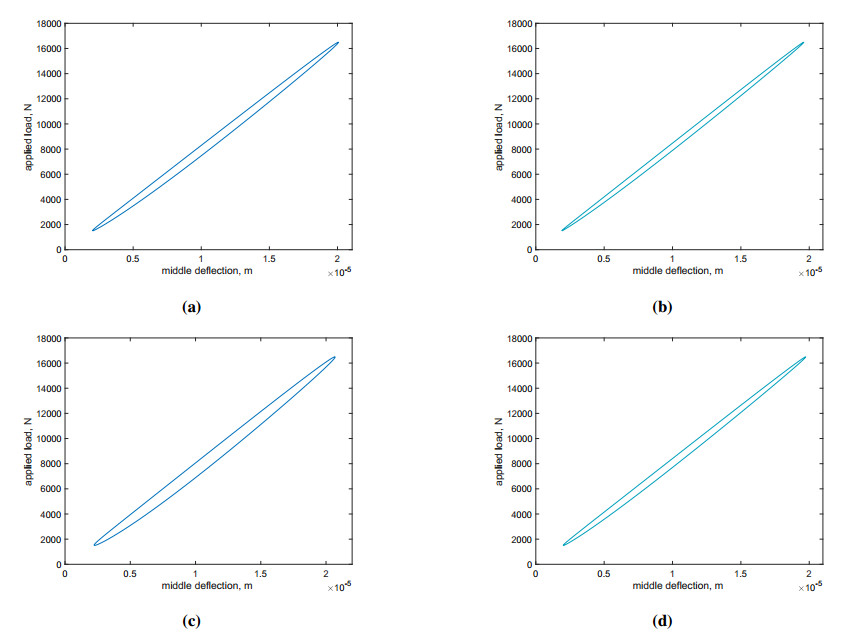
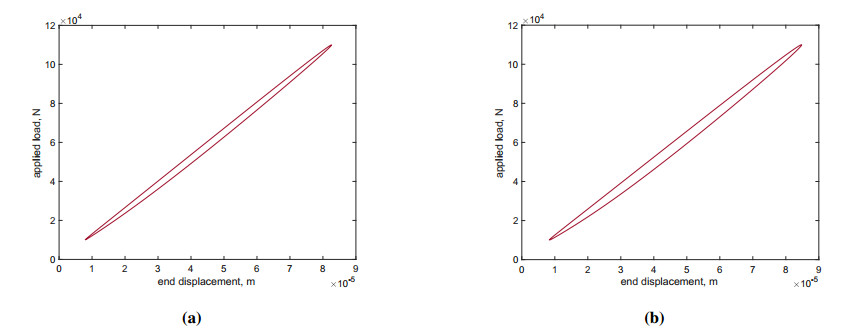
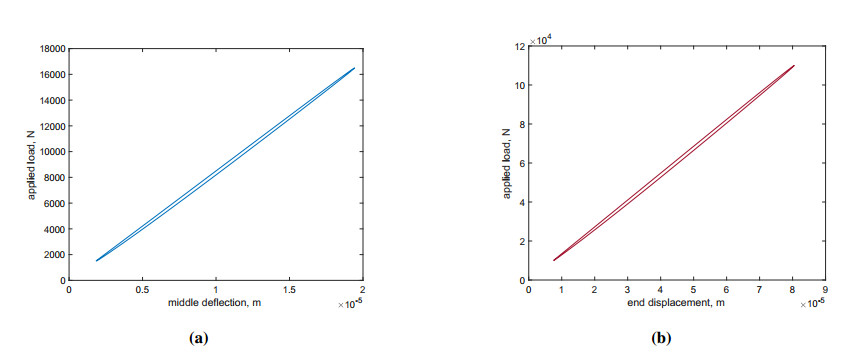
Figure 3 shows a cycle of loading and unloading for the two tests, namely, the three-point bending test and the compression test. Therefore, we can compare the two cases. The pictures display the external load versus the displacement of the loading point. The cycle area has been computed using a numerical approximated integral exploiting the trapezoidal rule. For the three-point bending test, we get a dissipated energy of 0.0074 J, and for the compression test, we evaluate a dissipated energy of 0.1699 J.

Figure 3.  Dissipative cycles for the three-point flexural test (a), and the compression test (b).

DownLoad: Full-Size Img PowerPoint

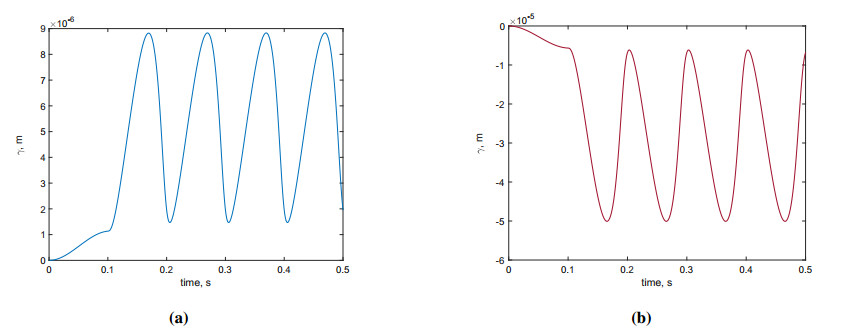
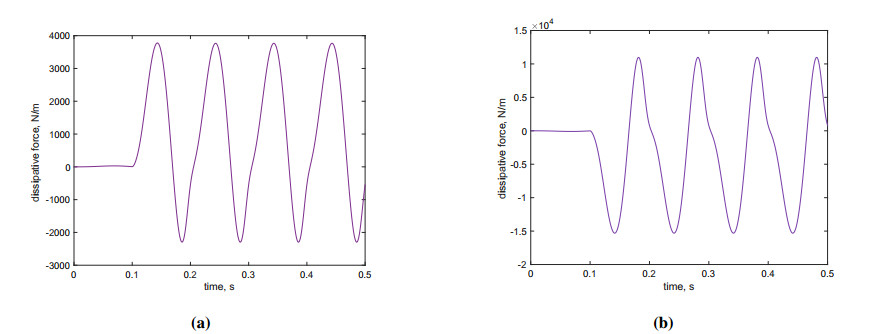
In order to provide a comprehensive understanding of the analyzed phenomenon, Figures 4 and 5 depict the time histories of the relative slip variable $\gamma$ and the friction forces, $\zeta_b \vert \varphi' \vert \tanh(\eta \dot{\gamma})$ and $\zeta_c \, \varsigma_C\vert u' \vert \tanh(\eta \dot{\gamma})$, at the points of maximum load, respectively. These observations were made in the center of the beam during the three-point bending test and at the point where the load was applied in the compression test. It is worth noting that the behavior of these variables related to the mechanics of the microcracks is nonlinear; thus, we might expect nonlinear behavior even at the microscopic level.

Figure 4.  Time history of the relative sliding, $\gamma$ for the three-point flexural test at the middle point (a), and for the compression test at the loading point (b).

DownLoad: Full-Size Img PowerPoint

Figure 5.  Time history of the friction force, $\zeta_b \vert \varphi' \vert \tanh(\eta \dot{\gamma})$, for the three-point flexural test at the middle point (a), and $\zeta_c \, \varsigma_C\vert u' \vert \tanh(\eta \dot{\gamma})$ for the compression test at the loading point (b).

DownLoad: Full-Size Img PowerPoint

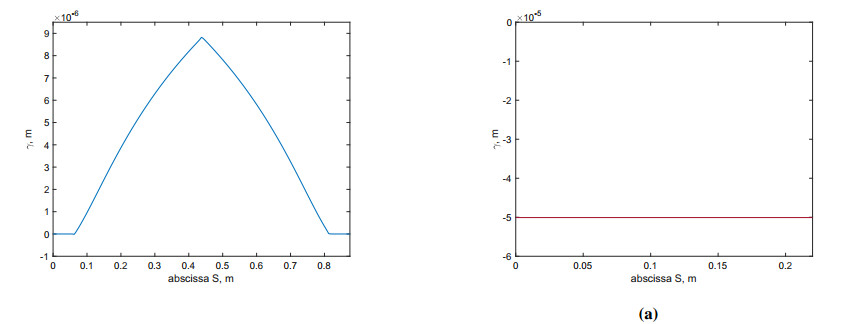
The relative sliding at the level of microcracks, $\gamma$ are depicted in Figure 6 at the time instant of about 0.15 s corresponding to a maximum in the load amplitude. For the three-point flexural test, the new variable $\gamma$ has significant values only in the portion of the beam where there is a flexural deformation, which, in turn, is directly related to compression in half of the cross-section, where the microcracks close and, due to some distortions in the shape of the beam, we can experience some sliding at that level of observation. For the compression test, instead, we observe that $\gamma$ is constant since the compression is as such.

Figure 6.  The relative sliding at the level of microcracks $\gamma$ at one maximum value of the force at about 0.15 s, for the three-point flexural test (a) and for the compression test (b).

DownLoad: Full-Size Img PowerPoint

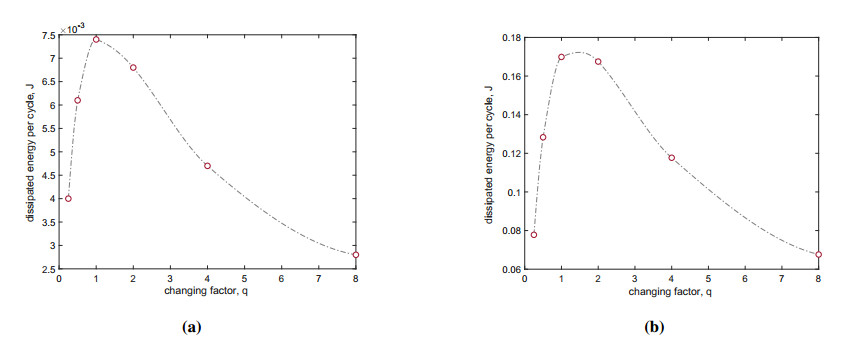
In order to obtain a more comprehensive understanding of the model outcomes, a parametric study is conducted. Specifically, we vary the amplitude of the friction force, denoted by $\zeta_b$ and $\zeta_c$, by employing a scale factor, $q$. This approach allows us to investigate the effects of altering the frictional force on the model performance and overall behavior. Through this study, we are able to draw meaningful conclusions that can inform future research and improve our understanding of the mechanisms underlying the model. Figure 7 shows the results of such a parametric study. In fact, for different multiplying factors $q$, specifically $\{0.25, 0.5, 2, 4, 8\}$, we compute the loading-unloading cycles for the two categories of tests and evaluate the area of the cycles, i.e., the lost energy of the system. We get the dissipated energy $\{0.0040, 0.0061, 0.0074, 0.0068, 0.0047, 0.0028\}$ J for the three-point bending tests and larger values $\{0.0778, 0.1283, 0.1699, 0.1675, 0.1177, 0.0676\}$ J for the compression tests. These results are summarized in a plot in Figure 7. The dotted lines are regressed curves made from each series of six simulations made for the considered tests. The simulations of both tests show the same trend, highlighting the presence of a maximum of dissipated energy. This behavior is typical of phenomena with two competitive aspects. In this case, we have that with low friction forces, the energy dissipated is little; in this range, if the friction coefficient is increased, more energy is dissipated. On the other hand, when the friction force is too large, the relative motion of the microcrack faces becomes increasingly smaller as the friction force increases, and, therefore, the dissipated energy inevitably decreases. Consequently, it is possible to determine a friction coefficient such as to have the maximum dissipated energy in this framework. From the perspective of engineering the cementitious material, this aspect is crucial since acting only on increasing the friction coefficient within the microcracks can even be counterproductive if the friction effect is exaggerated.

Figure 7.  Influence of the parameters $\zeta_b$ and $\zeta_c$ on the dissipative cycles for the three-point flexural test (a), and the compression test (b), respectively.

DownLoad: Full-Size Img PowerPoint

Turning our focus to the coupling parameters, we analyze the effect of the coefficient $\alpha_b$ increasing its value by 20 and 40% with respect to the reference value. Figure 8 presents the dissipative cycles obtained via simulations conducted for the previously considered tests. The plots depicted in the figure show that increasing the coupling $\alpha_b$ results in a more considerable dissipation. For the three-point flexural test, we evaluate a dissipated energy of 0.0114 and 0.0167 J, respectively, when the coupling increases by 20 and 40%. The same analysis has been conducted for the coupling coefficient $\alpha_s$. However, since this coefficient is less significant in the overall behavior, it is observed that with the same changes with respect to the reference case, the dissipation is almost the same. Therefore, the shear coupling has been increased by 100 and 200%, in the case of the three-point flexural test, resulting in a dissipation of energy of 0.0078 and 0.0097 J, respectively (see Figure 8). Overall, the general trend is the same but less effective.

Figure 8.  Influence of the parameter $\alpha_b$ on the dissipative cycles for the three-point flexural test with an amplifier factor of 1.2 (a) and 1.4 (c), and of $\alpha_s$ with 2 amplification (b), and 4 amplification (d).

DownLoad: Full-Size Img PowerPoint

Similarly, in the compression test, we obtain 0.2554 J and 0.36589 J of dissipated energy for a 20 and 40% increase in the the coupling $\alpha_e$, respectively (see Figure 9).

Figure 9.  Influence of the parameter $\alpha_e$ on the dissipative cycles for the compressive test with an amplifier factor of 1.2 (a) and 1.4 (b).

DownLoad: Full-Size Img PowerPoint

Therefore, in designing a building material to be earthquake-proof, i.e., capable of dissipating as much energy as possible, it seems very promising to concentrate our attention on those additives that increase these coupling coefficients without jeopardizing the mechanical strength and pursuing the optimal friction coefficient that provides the maximum level of dissipation simultaneously.

Finally, regarding the nonlinear stiffness $\text{k}_{m4}$, we carry out simulations to explore the influence of such a parameter. Figure 10 shows the dissipative cycles obtained by setting high values of $\text{k}_{m4}$. The dissipated energy obtained is 0.0043 J for the three-point flexural test with $\text{k}_{m4} = 1\times 10^{19}$ N/m$^4$. Meanwhile, for the compression test, 0.1210 J of energy is dissipated in the loading-unloading cycle with $\text{k}_{m4} = 1\times 10^{17}$ N/m$^4$. Thus, a greater stiffening of the asperities leads to a decrease in the energy dissipated.

Figure 10.  Influence of the parameter $\text{k}_{m4}$ on the dissipative cycles for the three-point flexural test (a), and the compression test (b).

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

In this paper, we propose a Timoshenko beam model augmented with a microcrack sliding descriptor that provides a promising framework for describing the mechanical behavior of cement-based materials. It is a very effective and efficient modeling tool that provides a beneficial computational advantage in evaluating both the strength of the material and also its dissipative behavior. Indeed, by introducing the variable $\gamma$ to represent the relative sliding of microcracks within the material, the model captures additional dissipative mechanisms that contribute to energy loss during loading-unloading cycles.

Finite element method-based numerical simulations conducted using COMSOL Multiphysics demonstrated the effectiveness of the model in replicating experimental tests. The simulations revealed the influence of various parameters on the mechanical response of the material, including the dissipated energy and the behavior of kinematic descriptors such as longitudinal and transverse displacement, cross-section orientation, and relative sliding at microcracks.

A parametric study investigating the effects of altering the frictional force parameters provided insights into the relationship between frictional forces and energy dissipation. The study revealed a nonlinear relationship between these parameters and dissipated energy, with an optimal frictional force value maximizing energy dissipation.

The model predictions align well with known experimental behavior observed in flexural and compression tests of cement-based materials. This validation underscores the model ability to capture the complex mechanical response of such materials under loading and unloading conditions.

The insights gained from this study can inform the design and optimization of cement-based structures, particularly in applications where energy dissipation and mechanical resistance are critical factors, for example, in the case of earthquakes. By accurately modeling the dissipation mechanisms within the material, engineers can develop more resilient and durable structures.

Further research could focus on refining the model by incorporating additional complexities, such as heterogeneities in material properties and multi-axial loading conditions. Additionally, experimental validation of the model predictions using a wider range of test configurations and material compositions would enhance its applicability and robustness.

Overall, the study underscores the importance of considering microstructural phenomena, such as microcrack sliding, in developing accurate models for predicting the mechanical behavior of cement-based materials. By integrating such phenomena into computational models, researchers can advance our understanding of material behavior and contribute to the development of more resilient and sustainable infrastructure solutions.

Author contributions

G.A., C.C., L.M.T. and E.B.: Conceptualization, Idealization, Methodology, Formal Analysis, Numerical Simulation, Writing. E.B.: Supervision, Revising.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflict of interest.