Effects of Bambara groundnut and Butternut blending on functional and sensory properties of sorghum flour porridge

1.   Introduction

With the development and use of network and wireless communications technologies, networked control systems (NCS) have gradually attracted attention for applications such as power networks, remote surgery, telephone networks, industrial and manufacturing systems, and new energy vehicles. It has some advantages such as convenience and efficiency in comparison to the conventional systems. In wireless network systems, signals can be exchanged through digital communication networks, which also presents new challenges for control engineers such as data quantization, event-driven sampling, etc. ^[1,2,3,4].

In some practical applications, such as unmanned submarines, UAVs, etc., limited resources are required for NCS due to the limited power supply of the device itself. The traditional control method is to use time-triggered control, where the controller transmits control signals to the system in a periodic manner, and the system transmits the state signals to the controller in a periodic manner. This leads to waste of resources and reduces the running time of the device. Therefore, the ET mechanism has been introduced, which helps reduce the burden on the network, saves resources and improves the efficiency of device resource utilization compared with the traditional periodic transmission. The fundamental principle behind the ET control approach is that the related sensors and controllers are only updated when an ET error exceeds a predetermined threshold or condition, also referred to as an ET rule ^{[5,6,7,8,9,10,11,12,13]}.

In NCS, a shared network is frequently required for data exchange on nodes distributed throughout space, however the network's constrained transmission capacity could result in network congestion phenomenon. Consequently, quantization is required, and a quantizer is a device that maps a transmitted signal to a subset set and takes segmented constants. By quantifying the triggered state of the system instead of the system state itself, the computational load on the system transmission is significantly reduced ^[14,15].

The presence of unmatched uncertainty may affect the stability of linear system when the control signal transmissions are made over a network channel. SMC is an effective control method in robust nonlinear controllers ^[16,17,18]. It has a wide range of applications in theory and practical life owing to its advantages of being insensitive to internal uncertainties and extrinsic disturbances, meeting the matched condition, and being easy to operate. The classical SMC design usually consists of two stages: the reaching stage and the sliding stage. In the reaching stage, the system state trajectory moves toward the SM manifold, while in the sliding stage, the system state trajectory slides along the SM manifold to the origin. When dealing with unmatched uncertainties, the SMC can be used with classical control design methods such as LMI method, adaptive method, etc., or the ISMC can be applied. The ISMC approach is to design a high-frequency switching gain to force the system state to reach the ISM manifold, and in the presence of unmatched uncertainty, the integral action of the ISM manifold continues to drive the system state to the equilibrium point ^[19].

There has been a lot of literature on ET control combined with SMC. In ^[20,21], the ET linear SMC is discussed and the practical SM band is introduced; Using a dynamic time-varying trigger threshold, ET ISMC of linear systems with perturbations is considered in ^[22]; And in ^[23], the ET ISMC for T-S fuzzy systems in the presence of uncertainty is considered, and novel triggering conditions are proposed. In ^[24], a class of networked linear systems is considered and a control input-based ET SMC control is proposed, where the ET rule is dependent on the changes of the input values. A unified class of ET SMC framework is proposed in ^[25], which can achieve finite-time reachability at the SM manifold and can enable finite-time stabilization of the system state. In ^[26], the delayed memristive neural network synchronization problem is investigated, and continuous-time sampling ET SMC is proposed, and based on this, periodic-time sampling ET SMC is proposed.

The quantization control can also be combined with the SMC. In ^[27], a class of linear uncertain systems with quantized feedback stability problem is studied by SMC. The influence of matched and unmatched uncertainties can be practically eliminated by the quantization parameter adjustment strategies. In ^[28], the problem of distributed quantization of SMC in complex networks is investigated, and the ISM surface is quantized using an adaptive filter. In ^[29], the problem of synchronization of discrete-time recurrent neural networks with time-varying delay is investigated, and the stability analysis is carried out using uniform quantizer and logarithmic quantizer, respectively.

In the general, the ET SMC and the quantized SMC are two different types of robust control methods. However, in recent years, the combination of the ET control, the quantized control, and the SMC has gradually gained attention. In ^[30], an ET approach was used to study the robust sedimentation problem of quantized feedback SMC for a class of uncertain linear systems, quantizing the ET states rather than the states themselves, using linear SM manifold. In ^[21], a linear SM manifold is also used, but the system states are first quantized and then an ET mechanism is added to the quantized states. In ^[31], the quantization-based ET SM tracking control problem for mechanical systems is investigated, and the ET rule uses the disparity between the quantized incremental triggering state and the quantized incremental state. Using a dynamic uniform quantizer, the ET SMC problem for a type of continuous-time system with actuator faults and output feedback signal quantization is investigated in ^[32]. In ^[33], the problem of robust sedimentation of perturbed linear time-invariant systems based on ET SMC is studied. A logarithmic quantizer is used to quantify the state and the triggering state.

The aforementioned literature considers, only under matched uncertainty, the combination of linear SMC, ET mechanism, and quantization mechanism, and this paper considers, in the existence of unmatched uncertainty, the combination of ET control, ISMC, and quantization control. The main challenges faced are as follows. 1) How to quantify the ET ISM manifold when the integral term is challenging to measure; 2) In the existence of unmatched uncertainty, how the system state guarantee a finite time to reach the practical SM band.

Based on ^[34], a matched and unmatched uncertain linear time-invariant system is considered, and the main objective is to design quantization-based ET ISMC to handle matched and unmatched uncertainties and perturbations. The main contributions of this paper are summarized as follows:

1) In this paper, the combination of quantization control, ET control, and ISMC is simultaneously considered. The quantized ET ISMC algorithm based on the convergence law subject to matched and mismatched uncertainties and perturbations is proposed to achieve finite time arrival of the linear system state at the SM surface and to realize asymptotic stability of the linear system state.

2) This paper proposes a quantization method for the ISM surface. The system state and the integral term are quantized separately for the ISM surface, and the virtual variable is introduced to replace the integral term, and two static uniform quantizers are used to quantize the system state and the virtual variable separately.

3) A positive lower bound on the inter-event time is derived to avoid Zeno behavior of the system.

The rest of the paper is organized as follows: Section 2 contains the preliminary and problem statements, including the construction of the ISM surface and the signal quantization approaches. In Section 3, the quantized ET ISMC is presented. And in Section 4, it is proved that the finite time to reach the ISM surface and that the system will not occur Zeno phenomenon during the operation of the system. Thus, simulation results of a numerical example and a mass-spring damping system are given in Section 5. In Section 6, this paper is concluded.

Notations: The sets of real numbers and integers are indicated by $\mathbb{R}$ and $\mathbb{Z}$ respectively. The set of positive real numbers and the set of positive integers are $\mathbb{R}_{ > 0}$ and $\mathbb{Z}_{ > 0}$. $\mathbb{R}^{n}$ denotes the $n$-dimensional Euclidean space in the real numbers. $\parallel\cdot\parallel$ denotes the matrix norm, and $\mid\cdot\mid$ denotes the absolute value.

2.   System description and problem formulation

Consider an uncertain linear NCS of the following form

where $\xi(t)\in\mathbb{R}^n$ is the system state, $u(t)\in\mathbb{R}$ indicates the control input, and $\xi(0) = \xi_{0}$ is assumed to be the initial value of the state $\xi(t)$. Thus, the matrice $A\in\mathbb{R}^{n\times n}$ is the system matrix and $b\in\mathbb{R}^{n}$ represents the input matrix. The $f_m(t, \xi)$ denotes the matched perturbation caused by external disturbance, and $p_{un}(t, \xi)$ denotes unmatched uncertainties. The modeling error $\Delta b$ is unknown and has the same dimension as $b$. Unmatched uncertainties are caused by modeling errors, inaccurate measurements, etc. Further, we can obtain the rewritten form of system (2.1) as follows

where $f_{u}(t, \xi) = \Delta b[u(t)+f_m(t, \xi)]+p_{un}(t, \xi)$. Suppose that the nominal system $\dot{\xi}(t) = A\xi(t)+bu(t)$ is controllable.

In this paper, the following assumption is required in the rest of the paper.

Assumption 1. Suppose that the matching and mismatching uncertainty $f_{m}(t, \xi)$ and $f_{u}(t, \xi)$ have known upper bounds, i.e., $\sup_{t\geq 0}|f_{m}(t, \xi)| \le F_{m}$, and $\sup_{t\geq 0}\Vert f_{u}(t, \xi)\Vert \le F_{u}$, where $F_{m}$ and $F_{u}$ are known positive constants.

Remark. 1 The above assumption are necessary for the proof of finite-time reachability of the SM surface and minimum inter-event time.

Here related lemma and definition are introduced.

Lemma 1. ^[35]Consider linear non-autonomous system $\dot{\xi} = f(t, \xi)$, $f(0) = 0$. Assume that there exists a continuous positive definite function $V(x):\mathbb{R}^{n} \to \mathbb{R}$ satisfying the following equation:

where $\eta_1 > 0$, $\eta_2 > 0$, and $\kappa\in(0, 1)$. Then the system is finite time stable. Furthermore, the convergence time satisfies

In order to construct the ISM surface represented by $\Theta$, the concepts of ideal and practical SM are presented as in ^[36].

Definition 1. (Ideal SM) There exists $t_1 \in [t_0, \infty)$ such that the SM trajectory is $\Theta = 0$ in the case of $t\geq t_1$, then it is called the ideal SM.

Definition 2. (Practical SM) There exists $t_1 \in [t_0, \infty)$ such that the SM trajectory stays in the vicinity of the SM surface with the bound given by $\varepsilon$ in the case of $t \geq t_1$, then it is called the practical SM. Here, $\varepsilon$ is referred to as practical SM band.

At the beginning, the ISM manifold is modeled as

where $G$ represents the projection matrix, and $G$ is usually taken to be $b^{T}$ in a way that makes $\det(Gb) \ne 0$. The ISM surface has no reaching stage, the system state is on the ISM surface at the beginning, which greatly reduces the chattering phenomenon.

In (2.2), the matched and unmatched uncertainties are assumed to be $0$, and the control input of the nominal system is $u_0$, the equation of the state trajectory of the ideal system is

Next, the nominal control $u_0(t)$ is designed so that the nominal system (2.6) is stable and SM motion occurs. The control law is now designed as

where $u_1(t)$ is the discontinuous control employed to counteract the uncertainty impacting the system. The control input $u_0(t)$ is intended to have state feedback controller in the following forms:

where $K\in\mathbb{R}^{1\times n}$ is the state feedback gain vector. Further, we choose the value of $K$ such that $(A-bK)$ is Hurwitz.

Taking the derivative of Eq (2.5) along system (2.2) and using (2.8), the result thus derive as

Replacing (2.2) into (2.9), and the result derived is

In ^[37], Gao has presented the constant plus proportional rate reaching law for continuous time systems. By considering the matching disturbances, the reaching law is reformulated as

where $Q_1$ and $Q$ will be mentioned below, equating relations (2.9) and (2.11) to solve for $u(t)$, then the ISMC result is obtained as

The resulting control law (2.12) guarantees a finite time for the system (2.2) to reach the SM surface, and it forces the SM motion.

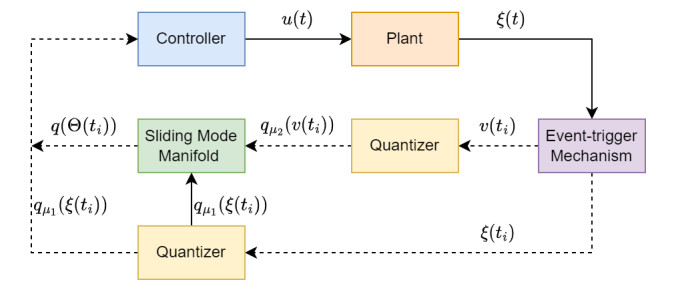
In this paper, SMC is investigated by ET control and quantization control, and the corresponding system block diagram is presented in Figure 1.

As can be seen from Figure 1, $\xi(t_i)$ and $v(t_i)$ are generated by the ET mechanism and transmitted to different quantizers through the network channels, respectively, and the resulting $q_{\mu_1}(\xi(t_i))$ and $q_{\mu_2}(v(t_i))$ are used to generate the quantized SM surface.

A quantizer is a piecewise constant function $q:\mathbb{R}^{r} \to \mathbb{D}$, where $\mathbb{D}$ is a finite subset of the vector space $\mathbb{R}^{r}$. Assuming that $z$ is the variable to be quantized, the quantizer can be seen as a device that converts a real-valued signal into a segmented constant-valued signal. Mathematically, it can be framed as a function $\text{round}(\cdot)$ that takes the nearest integer, i.e.,

where the quantizer parameter $\mu > 0$ is defined as the quantization sensitivity and $q_\mu(\cdot)$ is a uniform quantizer with its level $\mu$. Denote the quantization error as

Therefore, it can be obtained as

where $\Delta = \frac{\sqrt{p}}{2}$, $p$ is the dimensions of the vector $z$.

Defining $T_i$ as the inter-event time, and $T_i = t_{i+1}-t_i$. Denoting the ET error as

Setting the ET threshold, and furthermore, considering the positive constants $\alpha \in (0, \infty)$ and $\sigma \in (0, 1]$, it follows that

which is valid for all $t > 0$. Let the next ET moment be $t_{i+1}$. Therefore, the next ET moment $t_{i+1}$ is

In a NCS, the transmission signal uses an ET protocol in which the ET control law is only updated at the moment of sampling. In the controller, a zero-order keeper (ZOH) is employed in the ET controller to maintain the feedback information between any two triggering moments. Then, it is represented by

for $t\in[t_i, t_{i+1})$ and $i\in Z_{\geq 0}$, where $t_i, t_{i+1}\in T$, $T$ is the set of triggering moments, $\xi(t_i)$ is the value of the state $\xi(t)$ at the triggering moment. The value of the SM surface $\Theta(t)$ at the triggering moment is

Then, consider quantization of the triggering state $\xi(t_i)$

where $q_{\mu_1}(\xi(t_i))$ is the quantized value of the triggering state $\xi(t_i)$. Then the corresponding quantization error is

where $p_1$ is the dimensions of the vector ${\xi(t_i)}$, $\Delta_1 = \frac{\sqrt{p_1}}{2}$, $\mu_1 > 0$ is the quantization sensitivity.

To quantize the SM surface, the virtual variable $v(t)$ is introduced as

Then the value of $v(t_i)$ at the triggering instant is

Consider quantization of the virtual variable $v(t_i)$ is

where $q_{\mu_2}(v(t_i))$is the quantized value of the triggering state $v(t_i)$.

Therefore, the corresponding quantization error is

where $p_2$ is the dimensions of the vector $v(t_i)$, $\Delta_2 = \frac{\sqrt{p_2}}{2}$, $\mu_2 > 0$ is the quantization sensitivity. The quantized triggering SM surface $q(\Theta(t_i))$ is

3.   Design of quantized event-triggered integral sliding mode control

In the ET control law (2.19), the quantized ET control law (3.1) can be obtained by replacing the ET state ${\xi(t_i)}$ with the quantized ET state ${q_{\mu_1}(\xi(t_i))}$. Therefore, for the quantized ET implementation of the ISM, the control law (2.12) can be written as

for all $t\in[t_i, t_{i+1})$, and $i\in Z_{\geq 0}$.

The ET rule is designed so that the quantized ET control law (3.1) is updated at every $t_i$ only when the ET error exceeds some pre-defined threshold value. $q_{\mu_1}(\xi(t_i))$ is the ET state $\xi(t_i)$ obtained after quantization.

Remark. 2 During the sliding motion $\Theta(t) = \dot{\Theta}(t) = 0$, based on the Eq (2.9), it can be derived that the system state $\xi(t)$ is bounded and can be represented as $\Vert \xi(t)\Vert = \Vert\exp((A-bK)t)\xi_0(t) \Vert$. Further, we can choose $K$ such that $A-bK$ becomes $Hurwitz$ matrix, so that the norm of the system state $\xi(t)$ is bounded, i.e., $\Vert\xi(t)\Vert\le\delta\exp(-\beta t)$, where $\delta$ and $\beta$ are positive constants. If the last event of state $\xi(t)$ happened at the moment $t_i$, then

i.e.

From (2.20), (2.22), (2.26), (2.27), it is obtained that

we choose

then we have

Remark. 3 While the system state trajectory reaches the SM surface, if the control law is not updated, the system state trajectory will cross the SM surface and move away from it. The ET error starts to increase, and when the ET error exceeds the upper threshold, the signal is updated to redirect the system trajectory towards the SM surface. This process keeps going until the system state trajectory reaches its origin. From (2.16), it is known that

The sliding trajectory's greatest deviation is

The quantization error of SM function $\Theta(t)$ can be obtained by (3.4) and (3.8)

It can be derived that

The range of $\text{sgn}(\Theta(t))\neq \text{sgn}(q(\Theta(t_i)))$ is

4.   Main results

Theorem 1. Considering the system (2.2) in addition to the ISM manifold (2.5). Under the quantized ET control law (3.1), the system state trajectory can reach the SM surface in finite time even in the presence of unmatched perturbations, if there exist $Q$ satisfying

where $\eta$ is a positive scalar, and the practical SM is implemented in the vicinity of $\Theta(t) = 0$ within a band

Proof. Outside of the region $\Omega$, then it will satisfy $\text{sgn}(\Theta(t)) = \text{sgn}(q(\Theta(t_i)))$. Choose the Lyapunov candidate as $V = \frac{1}{2}\Theta^2$. Differentiating $V$ along the system (2.2) and using the derivative of the ISM surface in (2.9), then, we have

Substituting the designed control law in (3.1), it can be concluded that

From (2.16), we can obtain

Take (2.22), (2.17), and (3.6) into (4.5), one can further get that

Take the norm and sort it out,

It yields from Assumption 1 that

Substituting (4.1) into (4.8), one gets

Let $\eta_1 = \sqrt{2}\eta$ and $\eta_2 = 2Q_1$, then we obtain

Combining with Lemma 1, we have

When the system state trajectory has reached the SM manifold, the system state is asymptotically stable within the practical SM band. Thus, this proof of Theorem 1 is completed. □

Remark. 4 From (3.8), set $\Theta(t_i) = 0$, and then, the maximum SM band can be derived. The maximum band is given by (4.2).

Next, to guarantee that the system is Zeno-free, it must be demonstrated that the lower bound on the inter-event time must be greater than a positive constant. The following proof shows that there exists the lower bound on the inter-event time.

Theorem 2. Considering the system (2.2) in addition to the quantized ET ISMC in (3.1), if the inter-event execution time is generated from (2.18), the lower bound of the inter-event time indicates that

where

$k_1 = (|Gb|\Vert K\Vert+Q_1\Vert G\Vert)\Vert A\Vert+(Q_1\Vert GA\Vert+Q_1|Gb|\Vert K\Vert)$,

$k_2 = (|Gb|\Vert K\Vert+Q_1\Vert G\Vert)\Vert b\Vert \times \Vert -(Gb)^{-1}(GbKq_{\mu_1}(\xi(t_i))+Q_1q(\Theta(t_i))+Q\mathit{\text{sgn}}(q(\Theta(t_i))))\Vert$,

$k_3 = (|Gb|\Vert K\Vert+Q_1\Vert G\Vert)\Vert b\Vert F_m$,

$k_4 = (|Gb|\Vert K\Vert+Q_1\Vert G\Vert)F_u$.

Proof. Let $T_i$ be the inter-event time, i.e. the time required for the event error to grow from zero to $\sigma\alpha$. Define the set $\Gamma = (t:\Vert e(t)\Vert = 0)$ where $t \in [t_i, t_{i+1})$. From (2.2) and (2.9), we have

It yields from Assumption 1 that

Using the designed control law in (3.1) and (3.3), thus we obtain

Noticing that $e(t_i) = 0$, one can get that

Thus it yields that

The next event will occur only when the norm of the error exceeds a predefined threshold. Therefore, $T_i$ is expressed by (4.12), and that is the conclusion of the demonstration of the theorem. □

5.   Simulation examples

This section shows the effectiveness of the control strategy in two instances. The first example is a numerical model, and the second example employs a mass-spring damper system.

Example 1

This numerical example is to demonstrate the proposed perturbed continuous-time linear system under the quantized ET ISMC, and the system parameters are described as follows

The initial state of the linear system is designed to be $\xi_0 = [−1, 1, 1]^{T}$, the projection matrix $G$ is set as $G = b^{T} = [0, −3, 5]$. It was calculated that $K = [165.26, 52.9310, 82.3188]$, other design parameters are designed to be $\sigma = 0.4$, $\alpha = 50$, and the reaching gain $Q_1 = 4$. By calculation, the switching gain $Q$ is given as $Q = 291$. The quantization sensitivity $\mu_1$ and $\mu_2$ are both taken as 0.05.

Simulation results of the perturbed continuous-time linear system (2.2) with the designed quantized ET control law in (3.1) are presented in Figures 2–6. It can be noticed from Figures 2 and 4 that the system states can be well steered into the ISM surface in (2.5), then they finally slides to the origin. Figure 3 represents the proposed variation of the quantized ET ISMC. The evolution of $\Vert e(t) \Vert$ under the quantized ET ISMC is presented in Figure 5. Further, it shows from Figure 6 that no Zeno execution of ET condition occurs during the whole system implementation.

For resource-constrained systems, the fewer number of control signals updates means the system has a longer lifespan and a more efficient utilization of resources. Based on this, this paper proposes a performance index for comparing the number of control signals updates. In Table 1, we present the comparison between the number of control updates obtained by the time-triggered control scheme, the ET control scheme and the quantized ET control scheme. Thus, as can be observed in Table 1, the number of control updates in the quantized ET control method is fewer than in the ET control method and much fewer than in the time-triggered control method, which has resulted in reduced control calculations and minimum use of resources without affecting the stability of the system.

Example 2

The second example considers a mass-spring damper system with the system configuration shown in Figure 7. $u$ represents input control, the states $\xi_1$ and $\xi_2$ represent the position and speed of the car, respectively. $M$ represents the mass of the cart, and $k$ denotes the spring constant. The damping coefficient associated with the system is set as $h$. The perturbation term is chosen as $f$. The disturbance may be caused by the frictional forces acting on the mass-spring damper system. In practice, the spring constant $k$ and the damping coefficient $h$ shift their nominal values with time, and the actual velocity of the system is usually hard to acquire; therefore, system uncertainty $D$ needs to be taken into account when performing system modeling. Let $M = 1kg$, $k = 0.333N/m$, $h = 1.1Ns/m$, $f = 0.5sin(10t)$, $D = 0.1sin(10t)$.

The system equation of state is

The initial state of the system is designed to be $\xi_0 = [2.2, -1.7]^{T}$. Other parameters are designed as $G = b^{T} = [0, 1]$, $k = [25.1467, 9.0]$, $\sigma = 0.4$, $\alpha = 5$. $Q_1 = 4$, $F_m = 0.5$, $F_u = 0.1$, $Q = 3.5$. The quantization sensitivity $\mu_1$ and $\mu_2$ are both taken as 0.05.

Simulation results of the mass-spring damper system (5.1) with the designed quantized ET control law in (3.1) are presented in Figures 8–12. From Figure 8 and Figure 10, it can be drawn that the system state trajectory reaches the SM manifold in a finite time and is confined within the SM band. Figure 9 represents the proposed variation of the quantized ET ISMC. The evolution of $\Vert e(t) \Vert$ under the quantized ET ISMC is presented in Figure 11. In addition, it is observed from Figure 12 that no Zeno phenomenon occurs in the system during the operation of the system. Taking the performance index of Table 1 for comparison, the number of control updates for all strategies, such as time-triggered control strategy, ET control strategy, and quantized ET control strategy, are calculated and listed in Table 2. As can be seen from Table 2, the ET control strategy with quantized state measurements has much lesser control updates than the ET control strategy and lesser than the time-triggered control strategy in terms of the minimum use of control computations and resources.

6.   Conclusions

The stability problem of networked linear systems with matched uncertainty and unmatched uncertainty under quantized ET ISMC and the Zeno phenomenon problem are studied in this paper. To begin with, the priori knowledge such as finite-time reachability and actual SM band is introduced. The ISM surface is constructed, and the convergence law is used to derive the control input. On the basis of this, the system introduces the ET mechanism, and under the ET mechanism, the system state and SM surface are quantized respectively, which leads to quantized ET ISMC. Then, it is demonstrated that the system trajectory can reach the SM surface in a finite time, and no Zeno phenomenon occurs during the system operation. Finally, a numerical example and an example of a mass-spring damper are given to illustrate the effectiveness of the proposed quantized ET ISMC. In future work, we will continue to study the combination of quantized control, ET control, and SMC, and explore their applications under other conditions, such as nonlinear systems, fault-tolerant control, fuzzy systems, etc.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Shandong Provincial Natural Science Foundation ZR2022MF324 and ZR2021MF003, and the Shandong University of Science and Technology Research Fund 2018 TDJH101.

Conflict of interest

We declare that we have no conflict of interest.