A fractal hypernetwork model with good controllability

1.   Introduction

Since the term "fractal" was proposed by Mandelbrot ^[1], many researchers have been observed the fractal features in natural systems, such as crystals, plants, chemical molecules, rivers, and more ^[1]. Researchers model the real systems with fractal characteristics as fractal networks based on the graph theory ^{[2,3,4,5,6,7,8,9]}. And they have been found many interesting structural properties and dynamic behaviors in fractal networks ^{[2,3,4,5,6,7,8,9]}. Moreover, many researchers focus on how the fractal structure affects the performance of network, and have been obtained many important results ^[9,10,11,34].

In the field of complex networks, more and more researchers found that many real systems cannot be represented by networks based on the graph theory ^{[12,13,14,15,16,17,18,19,20,21]}. Hypergraph theory provide a powerful tool to solve such problems ^[22]. Many researchers have tended to represent more complex systems by hypergraphs ^{[12,13,14,15,16,17,18,19,20,21,23,24,25,26,27,28]}. They construct many hypernetwork models to describe the real complex systems. There are many real systems with fractal features in nature, which are more suitable modeled by fractal hypernetworks. Such as, the fractal plant systems and the fractal power systems. Because of the random structure of irregular hypernetworks, it is difficult to obtain the relationship between the structure and the performances in the hypernetworks, such as scale-free hypernetwork ^[12,14,27] and random hypernetwork ^[26]. However, in fractal hypernetworks, it is easier to obtain the exact results of properties, such as the node number, the hyperedge number, the hyperdegree distribution, and so on.

Controlling is one of the hot issues in complex systems ^{[10,29,30,31,32,33,34]}. The controllability is closely related to the dynamic behavior of the network ^[31,32,33]. For example, in the spread of rumors, if a few spreaders are controlled, the rumors will be controlled. A machine can run automatically only by controlling one switch. A complex system is controllable if imposing appropriate external signals on some elements, the system can be driven from any initial state to any final state in finite time ^[29,30]. It is important to control a hypernetwork system. For instance, the node represents the Wechat user and the hyperedge represents the Wechat group in Wechat user hypernetwork. The information is spread quickly in Wechat group. If we can control a few Wechat groups, we can control the spread of the information. Yuan studied the controllability of fractal networks based on graph and obtained some important results ^[10]. The controllability of fractal hypernetworks has not been studied yet. By analysis the controllability of the fractal hypernetworks, we will obtain how the fractal structure affects the controllability of the fractal hypernetworks.

In this paper, we construct a fractal hypernetwork model, which is named 2k uniform (1, 3) flower hypernetwork. In Section 2, the algorithm is proposed to construct the fractal hypernetwork model, and its topological properties are analyzed. In Section 3, we analyze the node controllability and the hyperedge controllability of the fractal (1, 3) flower hypernetwork by the exact controllability theory ^[29]. In Section 4, we compare the controllability of three hypernetworks. The last section concludes this paper.

2.   The fractal (1, 3) flower hypernetwork model and its topological properties

In this section, the algorithm for constructing the fractal (1, 3) flower hypernetwork is proposed. Moreover, we analyze some topological properties of the fractal hypernetwork.

2.1.   A hypernetwork model with fractal features

In ref. ^[5], researchers proposed a (1, 3) flower network model with fractal features based on graph. The fractal (1, 3) flower network has small-world characteristics, and its node degree distribution obey power law distribution. Inspired by the fractal (1, 3) flower network, we construct a 2k uniform (1, 3) flower hypernetwork model with fractal features.

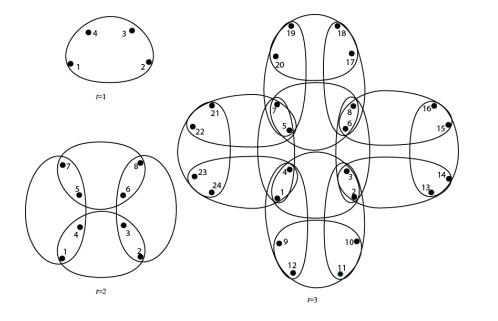
Let HF_2k(t) be the fractal 2k uniform (1, 3) flower hypernetwork after t time steps. The existing hyperedges at time t-1 are named as old hyperedges, and the hyperedges generated at time t are named as new hyperedges. Let N_2k(t) and E_2k(t) be the node number and the hyperedge number of HF_2k(t), respectively. An iterative algorithm for constructing 2k uniform (1, 3) flower hypernetwork is as follows:

Step 1: at the initial time t = 1, the hypernetwork HF_2k(1) has one hyperedge with 2k nodes, where N_2k(1) = 2k, E_2k(1) = 1.

Step 2: at time t = 2, the hypernetwork HF_2k(2) is an evolution hypernetwork from HF_2k(1) by adding 2k new nodes and 3 new hyperedges. One hyperedge contains 2k new nodes, other two hyperedges are consisted of k new nodes and k old nodes, respectively, where N_2k(2) = 4k, E_2k(2) = 4. In other words, each old hyperedge generates three new hyperedges.

Step 3: at time t (t > 2), the fractal hypernetwork HF_2k(t) is an evolution hypernetwork from HF_2k(t-1) by adding 2kE_2k(t-1) new nodes and 3E_2k(t-1) new hyperedges according to Step 2, then N_2k(t) = 2kE_2k(t-1)+N_2k(t-1), E_2k(t) = 4E_2k(t-1).

Figure 1 shows the iterative processes of 2k uniform (1, 3) flower hypernetwork with fractal features from time 1 to time 3.

The 2k uniform (1, 3) flower hypernetwork is a fractal hypernetwork. According to the construction process, we obtain some topological properties of 2k uniform (1, 3) flower hypernetwork.

2.2.   Some topological properties of 2k uniform (1, 3) flower hypernetwork

2.2.1.   The number of nodes and hyperedges

According to the iteration algorithm and Mathematical Induction method, after t iterations, it is easy to get (1) and (2).

According to (2), the hyperedge number of 2k uniform (1, 3) flower hypernetwork is just related to iteration time t. Table 1 shows the node number and the hyperedge number of the HF_2k(t). For k = 2, the node number of 4-uniform (1, 3) flower hypernetwork is ${N_4}\left( t \right) = 4\frac{{{4^{t - 1}} + 2}}{3} = \frac{{{4^t} + 8}}{3}$, and the hyperedge number is ${E_4}\left( t \right) = {4^{t - 1}}$

2.2.2.   Hyperdegree and hyperdegree distribution of 2k uniform (1, 3) flower hypernetwork

Let $d_{2k}^{t - 1}\left( i \right)$ be the hyperdegree of node i at time t-1 of 2k uniform (1, 3) flower hypernetwork and $\Delta d_{2k}^t\left( i \right)$ be the hyperdegree increment of node i from time t-1 to time t. Obviously, $d_{2k}^1\left( i \right) = 1$, Based on the iteration algorithm, if the node i is contained in $d_{2k}^{t - 1}\left( i \right)$ old hyperedges at time t-1, then the hyperdegree of the node i will be increase $d_{2k}^{t - 1}\left( i \right)$ at time t, which means that $\Delta d_{2k}^t\left( i \right) = d_{2k}^{t - 1}(i)$. Furthermore, each old hyperedge will generate 3 new hyperedges and 2k new nodes at time t. The hyperdegree of new nodes is 2 at time t > 1, namely $d_{2k}^t\left( j \right) = 2$, where j is a new node which is generated at time t. The hyperdegree of the old node i at time t is

The hyperdegrees of nodes in 2k uniform (1, 3) flower hypernetwork are related with the time of nodes being generated. The hyperdegrees of 2k nodes which are generated at time 1 are

The number of nodes joined to HF_2k(t) at time s is ${N_{2k}}\left( s \right) - {N_{2k}}\left( {s - 1} \right) = 2k{4^{s - 2}}$. And the hyperdegrees of these nodes are

Let $P\left( {d_{2k}^t} \right)$ be the hyperdegree distribution of 2k uniform (1, 3) flower hypernetwork, $N\left( {d_{2k}^t} \right)$ be the number of nodes with hyperdegree $d_{2k}^t$ at time t, then $P\left( {d_{2k}^t} \right) = \frac{{N\left( {d_{2k}^t} \right)}}{{{N_{2k}}\left( t \right)}}$.

By (4), we have ${2^{t - s + 1}} = d_{2k}^t$, then $s = t - {\log _2}d_{2k}^t + 1$, $N\left( {d_{2k}^t} \right) = 2k{4^{t - {{\log }_2}d_{2k}^t - 1}}$, ${N_{2k}}\left( t \right) = 2k\frac{{{4^{t - 1}} + 2}}{3}$. So, the hyperdegree distribution of 2k uniform (1, 3) flower hypernetwork is represented by (5).

Figure 2 shows the hyperdegree distribution of 4-uniform (1, 3) flower hypernetwork at time 7, which follows the power law distribution.

3.   The controllability of 2k uniform (1, 3) flower hypernetwork

According to the exact controllability theory ^[29] we analyze the node controllability and the hyperedge controllability of 2k uniform (1, 3) flower hypernetwork with fractal features in this section.

3.1.   The exact controllability theory

The following expression describes the controllability of network with N nodes,

In (6), the states of N nodes are represented by the vector x = (x₁, x₂, …, x_N)^T, and A is the N-order coupling square matrix of network. The vector u = (µ₁, µ₂, …, µ_m)^T represents the m controllers, and B is the input matrix of size $N\times m$. To completely control the network, we need to choose suitable B and u. For minimizing the number of signals added to driver nodes, a proper matrix B should be designed. The matrix B corresponds to the minimum number of input signals imposed on a minimum set of driver nodes. The controllability of complex network systems is defined by the fraction of driver nodes. A complex network system is controllable if the fraction of driver nodes is less than 1 ^[29,30].

Let N_D be the minimum driver node set (MDS) ^[29,30]. According to the results of Yuan ^[29] and Liu ^[30], N_D is the key to measure the controllability of complex network system, it is clearly that

Yuan et.al ^[29] proved that for an arbitrary network, the minimum number of N_D is determined by the maximum geometric multiplicity $\mu \left({\lambda }_{i}\right)$ of the eigenvalue ${\lambda }_{i}$ of A:

where ${\lambda _i} = (i = 1, 2, ..., l)$ are the distinct eigenvalues of A. If the coupling matrix A is symmetric, then the geometric multiplicity and the algebraic multiplicity of A are equal. In an undirected network, N_D is determined by the maximum algebraic multiplicity of $\delta \left( {{\lambda _i}} \right)$ of ${\lambda _i}$:

According to (8) and (9), we can calculate N_D of all networks.

In ref. ^[30], n_D denotes the measure of controllability, which is defined as follow:

According (10), a network is more controllable if it has smaller n_D, which means that the network is controllable if n_D < 1.

3.2.   Node controllability and hyperedge controllability of the hypernetwork

In this subsection, we put forward the methods to analyze the node controllability and the hyperedge controllability of hypernetwork, respectively.

3.2.1.   The method of analyzing the node controllability of hypernetwork

The node controllability in hypernetwork is similar to common network.

For a hypernetwork system with N nodes, if inputted suitable signals on a proper subset of nodes, the hypernetwork system can be driven from initial state to final state in finite time, then the hypernetwork system can be controlled by nodes. The minimal set of the proper node subset is called the minimum driven node set of hypernetwork (MDHS). Let ${H}_{{N}_{D}}$ be the number of the minimum driven node set of a hypernetwork, and ${H}_{{n}_{D}}$ be the node controllability measure of the hypernetwork, where ${H_{{n_D}}} = \frac{{{H_{{N_D}}}}}{N}$.

We propose a method to analyzing the node controllability of hypernetwork based on the 2- section graph of the hypergraph ^[22].

Let H = (V, E) be a hypergraph with N nodes, its 2-section graph is a common graph, written as [H]₂. The vertex set of [H]₂ is the vertex set of H. If two nodes are contained in the same hyperedge then they are connected by an edge in 2-section graph ^[22]. Figure 3 shows a hypergraph and its 2-section graph.

Let [HF_2k(t)]₂ be the 2-section graph of HF_2k(t). Figure 4 shows [HF₄(t)]₂ of HF₄(t) at time t (t = 1, 2, 3).

Inspired by ^[18], we can obtain the node controllability of 2k uniform (1, 3) flower hypernetwork by analyzing the node controllability in its 2-section graph network.

According the exact controllability theory ^[29], we give the analytical process of node controllability of 2k uniform (1, 3) flower hypernetwork as follows.

Let A_HF(t) be the adjacency matrix of [HF_2k(t)]₂. And let ${H_{{N_D}}}$ be the number of minimum driven node set at time t. The node controllability measure of HF_2k(t) at time t is written as ${H_{{n_D}}}\left( t \right)$. Moreover, let $\delta \left( {{\lambda _i}\left( t \right)} \right)$ be the maximum algebraic multiplicity of the eigenvalue ${\lambda _i}$ for A_HF(t).

By (9) and (10), we have ${H_{{N_D}}}\left( t \right) = \max \left\{ {\delta \left( {{\lambda _i}\left( t \right)} \right)} \right\}$, and ${H_{{n_D}}}\left( t \right) = \frac{{{H_{{N_D}}}\left( t \right)}}{{{N_{2k}}\left( t \right)}}$.

Figure 5 shows the curve of ${H_{{N_D}}}$ as a function of evolution time t, which shows that the minimum number of driven nodes ${H_{{N_D}}}$ increases with the nodes increasing. Figure 6 shows the curve of ${H_{{n_D}}}$ over time t, which shows that the measure of node controllability ${H_{{n_D}}} < 1$ at all times. Therefore, the fractal 2k uniform (1, 3) flower hypernetwork is a node controllable hypernetwork.

3.2.2.   The method of analyzing the hyperedge controllability of hypernetwork

For a hypernetwork system with E hyperedges, if the hypernetwork system, which is imposed suitable external signals on the proper hyperedge subset, can be driven from any initial state to any final state, then the hypernetwork system can be controlled by hyperedges. The minimal set of the proper hyperedge subset is called the minimum driven hyperedge set of hypernetwork (MDHES). In a hypernetwork, let ${H_{{E_D}}}$ be minimum number of the driven hyperedges and ${H_{{e_D}}}$ denote the measure of hyperedge controllability, then ${H_{{e_D}}} = \frac{{{H_{{E_D}}}}}{E}$.

We give a method to analyze the hyperedge controllability based on the line graph of hypergraph ^[22]. Let H = (V, E) be a hypergraph with N nodes and E hyperedges. The line graph of H is a graph, written as L(H), where the vertex set of L(H) is the hyperedge set E of H. If the intersection of two hyperedges in H is not empty, then their corresponding vertices are connected by an edge in L(H) ^[22]. Let $L\left({HF}_{2k}\right(t\left)\right)$ be the line graph of HF_2k(t).

Figure 7 shows a hypergraph and its line graph. Figure 8 shows $L\left({HF}_{4}\right(t\left)\right)$ of HF₄(t) at time t (t = 1, 2, 3).

We can obtain the hyperedge controllability of a hypernetwork by analyzing the node controllability of its line graph. We give the analytical process of the hyperedge controllability for HF₄(t) based on the exact controllability theory ^[29] as follows.

Let ${A_{{L_{HF}}}}\left( t \right)$ be the adjacency matrix of $L\left( {H{F_{2k}}\left( t \right)} \right)$, ${H_{{E_D}}}\left( t \right)$ be the number of minimum driven hyperedge set at time t. The hyperedge controllability measure of HF_2k(t) at time t is written as ${H_{{e_D}}}\left( t \right)$. Moreover, let $\delta \left( {{\lambda _i}\left( t \right)} \right)$ be the maximum algebraic multiplicity of the eigenvalue ${\lambda _i}$ for ${A_{{L_{HF}}}}\left( t \right)$.

By (9) and (10), we have ${H_{{E_D}}}\left( t \right) = \max \left\{ {\delta \left( {{\lambda _i}\left( t \right)} \right)} \right\}$, and ${H_{{e_D}}}\left( t \right) = \frac{{{H_{{E_D}}}\left( t \right)}}{{{E_{2k}}\left( t \right)}}$.

Figure 9 shows the curve of ${H_{{E_D}}}$ as a function of evolution time t. The result shows that the minimum number of driven hyperedges ${H_{{E_D}}}$ increases with the number of hyperedges increasing. Figure 10 shows the curve of the measure of hyperedge controllability ${H}_{{e}_{D}}$ as a function of evolution time t. The result shows that the measure of hyperedge controllability ${H_{{e_D}}} < 1$ in 4-uniform (1, 3) flower hypernetwork. The fractal 4-uniform (1, 3)-flower hypernetwork is a hyperedge controllable hypernetwork.

We compare the measures of the node controllability and the hyperedge controllability of 4-uniform (1, 3) flower hypernetwork with fractal feasures, which is drawn in Figure 11. As a result, the measure of hyperedge controllability is smaller than that of node controllability. It indicates that 4-uniform (1, 3) flower hypernetwork can be better controlled by its hyperedges.

4.   Comparisons for controllability of three hypernetworks

We design the simulation experiment to compare the controllability of 4-uniform (1, 3) flower hypernetwork with two hypernetworks which are 4-uniform linear hypertree network ^[35] and 4-uniform BA hypernetwork ^[12].

4.1.   The 4-uniform linear hypertree network

In ref. ^[35], the authors give a hypernetwork model with fractal features based on hypergraph. It is named k-uniform linear hypertree network. The 4-uniform linear hypertree network can be construct in an iterative way ^[35]. Figure 12 shows the iterative processes of 4-uniform linear hypertree network from time 1 to time 3.

4.2.   Comparisons for node controllability of two fractal hypernetworks

Figure 13 shows that the difference of node controllability measures between 4-uniform (1, 3) flower hypernetwork and 4-uniform linear hypertree network. These hypernetworks are both fractal hypernetworks. The results of Figure 13 indicate that 4-uniform (1, 3) flower hypernetwork has better node controllability than 4-uniform linear hypertree network.

4.3.   Comparisons for the hyperedge controllability measure of two fractal hypernetworks

Figure 14 shows that the hyperedge controllability measure of 4-uniform (1, 3) flower hypernetwork is smaller than 4-uniform linear hypertree network from time 2 to 7. Therefore, 4-uniform (1, 3) flower hypernetwork has better hyperedge controllability than 4-uniform linear hypertree network.

4.4.   Comparisons for node controllability of (1, 3) flower hypernetwork and BA hypernetwork

Figure 15 shows the node controllability measures of 4-uniform (1, 3) flower hypernetwork and 4-uniform BA hypernetwork. The results indicates that 4-uniform (1, 3) flower hypernetwork has better node controllability than 4-uniform BA hypernetwork.

4.5.   Comparisons for hyperedge controllability of (1, 3) flower hypernetwork and BA hypernetwork

Figure 16 shows the hyperedge controllability measures of 4-uniform (1, 3) flower hypernetwork and 4 uniform BA hypernetwork. The results indicate that 4-uniform (1, 3) flower hypernetwork has smaller measure of the hyperedge controllability than 4-uniform BA hypernetwork. In other words, the fractal 4-uniform (1, 3) flower has better hyperedge controllability.

4.6.   Comparisons for the controllability of three hypernetworks

In Figure 17, we compare the node controllability and the hyperedge controllability of three hypernetworks. We see that the node controllability measure of fractal 4-uniform (1, 3) flower hypernetwork is the smallest, so is the hyperedge controllability measure. It indicates that the fractal 4-uniform (1, 3) flower hypernetwork has better controllability than other two hypernetworks.

Figure 17 shows that the hyperedge controllability measures of three hypernetworks are smaller than their node controllability measures. It indicates that three hypernetworks are easier to control by their hyperedges

5.   Conclusions

In this paper, we construct a fractal (1, 3) flower hypernetwork model. We obtain the mathematical expressions of its topological properties, including the node number, the hyperedge number, the node hyperdegree and the node hyperdegree distribution. In particular, we analyze the node controllability and the hyperedge controllability of the fractal (1, 3) flower hypernetwork. The simulation results show that the controllability measures of node and hyperedge are both less than 1. It indicates that the fractal (1, 3) flower hypernetwork is controllable by nodes or hyperedges. Moreover, the fractal (1, 3) flower hypernetwork has better controllability than fractal linear hypertree network and BA hypernetwork. We compare the node controllability and the hyperedge controllability of three hypernetworks. The results show that three hypernetworks can be controlled easily by hyperedges. Because of the good controllability of fractal (1, 3) flower hypernetwork model, it suitable as the topology structure for some real systems with fractal features, such as, transmission system, communications system, power system, LAN, and so on.

Acknowledgments

This work is supported by Natural Science Foundation of Qinghai Province in China (No. 2019-ZJ-7012) and the National Natural Science Foundation of China (Nos. 11801296, 61603206).

Conflict of interest

All authors have no conflicts of interest to declare.