An epistasis and heterogeneity analysis method based on maximum correlation and maximum consistence criteria

1.   Introduction

Precision medicine is the most potential strategy to improve the clinical treatment of cancer. In-depth study of tumor heterogeneity is an important prerequisite for the implementation of precision medicine ^[1,2,3]. Tumor heterogeneity can be divided into two categories: inter-tumor heterogeneity and intra-tumor heterogeneity. The former refers to the molecular and cellular differences in the same organ tumors of different tumor patients, and the latter refers to the molecular and cellular differences in different tumor formation sites of the tumor tissue of the same patient ^[4,5,6,7]. Due to tumor heterogeneity, the same drugs and treatment measures have obvious clinical efficacy differences for different tumor subtypes ^[8,9,10]. For intra-tumor heterogeneity, there may be different tumor cell subclones in the same tumor tissue. When the drug only has a therapeutic effect on the primary clonal tumor cell, the remaining secondary subclonal cells will further evolve, leading to tumor recurrence and metastasis. More importantly, different tumor subtypes or different subclonal tumor cells may adopt different immune escape mechanisms, so that identifying their immune escape pathways in a targeted manner can implement immunotherapy more effectively ^{[11,12,13,14]}. In short, it is necessary to in-depth study tumor heterogeneity.

Fortunately, with the help of next-generation high-throughput sequencing technology, researchers can use different levels of omics data (e.g., genome ^{[15,16,17,18]}, transcriptome ^{[19,20,21,22]}, proteome ^[23,24], metabolome and epitome ^[25,26,27], etc.) to stratify tumor cohorts accurately. On the basis of accurately identifying the patient's tumor subtype, precision medicine can be implemented for the patient. Turashvili et al. summarized a comprehensive survey on inter-tumor heterogeneity and intra-tumor heterogeneity aspects for breast cancer ^[28]. For example, Hofree et al. proposed a network-based hierarchical method NBS which first converted somatic mutation data at the genome level into continuous analog signals through a network smoothing method, and then used a non-negative matrix factorization method to identify patient samples. In order to improve the robustness of the clusters, the consensus clustering algorithm was used to determine the number of clusters and the cluster relationship of samples ^[29]. For genome-level single nucleotide polymorphism (SNP) data, Li et al. proposed a three-stage processing framework based on techniques such as multi-objective optimization algorithm ^{[30,31,32,33]}, clustering algorithm ^[34] and deep learning ^{[35,36,37,38]}, which dealt with the problems of epistasis, heterogeneity ^[38,39,40] and tumor subtype prediction ^{[38,39,40,41,42,43]} respectively, which improved the efficiency of epistasis analysis and the accuracy of tumor heterogeneity recognition to a certain extent. Based on transcriptome data, Jiang et al. divided triple negative breast cancer (TNBC) into four subtypes and putative therapeutic targets or biomarkers were identified for each subtype ^[44]. To recognize dominate evasion pathway of different subtypes of breast cancer, Bou-Dargham et al. collected 1356 immune-related genes as clustering features based on cohorts' transcriptome data ^[45]. However, the occurrence and development of tumors usually involve a variety of biomolecules, and only a certain level of omics data is difficult to fully characterize its internal characteristics, resulting in difficult reproducibility, lack of interpretability, and so on. Therefore, with integrating multiple omics data such as genome, epigenome and transcriptome, Robertson et al. typed the 80 cases of uveal melanoma samples, and four subtypes with significant molecular differences and clinically relevant were identified ^[46]. More importantly, the role of single-cell sequencing data in tumor heterogeneity research has received widespread attention. For instance, Xiong et al. compared the heterogeneity among patients and subtypes based on CNV and revealed that there are four subtypes in Glioblastoma cells based on single-cell analysis ^[47]. Lawson et al. summarized cellular differentiation, diagnostics and therapy response, metastasis and heterogeneity in the microenvironment at single-cell resolution ^[48].

With the accumulation of genomic variation, different subclones are differentiated in tumor cells, each of which may be caused by different epistasis of pathogenic genes. Our research designs a new risk epistatic combination evaluation method, and then improves the heuristic genetic algorithm to search the epistasis combination space to overcome the combination explosion challenge. The multiple risk epistasis combinations identified by our method represent tumor heterogeneity. Using feature SNPs to train the XGBoostclassifier, the results of subtype classification show that accurately identifying tumor heterogeneity is beneficial to improve the performance of tumor subtype classification.

2.   Materials and method

This study mainly faces two challenges. One is that with the increase in the number of SNPs, the combination space of high-order epistasis increases sharply, which leads to a combination explosion. The other is that the epistasis between susceptible genes and the heterogeneity among tumor samples need to be considered. In order to solve these two problems, we first design multiple objectives evaluation criteria to evaluate the epistasis combination of susceptible genes from different angles and improves the heuristic genetic algorithm to efficiently search the combination space to screen multiple candidate epistasis combinations.

2.1.   Maximum correlation and maximum consistence criteria

A single optimization criterion can usually only find potential risk epistatic combinations from one angle, which may miss other feasible solutions, especially when there is heterogeneity in the sample ^[49]. In this study, two evaluation criteria are designed to evaluate candidate epistasis combinations. One is to examine the correlation between the epistasis combination and the target phenotype, and the other is to examine the rationality of genotypes distribution of the epistasis combination among the samples. These two goals have evaluated the superior combination from different angles and have a certain degree of complementarity.

Maximum correlation: It can be assumed that if a combination of loci is pathogenic, then the genotypes at these loci should have a strong correlation with the case/control states of the samples. Therefore, we can first use the maximum correlation to quantify and rank each candidate epistasis combination. Bayesian network consisted of nodes and directed edges can be used to describe the relationship between epistatic SNPs and disease. Given the Markov condition, the relationship between k SNPs and sample disease state can be simplified as the calculation of Eq (1), namely the joint probability distribution of epistatic combination in training samples.

where ${\pi \left({{X_i}} \right)}$ is the parents nodes of the node X_i and if $\pi\left(X_{i}\right) = \varnothing, P\left(X_{i} \mid \pi\left(X_{i}\right)\right)$ equals to a marginal distributions. K2 is a measure score for evaluating the structure of Bayesian network and it has been widely used in previous studies ^[30,50]. Since there is no prior knowledge about the known pathegenic SNPs in this study, the Dirichlet distribution $D\left[\alpha_{11} \ldots \alpha_{i j}\right]$ are set to be 1 in Eq (2).

where I is the combination space of k SNPs and each SNP has 3 states, namely heterozygous, wild homozygous and mutant homozygous, so that I = 3^k. r_i denotes the frequency of i-th epistatic combination in training samples and r_ij represents the frequency of i-th epistatic combination in samples with j-th state and j ∈(case, control).

Maximum consistence: Due to the heterogeneity in the samples, there may not be a strong correlation between some epistatic combinations and sample labels. Therefore, it is necessary to find these potentially susceptible genotypes from another perspective. It can be assumed that there is another susceptible genotype in the sample due to heterogeneity, and this genotype has a weaker association due to its small sample size. Therefore, this study believes that it can be investigated from the perspective of genotype consistency. If the genotype at the loci is more stable in the sample, then the genotype may be one of the main sources of case samples. Here, we applied Shannon entropy to measuring the uncertainty of genotype distribution. Of note, the smaller the information entropy value, the more stable the genotype at the loci is in the case samples, and the greater the possibility that the genotype is risky. The uncertainty of genotype distribution is defined as Eq (3).

where h refers to the number of genotypes actually present in the case samples and p_i is the possibility of the i-th genotype in the case samples.

2.2.   Adaptive genetic algorithm

The genetic algorithm simulates the phenomena of replication, crossover, and mutation that occur in natural evolution. Starting from the initial population, through random selection, crossover and mutation operations, a group of individuals (solution) more adapted to the environment (problem) are generated and finally converges to a group of individuals who are most adaptable to the environment. The genetic algorithm includes several main parts: coding, fitness value evaluation, selection, crossover, and mutation, which are briefly introduced below.

Individual coding: Individual coding is the first step in using genetic algorithms to solve specific problems. We encode each individual as a string of '0', '1', and the length of the string is equal to the number of SNPs, '0' means that the SNP is not selected, and '1' means that the SNP is selected to construct an epistatic combination. The goal of our study is to identify epistasis and heterogeneity. Therefore, multiple '1's on an individual solution indicate epistasis, and multiple near-optimal solutions correspond to heterogeneity.

Fitness evaluation: The evaluation of the solution not only affects the convergence speed of the population, but also determines whether to break out of the local optimum. Here, we combined the maximum correlation and maximum consistence criteria to evaluate each solution.

Selection operator: The selection operation simulates the rule of survival of the fittest in the natural evolution process. This operator keeps the more adaptable individuals in the population and recombines them to produce better next generations. In this study, each candidate solution is investigated with two criteria, and the sufficiently good solutions on any one goal are retained for the next generation.

Crossover operator: The size of the crossover probability P_c determines the abundance of the population. The larger the Pc, the higher the abundance of the population, but the higher the probability that good individuals will be destroyed ^[51]. In this study, we design an adaptive crossover probability adjustment strategy defined as Eq (4) to dynamically adjust based on the optimal fitness value and average fitness value of the population.

where f_max is the maximum fitness of the population and f_ave is the average fitness of the population. The f₁ and f₂ are the fitness of two individuals to be recombined. The k₁ and k₂ are constant values between 0 and 1.

Mutate operator: The size of the mutation probability P_m defined as Eq (5) determines whether it can jump out of the local optimum value to find the global optimal solution. The larger the P_m, the easier it is to jump out of the local optimum value to find the global optimal solution. However, a too large P_m value will degenerate genetic algorithm to Random search.

where f is the fitness of the individual to be mutated and k₃ and k₄ are constant values between 0 and 1.

2.3.   Tumor subtype recognition and classification

In this section, K-means clustering algorithm was introduced to recognize different tumor subtypes hidden in cases. For a given sample set, K-means divides the sample set into K clusters according to the distance between the samples. Make the points in the clusters as close together as possible, and make the distance between the clusters as large as possible. Assuming that the cases are divided into K clusters, namely (𝐶1, 𝐶2, ... 𝐶𝑘), then our goal is to minimize the squared error E defined in Eq (6). Of note, the K is set to be number of risky epistatic combinations, which means that each risk epistasis may lead to a subtype.

where $\mu_{i}$ is the centroid of i-th cluster, and is defined as Eq (7). The optimization objective can be solved by iterative algorithms.

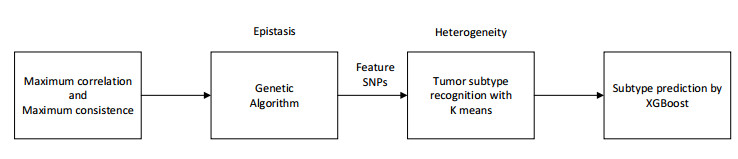
After using the K-means clustering algorithm to subdivide all case samples into different subtypes, our method proposes to use the XGBoost classifier to predict the subtype of a new sample. The XGBoost implements parallel tree boosting technique in a portable and efficient way ^[52]. The XGBoost prevents over-fitting through regularization items, and it can be optimized in parallel to improve training efficiency. To help researchers to solve classification problem in an easy-use, friendly way, R, Python, Ruby are provided. In order to more intuitively describe the computing framework proposed in this paper, we draw a flow chart in Figure 1 to describe the method in this paper.

3.   Datasets and evaluation measures

3.1.   Simulation datasets

In this study, to demonstrate the performance of the proposed method, extensive simulated datasets listed in Table 1 were generated by GAMETES_2.1 ^[53] which has been wildly used in previous studies ^[34,35]. With using GAMETES_2.1, researchers can customize epistatic datasets by setting parameters, such as minor allele frequency (MAF), epistatic order (k), heterogeneity proportion (HP), sample size, SNP size and so on.

In this study, we also simulated pure and heterogeneous dataset with using the same parameters as previous study ^[35]. The pure datasets were labelled with 'Pure' prefix, while heterogeneous datasets were labelled with 'Hete' prefix. The sample sizes of the data sets have five scales, namely 1000, 2000, 3000, 4000 and 8000, but the number of SNPs in each data set is fixed at 100. For pure datasets (HP = 1.0), 2 loci and 3 loci disease models were simulated and their MAFs are (0.2, 0.2) and (0.2, 0.2, 0.2) and their epistasis order are 2 and 3, respectively. For heterogeneous datasets, all these datasets are composed with two balanced disease models, so that the disease model H1 holds 50% and the H2 is also 50%. For instance, the HPs of 'Hete10' dataset are H1 = 50% and H2 = 50%, so that the 8000 samples are composed with 4000 samples caused by 3 loci disease model H1(0.2, 0.2, 0.2) and the rest 4000 samples caused by 3 loci disease model H2 (0.3, 0.3, 0.3).

3.2.   Performance evaluation measures

This study has dealt with the epistasis and heterogeneity of complex diseases at the same time, so different measures are used to evaluate the performance of our method. The Power is defined as Eq (8).

where n refers the frequency of correctly identifying the real pathogenic loci and N is the number of tests.

Accurately identifying heterogeneity in cases is a prerequisite for improving the accuracy of tumor subtype classification. In this study, the accuracy defined as Eq (9) is also applied to evaluating the performance of tumor subtype classification. In order to evaluate the accuracy of tumor subtype classification more objectively, this study adopted a 10-fold cross-validation strategy which divides the dataset into 10 equal parts, and then uses each part as the test set in turn, and the remaining parts as the training set and finally the results of the 10 tests are averaged ^{[25,54,55,56]}.

where N is the total number of cases and n represents the number of times the sample was correctly identified.

4.   Experimental results

In this section, our method MCMC (maximum correlation and maximum consistence) was compared with DPEH ^[34] and MDR ^[57]. The DPEH is a three-stage framework for epistasis detection, heterogeneity analysis and disease prediction based on deep learning. Note that DPEH adopted a ESMO method which applied an exhaustive search strategy to search epistasis with using two optimization objectives. The MDR reduces high dimensional multi-locus genotype into one dimension and also uses an exhaustive search strategy to find the riskiest epistatic combinations.

4.1.   Results on pure datasets

Since a sample in pure dataset only has two possible states: normal or case, there is no need to distinguish tumor subtypes, so that the diagnosis can be regarded as a binary classification problem.

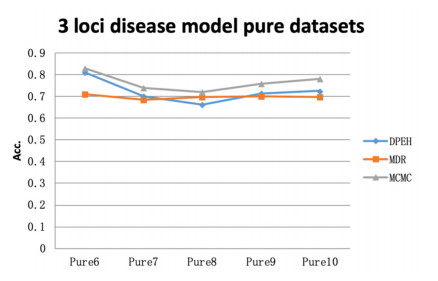
It can be seen from the results in the Figures 2 and 3 that the accuracy of our method MCMC is significantly improved compared with the other two methods, and the accuracy is increased by more than 5%. The increase in accuracy mainly comes from XGBoost's ability to more accurately describe the relationship between epistasis and disease status. In addition, on average, the prediction accuracy of the 3 loci dataset is slightly higher than that of the 2 loci dataset. The reason for this phenomenon may be that the increase in the number of features input to the prediction model XGBoost provides more information.

4.2.   Results on heterogeneous datasets

The heterogeneous simulation data set is generated by two kinds of pathogenic models, so there are 2 subtypes in the cases, and there are 3 categories in addition to the normal sample, so it is a triple classification problem. Since the MDR cannot directly deal with heterogeneous data, we use the same processing method as the DPEH to compare the accuracy of prediction with the MDR.

4.2.1.   The accuracy of 2 loci disease models

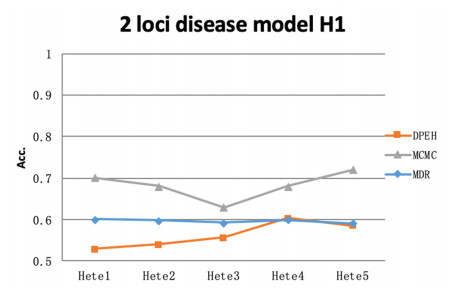
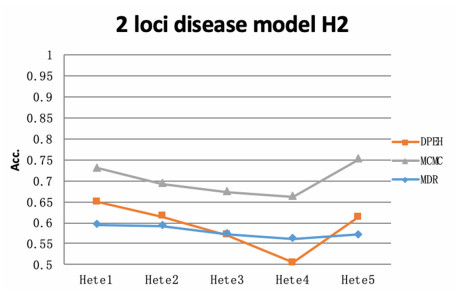
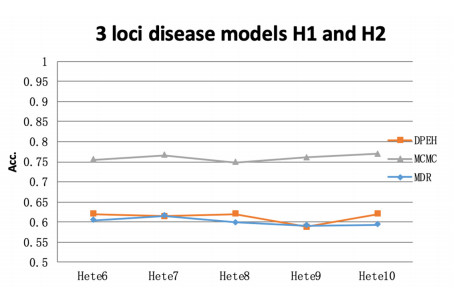
From the results in the Figures 4–6, it can be found that the MCMC is significantly improved compared with the subtype prediction of the DPEH and MDR methods. And it can be found that the accuracy of the pathogenic loci corresponding to the H2 model shown in Figure 5 as predictive features is higher than that of the H1 model shown in Figure 4. The reason may be that the MAFs of the H2 model are higher than the H1. It means that this mutation pattern of H2 in the case is more stable H1, which facilitates subtype identification. Comparing Figure 6 with Figures 4 and 5, it can be found that jointly inputting the pathogenic loci of the two models into the prediction model at the same time can further improve the prediction accuracy, because the information inputted to the model is more complete.

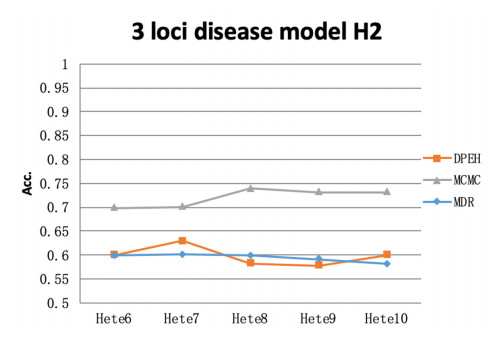
4.2.2.   The accuracy of 3 loci disease models

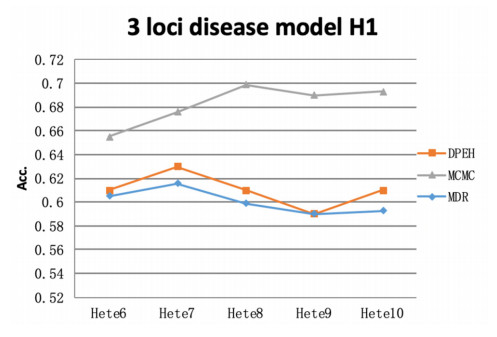
In Figures 7-9, we compared the results of DPEH, MDR and MCMC on 3 loci disease models. It can be found from the experimental results that the performance of the MCMC method is still significantly higher than the DPEH and MDR methods in this disease model. Similarly, the susceptibility loci corresponding to the H2 disease model can train more accurate subtype classifiers. In addition, the joint input of the pathogenic loci of the two disease models into the classifier can further improve the accuracy.

4.2.3.   The power on heterogeneous datasets

Table 2 details the detection efficiency of the two methods for each disease model. The bold numbers in the experimental results indicate that the performance of MCMC is more advantageous, so it can be found that in most cases, the performance of the MCMC method is significantly better than the DPEH method. More importantly, disease models with larger MAF are easier to accurately identify, and the detection efficiency of the 2 loci disease model is better than that of the 3 loci disease model.

5.   Discussion and conclusions

Tumor epistasis makes it difficult to find weakly effect susceptibility genes, while tumor heterogeneity makes it difficult to distinguish patient subtypes. Solving these two problems is the basic work of tumor precision medicine. In practical application, for tumors whose subtypes have not been fully defined, we can first treat the cohort for genome sequencing, and then use our method MCMC to analyze epistasis and heterogeneity, so as to fully identify tumor subtypes with different combinations of pathogenic sites. On the basis of fully defining tumor subtypes, our method can be used to classify new samples. Our computational framework proposed in this study has the following three advantages:

1) The MCMC method has more significant advantages than previous methods in terms of efficiency and accuracy.

2) The framework first uses improved genetic algorithms to optimize different epistasis evaluation criteria to identify multiple potential epistasis risk combinations. This multi-objective evaluation criterion improves the possibility of identifying weakly effect susceptible genes from different perspectives. Therefore, it is more conducive to the comprehensive discovery of target genes of complex diseases.

3) Adaptively determine the number of tumor subtypes based on high-confidence risk combinations, and then use a clustering algorithm to identify heterogeneity in case samples. Therefore, the MCMC method can adaptively deal with epistasis and heterogeneity at the same time, and has certain practical value.

Although the MCMC method designed in this study has achieved certain advantages in evaluation measures, there are still areas for further improvement. For example, there is still room for improvement in the efficiency of epistatic recognition and the classification accuracy of tumor subtypes. More important, it is necessary to apply our method to real tumor case-control study to further verify the reliability of tumor heterogeneity from the perspectives of tumor tissue morphology and tumor immune escape pathways.

Acknowledgments

This work was partially supported by Natural Science Foundation of Hunan Province of China (NO. 2020JJ7081). And, it was also supported by the Jiangxi Provincial natural science fund (No. 20192ACB21004 and 20204BCJL23035).

Conflict of interests

All authors declare no conflicts of interest in this paper.