Stagnant Stunting Rate despite Rapid Economic Growth

—An Analysis of Cross Sectional Survey Data of Undernutrition among Children under Five in Papua New Guinea

1.   Introduction

Electrical discharge machining (EDM) is an important non-traditional manufacturing method for machining electrically conductive and hard materials ^[1]. By the energy of electrical discharges between a tool electrode and a workpiece electrode in dielectric fluid environment, EDM is widely used to make dies, molds, and finishing parts for aerospace, automotive, and surgical components ^[1,2]. The performance of EDM is generally evaluated on the basis of material removal rate (MRR), tool wear rate (TWR), surface roughness (SR), surface kurtosis (Sku), and surface skewness (Ssk) ^[1,3,4]. A considerable amount of researches has been reported on the model construction of EDM performance response and the recognition of main EDM parameters. Based on central composite design (CCD), Gopalakannan et al. constructed a quadratic response surface model (RSM) to predict MRR, EWR and SR at different machining parameters on machining Al 7075 ^[3]. Their study reveals that the pulse current and pulse on time are main factors that affect MRR, EWR and SR ^[5]. Mohammadjafar et al. investigated the effects of different tool initial SR values and EDM parameters on the machined workpiece SR, TWR, MRR, and the tool SR ^[4]. The results showed that TWR increases and MRR decreases with the increase in tool surface roughness, while the initial tool SR has slight influence on final workpiece SR ^[6].

One of the most critical problems in EDM is to select proper parameters combination for optimum machining performance measures ^[7]. Usually, EDM parameters are selected on the basis of operator's experience or data reference provided by the manufactures ^[1]. To overcome this problem, many researches on EDM parameter optimization have been proposed. Somashekhar introduced the artificial neural network (ANN) for analyzing the material removal of micro-EDM to establish the parameter optimization model, and then optimize the process parameters for desired machining characteristics output ^[8]. Majumder uses fuzzy logic and particle swarm optimization (PSO) algorithm to determine the optimal machining parameters (pulse current, pulse on time, and pulse off time) for improving the machining performance (MRR and EWR) during the EDM of AISI 316LN stainless steel ^[9]. In Majumder's study, Taguchi L9 orthogonal array was generated to conduct the experimentation and the multiple least-square regression technique was introduced to model the relationship between the input factors and performance responses ^[9]. Based on a cost index combining MRR and TWR, D'Urso analyzed the influence of peak current, voltage and frequency and of their interactions on the process performance in micro-EDM drilling ^[10]. Parsana carried out the multi-objective EDM parameter optimization of Mg–RE–Zn–Zr alloy by using the Passing Vehicle Search (PVS) algorithm ^[11]. Through the Box–Behnken design, the influence correlativity of input parameters including the pulse-on, pulse-off and peak current on the MRR, TWR and roundness of holes are built using response surface method (RSM) ^[11]. To maximize the MRR and minimize the SR as well as the spark gap in EDM of Inconel 825, Rajyalakshmi and Ramaiah adopted the Taguchi grey relational analysis method to optimize the EDM process parameters ^[12]. The results showed that commonly used EDM parameters such as the pulse on time, pulse off time, and corner servo voltage et al. all be found to have significant influence on the EDM performance response in rough machining stage ^[12]. Using response surface methodology, Świercz investigated the influence of the EDM parameters on the surface integrity and MRR ^[13]. The results showed that the discharge current had the most influence (over the 50%) on the SR, the thickness of the white layer (WL), and the MRR, and MRR ^[13].

The study on the influence of EDM process parameters on machining responses has been carried out by many researchers. Commonly used methods in EDM performance modeling and parameter optimization include NSGA-II ^[14,15], response surface methodology ^[5,16], particle swarm optimization ^[9,17], artificial neural networks ^[18,19], Taguchi method ^[9,20,21] and grey relational analysis ^[20,22]. However, there are still some issues need to be solved. Orthogonal test design and CCD are generally used in existing method to construct the model of EDM performance, which leads to an unsatisfactory uniformity and projection of sample distribution. Moreover, the relationship between EDM performance characteristics and process parameters is highly nonlinear, but existing surrogate models used in EDM behave not so well for nonlinear problems. Further, the power consumption and air pollution are also needed to be considered in constructing the EDM parameter optimization model for clean production.

In this study, a novel EDM parameter optimization model is developed. The power consumption index UEC and air pollution indices (PM2.5 and PM10) are considered for clean production in proposed model. The RBF model which has good performance for nonlinear problem is used to model the relationship between EDM performance characteristics and process parameters. NSGA-II algorithm is applied to solve the multi-objective optimization model to obtain the optimal EDM parameter set.

The following of this paper is organized as follows. EDM materials and experiments are introduced in Section 2. Next is the proposed optimization model in Section 3. Then the optimization results are discussed in Section 4. Finally, conclusions are drawn in Section 5.

2.   Methods and experiments

In this study, EDM experiments are performed to obtain the data. EDM machine Changfeng 350 shown in Figure 1 is applied to machine the 304 steel. 304 steel used here because it's widely used in chemical, petrochemical, fertilizer, food processing, and pharmaceutical industries ^[23]. The chemical composition of 304 steel is shown in Table 1. The electrode is a copper bar with the length of 160 mm and section of 20 mm × 20 mm as shown in Figure 1(b).

Figure 1.  EDM experiments.

DownLoad: Full-Size Img PowerPoint

Table 1.  Chemical composition of 304 steel.

Element	C	Si	Mn	P	S	Cr	Ni	N
% Weight	≤ 0.08	≤ 1.0	≤ 2.0	≤ 0.035	≤ 0.03	18.0–20.0	5.0–10.5	≤ 1.0

---

 | Show Table

DownLoad: CSV

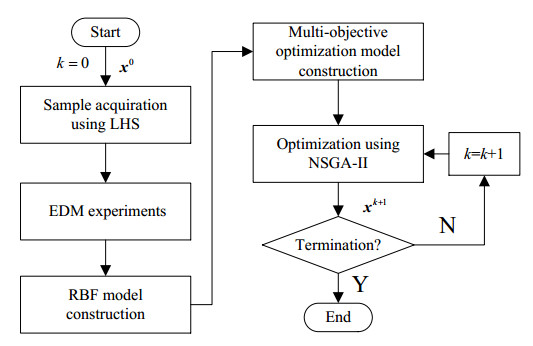
The flowchart of proposed EDM parameter optimization method is shown in Figure 2. The experiment and optimization procedure are detailed as follows.

Figure 2.  Flowchart of proposed EDM parameter optimization method.

DownLoad: Full-Size Img PowerPoint

Figure 3.  The main steps of the NSGA-II.

DownLoad: Full-Size Img PowerPoint

To reduce the number of EDM experiments but generate representative samples, Latin Hypercube Sampling (LHS) method is used select EDM parameter combinations in this study. Compared with orthogonal experimental design ^[15] and CCD ^[24], LHS can obtain well-distributed and representative samples in the design space. Moreover, LHS has the freedom to define the sample number, thereby providing greater flexibility for problem with different dimensionality ^[25].

LHS has been widely used due to its good spatial uniformity and projection characteristics. LHS is a global non-overlapping spatial sample filling method. The basic principle is to divide each dimension into n small regions evenly, and randomly take n sample points in all regions. The model for randomly selecting n LHS sample points in the m-dimensional design space is as follows:

Where $r(i)$ denotes a random integer arrangement of 1 to n, $U(0, 1)$ represents a random distribution over the interval [0, 1]. In Latin hypercube sampling, each sample point is taken with the same probability to ensure global representation of the design space. In addition, LHS has the advantages of flexible sample setting, high sampling efficiency and good balance. Therefore, it is proposed to use Latin hypercube sampling to select the sample points.

After sampling by LHS, the EDM experiments were carried out to collect the response data. In this paper, UEC, MRR, SR, PM2.5 and PM10 are selected as the EDM response outputs. The UEC (W/mm³) is defined as the energy consumption per unit volume. The MRR is identified indirectly as the ratio of the machined volume and the machined time. The SR was measured using Mahr MarSurf M300 roughness tester. The PM2.5 and PM10 data are measured using BOSCH cube Air particulates measure meter. The height of the air particulates measure meter is 1.6 m and the distance to the machining position is 1 m, which approximately simulates the actual position of the operator. The PM data is collected every 2 minutes until the end of machining. Then the mean value is calculated as the PM value at current EDM parameter combination.

The relationship between EDM parameter inputs and response outputs was approximated using the RBF model. In RBF, the Euclidean distance between the sample point and the point to be predicted is used as an input variable of a radially symmetric kernel function, and these radial symmetric kernel functions are used to perform linear combination. The expression of RBF is as follow:

Where ${\beta _0}$ represents a polynomial function, N is the number of sampling points, ${\beta _{\rm{i}}}$ is the weight coefficient of the radially symmetric kernel function, $\varphi $ is expressed as a radially symmetric kernel function. ${x_i}$ denotes a sample point in the known sample data, $\left\| \cdot \right\|$means the Euclid distance.

The RBF model has no specific requirement for response characteristics, and can fit well to any kind of function (especially for functions with high nonlinearity), and has strong robustness and adaptability. And it can deal with the problem of scattered points in multi-dimensional space, the convergence speed is faster, and the calculation cost is lower. Therefore, the RBF model is selected in this paper to model the implicit relationship between the EDM inputs and outputs. The type of the basis functions used for construct RBF model is Multiquadric.

3.   Multi-objective optimization

3.1.   EDM process parameters optimization model

In EDM, UEC is as small as possible to reduce the energy consumption. MRR is as great as possible to improve the machining efficiency. However, strong confliction between these two objectives is observed because a lower UEC is always along with a lower MRR, which leads lower energy consumption but lower machining efficiency ^[2]. Therefore, both UEC and MRR should be considered in EDM parameters optimization. The multi-objective optimization problem in this study is formulated as:

Where, ${\bar g_2}$ and ${\bar g_3}$ are determined according to Chinese National Standards. The lower limits and upper limits of EDM parameters are determined according to the EDM machine.

Unit energy consumption (UEC) is the power per unit volume, which is calculated as follows

Where, the voltage $U$ and the current $I$ are obtained using a multimeter; $t$ is the machining time, $S$ is the area of machined surface and $d$ is the machining depth.

MRR is calculated as follows

In this formula, $S$, $d$ and $t$ have the same definition as those in UEC calculation.

As can be seen from the above two formulas, UEC is inversely proportional to that of the MRR to an extent. Larger $S$, $d$ and smaller $t$ generates a larger MRR but a smaller UEC. Furthermore, the voltage $U$ and the current $I$ also have positive influence on UEC.

Different from existing EDM parameter optimization methods, the pollution indicators PM2.5 and PM10 are considered in this study. The PM10 is the particulate matter with an effective aerodynamic diameter smaller than 10 mm, which is reported to be correlated to the increase in hospital admissions for lung and heart disease ^[26]. The PM2.5 is the particulate matter with an aerodynamic diameter below 2.5 mm, which is sufficiently small to be ingested deep into human lungs ^[27]. For these reasons, the PM10 and PM2.5 are considered to ensure the health of operator in this paper.

3.2.   EDM process parameters optimization

The multi-objective optimization problem modeled in Eq 3 was solved by NSGA-II algorithm ^[28].

NSGA-II ^[11] is one of the most widely used Pareto dominance based multi-objective evolutionary algorithms (MOEAs) with fast non-dominating sorting procedure for discriminating solutions ^[29].

A multi-objective optimization problem (MOP) is formulated as follows

Where, $x$ is the decision variable, $F(x)$ is the objective function with $n$ objectives, and $G\left(x \right)$ is the constraint function with $m$ constraints. Considering two decision variables a and b, $F(a)$ is said to dominate $F(b)$ as follows

The Pareto optimal point ${x^*}$ is defined if there is no feasible $x$ such that $F(x)$ dominates $F\left(x^{*}\right)$. The set of all the Pareto optimal points is termed the Pareto set ^[30,31].

In NSGA-II, N initial population is generated firstly, and then N offspring population is generated from genetic operators such as fitness scaling, selection, crossover and mutation ^[32]. After that, 2N population, including N offspring population and N parent population, is ranked based on the non-dominations principle. Meanwhile, the crowded tournament selection operator is conducted for individuals of every non-dominated level. The new N parent population is generated according to the non-dominated relation and the crowding distance. More details of the theoretical background of NSGA-II can be found in literature ^[26].

In this study, the trained RBF model was embedded into the NSGA-II algorithm by serving as the objective and constraint function. The computer codes of the optimization algorithm were performed in MATLAB 7.11. To ensure the accuracy and efficiency of proposed method, different combinations of population size (${N_p}$ = 100,200,500), iteration number (${N_i}$ = 100,500, 1000), crossover probability (${P_c}$ = 0.3, 0.6, 0.9) and mutation probability (${P_m}$ = 0.02, 0.05, 0.1) are tested in NSGA-II to obtain respective non-dominated solutions. Then all the non-dominated solutions are merged to generate a new solution set. The number of non-dominated solutions is recalculated in the new solution set. Compared with other parameter combinations, more non-dominated solutions are observed when ${N_p}{\rm{ = }}200$, ${N_i}{\rm{ = }}500$, ${P_c}{\rm{ = }}0.9$, ${P_m}{\rm{ = }}0.05$. Therefore, ${N_p}{\rm{ = }}200$, ${N_i}{\rm{ = }}500$, ${P_c}{\rm{ = }}0.9$, ${P_m}{\rm{ = }}0.05$ is used in this study.

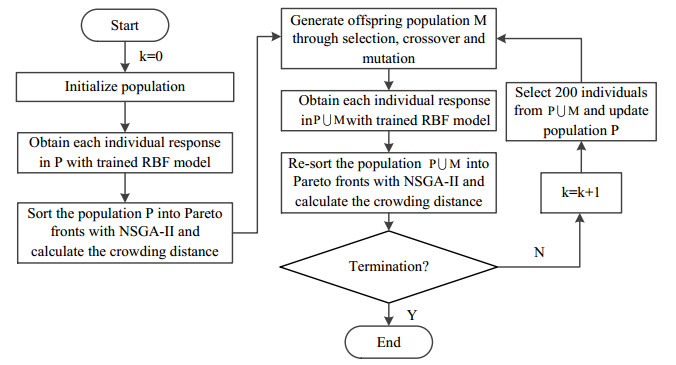
The main steps of the NSGA-II algorithm in EDM parameter optimization are listed as follows.

(1) Population initialization. 200 individuals (combinations of pulse current, time period and duty cycle) are randomly generated as the first generation population P;

(2) Response evaluation. Obtain the objective and constraint response for each individual in population P by calling the trained RBF model;

(3) Population sorting. Using the non-dominated sorting approach to sort the population P into Pareto fronts, and then calculate the crowding distance of every individual in each Pareto front ^[33];

(4) Offspring generation. From generation P, offsprings are generated through selection (using crowded-comparison-operator), crossover (using Simulated Binary Crossover) and mutation (using polynomial mutation). M is denoted in this study to represent the offspring population;

(5) Response re-evaluation. Obtain the objective and constraint response for each individual in population $P \cup M$ by calling the trained RBF model;

(6) Population re-sorting. Using the non-dominated sorting approach to sort the population P into Pareto fronts, and then calculate the crowding distance of every individual in each Pareto front;

(7) Population update. 200 individuals are selected from$P \cup M$, where the dominating Pareto fronts and the individuals with a larger crowded distance are first considered. Then the population P is updated to contain these 200 selected individuals;

(8) Termination. Steps (4)–(7) are repeated until the iteration number reaches 500. And then each individual in the first Pareto front is termed as an optimal solution.

4.   Results and discussion

The machined workpiece are shown in Figure 1(c). Table 2 shows the LHS samples and the responses of EDM experimental results in this paper. The RBF model approximating the relationship between EDM parameters (pulse current, time period and duty cycle) and performance characteristic (UEC, MRR, SR, PM2.5 and PM10) was built using these data.

Table 2.  LHS samples and the corresponding EDM responses.

No.	Pulse current(A)	Time Period ($\mu s$)	Duty cycle	UEC	MRR	SR	PM2.5	PM10
1	9.5	267	0.59	81.42	15.22	10.36	426.2	543.1
2	8.9	284	0.47	85.22	12.80	11.57	237.1	255.1
3	6.7	445	0.45	60.20	4.84	10.61	198.9	221.6
4	6.4	164	0.62	80.13	10.43	7.51	579.8	609.2
5	4.2	211	0.68	36.60	5.40	8.43	595.6	632.3
6	8.0	199	0.34	53.88	7.76	9.96	598.4	647.0
7	5.7	137	0.64	72.15	8.95	6.52	515.5	564.0
8	6.9	488	0.69	32.11	6.17	7.70	150.0	163.8
9	5.4	475	0.48	62.50	7.59	7.73	211.2	131.1
10	9.0	144	0.65	124.44	21.38	9.13	472.3	497.1
11	8.4	400	0.35	98.51	11.87	12.76	321.9	251.7
12	5.1	353	0.54	54.67	3.70	7.67	360.6	383.7
13	9.4	323	0.62	105.92	13.82	14.32	208.2	224.0
14	9.9	464	0.32	75.05	10.16	14.75	378.5	266.8
15	8.1	304	0.51	84.70	11.14	11.73	98.7	105.3
16	6.2	231	0.42	52.21	5.68	8.90	526.8	568.7
17	6.1	365	0.53	64.82	5.31	9.46	151.3	262.2
18	4.1	255	0.56	46.06	3.59	6.62	684.5	727.9
19	7.4	183	0.37	54.01	7.13	9.27	626.2	677.3
20	7.7	448	0.50	78.42	8.26	11.82	194.0	217.6
21	9.6	418	0.67	134.28	19.65	14.32	231.2	250.5
22	5.5	174	0.36	39.13	4.17	8.33	584.9	632.4
23	8.2	126	0.57	97.59	15.30	9.65	458.7	491.2
24	4.5	367	0.39	34.57	2.02	6.15	424.2	570.7
25	5.0	334	0.60	58.72	4.32	7.18	356.5	376.1
26	7.0	290	0.53	75.55	8.70	10.93	78.7	82.0
27	7.3	111	0.31	85.59	8.05	7.89	616.5	663.4
28	5.9	383	0.42	49.04	3.71	9.06	354.4	385.9
29	4.6	239	0.44	40.51	3.47	7.35	639.8	687.5
30	8.7	425	0.40	85.81	11.44	13.22	279.2	306.4

---

 | Show Table

DownLoad: CSV

For comparison, the commonly used surrogate model such as the second order polynomial response surface (PRS) ^[34,35], support vector regression (SVR) ^[36,37] and Kriging model (KRG) ^[38,39] are also used to fit the initial samples and corresponding EDM responses. To evaluate the fitting precision of each surrogate model, the multiple correlation coefficient (${R^2}$) based cross validation error is used in this study ^[40]. The calculation formula is as follows

Where, $m$ is the number of samples to construct the surrogate model; ${y_i}$ is the actual response function value, ${\hat y_i}$ is the predicted function value of surrogate model which is constructed using all samples except the $i$th sample; $\bar y$ is the mean value of the actual response function value of all $m$ samples. If the ${R^2}$ of the model approaches to 1, the model will be of high accuracy.

Using the multiple correlation coefficient (${R^2}$) based cross validation error to evaluate the accuracy of each surrogate model, the comparative results are shown in Table 3.

Table 3.  Accuracy comparisons of different surrogate model using ${R^2}$.

	UEC	MRR	SR	PM2.5	PM10
PRS	–0.1201	0.6878	0.6969	0.6315	0.5957
SVR	0.4581	0.6268	0.6547	0.7559	0.6579
KRG	0.4047	0.7597	0.7081	0.7819	0.7775
RBF	0.9027	0.9046	0.9145	0.9168	0.9236

---

 | Show Table

DownLoad: CSV

As can be seen from Table 3, if PRS, SVR and KRG are used to approximate the relationship of EDM parameters and performance responses, the fidelity cannot satisfy the approximation requirement (${R^2}$ is smaller than 0.9). It's worth noting that the relationship plot between UEC and EDM process parameters is highly nonlinear, which is quite different from that of the second order polynomial response surface. Therefore, the predication error is so huge that a negative R² generates for PRS. The ${R^2}$ of RBF is 0.9027, 0.9046, 0.9145, 0.9168 and 0.9236 for UEC, MRR, SR, PM2.5 and PM10. Therefore, RBF has high fitting accuracy for EDM performance responses (${R^2}$ is greater than 0.9) ^[2]. The reason is that RBF performs better for nonlinear problems compared to other surrogate model. Therefore, RBF is a reliable surrogate model to render the implicit relationship between EDM parameters and performance response.

There is no single optimum for all objective functions in multi-objective optimization problem ^[2]. Therefore, a set of different solutions named Pareto optimal set are acquired. Based on the regression model built to approximate the implicit relationship between EDM parameters and performance responses, NSGA-II is applied to solve the multi-objective optimization model in Eq 3. Theoretically, MRR and SR increase with increase in pulse current, time period and duty cycle. However, the relationship between the three above EDM parameters and UEC, PM2.5 and PM10 are complicated. Therefore, which parameter combinations are optimal for maximum MRR and minimum UEC is still a question.

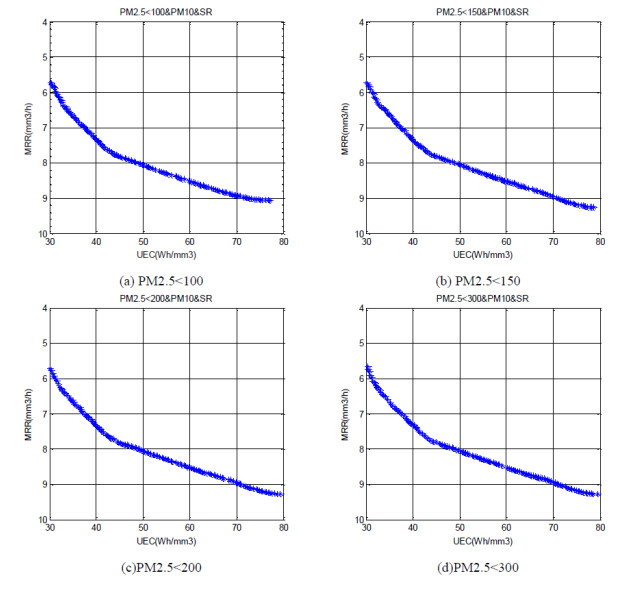
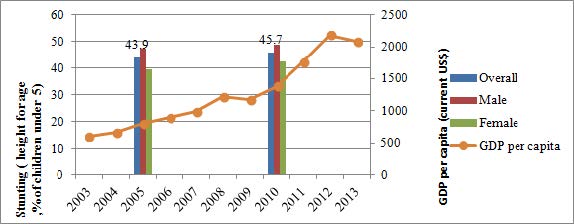
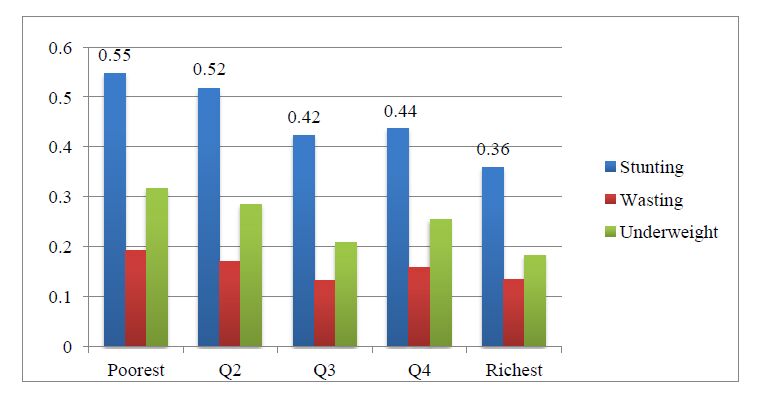
In this study, multiple constraints with different limits are considered in the optimization model. The limit of SR is 6.3 um because many electric discharge machined products require the surface roughness below than Ra6.3, which satisfies the requirements of many manufacturing enterprise. And the limits of PM2.5 and PM10 are determined according to Chinese National Standards (Seen in Table 4). It is worth noting that the excellent standard for PM2.5 (<50 ug/m³) and the primary standard for PM10 (<50 ug/m³) are not considered as constraints in this study because the values of all experiment samples in PM2.5 and PM10 are greater than 50. For each value of PM2.5, PM10 and SR combination, the Pareto plot is demonstrated in Figure 4. In a broad sense, these solutions (blue ${\rm{ \times }}$) are optimal that no other solutions in the design region are superior to them when both UEC and MRR are considered.

Table 4.  Values of PM2.5 and PM10 in Chinese national standards.

PM10 (ug/m3)		PM2.5 (ug/m3)
Primary standard	Secondary standard	Excellent	Good	Slightly polluted	Moderately polluted	Heavily polluted	Severely polluted
< 50	< 150	< 50	< 100	< 150	< 200	< 300	> 300

---

 | Show Table

DownLoad: CSV

Figure 4.  Pareto plots of proposed method with different PM2.5 constraints.

DownLoad: Full-Size Img PowerPoint

As can be seen from Figure 4, the Pareto plots with different PM2.5 constraints (PM2.5 < 100, PM2.5 < 150, PM2.5 < 200 and PM2.5 < 300) are almost overlapped, which means no obvious change of optimal solution set is generated with stricter PM2.5 constraints. The reason may be that other constraints (SR and PM10) play more significant roles on the results of multi-optimization in this study.

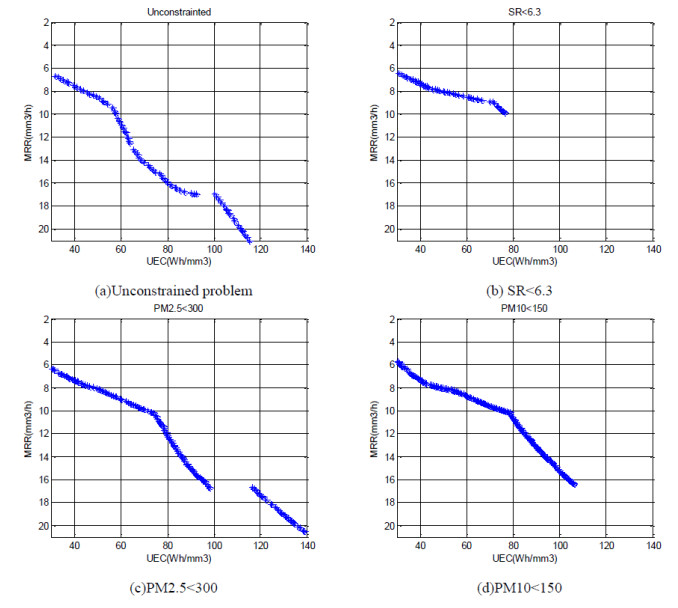
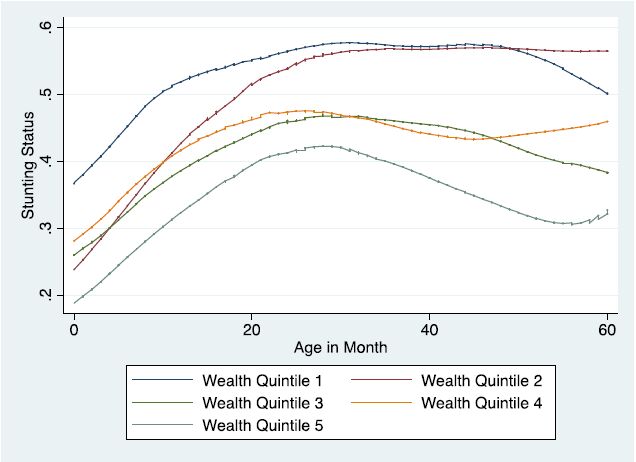
To demonstrate the above idea, additional optimization experiments are conducted. The Pareto plots for unconstrained problem, problem with only SR < 6.3 constraint, problem with only PM2.5 < 300 constraint and problem with only PM10 < 150 constraint are shown in Figure 5. The reason of Pareto plots breaking lies in the high nonlinearity of the objective functions. That's also an important reason to use RBF here. Compared with unconstrained problem, the Pareto plot for problem with only SR < 6.3 constraints is much shorter, which means many solutions are regarded as infeasible when SR < 6.3 constraint are imposed. The Pareto plot for only PM2.5 < 300 constraint is of similar shape to that of unconstrained problem. But the location is at the upper left of the Pareto plot for unconstrained problem, which means less feasible solutions are obtained when PM2.5 < 300 constraint is imposed. The shape and location of the Pareto plot for only PM10 < 150 constraint are both different from those of unconstrained problem, which means that PM10 has important influence for the multi-objective results in this study. Take all the four problems into consideration, conclusions can be drawn that SR < 6.3 and PM10 < 150 play the more important role in EDM parameter optimization.

Figure 5.  Pareto plots of proposed method with different constraints.

DownLoad: Full-Size Img PowerPoint

To further verify the agreement between the optimal solution and the real EDM experiment with optimal parameter, additional EDM experiment is performed. A point with asterisk in Figure 4(a) (UEC = 30.81, MRR = 5.90) was selected as an optimization solution, the corresponding EDM parameter is ([4.6 493 0.64]). Using these optimal parameters to carry out EDM experiments, the real experiment results are compared with the prediction results in Table 5. The relative error is calculated by $\left| {v - \bar v} \right|/v$.

Table 5.  Results comparisons of Actual Value and Predicted Value at selected optimum.

	UEC	MRR	SR	PM2.5	PM10
Actual Value ($v$)	31.42	6.14	3.7	89	92
Predicted Value ($\bar v$)	30.81	5.90	3.4	82	97
Relative Error (%)	1.94	3.91	8.11	7.87	5.15

---

 | Show Table

DownLoad: CSV

The relative errors of UEC, MRR, SR, PM2.5, and PM10 between predicted values and the real machining are 1.94%, 3.91%, 8.11%, 7.87%, and 5.15%, respectively. These errors are acceptable for EDM machining application ^[41]. This result confirms that the RBF model and the NSGA-II optimization algorithm are reliable for EDM parameter optimization with multiple constraints.

5.   Conclusion

In this study, the RBF model is applied to approximate the implicit relationships between EDM parameters and performance responses for 304 steel, which is called to conduct multi-objective optimization using NSGA-II algorithm. The main conclusions of this study are drawn as follows:

(1) The energy consumption index UEC and the air-pollution indices (PM2.5 and PM10) are considered in proposed multi-objective optimization model. UEC is considered as the objective function to reduce the machining cost and PM indices are termed as the constraints to protect the operators' health.

(2) The relationships between process parameters and performance responses are nonlinear in EDM parameter optimization. Using cross validation error based R² to verify the accuracy of commonly used surrogate models, the fidelities of PRS, SVR and KRG cannot be acceptable in this study. However, all the R² values of 5 performance responses using RBF is reliable (>0.9). Therefore, RBF is applied for accurate relationship approximation between EDM parameters and performance responses.

(3) The samples applied to construct the RBF model is selected using LHS method, which is of good spatial uniformity and projection characteristics.

(4) The Pareto plots of multi-objective optimization model with different PM2.5 constraint are obtain using NSGA-II. And the fitting plots of Pareto front for PM2.5 < 100, PM2.5 < 150, PM2.5 < 200, and PM2.5 < 300 are almost overlapped. The reason is that other constraints (SR and PM10) contribute most to the results of multi-optimization when PM2.5 < 300 in this study.

(5) Additional optimization experiments for unconstrained problem, problem with only SR < 6.3 constraint, problem with only PM2.5 < 300 constraint and problem with only PM10 < 150 constraint are conducted to demonstrate to prove the above idea. And conclusions can be drawn that SR < 6.3 and PM10 < 150 play the more important role in EDM parameter optimization.

The optimization results mean that using MRR and UEC as objective and using SR, PM2.5 and PM10 as constraints can be an effective method to provide appropriate process parameters for EDM machining.

Acknowledgments

This project is supported by National Natural Science Foundation of China (Grant No. 11602230), Key Scientific and Technological Research Projects in Henan Province (Grant No. 192102210069), Henan Key scientific research projects in Colleges and Universities (Grant No. 19A460031), Innovative Research Team (in Science and Technology) in University of Henan Province (Grant No. 18IRTSTHN015).

Conflict of interest

All authors declare no conflict of interest in this paper.