Study of single-electron tunneling oscillations using monte-carlo based modeling algorithms to a capacitive slanted two-dimensional array of tunnel junctions

Abbreviations: NT: Nanotechnology; SED: single-electron device; SE: single-electron; SET: singe-electron tunneling; PDF: probability density function; 2D: two-dimensional; 1D: one-dimensional; Diff.: Different; Simi.: Similar; L1: left1; L2: left2; R1: right1; R2: right2

1.   Introduction

Nanotechnologies (NT) are nowadays up-and-coming generic technologies encompassing several industrial sectors. Today, they are already contributing to many industrial successes. It is predicted that they will have a significant positive impact on technological progress and financial profits and health, the environment and social well-being. In the semiconductor field, where the integrated circuits are composed of transistors, which are nowadays as small as a few tens of nanometers in scale, the electronic circuits have still functioned with many electrons. The ultimate goal, in this respect, is the realization of integrated circuits at the single-electron level. Applied researches to date have taken an actual effort in the field of low-dimensional electronic conductors towards single-electron (SE) nanoelectronic to gain full control over single electron to be applicable and suitable for applications in the low dimensional semiconductor areas.

At present, it is possible to confine and manipulate single electrons in a very controlled way in semiconductor nanostructures such as nanowires or quantum dots composed of numerous nanoscale elements ^[1]. However, for the single electron circuits of the future to lead to useful applications, one requires a mechanism to transport and interconnect a single electron from one functional part of the course to another and manipulate it in a controlled way. Besides, coherent transport of quantum information has been demonstrated in many previous types of research in various stable state systems like transporting single electrons in multiple quantum dot networks, the coupling of superconducting qubits to microwave photons ^[2], or in both the 1D (one-dimensional) arrays ^[3,4] and the 2D (two-dimensional) arrays ^[5,6] of tunnel junctions. The essential structural feature that all these SEDs have in common is the small island composed of semiconductor or metal, in which electrons may be confined. This island of a nanoelectronic device assumes a role analogous to that of the FET transistor channel.

For these devices, the current passing a tunnel junction is governed by the Coulomb blockade phenomena. At low bias voltages and a given room temperature, operational SED at a nearly low temperature, T, satisfies the condition k_BT < < e²/2C, where C is the total capacitance and k_B is the Boltzmann constant. These SEDs could enter the Coulomb blockade region, and the tunneling of electrons in such a case is blocked, giving them essential unique properties ^[7]. However, a tunnel junction biased by a DC source may generate single-electron tunneling (SET) oscillations that are having an average frequency f_o proportional to the average current <I> estimated in that circuit, f_o = <I>/e, where e is the elementary electron charge ^[8]. This happens due to the gradual accumulation of the continuous charge on the junction capacitance. A sudden passage of one electron occurs through the junction, causing the charge profile to reach a certain critical charge threshold level (Q_c = ±e/2) ^[9]. The discreteness of charge transfer is one of the crucial issues that is facing the emerging nanoelectronic field. For all of that, there is a need to formulate the conditions under which the transport of charge through a conductor is considered as quasi-continuous charge transport. One example of those capable of quasi-continuous charge transfer is the 1D array of small tunnel junctions ^[10]. The 1D arrays have a key property that each additional electron jumping into one of its islands forms a series of gradually decreasing polarization charges. Hence, it is considered as a "single-electron soliton" with a characteristic that may be much larger than that of one single island ^[11]. In this study, the quality of oscillations has been investigated through the dynamic charging processes coupled with the possible instantaneous tunnel processes and then compared to previous research studies of similar structures.

The simulation tool uses algorithms based on the Monti-Carlo concept, a type of simulation that relies on repeated random sampling and statistical analysis to compute the results and trace the individual random tunneling events as well as collecting the data required to assess the quality of the resulting oscillations by adding the distribution of time between these events and then, calculating the finite frequency power spectral density of the resulting oscillations for the signal generated by those events. The modeling routine has been applied to characterize the operation of many sizes of homogeneous capacitive slanted two-dimensional arrays of small tunnel junctions. The rare event tunneling cases or the co-tunneling and the induced electrostatic background charges were excluded from this analytical work.

2.   Theory and model

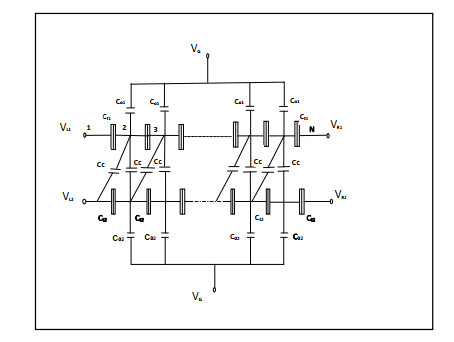
The equivalent nanostructure under study is shown in Figure 1 for the capacitive slanted two-dimensional arrays of tunnel junctions. Each collection set consists of a series of tunnel junctions 1, 2…, i, …, N, and they have tunnel capacitances C_t1 and C_t2, respectively, with assumed tunnel resistances R_t1 and R_t2, satisfying the condition R_t > > h/e², where h is the Plank's constant, for the purpose of minimizing the quantum mechanical effects. Both of them are connected by electrodes 1, 2…, i, …, N, at potential ф_i, and also, both are coupled to the ground plane via the stray capacitances C₀₁ and C₀₂, respectively. The two sets are linked together in the capacitive slanted manner by the capacitances Cc, before and after each junction of the lower and upper array, except their last junction connection, which is linked only before its junction. The circuit is capable of having voltage bias at its two left and two right voltage terminals.

The circuit architecture is different from that of the straight coupling using capacitances Cc of the 2D arrays as presented previously, as in ^[6], in how it has an extra capacitive element for each tunnel junction of the upper and lower array legs. The analysis is performed in a deficient voltage regime. For an excess single electron located at a given node inside any of the two arrays, the potential profile created will block further electrons from entering that part of the array. Under such conditions, the charges transport through the two sides of the array will be dominated by a single charge tunneling in each of the two arrays, from left to right or vice versa, until it finally exits at the other end. At higher bias conditions, the situation might change. More than one electron could be found inside the structure, and the time between events will be a combination of different sequences. The properties of the array resulting from such sequential tunneling mode could be studied in the time domain and its reflection in the frequency domain. Experimentally, it is most likely that successive tunneling events may take place across non-neighboring junctions. This would require the analysis of the various states transition multiple paths contributing to the transport processes. For the array nanostructure of Figure 1, when it is biased slightly near its bias V_th, the transport process is well defined by a single path for conduction, or the travel of the electron entering from one end. It moves to another one until it exits from the other end in only one direction, as considered in this study ^[12].

2.1.   Monte-Carlo computation method

The Monte-Carlo (MC) simulator tool starts with the Master Equation formalism to get the steady-state current I₀ passing in the tunnel junction network, and then computes the average time between the successive events. This is achieved by using several successive algorithms for identifying the list for the active states that hold the system in its steady-state. It is depicted that the steady-state and transport characteristics of single-electron circuits are strongly affected by the possible states in the system and the relationships between these states ^[13]. The simulator iterates "events" by repeatedly characterizing the circuit for a given set of input voltages and the clocked charge positions, and guesses the tunneling event that will occur next and updating the dependent and the independent circuit parameters accordingly by using the charge conservation law and the circuit matrix equations. The single-electron tunneling rate Γ through a tunnel junction depends on the change of the electrostatic free energy ∆E after and before a tunneling event, based on the Fermi golden role and the orthodox theory. The tunneling rate through the i^th tunnel junction is given as ^[8]:

where R_T is the tunnel resistance. Given the tunnel rate Γ for a tunneling event, the probability that the tunnel will occur in τ is given as ^[14]:

For small values of τ, that is for ∆τ, the tunnel interval ∆τ between two successive tunneling events is evaluated for all tunnel junctions by using a random number r uniformly distributed over the interval 0 ≤ r < 1, expressed as:

The tunneling event with the shortest ∆τ of all is chosen as the one that actually occurs. Then, the state of the circuit is updated. This simulation procedure is tracked repeatedly. Never the less, this MC method is precise; it is computationally expensive, especially for the larger extended systems of coupled devices. The model divides a total time of kT₀ (k~5, and T₀ is the average time between successive events) into W slots (W~1000). The Monte-Carlo simulation runs so that a total of M events crosses the junction under study (M~10⁷). The time between successive events is recorded in their corresponding time slots. The frequency components of the train of delta functions formed by the electrons crossing the reference tunnel junction are subsequently given by the Fourier relation:

where g_i(t) is the probability density function (PDF) for the time between successive events, considered as the percentage of the number of tunneling events counted in slot i to the number of events calculated within the time size of the slot and divided by the total M events crossing the junction under study. The probability density function is, therefore, estimated by the following relation:

where n_i is the number of tunneling events added up in slot i, ∆t is the slot's time frame size, and M represents the total events crossing the junction under study.

2.2.   Frequency spectrum analysis

The finite frequency spectrum of the current pulses detected at the measurement point is dependent on the pattern of tunneling events and the distribution of the time between these events (g_i), as stated above. The values obtained for g_i(t) is further used to get the power spectral density S(ω) expressed by the relation ^[15]:

where I₀ = <I> is the average tunneling current, G(ω) is the Fourier transform of the distribution of the time between events expressed in angular frequency (ω), and e is the electron charge. For a Poisson process, the power spectral density has a constant value, known as Scotty value, S(ω) = 2eI₀, independent of the frequency. It is considered a uniform noise power spectral density ^[15,16], as a result of the discreteness nature of the random tunneling for the events. The distribution of time between these events deviates from the Poisson behavior; in this case, the spectral density could be higher or lower than that of the Scotty value, and the curves for their probability density function shifts from the trend of the negative exponential distribution, depending on the distribution of the random tunneling events during a specific time of measurements, as reported previously for arrays of small tunnel junctions ^[6,17]. The tunnelling process in single electronic circuits is assumed to behave as Poisson point process. This Poisson point process is an arrival process described by a negative exponential distribution, f(t) = λe^-λt, where λ is the arrival rate of electrons. The time spent at any random state depends on the state's transition rates to any other states linked to this state by only one tunnel event. The PDF of the dwelling time at that state is obtained as ^[10,12]:

where Γ_j represents the tunnel rates for that state j. The time between two successive tunnel observations across the reference junction will correspond to the sum of all dwell times at all nodes in the array ^[12]. Let a variable T defines the time between successive events, which estimates the dwelling time at each node. The mean µ ( = <T> ) and the standard deviation σ for the time between successive events g_i(t) for the structure of the 2D array could be evaluated as follows:

Using Eq (8) above, we have:

where t_i represents the time measurement for the tunneling events across the junction under observation, i = 0, 1, 2, …, and ∆t is the time size of the slot. The charge passing through the junction could be subsequently found as:

The coefficient of variation β or the oscillation quality factor is defined as the ratio of the standard deviation divided by the mean. Using Eqs (9) and (10) above, it is equal to:

This quality factor β is a good measure for comparing different data sets to show their variability with their mean and standard deviation statistical analysis methods.

3.   Results and discussion

The present analysis aims to further investigate the characteristics of the electron transport through a homogeneous set of arrays built from small tunnel junctions. Few published studies for the structures are composed of two-dimensional arrays of tunnel junctions, as in ^[5,6]. One of them described the correlation behavior for the randomly generated tunneling events when applying a selected threshold bias condition to trigger the current passage across a targeted junction, as in ^[6]. As a result, there is a propagation of electrons throughout both arrays, until finally, they exit at either end of the two arrays. The SET's schematic circuit in this report differs from the earlier one in the coupling mechanism joining the two arrays. There is a direct straight coupling using one capacitive element joining the intersection points between the arrays set in the former circuit. In this latter one, the structure has additional capacitive components (capacitances Cc's) placed before each tunnel junction of them, except at their ends. This is done for better investigating the option of having an extra capacitive effect in the circuit operating conditions. Accordingly, it reflects the coherence of the random formed tunneling events. The circuit parameters entered as initial values for the simulation algorithms are the same as those figures assumed in modeling the previous study's equivalent circuit, as in ^[6]. Afterwards, these parameters have been adjusted for further tuning the outcome results as the new requirement needs i.e. the tunnel junction's capacitance C_t = 1.0e-17F, the ground plane (stray) capacitances C₀ = 1.0e-18F, the tunnel resistance R_t = 100kΩ, the coupling capacitances Cc = 1.0e-18F, and the nominal operation room temperature T = 1.0e-07K. These parameters are taken equal to each other and the corresponding ones in the different twin array. The arrays are attached to ideal voltage sources in both their left and right terminals. The bias voltage applied in any terminal is slightly above the threshold voltage. The analysis is conducted in a deficient voltage regime, i.e. the applied bias threshold voltage V_th is in terms of a few mille volts at either the left and the 2D arrays structure's right ends.

In this case study, the initial constant coupling relation estimated from the coupling capacitance Cc ratio and the tunneling capacitance Ct is assumed as Cc/Ct = 0.1. Moreover, the shorter arrays are referred to structures of lengths N = 3, 5, and 7 tunnel junctions, and that the relatively long arrays types are for those having N = 10, 15, 20, and 30 junctions, or more. For all these models, the bias conditions have been inspected for most possible combinations terminals from the upper and lower array leg's left and right sides. Also, the option of having a positive or a negative voltage injection is included. The case for operating only one array at a time is excluded. These bias different choices are used to select the proper potential arrangements in order to achieve the best modeling output results. Far ahead, it assists in plotting the distribution g_i(t)'s and the corresponding PDF charts having a close look at the optimum trends for these capacitive coupled nanostructures. As stated above, the simulator's hybrid part's initial stage uses the Master Equation (ME) approach for getting the steady-state current passing in the structure using the initial substituted parameters. In the ME stage, it is possible to address the best suitable bias from the profile of these single-electronic structures potential. Using these estimated bias voltages, the circuit would have an injected number of electrons that could transport in either array's legs.

Furthermore, it is ready to collect the rest of the results in the next step of the Monte-Carlo stage. The MC technique is very closely related to random experiments for which the specific outcome is not known in advance. One crucial characteristic is exploring the state's transition that is showing at any operation stage the electron transport patterns throughout these arrays for the three possible situations: the single electron, the electron-hole pair, and the combined single electron and electron-hole case. These state transitions are dependent primarily on Vth's setting, which are suitable for injection of a charge into these slanted coupled 2D arrays nanostructures ^[6].

A summary sheet is reported for the suitable threshold ranges for biasing to all the several length sizes of the nanostructures under study. Table 1, Table 2 and Table 3 below are three examples of the structure set of length N = 10 of small tunnel junctions. They list the possible triggering threshold voltage ranges, accompanied with the identified active states and followed by their observed random tunneling events, as well as their formed steady-state current measured at the reference junction. These tables were obtained from the simulated circuit for some chosen bias voltage ranges, before and after the initial parameter value of the coupling capacitance (Cc = 1.0E-18F), as the case for both options (A) and (B) in Tables 1 & 2. Then Cc is significantly changed (Cc = 0.50E-18F), as in option (C) in Table 3.

It is realized that any significant capacitive increase in Cc, is leading to a dramatic effect in the circuit's operation conditions, as it is demonstrated when comparing both options (A) & (B) to option (C) figures. In option (A), the circuit is injected from only its V_L1 and V_R2 terminals. It seemed that it has the better bias selection choice than option (B), which uses the left side terminals or V_L1 and V_L2. This, in terns, has a negative impact of increasing the total simulation time during the second important stage or the MC part, especially when considering larger values for the total number of events M for crossing the tested sample junction. When looking again to option (B), there is a larger counted number of states and events obtained in option (B) than that in (A), as the range of V_th has increased. Also, the steady-state currents have minimal values (<1.0E-15), and this is considered a numerical coding limitation in simulating this circuit; for that reason, option (A) is preferable to option (B). In Table 3 or option (C), and after substituting the new value for Cc, it appears that the V_th ranges are higher than the previously recorded ones in both Tables 1 & 2, but the corresponding states and events are considered as adequate and they could lead to good MC modeling tests. In this scenario logic steps, the best bias selection options have been assessed and made for all the other selected 2D structure lengths.

For observing the dynamics of the single-electron transport in these quantum dots structures, as well as the capacitive inter-array coupling touches for these nanoscale arrays, besides comparing their electronic oscillation characteristics against the previous remarks available for straight coupling style, as in ^[6], or these study findings with that reported to a similar structure circuit of an older one ^[5]. The array's initial parameter values are assumed constant ideal values with zero error tolerances. Besides, they are chosen equal to the previous ones, for having the same working conditions. Again here, the arrays were attached to an ideal voltage source. The output voltages, whether they are applied at any choice from the left and right terminals, are taken slightly above the selected threshold voltage. The analysis is carried out into a deficient voltage regime of a few voltages. At the same time, most probably, there is only one triggering terminal for either one of the two coupled arrays, and the remaining two ends were grounded. The development of a stable and reliable single-electronic system requires a setup of a precise schematic circuit design, besides the use of optimum parameter selections from within a suitable tested range for all its nominated elements, like the tunnel junction's capacitances and resistances, the stray capacitances, the arrays coupling capacitances and also, the nominal operation room temperature, to avoid the effect of other noise sources into the simulation study scope. What is left is only the shot noise, which in this case represents the signal itself or the created current fluctuations which are stochastics in nature, due to the generated random events. This applies to these long array structures as reported previously ^[15]. For example, an undesired small change in such ultra-small capacitances might significantly affect the numerical simulation outcomes and disturb the circuit operation's stability.

Figure 2 below illustrates the curves of the PDF for three shorter capacitive slanted linked 2D arrays of lengths (a) N = 3, (b) N = 5, and (c) N = 7 of small tunnel junctions. In each array size, all the possible MC simulated triggering choices for getting its g_i(t) density functions were plotted. This is in line with the earlier mentioned summary sheet that was obtained from the modeling beginning stage of the ME formalism, in which preliminary tests were done for exploring the arrays terminals selection from among the available four ends (V_L1, V_L2, V_R1, and V_R2) to bias the 2D array structure with a suitable threshold voltage. Here, these curves show the diversity found for the possible selection of the bias ends for a nanostructure specific length when comparing the oscillation characteristics or the distribution of time between events plots, in this case, for each choice.

It is observed in Figure 3 below, under the same previous experimental operation conditions, the density function g_i(t)'s curves or the distribution for the time between successive events leaving the array increases, while the structure length N is enlarged, as an expected result due to the rise in the number of the accumulated tunneling events that are needed to traverse the electrons in much longer arrays sizes. The reduction of the top trends for these probability density functions for the increase in N indicates that the time fluctuations between the events do increase in terms. This figure includes the g_i(t) curves for the arrays of lengths N = 3, 5, 7, 10, and 15. They have been drawn using the mentioned given above initial values. They also include two more extra plots for the arrays N = 10 & 15 for their g_i(t)'s after changing the coupling capacitances Cc to another larger value (Cc = 0.05E-18F). The correlation of these structures' generated tunneling events is noticed in a representation of a linear scale plot. For the shorter arrays of lengths N = 3, 5, and 7, all of them are having sharp peaks for their plotted PDF curves, and there is also an indicator for a presence of another peak within the same curve lines, as it is observed for arrays N = 5 and 7. For the arrays N = 10 and 15, the indication of their second peak are found in their extra added curves, named N = 10 (After) and 15 (After), as a reflection for the case of a new trends due to the increase in Cc capacitive value. Figure 4 represents the spectral densities S(f)'s curves for nanostructures of Figure 3 above. It shows, the tunneling events oscillations for the corresponding frequency contents again, and one more time, the bends of the peaks are visible in the frequency domain. These peaks are near the value of 0.5 of the normalized average oscillations frequency f_o and tend to reach its absolute value of 1.0; and the second peak or their second harmonic peak is closing to double this frequency value, as it is clearly noticed for N = 10 and 15, before increasing Cc. The oscillation characteristics seen here are in contrast and even look better in terms of its events correlation behavior than those reported previously for the straight coupling scenario, when comparing the trends for the same shorter sizes, as in ^[6]. Accordingly, it could be figured out that it is not possible to get some results in this work initially before increasing both Cc and the stray capacitances for their g_i(t)'s and S(f)'s for the longer arrays lengths N = 20 or 30, and even more. This remark is demonstrated in Figure 3, by showing the findings for arrays N = 10, before and after the addition of the capacitive effect, and it assists in the start for the appearance of another peak in their g_i(t)'s, or another second harmonic peak in their S(f)'s.

The oscillations trends for the relatively longer arrays N = 10, 15, 20, and 30 for the two slanted coupled one-dimensional arrays are shown in Figures 5 and 6, respectively. Results for arrays 20 and 30 were obtained only when all the stray capacitances for the two structure array legs values were changed to C₀₁ = 0.50E-18 & C₀₂ = 0.50E-18, respectively. This confirms that the stray capacitances or grounding capacitance are having an essential role in the functionality of operating these types of nanostructures in terms of controlling the suitable V_th ranges for biasing them using two terminals, as explained earlier in this study. The findings here in this work match those highlighted previously in an earlier report as in ^[5]. The values of the selected nanoscale elements used in this study simulation tool for either the capacitances Cc or C_0, are chosen such that the coupling factor is equal to 0.1 as mentioned earlier in this study, and thus C₀ is in its small limit. It is reported previously that V_th is proportional to 1/C_t (see Eq (24), in ^[5]). As C_t in this analysis work is fixed, it is evident that the suitable V_th ranges are proportional to the array lengths as remarked above in this work.

4.   Conclusion

In this work a comprehensive analysis is presented of single-electronic generated oscillations in scalable capacitive coupled two-dimensional arrays of nanoscale tunnel junctions, which operate similarly to nanostructures forming two series of quantum dots that are having surrounding Femi sea for injecting electron charges in them. It is concluded that the choice of adding a capacitive element enhances the performance of these nanoelectronic circuit operations, when compared to the straight coupling style, besides the importance of the special consideration of deciding on the other two important factors: the stray capacitances and the array lengths, as also both of them are having a role in determining the suitable threshold voltage ranges for triggering these 2D arrays nanostructures. It is expected that the overall indicators for the oscillation quality factor (β) will be enhanced better than that for the straight coupled 2D arrays, by choosing the best selection for the bias ends, as well as the precise values to be nominated for these three important nanoscale elements: the coupling capacitances, stray capacitances, and the array lengths. The capabilities of the scheme illustrated in this simulation for these coupled two-dimensional arrays are open for further extensions after more adjustments are done for the simulation algorithm's initial setup values for the two arrays.

Conflict of interest

The authors declare that there is no conflict of interest in this manuscript.