Weak Roman domination in rooted product graphs

1.   Introduction

The following approach to protection of a simple graph was described by Cockayne et al. ^[5]. Let $G$ be a simple graph with vertex set $V(G)$ and let $S\subseteq V(G)$ be a nonempty set. Suppose that one or more guards are stationed at the vertices belonging to $S$ and that a guard stationed at a vertex can deal with a problem at any vertex in its closed neighbourhood. We say that $G$ is protected under the placement of guards in $S$ if there is at least one guard available to handle a problem at any vertex. Consider a function $f: V(G)\longrightarrow \{0, 1, 2, \dots, k\}$ where $f(v)$ is the number of guards stationed at $v$, and let $V_i = \{v\in V(G):\; f(v) = i\}$ for every $i\in \{0, 1, 2, \dots, k\}$. Notice that $S = V(G)\setminus V_0$. We will identify the function $f$ with the sets $V_0, \dots, V_k$ induced by $f$ and write $f(V_0, V_1, \dots, V_k).$ The weight of $f$ is defined to be

A vertex $v\in V(G)$ is undefended with respect to $f$ if $f(v) = 0$ and $f(u) = 0$ for every vertex $u$ adjacent to $v$. We say that $G$ is protected under the function $f$ if $G$ has no undefended vertices with respect to $f$.

In fact, the simplest form of protection of a graph is known under the name of domination. We say that $f(V_0, V_1)$ is a dominating function (DF) if $G$ is protected under $f$. This classical method of protection has been studied extensively ^[10,11]. The domination number is defined to be

Obviously, $f(V_0, V_1)$ is a DF if and only if $V_1$ is a dominating set. A dominating set of cardinality $\gamma(G)$ is called a $\gamma(G)$-set.

We now define a particular subclass of protected graphs considered in ^[12]. The functions in this subclass protect the graph according to a certain strategy. Let $f(V_0, V_1, V_2)$ be a function on $G$. We say that $v\in V_0$ is protected under $f$ if there exists a neighbour $u$ of $v$ such that $u\in V_1\cup V_2$ and $G$ does not have undefended vertices under the function $f': V(G)\longrightarrow \{0, 1, 2\}$ defined by $f'(v) = 1$, $f'(u) = f(u)-1$ and $f'(z) = f(z)$ for every $z\in V(G)\setminus\{u, v\}$. In such a case, we say that $v$ is protected by $u$ under $f$. A weak Roman dominating function (WRDF) is a function $f(V_0, V_1, V_2)$ such that every $v\in V_0$ is protected under $f$. The weak Roman domination number is defined to be

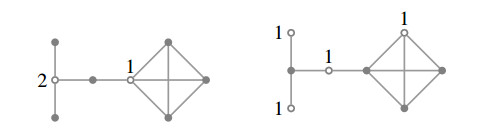
A WRDF of weight $\gamma_r(G)$ is called a $\gamma_r(G)$-function. For instance, for the graph shown in Figure 1, on the left, a $\gamma_r(G)$-function can place $2$ guards at the white-coloured vertex of degree three and one guard at the other white-coloured vertex. This concept of protection was introduced by Henning and Hedetniemi ^[12] and studied further, for instansce, in ^{[1,2,3,4,13,14,15,16,17,18]}.

The problem of computing $\gamma_r(G)$ is NP-hard^*, even when restricted to bipartite or chordal graphs. This suggests finding the weak Roman domination number for special classes of graphs or obtaining good bounds on these invariant. This is precisely the aim of this work in which we obtain closed formulae for the weak Roman domination number of rooted product graphs. As a particular case of the study, we derive the corresponding formula for corona graphs. Furthermore, we show that the use of rooted product graphs is a useful tool to show that the problem of computing the weak Roman domination number of a graph is NP-hard.

^*As the decision problem is NP-Complete ^[12].

Given a graph $G$ of order $n(G)$ and a graph $H$ with root vertex $v$, the rooted product $G\circ_v H$ is defined as the graph obtained from $G$ and $H$ by taking one copy of $G$ and $n(G)$ copies of $H$ and identifying the $i^{th}$ vertex of $G$ with the vertex $v$ in the $i^{th}$ copy of $H$ for each $i\in \{1, \dots, n(G)\}$.

For every $x\in V(G)$, the copy of $H$ in $G\circ_v H$ containing $x$ will be denoted by $H_x$ and for any WRDF $f$ on $G\circ_v H$, the restriction of $f$ to $V(H_x)$ and $V(H_x)\setminus \{x\}$ will be denoted by $f_x$ and $f_x^-$, respectively. Notice that $V(G\circ_v H) = \cup_{x\in V(G)}V(H_x)$ and so, if $f$ is a $\gamma_{r}(G\circ_v H)$-function, then

Throughout the paper, we will use the notation $K_t$, $K_{1, t-1}$, $C_t$ and $P_t$ for complete graphs, star graphs, cycle graphs and path graphs of order $t$, respectively. We will use the notation $G \cong H$ if $G$ and $H$ are isomorphic graphs. For a vertex $v$ of a graph $G$, $N(v)$ will denote the set of neighbours or open neighbourhood of $v$ in $G$. The closed neighbourhood, denoted by $N[v]$, equals $N(v) \cup \{v\}$. A vertex $v\in V(G)$ such that $N[v] = V(G)$ is said to be a universal vertex.

A leaf of a graph $H$ is a vertex of degree one, while a support vertex of $H$ is a vertex adjacent to at least one leaf. We denote the set of leaves of $H$ as $L(H)$ and the set of support vertices of $H$ as $S(H)$.

For the remainder of the paper, definitions will be introduced whenever a concept is needed.

2.   Weak Roman domination of rooted product graphs

To begin the analysis we need to establish some preliminary lemmas.

Lemma 2.1. Let $f(V_0, V_1, V_2)$ be a $\gamma_{r}(G\circ_v H)$-function. For any $x\in V(G)$, $\omega(f_x)\geq \gamma_{r}(H)-1$. Furthermore, if $\omega(f_x) = \gamma_{r}(H)-1$, then $f(x) = 0$.

Proof. Suppose that there exists $x\in V(G)$ such that $\omega(f_x)\leq\gamma_{r}(H)-2$. If $f(x) > 0$ then $f_x$ is a WRDF on $H_x$ of weight at most $\gamma_r(H)-2$, yielding a contradiction. Now, if $f(x) = 0$, then the function $g$, defined from $f_x$ by $g(v) = f_x(v)$ for every $v\neq x$ and $g(x) = 1$, is a WRDF on $H_x$ of weight $\omega(g)\leq \gamma_{r}(H)-1$, which is a contradiction. Therefore, $\omega(f_x)\geq \gamma_{r}(H)-1$ for every $x\in V(G)$.

Now, suppose that there exists $x\in V(G)$ such that $\omega(f_x) = \gamma_{r}(H)-1$. If $f(x) > 0$, then $f_x$ is a WRDF on $H$ of weight $\omega(f_x) < \gamma_{r}(H)$, which is a contradiction. Hence, $f(x) = 0$.

Given a $\gamma_{r}(G\circ_v H)$-function $f(V_0, V_1, V_2)$, we define the sets

and

By Lemma 2.1, if $\mathcal{B}_f\ne \emptyset$, then $\{\mathcal{A}_f, \mathcal{B}_f\}$ is a partition of $V(G)$ and so

Lemma 2.2. If $f(V_0, V_1, V_2)$ is a $\gamma_{r}(G\circ_v H)$-function, then every vertex in $\mathcal{B}_f$ is adjacent to a vertex in $\mathcal{A}_f\setminus V_0$.

Proof. By Lemma 2.1 we have that $\mathcal{B}_f\subseteq V_0$. Now, since $f$ is a $\gamma_{r}(G\circ_v H)$-function, if there exists $x\in \mathcal{B}_f$ such that $N(x)\cap V(G)\cap (V_1\cup V_2) = \emptyset$, then $f_x$ is a WRDF on $H_x$ of weight $\omega(f_x) = \gamma_r(H)-1$, which is a contradiction. Therefore, every vertex $x\in \mathcal{B}_f$ is adjacent to some vertex belonging to $V(G)\cap (V_1\cup V_2)\subseteq \mathcal{A}_f\setminus V_0$.

Corollary 2.3. If $f$ is a $\gamma_{r}(G\circ_v H)$-function, then $\mathcal{A}_f$ is a dominating set of $G$.

Lemma 2.4. If $f(V_0, V_1, V_2)$ is a $\gamma_{r}(G\circ_v H)$-function such that $\mathcal{B}_f\neq \emptyset$, then the following statements hold.

(i) $\omega(f_x) = \gamma_{r}(H)$ for every $x\in \mathcal{A}_f\cap (V_0\cup V_1)$.

(ii) $\omega(f_x)\leq \gamma_{r}(H)+1$ for every $x\in \mathcal{A}_f\cap V_2$.

Proof. Let $f$ be a $\gamma_{r}(G\circ_v H)$-function such that $\mathcal{B}_f\neq \emptyset$. First, suppose that there exists $x\in \mathcal{A}_f\cap (V_0\cup V_1)$ such that $\omega(f_x)\geq \gamma_{r}(H)+1$. Let $u\in \mathcal{B}_f$ and define a function $g$ on $G\circ_vH$ by $g(w) = f(w)$ for every $w\notin V(H_x)$, $g(x) = 1$ and $g_x^-$ is induced by $f_u^-$. It is readily seen that $g$ is a WRDF on $G\circ_vH$ and $\omega({g})\le \omega(f)-1 = \gamma_{r}(G\circ_v H)-1$, which is a contradiction. Hence, $\omega(f_x) = \gamma_{r}(H)$ for every $x\in \mathcal{A}_f\cap (V_0\cup V_1)$.

Now, suppose that there exists $x\in \mathcal{A}_f\cap V_2$ such that $\omega(f_x)\geq \gamma_{r}(H)+2$. Let $u\in \mathcal{B}_f$ and define a function $g$ on $G\circ_vH$ by $g(w) = f(w)$ for every $w\notin V(H_x)$, $g(x) = 2$ and $g_x^-$ is induced by $f_u^-$. It is readily seen that $g$ is a WRDF on $G\circ_vH$ and $\omega(g)\le \omega(f)-1 = \gamma_{r}(G\circ_v H)-1$, which is a contradiction. Hence, $\omega(f_x)\leq\gamma_{r}(H)+1$ for every $x\in \mathcal{A}_f\cap V_2$.

Let us define the sets

where $i\in \{0, 1, 2\}$, $j\in \{\gamma_r(H), \gamma_r(H)+1\}$. For simplicity, we will use the notation $m = \gamma_r(H)$ in some lemmas and proofs, specially when $\gamma_r(H)$ is a superscript.

From Lemma 2.4 we have the following consequence.

Corollary 2.5. If $f(V_0, V_1, V_2)$ is a $\gamma_{r}(G\circ_v H)$-function such that $\mathcal{B}_f\neq \emptyset$, then

Lemma 2.6. Let $f$ be a $\gamma_{r}(G\circ_v H)$-function. If $\mathcal{B}_f\neq \emptyset$, then there exists a $\gamma_{r}(G\circ_v H)$-function $g$ such that $\mathcal{B}_g = \mathcal{B}_f$ and

Proof. Let $f$ be a $\gamma_{r}(G\circ_v H)$-function with $\mathcal{B}_f\neq \emptyset$. Notice that, by Lemma 2.2, $\mathcal{A}_f\neq\emptyset$. Now, since $f$ is a $\gamma_{r}(G\circ_v H)$-function, if $\mathcal{A}_f^{2, m}\neq\emptyset$, then $\mathcal{A}_f^{2, m+1} = \emptyset$. Furthermore, if $\mathcal{A}_f^{1, m}\neq\emptyset$ and $\mathcal{A}_f^{0, m}\neq\emptyset$, then we fix $y\in\mathcal{A}_f^{1, m}$ and we define a $\gamma_{r}(G\circ_v H)$-function $g$ such that for every $x\in \mathcal{A}_f^{0, m}$, $g_x$ is induced by $f_y$ and $g_z = f_z$ for every $z\in V(G)\setminus \mathcal{A}_f^{0, m}$. In such a case, $\mathcal{A}_g^{1, m}\neq\emptyset$ and $\mathcal{A}_g^{0, m} = \emptyset$.

Using similar arguments we can show that if $\mathcal{A}_f^{2, m}\neq\emptyset$, then there exists a $\gamma_{r}(G\circ_v H)$-function $g$ such that $\mathcal{A}_g^{0, m}\cup \mathcal{A}_g^{1, m}\cup \mathcal{A}_g^{2, m+1} = \emptyset$.

Hence, by Corollary 2.5 we conclude that

Finally, if $\mathcal{A}_g^{0, m}\ne \emptyset$, then we fix $y\in \mathcal{B}_g$ and we define a function $h$ on $G\circ_v H$ by $h_z = g_z$ for every $z\in V(G)\setminus \mathcal{A}_g^{0, m}$ and for every $x\in \mathcal{A}_g^{0, m}$ we set $h(x) = 1$ and $h_x^-$ is induced by $g^-_y$. Notice that $h$ is a WRDF of weight $\omega(h) = \omega(g) = \omega(f)$ and $\mathcal{A}_h\in \{ \mathcal{A}_h^{1, m}, \mathcal{A}_h^{2, m}, \mathcal{A}_h^{2, m+1}, \mathcal{A}_h^{1, m}\cup\mathcal{A}_h^{2, m+1}\}.$ Therefore, the result follows.

Proposition 2.7. If there exists a $\gamma_r(G\circ_v H)$-function $f$ such that $\mathcal{B}_f\neq\emptyset$, then $\gamma_{r}(G\circ_v H)\leq n(G)(\gamma_r(H)-1)+\gamma_r(G)$.

Proof. Let $f$ be a $\gamma_r(G\circ_v H)$-function such that $\mathcal{B}_f\neq\emptyset$. Let $x\in\mathcal{B}_f$ and consider a $\gamma_r(G)$-function $h$. By Lemma 2.1, $f(x) = 0$, so that $f_x^-$ is a WRDF on $H_x-\{x\}$. Consider the function $g$ on $G\circ_v H$ such that for every vertex $u\in V(G)$, $g_u^-$ is induced by $f_x^-$ and $g(u) = h(u)$. Thus, $g$ is a WRDF on $G\circ_v H$ of weight $n(G)(\gamma_r(H)-1)+\gamma_r(G)$, concluding that $\gamma_{r}(G\circ_v H)\leq n(G)(\gamma_r(H)-1)+\gamma_r(G)$.

Theorem 2.8 (Trichotomy). For any graph $G$, any graph $H$ and any $v\in\; V(H)$,

Furthermore, the following statements hold for any pair of $\gamma_{r}(G\circ_v H)$-functions $f$ and $f'$.

● $\mathcal{B}_f = \; \emptyset$ if and only if $\mathcal{B}_{f'} = \; \emptyset$.

● $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$ if and only if $\mathcal{B}_f = \; \emptyset$.

Proof. Let $f(V_0, V_1, V_2)$ be a $\gamma_{r}(G\circ_v H)$-function. If $\mathcal{B}_f = \; \emptyset$, then $\omega(f_x)\ge \gamma_r(H)$ for every $x\in V(G)$, which implies that $\gamma_{r}(G\circ_v H)\ge n(G)\gamma_r(H)$. Hence, $\gamma_{r}(G\circ_v H) = n(G)\gamma_r(H)$, as we always can construct a WRDF $g$ such that $g_x = \gamma_r(H)$ for every $x\in V(G)$.

From now on we consider the case $\mathcal{B}_f\neq\emptyset$, and so we can assume that $f$ is a $\gamma_{r}(G\circ_v H)$-function which satisfies Lemma 2.6.

First, suppose that there exists $x\in \mathcal{B}_f$ such that $f(y) > 0$ for some $y\in N(x)\cap V(H_x)$. Let $S$ be a $\gamma(G)$-set and consider the function $g$ on $G\circ_v H$ where $g_u^-$ is induced by $f_x^-$ for every $u\in V(G)$, $g(u) = 1$ for every $u\in S$ and $g(u) = 0$ for every $u\in V(G)\setminus S$. Notice that for every $u\in V(G)$, $g_u^-$ is a WRDF on $H_u-\{u\}$. Moreover, since $S$ is a dominating set of $G$ and for every $u\in V(G)\setminus S$ there exists a vertex $y\in N(u)\cap V(H_u)$ with $g(y) > 0$, we conclude that every vertex $u\in V(G)\setminus S$ is protected under $g$ by some vertex in $S$. Hence, $g$ is a WRDF on $G\circ_v H$ of weight $n(G)(\gamma_r(H)-1)+\gamma(G)$, concluding that $\gamma_{r}(G\circ_v H)\leq n(G)(\gamma_r(H)-1)+\gamma(G)$. To show that in fact this is an equality, we observe that Corollary 2.3 and Lemma 2.4 lead to

Hence, $\gamma_{r}(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G)$.

From now on we suppose that $N(x)\cap V(H_x)\subseteq V_0$ for every $x\in \mathcal{B}_f$. Notice that in this case every vertex $x\in \mathcal{B}_f$ must be protected under $f$ by some vertex in $\mathcal{A}_f$. Furthermore, since $f$ satisfies Lemma 2.6, $\mathcal{A}_f\subseteq V_1\cup V_2$. Hence, the restriction of $f$ to $V(G)$ is a WRDF on $G$, and so

Since $f$ satisfies Lemma 2.6, we differentiate the following cases.

Case 1. $\mathcal{A}_f = \mathcal{A}_f^{1, m}$. In this case,

Hence, by Proposition 2.7 we conclude that $\gamma_{r}(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$.

Case 2. $\mathcal{A}_f = \mathcal{A}_f^{2, m}$. By Corollary 2.3 we have that $|\mathcal{A}_f|\ge \gamma(G)$, so that

To show the equality, we take a $\gamma(G)$-set $S$ and fix $x\in \mathcal{A}_f$ and $y\in \mathcal{B}_f$. Consider the function $g$ on $G\circ_v H$ such that for every $u\in S$, $g_u$ is induced by $f_x$ and for every $u\in V(G)\setminus S$, $g_u$ is induced by $f_y$. Then, $g(u) = 2$ for every $u\in S$ and we have that $g$ is a WRDF on $G\circ_v H$ of weight $n(G)(\gamma_r(H)-1)+\gamma(G)$, concluding that $\gamma_{r}(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_{}(G)$.

Case 3. $\mathcal{A}_f = \mathcal{A}_f^{2, m+1}$. By Corollary 2.3 we have that $|\mathcal{A}_f|\ge \gamma(G)$ and since $\gamma_r(G)\le 2\gamma(G)$ we deduce that

Hence, by Proposition 2.7 we conclude that $\gamma_{r}(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$.

Case 4. $\mathcal{A}_f = \mathcal{A}_f^{1, m}\cup\mathcal{A}_f^{2, m+1}$. In this case,

Thus,

Finally, by Proposition 2.7 we conclude that $\gamma_{r}(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$.

Therefore, $\gamma_{r}(G\circ_v H)\in \{n(G)(\gamma_{r}(H)-1)+\gamma_{}(G), n(G)(\gamma_{r}(H)-1)+\gamma_{r}(G), n(G)\gamma_{r}(H)\}.$ The remaining statements follow from the previous analysis.

We now proceed to consider the different cases of $\gamma_{r}(G\circ_v H)$. It is straightforward that for $G\cong \overline{K}_t$,

In order to stablish a sufficient and necessary condition to assure that $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$ when $G$ is nonempty, we need to state the following notation.

Given a nontrivial graph $H$ and a vertex $v\in V(H)$, the graph obtained from $H$ by removing vertex $v$ will be denoted by $H-\{v\}$. Notice that any $\gamma_{r}(H-\{v\})$-function can be extended to a WRDF on $H$ by assigning the value $1$ to $v$, which implies that the following lemma holds.

Lemma 2.9. For any nontrivial graph $H$ and any $v\in V(H)$,

We also need the following lemma.

Lemma 2.10. Let $f$ be a $\gamma_{r}(G\circ_v H)$-function. If $\mathcal{B}_f\ne \emptyset$, then $\gamma_{r}(H-\{v\}) = \gamma_{r}(H)-1$.

Proof. Let $x\in \mathcal{B}_f$. Notice that $\omega(f_x) = \gamma_{r}(H)-1$, by definition of $\mathcal{B}_f$. Now, by Lemma 2.1, $f(x) = 0$, which implies that that $f_x^-$ is a WRDF on $H_x-\{x\}$ of weight $\gamma_{r}(H)-1$, and so $\gamma_{r}(H-\{v\}) = \gamma_{r}(H_x-\{x\})\le \gamma_{r}(H)-1$. By Lemma 2.9 we conclude the proof.

Theorem 2.11. Let $G$ be a nonempty graph. Given a graph $H$ and a vertex $v\in V(H)$, $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$ if and only if $\gamma_{r}(H-\{v\})\ge \gamma_{r}(H)$.

Proof. Suppose that $\gamma_{r}(H-\{v\}) < \gamma_{r}(H)$. In such a case, $\gamma_{r}(H-\{v\}) = \gamma_{r}(H)-1$ by Lemma 2.9. Hence, from any $\gamma_{r}(H-\{v\})$-function and any $\gamma_{r}(G)$-function we can construct a WRDF on $G\circ_v H$ of weight $n(G)(\gamma_{r}(H)-1)+\gamma_{r}(G)$, concluding that $\gamma_{r}(G\circ_v H)\le n(G)(\gamma_{r}(H)-1)+\gamma_{r}(G) < n(G)\gamma_{r}(H)$. Therefore, if $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$, then $\gamma_{r}(H-\{v\})\ge \gamma_{r}(H)$.

Now, assume that $\gamma_{r}(H-\{v\})\ge \gamma_{r}(H)$ and let $f$ be a $\gamma_{r}(G\circ_v H)$-function. By Lemma 2.10 we have that $\mathcal{B}_f = \emptyset$, and so Theorem 2.8 leads to $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$.

From Lemma 2.9 and Theorems 2.8 and 2.11 we deduce the following result.

Theorem 2.12. Let $G$ be a nonempty graph. For any graph $H$ and any vertex $v\in V(H)$, the following statements are equivalent.

(ⅰ) $\gamma_{r}(H-\{v\}) = \gamma_{r}(H)-1$.

(ⅱ) $\gamma_{r}(G\circ_v H) = n(G)(\gamma_{r}(H)-1)+\gamma_r(G)$ or $\gamma_{r}(G\circ_v H) = n(G)(\gamma_{r}(H)-1)+\gamma(G)$.

We now focus on the case of graphs $G$ with $\gamma_r(G) > \gamma(G)$.

Theorem 2.13. Let $G$ be a graph such that $\gamma_r(G) > \gamma(G)$. For any graph $H$ and any vertex $v\in V(H)$, $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G)$ if and only if $\gamma_r(H-\{v\}) = \gamma_r(H)-1$ and one of the following conditions holds.

(ⅰ) There exists a $\gamma_r(H-\{v\})$-function $g$ such that $g(y) > 0$ for some $y\in N(v)$.

(ⅱ) There exists a $\gamma_r(H)$-function $h$ such that $h(v) = 2$.

Proof. Assume that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G)$. By Theorem 2.12, $\gamma_r(H-\{v\}) = \gamma_r(H)-1$. Suppose by contradiction that conditions (i) and (ii) do not hold. Let $f$ be a $\gamma_r(G\circ_v H)$-function. Since $\gamma(G) < \gamma_r(G)\le n(G)$, we have that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G) < n(G)\gamma_r(H)$, concluding that $\mathcal{B}_f\neq \emptyset$ by Theorem 2.8. We can assume that $f$ satisfies Lemma 2.6 and so $\mathcal{A}_f\in \{\mathcal{A}_f^{1, m}, \mathcal{A}_f^{2, m}, \mathcal{A}_f^{2, m+1}, \mathcal{A}_f^{1, m}\cup\mathcal{A}_f^{2, m+1}\}$. Moreover, $\mathcal{A}_f\neq \mathcal{A}_f^{2, m}$ since (ii) does not hold. Hence $\mathcal{A}_f\in \{\mathcal{A}_f^{1, m}, \mathcal{A}_f^{2, m+1}, \mathcal{A}_f^{1, m}\cup\mathcal{A}_f^{2, m+1}\}$. For any $x\in \mathcal{B}_f$, we have that $f(x) = 0$ (by Lemma 2.1), which implies that $f_x^-$ is $\gamma(H-\{x\})-$function, and since (i) does not hold, $N(x)\cap V(H_x)\subseteq V_0$. Hence, we only have to consider Cases 1, 3 and 4 of the proof of Theorem 2.8, to obtain that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$, which is a contradiction as $\gamma(G) < \gamma_r(G)$. Hence, conditions (i) and (ii) hold.

Now, assume that $\gamma_r(H-\{v\}) = \gamma_r(H)-1$. First, suppose that condition (i) holds. So, consider a $\gamma_r(H-\{v\})$-function $h$ such that $h(y) > 0$ for some $y\in N(v)$. Let $S$ be a $\gamma(G)$-set and consider the function $l$ on $G\circ_v H$ such that for every vertex $x\in V(G)$, $l^-_x$ is induced by $h$, $l(x) = 1$ if $x\in S$ and $l(x) = 0$ if $x\not\in S$. Notice that $l$ is a WRDF on $G\circ_v H$ of weight $\omega(l) = n(G)(\gamma_r(H)-1)+\gamma(G)$, which implies that $\gamma_r(G\circ_v H)\leq n(G)(\gamma_r(H)-1)+\gamma(G)$. Thus, by Theorem 2.12 we conclude that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G)$. Now, suppose that (i) does not hold and (ii) holds. As $\gamma_r(H-\{v\}) = \gamma_r(H)-1$ and $G$ is not empty, by Theorem 2.12 we have that $\gamma_r(G\circ_v H) < n(G)\gamma_r(H)$. Hence, by Theorem 2.8 we conclude that $\mathcal{B}_g\neq \emptyset$ for every $\gamma_r(G\circ_v H)$-function $g$. We can assume that $g$ satisfies Lemma 2.6, i.e., $\mathcal{A}_g\in \{\mathcal{A}_g^{1, m}, \mathcal{A}_g^{2, m}, \mathcal{A}_g^{2, m+1}, \mathcal{A}_g^{1, m}\cup\mathcal{A}_g^{2, m+1}\}$. Moreover, since condition (ii) holds, we can claim that $\mathcal{A}_g^{2, m}\ne\emptyset$, so that $\mathcal{A}_g = \mathcal{A}_g^{2, m}$. Now, for any $x\in \mathcal{B}_g$, we have that $g(x) = 0$ and $g_x^-$ is $\gamma(H-\{x\})$-function and, since (i) does not hold, $N(x)\cap V(H_x)\subseteq V_0$. To conclude the proof we only have to consider Case 2 of the proof of Theorem 2.8, obtaining that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G)$.

From Theorems 2.12 and 2.13 we inmediately have the following result.

Theorem 2.14. Let $G$ be a graph such that $\gamma(G) < \gamma_r(G)$. For any graph $H$ and any vertex $v\in V(H)$, $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$ if and only if $\gamma_r(H-\{v\}) = \gamma_r(H)-1$ and the following conditions hold:

(ⅰ) For every $\gamma_r(H-\{v\})$-function $g$, $g(y) = 0$ for every $y\in N(v)$.

(ⅱ) For every $\gamma_r(H)$-function $h$, $h(v)\neq 2$.

We now consider some particular cases of $G$ and $H$.

Theorem 2.15. Given a graph $G$, a nontrivial graph $H$ and a vertex $v\in V(H)$, $\gamma_r(G\circ_v H) = n(G)$ if and only if $H\cong K_t$, $t\ge 2$.

Proof. If $H \cong K_t$, where $t\ge 2$, then $\gamma_r(H-\{v\}) = \gamma_r(K_{t-1}) = 1$ for every vertex $v\in V(H)$. Hence, by Theorem 2.11 we have $\gamma_r(G\circ_v H) = n(G)\gamma_r(K_t) = n(G)$.

On the other hand, if $H\not \cong K_t$, then $\gamma_r(H)\ge 2$, and by Theorem 2.8 we have $\gamma_r(G\circ_v H)\ge n(G)(\gamma_r(H)-1)+\gamma(G) > n(G).$ Therefore, the result follows.

Theorem 2.16. Let $G$ be a graph, $H$ a connected graph and $v\in V(H)$. If $\gamma_r(H) = 2$, then the following statement hold.

(ⅰ) If $H-\{v\}\not\cong K_t$, then $\gamma_r(G\circ_v H) = 2n$.

(ⅱ) If $H-\{v\}\cong K_t$, then $\gamma_r(G\circ_v H) = n(G)+\gamma(G)$.

Proof. If $H-\{v\}\not\cong K_t$ then $\gamma_r(H-\{v\})\geq 2 = \gamma_r(H)$. Hence, Theorem 2.11 leads to $\gamma_r(G\circ_v H) = n(G)\gamma_r(H) = 2n(G)$. On the other hand, if $H-\{v\}\cong K_t$ then $\gamma_r(H-\{v\}) = 1 = \gamma_r(H)-1$. Now, since $H$ is connected and $H-\{v\} = K_t$, for any $y\in N(v)$ we can define a $\gamma_r(H-\{v\})$-function $g$ such that $g(y) = 1$ and $g(x) = 0$ for every $x\ne y$. Therefore, by Theorem 2.13 (and by Theorem 2.12 for the case $\gamma_r(G) = \gamma(G)$) we conclude that $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma(G) = n(G)+\gamma(G)$.

Theorem 2.17. Let $G$ be a graph, $H$ a connected graph and $u\in V(H)$. If $f(u) = 2$ for every $\gamma_r(H)$-function $f$, then $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$ for every $v\in N(u)$.

Proof. Assume that $f(u) = 2$ for every $\gamma_r(H)$-function $f$, and let $v\in N(u)$. Suppose that $\gamma_r(G\circ_v H)\neq n(G)\gamma_r(H)$. By Theorem 2.11 and Lemma 2.9 we conclude that $\gamma_r(H-\{v\}) = \gamma_r(H)-1$. Let $g$ be a $\gamma_r(H-\{v\})$-function. If $g(u) = 2$, then we define a function $h$ on $H$ such that $h(w) = g(w)$ for every $w\neq v$ and $h(v) = 0$. Observe that $h$ is a WRDF on $H$ with $\omega(h) = \omega(g) = \gamma_r(H)-1$, which is a contradiction. If $g(u)\leq 1$, then we define a function $h$ on $H$ such that $h(w) = g(w)$ if $w\neq v$ and $h(v) = 1$. In this case, $h$ is a $\gamma_r(H)$-function with $h(u)\neq 2$, which is a contradiction. Therefore, $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

The next theorem considers the case in which the root of $H$ is a support vertex.

Theorem 2.18. Let $G$ be a graph and $H$ a connected graph. If $v\in S(H)$ then $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

Proof. By Theorem 2.11, it is enough to show that $\gamma_r(H-\{v\})\geq\gamma_r(H)$. Let $u\in L(H)\cap N(v)$ and notice that for any $\gamma_r(H-\{v\})$-function $g$, $g(u) = 1$. Then the function $f$ on $H$ defined as $f(v) = 0$ and $f(w) = g(w)$ if $w\in V(H)-\{v\}$ is a WRDF on $H$ concluding that $\gamma_r(H-\{v\})\geq \omega(g) = \omega(f) = \gamma_r(H)$.

Theorem 2.19. Let $G$ be a graph, $H$ a graph and $v\in V(H)$. If $g(v)\neq 1$ for every $\gamma_r(H)$-function $g$, then $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

Proof. Assume that $g(v)\neq 1$ for every $\gamma_r(H)$-function $g$, and suppose that $\gamma_r(G\circ_v H)\neq n(G)\gamma_r(H)$. By Lemma 2.9 and Theorem 2.11 we have that $\gamma_r(H-\{v\}) = \gamma_r(H)-1$. Let $f$ be a $\gamma_r(H-\{v\})$-function and consider the function $h$ on $H$ such that $h(v) = 1$ and $h(u) = f(u)$ for every $u\ne v$. Notice that $h$ is a $\gamma_r(H)$-function on $H$ with $h(v) = 1$, which is a contradiction. Therefore, $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

Notice that if $v\in V(H)$ is an isolated vertex, then $\gamma_r(G\circ_v H) = n(G)(\gamma_r(H)-1)+\gamma_r(G)$. The following result concerns the case in which $v$ is not an isolated vertex.

Theorem 2.20. Let $G$ be a graph and $H$ a graph. If $v\in V(H)$ is not an isolated vertex and $g(v)\neq 0$ for every $\gamma_r(H)$-function $g$, then $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

Proof. Assume that $v$ is not an isolated vertex and $g(v)\neq 0$ for every $\gamma_r(H)$-function $g$. Suppose that $\gamma_r(G\circ_v H)\neq n(G)\gamma_r(H)$. By Lemma 2.9 and Theorem 2.11 we have that $\gamma_r(H-\{v\}) = \gamma_r(H)-1$. Let $f$ be a $\gamma_r(H-\{v\})$-function. Let $u\in V(H)\cap N(v)$. Now, we may consider the function $h$ on $H$ such that $h(v) = 0$, $h(u) = \min\{f(u)+1, 2\}$ and $h(w) = f(w)$ if $w\in V(H)\setminus\{u, v\}$. In this case, $h$ is a WRDF function on $H$ with $\omega(h)\le \omega(f) = \gamma_r(H)$ and $h(v) = 0$, which is a contradiction. Therefore, $\gamma_r(G\circ_v H) = n(G)\gamma_r(H)$.

Based on the two previous results, we can ask ourselves what happen in the cases in which $g(v)\ne 2$ for every $\gamma_r(H)$-function $g$, but in some cases $g(v) = 1$ and in others $g(v) = 0$. What we have observed is that $\gamma_r(G\circ_v H)$ can take all the possible values. In order to show this, we proceed to consider the case $H\cong P_t$ and $v\in L(P_t)$. To this end, we would emphasize that $\gamma_r(P_t) = \lceil \frac{3t}{7} \rceil$ for $t\geq 1$, which was shown in ^[12].

Theorem 2.21. If $G$ is a graph, $v\in L(P_t)$ and $t\geq 2$, then

Proof. Since $\gamma_r(P_t) = \left\lceil \frac{3t}{7} \right\rceil$ for every $t\geq 2$, we have that $\gamma_r(P_t) = \gamma_r(P_{t-1})$ for every $t\equiv 0, 2, 4, 6 \pmod7$, as $\left\lceil \frac{3t}{7}\right\rceil = \left\lceil \frac{3(t-1)}{7}\right\rceil$ for these cases. Hence, by Theorem 2.11 we can conclude that $\gamma_r(G\circ_v P_t) = n(G)\left\lceil \frac{3t}{7} \right\rceil$ for every $t\equiv 0, 2, 4, 6\pmod7$.

Let $P_t = (v = v_1, v_2, \ldots, v_t)$. If $t\equiv 1$ $\pmod7$, then $\gamma_r(P_t) = \left\lceil\frac{3(7k+1)}{7}\right\rceil = 3k+1$, $\gamma_r(P_{t-1}) = 3k$ and $\gamma_r(P_{t-3}) = 3k$ for some integer $k\ge 1$. Since in $P_t-\{v\}\cong P_{t-1}$ the only neighbour of $v_{2}$ is $v_{3}$, if there exists a $\gamma_r(P_{t-1})$-function $g$ such that $g(v_{2}) > 0$, then $\gamma_r(P_{t-3}) < 3k$, which is a contradiction. Hence, $g(v_{2}) = 0$ for every $\gamma_r(P_{t-1})$-function $g$, and by Theorem 2.14 (and by Theorem 2.12 for the case $\gamma_r(G) = \gamma(G)$) we conclude that $\gamma_r(G\circ_v P_t) = n(G)(\left\lceil \frac{3t}{7}\right\rceil-1)+\gamma_r(G)$ for every $t\equiv 1 \pmod7$.

Now, if $t\equiv 3\pmod7$ then $\gamma_r(P_t) = \left\lceil\frac{3(7k+3)}{7}\right\rceil = 3k+2$, $\gamma_r(P_{t-1}) = 3k+1$ and $\gamma_r(P_{t-3}) = 3k$ for some integer $k\ge1$. As $\gamma_r(P_{t-1}) = 3k+1$ and $\gamma_r(P_{t-3}) = 3k$, there exists a $\gamma_r(P_{t-1})$-function $h$ such that $h(v_{2}) = 1$. Also, since $\gamma_r(P_t-\{v\}) = \gamma_r(P_t)-1$, Theorem 2.13 (Theorem 2.12 for the case $\gamma_r(G) = \gamma(G)$) leads to $\gamma_r(G\circ_v P_t) = n(G)(\left\lceil \frac{3t}{7} \right\rceil-1)+ \gamma(G)$ for every $t\equiv 3\pmod7$.

The case $t\equiv 5\pmod7$ is analogous to the previous one.

It was shown in ^[12] that $\gamma_r(C_t) = \gamma_r(P_t) = \left\lceil \frac{3t}{7}\right\rceil$ for every $t\geq4$. Using similar arguments as in the previous theorem, we deduce the following result.

Theorem 2.22. If $G$ be a graph, $v\in V(C_t)$ and $t\geq 4$, then

3.   The case of corona graphs

Given two graphs $G$ and $H$, the corona product $G\odot H$ is defined as the graph obtained from $G$ and $H$ by taking one copy of $G$ and $n(G)$ copies of $H$, and making the $i^{th}$ vertex of $G$ adjacent to every vertex of the $i^{th}$ copy of $H$ for every $i\in \{1, \dots, n(G)\}$.

The join $G + H$ is defined as the graph obtained from disjoint graphs $G$ and $H$ by taking one copy of $G$ and one copy of $H$ and joining by an edge each vertex of $G$ with each vertex of $H$. Notice that the corona product graph $K_1\odot H$ is isomorphic to the join graph $K_1 + H$. Furthermore, any corona product graph $G\odot H$ can be seen as a rooted product, i.e.,

where $v$ is the vertex of $K_1$.

Theorem 3.1. For any graph $G$ and any graph $H$,

Proof. If $H\cong K_{t}$, then $\gamma_r(K_1+H) = 1 = \gamma_r(H)$. Now, if $H\not \cong K_{t}$, then $\gamma_r(K_1+H) = 2\le \gamma_r(H)$. Hence, by Theorem 2.11 we have that $\gamma_r(G\odot H) = n(G)\gamma_r(K_1+H)$. Therefore, the result follows.

4.   NP-hardness

Recent works have shown that graph products are useful tools to study problems related to computational complexity. For instance, Fernau and Rodríguez-Velázquez ^[7,8] showed how to use the corona product of two graphs to infer P-hardness results on the (local) metric dimension, based on known NP-hardness results on the (local) adjacency dimension. Analogously, Dettlaff et al. ^[6] have shown that the lexicographic product of two graphs is an appropriate tool to infer NP-hardness results on the super domination number, based on a well-known NP-hardness result for the independence number. Our next result shows that we can use the rooted product of two graphs to study the problem of finding the weak Roman domination number of a graph. In this case, the main tool is Theorem 2.21 which involves the domination number. It is well known that the dominating set problem is an NP-complete decision problem ^[9], i.e., given a positive integer $k$ and a graph $G$, the problem of deciding if $G$ has a dominating set $D$ of cardinality $|D|\le k$ is NP-complete. Hence, the optimization problem of computing the domination number of a graph is NP-hard. Obviously, the following result is well known^†, what is relevant here is the use of product graphs to prove it.

^†As the decision problem is NP-Complete ^[12].

Corollary 4.1. The problem of computing the weak Roman domination number of a graph is NP-hard.

Proof. By Theorem 2.21, for any graph $G$ and any integer $t\equiv 3, 5 \pmod 7$ we have that

where $v$ is a leaf of $P_t$. Hence, the problem of computing $\gamma(G)$ is equivalent to the problem of finding $\gamma_r(G\circ_v P_t)$, which implies that the problem of computing the weak Roman domination number of a graph is NP-hard.

5.   Conclusions

This article is a contribution to the theory of protection of graphs. In particular, it is devoted to the study of the weak Roman domination number of a graph. We obtain closed formulas for the weak Roman domination number of rooted product graphs and, as a particular case of the study, we derive the corresponding formula for corona graphs. Finally, we show that the use of rooted product graphs is a useful tool to show that the problem of computing the weak Roman domination number of a graph is NP-hard.

Among our main contributions we highlight the following.

$\bullet$ $\gamma_{r}(G\circ_v H)\in \{n(G)(\gamma_{r}(H)-1)+\gamma_(G), n(G)(\gamma_{r}(H)-1)+\gamma_{r}(G), n(G)\gamma_{r}(H)\},$ for any graphs $G$ and $H$, and any $v\in\; V(H)$ (Theorem 2.8).

$\bullet$ We characterize the graphs with $\gamma_{r}(G\circ_v H) = n(G)\gamma_{r}(H)$ (Theorem 2.11).

$\bullet$ We characterize the graphs with $\gamma_{r}(G\circ_v H) = n(G)(\gamma_{r}(H)-1)+\gamma_(G)$ (Theorem 2.13).

$\bullet$ We characterize the graphs with $\gamma_{r}(G\circ_v H) = n(G)(\gamma_{r}(H)-1)+\gamma_{r}(G)$ (Theorem 2.14).

$\bullet$ We characterize the graphs with $\gamma_r(G\circ_v H) = n(G)$ (Theorem 2.15).

$\bullet$ We obtain the weak Roman domination number of $G\circ_v P_t$ (Theorem 2.21) and $G\circ_v C_t$ (Theorem 2.22).

$\bullet$ $\gamma_r(G\odot H) = \left\{ \begin{array}{ll} n(G), & \texttt{if } H\cong K_t; \\ \\ 2n(G), & \texttt{otherwise.}\\ \end{array} \right.$ for any graphs $G$ and $H$ (Theorem 3.1).

$\bullet$ The problem of computing the weak Roman domination number of a graph is NP-hard (Corollary 4.1).

Conflict of interest

The authors declare that they have no conflict of interest.