Lie symmetry analysis of fractional ordinary differential equation with neutral delay

1.   Introduction

Fractional calculus has developed rapidly in recent decades. It has been successfully applied in many aspects of science and technology. At the same time, many related masterpieces emerged, such as S. Samko et al. ^[1], I. Podlubny ^[2], R. Hilfer ^[3], A. Kilbas et al. ^[4], etc.

Time delay is a common phenomenon in real world ^[5]. In order to describe the models more accurately in many practical systems, we need to take fractional calculus and delay into consideration together. Therefore, it has a significance to study the solutions and their characteristics of fractional differential equation with delay.

Many analytic techniques have been developed to deal with fractional differential equations (FDEs). Among them, the Lie symmetry analysis method is an effective technique to derive exact solutions of FDEs. This method was initially advocated by Norwegian mathematician Sophus Lie in the beginning of nineteenth century and was further developed by Ovsianikov ^[6] and others ^{[7,8,9,10,11,12]}. The Lie symmetry analysis method of differential equations has been extended to FDEs by Gazizov et al. ^[13] (see also ^[14,15]). The effectiveness of this method has widely been demonstrated in variety of nonlinear fractional partial differential equations occurring in different areas of applied science (see ^[16,17,18]).

Recently, there are some literatures studying delay fractional differential equations by Lie symmetry technique (see ^[19,20,21]). Complete Lie group classifications of first- and second-order delay ordinary differential equations are obtained by Dorodnitsyn et al. ^[22] and Pue-on and Meleshko ^[23], respectively.

In ^[19], Aminu M. Nass studied the Lie symmetry analysis of fractional ordinary differential equations with neutral delay as follows

The author use symmetry analysis method, establish infinite dimension symmetry algebras and obtain the exact solutions to the equation. Aminu M. Nass ^[20], Kassimu Mpungu and Aminu M. Nass ^[21] presented the complete Lie group classifications of delay fractional differential equations.

In this paper, we continue the study and extend the Lie symmetry analysis to the following equation

where the coefficients $a(x), b(x), d(x), e(x)$ and $g(x)$ are arbitrary functions with respect to independent variable $x$, the delay $\tau > 0$, and $0 < \alpha < 1$. This equation appears in many fields, such as population dynamics, prey-predator systems, viscoelasticity, heat flow and so on. we set out to obtain the Lie symmetries of (FODE) by the Lie point symmetry approach.

Moreover, we carry out the complete group classification of the equation, and get some concrete periodic invariant solutions to (FODE).

This paper is organized as follows. In Section 2, we recall the definition of the Riemann-Liouville fractional derivative and some relevant properties. In Section 3, we compute Lie symmetries for the fractional ordinary differential equation (FODE) and complete the group classification of the equation. In Section 4, some group invariant solutions for the (FODE) are constructed. The conclusion is given in the last section.

2.   Preliminaries

In this section, we recall some standard definitions and notations in fractional calculus. For convenience, we suggest that one refers to ^[1,2,3,4] for details.

Definition 2.1. The Riemann-Liouville fractional integral operator of order $\alpha > 0$ of the function f(t)$\in L^{1}(\left [a, b \right], \mathbb{R}_{+})$, denoted by $_{a}I_{t}^\alpha$, is defined by

where $\Gamma(s) = \int_{0}^{\infty }x^{s-1 }e^{-x}dx$ is the Gamma function.

Definition 2.2. The Riemann-Liouville fractional differential operator of order $\alpha > 0$ of the function f(t)$\in L^{1}(\left [a, b \right], \mathbb{R}_{+})$, denoted by $_{a}D_{t}^\alpha$, is defined by

for $t > a$.

If $\alpha = 0$, then $_{a}D_{t}^\alpha f(t) = f(t).$

Some properties for the Riemann-Liouville fractional derivative and integral are as follows:

The generalized Leibnitz rule for the Riemann-Liouville fractional derivative has the following form

where ${{\alpha}\choose{k}} = \frac{{\Gamma (\alpha + 1)}}{{\Gamma (\alpha -k + 1)}{\Gamma (k + 1)}}.$

If $a = 0$, we denote $_{a}D_{t}^\alpha f(t) = {}D^{\alpha}_{t}f(t)$ for simplicity.

3.   Lie symmetries of the fractional ordinary differential equation

Consider the fractional ordinary differential equation with neutral delay as follows,

where the coefficients $a(x), b(x), d(x), e(x)$ and $g(x)$ are arbitrary functions with respect to independent variable $x$, the delay $\tau > 0$, and $0 < \alpha < 1$.

We assume that the FODE (3.1) is invariant under the one-parameter($\epsilon$) Lie group of continuous point transformations in $(x, y)$ plane, i.e.,

for some smooth functions $\xi(x, y)$ and $\eta(x, y)$ known as infinitesimals, and $y_{\tau } = y(x-\tau)$, $\xi_{\tau } = \xi(x-\tau, y(x-\tau))$, $\eta_{\tau } = \eta(x-\tau, y(x-\tau))$.

According to the Lie group theory, the group generator $X$ of the point transformations (3.2) is expressed as

So the prolongation of the above group generator $X$ has the form

where

and $D_{x}$ is the total derivative with respect to $x$.

The prolongation of Lie-Bäcklund generator ^[10] equivalent to infinitesimal prolongation (3.4) is

where

From the definition of total derivative, we have

Since

we obtain

Remark: The infinitesimal transformations (3.2) should conserve the structure of the Riemann-Liouville fractional derivative operator, of which, the lower limit in the integral is fixed. Therefore, the manifold $x = 0$ should be invariant with respect to transformations (3.2). The invariance condition arrives at

The one-parameter Lie symmetry transformations (3.2) are admitted by FODE (3.1), if the following invariance criterion holds,

where the infinitesimal generator $\bar{X}$ is defined in (3.5). Eq (3.9) can be abbreviated as

which is known as the determining equation.

Put

into (3.10) and let coefficients of $y$, $y_\tau$ and their derivatives in the determining Eq (3.10) to be zero, we can obtain the over-determined system of differential equations as follows,

from the coefficients of $y''_\tau$, $y'^2$, $y'^2_\tau$ and $D^{\alpha-n}_{x}(y)$. From (3.11), (3.12) and (3.13), we get

where $\xi(x)$, $\psi _{1}(x)$ are periodic functions with period $\tau$, i.e.,

and $\psi _{2}(x)$ is an arbitrary function. Put (3.14) into the over-determined system, the simplified forms are

From (3.13), (3.14), (3.17) and $\xi(x, y)|_{x = 0} = 0$, we obtain

$(i):\ \ \xi(x) = 0, \ \ \psi_{1}(x) = c_{1}$

$(ii):\ \ \xi(x) = c_{1}\sin \frac{2\pi x }{\tau }, \ \ \psi_{1}(x) = c_{1}\frac{2\pi (\alpha-n)}{\tau(n+1) }\cos\frac{2\pi x }{\tau }, n\in\mathbb{N}$

$(iii):\ \ \xi(x) = c_{1}\sin \frac{2(n+1)\pi x }{\tau }, \ \ \psi_{1}(x) = c_{1}\frac{2\pi (\alpha-n)}{\tau }\cos\frac{2(n+1)\pi x }{\tau }, n\in\mathbb{N}$.

3.1.   Case (ⅰ): $\xi(x)=0, \psi_{1}(x)=c_{1}$

From $\xi(x, y) = 0$, $\eta(x, y) = \psi _{1}(x)y+\psi _{2}(x) = c_{1}y+\psi _{2}(x)$, we can get the following group generator of the FODE (3.1):

where, $c_{1}$ is an arbitrary constant, $\psi _{2}(x)$ satisfies Eq (3.19). For arbitrary functions $a(x), b(x), d(x), e(x)$ and $g(x)$, it is also difficult to obtain $\psi _{2}(x)$ from Eq (3.19). But for some special functions $a(x), b(x), d(x), e(x)$ and $g(x)$, we can get some concrete Lie symmetries.

For example, if $\psi _{2}(x)$ is an arbitrary function, we get

with functions $a(x), b(x), d(x), e(x)$ and $g(x)$ satisfying Eq (3.19).

If $\psi _{2}(x) = 0$, we get

with functions $e(x), g(x)$ satisfying $e(x) = g(x)$.

If $\psi_{2}(x) = c_{4}\ne0$, we get

with function $g(x)$ satisfying

In what follows, we present Lie symmetries for some special functions $a(x), b(x), d(x), e(x)$ and $g(x)$.

3.2.   Case (ⅱ): $\xi(x)=c_{1}\sin \frac{2\pi x }{\tau }, \psi_{1}(x)=c_{1}\frac{2\pi (\alpha-n) }{\tau(n+1) }\cos\frac{2\pi x }{\tau }, n\in\mathbb{N}$

By (3.15) and (3.16), we obtain

Put (3.14) into (3.17) and (3.18), we can get

Therefore, the FODE (3.1) admits infinite dimensional Lie algebra, which is spanned by the following group generators

for any functions $g(x)$ and $\psi_{2}(x)$ satisfying Eq (3.19), and the coefficient functions $a(x), b(x), d(x)$ and $e(x)$ defined in (3.20) and (3.21) with period $\tau$.

Particularly, for (3.19), we assume $\psi_{2} =$ constant $= c_{4}$, and obtain the following two forms of $g(x)$, i.e.,

Therefore, if $\psi_{2} = c_{4} = 0$, the FODE (3.1) admits one-dimension Lie algebra, which is spanned by

for given functions $a(x), b(x), d(x), e(x)$ and $g(x)$ defined in (3.20), (3.21) and (3.22).

In the same way, if $\psi_{2} = c_{4}\ne0$, the FODE (3.1) admits one extra dimensional Lie algebra spanned by the infinitesimal operators

for given functions $a(x), b(x), d(x), e(x)$ and $g(x)$ defined in (3.20), (3.21) and (3.23). Note, the $c_{i} (i = 1, \cdots, 6)$ are arbitrary constants.

3.3.   Case (ⅲ): $\xi(x)=c_{1}\sin \frac{2(n+1)\pi x }{\tau }, \psi_{1}(x)=c_{1}\frac{2\pi (\alpha-n)}{\tau }\cos\frac{2(n+1)\pi x }{\tau }, n\in\mathbb{N}$

In this case, we can obtain

from Eqs (3.15)–(3.18). Therefore, the FODE (3.1) admits infinite dimensional Lie algebra, which is spanned by the following infinitesimal operators

for any function $g(x)$ and $\psi_{2}(x)$ satisfying Eq (3.19), and the coefficient functions $a(x), b(x), d(x)$and $e(x)$ defined in (3.20) and (3.21) with period $\tau$.

As same as Case (ⅱ), we assume $\psi_{2} =$ constant $= c_{4}$, and obtain the following two forms of $g(x)$, i.e.,

Therefore, if $\psi_{2} = c_{4} = 0$, FODE (3.1) admits one-dimension Lie algebra, which is spanned by

for given functions $a(x), b(x), d(x), e(x)$ and $g(x)$ defined in (3.24), (3.25) and (3.26).

If $\psi_{2} = c_{4}\ne0$, FODE (3.1) admits one extra dimensional Lie algebra spanned by the differential operators

for given functions $a(x), b(x), d(x), e(x)$ and $g(x)$ defined in (3.24), (3.25) and (3.27), where $c_{i}(i = 1, \cdots, 6)$ are arbitrary constants.

4.   Invariant solutions

In this section, we use the admitted group generators to construct some analytical solutions for fractional ordinary differential equation with neutral delay (FODE).

4.1.   Case (ⅰ): $\xi(x)=0, \psi_{1}(x)=c_{1}$

According to the Lie group theory, we can not obtain a new solution, when $\psi _{2}(x) = 0$ with

$\psi_{2}(x) = c_{4}\ne0$ with

and $\psi _{2}(x)$ is an arbitrary function with

4.2.   Case (ⅱ): $\xi(x)=c_{1}\sin \frac{2\pi x }{\tau }, \psi_{1}(x)=c_{1}\frac{2\pi (\alpha-n) }{\tau(n+1) }\cos\frac{2\pi x }{\tau }, n\in\mathbb{N}$

4.2.1.   $\psi_{2}=0$

The characteristic equation associated with the group generator $X_{1}$ is

where

Solving (4.1), we have

where $c$ is a constant.

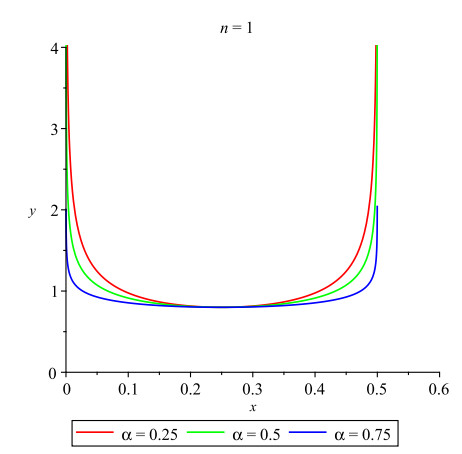
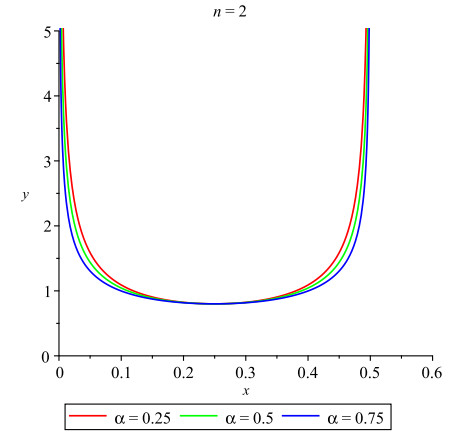
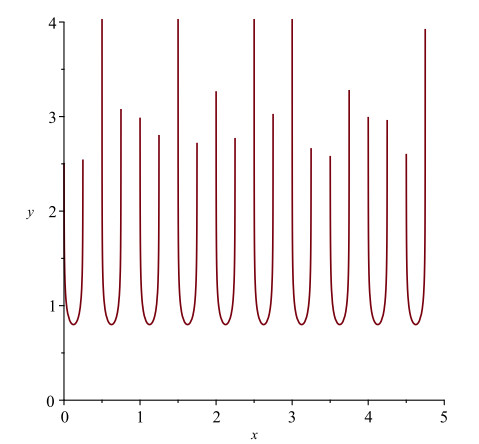
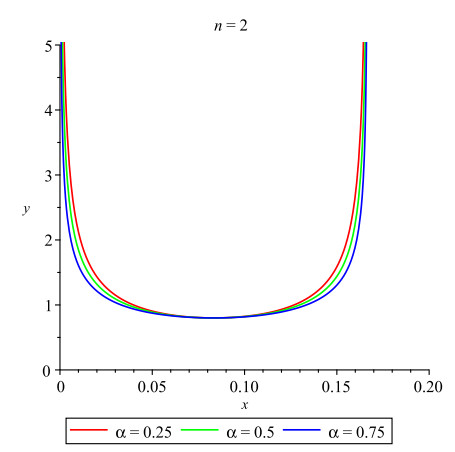
Graphical representations of the periodic solutions (4.2) are given in Figures 1–3. The behaviors of the solutions depend on the delay ($\tau$), the coefficient ($c$), the fractional order ($\alpha$) and the natural number ($n$). For example, in Figure 1, we set $\tau = 1$, $c = 0.8$, $\alpha = 0.5$ and $n = 1$.

4.2.2.   $\psi_{2}=c_{4}\ne0$

In this case, considering the linear combinations of the group generators $X_{1}$ and $X_{2}$, i.e.,

we can get the characteristic equation associated with the admitted operator $X_{1}+X_{2}$ as follows,

Its solutions are

where $c$ is a constant.

4.3.   Case (ⅲ): $\xi(x)=c_{1}\sin \frac{2(n+1)\pi x }{\tau }, \psi_{1}(x)=c_{1}\frac{2\pi (\alpha-n)}{\tau }\cos\frac{2(n+1)\pi x }{\tau }, n\in\mathbb{N}$

4.3.1.   $\psi_{2}=0$

The characteristic equation associated with the group generator $X_{1}$ is

where

Solving (4.5), we can get invariant solutions

where $c$ is a constant.

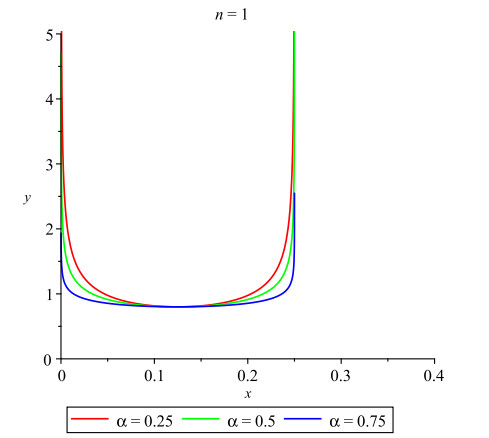
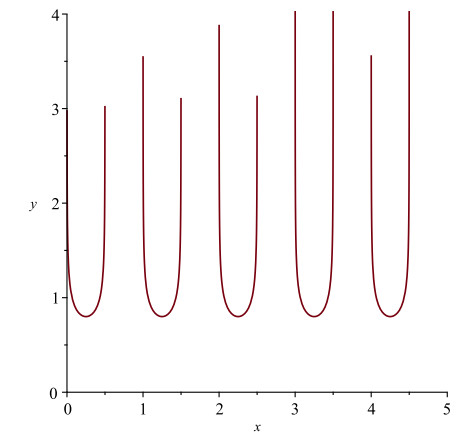
Graphical representations of the periodic solutions (4.6) are displayed in Figures 4–6. In Figure 4, we set $\tau = 1$, $c = 0.8$, $\alpha = 0.5$ and $n = 1$.

4.3.2.   $\psi_{2}=c_{4}\ne0$

In this case, considering the linear combinations of the group generators $X_{1}$ and $X_{2}$, i.e.,

we can get the characteristic equation associated with the admitted operator $X_{1}+X_{2}$ as follows,

Solving (4.7), we can obtain the following invariant solutions,

where $c$ is a constant.

5.   Conclusions

In this paper, it is proved that Lie symmetry technique is a powerful method to analysis the fractional ordinary differential equation with neutral delay, i.e.,

Firstly, we obtain the infinitesimal symmetries for the considered equation, and carry out a group classification. Secondly, we use the obtained Lie symmetries to construct the invariant solutions. Finally, we get some periodic solutions of the fractional ordinary differential equation with neutral delay.

Acknowledgments

The authors are grateful to the Editor and the anonymous Reviewers for their helpful comments and valuable suggestions. This work is partially supported by the State Key Program of National Natural Science Foundation of China (72031009) and the Open Project of State Key Laboratory of Environment-friendly Energy Materials (19kfhg08).

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.