Traveling waves in delayed reaction-diffusion equations in biology

1.   Reaction-diffusion equations without delay

Reaction-diffusion waves arise in various applications such as ecological invasions ^[1], tumor growth ^[2], cardiovascular events ^[3], combustion process ^[4] and many others. All these very different applications can be considered as some particular cases of a general mathematical theory developing during already almost one century and studying waves existence, stability, speed of propagation, and their nonlinear dynamics. In this review, we will speak about the state of the art in one of more recent developments of this theory related to delayed reaction-diffusion equations.

In this section we will briefly recall the main results about reaction-diffusion waves for the scalar equation without delay. They will help us to present the results for the delay equations in the following sections. We consider the equation

on the whole axis $ x \in \mathbb R $ with a sufficiently smooth function $ F(u) $ such that $ F(0) = F(1) = 0 $. Traveling wave solution of this equation is a solution of the form $ u(x, t) = w(x-ct) $, where $ c $ is the wave speed. It is an unknown constant which should be found together with the function $ w > 0 $ satisfying the equation

and such that

Systematic theory of reaction-diffusion waves begins in the 1930s with the works by Fisher ^[5] and Kolmogorov-Petrovskii-Piskunov ^[1] in population dynamics, by Zeldovich and Frank-Kamenetskii in combustion theory ^[6], and by Semenov in chemical kinetics ^[7], but the first works by Mikhelson ^[8] and Luther ^[9] appeared several decades earlier.

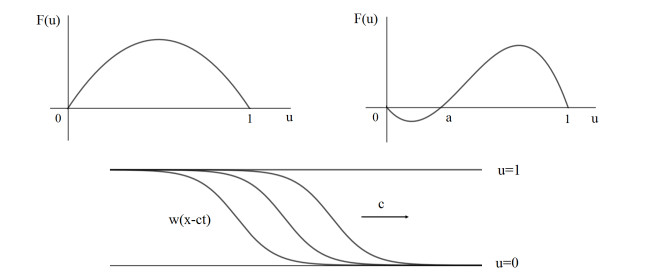
Existence and stability of reaction-diffusion waves depend on the nonlinearity $ F(u) $. It is convenient to introduce the classification of the functions $ F(u) $ according to the stability of the stationary points $ u = 0 $ and $ u = 1 $ of the equation $ du/dt = F(u) $. In the bistable case, both of them are stable; in the monostable case, one point is stable while another one is unstable; in the unstable case, both of them are unstable, see Figure 1, upper row. A further classification of monostable and bistable nonlinearities can be found in section 2.1 of ^[10].

Wave existence. Existence of solutions of problem (1.2), (1.3) can be studied by the phase plane analysis for the corresponding system of first-order equations. In the monostable case, under the assumption that $ F(u) > 0 $ for $ 0 < u < 1 $, monotonically decreasing solutions of this problem exist for all values of speed $ c $ greater than or equal to some minimal speed $ c_0 > 0 $. We will see below that the monotone waves are stable, while non-monotone waves are unstable. The latter exist for all positive $ c $. If in addition $ F(u) \leq F'(0)u, \ u \geq 0 $, then $ c_0 = 2 \sqrt{F'(0)} $. Without the assumption that the monostable nonlinearity $ F(u) $ is positive in the interval $ [0, 1] $, a solution of problem (1.2), (1.3) may not exist. If it exists, then it is possible to affirm that the $ [0, 1] $-waves, that is, solutions of Eq (1.2) with limits (1.3), exist in some interval $ [c_0, c_1) $ of speeds. If such waves do not exist, then the solution of the Cauchy problem for equation (1.1) is described by systems of waves (see below).

In the simple bistable case where $ F(u) < 0 $ for $ 0 < u < u_0 $, $ F(u) > 0 $ for $ u_0 < u < 1 $, and some $ u_0 \in (0, 1) $, there exists a solution of problem (1.2), (1.3) for a unique value of speed $ c $. In the general bistable case, if the $ [0, 1] $-wave exists, then the speed is unique. If it does not exist, then, as before, there are systems of waves. Finally, in the unstable case, such wave does not exist.

Wave stability. There are different types of wave stability. Solution $ u(x, t) $ of Eq (1.1) with some initial condition $ u(x, 0) = u_0(x) $ converges to a wave $ w(x) $ in form and in speed if there exists a function $ m(t) $ such that $ u(x, t) \to w(x-m(t)) $ as $ t \to +\infty $, uniformly in $ \mathbb R $, and $ m'(t) \to c $. This convergence (in other terms) and the corresponding method to study it were introduced in KPP ^[1]. Uniform convergence implies that $ u(x, t) \to w(x-ct-h) $ uniformly in $ \mathbb R $ for some constant $ h $. Convergence in form and in speed follows from the uniform convergence but the opposite may not be true.

In the monostable case, solution of the Cauchy problem converges to one of the $ [0, 1] $-waves depending on the initial condition $ u_0(x) $. Namely, if $ u_0'(x)/u_0(x) \to - \lambda $ as $ x \to +\infty $, where $ \lambda = c/2 - \sqrt{c^2/4-F'(0)} $, and $ \underline \lim_{x \to -\infty} u_0(x) > 0 $, then the solution converges in form and in speed to the wave with the speed $ c \geq c_0 $. If $ \lambda \leq c_0/2 - \sqrt{c_0^2/4-F'(0)} $, then the convergence occurs to the wave with the minimal speed $ c_0 $. More general results are also known (see ^[11] and the references therein). In applications, initial conditions such that $ u_0(x) \equiv 0 $ for $ x $ sufficiently large are often considered. In this case, the solution converges to the wave with the minimal speed. The uniform convergence in the monostable case occurs under some additional conditions.

In the bistable case, the $ [0, 1] $-wave is globally asymptotically stable in the sense of uniform convergence if $ F'(0) < 0, F'(1) < 0 $ and for a large class of initial conditions. The convergence in form and in speed occurs without the last condition on the derivatives.

In general, monotone waves for the scalar reaction-diffusion equations are stable, and non-monotone waves are unstable. This can be seen from the analysis of the spectrum. In the bistable case, it can be easily verified that the linearized operator $ L v = v'' + cv' + F'(w(x))v $ has a zero eigenvalue with the corresponding eigenfunction $ v_0(x) = - w'(x) $. If $ w(x) $ is a monotonically decreasing function, then the eigenfunction $ v_0(x) $ is positive. Therefore, $ 0 $ is the eigenvalue with the maximal real part (the principal eigenvalue) ^[12], and all other spectrum lies in the left-half plane of the complex plane. Such structure of the spectrum provides asymptotic stability of waves with shift with respect to small perturbations. If the wave is non-monotone, then the eigenfunction $ v_0(x) $ has variable sign. Hence, $ 0 $ is not the principal eigenvalue, and there is a positive eigenvalue of the operator $ L $. Thus, the wave is unstable. In the monostable case, the situation is more complex because of the essential spectrum but the result about stability of monotone waves (in certain sense) and instability of non-monotone waves remains valid.

Systems of waves. If the $ [0, 1] $-waves do not exist, then behavior of solutions of the Cauchy problem is determined by systems of waves. In order to explain this notion, consider the following example. Suppose that $ F(0) = F(u_0) = F(1) = 0 $ for some $ u_0 \in (0, 1) $, and $ F'(0), F'(u_0), F'(1) < 0 $. Hence, we can consider the bistable $ [0, u_0] $-wave and another bistable $ [u_0, 1] $-wave assuming that they exist. Denote by $ c_1 $ the speed of the former and by $ c_2 $ of the latter. If $ c_1 > c_2 $, then there are two waves propagating one after another with different speeds, and the solution $ u(x, t) $ converges to a two-step function formed by these waves. If $ c_1 < c_2 $, then the two waves merge, and there is a single $ [0, 1] $-wave. Such solutions were first studied in combustion theory. In the mathematical context they were introduced and studied in ^[13,14] (called there minimal decomposition of waves). For general functions $ F(u) $ they were studied in ^[15,16].

Monotone systems. Consider now equation (1.1) with the vector variables $ u = (u_1, ..., u_n) $, $ F = (F_1, ..., F_n) $. This system of equations is called a monotone system if the following inequalities

are satisfied for all $ u \in \mathbb R^n $. This is a class of systems for which the maximum principle and comparison theorems, conventionally used for the scalar equation, remain valid. These properties of monotone systems provide the results on the wave existence and stability similar to the results presented above for the scalar equation ^[12,11]. Furthermore, the minimax representation of the wave speed and the results on the systems of waves are also applicable for the monotone systems.

For a more general class of locally monotone systems, the inequalities (1.4) are supposed to hold only on the surfaces $ F_i = 0 $. In this case, the maximum principle is not applicable but it is still possible to prove wave existence in the bistable case.

2.   Traveling waves in continuous scalar delayed reaction-diffusion equations

2.1.   Waves in scalar reaction-diffusion equations with spatiotemporal delays

The fundamentals of the theory of parabolic functional differential equations (including reaction-diffusion equations with delays) were developed in the 1970s ^[19], with the earlier contributions by Artola ^[17,18] and later extensive studies in ^[20,21] (among many other papers: see the aforementioned works for more history and references).

Particularly, the existence and uniqueness of traveling waves for scalar equations with non-local diffusion and with reaction allowing spatiotemporal delays were already considered in 1980 by Schumacher ^[22]. Even so, the first systematic and comprehensive studies of wave solutions for scalar reaction-diffusion equations with discrete delays were realized by Schaaf ^[23] in 1987.

It is worth mentioning that the biggest part of mathematical models given by parabolic functional differential equations is related to biological and ecological applications. In fact, the celebrated Kolmogorov-Petrovskii-Piskunov-Fisher studies of propagation of advantageous genes ^[5,1] are often taken as a starting point for further improvements considering elaborated spatiotemporal interactions, cf. recent studies in ^{[24,25,26,27,28]}. In continuation, we touch briefly on the variety of parabolic functional differential equations that appear in the theory of traveling waves.

2.2.   On the diversity of delayed continuous reaction-diffusion equations in biological modeling

In the next sections, we are considering biological systems^* whose evolution is determined by the interaction of a linear diffusion $ {\mathcal D} $ and appropriate nonlinear response $ {\mathcal R} $ incorporating delayed effects:

^* Evolving in a continuous environment; note that there exists a vast bibliography on traveling waves for delayed reaction-diffusion equations describing biological models in patchy habitats ^[30]

In the ecological models, the term $ {\mathcal D}u $ describes random motion of individuals. The derivation of the diffusion term in (2.1) was analyzed by many authors, e.g. see ^[31,1,32]. In particular, Kolmogorov et al. ^[1] explain how random spatial walk can be naturally represented by non-local diffusion operators of the form

where $ K*u $ is the space-convolution and $ K\geq 0 $ is some normalized (probabilistic) kernel,

If non-local diffusion is isotropic and short-ranged, then it can be approximated ^[1] by the local diffusion operator given by the Laplacian

where $ k > 0 $ is some diffusion coefficient. In Chapter 11 of ^[32], J. Murray presented a simplified random walk derivation of the diffusion operator (2.2). Furthermore, the Fokker-Planck theory provides a rigorous justification for the form (2.2).

In most biological applications, delayed Eq (2.1) is considered with Fickian diffusion (2.2) and therefore $ ({\mathcal D}u)(t, x) $ depends only on the current values of $ u(t, x) $ (see ^[28,29] for other examples). Delayed continuous reaction-diffusion equation with delay-independent nonlocal diffusion were studied by many authors, see for more references ^{[33,30,34,35,36,37]}.

Next, as it was first suggested by Britton ^[38,39], nonlocal space interactions (or, more generally, spatio-temporal competitive effects in a population) can be taken into account by considering the delayed reaction term

Here $ f(u, v) $ and $ g(u) $ are some appropriate continuous functions of real variables, $ h > 0 $ is time delay and $ K*g(u) $ is the space-convolution of $ g(u) $ and some normalized non-negative kernel $ K $. Instead, one can also consider more general spatio-temporal convolution $ K**g(u) $,

There are also some other biological applications related to the analysis of age-structured populations and leading to the same form of reaction term (2.3). Based on earlier work by Smith and Thieme ^[40,41], corresponding theory was developed in ^[31,42] to analyze evolution of the total matured sub-community of a single species population with age structure and a fixed maturation period $ h $.

In the simplified but nonetheless representative and non-trivial case when the spatial intraspecific interaction is ignored in the reaction term and the influence of the past history on the current evolution at each moment $ t $ is expressed only by the values of $ u(t-h, x) $, we obtain

The surveys ^[31,43,44] discussed a series of specific biological situations which can be modeled by equation (2.1) with $ {\mathcal D} $ and $ \mathcal R $ of the types (2.2), (2.3), respectively. Moreover, the question of traveling waves and their properties was studied in ^[31,44]. After the publication of the aforementioned papers, an important piece of work has been done by different authors. It includes studies of key questions of the theory concerning existence, stability, uniqueness, genesis of waves etc, by different methods and for various families of equations. Since almost each such family incorporates either Kolmogorov type equation with some appropriate specific rate of increase $ f(u, v) $ and normalized non-negative kernel $ K(x) $

or the diffusive Mackey-Glass type equations

with some birth and mortality rates $ f(u), g(v) $, it is both natural and instructive to illustrate results obtained in last decade or so on the above models. This will be our main goal in the next sections, where we will be concerned with both bistable and monostable plane traveling waves $ u = \phi(\nu\cdot x +ct) $, where $ \nu \in \mathbb R^n, \ |\nu| = 1 $, is direction of wave propagation. Planarity of wave motion simplifies its analysis which actually shows that the spatial dimension $ n $ is irrelevant in various aspects. Therefore in subsequent sections we will always assume that $ n = 1 $ and $ x \in \mathbb R $.} The exposition below reflects the personal interests of the authors taking into account that it would be rather difficult to mention all recent valuable contributions to the theory of traveling waves in Eqs (2.4) and (2.5).

3.   Traveling waves in continuous scalar delayed equations with monotonicity

Equations (2.4) and (2.5) are called quasi-monotone in the case when the birth functions $ f(u, v), f(v) $ are monotonically increasing, with respect to the variable $ v $, between the equilibria connected by the traveling wave $ u = \phi(x+ct) $. Similarly to (1.4), this property enables direct application of the comparison principle and sliding techniques for the analysis of waves in (2.4), (2.5) and the related equations, including the following profile equations:

Actually, the use of comparison arguments led to the development of general theories of wave propagations in abstract monotone evolution systems which include conveniently the quasi-monotone models (2.4), (2.5). Within an abstract setting, the bistable case was considered in ^[45,46] and ^[47] while the monostable one was studied in ^[48,50] (see also in ^[51,52] and references therein for an abstract recursive approach). In the next subsections, we discuss basic properties of our quasi-monotone models.

3.1.   The diffusive Eq (2.5) with the monostable monotone birth function

Assume that $ g, f $ are increasing $ C^1 $-smooth functions on some interval $ [0, \kappa] $ and that the following monostability conditions are satisfied:

Depending on the boundary conditions imposed on the wave profile at $ \pm \infty $, we will consider the leftward traveling waves (wavefronts)

and the rightward traveling waves

The first fundamental result concerns the structure of the set of all admissible wave speeds:

Proposition 3.1. There exist two extended real numbers (called rightward and leftward minimal speeds) $ c^*_-, c^*_+ \in \mathbb R\cup\{\pm\infty\} $, $ c^*_- < c^*_+ $, such that (2.5) has a leftward [respectively, rightward] traveling wave with monotone profile $ \phi $ if and only if $ c\geq c^*_+ $ [respectively, if $ c\leq c^*_- $] ^[50]. Furthermore, $ c^*_-, c^*_+ $ are the spreading speeds in the following sense: if $ u(t, x, u_0) $ solves, for Eq (2.5), the initial value problem $ u(s, x, u_0) = u_0(s, x), $ $ s \in [-\tau, 0], \ x \in \mathbb R $, with continuous and compactly supported initial datum $ u_0: [-\tau, 0]\times \mathbb R \to [0, \kappa) $, then

On the other hand, for each $ \epsilon \in (0, \kappa) $ and each pair $ (c'', c'), $ satisfying $ c^*_- < c'' < c' < c^*_+ $, there exists positive $ r_\epsilon $ such that if the initial function $ u_0 $ satisfies the inequality $ u_0(s, x) \geq \epsilon $ for all $ s\in [-\tau, 0], $ $ \ x \in [a, a+r_\epsilon] $ and some real $ a $, then uniformly in $ x $

Proof. In view of Remark 4.1 in ^[50], the above result follows from Theorems 3.4 and 4.4 (proved by means of an abstract recursive approach) of the same paper. The waves propagating with the minimal speeds are called the minimal (or critical) waves.

Remark 3.2. In Eq (2.5), the properties of the extended numbers $ c^*_\pm $ depend essentially on the normalized non-negative kernel $ K $. For example, if the bilateral Laplace transform $ \mathcal{K}(\lambda) = \int_ \mathbb R e^{-\lambda s}K(s)ds $ is defined for all real $ \lambda $, both numbers $ c^*_\pm $ are finite and $ c^*_- < c^*_+ $. In general, both of these numbers can be nonpositive (or nonnegative). This means that a rightward wave can actually propagate in the the left direction (in such a case, we obtain an extinction wavefront instead of an invasion wave). However, if $ K $ is an even (symmetric) function this situation can not happen since $ c^*_- = - c^*_+ < 0 $. Now, if $ K(s) $ converges slowly to $ 0 $ at $ \infty $ (for example, the convergence is algebraic and $ \mathcal{K}(\lambda) $ is defined only for $ \lambda = 0 $), a different type of waves must be considered.

The earlier (weaker) versions of Proposition 3.1 were established under the additional sub-tangency inequality

The non-negativity of the function $ f'(0)u-f(u) $ simplifies essentially the respective proofs and allows the explicit calculation of the speeds $ c^*_\pm $ from the characteristic equation

It is easy to see that there exists a unique value $ c^\#_- $ [respectively, $ c^\#_+ $] of parameter $ c $ for which $ \chi(\cdot, c) $ has a negative [respectively, positive] double zero. If (3.3) is assumed then $ c^*_\pm = c^\#_\pm $ and it may happen that $ c^*_- < c^\#_- $ and/or $ c^*_+ > c^\#_+ $ in the opposite case. The minimal wavefront propagating with the speed different from $ c^\#_\pm $ is called pushed ^[53].

The nonlinear stability (see Section 7 ^[54] for a formal definition of this concept) of the monostable wavefronts (including monotone wavefronts as a particular case) to Eq (2.5) with $ n = 1 $ was analyzed by means of the energy methods developed by Ming Mei et al. in a series of papers ^{[55,56,57,58,59,60]}. See also ^[61,62] where additionally quasi-monotonicity condition was assumed. Since the energy approach can be equally used for non-quasi-monotone nonlinearities, respective stability results will be discussed later, in section 4. Instead, in Theorem 3.3 below we present one global convergence result from ^[63] proved for the quasi-monotone delayed equation

by means of the Chen's ^[45] squeezing techniques (the same techniques were also used in ^[64] for establishing the global stability of non-critical monotone waves for the general Eq (2.1) with the monostable quasi-monotone non-local nonlinearity (2.3). However, in contrast to the previous works, the sub-tangency condition (3.3) was not assumed in the mentioned theorem from ^[63]).

We start by observing that $ \chi(z, c) $ has exactly two positive zeros (counting multiplicity) $ \lambda_1 = \lambda_1(c) \leq \lambda_2 = \lambda_2(c) $ if and only if $ c \geq c^\#_+ $. Set $ \lambda_*: = \lambda_1(c_+^*) $, then $ 0 < \lambda_* \leq \lambda_1(c_+^\#). $

Proposition 3.3. Assume that the initial function $ w_{0} $ satisfies [63, Theorem 1]

$(IC_1)$ $ \quad 0\leq w_0(s, x)\leq |w_0|_\infty: = \sup_{(s, x)\in \Pi_0}w_0(s, x) < \infty, \quad (s, x) \in [-h, 0]\times \mathbb R \subset \mathbb R^2; $

$(IC_2)$ $ \liminf_{x \to +\infty} \min_{s\in[-h, 0]} w_0(s, x) > 0 $,

and, for some $ A > 0 $ and $ c > c_* $,

uniformly on $ s\in[-h, 0] $. If, in addition, the birth function $ g\in C^{1, \gamma}[0, \kappa] $ is strictly increasing then the solution $ u(t, x) $ of the initial value problem $ u(s, x) = w_0(s, x), \ s \in [-h, 0], \ x \in \mathbb R, $ for Eq (3.4) satisfies

where $ a = (\lambda_1(c))^{-1}\ln A $ and the front profile $ \phi $ (existing in virtue of the assumption $ c > c_* $) is normalised by $ \lim_{x\to-\infty}e^{-\lambda_1(c)x}\phi(x) = 1 $.

Clearly, Theorem 3.3 also allows to answer the velocity selection question for solutions with initial data possessing exponential decay at $ -\infty $.

The pushed wavefronts (i.e. when $ c = c^*_+ > c^\#_+ $) for the quasi-monotone Eq (3.4) were further analyzed in ^[35] and their global attractivity properties were established in ^[65] by means of the squeezing approach combined with the Berestycki and Nirenberg method of the sliding solutions ^[35，66] as well as some ideas developed by Ogiwara and Matano in ^[46]:

Proposition 3.4. Let $ g\in C^{1, \gamma}[0, \kappa] $ be monotone and the initial data $ w_0 $ satisfy $ (IC_1) $, $ (IC_2) $ together with [65, Theorem 1.5]

for some $ \mu > \lambda_1(c_*) $ and $ K > 0 $. Next, fix a positive number $ \lambda < \mu $ such that $ \lambda \in (\lambda_1(c_*), \lambda_2(c_*)) $. Then the solution of the initial value problem $ u(s, x) = w_0(s, x), \ s \in [-h, 0], \ x \in \mathbb R, $ for Eq (3.4) asymptotically converges to a shifted pushed front: for some $ s_0\in \mathbb R $,

Observe that Theorems 3.3 and 3.4 do not give any estimation of the rate of convergence of the solution $ u(t, x) $ to its associated limit wavefront. It was conjectured in ^[63,65] that the convergence rate in (3.5) and (3.6) is of the exponential type. In the particular case of the pushed waves, by enhancing the squeezing method with some ideas of Chen ^[45] (Theorem 3.1) and Smith et al. ^[67] (Theorem 3.3), this conjecture was affirmatively solved by Wu et al. in ^[68] while the case of the pulled wavefronts ($ c > c^*_+ $) still remains open.

The above stability results imply that two wavefronts to (3.4) propagating at the same speed $ c > c_+^* $ and having the same rate of exponential growth at $ -\infty $ should coincide (possibly, after a translation). See also Theorem 1.2 of ^[35] for an alternative proof (based on the sliding solution method of Berestycki and Nirenberg) of this uniqueness property of wavefronts (which are necessarily monotone under the quasi-monotonicity assumption). If the birth function $ f $ meets the following special Lipschitz condition (which implies (3.3))

then the uniqueness of wavefronts (including the minimal ones) for the non-local equations (2.5) is assured by the Diekmann-Kaper theory ^[33,69]. Without condition (3.7), as far as we know, the uniqueness of wavefronts for the non-local equations is an open question even if the birth function is assumed to be monotone. A weaker uniqueness property within the class of monotone wavefronts for (2.5) was shown in ^[70] for the monotone $ C^1 $-smooth nonlinearities satisfying

(importantly, the latter inequality does not exclude the weak Allee effect ^[71,72]).

Finally, it is worth mentioning than several results proved for non-quasi-monotone equations and mentioned in section 4 are also valid for more simple monotone case.

3.2.   The diffusive Eq (2.1) with the bistable monotone nonlinearity (2.3)

Consider the reaction term $ {\mathcal R}u $ defined in (2.3),

We will say that the diffusive Eq (2.1) is of the bistable type if $ C^1 $-smooth function $ F(u): = f(u, g(u)), \ u \in [0, \kappa], $ is such that

The bistable Eq (2.1) is called quasi-monotone if, in addition, $ f(u, g(v)) $ is an increasing function of $ v $. The definition of the bistable wavefront for bistable quasi-monotone Eq (2.1) is the same as given at the beginning of section 3.1. It should be noted that (2.1) also can have monostable wavefronts connecting the equilibria $ a $ and $ \kappa $.

In 1987, for the particular quasi-monotone nonlinearity $ ({\mathcal R}u)(t, x) = f(u(t, x), u(t-h, x)) $, Schaaf ^[23] established the existence and uniqueness of the bistable wavefront. What is not very typical for the delayed systems, the phase space arguments were used in the cited work. This wave solution (propagating at some speed $ c_*(h) $) has strictly increasing profile $ \phi_h $. Furthermore, $ \phi_h $ and $ c_*(h) $ depend continuously on $ h $, $ c_*(h) $ is monotone decreasing and sign $ c_*(h) = $ sign$ \int_0^\kappa F(u)du $. As it was showed by Ogiwara and Matano in Theorem 7.2 of ^[46] on the base of their general convergence theorem for abstract order preserving systems under a group action, obtained bistable wavefront is necessarily locally asymptotically stable with phase shift. Moreover, by using the squeezing technique within the general framework of the theory of abstract functional differential equations ^[20], Smith and Zhao ^[67] proved that this bistable wave is globally and exponentially asymptotically stable with phase shift.

Next, in 1997, Chen ^[45] considered an abstract scalar evolution equation of the bistable quasi-monotone type. By introducing new ideas and partially motivated by the seminal work of Fife and McLeod ^[13], Chen successfully approached the questions of the existence, uniqueness and asymptotic stability of the bistable wavefronts for his abstract (non-delayed but generally non-local) evolution equation. For non-delayed Eq (2.1) with bistable quasi-monotone nonlinearity (2.3), Theorem 5.1 ^[45] guarantees the existence and uniqueness of the bistable wavefront (which, in addition, should be monotonic). Moreover, an explicit a priori estimate for the absolute value $ |c_*(h)| $ (not depending on $ h $) can be drawn from Theorem 3.5 ^[45]. In 2007, developing further the comparison and squeezing technique of ^[45], Ma and Wu ^[73] proved the global exponential stability with phase shift of the unique monotone wavefront in the bistable quasi-monotone Eq (2.5). For a family of nonlocal delayed advection-diffusion equations (which include the model (2.1) with (2.3)) the existence, uniqueness and stability results of similar kind were obtained by Wang et al. ^[74].

Finally, a completely different approach for proving wave exponential stability (in the case of quasi-monotone non-local but non-delayed bistable equation) was developed by Ducrot et al. in ^[75]. It requires a careful analysis of the spectral properties of some associated linear elliptic operator with a nonlocal term. As it was noted by authors of ^[75], their method may also apply to reaction–diffusion equations with delay.

4.   Traveling waves in continuous scalar delayed equations without monotonicity

Suppose now that the birth function $ f(u, v) $ is not monotone increasing with respect to the second variable. For example, such situation happens when $ f(u, v) = u(1-v) $ (the case of the KPP-Fisher delayed or nonlocal equations) or when $ f(v) $ in the Mackey-Glass type Eq (3.4) is not increasing between equilibria. This lack of the monotonicity has at least three following immediate negative (and partially related among them) consequences for the studies of Eq (2.1) with non-monotone nonlinearity (2.3):

i) Restricted application of the comparison arguments;

ii) Limitations in the use of various efficient approaches (e.g. the monotone iterative technique ^[76] and the sliding solution method);

iii) More complex spectral theory for the linearized equation at the positive equilibrium $ \kappa $ (on the other hand, for the above mentioned biological models, there are not qualitative changes in the spectral analysis of the linearized equation at the zero equilibrium). In particular, the spectrum $ \Sigma(\kappa) $ of the mentioned equation can have an empty intersection with the real negative semi-axis and therefore generally wave profiles are oscillating around the positive equilibrium ^{[26,28,56,77,78,79,80]} (each positive wave developing non-decaying oscillations around the positive equilibrium and converging to $ 0 $ at the opposite end of the real line will be referred to as a semi-wavefront). But even when $ \Sigma(\kappa) $ contains negative eigenvalues, a new class of non-oscillating and non-monotone stable wavefronts appear in several relevant biological models as a consequence of delayed effects ^[81,82,83]. Observe that stable wavefronts for scalar non-delayed bistable equations are necessarily monotone, cf. ^[46].

As a result, till the present moment the theory of traveling waves for non-monotone delayed equations did not obtained such a finished form as in the case of quasi-monotone equations. In general, even the basic questions concerning the existence and uniqueness of waves are not completely answered (surprisingly, even adequate definition of the minimal speeds of propagation for monostable equations including (3.4) is an open question ^[84,85]). Nevertheless, there are a series of rather satisfactory results concerning the existence, uniqueness, stability, geometric and convergence properties of wavefronts for some particular subclasses of non-monotone delayed reaction-diffusion equations. Let us mention some of these findings:

Existence of monostable semi-wavefronts. The abstract recursive approach ^[50] mentioned in section 3.1 is an efficient tool to study the spreading properties of solutions to the nonlocal delayed diffusive equations. Its extension in ^[37,86] for some classes of non-monotone systems also allows to solve the wave existence problem. In contrast with ^[50], the sub-tangency assumption (3.3) was assumed in these works (cf. ^[37] inequality (4.4) and ^[86] condition (GC)) to prove the existence of the minimal speed for the semi-wavefronts propagation. By amplifying the Diekmann-Kaper theory of a nonlinear convolution equation ^[69], an alternative abstract approach to the semi-wavefront existence problem was proposed in ^[87]. It also requires the dominance condition (3.3). For Eq (3.4), the abstract settings of ^[37,86] and ^[87] yield essentially the same conclusions as the earlier remarkable contribution ^[37,86,88] by Ma (see also ^[87,89,90,] for the further references).

Quasi-monotonicity in the sense of Wu and Zou: existence of monostable monotone wavefronts. Even if the Eq (2.1) has a non-monotone nonlinearity (2.3), it can still have the monotone wavefronts for some range of the propagation speeds. In particular, this happens if the non-monotone differential wave profile equation can be rewritten in the equivalent integral form possessing good monotonicity properties. As it was indicated in the pioneering work ^[76] by Wu and Zou, sometimes it is possible to impose a special quasi-monotonicity condition on the birth function (which is not monotone increasing with respect to delayed variable) which allows to implement such a transformation ^[28]. Remarkably, further developments of the Wu and Zou idea allowed to obtain simple criteria for the existence of the monotone wavefronts in the non-local delayed (including some neutral types) KPP-Fisher and Mackey-Glass equations ^{[28,70,91,92]}. It should be noted here that for the latter equation, apart of inequality (3.3), a similar condition at the positive equilibrium was required in ^[70].

Hale-Lin functional analytic-approach and global continuation of monotone wavefronts. Assuming that Eq (2.1) has a wave solution for certain parameters (e.g., for some fixed speed and delay), sometimes it is possible to use the Lyapunov-Schmidt reduction method in appropriate functional spaces to extend this solution for close values of parameters. For instance, since the wave existence problem simplifies for the parameters $ \epsilon = 1/c = 0 $ (and some fixed delay $ \tau > 0 $) or for $ \tau = 0 $ (and some fixed admissible speed), it is convenient to the extend wave solutions existing either for non-delayed equations (when $ \tau = 0 $) or for simpler first-order delay differential equations (when the propagation speed $ c = \infty $). The idea behind this method goes back to the Hale and Lin studies ^[34,93] of the heteroclinic connections for the delayed equations. As a perturbation technique for establishing the persistence of fast monostable wave solutions in general delayed systems, it was invoked for the first time by Faria et al. in ^[49]. Application of this method requires a detailed analysis of the Fredholm properties of the linearization about the original wave solution. The presence of positive delay complicates this analysis considerably. In a series of subsequent works, the functional analytic approach was successfully applied to study the existence of periodic waves and semi-wavefronts periodically oscillating around the positive equilibrium ^[95,96], the persistence of wavefronts in nonlocal reaction-diffusion equations for small delays ^[97,98], the positivity and oscillation properties of the wavefronts ^[77,99], the uniqueness of fast wavefronts in the Mackey-Glass type equations ^[100], the non-uniqueness of semi-wavefronts in the non-local KPP-Fisher equations ^[78], the existence of non-oscillating non-monotone wavefronts in the Kolmogorov ecological equation ^[82]. Moreover, as it was shown in ^[101] for the unimodal monostable equations and in ^[102] for the unimodal bistable equations, the Hale-Lin approach allows to obtain rather optimal global continuation results for the case of monotone wavefronts.

Leray-Schauder continuation principle. The main idea of this method is to transform continuously a non-quasi-monotone model to a quasi-monotone one while keeping track of traveling wave solutions. It was successfully applied to prove the existence: a) of bistable wavefronts for a series of non-delayed models (see ^[11,103,104] for more references and further discussion); b) of the minimal pulled monostable semi-wavefronts in the non-local KPP-Fisher equation ^[105]; c) of the wavefronts to non-delayed combustion models ^[66]. Recent works ^[106,107] show that the version of the Leray-Schauder theory elaborated in ^[103,104] allows to prove the existence of monotone wavefronts for the non-quasi-monotone model

proposed in ^[108] in order to understand spatiotemporal dynamics of virus infection spreading in tissues (see section 5 for more details). According to its biological meaning explained in ^{[106,107,108]} it was assumed in ^[106,107] that smooth function $ g $ has a unique critical (global maximum) point and $ g(0) > 1 $, $ g'(0) > 0 $,

Observe that in the spatially local case with single discrete delay, Eq (4.1) was also analyzed in ^[108] (by using the phase plane method) and in ^[102] (under more realistic conditions on $ g $ and inside the Hale-Lin functional-analytical framework).

Now, for the bistable types of Eq (3.4) and non-local Eq (2.4) (with $ f(u, v) = (u-\theta)(1-v) $), Alfaro et al. ^[109,110] appealed to the Leray-Schauder topological degree argument to prove the existence of both monotone fronts and non-monotone semi-wavefronts. In contrast to ^{[103,104,111]} (where topological degree was constructed for general elliptic problems in unbounded domains) but similarly to ^[66,105], the continuation method in ^[109,110] was applied to establish the existence of a 'truncated semi-wavefronts' $ \phi_a $ on finite intervals $ [-a, a] $, then the required wave was obtained by letting $ a \to +\infty $.

Uniqueness of semi-wavefronts. For a broad series of autonomous delayed and non-local equations, the Diekmann-Kaper theory of a nonlinear convolution equation ^[69] and its versions developed in ^{[28,33,91,92]} allowed to answer the uniqueness question in the case of the monostable semi-wavefronts, both critical and non-critical: each semi-wavefront propagating with a fixed velocity $ c $ is unique up to translation. Application of this theory, however, requires a rather strong linear dominance condition, like (3.7) for the model (3.4). Now, as it was recently shown in ^[112], the condition (3.7) can be weaken for a broad class of reaction-diffusion models with distributed but finite delays. For example, by Corollary 4 in ^[112], for the particular case of Eq (3.4), the inequality

implies the uniqueness. An analog of this condition also holds for the delayed logistic (i.e. KPP-Fisher) model that allowed to prove the uniqueness of semi-wavefronts for this equation.

In the case of both bistable and monostable pushed semi-wavefronts, the above-mentioned dominance type conditions are not longer available: as a consequence, even for such simple equation as (3.4), the uniqueness of either bistable or pushed semi-wavefront remains to be an open question ^[110].

Importantly, as the studies ^[78,113,114] reveal, for some non-local monostable models, including the non-local KPP-Fisher equation, the wave's uniqueness property fails to hold. It would be interesting to find an adequate biological interpretation of such a non-uniqueness phenomenon.

Stability of semi-wavefronts. The stability of monostable wavefronts (both monotone and oscillating) to non-quasimonotone version of Eq (2.5) with $ n = 1 $ was an object of investigation in several recent papers by Mei and his collaborators ^{[59,60,115,116]}. The technical weighted energy approach was combined with other analytical tools in these works. For example, for Eq (3.4) satisfying (3.7), Theorem 1.1 in ^[116] presents a rather optimal global stability result, showing that all non-critical wavefronts are globally exponentially stable and all critical waves are globally algebraically stable (with the convergence rate $ O(t^{-1/2}) $ as $ t\to +\infty $ in the usual $ \sup $-norm for $ C(\mathbb R, \mathbb R) $). It is unclear at this point whether a similar stability result could be obtained: a) for the proper (not converging) semi-wavefronts; b) in situation when (3.7) is not assumed and the wave speed is close to the minimal one.

Recently, a different approach to the stability of oscillating monostable semi-wavefronts (both critical and non-critical) was proposed by Solar et al. in ^{[54,63,117,118]}. It is based on maximum principle arguments and requires the dominance of the linearization of (2.5) at zero equilibrium over the whole Eq (2.5). The obtained results complement the studies in ^{[59,60,115,116]} and can be considered as the first steps in the solution of the above mentioned problems a) and b). Furthermore, Benguria and Solar ^[24] developed a technique which allowed to demonstrate local stability (on infinite semi-axes) of each semi-wavefront propagating with the velocity $ c\geq 2\sqrt{2} $ to delayed version of the celebrated KPP-Fisher equation

(see ^{[27,76,92,94,101,119,120]} for more references about this model). Since the minimal speed $ c_* $ in (4.2) is equal to $ c_* = 2 $, the stability problem for this model remains open in the case of slow semi-wavefronts.

Finally, we refer to ^{[37,54,63,71]} for related asymptotic properties of solutions to non-quasimonotone delayed monostable equations. In should be noted that the stability (and even a weaker question of uniqueness) of both bistable and pushed semi-wavefronts for non-quasimonotone delayed equations seems to be unexplored in the existing literature.

5.   Delay RDEs in mathematical immunology

Virus density distribution in the tissue $ u(x, t) $ can be described by the delayed reaction-diffusion equation ^{[108,121,122]}:

where the first term in the right-hand side characterizes its random motion, the second term determines virus reproduction considered in the logistic form, and the last term its elimination by the immune cells. Time delay $ \tau $ in the function $ f(u_\tau) $, where $ u_\tau(x, t) = u(x, t-\tau) $, characterizes clonal expansion of immune cells. Parameters $ D $ and $ k $ are positive constants, the function $ f(u) $ describes the intensity of immune response depending on viral load. It is a non-negative sufficiently smooth function defined for $ u \geq 0 $, it is growing for sufficiently small values of $ u $ and decaying for $ u $ large enough. Its characteristic form can be qualitatively described by the function $ f(u) = (a_1u + a_2) e^{-a_3 u} $, where $ a_1, a_2, a_3 $ are some positive constants. It will be used below for convenience of presentation. Let us note that $ f(0) $ corresponds to immune response in the absence of pathogen, that is, to the level of acquired immunity.

RDE without time delay. The function $ F(u) = k u (1-u) - f(u) u $ vanishes at $ u_0 = 0 $ and it has up to three positive zeros. For a single positive zero $ u = u_1 $, there exist $ [u_0, u_1] $-waves, that is, the waves with the limits $ u(-\infty) = u_1, u(\infty) = 0 $, for all values of the speed $ c \geq c_0 $, where $ c_0 = 2 \sqrt{k-f(0)} $ is the minimal speed (monostable case). These waves are stable in appropriate weighted norms.

If there are two positive zeros, $ u_1 $ and $ u_2 $, $ u_1 < u_2 $, and $ u_0 $ and $ u_2 $ are stable stationary points of the equation $ du/dt = F(u) $ (bistable case), then the $ [u_0, u_2] $-wave exists for a single value of $ c $. This wave is globally asymptotically stable.

In the case of three positive zeros, $ u_1, u_2, u_3 $, $ u_1 < u_2 < u_3 $, there are monostable $ [u_0, u_1] $-waves and a bistable $ [u_1, u_3] $-wave. If the speed $ c_1 $ of the $ [u_1, u_3] $-wave is greater than the minimal speed $ c_0 $ of the $ [u_0, u_1] $-waves, then there are $ [u_0, u_3] $-waves. Otherwise, such waves do not exist, and there are two consecutive waves propagating with different speeds. Convergence of the solution of the Cauchy problem to waves and systems of waves in known ^{[13,14,15,16]}.

Time delay. If the function $ f(u) $ is decreasing, then the existence of waves in the monostable and bistable cases can be proved using the methods based on the maximum principle and comparison theorems ^[45,73]. For a non-monotone function $ f(u) $ such methods are not applicable. In the bistable case, the wave existence is proved in ^[106] by the Leray-Schauder method and in ^[102] by the Hale-Lin approach (see section 4).

If $ f'(u_1) > 0 $, where $ u_1 $ is the first positive zero of the function $ F(u) $, then the stationary solution $ u = u_1 $ of the delay differential equation

loses it stability for the values of $ \tau $ greater than some critical value $ \tau_c $. Periodic time oscillations, period doubling bifurcations and transition to chaos occur as $ \tau $ increases ^[123].

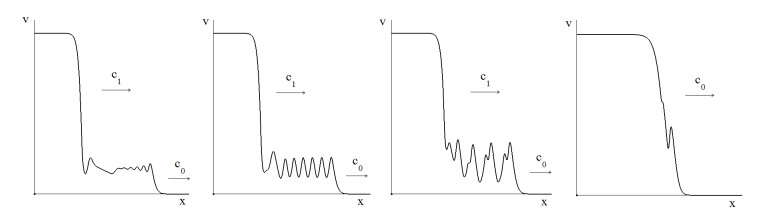
Periodic time oscillations of solutions of Eq (5.2) influence the propagation of monostable $ [u_0, u_1] $-waves and monostable-bistable waves. Figure 1 shows some examples of wave propagation in the monostable-bistable case ^[108]. The monostable wave with the minimal speed in this example propagates faster than the bistable wave. The monostable wave becomes non-monotone with decaying or persistent oscillations behind the wave front. The speed of the bistable wave increases with the increase of time delay, and for $ \tau $ sufficiently large, the two waves merge forming a single wave with the speed $ c_0 $ of the monostable wave.

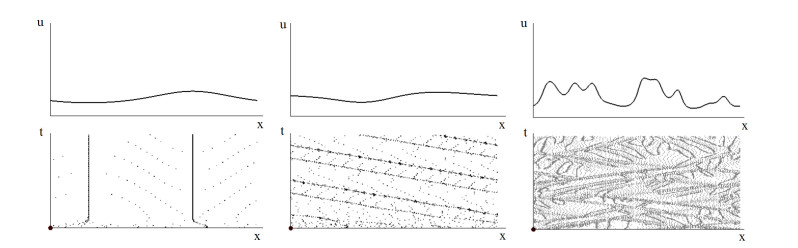
Another mechanism of the emergence of spatiotemporal patterns described by Eq (5.1) is related to secondary bifurcations of the homogeneous in space periodic time oscillations. The loss of stability of such oscillations with respect to spatial perturbations leads to the emergence of standing waves, periodic waves, and more complex aperiodic regimes (Figure 3) ^[123,124].

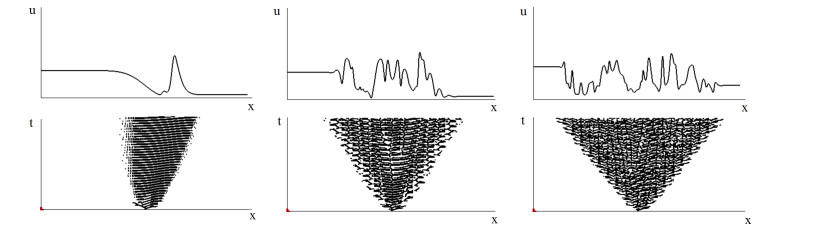
Behavior of solutions of this equation is different for the initial condition of $ u(x, 0) = u_0(x) $ considered as a piece-wise constant function, $ u_0(x) = u_1 $ for $ 0 \leq x\leq x_0 $ and $ u_0(x) = u_2 $ for $ x_0 < x \leq L $, where $ L $ is the length of the interval, $ x_0 \in (0, L) $, $ u_1 $ and $ u_2 $ are some constants. Two different time-oscillating solutions of Eq (5.2) with the initial conditions $ u(0) = u_1 $ and $ u(0) = u_2 $ are observed in the left and in the right parts of the interval $ [0, L] $ separated by a transition zone between them. The width of this transition zone grows in time with a decaying rate (Figure 4, left) or with a constant rate (Figures 4, middle and right). The former is determined by diffusion, and the latter by a wave propagating between a constant in space and periodic in time solution and spatiotemporal oscillations in the middle of the interval. These oscillations can be close to periodic with a single spike moving back and forth along the transition zone (Figure 4, left) or they can have a more complex structure with multiple spikes (Figures 4, middle and right). Though such oscillations are not periodic, they have some characteristic space and time scales which can be identified in the patterns formed by the maxima of solutions (Figure 4, lower row).

Multi-dimensional equation. The 2D equation

is introduced in ^[125] (without time delay) in order to study dynamics of virus distribution with respect to the space variable $ x \in \mathbb R $ and genotype variable $ y \in [-L, L] $. Here $ I(u) = \int_{-L}^L u(x, y, t)dy $ is the total virus density for all genotypes. Dependence of the function $ f(I(u)) $ on this integral signifies that the strength of immune response depends on the total virus density for all genotypes. A non-negative function $ \sigma(y) $ characterized genotype-dependent virus mortality.

If $ \sigma(y) \equiv 0 $, then for the boundary condition

and the initial condition independent of $ y $, dynamics of this solution is similar to the dynamics for the 1D equation described above.

The corresponding 1D equation with respect to the genotype variable $ y $ and the function $ \sigma(y) $ different from $ 0 $ was studied in ^[126,127]. Positive stationary solutions of this equation decaying at infinity correspond to virus quasi-species. The condition of their existence is determined by the properties of the genotype-dependent mortality $ \sigma(y) $ and by the mutation rate $ D_y $.

If $ \sigma(y) \neq 0 $, then the solution of Eq (5.3) is essentially two-dimensional. However, in the particular case $ b = 0 $ it can be reduced to 1D equation by the methods of separation of variables. Set $ u(x, y, t) = u(x, t) \phi(y) $. Then problem (5.3), (5.4) can be reduced to the 1D equation for the function $ v(x, t) $:

where $ \lambda $ is the principal eigenvalue of the problem

with $ \int_{-L}^L \phi(y)dy = 1 $. Equation (5.5) is similar to Eq (5.1) with a modified nonlinearity. Dynamics of its solutions can be analyzed by the same methods.

Systems of equations. A more complete model of infection development consists of the equations for the virus density and for the concentration of immune cells:

where $ D_u, D_c, k $, and $ \sigma $ are positive parameters, $ \phi(u) $ and $ \psi(u) $ are some non-negative functions. Equation (5.7) is similar to Eq (5.1) where the concentration $ c $ of immune cells is replaced by the function $ f(u_\tau) $ (see below). The right-hand side of Eq (5.8) describes random motion of immune cells, their reproduction, and death. The last two terms depend on the virus density with time delay. Under the quasi-stationary approximation in Eq (5.8), from the equality $ \phi(u_\tau) c (1-c) - \psi(u_\tau) c = 0 $, we get $ c = f(u_\tau) $, where $ f(u) = 1 - \psi(u)/\phi(u) $. This approximation allows us to reduce system (5.7), (5.8) to Eq (5.1).

If the function $ f(u) $ is strictly decreasing, then system (5.7), (5.8) with $ \tau = 0 $ can be reduced to a locally monotone system. The existence of waves in this case is proved by the Leray-Schauder method based on the topological degree for elliptic problems in unbounded domains and a priori estimates in some properly chosen weighted spaces ^[12]. If this function is not monotonically decreasing, this reduction cannot be done. The wave existence in the bistable case without time delay is proved in ^[128] and with time delay in ^[111]. Dynamics of waves is studied numerically in ^[108,129]. Depending on the values of parameters, these waves convert the disease-free equilibrium either in the virus-free equilibrium, corresponding to infection elimination, or to virus-positive equilibrium corresponding to persistent infection.

6.   Neural field models

Neural field models describe the distribution of electric potential in the brain cortex. Ensemble of neurons in these models is considered as a continuous medium. Neurons receive signals from other neurons and fire if this signal exceeds some threshold level. Neural field models describe various waves and patterns observed in different types of brain activity ^{[130,131,132,134]}.

The investigation of neural field models begins with the work by Wilson and Cowan ^[133] who introduced delay integro-differential equations for the densities of activating and inhibiting neurons. This work was followed by many others with a variety of models and results. Typically, neural field model can be considered as a system of two equations

where the integrals

describe total signals coming from all points $ y $ to the point $ x $, $ W_{11} $ and $ W_{21} $ correspond to the activating signals and $ W_{12} $ and $ W_{22} $ to inhibiting signals. Time delay $ |x-y|/q_i $ corresponds to the delay in signal transmission, where its speed $ q_i $ can be different for activating and inhibiting signals, and $ \tau_i $ is time delay in the response function $ S_{ij} $ due to signal processing. The connectivity functions $ \phi_{ij} $ characterize the intensity of neuron connection as a function of distance between them. They are usually considered as exponentially decaying functions of the argument $ |x-y| $, while the neuron response functions $ S_{ij} $ are sigmoid-type functions. The last terms in right-hand sides in Eqs (6.1), (6.2) describe signal decay. Neural field models are often considered without the diffusion terms ^[135]. In this case, signal transmission occurs along the axons, and it is taken into account in the integral terms. For the sake of generality and taking into other possible mechanisms (molecular diffusion), we consider the case of nonzero diffusion coefficient. Signal transmission speed $ q_i $ are sufficiently fast ^[136], and the terms $ |x-y|/q_i $ can be neglected.

We will consider various particular cases of the model (6.1), (6.2) and will describe their main properties from the point of view of the existence of wave fronts and periodic waves.

Activation without inhibition. Assuming that the coefficients in Eqs (6.1) and (6.2), as well as connectivity and response functions are equal to each other, we get $ u(x, t) \equiv v(x, t) $ for all $ x $ and $ t $, if this equality is satisfied for the initial condition. Therefore, the system of two equations can be reduced to a single equation. Next, if the response function for inhibiting neurons is set $ 0 $, then we obtain the scalar equation for the density of activating neurons (signals):

The subscripts are omitted here for simplicity of notation. Existence and stability of wave fronts for a similar equation in the context of population dynamics was studied in ^[73]. The wave speed in a partially damaged tissue due to stroke, where the connectivity and response function are modified, decreases with respect to the normal tissue ^[137]. If the damage of the tissue is not too strong, the wave speed can be restored by the external stimulation.

A modified equation, where the integral and the nonlinearity are inverted, $ S(J(u)) $ with $ J(u) = \int_{-\infty}^\infty \phi(x-y) u(y, t-\tau) dy $, instead of $ J(S(u)) $ in (6.3), are also considered in neural field models and in other applications. It is shown that the wave speed for this equation can be determined either by diffusion or by neuron connectivity depending on their relative contribution ^[138].

Activation and inhibition. In the presence of inhibition, system (6.1), (6.2) can be reduced to the single equation

(with the corresponding subscripts). Assuming that $ S_1(0) = S_2(0) = 0 $, then $ u = 0 $ is a homogeneous in space stationary solution of this equation. Linear stability analysis shows that this solution can lose its stability leading to the bifurcation of homogeneous in space periodic time oscillations or of stationary periodic in space solutions. Periodic traveling waves bifurcate from the unstable solution $ u = 0 $. Therefore, they are unstable near the bifurcation point but they can become stable for sufficiently large time delay $ \tau_2 $ ^[139]. It is interesting to note that different waves can coexist for the same values of parameters. This result corresponds to the existence of periodic waves with different frequencies and speeds observed in the brain cortex.

Reduction of system (6.1), (6.2) to the single equation imposes some constraints on parameters and dynamics of solutions. Bifurcation of stable periodic waves can occur for the system of two equations, various other patterns and waves are observed ^[135].

Other models. Models with distributed time delay can also manifest complex dynamics with periodic traveling waves, stationary and time-dependent patterns ^[140,141]. Neural field model with refractoriness ^[142] takes into account time delay after neuron firing. Traveling waves in delay reaction-diffusion equations for some other applications are considered in ^[143,144].

7.   Conclusions

Delayed reaction-diffusion equations arise in various biological and biomedical applications where time delay in the reaction term takes into account duration of some production or elimination processes, such as duration of cell cycle in cell proliferation or virus replication inside cell, and so on. The derivation of these models should be done with certain precaution because time delay in negative terms can lead to the loss of positivity of solutions. Furthermore, the combination of delay with random motion (diffusion) can false the density distribution because the 'particle' moves during delay period. Therefore, the reaction term $ f(u(x, t-\tau)) $ taken at the space point $ x $ at time $ t-\tau $ does not necessarily correspond to the density variation $ \frac{\partial u}{\partial t}(x, t) $ at the same space point but some time later. In this case, the assumption that motion and proliferation are mutually exclusive, as it is the case in some models of tumor growth, can be appropriate.

Introduction of time delay in biological models allows us sometimes to simplify the model excluding some processes occurring at a lower space scale. If the model concerns, for example, a cell population, then we can possibly bypass complex and often not sufficiently well known intracellular regulation. On the other hand, if the characteristic diffusion time is much larger than time delay in the reaction term, then the introduction of time delay is not justified. As such, in the evolutionary models with time scale measured in dozens of generations, we do not take into account the duration of gestation.

From the mathematical point of view, delayed equations represent an interesting development of the classical theory of reaction-diffusion equations. We can identify two sub-classes of such equations, satisfying or not the maximum principle (quasi-monotonicity). If it is satisfied, then conventional methods to study existence and stability of traveling waves remain usually applicable, though they can be technically more involved. Much less can be done if quasi-monotonicity is not satisfied. In this case, some other methods, such as various continuation methods (including Leray-Schauder method), are developed for some particular types of equations.

Similar to ODEs where time delay can lead to time oscillations, time delay in reaction-diffusion equations makes their dynamics more complex and interesting. Numerical simulations show the emergence of periodic waves and other spatiotemporal patterns. Complex nonlinear dynamics of delayed reaction-diffusion equation is not yet well investigated. The same is true for many other questions including distributed and state dependent delay in reaction-diffusion equations, systems of delayed equations, multi-dimensional equations.

Acknowledgments

S. Trofimchuk was partially supported by FONDECYT (Chile), project 1190712 (Sections 2–4). V. Volpert is supported by the Ministry of Science and Higher Education of the Russian Federation: agreement no. 075-03-2020-223/3 (FSSF-2020-0018) (Sections 1, 5–7).

Conflict of interest

The authors declare no conflict of interest.