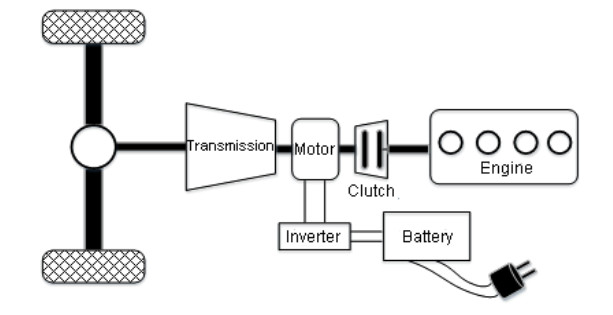
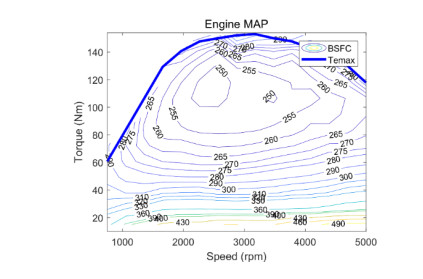
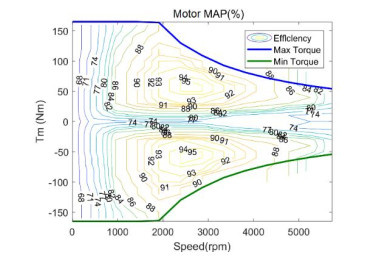
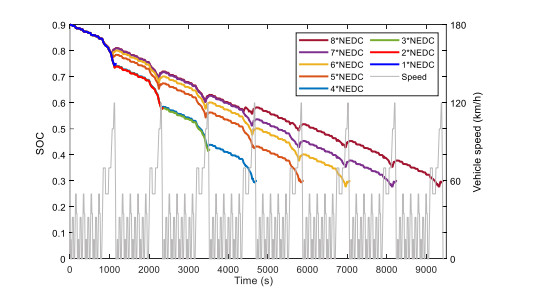
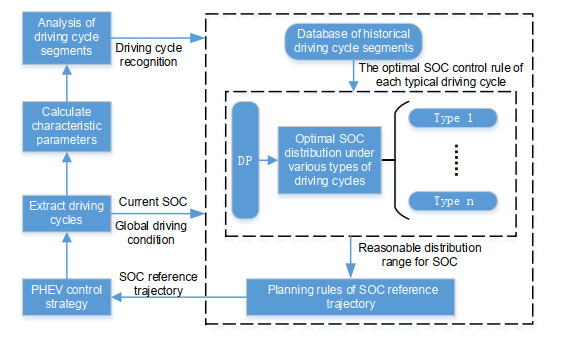
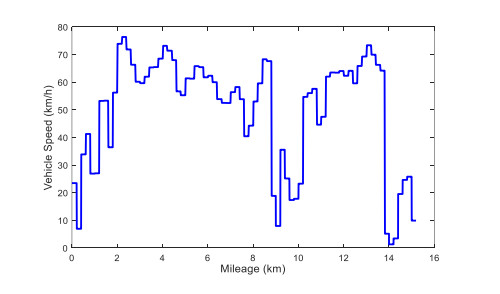
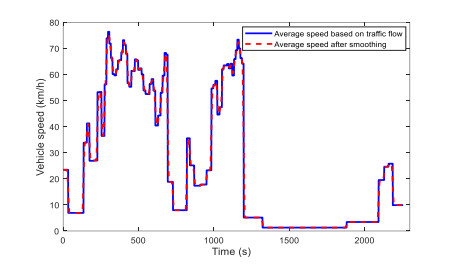
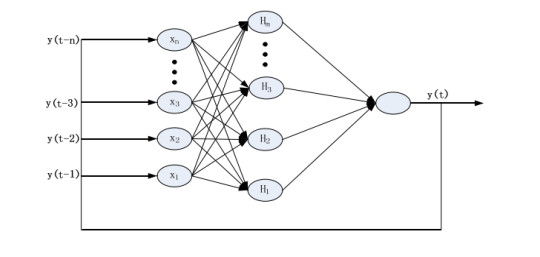
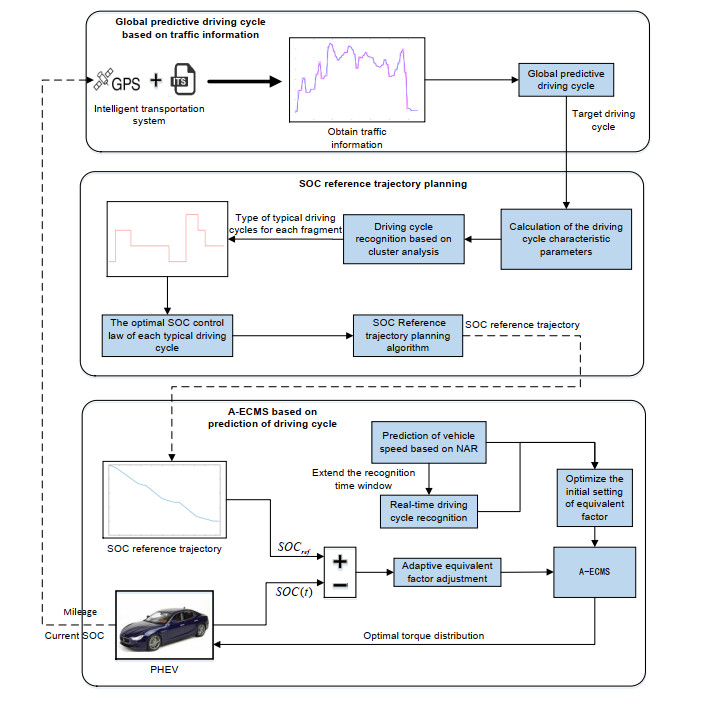
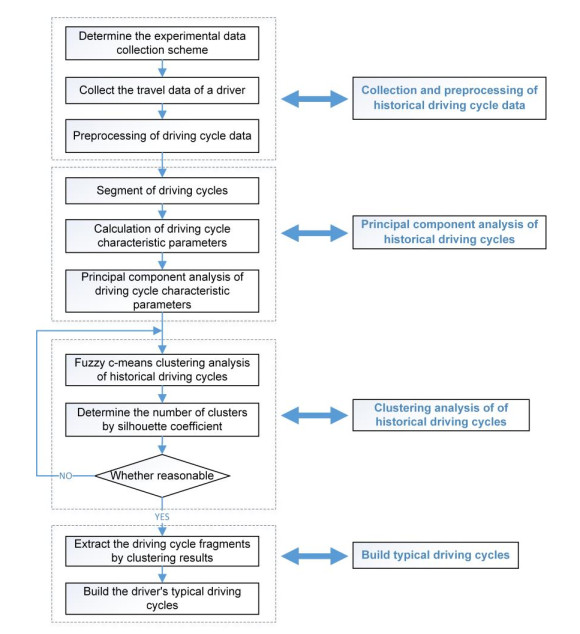
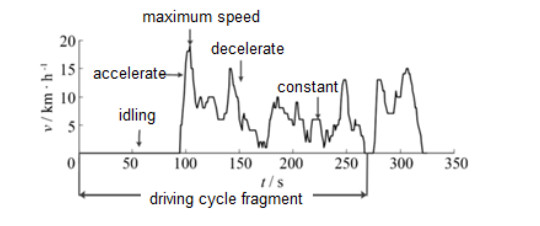
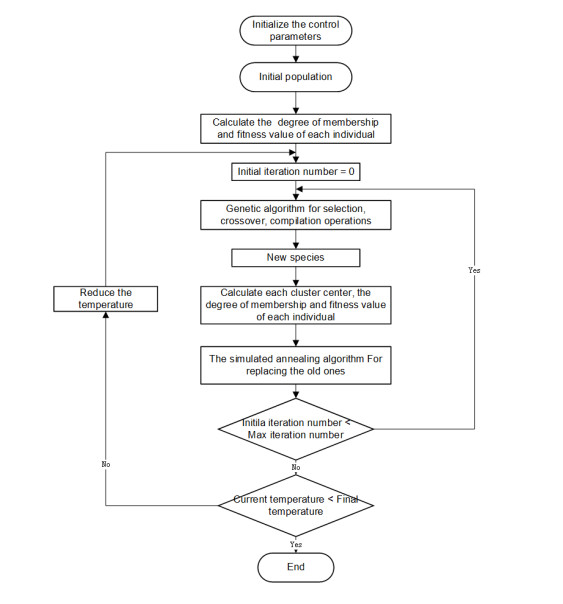
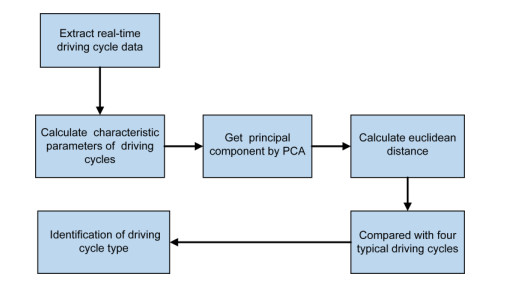
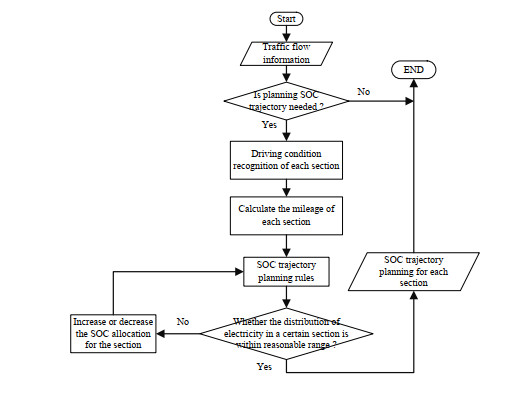
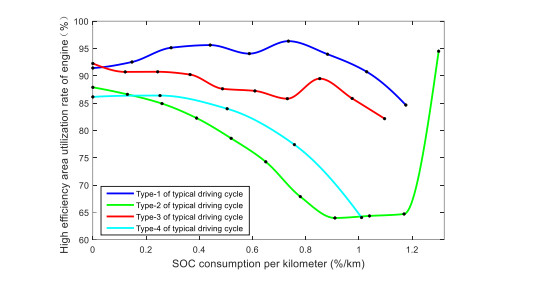
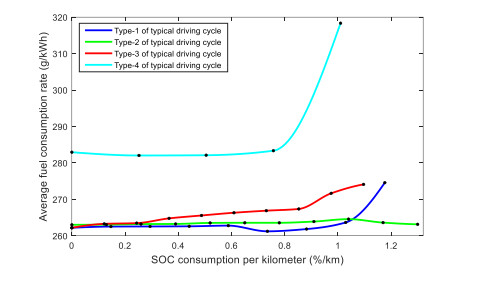
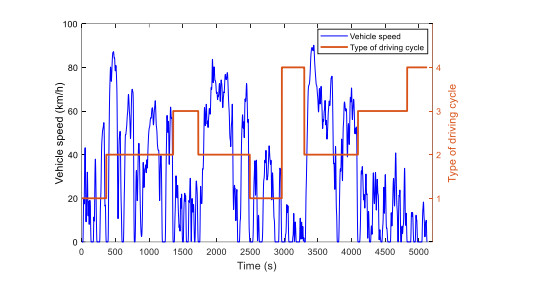
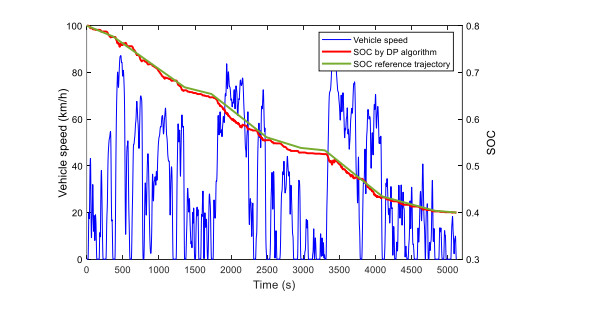
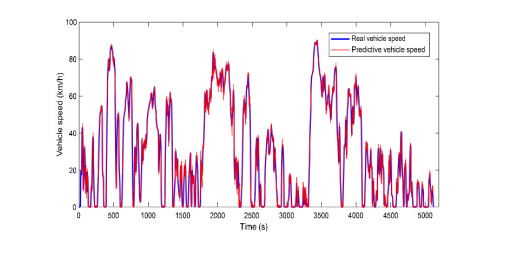
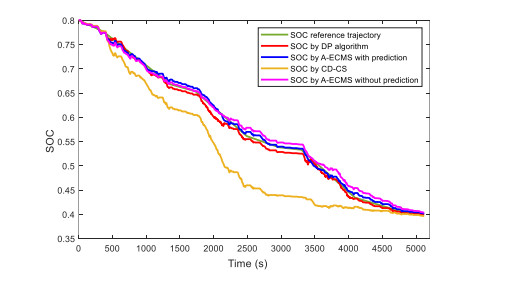
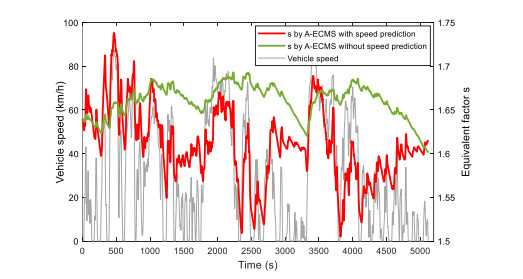
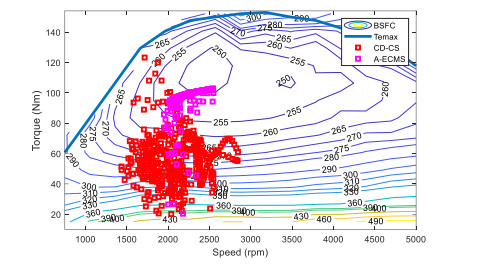
Energy management plays an important role in improving the fuel economy of plug-in hybrid electric vehicles (PHEV). Therefore, this paper proposes an improved adaptive equivalent consumption minimization strategy (A-ECMS) based on long-term target driving cycle recognition and short-term vehicle speed prediction, and adapt it to personalized travel characteristics. Two main contributions have been made to distinguish our work from exiting research. Firstly, online long-term driving cycle recognition and short-term speed prediction are considered simultaneously to adjust the equivalent factor (EF). Secondly, the dynamic programming (DP) algorithm is applied to the offline energy optimization process of A-ECMS based on typical driving cycles constructed according to personalized travel characteristics. The improved A-ECMS can optimize EF based on mileage, SOC, long-term driving cycle and real-time vehicle speed. In the offline part, typical driving cycles of a specific driver is constructed by analyzing personalized travel characteristics in the historical driving data, and optimal SOC consumption under each typical driving cycle is optimized by DP. In the online part, the SOC reference trajectory is obtained by recognizing the target driving cycle from Intelligent Traffic System, and short-term vehicle speed is predicted by Nonlinear Auto-Regressive (NAR) neural network which both adjust EF together. Simulation results show that compared with CD-CS, the fuel consumption of A-ECMS proposed in the paper is reduced by 8.7%.
1.
Introduction and definitions
The theory of the basic and the fractional quantum calculus, that is, the basic (or q-) calculus and the fractional basic (or q-) calculus, play important roles in many diverse areas of the mathematical, physical and engineering sciences (see, for example, [10,15,33,45]). Our main objective in this paper is to introduce and study some subclasses of the class of the normalized p-valently analytic functions in the open unit disk:
by applying the q-derivative operator in conjunction with the principle of subordination between analytic functions (see, for details, [8,30]).
We begin by denoting by A(p) the class of functions f(z) of the form:
which are analytic and p-valent in the open unit disk U. In particular, we write A(1)=:A.
A function f(z)∈A(p) is said to be in the class S∗p(α) of p-valently starlike functions of order α in U if and only if
Moreover, a function f(z)∈A(p) is said to be in the class Cp(α) of p-valently convex functions of order α in U if and only if
The p-valent function classes S∗p(α) and Cp(α) were studied by Owa [32], Aouf [2,3] and Aouf et al. [4,5]. From (1.2) and (1.3), it follows that
Let P denote the Carathéodory class of functions p(z), analytic in U, which are normalized by
such that ℜ(p(z))>0.
Recently, Kanas and Wiśniowska [18,19] (see also [17,31]) introduced the conic domain Ωk(k≧0), which we recall here as follows:
or, equivalently,
By using the conic domain Ωk, Kanas and Wiśniowska [18,19] also introduced and studied the class k-UCV of k-uniformly convex functions in U as well as the corresponding class k-ST of k-starlike functions in U. For fixed k, Ωk represents the conic region bounded successively by the imaginary axis when k=0. For k=1, the domain Ωk represents a parabola. For 1<k<∞, the domain Ωk represents the right branch of a hyperbola. And, for k>1, the domain Ωk represents an ellipse. For these conic regions, the following function plays the role of the extremal function:
with
where κ is so chosen that
Here K(κ) is Legendre's complete elliptic integral of the first kind and
that is, K′(κ) is the complementary integral of K(κ) (see, for example, [48,p. 326,Eq 9.4 (209)]).
We now recall the definitions and concept details of the basic (or q-) calculus, which are used in this paper (see, for details, [13,14,45]; see also [1,6,7,11,34,38,39,42,54,59]). Throughout the paper, unless otherwise mentioned, we suppose that 0<q<1 and
Definition 1. The q-number [λ]q is defined by
so that
.
Definition 2. For functions given by (1.1), the q-derivative (or the q-difference) operator Dq of a function f is defined by
provided that f′(0) exists.
We note from Definition 2 that
for a function f which is differentiable in a given subset of C. It is readily deduced from (1.1) and (1.8) that
We remark in passing that, in the above-cited recently-published survey-cum-expository review article, the so-called (p,q)-calculus was exposed to be a rather trivial and inconsequential variation of the classical q-calculus, the additional parameter p being redundant or superfluous (see, for details, [42,p. 340]).
Making use of the q-derivative operator Dq given by (1.6), we introduce the subclass S∗q,p(α) of p-valently q-starlike functions of order α in U and the subclass Cq,p(α) of p-valently q-convex functions of order α in U as follows (see [54]):
and
respectively. From (1.10) and (1.11), it follows that
For the simpler classes S∗q,p and C∗q,p of p-valently q-starlike functions in U and p-valently q-convex functions in U, respectively, we have write
Obviously, in the limit when q→1−, the function classes S∗q,p(α) and Cq,p(α) reduce to the familiar function classes S∗p(α) and Cp(α), respectively.
Definition 3. A function f∈A(p) is said to belong to the class S∗q,p of p-valently q-starlike functions in U if
In the limit when q→1−, the closed disk
becomes the right-half plane and the class S∗q,p of p-valently q-starlike functions in U reduces to the familiar class S∗p of p-valently starlike functions with respect to the origin (z=0). Equivalently, by using the principle of subordination between analytic functions, we can rewrite the condition (1.13) as follows (see [58]):
We note that S∗q,1=S∗q (see [12,41]).
Definition 4. (see [50]) A function p(z) given by (1.5) is said to be in the class k-Pq if and only if
where pk(z) is given by (1.6).
Geometrically, the function p∈k-Pq takes on all values from the domain Ωk,q (k≧0) which is defined as follows:
The domain Ωk,q represents a generalized conic region which was introduced and studied earlier by Srivastava et al. (see, for example, [43,50]). It reduces, in the limit when q→1−, to the conic domain Ωk studied by Kanas and Wiśniowska [18]. We note the following simpler cases.
(1) k-Pq⊆P(2k2k+1+q), where P(2k2k+1+q) is the familiar class of functions with real part greater than 2k2k+1+q;
(2) limq→1−{k-Pq}=P(pk(z)), where P(pk(z)) is the known class introduced by Kanas and Wiśniowska [18];
(3) limq→1−{0-Pq}=P, where P is Carathéodory class of analytic functions with positive real part.
Definition 5. A function f∈A(p) is said to be in the class k-STq,p if and only if
or, equivalently,
The folowing special cases are worth mentioning here.
(1) k-STq,1=k-STq, where k-STq is the function class introduced and studied by Srivastava et al. [50] and Zhang et al. [60] with γ=1;
(2) 0-STq,p=Sq,p;
(3) limq→1{k-STq,p}=k-STp, where k-STp is the class of p-valently uniformly starlike functions;
(4) limq→1{0-STq,p}=Sp, where S∗p is the class of p-valently starlike functions;
(5) 0-STq,1=S∗q, where S∗q (see [12,41]);
(6) limq→1{k-STq,1}=k-ST, where k-ST is a function class introduced and studied by Kanas and Wiśniowska [19];
(7) limq→1{0-STq,1}=S∗, where S∗ is the familiar class of starlike functions in U.
Definition 6. By using the idea of Alexander's theorem [9], the class k-UCVq,p can be defined in the following way:
In this paper, we investigate a number of useful properties including coefficient estimates and the Fekete-Szegö inequalities for the function classes k-STq,p and k-UCVq,p, which are introduced above. Various corollaries and consequences of most of our results are connected with earlier works related to the field of investigation here.
2.
A set of Lemmas
In order to establish our main results, we need the following lemmas.
Lemma 1. (see [16]) Let 0≦k<∞ be fixed and let pk be defined by (1.6). If
then
and
where
and t∈(0,1) is so chosen that
K(t) being Legendre's complete elliptic integral of the first kind.
Lemma 2. Let 0≦k<∞ be fixed and suppose that
where pk(z) be defined by (1.6). Then
where Q1 and Q2 are given by (2.1) and (2.2), respectively.
Proof. By using (1.6) in (2.3), we can easily derive (2.4).
Lemma 3. (see [26]) Let the function h given by
be analytic in U and satisfy ℜ(h(z))>0 for z in U. Then the following sharp estimate holds true:
The result is sharp for the functions given by
Lemma 4. (see [26]) If the function h is given by
then
When ν>1, the equality holds true if and only if
or one of its rotations. If 0<ν<1, then the equality holds true if and only if
or one of its rotations. If ν=0, the equality holds true if and only if
or one of its rotations. If ν=1, the equality holds true if and only if the function h is the reciprocal of one of the functions such that equality holds true in the case when ν=0.
The above upper bound is sharp and it can be improved as follows when 0<ν<1:
and
3.
Main results
We assume throughout our discussion that, unless otherwise stated, 0≦k<∞, 0<q<1, p∈N, Q1 is given by (2.1), Q2 is given by (2.2) and z∈U.
Theorem 1. If a function f∈A(p) is of the form (1.1) and satisfies the following condition:
then the function f∈k-STq,p.
Proof. Suppose that the inequality (3.1) holds true. Then it suffices to show that
In fact, we have
The last expression is bounded by 1 if (3.1) holds true. This completes the proof of Theorem 1.
Corollary 1. If f(z)∈k-STq,p, then
The result is sharp for the function f(z) given by
Remark 1. Putting p=1 Theorem 1, we obtain the following result which corrects a result of Srivastava et al. [50,Theorem 3.1].
Corollary 2. (see Srivastava et al. [50,Theorem 3.1]) If a function f∈A is of the form (1.1) (with p=1) and satisfies the following condition:
then the function f∈k-STq.
Letting q→1− in Theorem 1, we obtain the following known result [29,Theorem 1] with
Corollary 3. If a function f∈A(p) is of the form (1.1) and satisfies the following condition:
then the function f∈k-STp.
Remark 2. Putting p=1 in Corollary 3, we obtain the result obtained by Kanas and Wiśniowska [19,Theorem 2.3].
By using Theorem 1 and (1.18), we obtain the following result.
Theorem 2. If a function f∈A(p) is of the form (1.1) and satisfies the following condition:
then the function f∈k-UCVq,p.
Remark 3. Putting p=1 Theorem 1, we obtain the following result which corrects the result of Srivastava et al. [50,Theorem 3.3].
Corollary 4. (see Srivastava et al. [50,Theorem 3.3]) If a function f∈A is of the form (1.1) (with p=1) and satisfies the following condition:
then the function f∈k-UCVq.
Letting q→1− in Theorem 2, we obtain the following corollary (see [29,Theorem 1]) with
Corollary 5. If a function f∈A(p) is of the form (1.1) and satisfies the following condition:
then the function f∈k-UCVp.
Remark 4. Putting p=1 in Corollary 5, we obtain the following corollary which corrects the result of Kanas and Wiśniowska [18,Theorem 3.3].
Corollary 6. If a function f∈A is of the form (1.1) (with p=1) and satisfies the following condition:
then the function f∈k-UCV.
Theorem 3. If f∈k-STq,p, then
and, for all n=3,4,5,⋯,
Proof. Suppose that
where
Eq (3.4) can be written as follows:
which implies that
Comparing the coefficients of zn+p−1 on both sides of (3.5), we obtain
By taking the moduli on both sides and then applying the following coefficient estimates (see [50]):
we find that
We now apply the principle of mathematical induction on (3.6). Indeed, for n=2, we have
which shows that the result is true for n=2. Next, for n=3 in (3.7), we get
By using (3.7), we obtain
which is true for n=3. Let us assume that (3.3) is true for n=t(t∈N), that is,
Let us consider
Therefore, the result is true for n=t+1. Consequently, by the principle of mathematical induction, we have proved that the result holds true for all n(n∈N∖{1}). This completes the proof of Theorem 3.
Similarly, we can prove the following result.
Theorem 4. If f∈k-UCVq,p and is of form (1.1), then
and, for all n=3,4,5,⋯,
Putting p=1 in Theorems 3 and 4, we obtain the following corollaries.
Corollary 7. If f∈k-STq, then
and, for all n=3,4,5,⋯,
Corollary 8. If f∈k-UCVq, then
and, for all n=3,4,5,⋯,
Theorem 5. Let f∈k-STq,p. Then f(U) contains an open disk of the radius given by
Proof. Let w0≠0 be a complex number such that f(z)≠w0 for z∈U. Then
Since f1 is univalent, so
Now, using Theorem 3, we have
Hence
This completes the proof of Theorem 5.
Theorem 6. Let the function f∈k-STq,p be of the form (1.1). Then, for a complex number μ,
The result is sharp.
Proof. If f∈k-STq,p, we have
From the definition of the differential subordination, we know that
where w(z) is a Schwarz function with w(0)=0 and |w(z)|<1 for z∈U.
Let h∈P be a function defined by
This gives
and
Using (3.10) in (3.9), we obtain
and
Now, for any complex number μ, we have
Then (3.11) can be written as follows:
where
Finally, by taking the moduli on both sides and using Lemma 4, we obtain the required result. The sharpness of (3.8) follows from the sharpness of (2.5). Our demonstration of Theorem 6 is thus completed.
Similarly, we can prove the following theorem.
Theorem 7. Let the function f∈k-UCVq,p be of the form (1.1). Then, for a complex number μ,
The result is sharp.
Putting p=1 in Theorems 6 and 7, we obtain the following corollaries.
Corollary 9. Let the function f∈k-STq be of the form (1.1) (with p=1). Then, for a complex number μ,
The result is sharp.
Corollary 10. Let the function f∈k-UCVq be of the form (1.1) (with p=1). Then, for a complex number μ,
The result is sharp.
Theorem 8. Let
and
If the function f given by (1.1) belongs to the class k-STq,p, then
Furthermore, if σ1≦μ≦σ3, then
If σ3≦μ≦σ2, then
Proof. Applying Lemma 4 to (3.12) and (3.13), respectively, we can derive the results asserted by Theorem 8.
Putting p=1 in Theorem 8, we obtain the following result.
Corollary 11. Let
and
If the function f given by (1.1) (with p=1) belongs to the class k-STq, then
Furthermore, if σ4≦μ≦σ6, then
If σ3≦μ≦σ2, then
Similarly, we can prove the following result.
Theorem 9. Let
and
If the function f given by (1.1) belongs to the class k-UCVq,p, then
Furthermore, if η1≦μ≦η3, then
If η3≦μ≦η2, then
Putting p=1 in Theorem 9, we obtain the following result.
Corollary 12. Let
and
If the function f given by (1.1) (with p=1) belongs to the class k-UCVq, then
Furthermore, if η4≦μ≦η6, then
If η3≦μ≦η2, then
4.
Concluding remarks and observations
In our present investigation, we have applied the concept of the basic (or q-) calculus and a generalized conic domain, which was introduced and studied earlier by Srivastava et al. (see, for example, [43,50]). By using this concept, we have defined two subclasses of normalized multivalent functions which map the open unit disk:
onto this generalized conic domain. We have derived a number of useful properties including (for example) the coefficient estimates and the Fekete-Szegö inequalities for each of these multivalent function classes. Our results are connected with those in several earlier works which are related to this field of Geometric Function Theory of Complex Analysis.
Basic (or q-) series and basic (or q-) polynomials, especially the basic (or q-) hypergeometric functions and basic (or q-) hypergeometric polynomials, are applicable particularly in several diverse areas [see, for example, [48,pp. 350-351]. Moreover, as we remarked in the introductory Section 1 above, in the recently-published survey-cum-expository review article by Srivastava [42], the so-called (p,q)-calculus was exposed to be a rather trivial and inconsequential variation of the classical q-calculus, the additional parameter p being redundant or superfluous (see, for details, [42,p. 340]). This observation by Srivastava [42] will indeed apply to any attempt to produce the rather straightforward (p,q)-variations of the results which we have presented in this paper.
In conclusion, with a view mainly to encouraging and motivating further researches on applications of the basic (or q-) analysis and the basic (or q-) calculus in Geometric Function Theory of Complex Analysis along the lines of our present investigation, we choose to cite a number of recently-published works (see, for details, [25,47,51,53,56] on the Fekete-Szegö problem; see also [20,21,22,23,24,27,28,35,36,37,40,44,46,49,52,55,57] dealing with various aspects of the usages of the q-derivative operator and some other operators in Geometric Function Theory of Complex Analysis). Indeed, as it is expected, each of these publications contains references to many earlier works which would offer further incentive and motivation for considering some of these worthwhile lines of future researches.
Conflicts of interest:
The authors declare no conflicts of interest.













 DownLoad:
DownLoad: