Existence of nonradial positive and nodal solutions to a critical Neumann problem in a cone

1.   Introduction

Coronavirus disease 2019, COVID-19, is a new infectious disease that emerged at the end of 2019. Within three months, became a global epidemic ^[1]. As of December 26, 2021, the number of confirmed cases around the world had reached 278,714,484 ^[2]. The epidemic affected various aspects of life, including the economic, health and social aspects.

Several researchers have discussed the disease dynamics and characteristics of COVID-19 patients in different regions of the world. Individuals infected with COVID-19 may or may not have symptoms that range from mild to severe. Individuals who experience a fever, dry cough, fatigue and headaches as mild symptoms or acute respiratory distress syndrome as a severe symptom ^[3] are called symptomatic individuals. Individuals who do not show any signs and their infection is confirmed through real-time reverse transcriptase-polymerase chain reaction (RT-PCR), i.e., a type of diagnostic test for COVID-19, are called asymptomatic individuals ^[4]. These patients can also transmit the disease to other individuals ^[5,6].

The presence of asymptomatic patients has led researchers to focus on studying this class of patients. Some research has described the clinical characteristics of asymptomatic and symptomatic patients of COVID-19 ^[7,8]. Kim et al. ^[7] determined the spread of asymptomatic cases in South Korea. Of 213 infected individuals with COVID-19, 41 ($19.2\%$) were asymptomatic. They concluded that as much as one-fifth of infected individuals with COVID-19 are asymptomatic. Therefore, strict social distancing must be applied to prevent the transmission of the disease through these individuals. AlJishi et al. ^[8] described the spread of COVID-19 at the epicenter of its spread in Saudi Arabia, in the eastern region of the kingdom. They concluded that most COVID-19 cases were asymptomatic and returned from travel. In addition, Alsofayan et al. ^[9] emphasized the need to give attention to asymptomatic individuals and health care workers because they contribute to the spread of the disease.

Several studies have proposed a mathematical model that considers asymptomatic and symptomatic infected individuals ^{[10,11,12,13,14,15,16,17,18]}. A mathematical model was proposed in ^[10] to discover the effect of asymptomatic infected people and estimate the number of beds needed in hospitals and intensive care units in Saudi Arabia. They concluded that asymptomatic people are more effective in increasing the number of infections than symptomatic people. However, the increase in COVID-19 testing and social distancing reduces the infection by asymptomatic individuals. Sun and Weng ^[15] established a mathematical model to discuss the effect of asymptomatic and imported patients in the Jiangsu and Anhui provinces in China. Their analysis found that asymptomatic patients are more dangerous than imported patients. Moreover, asymptomatic patients can rapidly cause an outbreak of the disease without strict preventive measures.

Serhani and Labbardi ^[16] analyzed two mathematical models to study the spread of COVID-19 in Morocco without and with containment of the pandemic. They found that the free equilibrium point is asymptotically stable when the containment coefficient exceeds the basic reproduction number $\mathcal{R}_{0}$. Furthermore, increasing the containment rate decreases the number of asymptomatic and symptomatic individuals. Huo et al. ^[17] studied the spread of COVID-19 and the effect of non-pharmaceutical interventions in Wuhan. They estimated that $20\%$ of patients remain asymptomatic during infection, and that their ability to transmit is around $70\%$ of the symptomatic patients' ability.

Moreover, in ^[13,14], the authors analyzed mathematical models for COVID-19 in Saudi Arabia. The models assumed the transmission of infection is due to the environment and occurs through contact with exposed, asymptomatic and symptomatic individuals. Alzahrani et al. ^[13] dealt with a fractional model. Alqarni et al. ^[14] used a classical epidemic model and concluded that the cases in Saudi Arabia would decrease if contact with exposed individuals and the environment decreases.

With the increasing number of infections and the contribution of asymptomatic individuals to the transmission of the disease, there have been efforts in various countries to constrain the epidemic. Several precautions have been imposed to keep susceptible individuals away from infected individuals. Studies have demonstrated the effectiveness of preventive measures, such as lockdowns ^[19,20,21], social distancing ^[22,23,24], quarantining ^[12,16] and isolation ^[25,26]. Nevertheless, we need measures to detect asymptomatic patients, particularly at the beginning of the disease and before treatment is available, to limit its spread and reduce the number of deaths, an example of such a measure is diagnosis testing ^[27].

Al-Salti et al. ^[18] developed a mathematical model to analyze the optimal control strategies, especially diagnosis and quarantining, for the spread of COVID-19 in the Sultanate of Oman. It was concluded that diagnosis and quarantining are the most important strategies for controlling the disease. Similarly, in ^[11], Ahmed et al. confirmed the effectiveness of the diagnosis in reducing the infected cases. In addition, Khan et al. ^[28] studied the effectiveness of Saudi Arabia's experience in producing the diagnosis of COVID-19. From April 14 to mid-July of 2020, the Saudi's diagnostic program for COVID-19 was conducted in three stages ^[28,29]. The first stage was performing random diagnostic tests on people in crowded places such as workers' housing, which included 807 locations from April 16 to May 5, 2020 ^[30]. The second stage was conducting diagnostic tests in specific health centers through an application (Mawid) from May 3 to May 19, 2020. The third stage was conducting rapid tests at medical centers through drive-in vehicles, which started on May 29, 2020 ^[31,32]. Also, the government of Saudi Arabia has continued to expand the diagnostic procedures for COVID-19 ^{[33,34,35,36]}.

This paper describe the study of the impact of detecting asymptomatic COVID-19 patients through random diagnostic testing in Saudi Arabia. Random diagnosis means diagnosing COVID-19 for suspected individuals at random, whether they show symptoms or not. In other words, officials in the Ministry of Health go to homes and diagnose individuals in places where there are factors that contribute to the spread of the disease, such as overpopulation.

We extend our model in ^[37] to include the asymptomatic COVID-19 patients and analyze the impact of random diagnostic tests. Therefore, this model contains three control measures that have been implemented in Saudi Arabia: lockdown, social distancing and random diagnostic testing. The analysis of this model attempts to determine if it is possible to rely on random diagnosis while reducing or eliminating lockdown and social distancing. This paper is organized as follows. In Section 2, we formulate the model and prove that it is well posed. In Section 3, we demonstrate the qualitative analysis, including the equilibrium points, basic and control reproduction numbers, and the local and global stability of the equilibrium points. Section 4 presents the numerical analysis, which includes the fitting of the model to COVID-19 cases in Saudi Arabia and the estimation of the model parameters. Furthermore, we describe numerical experiments that were conducted to confirm the qualitative analysis results and investigate the sensitivity analysis for the control reproduction number. Finally, we analyze different scenarios for control strategies, random diagnostic testing, lockdown and social distancing.

2.   Mathematical model

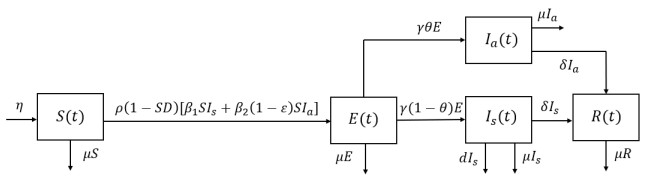
The model was formulated to examine the effect of the random diagnostic tests for asymptomatic patients on the spread of COVID-19 in Saudi Arabia. The Saudi population, $N$, comprises five compartments: susceptible individuals, $S$, exposed individuals, $E$, asymptomatic infected individuals (with no symptoms), $I_{a}$, symptomatic infected individuals (with symptoms), $I_{s}$, and recovered individuals, $R$. Individuals move from the susceptible compartment to the exposed compartment after interacting with infected individuals, symptomatic or asymptomatic, at the transmission rates $\beta_{1}$ and $\beta_{2}$, respectively. The control measures, i.e., the lockdown ($\rho(t)\in(0, 1]$) and the social distancing ($SD(t)\in[0, 1)$), impact the transmission rates $\beta_{1}$ and $\beta_{2}$. However, the random diagnostic testing for asymptomatic individuals affects only $\beta_{2}$. The function $\varepsilon(t)\in [0, 1]$ represents the effectiveness of the random diagnostic testing for $I_{a}$. If $\varepsilon = 1$, then the random diagnostic test was administered to all asymptomatic individuals in the community. Conversely, no random diagnostic test is performed for $I_{a}$ when $\varepsilon = 0$. After completing the incubation period, $1/\gamma$, individuals in the exposed compartment move to the asymptomatic compartment with the probability $\theta$, where $\theta\in(0, 1)$; and the rest of the individuals $(1-\theta)$ move to the symptomatic compartment. We assume that individuals in the exposed compartment may or may not show symptoms by the end of the incubation period. Also, individuals in the asymptomatic compartment can transmit the disease more than individuals in the symptomatic compartment, that is, $\beta_{2} > \beta_{1}$. Moreover, individuals die due to COVID-19 only from the symptomatic compartment at a rate $d$. Infected individuals, asymptomatic and symptomatic, recover and gain immunity to COVID-19 at a rate $\delta$. The natural death rate for each compartment is $\mu$, and $\eta$ is the natural birth rate.

Figure 1 displays the model's dynamics. We express the model mathematically with the following nonlinear system of ordinary differential equations:

where all parameters belong to the interval $(0, 1]$ and $N = S(t)+E(t)+I_{a}(t)+I_{s}(t)+R(t)$.

We start the analysis by proving that the state variables of Model (2.1) are epidemiologically meaningful, that is, non-negative and bounded.

Theorem 1

If $(S, E, I_{a}, I_{s}, R) \in \mathbb{R}_{\ge0}^{5}$, then the set

is positively invariant for Model (2.1).

Proof.

Let $(S(0), E(0), I_{a}(0), I_{s}(0), R(0))\in \Omega$. We have

Thus, all non-negative solutions remain non-negative for $t\ge 0$. By adding all of the equations of Model (2.1), we get

Multiplying the above inequality by the integrating factor $(e^{\mu r})$, we have

By integrating both sides over the interval $[0, t]$, we obtain

Hence,

Therefore, for $t\ge 0,$ the solutions of Model (2.1) are non-negative and bounded. Thus, $\Omega$ is positively invariant.

3.   Qualitative analysis

We qualitatively investigate Model (2.1). First, we determine the equilibrium points and the expression of the control reproduction number. Second, we examine the local and global stability of the equilibrium points.

3.1.   Equilibrium points and control reproduction number

The equilibrium points of the model are determined by setting the rates for Model (2.1) to zero:

System (3.1) produces two steady-state solutions: the COVID-19 free equilibrium point, $P_{0} = \left(\eta / \mu, 0, 0, 0, 0\right)$, which always exists, and the COVID-19 endemic equilibrium point, $P_1 = \left(S_{1}, E_{1}, I_{a_{1}}, I_{s_{1}}, R_{1}\right)$, where

Here,

The endemic equilibrium $P_1$ exists only if $\mathcal{R}_{c} > 1$.

Control reproduction number. We use the next-generation matrix method ^[38] to find the control reproduction number. Let the infected compartments $\mathcal{O} = (E, I_{a}, I_{s})^T$; then, the exposed class, asymptomatic class and symptomatic class equations of Model (2.1) can be rewritten as $\dot{\mathcal{O}} = \mathscr{F}(\mathcal{O}) - \mathscr{V} (\mathcal{O})$, where

and

Evaluating the Jacobian matrix of $\mathscr{F}$ and $\mathscr{V}$ at the COVID-19 free equilibrium point $P_{0}$, we get, respectively,

and

The next-generation matrix is

where

Hence, the control reproduction number is the spectral radius of the matrix $FV^{-1}$, that is,

Also, we can rewrite Expression (3.2) as follows: $\mathcal{R}_{c} = \rho(1-SD)\left(\mathcal{R}_{s}+(1-\varepsilon)\mathcal{R}_{a}\right)$, where $\mathcal{R}_{s}$ gives the secondary cases of COVID-19 by one symptomatic individuals, and $\mathcal{R}_{a}$ gives the secondary cases of COVID-19 by one asymptomatic individuals.

The terms in $\mathcal{R}_c$ are explained further as follows. First, for $\mathcal{R}_{s}$, the term that expresses the incidence of new infections by symptomatic individuals is $\beta_{1}SI_{s}$. Thus, the number of secondary cases by one symptomatic individual ($I_{s} = 1$) in a population containing only susceptible individuals is $\beta_{1} S_{0}$, where $S_0 = \eta / \mu$. Moreover, $1/ (\delta+d+\mu)$ represents the average time spent by one symptomatic individual in the symptomatic compartment. Also, $\gamma(1-\theta)/(\gamma+\mu)$ is the proportion of newly symptomatic individuals that survived the incubation period. Second, for $\mathcal{R}_{a}$, the term that represents the incidence of new infections by asymptomatic individuals is $\beta_{2}SI_{a}$. Therefore, the number of secondary cases by one asymptomatic individual ($I_{a} = 1$) in a population containing only susceptible individuals is $\beta_{2} S_{0}$, where $S_0 = \eta / \mu$. Further, $1/ (\delta+\mu)$ expresses the average time spent by one asymptomatic individual in the asymptomatic compartment. Again, $\gamma\theta/(\gamma+\mu)$ is the proportion of newly asymptomatic individuals that survived the incubation period.

3.2.   Local stability analysis

We employ the linearization method ^[39] to examine the local stability of the equilibrium points of Model (2.1).

Theorem 2

The COVID-19 free equilibrium point $P_{0}$ is locally asymptotically stable if $\mathcal{R}_{c} < 1$.

Proof.

The Jacobian matrix of Model (2.1) evaluated at $P_{0}$ yields

By solving the characteristic equation $\mid J(P_0)- \lambda I\mid = 0$, we obtain the eigenvalues $\lambda_{1, 2} = - \mu$, and $\lambda_{3, 4, 5}$ are roots of the following equation:

where

We use the Routh-Hurwitz criteria ^[39] to determine the signs of the remaining eigenvalues $\lambda_{3, 4, 5}$. They are negative if $a_{1} > 0, a_{3} > 0$ and $a_{1}a_{2}-a_{3} > 0$. Clearly, $a_{1} > 0$. Also, $a_{3} > 0$ if $\mathcal{R}_{c} < 1$. Moreover,

If $\mathcal{R}_{c} = \rho(1-SD)[\mathcal{R}_{s}+(1-\varepsilon)\mathcal{R}_{a}] < 1$, then $\rho(1-SD)\mathcal{R}_{s} < 1$ and $\rho(1-SD)(1-\varepsilon)\mathcal{R}_{a} < 1$. Thus, $a_{1}a_{2}-a_{3} > 0$. Hence, $P_0$ is locally asymptotically stable if $\mathcal{R}_{c} < 1$.

Theorem 3

The COVID-19 endemic equilibrium point $P_1$ is locally asymptotically stable if $\mathcal{R}_{c} > 1$.

Proof.

The Jacobian matrix of Model (2.1) evaluated at $P_{1}$ yields

where

The characteristic equation, $\mid J(P_1)- \lambda I\mid = 0$, has the eigenvalues $\lambda_{1} = - \mu$, and $\lambda_{2, 3, 4, 5}$ are the roots of the following equation:

where

Clearly, $a_{1} > 0$ and $a_{4} > 0$. Also, since $\mathcal{R}_{c} = \rho(1-SD)(\mathcal{R}_{s}+(1-\varepsilon)\mathcal{R}_{a}) > 1$, then $a_{2} > 0$ and $a_{3} > 0$. By the Descartes' rule ^[40], the characteristic equation given by Eq (3.3) has no positive roots since there is no change in the signs of the coefficients. When substituting for ($\lambda$) by ($-\lambda$) in Eq (3.3), the signs of the coefficients change as follows:

The number of sign changes is four; therefore, the characteristic Eq (3.3) has four negative eigenvalues. Hence, $P_{1}$ is locally asymptotically stable if $\mathcal{R}_{c} > 1$.

3.3.   Global stability analysis

We utilize the Lyapunov and Krasovkii–LaSalle stability theorems ^[41,42,43] to examine the global stability of the equilibrium points of Model (2.1). Also, we use the function $W(u) = u-1-\ln{u}$, which is a positive function, in the following proofs.

Theorem 4

The COVID-19 free equilibrium point $P_0$ is globally asymptotically stable if $\mathcal{R}_{c} < 1$.

Proof.

Define the Lyapunov function $L_{0}(S, E, I_{a}, I_{s}, R)$ as follows:

If $\mathcal{R}_{c} < 1$, then $L_{0}$ is positive-definite since $L_{0}(S, E, I_{a}, I_{s}, R) > 0$ for all $(S, E, I_{a}, I_{s}, R)\in \Omega$ and $L_{0}(P_0) = 0$. Computing the time derivative of $L_{0}$ along the solutions of Model (2.1), we get

Since $S_{0} = \eta/ \mu$, then $\eta = \mu S_{0}$. Collecting terms, we get

After simplifications by using expressions of $\mathcal{R}_{a}$ and $\mathcal{R}_{s}$, we obtain

If $\mathcal{R}_{c} < 1$, then $dL_{0}/dt \leq 0$ for all $S, R > 0$. Also, $dL_{0}/dt = 0$ when $S(t) = S_{0}$, and $R(t) = 0$. Applying the Krasovkii-Lasalle theorem, we suppose that

and $M_{0}$ is the largest invariant subset of $\mathscr{I}_{0}$, where all elements in it satisfy $S(t) = S_{0}$ and $R(t) = 0$. Then, from the fifth equation of Model (2.1), we get

Substituting this into the third equation of Model (2.1), we have

Hence, $M_{0} = \big\{P_0\big\}$; thus, the equilibrium $P_0$ is globally asymptotically stable if $\mathcal{R}_{c} < 1$.

Theorem 5

The COVID-19 endemic equilibrium point $P_1$ is globally asymptotically stable if $\mathcal{R}_{c} > 1$.

Proof.

Define the Lyapunov function $L_{1}(S, E, I_{a}, I_{s}, R)$ as follows:

Clearly, $L_{1}(S, E, I_{a}, I_{s}, R)$ is a positive semi-definite function since $L_{1}\geq 0$ for all $(S, E, I_{a}, I_{s}, R) \in \Omega$ and $L_{1}(S_{1}, E_{1}, I_{a_{1}}, I_{s_{1}}, R_{1}) = 0$. The time derivative of $L_{1}$ along the solutions of Model (2.1) is given by

From the equilibrium described by Eq (3.1) for $P_{1}$, we have

Then,

Now, we substitute for $S_{1} = \eta/\mu\mathcal{R}_{c}$ in the coefficient of $E$ in Eq (3.4) and use the formula of $\mathcal{R}_{c}$. Moreover, we substitute the values of $E_1, \ 1/I_{a_{1}}\ {\rm{and}} \ 1/I_{s_{1}}$ in the following terms:

After simplifying Eq (3.4), we obtain

Since the arithmetic mean is greater than or equal to the geometric mean, we have

Hence, $dL_{1}/dt \leq 0$ for all $S, E, I_{a}, I_{s} > 0$ and $dL_{1}/dt = 0$ when $S(t) = S_{1}, \ E(t) = E_{1}, \ I_{a}(t) = I_{a_{1}}$ and $I_{s}(t) = I_{s_{1}}$. Applying the Krasovkii-Lasalle theorem, we consider the set

and $M_{1}$ is the largest invariant subset of $\mathscr{I}_{1}$, where all elements satisfy $S(t) = S_{1}, \ E(t) = E_{1}, \ I_{a}(t) = I_{a_{1}}$ and $I_{s}(t) = I_{s_{1}}$; it remains to be proven that $R(t) = R_{1}$. Assume that $(S(t), E(t), I_{a}(t), I_{s}(t), R(t))$ is a solution to Model (2.1) belonging to the set $M_{1}$; thus, we have

Solving Eq (3.5) by using the integrating factor method, we obtain

Note that, $\delta(I_{a_{1}}+I_{s_{1}})/\mu = R_{1}$. From Eq (3.6), as time increases, $R(t)$ approaches $R_1$, that is, $\lim_{t \to \infty}R(t)\longrightarrow R_1$. The solution $(S(t), E(t), I_{a}(t), I_{s}(t), R(t))$ will stay at the set $M_{1}$; hence, $M_{1} = \big\{P_1\big\}$. Therefore, the equilibrium $P_1$ is globally asymptotically stable if $\mathcal{R}_{c} > 1$.

4.   Numerical analysis

Here, we fit Model (2.1) to the actual data of COVID-19 cases in Saudi Arabia and estimate the parameters that make it compatible with reality. Also, we perform numerical experiments to demonstrate the agreement with the qualitative results. Furthermore, we discuss the sensitivity analysis for the control reproduction number, $\mathcal{R}_{c}$. Finally, we examine different scenarios for the control measures in the model, namely, lockdown, social distancing and the detection of asymptomatic individuals through random diagnostic testing.

4.1.   Model fitting and estimation of parameters

We estimate the parameters of Model (2.1) to validate it with the actual data of infected cases in Saudi Arabia. The data of the infected cases were taken from the COVID-19 dashboard of the Saudi Ministry of Health for the period of March 12, 2020 to September 23, 2020 ^[45].

The health care workers in the Saudi Ministry of Health have applied random diagnostic testing for asymptomatic and symptomatic individuals in dense regions. The random diagnostic tests were done between April 16, 2020 and May 3, 2020, for $42,765$ individuals. The number of confirmed cases (positive test result) was 7,776 ($18.18\%$) individuals ^[28]. We estimate that the effectiveness of the random diagnostic tests for the asymptomatic individuals, $\varepsilon$, to be approximately zero because of the insufficient information about the number of asymptomatic individuals at the time of implementing these tests. Also, the period for these tests is small compared to the time interval of the data considered from the COVID-19 dashboard.

The parameters $\eta, \ \mu, \delta, \ d, \ \rho, \ SD$ and $\gamma$ have the same values as in ^[37]. As for the values of the remaining parameters of Model (2.1), we estimate the value of $\beta_{2}$ to be greater than $\beta_{1}$ based on the model's assumption, which is similar to ^[10,13].

The parameter values are presented in Table 1. In Table 2, we display the values of lockdown, $\rho$, social distancing, $SD$ and the corresponding values of $\mathcal{R}_{c}$. These values were taken from ^[37], where Saudi Arabia implemented different levels of lockdown and social distancing, which led to dividing the study period into seven phases.

Model (2.1) was solved numerically by using the MATLAB package ode45 with the following initial values: $S(0) = 34813577, \ E(0) = 150, \ I_{a}(0) = 95, \ I_{S}(0) = 44$ and $R(0) = 1$. We assumed that each initial value for the exposed class was set to be greater than those for the infected classes, as in ^[13,23,46]. Also, each initial value of the asymptomatic class was set to be greater than those for the symptomatic class based on the results in ^[8], which demonstrated that most of the COVID-19 cases at the beginning of the spread in Saudi Arabia were asymptomatic and returning from imported. Moreover, Li et al. ^[6] estimated the undocumented infections (infections with mild, limited or loss of symptoms) to be $86\%$ of the infections in China before imposing travel restrictions on January 23, 2020.

The results of fitting Model (2.1) to the COVID-19 infected cases (symptomatic and asymptomatic) in Saudi Arabia from March 12, 2020 to September 23, 2020 are illustrated in Figure 2, which shows good agreement.

4.2.   Numerical experiments

This section demonstrates the agreement between the numerical solution of Model (2.1) and the qualitative analysis offered in Section 3. We conducted numerical simulations of the model for different initial values in the feasible set to show the tendency of the solution curves to equilibrium $P_0$ if $\mathcal{R}_{c} < 1$, or equilibrium $P_1$ if $\mathcal{R}_{c} > 1$. We start by rescaling the state variables in the model. Let

Thus, the rescaled Model (2.1) becomes (omitting the bar onward)

Note that we have used the limiting value of $N$ in the model, i.e., $N = \eta/\mu$. We numerically solve Model (4.2) with parameters chosen to satisfy the stability conditions from the qualitative analysis, and with the following different initial conditions belonging to the set $\Omega$:

IC1: $S(0) = 0.8, \ E(0) = 0.1, \ I_{a}(0) = 0.05, \ I_{s}(0) = 0.02, \ R(0) = 0.01,$

IC2: $S(0) = 0.6, \ E(0) = 0.2, \ I_{a}(0) = 0.08, \ I_{s}(0) = 0.07, \ R(0) = 0.05,$

IC3: $S(0) = 0.4, \ E(0) = 0.3, \ I_{a}(0) = 0.12, \ I_{s}(0) = 0.10, \ R(0) = 0.07$.

$\bf Experiment\; 1:$ Assume the parameters of Model (4.2) have the following values: $\mu = 0.04, \ \eta = 1250, \ \gamma = 0.167, \ \beta_{1} = 0.0554\times10^{-4}, \ \beta_{2} = 1.0596\times10^{-4}, \ \varepsilon = 0.50,$ $\theta = 0.54, \ \delta = 3.2772\times10^{-1}, \ d = 2.3724\times10^{-1}, \ \rho = 0.5$ and $SD = 0.75$. Thus, $\mathcal{R}_{c} = 0.2585 < 1$. Therefore, we expect that the solution curves of the model tend to the COVID-19 free equilibrium point $P_0 = (1, \ 0, \ 0, \ 0, \ 0)$. This is evident in Figure 3; the numerical solutions eventually reach $P_0$ for different initial conditions. Accordingly, COVID-19 diminishes.

$\bf Experiment\; 2:$ In this experiment, we increased the value of the parameter $\rho$ and decreased the values of the parameters $\varepsilon$ and $SD$. That is to say, the control measures of lockdown, social distancing and random diagnostic testing were reduced. We assume the parameters of Model (4.2) have the following values: $\mu = 0.04, \ \eta = 1250, \ \gamma = 0.167, \ \beta_{1} = 0.0554\times10^{-4}, \ \beta_{2} = 1.0596\times10^{-4}, \ \varepsilon = 0.10,$ $\theta = 0.54, \ \delta = 3.2772\times10^{-1}, \ d = 2.3724\times10^{-1}, \ \rho = 0.85$ and $SD = 0.30$. Therefore, $\mathcal{R}_{c} = 2.1639 > 1$. Hence, we expect the solution curves of the model to approach the COVID-19 endemic equilibrium point $P_1$. This is displayed in Figure 4; the numerical solutions eventually tend to $P_1 = (0.4621, \ 0.1039, \ 0.0255, \ 0.0132, \ 0.3170)$ for different initial conditions. Consequently, COVID-19 remains at a specific percentage.

We conclude from the experiments that the numerical results are in good agreement with the qualitative results.

4.3.   Sensitivity analysis for $\mathcal{R}_{c}$

To determine which parameters influence the spread of COVID-19, we investigated the sensitivity of the control reproduction number for Model (2.1). The sensitivity of $\mathcal{R}_{c}$ was examined analytically by evaluating $\partial \mathcal{R}_{c} / \partial \mathcal{P}$, where $\mathcal{P} = (\eta, \beta_1, \beta_2, \rho, SD, \gamma, \delta, \varepsilon, \theta, d, \mu)$. The changes in $\mathcal{R}_{c}$ corresponding to one parameter at a time are as follows:

where $\omega = \varepsilon+\left(\beta_{1}(\delta+\mu)/ \beta_{2}(\delta+d+\mu)\right)$. From Eq (4.3), we see that an increase in $\varepsilon, \ SD, \ \delta, \ d$ or $\mu$ leads to a decrease in $\mathcal{R}_{c}$. Conversely, an increase in $\beta_{1}, \ \beta_{2}, \ \rho, \ \gamma$ or $\eta$ leads to an increase in $\mathcal{R}_{c}$. Finally, the sensitivity of $\mathcal{R}_{c}$ with respect to $\theta$ depends on the value of $\omega$. If $\omega > 1$, then $\mathcal{R}_{c}$ decreases, and if $\omega < 1$, $\mathcal{R}_{c}$ increases. Figure 5 illustrates these results.

The normalized sensitivity index (elasticity) of $\mathcal{R}_{c}$ with respect to the model parameters $\mathcal{P}$ is defined as follows ^[47]:

By applying the formula in Eq (4.4), we get

Table 3 exhibits the elasticity of $\mathcal{R}_{c}$ with respect to the model parameters. The parameter values were taken from Table 1, in addition to $\rho = 0.80, \ SD = 0.60$ and $\varepsilon = 0.40$. Any positive value for the elasticity in Table 3 means that the contribution of the parameter to $\mathcal{R}_{c}$ is to increase its value. For instance, $\Gamma_{\mathcal{R}_{c}}^{\beta_{2}} = 0.9587$ means that an increase in $\beta_{2}$ by $1\%$ will increase $\mathcal{R}_{c}$ by $0.9587\%$. On the contrary, any negative value for the elasticity means that the contribution of the parameter to $\mathcal{R}_{c}$ is to decrease its value. For example, $\Gamma_{\mathcal{R}_{c}}^{\varepsilon} = -0.6391$ means that an increase in $\varepsilon$ by $1\%$ will decrease $\mathcal{R}_{c}$ by $0.6391\%$. We notice that the most sensitive parameters are $\beta_{2}, \ \rho, \ SD$ and $\varepsilon$. Therefore, the increase in imposing social distancing and lockdown measures and detecting asymptomatic individuals through random diagnostic testing reduces the spread of the disease.

4.4.   Different scenarios for control strategies

Model (2.1) examines some of the policies that have been applied in Saudi Arabia to control COVID-19, namely, the effectiveness of random diagnostic testing on the asymptomatic class ($\varepsilon$), lockdown ($\rho$) and social distancing ($SD$). We executed several scenarios to investigate the impact of these policies by simulating Model (2.1) for infected cases. Figure 2 shows the actual data in Saudi Arabia and the fitting curve for Model (2.1) for infected cases from March 12, 2020 to September 23, 2020. We solve Model (2.1) numerically with the following initial values: $S(0) = 34813577, \ E(0) = 150, \ I_{a}(0) = 95, \ I_{s}(0) = 44, \ R(0) = 1$ and the parameter values given in Table 1. The parameters $\varepsilon, \ \rho$ and $SD$ took different values for each scenario. We describe different scenarios in Table 4. For the fitting values of $\rho$ and $SD$, refer to Table 2.

The results of applying the scenarios ($1^{st}-7^{th}$) are summarized in Tables 5–11 and illustrated in Figures 6–12. We compared the scenarios with the peak value of the infected cases in the fitting of Model (2.1), that is, $59,830$, which occured on Day $123$.

The $1^{st}$ scenario examines the impact of detecting asymptomatic individuals by applying random diagnostic testing in Saudi Arabia. At the same time, the lockdown and social distancing are kept as the fitting values. Figure 6 illustrates that the peak of infected cases decreases with increasing $\varepsilon$. For instance, when detecting only $2\%$ of the asymptomatic individuals ($\varepsilon = 0.02$) by random diagnostic testing, the cases will reach 45,140 on Day 122. Compared with actual data, the number of cases decreased by $24.55\%$ (see Table 5). This indicates the importance of applying the random diagnostic testing to find asymptomatic individuals and reduce the cases.

The $2^{nd}$ scenario was applied to determine whether it is possible to rely only on detecting asymptomatic individuals through random diagnostic testing without imposing social distancing and a lockdown. Figure 7 shows that the infected cases will far surpass the actual data. For example, if the detection of asymptomatic cases reaches $60\%$ ($\varepsilon = 0.60$), the peak of cases will be $2,332,000$ on Day $97$ (see Table 6). That is an increase of $3797.71\%$ relative to the peak value of the actual data. We concluded that detecting asymptomatic individuals is insufficient without imposing social distancing and lockdown.

The $3^{rd}$ scenario analyzes four different values for the level of lockdown ($\rho = 1, \ 0.85, \ 0.75, \ 0.55$) the values for social distancing were kept as the fitting values. When $\rho = 1$, there is no lockdown implementation. The remaining values of $\rho$ correspond to the lockdown level undertaken by Saudi Arabia in Phase 1, Phase 2 and Phase 4, respectively ^[37].

Figure 8 shows that increasing the lockdown level leads to a decrease in the infected cases. Note that increasing the lockdown level means decreasing the value of $\rho$. Moreover, increasing the lockdown level requires a smaller value for detecting asymptomatic individuals through random diagnostic testing to reach case numbers lower than the actual data. To explain further, when the lockdown level is equal to $1, \ 0.85, \ 0.75\ {\rm{or}}\ 0.55$, we need to apply a $40, \ 30, \ 20 \ {\rm{or}}\ 10\%$ level of random diagnostic testing, respectively, to detect the asymptomatic individuals (see Table 7).

The $4^{th}$ scenario investigates the impact of social distancing while keeping the value of $\rho$ equal to the fitting values. Figure 9 illustrates that increasing the application of social distancing delays peak days; however, only when $SD = 0.70$ and $\varepsilon = 0.40$ does the cases reach a value that is lower than the actual data by $51.81\%$, i.e., $28,830$ (see Table 8).

The $5^{th}$ and $6^{th}$ scenarios examine the impact of imposing a lockdown at low levels and relying on social distancing and random diagnostic testing. We let $\rho = 0.85\ {\rm{and}}\ 0.75$ for the $5^{th}$ and $6^{th}$ scenarios, respectively. Figures 10 and 11 show that it is possible to reach a lower number of infected cases than in the actual data if $SD = 0.70$, where $\varepsilon = 0.40$ for the case where $\rho = 0.85$ (see Table 9), and $\varepsilon = 0.30$ for the case where $\rho = 0.75$ (see Table 10). This indicates that enforcing low lockdown levels is effective with a high level of social distancing implementation and $30\%$ or more of the detection of asymptomatic individuals through random diagnostic testing.

The $7^{th}$ scenario was designed to determine the effect of different values of $\varepsilon$ through the phases. We assume that the value of $\varepsilon$ is $\varepsilon_{1}$ in Phase 1 to Phase 2, $\varepsilon_{2}$ in Phase 3 to Phase 5 and $\varepsilon_{3}$ in Phase 6 to Phase 7 (see Table 11). Figure 12(a) and (b) show that performing random diagnostic tests in the middle phases (Phase 3–5) and the beginning phases (Phase 1 and 2), rather than the last phases (Phase 6 and 7), gives better results. Furthermore, applying the tests in all phases reduces the number of cases, as seen in Figure 12(c).

We conclude from the analysis of the $1^{st}$ to the $6^{th}$ scenarios that applying random diagnostic testing alone is inadequate without imposing social distancing and lockdown. The importance of using random diagnostic testing to find asymptomatic individuals is apparent when lockdown and social distancing measures are enforced; only then does the number of cases decline. An increase in the level of lockdown decreases the required percentage of random diagnostic tests to lower the number of cases. However, an increase in social distancing does not have the same effect as a lockdown; a high percentage of random diagnostic tests is needed to reduce the number of cases. On the other hand, implementation of lower levels of lockdown is possible only when a high level of social distancing and a high percentage of random diagnostic tests are imposed.

As for the $7^{th}$ scenario, we deduce that performing the random diagnostic tests in all phases is effective in lowering the number of cases. However, applying the random diagnostic tests in the early and middle phases is sufficient to reduce the cost of conducting these tests.

5.   Conclusions

This study was purposed to develop a mathematical model to examine the impact of random diagnostic testing on COVID-19 patients in the presence of a lockdown and social distancing in Saudi Arabia. Qualitative and numerical analyses were applied to the model. The model was well posed and had two equilibrium points. The COVID-19 free equilibrium existed and was locally and globally asymptotically stable if $\mathcal{R}_{c} < 1$. Conversely, the COVID-19 endemic equilibrium existed and was locally and globally asymptotically stable if $\mathcal{R}_{c} > 1$.

The model was validated by using the data from the COVID-19 dashboard of the Saudi Ministry of Health spanning March 12, 2020 to September 23, 2020. In addition, the numerical experiments performed using the model showed the consistency of the numerical solutions with the qualitative analysis.

Furthermore, the sensitivity analysis for $\mathcal{R}_{c}$ revealed that the most influential parameter in terms of increasing $\mathcal{R}_{c}$ was the transmission rate due to contact with asymptomatic individuals ($\beta_{2}$). However, the control parameters, i.e., the lockdown ($\rho$), social distancing ($SD$) and the effectiveness of random diagnostic testing for asymptomatic individuals ($\varepsilon$), played a significant role in decreasing $\mathcal{R}_{c}$. Finally, we analyzed different scenarios numerically for the control strategies applied in Saudi Arabia.

We concluded that applying random diagnostic testing to detect asymptomatic individuals in the presence of a lockdown and social distancing significantly reduced the cases. On the other hand, it was impossible to rely on random diagnostic testing without imposing a lockdown and social distancing. Moreover, implementing a lockdown at low levels required increased social distancing levels and a high percentage of random diagnostic testing.

Conflict of interest

The authors declare that there is no conflict of interest.