Integrating release and dispatch policies in production models

1.   Introduction

As of August 2021, COVID-19 is still spreading in Japan and throughout the world. To overcome this infectious disease, various measures have been implemented (e.g., hand sanitization, mask-wearing, telework ^[1], quarantine at airports ^[2], and contact-tracing applications ^[3]). However, new variants, such as B.1.1.7 (alpha) ^[4] and B.1.617 (delta) ^[5] have appeared with even higher infectivity.

In complex situations that combine various conditions, it is important to perform simulations to determine the future infection spread. Before COVID-19 appeared, simulation studies of various viral infectious diseases were reported ^[6,7]. Moreover, COVID-19 simulations have been reported in various countries ^[8,9,10,11]. Simulations have been conducted to verify the efficacy of remote working ^[12], airport quarantines ^[13], stay-at-home orders ^[14], and contact-tracing applications ^[15]. Using the simulation approach, other studies ^[16,17] have analyzed the fatality curve of COVID-19 infected individuals. As we found in these studies, various complex situations can be surveyed using mathematical models.

To decrease the number of infected individuals, COVID-19 vaccinations (i.e., BNT162b (Pfizer) ^[18], mRNA-1273 (Moderna) ^[19], and ChAdOx1 (AstraZeneca) ^[20]) have been promulgated. In Japan, vaccination began in February 2021 ^[21], and second vaccinations had been given to $ 3 \times 10^7 $ individuals as of August 2021 ^[22]. To determine the effect of vaccination, it is necessary to perform simulations using mathematical models. For example, there are some case studies that considered the effect of the vaccine in Malaysia ^[23], United States ^[24,25], Spain ^[26], and Saudi Arabia ^[27]. However, a case study focused only on Japan is lacking. Therefore, we fill this gap by performing a simulation to account for the effects of vaccination in Japan.

2.   Mathematical model

The susceptible–infected–recovered–vaccination (SIRV) model ^{[28,29,30,31]} and the susceptible–infected–recovered–vaccination–death (SIRVD) model ^[32] have been proposed to estimate the state of vaccinations worldwide. However, those models can only account for the first dose. The effects of the first and second vaccinations differ in the case of COVID-19 ^[33]. Because the previous models ^{[28,29,30,31,32]} cannot represent first and second vaccinations, we consider it difficult to appropriately verify the effects of multiple vaccinations. Therefore, we used the susceptible–infected–recovered–vaccination1–vaccination2–death (SIRVVD) model, which represents the first and second vaccinations for the simulation. In this section, we describe the SIRVVD model.

2.1.   Equations

The set $ T $ of the simulation periods is

where $ t_\mathrm{end} $ indicates the final day of the simulation. From the basic SIR model, time $ t $ is a real number. However, in the case of COVID-19, the Japanese government reports newly infected individuals every other day (one time per day). Therefore, we consider it desirable that time $ t $ takes the form of set $ T $.

Herein, we define the number of infected individuals on day $ t \in T $ as

where, $ I_0(t) $ is the number of infected individuals who do not receive the vaccination. $ I_{\{1, 2\}}(t) $ is the number of infected individuals who received the first and second vaccinations, respectively (despite being vaccinated and infected).

Then, we define the number of susceptible persons $ S(t+1) $, the number of infectors $ I_{\{0, 1, 2\}}(t+1) $, the number of vaccinated persons $ V_1(t+1) $ (first dose) and $ V_2(t+1) $ (second dose), the number of recovered persons $ R(t+1) $, and the number of dead persons $ D(t+1) $, as

Variable $ \beta(t) $ is the infectivity on a day $ t $. $ \theta_0 $ is the reduction rate of antibodies from a natural infection. $ \theta_{\{1, 2\}} $ are the reduction rates of antibodies from the first and second vaccinations, respectively. $ \alpha_1 $ is the rate of the first dose of vaccination for susceptible persons, $ S(t) $. $ \alpha_2 $ is the rate of the second vaccination of persons who received the first dose of vaccine $ V_1(t) $. $ \sigma_{\{1, 2\}} $ are the effectiveness of the first and second vaccinations for reducing the infection probability, respectively. $ \gamma $ is the removal rate of the infected individuals. $ \delta_0 $ is the fatality rate of the infected individuals who did not receive vaccination. $ \delta_{\{1, 2\}} $ are the fatality rates of infected individuals who received the first and second vaccinations, respectively. Because we assume that the validity periods of vaccinations and antibodies from natural infection follow an exponential distribution, $ \theta_{\{0, 1, 2\}} $ are the inverse values of their average periods. Likewise, because we assume that the infection period follows an exponential distribution, $ \gamma $ is the inverse of the average infection period. In the case of the SIR model, some studies have adopted the inverse value of the average infection period as $ \gamma $ ^[34,35]. Moreover, the total population $ N $ is

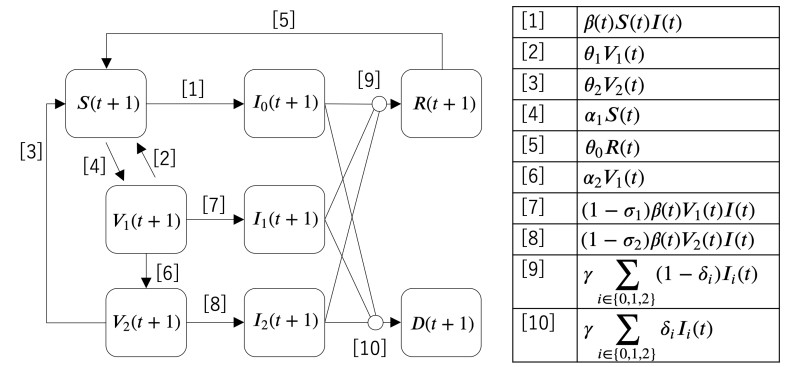
We show the states transition model in Figure 1. Paths 1, 7, and 8 mean infection. Paths 4 and 6 mean vaccination. Paths 2 and 3 mean the effects of vaccine disappear by elapsed time. Paths 9 and 10 mean recovering and deaths, respectively. The models shown in Figure 1 and Equations (2.3)–(2.10) correspond to each other. Therefore, we can represent the transition of infection states considering the first and second vaccinations using this model.

Figure 1.  SIRVVD model considering first and second doses of vaccination.

DownLoad: Full-Size Img PowerPoint

It is desirable to consider that there is a limit to the number of vaccines available. Therefore, we calculate the amount of vaccinations by

where $ N_{\{1, 2\}}(t+1) $ are the numbers of first and second vaccinations on day $ t+1 $, respectively.

Moreover, in the case of COVID-19, the number of newly infected individuals is reported every other day. In this model, the number of new infectors $ I^+(t) $ on day $ t $ is

$ I^+(t) $ is the summation of paths 1, 7, and 8.

In this subsection, we explain the proposed SIRVVD model. We carried out a mathematical analysis of the impact of the vaccination on $ I_j(t) $ as a supplement. This detail is shown in the Appendix section.

2.2.   Calculation examples

Herein, we present simple calculation examples to understand the features of the mathematical model by using parameters that are easy to understand. First, we explain the adopted parameters (note that the simulations below are fictitious locations and viruses). The total population $ N $ is $ 10^4 $ persons. The initial infectors $ I_0(0) $ are $ 10^1 $ persons. Initial susceptible persons comprise $ S(0) = N - I_0(0) = 9,990 $ individuals. The initial numbers of other statuses are $ V_{\{1, 2\}}(0) = I_{\{1, 2\}}(0) = R(0) = D(0) = 0 $. The end of the day of simulation $ t_\mathrm{end} $ is 100. The infectivity is $ \beta(t) = 10^{-4.5}, \forall t \in T $. The reduction rates of antibodies by vaccination or natural infection $ \theta_{\{0, 1, 2\}} $ are $ 10^{-2} $. The effectiveness of the first and second vaccinations is $ \sigma_1 = 0.5 $ and $ \sigma_2 = 0.9 $, respectively. The removal rate from infection is $ \gamma = 0.15 $. The fatality rates are $ \delta_0 = 0.10 $, $ \delta_1 = \delta_0 \times (1-0.40) $, and $ \delta_2 = \delta_0 \times (1-0.80) $. This means that the reduction values of the fatality rate by the first and second vaccinations are 40% and 80%, respectively.

The above parameters are fixed values. In contrast, we set some values to $ \alpha_{\{1, 2\}} $ to check the effectiveness of the vaccination. These are

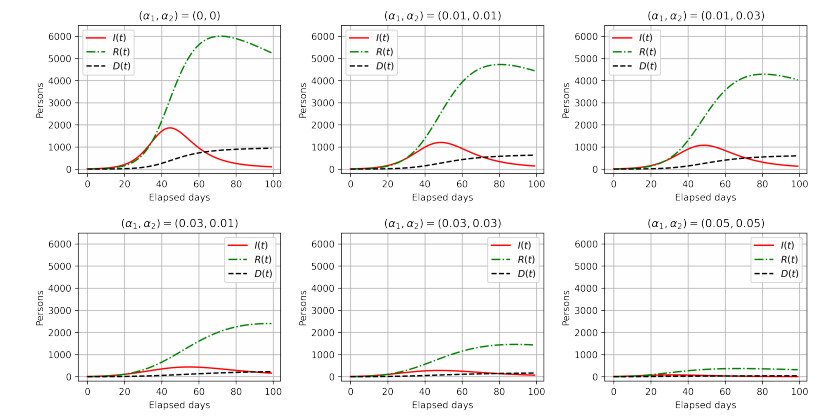
The simulation results for $ I(t), R(t) $, and $ D(t) $ are shown in Figure 2. The more $ \alpha_{\{1, 2\}} $ increases, the more $ I(t), R(t), $ and $ D(t) $ decreases, owing to the effectiveness of the vaccination. It was found that the spread of infection slowed with respect to the progress of vaccinations. This change can be understood by reading the discussion given in the Appendix. If we compare $ (\alpha_1, \alpha_2) = (0.01, 0.03) $ and $ (0.03, 0.01) $, the number of infected individuals of $ (0.03, 0.01) $ is less than that of $ (0.01, 0.03) $. $ \alpha_2 $ is the parameter for transition from $ V_1(t) $ to $ V_2(t) $. Therefore, if $ V_1(t) $ is small, even if $ \alpha_2 $ is high, $ V_2(t) $ is small. To increase $ V_1(t) $, it is necessary to set the high value as $ \alpha_1 $. Therefore, if $ \alpha_1 $ is small, and $ \alpha_2 $ is high, such as $ (\alpha_1, \alpha_2) = (0.01, 0.03) $, the effect of vaccination on reducing infected individuals is small.

Figure 2.  Calculation examples: $ I(t), R(t), $ and $ D(t) $.

DownLoad: Full-Size Img PowerPoint

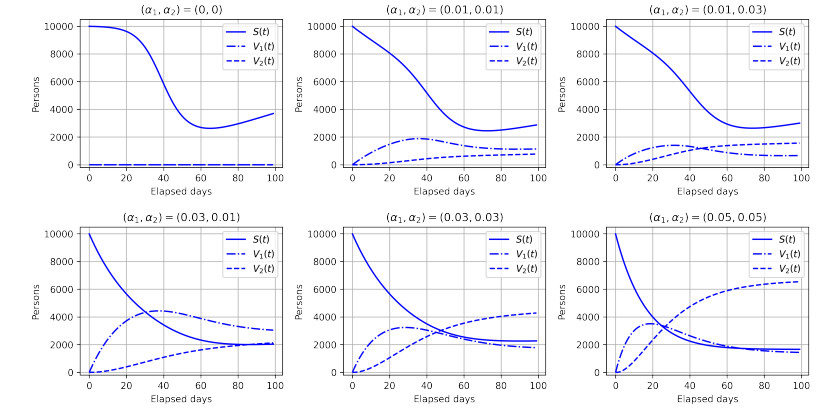
The simulation results for $ S(t) $, $ V_1(t) $, and $ V_2(t) $ are shown in Figure 3. In all cases, $ S(t) $ decreases with the elapsed time. In cases where $ \alpha_1 $ is small, such as $ (\alpha_1, \alpha_2) = (0.01, 0.01), $ and $ (0.01, 0.03) $, $ V_1(t) $ is also small because $ V_1(t) $ and $ V_2(t) $ are also small. The higher the $ \alpha_1 $, the higher the $ V_1(t) $. In the case of $ (\alpha_1, \alpha_2) = (0.05, 0.05) $, because the number of transitions from $ S(t) $ to $ V_1(t) $ and from $ V_1(t) $ to $ V_2(t) $ is high, $ V_2(t) $ is also high. Figures 2, 3 indicate that vaccination effectively reduces the number of infected individuals and deaths.

Figure 3.  Calculation examples: $ S(t), V_1(t), $ and $ V_2(t) $.

DownLoad: Full-Size Img PowerPoint

2.3.   Comparison between SIRVD and SIRVVD models

Herein, we compare SIRVD to the proposed SIRVVD model. If we substitute zero for $ \alpha_2 $, $ I_2(0) $, and $ V_2(0) $, which are the parameters related to the vaccine, $ V_2(t) $ and $ I_2(t) $ are

When we substitute these values for the proposed SIRVVD model defined by Equations (2.3) – (2.10), the model can be expressed as

The forms of Equations (2.17)–(2.22) are similar to the SIRV model to represent the first dose of vaccination, which was proposed by Ishikawa ^[30] (see Equations (1)–(4). Note that Ishikawa's model cannot represent the state of death caused by infection. To compare the SIRVD and SIRVVD models, we set $ \alpha_1 = 0.01, 0.03 $ to the SIRVD model expressed by Equations (2.17) – (2.22) and performed simulations. The values of the other parameters are the same as those described in Subsection 2.2.

The maximum number of infected individuals $ \mathrm{Max}_t I(t) $, and dead persons at the end of simulation $ D(t_\mathrm{end}) $ by the SIRVD model are shown in Table 1. To compare the SIRVD and SIRVVD models, we also show the results of the SIRVVD model (see Subsection 2.2 and Figure 2 for details). In all cases ($ \alpha_1 = 0.01, 0.03 $), $ \mathrm{Max}_t I(t) $ and $ D(t_\mathrm{end}) $ by the SIRVD model were higher than those of the SIRVVD model. This is because the SIRVD model cannot represent the effect of the second dose of vaccination. Because the effects of the first and second vaccinations are different ^[33] in the case of COVID-19, we consider that the proposed SIRVVD model expressed by Equations (2.3)–(2.10) is important.

Table 1.  Comparison between the SIRVD model expressed by Equations (2.17)–(2.22) and the proposed SIRVVD model expressed by Equations (2.3)–(2.10) on the maximum infected individuals $ \mathrm{Max}_t I(t) $, and the dead persons of the end of the simulation $ D(t_\mathrm{end}) $.

Model	$ \alpha_1 $	$ \alpha_2 $	$ \mathrm{Max}_t I(t) $	$ D(t_\mathrm{end}) $
SIRVD model	0.01	-	1,299	653
SIRVVD model	0.01	0.01	1,204	630
SIRVVD model	0.01	0.03	1,077	598
SIRVD model	0.03	-	623	288
SIRVVD model	0.03	0.01	438	229
SIRVVD model	0.03	0.03	281	164

---

 | Show Table

DownLoad: CSV

3.   Simulations assumed in actual Japan

3.1.   Objective and condition

We performed simulations assumed in Japan using the model shown in Figure 1. The simulation period was from February 12, 2020 ($ t = 0 $), to January 31, 2021 ($ t = t_\mathrm{end} = 354 $ days). During this period, there were no vaccinations in Japan. Therefore, the objective of our simulations is to compare the presence and absence of vaccines in Japan. To do this, we used the open data of newly infected individuals reported by the Japanese government ^[36].

Kobayashi et al. ^[37] reported that the removal rate $ \gamma $ of COVID-19 in Japan ranges from 0.13 to 0.17. Therefore, we adopt $ \gamma = 0.15 $. As mentioned in Section 2.1, we assume that the infection period follows an exponential distribution. In other words, $ \gamma^{-1} $ is the average infection period, which is $ \gamma^{-1} = (0.15)^{-1} = 6.67 $ days. We define $ f(t; \gamma) $ as the exponential distribution of the infection period. In this case, we can estimate the probability of recovering or death $ F(x; \gamma) $ from 0 to $ x $ days by integrating $ f(t; \gamma) $ as follows:

Note that we can only calculate the cases of $ \gamma > 0 $. For example, $ F(14; 6.67) = 0.878 $ and $ F(20; 6.67) = 0.950 $, which indicates that approximately 88% and 95% of all infected individuals recovered or died within 14 and 20 days, respectively.

Because the total population in Japan is $ 1.2 \times 10^8 $, we adopted $ N = 1.2 \times 10^8 $. The number of initial infected individuals $ I_0(t = 0) $ is the sum of infected individuals from 1 week before the start of the simulation. As a result, $ I_0(t = 0) = 2 $ individuals. Because the simulation starting time is February 12th, 2020, this range is from February 5th, 2020, to February 11th, 2020. The infection was not widespread at the start of the simulation, and there were no vaccinations. Therefore, we set $ R(t = 0), D(t = 0), V_1(t = 0), V_2(t = 0), I_1(t = 0), $ and $ I_2(t = 0) $ as $ 0 $. Moreover, $ S(t = 0) = N - I_0(t = 0) $.

If we assume that the effective period of the antibody by vaccination and natural infection follows an exponential distribution, $ \theta_{\{0, 1, 2\}}^{-1} $ is the average effective period of the antibody. A previous study on the effective period of an antibody by Dan et al. ^[38] reported that the antibody of COVID-19-infected individuals varies between 6 and 8 months. Therefore, we assume the average effective period to be 7 months ($ 7 \times 30 = 210 $ days) and adopt $ \theta_{\{0, 1, 2\}} = 1/210 $.

Dagan et al. ^[33] reported that by undergoing the first and second doses of the vaccine (BNT162b2), the infection probability decreases by 60% and 92%, respectively (Israeli data source). In the case of Japan, these values were almost the same ^[40] (note that for the B.1.617 delta variant, the effect might decrease ^[39]). Therefore, we adopted $ \sigma_1 = 0.60 $ and $ \sigma_2 = 0.92 $. Moreover, in Japan, as of February 10th, 2021, the total number of infected and dead persons was 408,000 and 6,507 people, respectively, ^[41]. Therefore, we adopted $ \delta_0 = 6,507/408,000 = 0.016 $ as the fatality rate. Dagan et al. ^[33] reported that the fatality rate decreased by 84% with the first dose of vaccination (second doses not reported). Therefore, we adopted $ \delta_1 = \delta_2 = \delta_0 \times (1-0.84) $ as the fatality rate after vaccination.

The research objective is to simulate the actual Japanese conditions. Hence, it is necessary to obtain an infectivity parameter that can reproduce the Japanese spreading rate. Therefore, we searched for infectivity $ \beta(t) $ such that the differences between the SIRVVD model based on the number of newly infected individuals $ I^+(t) $ defined by Equation (2.14) and the number of newly infected individuals in the case of actual Japan ^[36] were minimal. The best infectivity $ \beta^\mathrm{opt}(t) $ is defined by

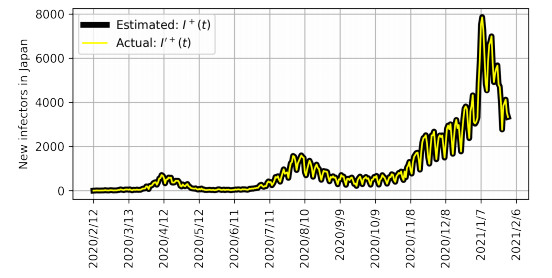
In Figure 4, we show the actual newly infected individuals in Japan $ I'^{+}(t) $ ^[36], and the newly infected individuals $ I^+(t) $ reproduced by the SIRVVD model (Equation (2.14)) by using $ \beta^\mathrm{opt}(t) $. Because these are almost the same, we consider $ \beta^\mathrm{opt}(t) $ to represent infectivity in Japan.

Figure 4.  Reported newly infected individuals in actual Japan $ I'^+(t) $ and the number of estimated newly infected individuals, $ I^+(t) $, by the SIRVVD model using $ \beta^\mathrm{opt}(t) $.

DownLoad: Full-Size Img PowerPoint

Because the research objective is to verify the effects of vaccination, we set some values as $ (\alpha_1, \alpha_2) $, which are the coefficients for vaccination. These are

Scenario $ (\alpha_1, \alpha_2) = (0, 0) $ represents the absence of a vaccine in Japan. Therefore, the amount reduced from the infected individuals in scenario $ (\alpha_1, \alpha_2) = (0, 0) $ indicates the effectiveness of the vaccination.

3.2.   result and discussion

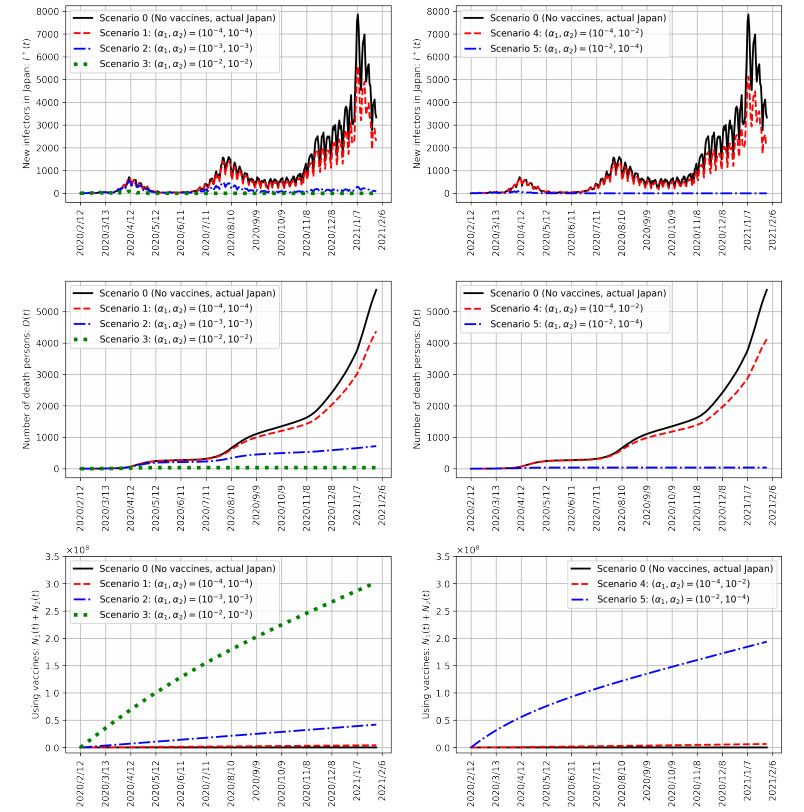
Figure 5 shows the simulation results based on the conditions described in Section 3.1. This indicates that the higher the $ (\alpha_1, \alpha_2) $, the fewer the newly infected individuals $ I^+(t) $ and dead persons $ D(t) $. It is clear that the speed of the infection spread is suppressed by the vaccination. As the vaccination progresses, the slower the infection spreads, which can be roughly understood by the discussion given in the Appendix. In contrast, in the case of scenario $ (\alpha_1, \alpha_2) = (10^{-4}, 10^{-2}) $, the number of newly infected individuals and dead persons is large. This is because $ V_1(t) $ is small; even if $ \alpha_2 $ is high, $ V_2(t) $ becomes small. Therefore, it is important to increase $ V_1(t) $ by substituting a high value for $ \alpha_1 $. We show the number of vaccinations $ N_1(t) + N_2(t) $ in the underside of Figure 5. It is desirable to substitute high values for $ (\alpha_1, \alpha_2) $; however, the preparation of many vaccines is required. For example, in the case of $ (\alpha_1, \alpha_2) = (10^{-2}, 10^{-2}) $, approximately $ 3 \times 10^8 $ vaccines are required for approximately a year. In Japan, the total vaccination rate was $ 8 \times 10^7 $ for approximately 3 months from May to August 2021 ^[22]. If Japan can keep this pace, it may achieve approximately $ 3 \times 10^8 $ vaccinations for about a year.

Figure 5.  Relationship between $ (\alpha_1, \alpha_2) $ and some variables ($ I^+(t), D(t), N_1(t)+N_2(t) $).

DownLoad: Full-Size Img PowerPoint

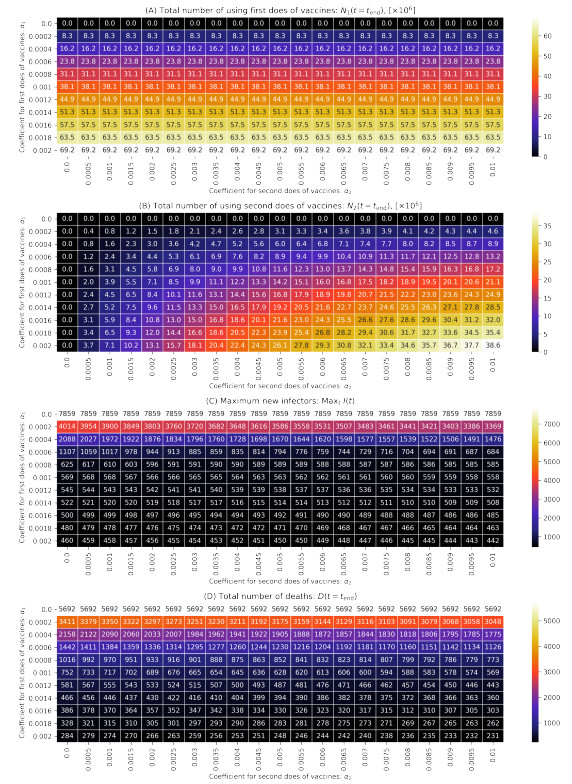
To discuss the effect of the vaccination in detail, the results of substituting various values for $ (\alpha_1, \alpha_2) $ are shown in Figure 6. The other parameters are the same as in the case of Figure 5, meaning that these simulations are assumed to be actual Japan. Figures 6 (A) and (B) show the numbers of first and second doses of the vaccination $ N_1(t_\mathrm{end}) $ and $ N_2(t_\mathrm{end}) $ at the end of the simulation $ t_\mathrm{end} $, respectively. Figure 6 (A) shows that as $ \alpha_1 $ increases, so does $ N_1(t_\mathrm{end}) $. Moreover, even if we substituted a high value for $ \alpha_2 $, in the case of substituting a small value for $ \alpha_1 $, $ N_2(t_\mathrm{end}) $ is small. We can also understand this phenomenon by examining Figure 5. Figures 6 (C) and (D) show the maximum numbers of newly infected individuals $ \mathrm{Max}_t I(t) $ and the number of dead persons $ D(t_\mathrm{end}) $ at the end of the simulation, respectively. Because $ N_1(t_\mathrm{end}) $ increases with an increasing $ \alpha_1 $, $ \mathrm{Max}_t I(t) $ and $ D(t_\mathrm{end}) $ decreases, owing to the effect of the vaccination. We can see that $ \alpha_2 $ also has an effect on reducing $ \mathrm{Max}_t I(t) $ and $ D(t_\mathrm{end}) $. Moreover, the amount of change in $ \mathrm{Max}_t I(t) $ and $ D(t_\mathrm{end}) $ in the case of a small $ \alpha_1 $ is larger than that in the case of a high $ \alpha_1 $. For example, if we compare $ (\alpha_1, \alpha_2) = (0.0002, 0) $ and $ (0.0006, 0) $, the difference between the maximum number of newly infected individuals is approximately 3,000. By contrast, if we compare $ (\alpha_1, \alpha_2) = (0.0012, 0) $ and $ (0.0016, 0) $, the difference between the maximum number of newly infected individuals is only approximately 50. These results indicate that the relationship between the number of vaccinations and the effect of reducing infected individuals is logarithmic. Therefore, even if the Japanese government prepares only a few vaccines, we infer that there would be a certain effect on reducing infected persons.

Figure 6.  Comprehensive simulation results focused on Japan.

DownLoad: Full-Size Img PowerPoint

4.   Conclusion

In this paper, we presented simulations of COVID-19 infections spreading in Japan considering first and second vaccination events. The mathematical models are found in Equations (2.3)–(2.10), which represent the effect of the first and second doses on reducing the mortality rate and infectivity. For simulation in Japan, we adopted the vaccine, "BNT162b2" ^[33]. The efficacy of the first and second doses were 60% and 92%, respectively ^[33]. Note that in the case of the B.1.617 delta variant, the effect of vaccinations may decrease ^[39]). As shown in Figures 5 and 6, vaccination reduces the number of newly infected individuals and dead persons in Japan.

As of August 8, 2021, the rate of second vaccinations in Japan was approximately 30%. Because this rate is insufficient, COVID-19 infection will continue to spread. However, in the near future, assuming that the rate of vaccination will increase in Japan, the number of infected individuals is expected to decrease. Because there is a possibility of developing new virus variants of COVID-19, we cannot be optimistic. Overcoming COVID-19 infection requires continued performance of various measures to decrease the number of infected individuals, such as vaccination, mask-wearing, teleworking, and contact tracing ^[15].

Acknowledgments

This work was supported in part by the Telecommunications Advancement Foundation (Grant No. 20203002 to Y. Omae) and a JSPS Grant-in-Aid for Scientific Research (C) (Grant No. 21K04535 to J. Toyotani).

Appendix

Theoretical remarks on SIRVVD model

Here, we discuss the effect of two-step vaccinations on the number of infected individuals. To obtain analytical insights, we simplify the situation: the infectivity $ \beta(t) $, the number of susceptible persons $ S(t) $, and vaccinated persons $ V_1(t), V_2(t) $ are constants with respect to time $ t $, respectively. This is valid when the time scale of the infection spread or reduction is much faster than those of $ \beta(t), S(t), V_1(t), $ and $ V_2(t) $. In this situation, Equations (2.6) – (2.8) in the form of a differential equation can be written as

These equations can be formally solved when one treats the second terms on the right-hand side of each equation as non-homogeneous (source terms). The solutions are given as

where the characteristic time scales, $ \tau_0, \tau_1 $, and $ \tau_2 $, are given as

The first term in each solution has a typical time scale determined by its own contribution, which stems from the first terms in Equations (4.1)–(4.3). The relationships among these time scales are generally

Thus, the typical time scale for the infection spread is directly affected by the vaccination: the time scale without the vaccination is much faster than those with the vaccination. These time scales are estimated as $ \tau_0 = 15.81 $ days, $ \tau_1 = 39.53 $ days, and $ \tau_2 = 197.64 $ days, where the following values are used: $ S = V_1 = V_2 = 2,000 $, $ \beta = 10^{-4.5} $, $ \gamma = 0 $, $ \sigma_1 = 0.60 $, and $ \sigma_2 = 0.92 $, the vaccine BNT162b2 ^[33]. These values indicate that the impact of the second vaccination was significant. In addition to the direct contribution (the first terms in Equations (4.4)–(4.6)) for each $ I_j(t) $ $ (j = 0, 1, 2) $, there are interference terms from the infected individuals with the other vaccination counts, which correspond to the second terms on the right-hand side of Equations (4.4)–(4.6). Owing to the interference terms, multiple time scales exist in each $ I_j(t) $; for example, not only does the typical time scale $ \tau_1 $ appear in the time evolution of $ I_1(t) $, but so does $ \tau_0 $ and $ \tau_2 $. Therefore, when $ I_0(t)\gg I_1(t), I_2(t) $, which corresponds to the situation immediately after starting vaccinations, $ I_0(t) $ and $ I_2(t) $ grow with the time scale of $ \tau_0 $. Additionally, when $ I_2(t)\gg I_0(t), I_1(t) $, which corresponds to the case when the vaccination is completed, the number of infected individuals varies with the time scale of $ \tau_2 $. Thus, vaccination drastically affects the time scale for the spread of infection.