Performance enhanced Kalman filter design for non-Gaussian stochastic systems with data-based minimum entropy optimisation

1.   Introduction

In order to control and optimise the system performance, the system state observiation is a significant concept since the system state can reflect the internal properties of the dynamic system. However, for most of the practical systems, the system state cannot be measured directly, meanwhile, the random noise would affect the state and the measurement. To estimate the system state using system output measurement, Kalman filter has been presented in 1960 ^[3].

Kalman filter is well-developed for linear stochastic systems which are subjected to Gaussian noises. To deal with the non-linearities of the stochastic systems, extended Kalman filter (EKF) ^[6] has been presented by adding the linearisation operation into the Kalman filter design. In this case, the non-linear system model has been converted to linear model locally for each instant. Due to the fact that the Kalman filter and EKF have simple parametric structure, they are widely used in practice. Notice that both Kalman filter and EKF have adopted Gaussian assumption. In other words, the performances of Kalman filter and EKF would be deteriorated if the systems are subjected to non-Gaussian noises.

Motivated by non-Gaussian distribution shaping control, the non-Gaussian systems widely exist in industrial process, for example, paper-making process, networked systems ^[7], neural interaction systems ^[16,17], etc, it is important to investigate the filtering problem subjected to non-Gaussian noises. Note that the states or outputs will be non-Gaussian even if the noise is Gaussian due to the influences of the non-linear dynamics ^[8]. The performance enhancement problem for non-Gaussian control system design has been analysed in ^[19,20], where the entropy criterion has been adopted to enhance the performance of the exiting fixed control loop. Similarly, this approach can be extended to filtering problem in order to overcome the fore-mentioned shortcomings.

In particular, the filter design cannot be adjusted anymore once the system integration is completed, which means the filter cannot adapt to the model time-variant dynamics, unexpected damage, non-Gaussian noise, etc. Therefore, the performance enhancement strategy should be considered based on the existing system structure and a new compensative framework for the estimated states should be established. We assume that the existing EKF design has been completed for the system and a compensative non-linear term is added to the estimated state directly. Following this approach, the residuals and un-modelled dynamics can be compensated by the non-linear term. In particular, our objective is to design an optimal non-linear term to enhance the performance.

In this paper, the non-linear term has been re-expressed by polynomial while the coefficients of the polynomial can be optimised in real time to minimise the performance criterion, where entropy has been used as performance criterion to describe the randomness of the estimation error ^[4]. Comparing with the existing minimum entropy filter, the convergence analysis of the presented algorithm would be obtained based upon the existing EKF structure, while the non-Gaussian effects will be attenuated by entropy optimisation. Moreover, the entropy can be estimated by kernel density estimation (KDE) with data. As a result, the analytical evolution is not essential. Different from the Kalman framework, not only the variance has been considered in the design but also the whole distribution of the estimation error has been taken into account which implies that our design includes more information and makes the performance enhancement feasible. Since the presented filtering algorithm can improve the estimation accuracy, it would affect a lot of related research topics such as fault diagnosis ^[5], probabilistic decoupling ^[15,18] and even non-linear filtering problem ^[13].

The rest of this paper is organised as follows: in Section 2, the preliminaries are briefly introduced including the problem formulation, EKF and KDE. Section 3 shows the main algorithm where the compensation loop has been designed and the optimisation has been achieved. In Section 4, the convergence of the presented algorithm has been analysed. To validate the effectiveness of the presented filtering framework, the simulation results have been illustrated in Section 5. As the last part of the paper, further discussion and conclusions have been given by Section 6 and Section 7, respectively.

2.   Preliminaries

Consider the stochastic non-linear system model:

where $x\in\mathbb R^n$ and $y\in\mathbb R$ denote the system state vector and system output, respectively. $w\in\mathbb R^n$ and $v\in\mathbb R$ stand for the random noises with arbitrary stochastic distributions where $E\left\{w_k\right\} = 0$ and $E\left\{v_k\right\} = 0$. $k$ is the sampling index. $f: \mathbb R^n \to \mathbb R^n$ and $h: \mathbb R^n\to \mathbb R$ are known differentiable non-linear functions where $f\left(0\right) = 0$ and $h\left(0\right) = 0$. Note that $E\left\{ \cdot \right\}$ denotes the operation for calculating the mean value.

Remark 1. For the filtering problem, single-output means the limited measurable information which demonstrates the benefit of the system state estimation. Actually, the multi-output model can be covered using the presented algorithm with the generalised joint-entropy minimum optimisation. Without loss of the generality, the single-output model is adopted in this manuscript for simplifying the formulation.

2.1.   Extended Kalman filter

Based upon the structure of the system model, the EKF design can be started with linearisation as follows:

After system linearisation, the investigated system model (2.1) can be re-presented as follows:

where $\bar f\left({{x_k}} \right)$ and $\bar h\left({{x_k}} \right)$ stand for the un-modelled dynamics of the investigated system model (2.1).

The EKF filter structure can be given by Eq. (2.4)

where $\hat x_k$ denotes the estimated system state $x_k$ for sampling index $k$, ${{\tilde y}_k} = {y_k} - h\left({{{\hat x}_k}} \right)$ stand for the estimation error of the system output $y_k$ and the filter gain $K_k\in\mathbb R^{n\times 1}$ can be calculated recursively as follows:

while the $P$ matrix is governed by the following Riccati equation.

Note that $R_k$ and $Q_k$ stand for the covariance matrix for $w_k$ and $v_k$ which implies these matrices are time-varying symmetric positive definite matrices and

The filtering design objective can be formulated as

where ${{\tilde x}_k} = {x_k} - {{\hat x}_k}$ denote the estimation error of the system state $x_k$ and $\hat x_0$ is the initial value of the filter.

For theoretical analysis, the following assumptions can be made for the investigated system model (2.1).

Assumption 1. There exists one positive real number $L_{1, k} < 1$, such that the inequality (2.9) holds for any sampling instant $k$.

where $\left\| \cdot\right\|$ denotes the norm operation.

Assumption 2. There exists one positive real number $L_{2, k} < 1$, such that the inequality (2.10) holds for any sampling instant $k$.

Remark 2. Since the noises are unmeasurable, the covariance matrices $R_k$ and $Q_k$ cannot be obtained accurately, while the approximation also results in the performance decay. It affects the performance strongly for non-Gaussian systems because the non-Gaussian distribution cannot be characterised sufficiently by $1$st-order and $2$nd-order moments.

2.2.   Kernel density estimation

Note that Kalman-like filters are based on quadratic cost function which means that the optimal result is obtained using $2$nd-order moment such as variance and covariance. However, since the variance and covariance cannot be used to deal with the non-Gaussian distribution properly, the concept of entropy can be introduced to describe the signal randomness which is subjected to the non-Gaussian noise. In particular, the quadratic Rényi entropy has been used in this paper.

where $\bar \omega$ denotes random variable, $\Omega$ denotes the sample space and $\gamma\left(\cdot\right)$ stands for the probability density function (PDF). Notice that the entropy is equivalent to variance for Gaussian random variable.

Once the samples of the random variable $\bar \omega$ can be collected as a data set $\left\{ \bar \omega_1, \bar \omega_2, \ldots, \bar \omega_N \right\}$, then the PDF of $\bar \omega$ can be estimated by kernel density estimation (KDE) as follows:

where $G$ denotes the Gaussian kernel function. $\Sigma$ stands for the covariance matrix of the kernel function.

Substituting the KDE equation into the definition of Rényi entropy, the estimation of entropy can be formulated as follows:

Note that logarithm is a monotonic function, the entropy optimisation can be rewritten as information potential optimisation equivalently, where the information potential has been defined as

3.   Performance enhanced filtering algorithm using polynomial compensation

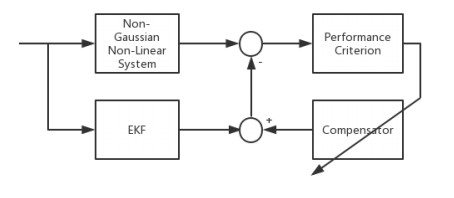
Based upon the analysis above, the accuracy will be improved if a compensative term can be added to the EKF filter, where the EKF has been design as fixed component in terms of structure and parameters. The additional term can be inserted onto the existing filter directly which is shown as follows:

Since the non-linear function $g\left({{{\tilde y}_k}}\right)$ is difficult to estimate for sampling instant $k$, the polynomial form can be adopted as follows:

where $\alpha_i$ denotes the coefficient of the polynomial. Note that $g\left(0 \right) = {\alpha _0}$ which results in $\alpha_0 = 0$ since $g\left(0 \right) = 0$. Potentially, the polynomial can be simplified with $\alpha_0 = 0$.

Equivalently, the polynomial can be re-written based on parametric structure with optimisation purpose.

where

while $i$ denotes the order for polynomial estimation. Generally, high-order polynomial will lead to better estimation however the order should be pre-specified considering the computational load. Without loss of generality, we can choose $m$ as the order of the estimation. Notice that $m = 1$ results in a linear compensator. In addition, Eq. (3.3) can be further simplified since $g\left(0\right) = 0$. As a result, $\alpha_0 = 0$ while the first element can be removed from Eq. (3.5) and $\alpha_0$ can be also removed from Eq. (3.4).

Since $\phi _k$ is known for any sampling instant $k$, the parameter matrix $\Lambda _k$ should be obtained with the entropy optimisation. Using KDE and information potential definition, we use information potential to describe the randomness while it can be approximated as follows:

where $G$ denotes the Gaussian kernel function. $\Sigma$ stands for the covariance matrix of the kernel function.

Based upon the obtained entropy value, Eq. (3.7) can be considered as the performance criterion for the optimisation.

where $R_1$, $R_2$ and $R_3$ are the weighting constants.

To minimise the performance criterion (3.7), the gradient descent optimisation can be adopted as follows:

where $\varepsilon _k$ is the time-varying step for optimisation.

Note that there always exists a real sufficient large-value constant $R_2$, such that the inequality (3.9) can be satisfied.

which results in the existence of the optimum.

To illustrate the presented algorithm, the block diagram is given by Figure 1.

4.   Convergence

The convergence analysis of the presented filtering algorithm should be started from the dynamics of the system state estimation error. Particularly, substituting the designed filter (3.1) (3.3) into the system model (2.1), we have

Moreover, we have

Substituting $\tilde y_k$ and $\Lambda_k$ into the equations (4.2) and (4.3), we have

Using Assumption A2, the inequality (4.4) can be obtained.

which leads to

Using the structure of $\phi_k$, there always exist two real positive numbers ${\bar L}_{2, k}$ and ${\bar \sigma }_k$, such that,

where ${{\bar \sigma }_k}$ denotes the upper bound for $\alpha_0$ for all sampling instants.

Substituting Eqs. (4.5) and (4.6) to Eq. (4.3) with Assumption A1, we have

Note that the estimation error $\tilde x_k$ is bounded if

In addition, the selected step $\varepsilon _{k - 1}$ makes the inequality (4.9) holds, naturally.

which leads that the upper bound ${\bar \sigma }_k$ is decreasing along $k$. In other words, ${\bar \sigma }_k\to 0$ implies that the estimation error converges to $0$ in mean-norm sense. In this paper, ${{\bar \sigma }_k} = 0$ since $\alpha_0 = 0$ which simplifies Eq. (4.8) as follows:

Note that $\left\| {{F_k} - {K_k}{H_k}} \right\| < 1$, ${L_{1, k}} < 1$ and ${L_{2, k}} < 1$, Eq. (4.8) is implementable. For any sampling instant $k$, the system evaluation is governed by the pre-specified step $\varepsilon_{k-1}$. Note that the convergence can be achieved with the information from the previous sampling instant then $J_k$ is always bounded.

Based upon the convergence analysis, the design procedure can be demonstrated using the following pseudo-code: Algorithm 1.

5.   Simulation

In order to demonstrate the effectiveness of the presented algorithm especially for practical application, the two-tank system model, shown by Figure 2, has been investigated in terms of level control. In particular, the water in the pool is injected into tank 1 with controlling the pump $u_{2, k}$ and flow from tank 2 to tank 1 goes through the intercommunicating valve, while the valve opening ratio $u_{1, k}$ and the discharge vale of tank 2 are closed. Based on ^[13], the system model can be formulated as follows:

where $x_1$ is the level of tank 1and $x_2$ denotes the level of tank 2. $A_1$ and $A_2$ are the cross-sectional area. $c_1$ and $c_2$ are constant parameters of the valves and pumps. $k_0, k_1, k_2, k_3$ and $k_4$ stand for the ratio of the valves. Note that $w$ and $v$ are the process noise and measurement noise, respectively. Furthermore, $w$ and $v$ are non-Gaussian noises although they are with zero mean values.

To apply the presented filtering algorithm, the discrete-time model can be obtained following the discretisation of system model (5.1) where the sampling time is selected as 0.1s. In addition, the parameters of the model can be pre-measured as $A_1 = A_2 = 167.4 cm^2$, $k_0 = 0.7$, $k_1 = 0.25$, $k_2 = k_3 = 0$, $k_4 = 0.1$, $c_1 = 0$ and $c_2 = 2.88$. Since the value of tank 1 is assumed as closed, we have $u_1 = 0$ while the system is driven by $u_2$ only where it has been pre-specified as $u_2 = 30$.

Without loss of generality, we choose $m = 2$ which results in a $2$-nd order polynomial based compensator and $\alpha_0 = 0$. The weighting constants are given as $R_1 = R_3 = 1$ and $R_2 = 50$. Before $k = 3000$, only EKF is used where the EKF can give a good tracking property for any initial value, however the entropy of each instant has not been optimised. The enhanced performance scheme will be adopted based on existing EKF design after $k = 3000$ while the entropy will be attenuated by the additional compensation.

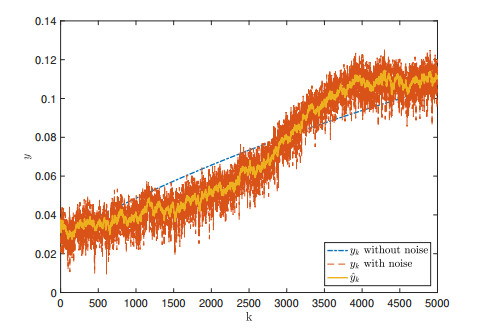
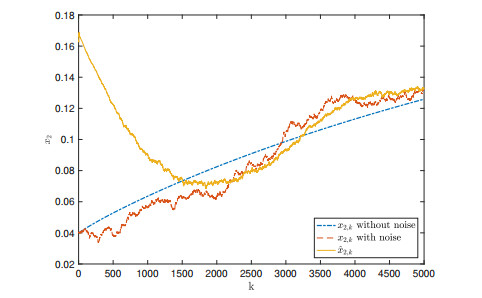
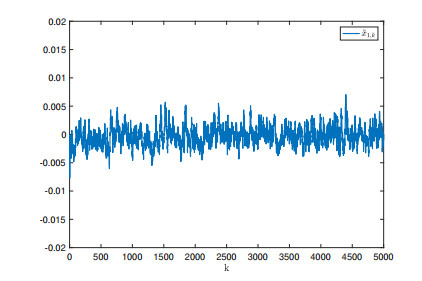
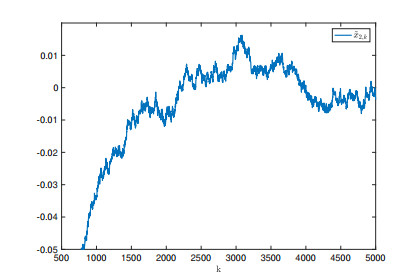
In particular, Figure 3 shows the performance of the estimation for system output, where the measurement noise $v$ has been attenuated. And based on the estimation error $\tilde y_k$, the system state $x_1$ and $x_2$ can be estimated while performances have been illustrated by Figures 4 and 5. It has been shown that the non-Gaussian noise strongly affects the process. The presented algorithm can supply the good performance for system state estimation subject to the non-Gaussian noise. In addition, the estimation errors $\tilde x_1$ and $\tilde x_2$ are given by Figures 6 and 7, where the estimation errors are bounded and close to zero.

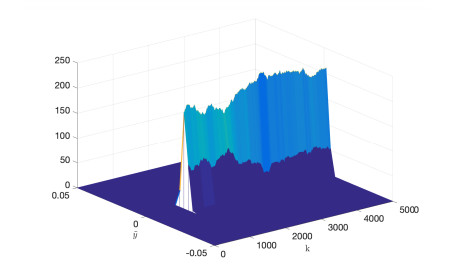
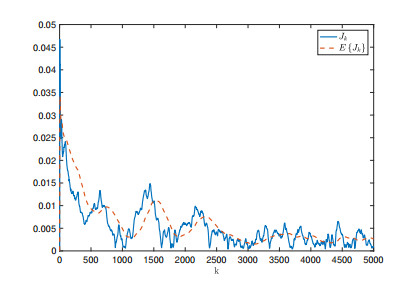
Based upon the performance enhancement via entropy attenuation, the probability density function of the system output estimation error should become sharp which has been shown by Figure 8. Note that after $k = 3000$, the probability density function becomes sharper which implies that the entropy value has been attenuated and the randomness of the estimation error has been reduced. Meanwhile, the performance criterion is given by Figure 9 where the value of the entropy-based cost function has been minimised. Figure 8 also illustrates the comparison of the performance between the EKF and the presented filtering scheme, where the performance has been enhanced in terms of minimum randomness of the estimation. Note that the EKF can be used firstly and then the filter design can be switched to the enhancement scheme as the presented algorithm will not affect the existing design loop. Meanwhile, the convergence is much easier to achieved once the estimation error has been governed within a neighbourhood of zero point.

6.   Further discussion

The contribution of the presented algorithm can be considered as the framework. In particular, most of the practical system structures cannot be changed after the design progress. In other words, it is significant to enhance the performance without changing the existing design from the view of the implementation. Moreover, this paper shows the framework with EKF as a standard example. The approach can be adopted with all the other filter design such as high-gain^[2], NN-based filter^[13], even particle filter^[14], etc. On the other hand, the performance criterion can also be replaced by other optimisation objectives such as the economic dispatch ^[9], etc.

Notice that the presented algorithm will not increase the complexity of the algorithm implementation. For each instant, the optimisation operations have been merged into the EKF algorithm, however, only one iteration has been adopted for each instant optimisation which means the addition complexity for each instant $k$ is equal to $O\left(M\right)$, where $M$ is a positive integer constant denoting the operation number for optimisation at each instant. In other words, along the system runs $k \to \infty$, the additional compensator complexity will be kept at the same level comparing to the existing filter design algorithm.

Since a number of the exciting fault diagnosis approaches are based on the filter or observer designs. The presented framework has a direct perspective for practical applications. Due to the fact that the probability density function based design has been used for fault diagnosis and tolerance control^[1,12], the entropy performance enhancement can be merged into the existing methods directly. Another perspective is the potential applications for operation control of industrial processes, such as magnesium furnaces ^[10,11], etc.

7.   Conclusions

In this paper, a novel filtering algorithm has been proposed in order to enhance the estimation accuracy for the non-Gaussian system based upon the existing EKF design. Basically, the existing EKF design has not been changed in terms of the structure and the parameters. An additional compensation loop has been designed using the non-linear compensator in the polynomial format with adjustable coefficients. Moreover, this addition non-linear term can be restated as a gain vector with a measurable vector, then the optimal coefficients should be obtained as the gain of the compensator. To achieve this optimisation, the concept of the entropy and kernel density estimation (KDE) have been adopted where the parameters have been optimised with the minimum entropy cost function using the gradient descent approach. The theoretical analysis demonstrates that the additional compensative loop design is able to guarantee the convergence of the estimation error and the simulation results indicate the effectiveness of the presented algorithm.

Acknowledgments

We would like to thank the editor and reviewer for their valuable comments which improve the quality of this paper strongly.

Conflict of interest

The author declares no conflicts of interest in this paper.