1. Introduction

In biology and medicine we may observe a wide spectrum of self-organization phenomena. This may happen at any scale; from the cellular scale of embryonic tissue formation, wound healing or tumor growth, and angiogenesis, to the much larger scale of animal grouping. Such phenomena are usually explained in terms of a collective behavior driven by "forces", either external and/or internal, acting upon individuals (cells or organisms). In most of these organization phenomena, randomness plays a major role; here we wish to address the issue of the relevance of randomness as a key feature for producing nontrivial organization of biological structures (see [8] for a general discussion on this topic). As a working example we offer a review of papers by the same authors in which tumor-driven angiogenesis has been analyzed [10], [4], [41]. In this case cells organize themselves as a capillary network of vessels, the organization being driven by a family of underlying fields, such as nutrients, growth factors and alike [22,25,13,19,21,15,14].

Actually an angiogenic system is extremely complex due to its intrinsic multiscale structure. When modelling such systems, we need to consider the strong coupling between the kinetic parameters of the relevant microscale branching and growth stochastic processes of the capillary network and the family of interacting macroscale underlying fields. Capturing the keys of the whole process is still an open problem while there are many models in the literature that address some partial features of the angiogenic process [2,36,30,31,27,37,38,35,10,39,34,20].

The importance of using an intrinsically stochastic model at the microscale to describe the generation of a realistic vessel network has been the subject of a series of papers by one of the present authors [8,11].

Typical models treat vessel cells on the extracellular matrix as discrete objects, and different cell processes like migration, proliferation, etc. occur with certain probabilities. The latter depend on the concentrations of certain chemical factors which satisfy systems of reaction-diffusion equations (RDEs) [2,24,42,34].

Viceversa, the RDEs for such underlying fields contain terms that depend on the spatial distribution of vascular cells. As a consequence, a full mathematical model of angiogenesis consists of the (stochastic) evolution of vessel cells, coupled with a system of RDEs containing terms that depend on the distribution of vessels. The latter is random and therefore the equations for the underlying fields are random RDEs, which are supposed to drive the kinetic parameters of the stochastic geometric processes of birth (branching), growth (vessel extension), and death (anastomosis).

This strong coupling leads to an highly complex mathematical problem from both analytical and computational points of view. A possibility to reduce complexity is offered by the so called hybrid models, which exploit the natural multiscale nature of the system.

The idea consists of approximating the random RDEs by deterministic ones, in which the microscale (random) terms depending on cell distributions are replaced by their (deterministic) mesoscale averages. In this way only a simple stochasticity of the geometric processes of branching -vessel extension -anastomosis is kept, driven now by deterministic kinetic parameters depending upon the above mentioned mean field approximation of the concentrations of the relevant fields [10,28].

Our analysis has shown that nontrivial problems arise when deriving deterministic equations for the mean spatial densities of the relevant stochastic entities modelling the vessels' evolution at the microscale.

In the literature there are examples of rigorous derivations of mean field equations of stochastic particle dynamics [29,40,17,6]. However, to the best of the authors' knowledge, the kind of models considered here have not yet been studied and require further investigation.

In angiogenesis, the leading mechanisms driven by the underlying fields consist of vessel branching, elongation and anastomosis. This last one has been the major and critical addition to the model proposed in [10]. In [4] anastomosis has been modelled as a death process of a tip that encounters an existing vessel and is therefore coupled with the density of the full vessel network. In order to cope with anastomosis, the vessel network has been modelled as a stochastic geometric process of Hausdorff dimension one, as opposed to the system of tips which form a usual stochastic particle system of Hausdorff dimension zero.

In [4] we have been able to derive (at least formally) a mean field equation for the spatial density of tips, as a function of spatial location and velocity. This equation is a parabolic integrodifferential equation of a Fokker-Planck type, having a source term and a noninvertible diffusion matrix; it is second order in the derivatives with respect to the velocities, and first order in the derivatives with respect to the position coordinates. Apparently, together with the mean field equations for the underlying fields, we have thus found an independent (deterministic) integrodifferential system whose solution can provide the required (deterministic) kinetic parameters, which drive the stochastic system for the tips, eventually leading to the stochastic vessel network, at the microscale.

Mean field equations that follow from the "propagation of chaos" assumption (law of large numbers) (see [29], [40], and references therein) are quite convenient as they hold for any given realization of the underlying self-averaging stochastic processes, but this requires a large number of tips at any location in the phase space, and at any time.

Unfortunately anastomosis is responsible for a significant decay of the number of tips, so to make inapplicable laws of large numbers on a single realization of the stochastic process (a replica of the system), according to the "propagation of chaos".

However by re-examining the derivation given in [4], in [41] we have noticed that the same deterministic description holds for vessel tip densities calculated by averaging over replicas. This is close to J.W. Gibbs' original ensemble average interpretation of equilibrium statistical mechanics [23], except that, of course, our system is always very far from equilibrium. In either cases, though with a different interpretation of the solution, the deterministic description consists of a reaction-diffusion equation for the tumor angiogenic factor (TAF) concentration coupled to a Fokker-Planck type equation for the vessel tip density. To conclude, randomness cannot be avoided; the deterministic description represents the evolution of an ideal "mean" angiogenesis system and the evolution of a particular replica may deviate significantly from it. These deviations are important and deserve further study, but this is outside the scope of the present paper (see [8]).

The paper is organized as follows. Section 2 describes how our stochastic model treats vessel branching, extension and anastomosis. In the subsequent three sections we present the mathematical ingredients to be used in the sequel. In Section6 we derive the mean field approximation based on the propagation of chaos assumption. In Section 7 a discussion is presented based on the outcomes of the numerical simulations of the stochastic model as opposed to the mean field model. In Section 8 the ensemble average approach is presented to derive an equation of Fokker-Planck type for the density of vessel tips and the TAF's RDE. In Section 9 numerical simulations of the deterministic averaged model are presented as opposed to the stochastic model. Finally Section 10 contains our conclusions.

---

2. The mathematical model

Based on the above discussion, the main features of the process of formation of a tumor-driven vessel network that we have considered are (see [18,30,10])

ⅰ) vessel branching;

ⅱ) vessel extension;

ⅲ) chemotaxis in response to a generic tumor angiogenic factor (TAF), released by tumor cells;

ⅳ) haptotactic migration in response to fibronectin gradient, emerging from the extracellular matrix and through degradation and production by endothelial cells themselves;

ⅴ) anastomosis, the coalescence of a capillary tip with an existing vessel.

Let $N_0$ denote the initial number of tips, $N(t)$ the number of tips at time $t.$ Each particle tip is characterized by its space $\mathbf{X}^i(t)$ and velocity $\mathbf{v}^i(t)$ coordinates, so that the whole process is characterized by the stochastic processes $\{(\mathbf{X}^i(t),\mathbf{v}^i(t)),\, i = 1, . . .,N(t),\, t\in\mathbb R_+\}$. We model the capillary network of endothelial cells $\mathbf{X}(t)$ as the union of all random trajectories representing the extension of individual capillary tips from the (random) time of birth (branching) $T^i,$ to the (random) time of death (anastomosis) $\Theta^i,$

$\mathbf{X}(t)=\displaystyle\bigcup\limits_{i=1}^{N(t)} \{\mathbf{X}^i(s), T^i\le s\le \min\{t, \Theta^i \} \}, \label{network} $

(1)

giving rise to a stochastic network. It is clear that $\mathbf{X}^i(t)$ is a random closed set of Hausdorff dimension zero, while $\mathbf{X}(t)$ is a random closed set of Hausdorff dimension one.

We may describe both random sets by means of random distributions á la Dirac-Schwarz [12]; $\delta_{\mathbf{X}^i(t)}(\mathbf{x})$ is the random distribution of the tip $\mathbf{X}^i(t)$ localized at point $\mathbf{x}$, for $i=1,\ldots,N(t);$ $\delta_{\mathbf{X}(t)}(\mathbf{x})$ is the random distribution of the whole network $\mathbf{X}(t)$ localized at point $\mathbf{x}$.

For convenience of the reader, we remind here that, under sufficient regularity assumptions on a random set $\mathbf{\Xi},$ it may admit a mean density $\lambda_{\mathbf{\Xi}},$ given by the expectation of the random distribution [12] [1]

$ \lambda_{\mathbf{\Xi}}(\mathbf{x})=\mathbb{E} [\delta_{\mathbf{\Xi}}](\mathbf{x}).\label{mean_density} $

(2)

---

2.1. The underlying fields

TAF, fibronectin and matrix degrading enzymes activate the migration of endothelial cells.

TAF diffuses, and it decreases where endothelial cells are present; we will adopt the following model for the TAF evolution, according to which "consumption" (actually molecular binding) is due to the additional endothelial cells producing vessels' extension. Consumption is then taken proportional to the velocity $\mathbf{v}^i, i=1,\ldots, N(t)$, of the tips, hence

$ $$\begin{array}{l} \frac{\partial}{\partial t}C(t,\mathbf{x}) \,=\, d_0 \delta_A(\mathbf{x})&+& d_2 \triangle C(t,\mathbf{x}) \nonumber \\ &-& \eta C(t,\mathbf{x}) \frac1N \sum\limits_{i=1}^{N(t)}|\mathbf{v}^i(t)| (K_N \ast \delta_{ \mathbf{X}^i(t)} )(\mathbf{x}). \end{array}$$ $

(3)

Parameters $ d_2, \eta >0 $ denote the diffusivity and the rate of consumption, respectively, while $d_0$ represents the rate of production by a source located in a region $A\subset \mathbb R^d$, modelling e.g. a tumor mass. Later we will include the production term in the evolution equation for $C(t,\mathbf{x})$ only via the boundary conditions, meaning that the tumor is located at the boundary of the relevant domain.

Model (3) considers a dependence upon the (mollified) empirical distribution of the variation in length of the existing vessels, per unit time.

The parameter $N$ represents a scale parameter, corresponding to the order of magnitude of the number of vessels in the network, so that the action of each existing vessel is reduced accordingly. Convolution with the kernel $K_N( \mathbf{x})$ provides a mollified version of the relevant random distributions; from a modelling point of view this may correspond to a nonlocal reaction with the relevant modelling fields (see e.g. [38]). Correspondingly, the mollifier kernel $K_N$ is chosen such that $\lim\limits_{N\rightarrow \infty}K_N( \mathbf{x}) =\delta_0(\mathbf{x})$.

Specific choices about the dependence of the kernel $K_N$ upon $N$ may allow the convergence, for $N$ tending to infinity, of the mollified random distributions to the corresponding mean densities, thanks to suitable laws of large numbers.

Fibronectin is bound to the extracellular matrix and does not diffuse [3]. Degradation of fibronectin, characterized by a coefficient $\zeta_1$, depends on the concentration of matrix degrading enzyme(MDE), produced by the cells [35].

$ \frac{\partial}{\partial t}f(t,\mathbf{x}) \,=\, -\zeta_1 m(t,\mathbf{x}) f(t,\mathbf{x}) + \zeta_2 \frac1N\sum\limits_{i=1}^{N(t)}({K_N \ast \delta_{ \mathbf{X}^i(t)}})(\mathbf{x}). \label{fibronectin_evolution} $

(4)

The MDE, once produced at a rate $\nu_1$, diffuses locally with a diffusion coefficient $\epsilon_1$, and is spontaneously degraded at a rate $\nu_2$.

$ \frac{\partial}{\partial t}m(t,\mathbf{x}) \,=\, \epsilon_1 \triangle m(t,\mathbf{x}) -\nu_2 m(t,\mathbf{x}) + \nu_1 \frac1N\sum\limits_{i=1}^{N(t)}({K_N \ast \delta_{\mathbf{X}^i(t)}})(\mathbf{x}). \label{mde_evolution} $

(5)

All these (random) partial differential equations are subject to suitable boundary and initial conditions.

For the sake of technical simplification, in the sequel we will not consider the last two underlying fields $f$ and $m.$

---

3. The relevant empirical measures

Let us assume that, at any time $t\geq 0$, the number of tips, $N(t)$, and the number of vessels per unit volume is of the same order $O(N)$, where $N$ is a scale parameter; at first we shall consider the "propagation of chaos" approach according to which $N$ can be taken as a sufficiently large positive integer, uniformly in space and time; the main issue of this paper is that this assumption may be false, as shown by the numerical simulations of the model presented here (see Section 7, and the following ones).

There are two fundamental random measures describing the system at any time $t \ge 0.$ The global random empirical measure $Q_N$ of the joint process $\{(\mathbf{X}^k(t),\mathbf{v}^k(t)), k=1,\ldots, N(t), t \in \mathbb R_+\}$ is defined as

$ Q_N(t):=\frac{1}{N} \sum\limits_{k=1}^{N(t)}\epsilon_{(\mathbf{X}^k(t),\mathbf{v}^k(t))}. \label{def: _empirical measure_global} $

(6)

Here $\epsilon_{(\mathbf{x},\mathbf{v})}$ is the usual Dirac measure on $\mathcal B_{\mathbb R^d \times \mathbb R^d }.$

Consequently, the random empirical measure of the process $\{(\mathbf{X}^k(t)),\, k=1,\ldots, N(t), t \in \mathbb R_+\}$ will be given by

$ T_N(t)=\frac{1}{N} \sum\limits_{k=1}^{N(t)}\epsilon_{\mathbf{X}^k(t)}= Q_N(t)(\cdot\times\mathbb R^d). \label{def: _empiricalmeasure_tips} $

(7)

---

4. The dynamics

---

4.1. Tip branching

Two kinds of branching have been identified; either from a tip or from a mature vessel; here for the sake of simplicity, we shall consider only tip branching.

The birth process of new tips can be described in terms of a marked point process (see e.g. [5]), by means of the random measure $\Phi$ on ${\mathcal B}_{\mathbb R^+\times \mathbb R^d\times \mathbb R^d}$ such that, for any $t\ge 0$ and any $B\in {\mathcal B}_{\mathbb R^d\times \mathbb R^d}$,

$ \Phi((0,t]\times B): =\int_0^t\!\int_B\Phi(ds\times d{\mathbf{x}}\times d{\mathbf{v}}), \label{PHI} $

(8)

where $\Phi(ds\times d{\mathbf{x}}\times d{\mathbf{v}})$ is the random variable that counts those tips born from an existing tip during times in $(s,s+ds]$, with positions in $({\mathbf{x}},{\mathbf{x}}+d {\mathbf{x}}]$, and velocities in $({\mathbf{v}},{\mathbf{v}}+d{\mathbf{v}}]$.

We assume that the probability that a tip branches from one of the $N(t)$ existing ones during an infinitesimal time interval $(t, t + dt]$ is function of the TAF concentration $C(t,\mathbf{x})$

$ prob\!\left(N(t+dt)-N(t)=1 |\mathcal F_{t^-}\right) =\sum\limits_{i=1}^{N(t)}\alpha(C(t,\mathbf{X}^i(t)))\, dt, \label{prob_nuova_nascita_tip} $

(9)

where $\alpha(C)$ is a non-negative function; for example, we may take

$ \alpha(C)=\alpha_1\frac{C}{C_R+C}, $

(10)

where $C_R$ is a reference density parameter [10].

Here $\mathcal{F}_{t^-}$ denotes the history of the whole process up to time $t^-.$

As a technical simplification, we will further assume that whenever a tip located in $\mathbf{x}$ branches, the initial value of the state of the new tip is $(\mathbf{X}^{N(t)+1},\mathbf{v}^{N(t)+1}) = (\mathbf{x},\mathbf{v}_0)$, where $\mathbf{v}_0$ is a non random velocity. Later, as in [41], a newly created tip will be taken to assume an initial velocity selected out of a normal distribution with mean $\mathbf{v}_0,$ and some variance.

We then claim that the compensator of the random measure $\Phi(ds \times d{\mathbf{x}}\times d{\mathbf{v}})$ is

$\alpha(C(s,{\mathbf{x}}))\delta_{{\mathbf{v}}_0}(\mathbf{v})\, N Q_N(s)(d(\mathbf{{x}},\mathbf{{v}}))\, ds. \label{branching_compensator} $

(11)

---

4.2. Vessel extension

We describe vessel extension by the Langevin system

$ $$\begin{array}{l} d\mathbf{X}^k(t)&=&\mathbf{v}^k(t)\, dt\nonumber\\ d\mathbf{v}^k(t)&=& \left[- k\, \mathbf{v}^k(t)+ \mathbf{F}\!\left(C(t,\mathbf{X}^k(t))\right)\! \right]\! dt + \sigma\, d\mathbf{W}^k(t), \end{array}$$ $

(12)

for all those $k=1, \ldots, N(t)$ for which $T^k <t < \Theta^k.$ Besides the friction force, there is a force due to the underlying TAF field $C(t,\mathbf{x})$ [30,35]:

$ \mathbf{F}(C)= \frac{d_1}{(1+\gamma_1C)^q}\nabla_x C. \label{Fvector} $

(13)

---

4.3. Anastomosis

When a vessel tip meets an existing vessel it joins it at that point and time and it stops moving. This process is called tip-vessel anastomosis.

As in the case of the branching process, we have modelled this process via a marked counting process; anastomosis is modelled as a "death" process.

Let $\Psi$ denote the random measure on ${\mathcal B}_{\mathbb R^+ \times \mathbb R^d \times \mathbb R^d} $ such that, for any $t \ge 0,$ and any $B \in \mathcal B_{\mathbb R^d \times \mathbb R^d}$,

$ \Psi((0,t] \times B) := \int_0^t \int_B \Psi(ds\times d{\mathbf{x}} \times d{\mathbf{v}}) \label{psiB} $

(14)

where $\Psi(ds\times d{\mathbf{x}} \times d{\mathbf{v}})$ is the random variable counting those tips that are absorbed by the existing vessel network during time $(s,s+ds],$ with position in $({\mathbf{x}}, {\mathbf{x}}+d{\mathbf{x}}],$ and velocity in $({\mathbf{v}}, {\mathbf{v}}+d{\mathbf{v}}].$

Thanks to the choice of a Langevin model for the vessels extension, we may assume that the trajectories are sufficiently regular and have an integer Hausdorff dimension $1.$

Hence [12] the random measure

$ A \in \mathcal B_{\mathbb R^d} \mapsto \mathcal H^1 ({\mathbf{X}}(t)\cap A) \in \mathbb R_+ $

(15)

admits a random generalized density $\delta_{{\mathbf{X}}(t)}(\mathbf{x})$ with respect to the usual Lebesgue measure on $\mathbb R^d$ such that, for any $A \in \mathcal B_{\mathbb R^d},$

$ \mathcal H^1 ({\mathbf{X}}(t)\cap A)= \int_A \delta_{\mathbf{X}(t)}(\mathbf{x})d \mathbf{x} . $

(16)

Given the definition of ${\mathbf{X}}(t)$ as the union of all trajectories up to time $t,$ the Hausdorff measure associated with the stochastic network ${\mathbf{X}}(t)$ can be expressed in terms of the occupation time of a region $A \in \mathcal B_{\mathbb R^d}$ by tips existing up to time $t>0$ (see [32], [26])

$ $$\begin{array}{l}\mathcal H^1 ({\mathbf{X}}(t)\cap A) &=& \gamma \displaystyle \int_0^t ds\sum\limits_{i=1}^{N(s)} \, \mathbb I_A({\mathbf{X}}^i(s)) \nonumber \\ &=&\displaystyle \gamma \int_0^t ds\sum\limits_{i=1}^{N(s)}\epsilon_{{\mathbf{X}}^i(s)} (A), \end{array}$$ $

(17)

where $\mathbb I_A({\mathbf{x}})=1$ if ${\mathbf{x}}\in A$, 0 otherwise, and $\epsilon_{{\mathbf{x}}}$ denotes the usual Dirac measure associated with the point ${\mathbf{x}}$. $\gamma$ is a suitable dimensional constant taking into account an average velocity of growth of the vessels; it can be used to fit the model with real data.

The latter has the Dirac delta as its generalized derivative with respect to the usual Lebesgue measure on $\mathbb R^d.$ Hence,

$ \delta_{\mathbf{X}(t)}(\mathbf{x})= \gamma \displaystyle \int_0^t ds\sum\limits_{i=1}^{N(s)} \,\delta_{\mathbf{X}^i(s)}(\mathbf{x}). $

(18)

We assume that the probability per unit time that a typical tip ${\mathbf{X}}^k(t)$ meets the existing vessel network ${\mathbf{X}}(t)$ (and "dies") is a linear function of the scaled random distribution $N^{-1} \delta_{{\mathbf{X}}(t)}$ of the stochastic network at point ${\mathbf{X}}^k(t)$ and time $t,$ so that the probability that an active tip dies during an infinitesimal time interval is given by

$ prob\!\left(N(t+dt)-N(t)=-1 |\mathcal F_{t^-}\right) = N^{-1} \sum\limits_{i=1}^{N(t)} ( K_N \ast \delta_{\mathbf{X}(t)} )(\mathbf{X}^i(t)) dt. \label{prob_morte_tip} $

(19)

We then claim that the compensator of the random measure $\Psi(ds\times d{\mathbf{x}} \times d{\mathbf{v}})$ is

$ N^{-1} ( K_N \ast \delta_{\mathbf{X}(s)} )(\mathbf{x})N Q_N(s)(d({\mathbf{x}},{\mathbf{v}}))ds. $

(20)

---

5. Complexity

Our stochastic model is thus described by a set of Ito stochastic differential equations (SDEs), a marked point process describing tip branching (a birth process), and a marked point process describing anastomosis (a death process). The latter process depends on the past history of a given realization of the overall stochastic process. In addition, the TAF concentration is itself a random process since it depends on the stochastic evolution of the tips as indicated by Equation (3). Hence $C(t, \mathbf{x})$ is a random spatial field, which is supposed to drive the kinetic parameters of branching and extension of vessels (see Equations (9), and (12)); as a consequence the fully stochastic system described in the previous sections results to be of high complexity, both analytical and computational, especially in presence of a large vessel network. In most of the current literature a reduction of the complexity is reached by taking a deterministic mean field approximation of the stochastic reaction term in the evolution equation of the underlying fields. In this way the stochastic processes of branching and extension are driven by deterministic parameters. The usual assumption is the "propagation of chaos"; as we had anticipated in Section 3 this is possible only if one can claim that the scale parameter $N$ can be taken as a sufficiently large positive integer, uniformly in space and time. Next section is devoted to that approach.

---

6. Mean field approximation

By Itô's formula (see e.g. [9], p. 270), we may obtain the evolution equation of the random measure $(Q_N(t))_{t \in \mathbb R_+}$ as follows. For any test function $g\in C_b(\mathbb R^d\times \mathbb R^d),$

$ $$\begin{array}{l} \int\! g(\mathbf{x},\mathbf{v})\, Q_N(t)(d(\mathbf{x},\mathbf{v})) = \!\int\! g(\mathbf{x},\mathbf{v})\, Q_N(0)(d(\mathbf{x},\mathbf{v})) \\ \,+\int_0^t\!\int\!\mathbf{v}\cdot\nabla_xg(\mathbf{x},\mathbf{v}) Q_N(s)(d(\mathbf{x},\mathbf{v}))\, ds \\ \, +\!\! \int_0^t\!\!\!\int\! [\mathbf{F}(C(s,\mathbf{x}))-k\mathbf{v}]\!\cdot\!\nabla_v g(\mathbf{x},\mathbf{v}) Q_N(s)(d(\mathbf{x},\mathbf{v}))\, ds \nonumber\\ \,+ \int_0^t\int\! \frac{\sigma^2}{2}\Delta_v g(\mathbf{x},\mathbf{v}) Q_N(s)(d(\mathbf{x},\mathbf{v})) ds\nonumber\\ \, + \int_0^t \! \!\int\!\alpha(C(s,\mathbf{x}))\delta_{\mathbf{v}_0}(\mathbf{v}) g(\mathbf{x},\mathbf{v})Q_N(s)(d(\mathbf{x},\mathbf{v}))\, ds \nonumber\\ \,- \int_0^t\!\! \int\! \frac{1}{N} (K_N\ast \delta_{\mathbf{X}(s)})(\mathbf{x}) g(\mathbf{x},\mathbf{v}) Q_N(s)(d(\mathbf{x},\mathbf{v}))\, ds \nonumber\\ \,+ \tilde{M}_N(t), \end{array}$$ $

(21)

where

$\tilde{M}_N(t)= \tilde{M}_{1,N}(t) + \tilde{M}_{2,N}(t) + \tilde{M}_{3,N}(t),$

with

$ \tilde{M}_{1,N}(t)= \!\int_0^t\!\frac{1}{N} \sum\limits_{k=1}^{N(s)}\!\nabla_v g(\mathbf{X}^k(s),\mathbf{v}^k(s))\cdot d\mathbf{W}^k(s),\label{mtilde} $

(22)

$ $$\begin{array}{l}\tilde{M}_{2,N}(t)= \!\int_0^t\!\! \int g(\mathbf{x},\mathbf{v}) [\Phi_N(ds\times d\mathbf{x}\times d\mathbf{v}) \\ \;\;\;\;\;\;\; - \alpha(C(s,\mathbf{x}))\delta_{\mathbf{v}_0}(\mathbf{v}) Q_N(s)(d(\mathbf{x},\mathbf{v}))ds], \end{array}$$ $

(23)

$ $$\begin{array}{l} \tilde{M}_{3,N}(t)&\!=\!&\!\int_0^t\!\! \int g(\mathbf{x},\mathbf{v}) [\Psi_N(ds\times d\mathbf{x} \times d\mathbf{v})\nonumber\\ &\!-\!&\! \left.\frac{1}{N} (K_N\ast \delta_{\mathbf{X}(s)})(\mathbf{x})Q_N(s)(d(\mathbf{x},\mathbf{v}))ds\right]\!\!. \end{array}$$ $

(24)

All $(\tilde{M}_{1,N}(t))_{t \in \mathbb R_+},$ $(\tilde{M}_{2,N}(t))_{t \in \mathbb R_+},$ and $(\tilde{M}_{3,N}(t))_{t \in \mathbb R_+}$ are zero mean martingales, so that $(\tilde{M}_{N}(t))_{t \in \mathbb R_+}$ is itself a zero mean martingale.

By Doob's inequality

$\tilde M_N(t) \mathop{\longrightarrow}\limits ^{P}_{N \rightarrow \infty} 0.$

This is the substantial reason of the possible deterministic limiting behavior of the process, as $N\rightarrow \infty.$

As a consequence, if we suppose that indeed, for a large value of the scale parameter $N,$ we may claim

$Q_N(t)(d(\mathbf{x},\mathbf{v}))\rightarrow Q_{\infty}(t)(d(\mathbf{x},\mathbf{v}))=p(t,\mathbf{x},\mathbf{v})d\mathbf{x} \, d\mathbf{v}. \label{LLN_Q} $

(25)

Assuming that (25) holds true, the scaled stochastic distribution of vessels $ \displaystyle \frac{1}{N} ( K_N \ast \delta_{\mathbf{X}(t)}) (\mathbf{x})$ can be itself approximated by the mean value

$ \lambda(t,{\mathbf{x}})= \mathbb{E}[\delta_{\mathbf{X}(t)}] (\mathbf{x})= \gamma \displaystyle \int_0^t \tilde{p}(s,{\mathbf{x}})\, ds, $

(26)

where

$ \tilde{p}(t,\mathbf{x}) = \mathbb{E}[\delta_{\mathbf{X^i}(t)}](\mathbf{x}) =\int p(t,\mathbf{x},\mathbf{v}')\, d\mathbf{v}'\label{reduced_density} $

(27)

is the marginal density of $p(t,\mathbf{x},\mathbf{v})$.

A formal justification of the above is the following one. According to a previous discussion

$ \frac{1}{N}\delta_{\mathbf{X}(t)}(\mathbf{x})= \gamma \int_0^t ds \displaystyle{\frac{1}{N} \sum\limits_{i=1}^{N(s)} \delta_{\mathbf{X}^i(s)}(\mathbf{x})} .$

In the mean field approximation we are assuming that a "law of large numbers" may be applied, so that $ \displaystyle{\frac{1}{N} \sum_{i=1}^{N(s)} \delta_{\mathbf{X}^i(s)}(\mathbf{x})}$ is an approximation of $ \tilde{p}(s,{\mathbf{x}}),$ and consequently, $ \displaystyle{\frac{1}{N} (K_N \ast \delta_{\mathbf{X}(t)})(\mathbf{x})}$ is an approximation of $ \gamma \displaystyle \int_0^t \,\tilde{p}(s,\mathbf{x}) ds.$

For objects of Hausdorff dimension $0,$ as they are $(\mathbf{X}^i(t),\mathbf{v}^i(t)),$ it is well known that the only request for stating that their expected value $p(t,\mathbf{x},\mathbf{v})$ is a classical function, is that they are absolutely continuous random vectors, and this is the case for solutions of SDEs. On the other hand, the possibility that the generalized function $\delta_{\mathbf{X}(t)}$ describing the vessel network, of Hausdorff dimension $1,$ is an absolutely continuous random object is based on the crucial assumption of a Langevin model for the vessels' extension (see System (12)). Indeed under this choice we may state that almost all trajectories are rectifiable; a pure Brownian motion model would have led to trajectories that are not rectifiable though continuous (the mathematical theory of random densities is presented in [12]).

Finally the consumption term in (3) is an approximation of the flux density

$ \mathbf{j}(t,\mathbf{x})= \int \mathbf{v}' p(t,\mathbf{x},\mathbf{v}')\, d \mathbf{v'}, \label{flux_max} $

(28)

so that the evolution equation (3) may be approximated by its (deterministic) mean field version

$ \frac{\partial}{\partial t}\widetilde{C}(t,\mathbf{x}) = d_2 \Delta_x \widetilde{C}(t,\mathbf{x}) - \eta \widetilde{C}(t,\mathbf{x})|\mathbf{j}(t,\mathbf{x})| . $

(29)

TAF injection from the tumor is realized as a nonzero flux boundary condition for this equation [4], instead of including it explicitly as in (3).

Based on the above discussion, one might claim that the evolution equation for the density $p(t,\mathbf{x},\mathbf{v})$ is the following one

$ $$\begin{array}{l} \frac{\partial}{\partial t} p(t,\mathbf{x},\mathbf{v})&= \frac{\alpha_1\widetilde{C}(t,\mathbf{x})}{C_R+\widetilde{C}(t,\mathbf{x})}\, p(t,\mathbf{x},\mathbf{v})\delta_{\mathbf{v}_0}(\mathbf{v}) \nonumber \\ &- \gamma p(t,\mathbf{x},\mathbf{v}) \int_0^t \tilde{p}(s,\mathbf{x})\, ds \nonumber \\ &- \mathbf{v}\cdot \nabla_x p(t,\mathbf{x},\mathbf{v}) \nonumber \\ & + k \nabla_v \cdot (\mathbf{v} p(t,\mathbf{x},\mathbf{v})) \nonumber \\ &- d_1\nabla_v \cdot \left[\frac{\nabla_x \widetilde{C}(t,\mathbf{x})}{[1+\gamma_1\widetilde{C}(t,\mathbf{x})]^q}\, p(t,\mathbf{x},\mathbf{v}) \right]\! \nonumber \\ &+ \frac{\sigma^2}{2} \Delta_{v} p(t,\mathbf{x},\mathbf{v}). \end{array}$$ $

(30)

The coupled system (29), (30) is subject to suitable boundary and initial conditions, to be discussed later.

This approach is called "hybrid", since we have substituted all stochastic underlying fields by their "mean" counterparts; most of the current literature could now be reinterpreted along these lines. Indeed, one should check that the hybrid system is fully compatible with a rigorous derivation of the evolution for the vessel densities. Nonlinearities in the full model are a big difficulty in this direction; a rigorous derivation of the convergence results requires a nontrivial mathematical analysis, which is under investigation; for this it is instrumental a proof of existence, uniqueness and sufficient regularity of the solution of the mean field equations (see [29], and [6]). We wish to stress that anyhow substituting mean geometric densities of tips or of full vessels to the corresponding stochastic quantities leads to an acceptable coefficient of variation (percentage error) only when a law of large numbers can be applied, i.e. whenever the relevant numbers per unit volume are sufficiently large; otherwise stochasticity cannot be avoided, and in addition to mean values, the mathematical analysis and/or simulations should provide confidence bands for all quantities of interest (see e. g. [7]). An interesting case in this direction is discussed in [11].

---

7. Numerical simulations

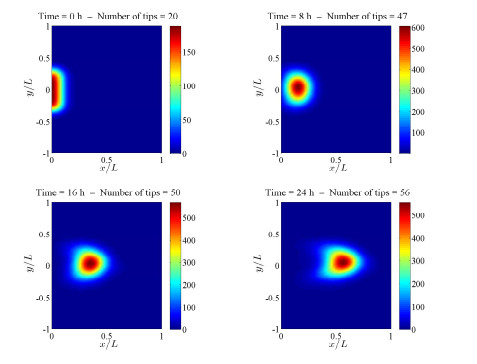
Figure 1 shows the outcome of a numerical simulation of the fully stochastic model. The values of all parameters are discussed in [4] and [41]; in particular all kernels have been taken as Gaussians centered at $0$. Tips proliferate by branching but they tend to crowd in a relatively narrow region due to chemotaxis. The number of active tips is kept below a hundred by anastomosis and, as a result, there never are enough tips for the law of large numbers to produce self-averaging of realizations. In fact, the fluctuations of tip density or velocity observed in simulations are not small at any time. Thus a deterministic description of vessel tip density based on self-averaging due to the law of large numbers does not seem correct.

However, there is another interpretation of the numerical simulations for which a deterministic description is correct. While the vessel network may look different for different replicas of the stochastic process, tip densities associated to averages over replicas are described by Equation (30) [41]. How is this possible? Let $\mathcal{N}$ be the number of independent replicas (realizations) of the angiogenic process having the same initial number of vessel tips but otherwise random initial conditions. For any replica $\omega$ of the stochastic simulation, let us define the stochastic distribution of tips per unit volume in the $(\mathbf{x},\mathbf{v})$ phase space by

$ Q_N^*(t,\mathbf{x},\mathbf{v},\omega) \,\,\!\!\!=\!\!\!\sum\limits_{i=1}^{N(t,\omega)}\delta_{\mathbf{X}^i(t,\omega)}(\mathbf{x})\,\delta_{\mathbf{v}^i(t,\omega)}(\mathbf{v}). \label{eq99_1} $

(31)

Here the number of tips at time $t$, $N(t,\omega)$, may be different for different replicas. Similarly at time $t$, the stochastic distribution of tips per unit volume in physical space is given by

$ \tilde{Q}_N^*(t,\mathbf{x}, \omega)= \sum\limits_{i=1}^{N(t,\omega)}\delta_{\mathbf{X}^i(t,\omega)}(\mathbf{x}), \label{eq99_2} $

(32)

and

$ \delta_{\mathbf{X}(t,\omega)}(\mathbf{x}):= \gamma \int_0^t\sum\limits_{i=1}^{N(s,\omega)}\delta_{\mathbf{X}^i(s,\omega)}(\mathbf{x})ds $

(33)

represents the concentration of all vessels per unit volume in physical space, at time $t,$ i.e., the vessel network.

By following a similar approach as in our previous paper [4], we may then obtain the weak formulation of the stochastic evolution of $Q_N^*(t,\mathbf{x},\mathbf{v},\omega),$ by following similar steps as in Equation (21):

$ $$\begin{array}{l} \int\! g(\mathbf{x},\mathbf{v})\, Q_N^*(t,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v} &=& \!\int\! g(\mathbf{x},\mathbf{v})\, Q_N^*(0,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v} \nonumber\\ &+&\int_0^t\!\int\!\mathbf{v}\cdot\nabla_xg(\mathbf{x},\mathbf{v}) Q_N^*(s,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v}\, ds \nonumber\\ &+&\!\! \int_0^t\!\!\!\int\! [\mathbf{F}(C(s,\mathbf{x}))-k\mathbf{v}]\!\cdot\!\nabla_v g(\mathbf{x},\mathbf{v}) Q_N^*(s,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v}\, ds \nonumber\\ &+& \int_0^t\int\! \frac{\sigma^2}{2}\Delta_v g(\mathbf{x},\mathbf{v}) Q_N^*(s,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v} ds\nonumber\\ &+& \int_0^t \! \!\int\!\alpha(C(s,\mathbf{x}))\delta_{\mathbf{v}_0}(\mathbf{v})g(\mathbf{x},\mathbf{v})Q_N^*(s,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v}\, ds \nonumber\\ &-& \int_0^t\!\! \int\! \delta_{\mathbf{X}(s)}(\mathbf{x}) g(\mathbf{x},\mathbf{v}) Q_N^*(s,\mathbf{x},\mathbf{v})d\mathbf{x} d\mathbf{v}\, ds \nonumber\\ &+& \overline{M}_N(t), \end{array}$$ $

(34)

where we have omitted the variable $\omega$ not to encumber the formulas. Here $\overline{M}_N(t)$ is again a zero mean martingale that collects all source of randomness of the system, $g(\mathbf{x},\mathbf{v})$ is a smooth test function.

By mimicking the typical kernel density estimation approach in Statistics (see e.g. [33], page 489), we introduce the (random) empirical distribution of tips per unit volume in the $(\mathbf{x},\mathbf{v})$ phase space,

$ $$\begin{array}{l} p_{\mathcal{N}}\!(t,\mathbf{x},\mathbf{v})\!&=&\!\frac{1}{\mathcal{N}}\sum\limits_{\omega=1}^\mathcal{N}(K_{\mathcal N} \ast Q_N^*(t, \cdot, \cdot, \omega))(\mathbf{x},\mathbf{v}). \end{array}$$ $

(35)

Here the mollifying kernel $K_{\mathcal N}(\mathbf{x},\mathbf{v})$ tends to a Dirac delta function $\delta_{\mathbf{0},\mathbf{0}}$ as $\mathcal N\rightarrow \infty$. Correspondingly, the empirical distribution of tips per unit volume in the physical space and the vessel tip flux are,

$ \tilde{p}_{\mathcal N}(t,\mathbf{x})\,\,\!\!=\!\frac{1}{\mathcal{N}}\sum\limits_{\omega=1}^\mathcal{N}(K_{\mathcal N} \ast \widetilde{Q}_N^*(t, \cdot, \omega))(\mathbf{x}), \label{eq11} $

(36)

$ \mathbf{j}_{\mathcal N}(t,\mathbf{x})\,\,\!\!=\!\frac{1}{\mathcal{N}}\!\sum\limits_{\omega=1}^\mathcal{N}\!\sum\limits_{i=1}^{N(t,\omega)}\!\!\mathbf{v}^i(t,\omega) (K_{\mathcal N} \ast \delta_{\mathbf{X}^i(t,\omega)})(\mathbf{x}),\label{eq12} $

(37)

respectively. We now conjecture that the following limit exists

$ $$\begin{array}{l} p(t,\mathbf{x},\mathbf{v})\!\!\!&=&\!\!\!\lim\limits_{\mathcal{N}\to\infty} p_{\mathcal{N}}(t,\mathbf{x},\mathbf{v}), \end{array}$$ $

(38)

and that $p(t,\mathbf{x},\mathbf{v})$ is the deterministic distribution of tips per unit phase space volume. The proof of this statement is not trivial (and out of the scope of this paper), as the usual assumptions on the kernel density estimation (see page 489 of [33]) may not apply. Correspondingly the deterministic distribution of tips per unit volume in the physical space should exist as the following limit

$ $$\begin{array}{l} \tilde{p}(t,\mathbf{x})&=&\lim\limits_{\mathcal{N}\to\infty} \tilde{p}_{\mathcal N}(t,\mathbf{x}). \end{array}$$ $

(39)

Finally, we may obtain the deterministic version of the vessel tip flux as

$ $$\begin{array}{l} \mathbf{j}(t,\mathbf{x})\!\!&=&\!\!\lim\limits_{\mathcal{N}\to\infty}\mathbf{j}_{\mathcal N}(t,\mathbf{x}). \end{array}$$ $

(40)

Figure 2 shows the marginal tip density $\tilde{p}(t,x,y)\approx\tilde{p}_{\mathcal N}(t,x,y)$ calculated from (36) with $\mathcal{N}=50$ replicas at the times represented in Figure 1. The tips proliferate after a few hours and reach a high value by branching onto the free space ahead of them. Influenced by chemotaxis, the marginal tip density thickens about the $x$ axis and it forms a lump that advances toward the tumor. Behind the lump, the density drops to a low value as few active tips remain. As shown by Figure 1, the network of vessels is quite dense in the wake of the tips and therefore anastomosis reduces enormously the number of active tips there. They are numerous only at the leading part of the lump where free space is available. Thus the definition of marginal tip density based on ensemble average over replicas provides a better deterministic description of angiogenesis than the density based on the law of large numbers. There are no tips or very few ones in large regions of the physical space.

---

8. Ensemble average description

On the basis of the above convergence assumptions and considering

$ \lim\limits_{\mathcal{N}\to\infty} \frac{1}{\mathcal{N}}\!\sum\limits_{\omega=1}^\mathcal{N} \overline{M}_N(t, \omega)=0,$

we may expect that the ensemble average of the stochastic equation (34) tends in its strong form to the same equation of Fokker-Planck type as (30):

$ $$\begin{array}{l} \frac{\partial}{\partial t} p(t,\mathbf{x},\mathbf{v})\!&=&\! \frac{\alpha_1C(t,\mathbf{x})}{C_R+C(t,\mathbf{x})}\, p(t,\mathbf{x},\mathbf{v})\delta_{\mathbf{v}_0}(\mathbf{v}) \nonumber\\ &-& \gamma p(t,\mathbf{x},\mathbf{v}) \int_0^t \tilde{p}(s,\mathbf{x})\, ds - \mathbf{v}\cdot \nabla_x p(t,\mathbf{x},\mathbf{v}) \nonumber\\ &+& k \nabla_v \cdot [\mathbf{v} p(t,\mathbf{x},\mathbf{v})] - d_1\nabla_v \cdot \left[\frac{\nabla_x C(t,\mathbf{x})}{[1+\gamma_1C(t,\mathbf{x})]^q}\, p(t,\mathbf{x},\mathbf{v}) \right]\! \nonumber\\ &+& \frac{\sigma^2}{2} \Delta_{v} p(t,\mathbf{x},\mathbf{v}). \end{array}$$ $

(41)

Here the marginal vessel tip density,

$ \tilde{p}(t,\mathbf{x}) = \int p(t,\mathbf{x},\mathbf{v}')\, d\mathbf{v}',\label{eq19} $

(42)

is the marginal density of $p(t,\mathbf{x},\mathbf{v})$. As an additional consequence of the above, Equation (41) for $p(t,\mathbf{x},\mathbf{v})$ is coupled with a deterministic reaction-diffusion equation for the TAF concentration,

$ \frac{\partial}{\partial t}C(t,\mathbf{x})=d_2 \Delta_x C(t,\mathbf{x})- \eta\, C(t,\mathbf{x})\!\left| \mathbf{j}(t,\mathbf{x})\right|\!,\label{eq20} $

(43)

where $\mathbf{j}(t,\mathbf{x})$ is the ensemble-averaged current density (flux) vector at any point $\mathbf{x}$ and any time $t\geq 0$,

$ \mathbf{j}(t,\mathbf{x})= \int \mathbf{v}' p(t,\mathbf{x},\mathbf{v}')\, d \mathbf{v'}. \label{eq21} $

(44)

A crucial point in the derivation of (41) as the ensemble average of Equation (34) is the approximation of nonlinear terms in the latter, e.g. the anastomosis term. Had the law of large numbers been applicable (on the single replica, according to the propagation of chaos assumption), the mean values of nonlinear terms could be factorized. With the ensemble average description, factorization of nonlinear terms requires further investigation, and this is out of the scope of the present paper. By assuming factorization occurs, we may expect that the ensemble average of Equation (34) tends in its strong form to (41).

By an abuse of notations, we are using in Equation (43) the same letter $C$ for the deterministic counterpart of the TAF field, too.

We need to stress here that the $p(t,\mathbf{x}, \mathbf{v})$ appearing in Equation (30) represents a scaled density in phase space, the integral of which over the whole phase space is $N(t)/N$, where $N(t)$ is the mean number of tips at time $t$. This number coincides with the number of tips in a single realization of our supposed self-averaging stochastic process. In contrast to this, the $p(t,\mathbf{x}, \mathbf{v})$ appearing in Equation (41) represents the true concentration per unit volume of phase space.

For appropriate initial and boundary data, it is possible to prove that (41) and (43) have a unique smooth solution [16].

---

8.1. Boundary and initial conditions

We have solved the system of equations (41) and (43) in a two dimensional strip geometry using the initial and boundary conditions introduced in [4]. The strip is $\Omega=[0,L]\times\mathbb R \subset \mathbb R^2$, its left boundary $\Omega_0=(0,y)$, $y\in\mathbb R$, is the primary vessel issuing new vessels, and $\Omega_L=(L,y)$, $y\in\mathbb R$, represents the tumor which is a source of the TAF $C.$ Let $c_1(y)$ be the TAF flux emitted by the tumor at $x=L$. As boundary conditions for the TAF we have taken

$ $$\begin{array}{l} &\frac{\partial}{\partial x} C(t,0,y)=0, \frac{\partial}{\partial x} C(t,L,y)=\frac{c_1(y)}{d_2}, \end{array}$$ $

(45)

and $C\to 0$ as $|y|\to\infty$. We have used a Gaussian as the initial condition for the TAF

$ C(0,x,y)=1.1\, C_R e^{-[(x-L)^2/c^2+y^2/b^2]},\label{eq24} $

(46)

for appropriate $b$ and $c$.

As boundary conditions for the tip density we have taken

$ $$\begin{array}{l} & p^+(t,0,y,v,w) =\frac{e^{-\frac{k|\mathbf{v}-\mathbf{v}_0|^2}{\sigma^2}}}{\int_0^{\infty}\!\int_{-\infty}^{\infty} v' e^{-\frac{k|\mathbf{v}'-\mathbf{v}_0|^2}{\sigma^2}}dv'\,dw'} \nonumber \\ & \times\! \left[j_0(t,y)\! -\! \int_{-\infty}^0\!\int_{-\infty}^{\infty}\!\! v' p^-(t,0,y,v',w')d v' dw'\right]\!\!, \end{array}$$ $

(47)

$ $$\begin{array}{l} p^-(t,L,y,v,w)=\frac{e^{-\frac{k|\mathbf{v}-\mathbf{v}_0|^2}{\sigma^2}}}{\int_{-\infty}^0\!\int_{-\infty}^{\infty} e^{-\frac{k|\mathbf{v}'-\mathbf{v}_0|^2}{\sigma^2}}dv'\,dw'}\\ \times \!\left[\tilde{p}(t,L,y)\! -\!\int_0^{\infty}\!\!\int_{-\infty}^{\infty}\! p^+(t,L,y,v',w')dv' dw'\!\right]\!\!, \end{array}$$ $

(48)

$ p(t,\mathbf{x},\mathbf{v})\to 0 \mbox{ as } |\mathbf{v}|\to \infty, $

(49)

where $p^+=p$ for $v>0$ and $p^-=p$ for $v<0$, $\mathbf{v}=(v,w)$. These phenomenological conditions give the tip density for velocities entering the slab region in terms of the tip density for velocities exiting the slab region. They are constructed so that they give the marginal tip density at $x=L$ and the tip flux density at $x=0$, which is [4]

$ j_0(t,y)=\frac{v_0\, L}{\sqrt{v_0^2+w_0^2}}\alpha(C(t,0,y))\, p(t,0,y,v_0,w_0), \label{eq28} $

(50)

for the vector velocity $\mathbf{v}_0=(v_0,w_0)$. Improving the boundary conditions requires a separate and detailed work comparing stochastic and deterministic descriptions of the angiogenesis process.

Finally as initial condition for the tip density we have taken

$ $$\begin{array}{l} p(0,x,y,v,w)&=& \frac{2e^{-x^2/l_x^2}}{\pi^{3/2}l_x\sigma_v^2}\,e^{-|\mathbf{v}-\mathbf{v}_0|^2/\sigma_v^2} \sum\limits_{i=1}^{N_0}\frac{1}{\sqrt{\pi}l_y} e^{-|y-y_i|^2/l_y^2}. \end{array}$$ $

(51)

As $l_x$ and $l_y$ tend to zero, (51) becomes

$ p(0,x,y,\mathbf{v})\!=\! 2\delta^{\sigma_v}_{\mathbf{v}_0}(\mathbf{v})\delta_{0}(x)\sum\limits_{i=1}^{N_0}\delta_{y_i}(y),\label{eq30} $

(52)

where $\delta^{\sigma_v}_{\mathbf{v}_0}(\mathbf{v})$ is the mollified version of the usual Dirac delta by a Gaussian kernel. This initial condition corresponds to the following initial condition for the stochastic process: There are $N_0$ equally spaced initial tips at $x=0$, with vertical positions $y_i$ equally spaced on the interval $[-L_y,L_y]$, whose initial velocities are normally distributed about $\mathbf{v}_0$ with standard deviation $\sigma_v$.

---

9. Numerical results and comparison with the stochastic simulations

We have used the parameter values that have been extracted from experiments as explained in [4]. The anastomosis coefficient $\gamma$ had been given an arbitrary value in [4], whereas we estimate it here so as to get a good agreement between simulations of the stochastic equations and solutions of the deterministic equations (see [41]). We have suitably nondimensionalized the governing equations of our model, (41) and (43), according to the units given in [4], thereby obtaining

$ $$\begin{array}{l} \frac{\partial p}{\partial t} &=& \frac{A\, C}{1+C}p\, \delta_{\mathbf{v}_0}(\mathbf{v}) - \Gamma p\! \int_0^t \tilde{p}(s,\mathbf{x})\, ds - \mathbf{v}\cdot \nabla_x p \nonumber\\&-& \nabla_v \cdot\left[\!\left(\frac{\delta\, \nabla_x C}{(1+\Gamma_1C)^q}-\beta\mathbf{v}\right)\! p\right] +\frac{\beta}{2}\, \Delta_{v} p, \end{array}$$ $

(53)

$ $$\begin{array}{l} \frac{\partial C}{\partial t} &=& \kappa\, \Delta_x C - \chi\, C\, |\mathbf{j}| . \end{array}$$ $

(54)

The dimensionless parameters appearing in these equations are defined in Table 1 (see [4], [41]). In the computations for the generalized function $\delta_{\mathbf{v_0}}(\mathbf{v})$ that appears in (53) we have used the mollified version $\delta_{v}(\mathbf{v})$ with $\sigma_v^2=\sigma^2\epsilon^2/k$ in (52) as the variance in the Gaussian mollifying kernel, and obtained the nondimensional function,

$ \delta_{v}(\mathbf{v})= \frac{1}{\pi\epsilon^2}e^{-|\mathbf{v}|^2/\epsilon^2}. \label{eq33} $

(55)

We have used $\epsilon = 0.08$ in the numerical simulations.

The nondimensional boundary conditions for $C$ are

$ \frac{\partial C}{\partial x}(t,0,y)=0, \frac{\partial C}{\partial x}(t,1,y)=f(y), \, \lim\limits_{y\to\pm\infty}C= 0, \label{eq34} $

(56)

where $f(y)=L\, c_1(Ly)/(C_Rd_2)$ is a nondimensional flux, following from (45). We have used $c_1(y)=a\, e^{-y^2/b^2}$, with $a=5.5\times 10^{-27}$ mol/(ms), $d_2=10^{-13}$ m$^2$/s, and $b=0.6$ mm ($b$ is about half the assumed tumor size). The initial condition for the TAF (46) yields

$ C(0,x,y)=1.1\, e^{-[(x-1)^2L^2/c^2+y^2L^2/b^2]},\label{eq35} $

(57)

with $b/L=0.3$, $c/L=1.5$, whereas the nondimensional initial vessel density is

$ $$\begin{array}{l} p(0,x,y,v,w)&=& \frac{2 L e^{-x^2 L^2/l_x^2}}{\pi^{3/2}l_x\,\epsilon^2}\,e^{-|\mathbf{v}-\mathbf{v}_0|^2/\sigma_v^2} \sum\limits_{i=1}^{N_0}\frac{L}{\sqrt{\pi}l_y} e^{-|y-y_i|^2 L^2/l_y^2}, \end{array}$$ $

(58)

with $l_x/L=0.06$ and $l_y/L=0.08$, that corresponds to $N_0=20$ initial vessel tips. In nondimensional form, the boundary conditions (47)-(48) for $p$ become

$ $$\begin{array}{l} p^+(t,0,y,v,w) =\frac{e^{-|\mathbf{v}-\mathbf{v}_0|^2}}{\int_0^{\infty}\!\int_{-\infty}^{\infty} v' e^{-|\mathbf{v}'-\mathbf{v}_0|^2} dv'\,dw'} \\ \times\! \left[j_0(t,y)\! -\! \int_{-\infty}^0\!\int_{-\infty}^{\infty}\!\! v' p^-(t,0,y,v',w')d v' dw'\right]\! \end{array}$$ $

(59)

for $x=0$ and $v>0,$

$ $$\begin{array}{l} &p^-(t,1,y,v,w)=\frac{e^{-|\mathbf{v}-\mathbf{v}_0|^2}}{\int_{-\infty}^0\!\int_{-\infty}^{\infty} e^{-|\mathbf{v}'-\mathbf{v}_0|^2}dv'\,dw'} \nonumber\\ & \times \!\left[\tilde{p}(t,1,y)\! -\! \int_0^{\infty}\!\!\int_{-\infty}^{\infty}\! p^+(t,1,y,v',w')dv' dw'\right]\! \end{array}$$ $

(60)

for $x=1$ and $v<0$. Eq. (50) produces the nondimensional flux $j_0$:

$ j_0(t,y)=A\, v_0\frac{C}{1+C}\, p(t,0,y,v_0,w_0) \label{eq39} $

(61)

($\sqrt{v_0^2+w_0^2}=|\mathbf{v}_0|^2=1$ in nondimensional units).

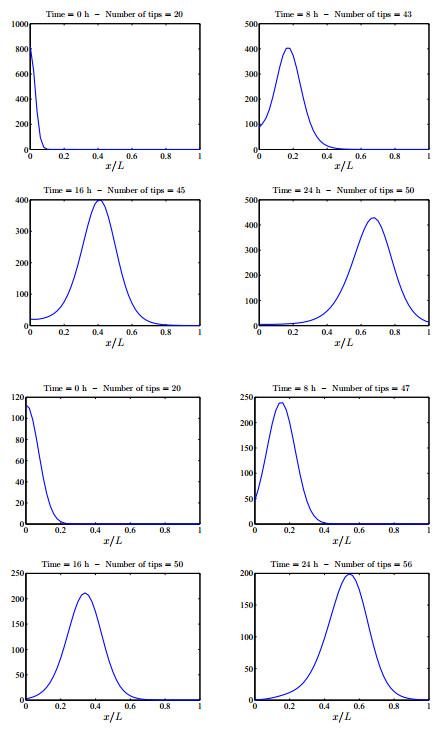
In [4], we have shown the consistency of the deterministic model by depicting TAF concentration, marginal tip density and overall network density at different times. Figure 3 shows that the marginal tip density obtained by numerically solving the deterministic equations (53)-(61) agrees quite well with the ensemble average over 50 replicas of the stochastic process depicted in Figure 2.

Figure 4 compares the deterministic and averaged stochastic descriptions of the marginal tip density at the $x$ axis, $\tilde{p}(t,x,y=0)$. The marginal density of the vessel tips advances as a lump toward the tumor at $x=L$, and its projection onto the $x$ axis is a moving pulse. While both descriptions agree qualitatively, there are quantitative discrepancies: the pulse maximum is larger for the solution of the deterministic equations. The agreement improves by increasing the number of replicas and fine-tuning the anastomosis coefficient $\Gamma$ as done in [41]. The value given in Table 1, $\Gamma=0.145$, produces the best agreement between the integer part of $\int\tilde{p}(t,\mathbf{x})\, d\mathbf{x}$ calculated by solving the deterministic equations and by ensemble averages of the stochastic process [41].

---

10. Conclusions

In our recent papers [4] and [41] we have explored the behavior of a stochastic angiogenesis model, and of its possible deterministic approximation. In this model, the tips undergo a stochastic process of tip branching, vessel extension and anastomosis whereas TAF is described by a reaction-diffusion equation with a sink term proportional to the tip flow.

In [4] the empirical measure describing the tip distribution had been assumed to satisfy a "law of large numbers" for any single replica of the process, i. e. the classical "propagation of chaos" assumption (see e.g. [40], and references therein), so that it admits a position-velocity density which is shown to satisfy a nonlinear integro-differential equation of a Fokker-Planck type, coupled with a reaction-diffusion equation for the TAF concentration, in which the stochastic tip flow has been replaced by its mean field approximation, deriving from the tip mean density.

On the other hand, in [41] we have solved numerically the stochastic model for many realizations (independent replicas of the system). Numerically calculated velocity fluctuations have revealed that they do not decay even as the number of initial vessel tips increases. This shows that the stochastic model is not self-averaging and therefore we cannot use the "propagation of chaos" assumption to derive a mean field deterministic approximation of the stochastic model. The main reason being that anastomosis eliminates many vessel tips, resulting in the fact that there never are enough tips for a law of large numbers apply on a single replica. The vessel network has shown to be quite different for different replicas of the stochastic process.

However by re-examining the derivation given in [4], we conclude that the same deterministic description holds for vessel tip densities calculated by averaging over replicas. The deterministic description consists of a reaction-diffusion equation for the TAF concentration coupled to a Fokker-Planck type equation for the vessel tip density. The latter contains a birth term corresponding to tip branching and a death integral term corresponding to anastomosis or tip merging. The coefficient of the latter term has been fitted by comparison with the stochastic description: optimal selection produces a good fit for the evolution of the total number of tips.

For the averaged deterministic reaction-diffusion system, boundary conditions have been proposed in [41], which describe the flux of vessel tips injected from a primary blood vessel in response to TAF emitted by the tumor and the tip density eventually arriving at the tumor. Numerical solution of the model in a simple geometry shows how tips are created at the primary blood vessel, propagate and proliferate towards the tumor and may or not reach it after a certain time depending on the parameter values. This is consistent with known biological facts.

Actually nontrivial additional investigation is required for a rigorous derivation of the deterministic approximation of the relevant empirical measures and their evolution equations. Anyhow we wish to convey a general message elicited by the proposed angiogenesis model: in stochastic models containing birth and death processes in addition to Brownian motion (Langevin equations), the death processes may preclude reaching the large number of individuals required to have self-averaging and a deterministic description based on the "propagation of chaos". Nevertheless, deterministic equations for macroscopic densities and fluxes may follow from using ensemble averages over a large number of replicas.

The significant consequence concerns the variance; though the mean behavior can be described by the same PDE, the case of self-averaging does not carry any variance; but the variance cannot be ignored in the case of ensemble averaging, which implies the use of confidence bands in predicting the evolution of a real vessel network! The authors are well aware of the limits of their own analysis, but they wish to stimulate more attention to the mathematical issues raised by this important biomedical problem. Only accurate models can support medical intervention for prevention and cure. Simulations are surely useful as a first insight, but therapies (optimal control) require accurate mathematical models, validated by comparison with real data (inverse problems -statistics of random geometric structures).

Apart from the specific application we have been dealing with, in this paper methodological contributions have been given for a sound mathematical modelling of stochastic vessel networks: a) the use of stochastic distributions, and their mean densities, describing the vessels -random objects of Hausdorff dimension $1;$ b) reduction of vessel distributions to integrals over time of tip distributions -random objects of Hausdorff dimension $0;$ c) use of a Langevin model for vessel extensions, thus leading to the required regularity for the existence of vessel mean densities [1].

---

Acknowledgments

The authors acknowledge the contribution of the anonymous Referees for a significant improvement of the manuscript. This work has been supported by the Spanish Ministerio de Economí a y Competitividad grant MTM2014-56948-C2-2-P. VC has been supported by a Chair of Excellence UC3M-Santander at the Universidad Carlos Ⅲ de Madrid. It is a great pleasure to acknowledge fruitful discussions with Daniela Morale of the Department of Mathematics of the University of Milan.

---