1. Introduction

In this paper, we estimate the connectedness of the Italian banking system through in- and out-of-sample dynamic of the set of measures introduced in Diebold and Yilmaz(2009, 2012, 2014, 2015) and further developed in Gätjen and Schienle (2015). This method aims to assess the existence and to measure any spill-overs between different banks through the recursive, rolling window application of forecast error variance decomposition in a general, flexible vector autoregressive (VAR) framework. Such a variance decomposition is defined in Lütkepohl (2005) as "the proportion of the H-step forecast error variance of variable i accounted for by innovations in variable j". Given two variables of interest i and j, the more variable j affects the forecast error variance of variable i, the more we consider the former to be connected to the latter. Specifically, in our application the variables of interest are the (logarithms of) the daily variances of the share price of pairs of financial institutions.¹

¹ As suggested in Diebold and Yilmaz(2014, 2016), we choose as the reference variable for our model the logarithm the intraday share price volatility of each bank and apply a generalized variance decomposition following the seminal work by Koop, Pesaran, and Potter (1996) and Pesaran and Shin (1998). The underlying assumption is that the stock market is informationally efficient and the public information about the connectedness between financial institutions is incorporated in the stock price. Moreover, the logarithmic transformation helps ensure that at least in approximate terms the majority of the variables follows an approximate marginal normal distribution, which is in principle required by the variance decomposition technology.

The empirical application to the Italian banking system turns out to be particularly interesting; indeed, despite the systemic, global threats that it would pose to the rest of the World have been largely debated by financial commentators (see e.g., Davies, 2017; Friedman, 2016; The Economist, 2016), there is limited academic literature that explores the interconnectedness of the Italian banks. For instance, Gropp and Moerman (2014) examine contagion in a sample of 67 large European banks (including all major Italian banks) aiming to identify systematically important financial institutions. Betz et al. (2016) analyze a sample of 51 European banks to show how banking sector fragmentation and sovereign-bank linkages evolved over the European sovereign debt crisis. With reference to network measures of systemic risk in the Italian banking system, Borri et al. (2014) have proposed to use differential CoVaR to measure the contribution of each bank to the overall VaR of the financial system when that bank is in a state of distress. Di Biase and D'Apolito (2012) find regression evidence based on bank stock betas consistent with the fact that the systemic risk of Italian banks would grow with their size but not with leverage. However, in contrast to ours, none of these papers adopts an explicit network VAR decomposition approach.

Beside the relevant empirical application, our goal is to perform a comparison of two alternative methodologies to infer network connectedness from VAR models. In fact, we derive connectedness measures using both the in-sample estimation first proposed by Diebold and Yilmaz(2014, 2015) and the out-of-sample approach of Gätjen and Schienle (2015), under a range of VAR(p) specifications. Similarly to earlier literature, we implement a dynamic version of the two methods based on a one-sided rolling window estimation/forecasting approach. Moreover, we proceed to carefully test the significance of each of the two measures by bootstrapping the test distributions under the null hypothesis of absence of connectedness. Because the application of sequential testing to time series of spill-over measures based on a rolling window scheme complicates the distribution of the test statistics (even when they are bootstrapped) because the sample test statistics are based on overlapping data, we also apply recent methods appropriate to sequential p-values to control the false discovery rate. Finally, in order to assess the differential reliability of the two types—in- vs. out-of-sample—connectedness measures, we also (rank) correlate them with a range of five additional measures of connectedness and systemic risk, including the well-known Marginal Expected Shortfall, CoVaR, and change in CoVar measures.²

² Systemic risk shall be defined as the risk of collapse of the entire financial system, triggered by the default of one, or more, interconnected financial institutions.

We find three key results. First and foremost, as far gross connectedness measures are concerned, adopting in- or out-of-sample measures makes no substantial or qualitative difference in terms of resulting economic implications. Even though in general the out-of-sample measures tend to be higher than the in-sample ones, their dynamics is strikingly similar. This result partially differs from Gätjen and Schienle's (2015), who, however, study contagion and spill-over in the European sovereign market. Second, yet we find more important differences in the empirical implications of in- vs. out-of-sample measures when these are applied to estimate net network connectedness. Indeed, even modest differences in gross measures seem (they do not necessarily have) to compound in non-negligible divergences in net measures. Third, and this appears in line with the existing limited empirical evidence (see e.g., Betz et al., 2016), the Italian banking system is characterized by a substantial degree of connectedness which makes it prone to contagion and systemic crisis. The highest gross connectedness scores concern the largest banks that are especially inclined to export variance to the other smaller banks, but also appear to be rather susceptible to shocks coming from all other banks under examination. Interestingly, under in-sample variance decomposition, we obtain evidence that no Italian bank is consistently exporting or importing volatility on a net basis and appears to be producing a negative externality or to bear the costs of systemic risk. In contrast, when we adopt the out-of-sample method, we find that there may be a few large, net exporters of volatility among Italian banks, that should be on the top of the list of supervised and regulated banks (at the European level, one may add, in the light of the global importance of the Italian banking system).³

³ Our focus on Italian banks in isolation from global influences finds justification in recent results by Demirer, Diebod, Liu, and Yilmaz (2018) who study global network connectedness by addressing the dimensionality problem in standard VAR-based analysis applied to 150 important banks globally, using Least Absolute Shrinkage and Selection Operator (LASSO) methods. Over a 2004–2014 sample, they find that banks' connectedness has a strong geographical component and that this increases during crises. Also, Italian banks have long been mostly dependent upon domestic funding sources; additionally, after the subprime mortgage crisis, the banking sectors in the Euro Area considerably reduced their degree of cross-border integration. Betz et al. (2016) report a similar finding using a rather different method.

There is an ever-expanding literature on measuring and testing network connectedness with the aim of controlling and managing potential network spillover risks. In a series of papers, Diebold and Yilmaz(2009, 2012, 2014, 2016) show how VAR models and the associated variance decompositions may be used—under a variety of identification schemes of structural shocks—as tools to produce variance contribution matrices that are informative on network structure. Diebold and Yilmaz (2015) show that such methods are equivalent to classical empirical (directed) network methods and concepts (for instance based on the notion of nodes, degrees, and distance among nodes), when the adjacency matrix is identified with the matrix of bilateral variance decompositions. We contribute to this literature by providing an additional application and especially by performing a comparison between in-sample and out-of-sample forecast error-based variance decompositions.⁴

⁴ It could be also interesting to incorporate in the analysis other markets/asset classes. For instance, Fengler and Gisler (2015) evaluate the relevance of covariances in the transmission mechanism of spillovers across US stock, bond, and gold markets, in the period July 2003–December 2012. They adapt Diebold and Yilmaz's forecast-error variance decomposition methods by incorporating covariances into the VAR measurement of variance spillovers.

Of course, other approaches to the empirical estimation of network structure would have been possible. For instance, there is a growing literature based on Bayesian graphs that has addressed the same issues in our paper. Ahelegbey et al. (2016) apply a Bayesian graph-based MCMC approach to identification in structural VARs applied to systemic risk and report evidence of strong, unidirectional linkages from financial to non-financial super-sectors in the Eurozone from the 2007–2009 financial crisis but of bi-directional linkages during the 2010–2013 European sovereign debt crisis.

There are also other strands of literature that have used a variety of methods to jointly assess the existence of spillovers and network effects among banks and sovereign debt. For instance, Alter and Beyer (2015) assess the dynamics of financial contagion among sovereigns and banks using medium-size VARs with exogenous common factors that account for common global and regional trends. They report that the strength of contagion fluctuated within a stable interval between October 2009 and July 2012 but the components from banks-to-sovereigns and sovereigns-to-banks increased signaling an intensifying feedback loop between euro area banks and sovereigns. Betz et al. (2016) stress that for regulatory purposes, network dependencies in extreme risks are more relevant than simple correlations. This requires focusing on connections between time-varying tails, as, e.g., represented by conditional quantiles. They quantify the systemic impact of an individual bank with the marginal effect of its Value-at-Risk (VaR) on the VaR of the system, giving rise to an estimated risk network. They report that the density of the tail dependence network based on equity prices increased after 2006 peaking around the height of the global financial crisis and significantly declined thereafter. However, during the European debt crisis in 2011–2012, the markets were characterized by increased interconnectedness between sovereigns and banks and fragmented along national borders as reflected by a strong increase of within-country linkages, which are more pronounced for countries engulfed by the sovereign crisis, like Italy.

The rest of the paper is structured as follows. Section 2 reviews the key elements of our VAR/variance decomposition-based methodologies and compares the key choice that is tested in our paper, i.e., in-sample vs. out-of-sample variance decompositions. Moreover, a number of innovative methods geared towards testing the statistical significance of the estimated connectedness measures are developed that can keep track of the inferential problems created by the sequential nature of the measures estimated in this paper, such as the false discovery rate. A few benchmarks useful to assess the economic meaning and significance of our connectedness measures are also defined. Section 3 presents the data and summary statistics. Section 4 contains our novel empirical results and it is organized along two axes: First, the comparison between the estimates and economic plausibility of connectedness measured estimates on in-sample vs. out-of-sample variance decompositions; second, the key empirical insights we derive on the state and nature of the Italian banking system. Section 5 concludes.

---

2. Methodology

---

2.1. Definition of the connectedness measures

We follow Diebold and Yilmaz (2014) in defining the connectedness measures that we shall analyze in this paper. If we denote the proportion of the H-step ahead forecast error variance of a variable ${{x}_{i, t}}$ explained by the innovations in the variable ${{x}_{j, t}}$ by $\tilde{d}_{i, j}^{H}$, we can arrange such variance decomposition terms/effects into a $N\times N$ variance decomposition matrix ${{\mathit{\boldsymbol{\tilde D}}}^H} \equiv \left[ {\tilde d_{i, j}^H} \right]$, where N is the number of variables under investigation. The matrix ${{\mathit{\boldsymbol{\tilde D}}}^H}$ defined in this way, is not symmetric, which means that the connectedness $\tilde d_{j, i}^H$ from ${x_{j, t}}$ to ${x_{i, t}}$ is in general different from the connectedness $\tilde d_{i, j}^H$ from ${x_{i, t}}$ to ${x_{j, t}}$. The main advantage of this pairwise directional connectedness measure is that, for each variable, we can distinguish the connectedness arising from the other variables and reflected by the variable, from its connectedness transmitted to the other variables. We thus define the connectedness "from-others" for the ith variable as:

$C_{FROM, i}^H = \mathop \sum_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^N \tilde d_{i, j}^H,$

(1)

which is the total proportion of the forecast error variance not explained by innovations to the ith variable itself. In turn, we define the connectedness "to-others" for the jth variable as:

$C_{TO, j}^H \equiv \mathop \sum_{\begin{array}{*{20}{c}} {i = 1}\\ {i \ne j} \end{array}}^N \tilde d_{i, j}^H$

(2)

These two measures are the sums by row and by column, respectively, of the elements in ${{\mathit{\boldsymbol{\tilde D}}}^H}$ without considering its main diagonal. In a similar way, we define the net connectedness for the ith variable as:

$C_{NET, i}^H = C_{TO, i}^H - C_{FROM, i}^H,$

(3)

which measures its connectedness to the other variables net of the connectedness from the other variables. Lastly, we define total connectedness as:

$C_{TOTAL}^H = \frac{1}{N}\mathop \sum_{\begin{array}{*{20}{c}} {i, j = 1}\\ {i \ne j} \end{array}}^N \tilde d_{i, j}^H = \frac{1}{N}\mathop \sum_{i = 1}^N C_{FROM, i}^H = \frac{1}{N}\mathop \sum_{i = 1}^N C_{TO, i}^H$

(4)

with the objective of measuring the overall connection between the N variables under investigation.

---

2.2. In-sample variance decomposition

The in-sample variance decomposition method is based on the generalized impulse function of Pesaran and Shin (1998). Similarly to Diebold and Yilmaz(2014, 2016), the generalized error variance decomposition is preferred over a standard Cholesky-factor decomposition because it is independent from the ordering of the variables. Consider a vector stochastic process $\left\{ {{\mathit{\boldsymbol{x}}_t}} \right\}$ of N random variables which follows a vector autoregressive model of order p:

${\mathit{\boldsymbol{x}}_t} = \mathop \sum_{i = 1}^p {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_{t - i}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_t} + {\mathit{\boldsymbol{\varepsilon }}_t}, t = 1, 2, \ldots, T,$

(5)

where ${\mathit{\boldsymbol{w}}_t}$ is a $q \times 1$ vector of deterministic variables, ${\mathit{\boldsymbol{A}}_i}$ and B are $N \times N$ and $N \times q$ coefficient matrices, and ${\mathit{\boldsymbol{\varepsilon }}_t}$ is a N-dimensional innovation process with $E\left({{\varepsilon _t}} \right) = \mathit{\boldsymbol{0}}$, $E\left({{\mathit{\boldsymbol{\varepsilon }}_t}\mathit{\boldsymbol{\varepsilon }}_t'} \right) = {\bf{\Sigma }}_\varepsilon ^{IS}$ and $E\left({{\mathit{\boldsymbol{\varepsilon }}_t}|{\mathit{\boldsymbol{w}}_t}} \right) = \mathit{\boldsymbol{0}}$ for ∀t, $E\left({{\mathit{\boldsymbol{\varepsilon }}_t}\mathit{\boldsymbol{\varepsilon }}_{t'}'} \right) = \mathit{\boldsymbol{O}}$ for $t \ne t'$. Assuming that the process in 5 is covariance stationary, the VAR(p) model in 5 can be expressed as an infinite-order vector moving average process⁵:

⁵ This is equivalent to assume that the roots of det (${I_N} - \mathop \sum_{i = 1}^p {\mathit{\boldsymbol{A}}_i}{z^i}) = 0$ fall outside the unit circle, see Guidolin and Pedio (2018) for details.

${\mathit{\boldsymbol{x}}_t} = \mathop \sum_{i = 0}^\infty {{\bf{\Phi }}_i}{\mathit{\boldsymbol{\varepsilon }}_{t - i}} + \mathop \sum_{i = 0}^\infty {{\bf{\Phi }}_i}\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_{t - i}}, t = 1, 2, \ldots, T$

(6)

where the sequence of coefficient matrices Φ_i can be recursively calculated as:

${{\bf{\Phi }}_i} = 0ifi < 0, {{\bf{\Phi }}_0} = {\mathit{\boldsymbol{I}}_N}, {{\bf{\Phi }}_i} = \mathop \sum_{l = 1}^p {\mathit{\boldsymbol{A}}_l}{{\bf{\Phi }}_{i - l}}$

(7)

Given 6, Pesaran and Shin (1998) derive the fraction of the H-step ahead general forecast error variance of the ith variable explained by innovations in the jth variable as:

$d_{ij}^{IS, H} = \frac{{{{\left({\sigma _{jj}^{IS}} \right)}^{ - 1}}\mathop \sum \nolimits_{l = 0}^{H - 1} {{\left({\mathit{\boldsymbol{e}}_i'{{\bf{\Phi }}_l}{\bf{\Sigma }}_\varepsilon ^{IS}{\mathit{\boldsymbol{e}}_j}} \right)}^2}}}{{\mathop \sum \nolimits_{l = 0}^{H - 1} \left({\mathit{\boldsymbol{e}}_i'{{\bf{\Phi }}_l}{\bf{\Sigma }}_\varepsilon ^{IS}{\bf{\Phi }}_l'{\mathit{\boldsymbol{e}}_i}} \right)}}$

(8)

Where e_i is the column vector with ith element equal to 1 and 0 otherwise, Φ_l are the coefficient matrices in 6, ${\bf{\Sigma }}_\varepsilon ^{IS}$ is the covariance matrix of innovations in 5 and $\sigma _{jj}^{IS}$ is the jth element on the diagonal of ${\bf{\Sigma }}_\varepsilon ^{IS}$. As the innovations are not orthogonal and the sum of the contributions to forecast error variance by the ith variable is not 1, in the in-sample variance decomposition matrix ${{\mathit{\boldsymbol{\tilde D}}}^{IS, H}}$, in what follows we shall use a $\tilde d_{i, j}^{IS, H}$ re-scaled as:

$\tilde d_{ij}^{IS, H} \equiv \frac{{d_{ij}^{IS, H}}}{{\mathop \sum \nolimits_{j = 1}^N d_{ij}^{IS, H}}}$

(9)

so that $\mathop \sum_{i = 1}^N \tilde d_{ij}^{IS, H} = 1$ and $\mathop \sum_{i, j = 1}^N \tilde d_{ij}^{IS, H} = N$ by construction.

---

2.3. Out-of-sample variance decomposition

Gätjen and Schienle (2015) propose a modification of 8 in which the variance decomposition is based on the out-of-sample (OOS) forecast error variance, rather than the in-sample forecast error variance as in Diebold and Yilmaz (2014). Given the VAR(p) in 5 and under the same assumptions on the N-dimensional innovation process ${\mathit{\boldsymbol{\varepsilon }}_t}$ introduced before, we define the OOS, H-step ahead forecast error variance-covariance matrix as:

${{\bf{\Sigma }}^{OOS, H}} = E\left[ {\left({{\mathit{\boldsymbol{x}}_{t + H}} - {{\mathit{\boldsymbol{\hat x}}}_{t + H|t}}} \right){{\left({{\mathit{\boldsymbol{x}}_{t + H}} - {{\mathit{\boldsymbol{\hat x}}}_{t + H|t}}} \right)}'}} \right],$

(10)

where ${{\mathit{\boldsymbol{\hat x}}}_{t + H|t}}$ is the minimum mean square error (MSE) forecast of ${\mathit{\boldsymbol{x}}_{t + H}}$ conditional on information up to t. Thus, the proportion of the out-of-sample, H-step ahead forecast error variance of the ith variable explained by innovations in the jth variable may be defined as:

$d_{ij}^{OOS, H} = \frac{{{{\left({\mathit{\boldsymbol{e}}_i'{{\bf{\Sigma }}^{OOS, H}}{\mathit{\boldsymbol{e}}_j}} \right)}^2}}}{{\left({\mathit{\boldsymbol{e}}_i'{{\bf{\Sigma }}^{OOS, H}}{\mathit{\boldsymbol{e}}_i}} \right)\left({\mathit{\boldsymbol{e}}_j'{{\bf{\Sigma }}^{OOS, H}}{\mathit{\boldsymbol{e}}_j}} \right)}}$

(11)

As before, in the OOS variance decomposition matrix ${{\mathit{\boldsymbol{\tilde D}}}^{OOS, H}}$, we use a re-scaled version of 11 calculated as:

$\tilde d_{ij}^{OOS, H} \equiv \frac{{d_{ij}^{OOS, H}}}{{\mathop \sum \nolimits_{j = 1}^N d_{ij}^{OOS, H}}}$

(12)

so that $\mathop \sum_{i = 1}^N \tilde d_{ij}^{OOS, H} = 1$ and $\mathop \sum_{i, j = 1}^N \tilde d_{ij}^{OOS, H} = N$, by construction.

---

2.4. The estimation of the connectedness measures

We follow Diebold and Yilmaz (2014) and focus our analysis on a predictive horizon of H = 12 days, which seems economically meaningful to traders and also supervisory authorities in the context of episodes of panic and contagion. As we keep this parameter fixed throughout the entire paper, we omit the H superscript in the subsequent notation. To obtain robust results, we use two different VAR(p) specifications with different deterministic variables, ${\mathit{\boldsymbol{w}}_t}$: We will refer to the model with a constant term ${w_t} = \left[ 1 \right]$ as the VAR_C(p) and to the model with both a constant and a linear trend ${\mathit{\boldsymbol{w}}_t} = {\left[ {\begin{array}{*{20}{c}} 1&t \end{array}} \right]'}$ as the VAR_CT(p). To account for time-varying parameters and, most importantly, time-varying connectedness, we estimate the connectedness measures using a one-sided rolling window of length ${T_C}$. As in Diebold and Yilmaz(2014, 2016), we use the observations ${\mathit{\boldsymbol{x}}_t}$, $t = \tau - {T_C} + 1, \ldots, \tau$ to estimate the parameters of model 5 by standard OLS, given that the model is unrestricted. The estimated values ${{\mathit{\boldsymbol{\hat A}}}_{i, \tau }}$ (i = 1, 2, …, p) and ${\bf{\hat \Sigma }}_{\varepsilon, \tau }^{IS}$ are used in equations 7–9 to obtain the in-sample variance decomposition matrix $\mathit{\boldsymbol{\tilde D}}_\tau ^{IS}$ at time $\tau$ and the respective in-sample connectedness measures at time $\tau$, as defined in 1–4. In the case of the out-of-sample connectedness, we employ two one-sided rolling windows as in Gätjen and Schienle (2015):

1. The first is a window of length ${T_M}$ used to estimate the VAR(p) model in 5 by OLS using observations ${\mathit{\boldsymbol{x}}_t}$, $t = \tau - {T_M} + 1, \ldots, \tau$ to obtain the time series of the minimum MSE estimator ${{\mathit{\boldsymbol{\hat x}}}_{\tau + H|\tau }}$;

2. The second window of length ${T_C}$ is used to estimate the out-of-sample H-step ahead forecast error covariance matrix:

${\bf{\hat \Sigma }}_\tau ^{OOS} = \frac{1}{{{T_C}}}\mathop \sum_{t = \tau - {T_C} - H + 1}^{\tau - H} \left[ {\left({\left({{\mathit{\boldsymbol{x}}_{t + H}} - {{\mathit{\boldsymbol{\hat x}}}_{t + H|t}}} \right){{\left({{\mathit{\boldsymbol{x}}_{t + H}} - {{\mathit{\boldsymbol{\hat x}}}_{t + H|t}}} \right)}'}} \right)} \right]$

(13)

The estimator ${\bf{\hat \Sigma }}_\tau ^{OOS}$ is then used in 11–12 to obtain the OOS variance decomposition matrix $\mathit{\boldsymbol{\tilde D}}_\tau ^{OOS}$ at time $\tau$ and the corresponding OOS connectedness measures at time $\tau$ defined as in equations 1–4. Both procedures are applied to both the VAR_C(p) and the VAR_CT(p) specifications. We set ${T_C} = 200$ days and ${T_M} = 200$ days as in Gätjen and Schienle (2015). The lag order p in the VAR(p) models is chosen for each rolling window by minimization of the Akaike Information Criterion, which in any event, always determined p = 1 as the optimal selection for all the applications that we present.

---

2.5. Testing the statistical significance of the connectedness measures

We are interested in assessing the significance of the connectedness measures in order to perform meaningful comparisons between different methodological specifications, across different financial institutions, and over time. In particular, we aim at testing the null hypothesis of the absence of connectedness between the N realized volatility series whose dynamics shall be jointly modelled in 5. To limit the number of assumptions under which we conduct the tests, we do not impose any distribution on the innovations ${\mathit{\boldsymbol{\varepsilon }}_t}$ under the null hypothesis. We use instead a parametric, residual-based bootstrap as in Mackinnon (2009) to determine p-values of our tests. Because the in- and out-of-sample connectedness measures are formulated differently, the associated null hypotheses and bootstrapping procedures are different. However, the underlying intuition is that, in absence of connectedness, each variable follows a univariate autoregressive process of order p and is unaffected by either the realized values or the innovations of the other variables.

In the case of in-sample connectedness, the null hypothesis is based on 5 as follows:

$\left\{ {\begin{array}{*{20}{c}} {H_0^{IS}:}&{\forall i \Rightarrow {\mathit{\boldsymbol{A}}_i} = \mathit{\boldsymbol{A}}_i^0 \wedge {\bf{\Sigma }}_\varepsilon ^{IS} = {\bf{\Sigma }}_\varepsilon ^{0, IS}}\\ {H_a^{IS}:}&{\exists i \Rightarrow {\mathit{\boldsymbol{A}}_i} \ne \mathit{\boldsymbol{A}}_i^0 \vee {\bf{\Sigma }}_\varepsilon ^{IS} \ne {\bf{\Sigma }}_\varepsilon ^{0, IS}} \end{array}} \right.,$

(14)

where $i \in \left\{ {1, 2, \ldots, p} \right\}$ and $\mathit{\boldsymbol{A}}_i^0$ and ${\bf{\Sigma }}_\varepsilon ^{0, IS}$ are diagonal matrices. A valid bootstrapping procedure is illustrated in Appendix A. In the case of out-of-sample connectedness, the null hypothesis must be broadened to also include ${{\bf{\Sigma }}^{OOS, H}}$, on the basis of which we calculate the OOS variance decomposition matrix:

$\left\{ {\begin{array}{*{20}{c}} {H_0^{OS}:}&{\forall i \Rightarrow {\mathit{\boldsymbol{A}}_i} = \mathit{\boldsymbol{A}}_i^0 \wedge {\bf{\Sigma }}_\varepsilon ^{IS} = {\bf{\Sigma }}_\varepsilon ^{0, IS} \wedge {{\bf{\Sigma }}^{OOS}} = {{\bf{\Sigma }}^{0, OOS}}}\\ {H_1^{OS}:}&{\exists i \Rightarrow {\mathit{\boldsymbol{A}}_i} \ne \mathit{\boldsymbol{A}}_i^0 \vee {\bf{\Sigma }}_\varepsilon ^{IS} \ne {\bf{\Sigma }}_\varepsilon ^{0, IS} \vee {{\bf{\Sigma }}^{OOS}} \ne {{\bf{\Sigma }}^{0, OOS}}} \end{array}} \right.,$

(15)

where $i \in \left\{ {1, 2, \ldots, p} \right\}$ and $\mathit{\boldsymbol{A}}_i^0$, ${\bf{\Sigma }}_\varepsilon ^{0, IS}$ and ${{\bf{\Sigma }}^{0, OOS}}$ are diagonal matrices. The bootstrapping procedure consists of steps detailed in Appendix B. We apply the bootstrap with $M = 5000$ re-samples which guarantees a good balance between calculation speed—given the many complex iterations to be performed—and the accuracy (granularity) of the bootstrap distribution of the test statistics. Because in the case of both in- and out-of-sample connectedness, the bootstrap is applied to rolling windows of data, the resulting output for the hypotheses tests consists of $12N + 4$ time-series of p-values, one for each connectedness measures under analysis.

A first issue is that, in the context of the multiple, sequential hypothesis tests that we plan to perform, comparing the p-values of each test with a threshold $\alpha$ is generally invalid because the probability of making a type I error increases with the number of hypotheses sequentially tested. Unfortunately, this is our case, as for each connectedness measure ($\star$), we have a time series of p-values $\left\{ {{p_{ \star, t}}} \right\}_{t = 1}^L$ of length L, which takes values ${L^{IS}} = 3207$ for the in-sample measures and ${L^{OOS}} = 2996$ for the OOS measures. As a result, a first statistic that we can calculate on the basis of the sequence $\left\{ {{p_{ \star, t}}} \right\}_{t = 1}^L$ is the true null ratio ${\pi _{ \star, 0}} = {\raise0.7ex\hbox{${{L_{ \star, 0}}}$} \!\mathord{\left/ {\vphantom {{{L_{ \star, 0}}} {{L_ \star }}}}\right.} \!\lower0.7ex\hbox{${{L_ \star }}$}}$, which is the ratio between the number of "true" null hypotheses ${L_0}$ over the total number of hypotheses under testing. We use the estimator of the true null ratio for one-sided tests introduced in Pounds and Cheng (2006):

${{\hat \pi }_{ \star, 0}} = \min \left[ {\begin{array}{*{20}{c}} {1, }&{\frac{4}{{{L_ \star }}}\mathop \sum_{t = 1}^{{L_ \star }} min\left({{p_{ \star, t}}, 1 - {p_{ \star, t}}} \right)} \end{array}} \right]$

(16)

This estimator is conservatively biased, in the sense that $E\left[ {{{\hat \pi }_{ \star, 0}}} \right] \ge {\pi _{ \star, 0}}$. Even though it is biased, its conservativeness will not invalidate the following analysis because a large value of ${\pi _{ \star, 0}}$ implies high connectedness and this is—at least on logical grounds—what our paper intends to empirically prove.

Yet, we want to focus on controlling the False Discovery Rate (henceforth, FDR), i.e., the expected proportion of rejected hypotheses which are falsely positive. Given the time-series nature of our sequence of p-values, we are not interested in rejecting the intersection of all null hypotheses, but rather in assessing the reliability of the connectedness measures when they suggest a significant connection in the banking system. Here the main issue is that the p-values in the sequence $\left\{ {{p_{ \star, t}}} \right\}_{t = 1}^L$ cannot be generally assumed to be independent because they are obtained from overlapping windows of data. However, Benjamini and Yekutieli (2001) have proven that a modification of the Benjamini-Hochberg procedure controls the FDR at a level less than or equal to $\frac{{{L_0}}}{L}q$ (for a given selection of the parameter q), even under non-independence of the time series of p-values. Their procedure is as follows. Let ${p_{ \star, \left(1 \right)}} \le {p_{ \star, \left(2 \right)}} \le \ldots \le {p_{ \star, \left(m \right)}}$ be the ordered p-values under the null hypotheses $H_{\left(1 \right)}^0, H_{\left(2 \right)}^0, \ldots, H_{\left(m \right)}^0,$ respectively. Define the index k as:

$k = max\left\{ {i:{p_{ \star, \left(i \right)}} \le \frac{{iq}}{L}/\mathop \sum_{j = 1}^L \frac{1}{j}} \right\}$

(17)

If we reject the first k ordered null hypotheses $H_{\left(1 \right)}^0, H_{\left(2 \right)}^0, \ldots, H_{\left(k \right)}^0$, for which it holds that ${p_{ \star, \left(i \right)}} \le {p_{ \star, \left(k \right)}}$ for $i = 1, \ldots, k$, the procedure always controls the FDR at a level:

$FDR \le \frac{{{L_0}}}{L}q = {\pi _0}q$

(18)

We proceed by setting a maximum level of false discovery ratio $FD{R^{MAX}} = 0.05$ and we divide it by the estimated true null ratio in 16 to obtain the constant q to use in 17, as in 18, $q = FDR/{{\hat \pi }_0}$. Subsequently, we use kth p-value $p_ \star ^{FDR} = {p_{ \star, \left(k \right)}}$ as our reference and simply reject all null hypotheses for which the p-value is smaller than $p_ \star ^{FDR}$.

Because the estimator defined in 16 is conservatively biased, on average we obtain a higher q than the one that could be computed using the true value ${\pi _{ \star, 0}}$. Thus, we expect k to be higher than needed and to reject more null hypotheses than we should. However, this fact does not diminish the achieved reliability in the matter of the rejection of $H_{\left(1 \right)}^0, H_{\left(2 \right)}^0, \ldots, H_{\left(k \right)}^0$, because the modified Benjamini-Hochberg procedure guarantees that the expected proportion of false positives is below the value $FD{R^{MAX}}$ we have set.

---

2.6. The definition of the benchmarks and associated comparisons

To favor the economic interpretation of our empirical results, we also compare the connectedness measures estimated on the basis of the variance decompositions against a set of benchmark indexes which quantify connectedness in a broader sense, that is not linked to a structural framework that measures interdependence in variance, differently from the VAR(p) in equation 5.

The first benchmark is simply the sample linear correlation coefficient between the logarithmic return of the sector (bank) market index ${R_{mkt, t}}$ and the contemporaneous logarithmic return of the jth bank ${R_{j, t}}$:⁶

⁶ We define the market index as the equally weighted portfolio that includes all banks in our sample, so that it is effectively a sectoral sub-index.

$B_{j, t}^1 = \hat \rho \left({{R_{mkt, t}}, {R_{j, t}}} \right)$

(19)

The higher $B_{j, t}^1$ is across different financial institutions, the more they will also move together. The second benchmark is the sample correlation coefficient between ${R_{mkt, t}}$ and the H-lagged logarithmic return of the jth bank ${R_{j, t - H}}$:

$B_{j, t}^2 = \hat \rho \left({{R_{j, t - H}}, {R_{mkt, t}}} \right)$

(20)

20 attempts to capture the ability of the equity valuation of the jth bank to influence the overall index H periods ahead, where H is the predictive horizon used in 8–10. Both $B_{j, t}^1$ and $B_{j, t}^2$ are estimated using the sample linear correlation over a rolling window of length ${T_C}$.

The third benchmark is Marginal Expected Shortfall (MES), defined as:

$B_{j, t}^3 = ME{S_{\alpha, j, t}} = - E\left({{R_{j, t}}{\rm{|}}{R_{mkt, t}} \le - VaR_\alpha ^{mkt}} \right)$

(21)

Where $VaR_\alpha ^{mkt}$ is the Value at Risk at $\alpha \%$ of the sector market index. MES estimates the expected loss conditional on the occurrence of a left-tail event in the sector. Similarly to the connectedness from-others, MES is the higher the stronger the spill-over of the whole banking system on the jth bank. We estimate 30 using the historical returns over a rolling window of length ${T_C}$:

$\hat B_{j, t}^3 = - \frac{{\mathop \sum \nolimits_{\tau = 1}^{{T_C}} {R_{j, t - \tau }}I\left({{R_{mkt, t - \tau }} \le \hat q_{t - {T_C}, t}^{\alpha, mkt}} \right)}}{{\mathop \sum \nolimits_{\tau = 1}^{{T_C}} I\left({{R_{mkt, t - \tau }} \le \hat q_{t - {T_C}, t}^{\alpha, mkt}} \right)}}$

(22)

where $I\left(\cdot \right)$ is the indicator function and $\hat q_{t - {T_C}, t}^{\alpha, mkt}$ is the estimator of the $\alpha \%$ percentile of the sector index returns between $t - {T_C}$ and t.

The fourth benchmark is the market index CoVaR conditional to the jth bank:

$B_{j, t}^4 = CoVaR_{\alpha, t}^{mkt|j},$

(23)

defined as:

$Pr\left({{R_{mkt, t}} \le - CoVaR_{\alpha, t}^{mkt|j}{\rm{|}}{R_{j, t}} = - VaR_\alpha ^j} \right) = \alpha,$

(24)

where $VaR_\alpha ^j$ is the Value at Risk at $\alpha \%$ of the jth bank. The CoVaR measures the left-tail risk measured with reference to the whole system if the jth bank is in distress. Because it measures the tail impact of the jth bank on the other banks, it is comparable to the connectedness to-others. We estimate $CoVaR_{\alpha, t}^{mkt|j}$ through a quantile regression over a rolling window of length ${T_C}$, assuming that ${R_{mkt, t}}$ follows:

$Pr\left({{R_{mkt, t}} < Z_{mkt, t}^\alpha } \right) = F\left({Z_{mkt, t}^\alpha - {\beta _1} - {\beta _2}{R_{j, t}}} \right) = \alpha,$

(25)

and estimating the parameters ${\beta _1}$ and ${\beta _2}$ for the $\alpha \%$ quantile following Koenker and Bassett (1978). Therefore, the estimated $\alpha \%$ quantile of the market return, conditional on the return of the jth bank, is:

$\hat Z_{mkt, t}^\alpha = \hat \beta _1^\alpha + \hat \beta _2^\alpha {R_{j, t}}$

(26)

From 26, we can derive the estimator of $CoVaR_{\alpha, t}^{mkt|j}$ as:

$\hat B_{j, t}^4 = \widehat {CoVaR}_{\alpha, t}^{mkt|j} = - \hat \beta _1^\alpha + \hat \beta _2^\alpha \widehat {VaR}_\alpha ^j,$

(27)

where $\widehat {VaR}_\alpha ^j = \hat q_{t - {T_C}, t}^{\alpha, j}$ is the estimator of the $\alpha \%$ percentile of the returns of the jth bank.

The fifth benchmark is the market index ${\rm{\Delta }}CoVaR$ conditional on the jth bank:

$B_{j, t}^5 = {\rm{\Delta }}CoVaR_{\alpha, t}^{mkt|j} = CoVaR_{\alpha, t}^{mkt|j} - CoVaR_{\alpha, t}^{mkt|Med\left(j \right)},$

(28)

where ${\rm{CoVaR}}_{\alpha, t}^{mkt|j}$ is defined as in 24 and $CoVaR_{\alpha, t}^{mkt|Med\left(j \right)}$ is defined as:

$Pr\left({{R_{mkt, t}} \le - CoVaR_{\alpha, t}^{mkt|Med\left(j \right)}{\rm{|}}{R_{j, t}} = Med\left({{R_{j, t}}} \right)} \right) = \alpha,$

(29)

i.e., $Med\left({{R_{j, t}}} \right)$ is the median of ${R_{j, t}}$. ${\rm{\Delta }}CoVaR_{\alpha, t}^{mkt|j}$ measures the increase in left-tail risk in the banking system due to the jth bank being in an ordinary state (as represented by its median return) rather than in a distressed one. Because it is directly derived from $CoVaR_{\alpha, t}^{mkt|j}$, it is analogous to the connectedness to-others. We estimate ${\rm{\Delta }}CoVaR_{\alpha, t}^{mkt|j}$ through a rolling window of length ${T_C}$ as:

$\hat B_{j, t}^5 = \widehat {{\rm{\Delta }}CoVaR}_{\alpha, t}^{mkt|j} = \hat \beta _2^\alpha \left({\widehat {VaR}_\alpha ^j - \hat q_{t - {T_C}, t}^{0.5, j}} \right),$

(30)

where $\hat \beta _2^\alpha$ is the same as in 36 and $\hat q_{t - {T_C}, t}^{0.5, j}$ is the estimated median return of the jth bank.

Once we have estimated all five benchmarks, we proceed to compare them with the connectedness measures based on the forecast error variance decomposition. To do so, we compute the Spearman's rank correlation coefficient between each connectedness measure $\left(\star \right)$ and each benchmark:

$\hat \rho _{ \star, k, j}^S = {\rho ^S}\left({C_j^ \star, B_j^k} \right)k = 1, \ldots, 5.$

(31)

We resort to the Spearman's rank correlation as it does not impose a linear relationship between the connectedness measure and the benchmarks, but it assumes only a monotonic relationship between the two. The non-parametric nature of the Spearman's coefficient allows us to capture the common behavior between the time-series from which it is computed, while being unaffected by their different range of values.⁷ In fact, we test the null hypothesis of absence of correlation, against the alternative of a positive rank correlation:

⁷ For instance, note that the connectedness from-others indices, B¹ and B² are bounded, while the other measures are unbounded.

$\left\{ {\begin{array}{*{20}{c}} {{H_0}:}&{\rho _{ \star, k, j}^S = 0}\\ {{H_1}:}&{\rho _{ \star, k, j}^S > 0} \end{array}} \right.$

(32)

Under the null hypothesis, the statistic:

$t = \hat \rho _{ \star, k, j}^S\sqrt {\frac{{n - 2}}{{1 - {{\left({\rho _{ \star, k, j}^S} \right)}^2}}}}$

(33)

is distributed as a t-student distribution with n-2 degrees of freedom, where n is the number of observations used to compute $\hat \rho _{ \star, k, j}^S$.

---

3. Data

We include in our sample 10 Italian banks which were quoted in the MTA segment of Borsa Italiana over the period July 1, 2003–December 22, 2016. Table 1 shows the composition of our sample, together with the bank's tickers and the value of their total assets as of the end of fiscal year 2015. The data consist of the daily open, high, low and close quotes for each trading day over sample period. We estimate their intraday realized volatility ${\sigma _t}$ using the range-based estimator of Garman and Klass (1980):

${{\hat \sigma }_t} = \sqrt {0.511{{\left({u - d} \right)}^2} - 0.019\left[ {c\left({u + d} \right) - 2ud} \right] - 0.383{c^2}},$

(34)

where $u = log\left({High/Open} \right)$, $d = log\left({Low/Open} \right)$ and $c = log\left({Close/Open} \right)$. The opening quotes of CE, Banco di Desio e della Brianza, Banca Piccolo Credito Valtellinese, and Banca Carige are not reported with continuity, so we estimate their intraday volatility using Garman and Klass's (1980) estimator:

${{\hat \sigma }_t} = \sqrt {\frac{{{{\left[ {log\left({\frac{{High}}{{Low}}} \right)} \right]}^2}}}{{4log\left(2 \right)}}, }$

(35)

which is based solely on the daily high and low quotes. Table 2 shows the summary statistics of estimated intraday volatilities for each bank. As in Diebold and Yilmaz(2014, 2016) we estimate the VAR(p) in 5 on ${x_{i, t}} = {\rm{log}}\left({{{\hat \sigma }_t}} \right)$, the logarithm of intraday volatility. Panel B of Table 2 shows in fact that by considering the natural logarithm of estimating decreases both the skewness and the excess kurtosis of the data, even though the Jarque-Bera test reject normality for most banks (the 5% size critical value is approximately 5.99). According to the Augmented Dickey-Full statistic, we can reject the null hypothesis of a unit root in the data at a 1% size for all banks, thus we can model the data with a VAR(p) model without taking into account cointegration, e.g., differently from Heinz and Sun (2014) in their application to CDS and bond yields data.

---

4. Empirical results

---

4.1. In-sample connectedness

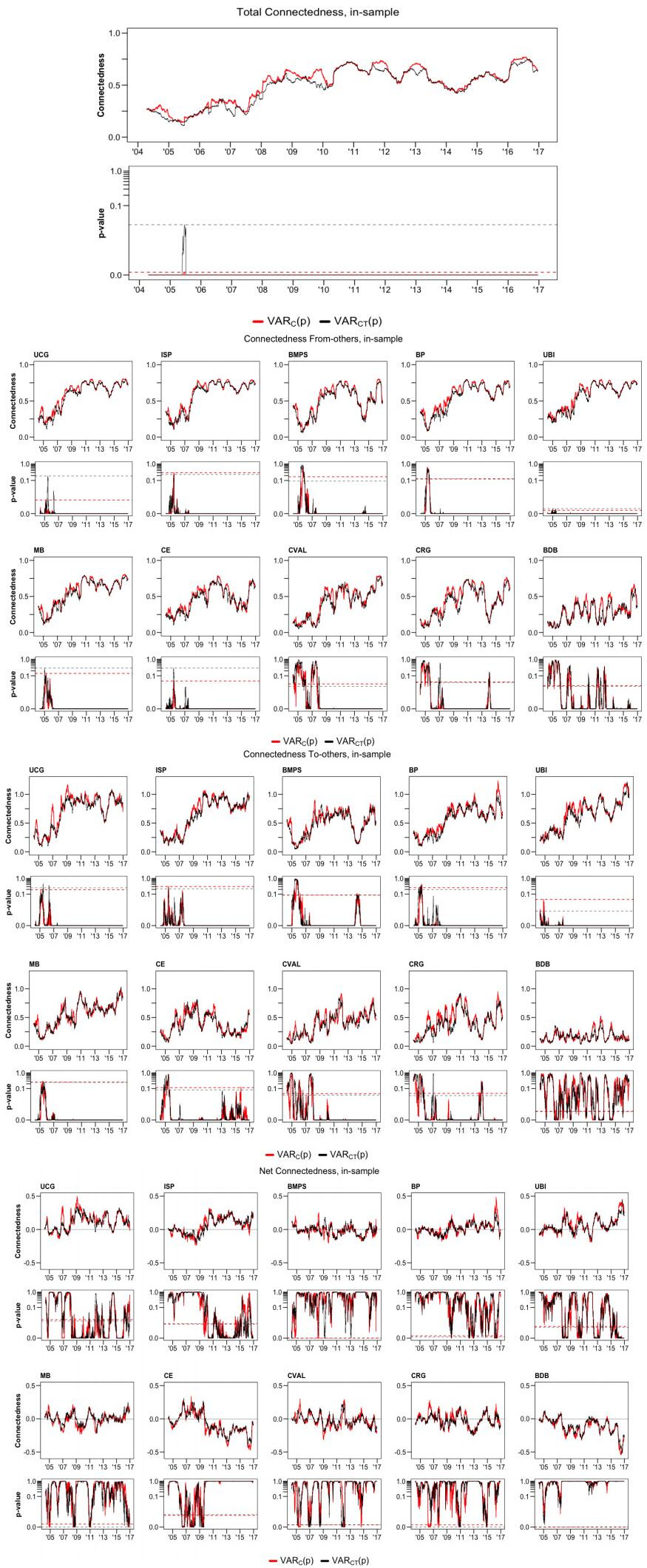
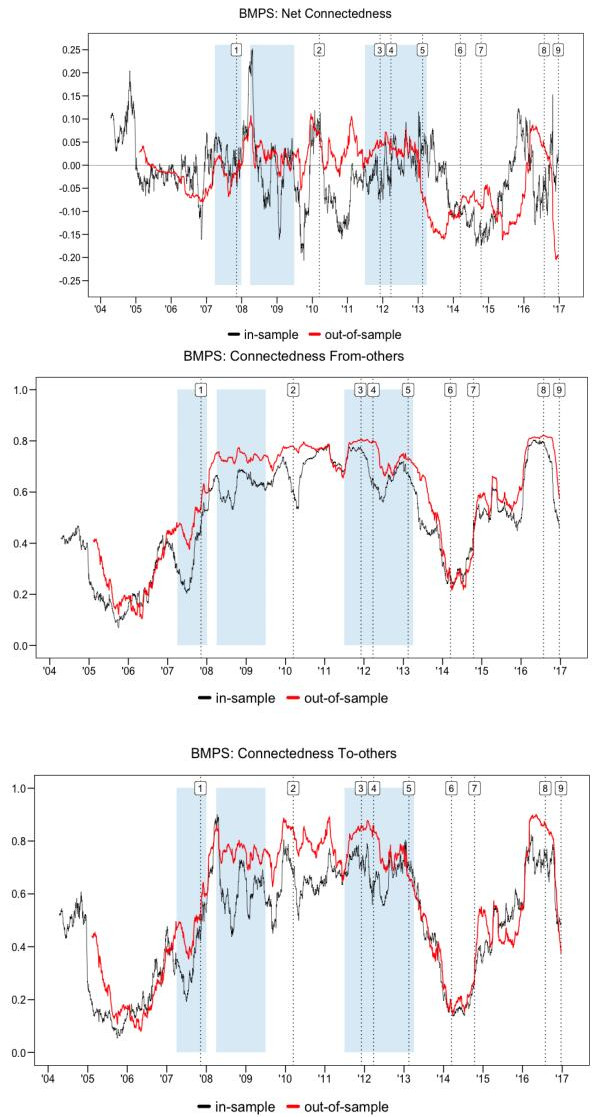
We start by estimating the connectedness of the Italian banking system using the in-sample method of Diebold and Yilmaz(2014, 2016). Figure 1 shows the time series of the resulting measures. Observing the plots, we note that there is no noteworthy difference between the VARC(p), in red, and the VARCT(p), in black, specifications: The time series of total connectedness evolve in similar ways. The total connectedness of the banking system in panel A shows a general upward trend starting in mid-2005 and ending in 2012, which includes the Financial Crisis of 2007–2008 and the European Debt Crisis of 2009–2012. Even though the total connectedness started rising two years before the subprime crisis in the United States, it is when the US crisis propagates to Europe and takes "trans-Atlantic" proportions (see Diebold and Yilmaz, 2016) that total connectedness increases sharply and reaches 0.65 at the end of 2008, doubling the starting level in 2005. Such an alarmingly high level is only exceeded between 2010 and 2012, when Italian banks came directly under market pressures and were often alleged to be on the brink of default because of their large holdings of peripheral sovereign debt, as total connectedness came to oscillate in the range 0.55–0.70.⁸ The last four years in our time-interval record a decline in 2013–2014 followed by an increase in 2015–2016, which are marked by the demise of Banca Monte dei Paschi di Siena (rescued by the government) and the obvious difficulties of Carige. Clearly, the connectedness is found to be highly significant throughout the entire sample (see lower plot in Figure 1, panel A), with p-values that are always below the FDR threshold.

⁸ The Italian banking sector was severely hit by the sovereign debt crisis in 2010–2011, when the Italian FTSE Bank Index dropped by nearly 50 per cent (10 percent more than the MSCI‐EMU Bank Index). Italian banks directly or indirectly owned a large share of the domestic government debt and, at the end of 2011, the total exposure of the Italian banking system to the domestic public sector amounted to €272 billion, 10 per cent of their total assets (source: Bank of Italy).

The plots concerning connectedness from-others in Figure 1, panel B follow roughly the same evolution as general connectedness in panel A. An inspection of the plots for individual banks reveal that the decline in connectedness from- during 2013–2014 has been more pronounced for BMPS, CE and CRG (see Table 1 for a definition of all acronyms). For these three banks the connectedness returns to the pre-crisis level before reverting to high levels during the last two years in our sample. Although the case of CE is not completely obvious (or it may simply have a benign interpretation), BMPS and CRG benefitted from rescue attempts in 2013–2014 that are likely to have temporarily "detached" them from the rest of the banks in the sector. However, the two most important banks, UCG and ISP, are characterized by a rather permanent increase in the sensitivity to volatility shocks from other banks, as their estimated connectedness simply increases from 0.2–0.3 in 2004, to approximately 0.7 by the end of the sample. Because the same pattern also characterized major banks such as UBI and MB, this represents a worrisome development. By the end of the sample, the connectedness from of all banks turns out to be highly statistically significant, with the only exceptions/doubts concerning BDB, which appears in fact rather disconnected from the rest of the system.

The connectedness to-others measures in panel C show a more heterogeneous behavior. The connectedness of UCG, ISP, BMPS and BP, the largest banks according to total assets, follows the same pattern described in panels A and B, while the other banks show a fluctuating upward trend in connectedness with peaks in 2008 and 2011. Here a few empirical results are unexpected and isolate the most systematically "dangerous"—in terms of their volatility being transmitted to others—banks in the Italian system. Besides UCG, ISP, and BP that are expected to be able to "export" volatility because of their size, banks such as UBI and MB are estimated to have recorded an increase in their connectedness to-others from 0.25–0.3 in 2005 to an index close or even in excess of 1.0 by the end of our sample. Interestingly, the connectedness of BDB, which is the bank with the smallest total assets at the end of FY 2015 in our sample, stays to a low level for the entire period under analysis and it is frequently not statistically significant.

Although it is characterized by the least statistical significance in Figure 1, panel D is in some way the most interesting among the panels. With few exceptions, the estimated net connectedness measures fail to follow any particular pattern, except a rather unsurprising peak in 2009–2010 concerning the banks with higher total assets. This means that in the banking system, all banks influence and are influenced by all other banks, creating an approximately homogeneous and compact system. The exceptions are represented by UBI which, after 2015, has taken to export much more volatility than it imports from the rest of the banking system, and CE and BDB (the former, after 2010) that on the contrary play a passive role and import more risk than they export. Interestingly, the most troubled Italian banks during our sample period, BMPS and CRG, display an approximate zero net connectedness that is hardly ever statistically different from zero.

Table 3 offers a summary of these results by reporting the estimated Pounds and Cheng's true null ratio ${{\hat \pi }_{ \star, 0}}$ and Benjamini and Yekutieli's k-th p-value that maximizes 26 controlling for the possibility of false discovery caused by the sequential nature of the tests performed by setting a maximum level of false discovery ratio $FD{R^{MAX}} = 0.05$. While with the former test, the lower is ${{\hat \pi }_{ \star, 0}}$ the stronger is the evidence against the null hypothesis of no connectedness in the data, under the second methodology, because one rejects all null hypotheses for which the p-value is smaller than $p_ \star ^{FDR}$, the higher is $p_ \star ^{FDR}$ the stronger is the evidence in the data against the null hypothesis of no connectedness. While total connectedness is highly significant under both VAR_C(p) and VAR_CT(p) in terms of ${{\hat \pi }_{ \star, 0}}$, the evidence is more mixed when one accounts for the FDR, as the smallest $p_ \star ^{FDR}$ is 0.0002, which is well below a classical 0.05. As one would expect from Figure 1, there is little evidence of non-zero net connectedness in the data, as all estimated ${{\hat \pi }_{ \star, 0}}$s are large while the values for $p_ \star ^{FDR}$ are generally small, occasionally 0.000. There is instead no doubt that, even when FDR effects are considered, the connectedness to- and from-others measures are largely statistically significant in overall terms. This is certainly the case of UCG, ISP, BMPS, BP, MB, and CE, in some ways the largest banks and a few more; however, the smaller banks seem to be on the verge of no gross connectedness, as signaled by ${{\hat \pi }_{ \star, 0}}$ exceeding 0.1 and $p_ \star ^{FDR}$ never exceeding 0.05, which may be indicators of weak evidence in the data. This confirms the picture found above: the Italian banking systems appear to be mildly connected—especially as far as the largest banks are concerned—the large banks are both active exporting and importing volatility with a net balance close to zero, and only the smallest banks such as CVAL, CRG, and BDB carry weaker links.

---

4.2. Out-of-sample connectedness

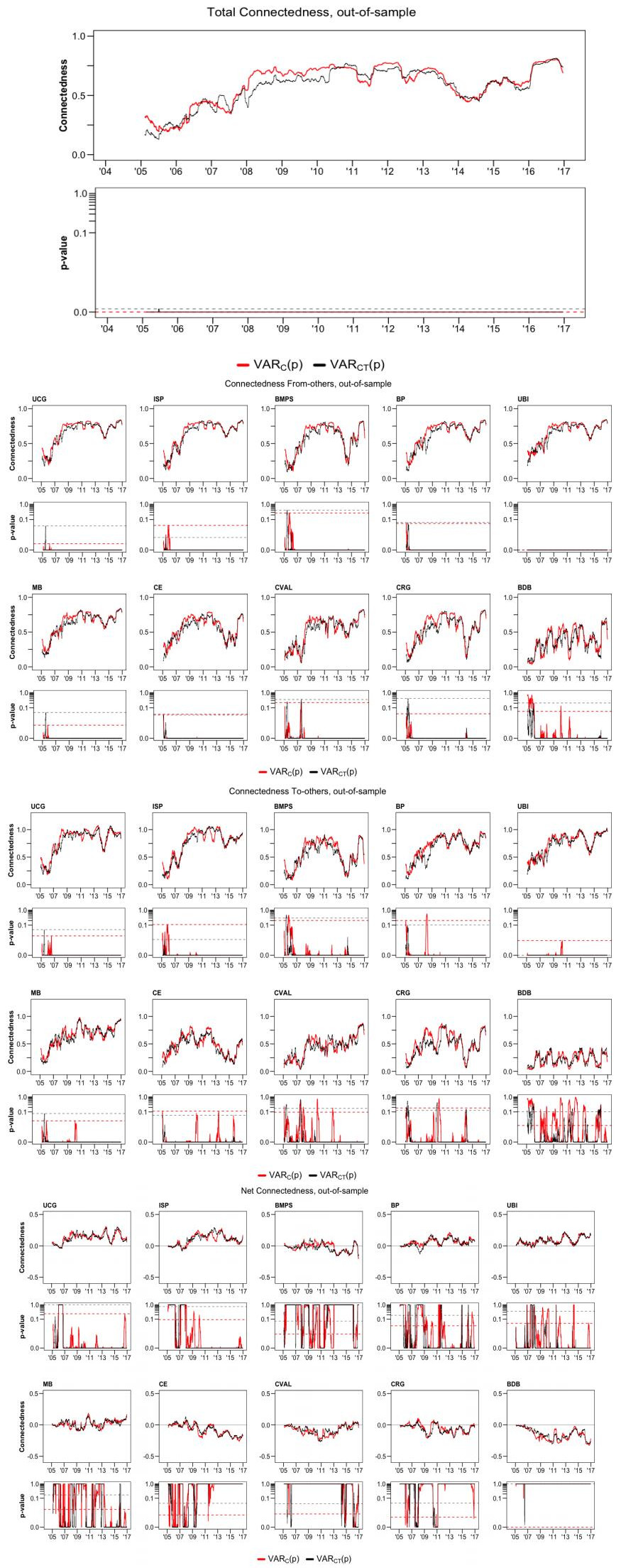
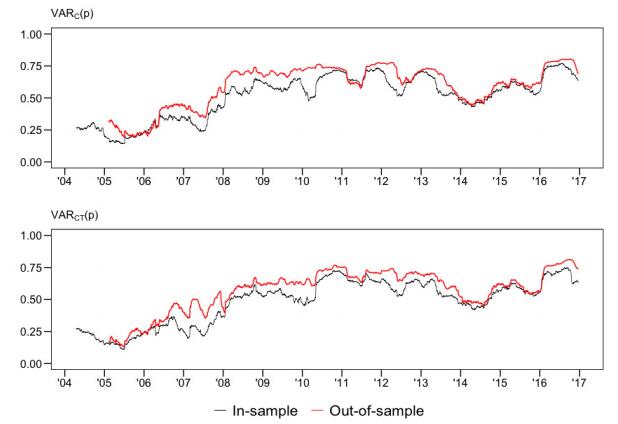
In Figure 2, we present results based on the OOS realized forecast error variance decomposition methodology proposed by Gätjen and Schienle (2015). While Figure 2 has a structure that is identical to Figure 1, Figure 3 directly compares the in- and out-of-sample connectedness estimates derived from the two methods.

Panel A of Figure 2 is virtually indistinguishable from panel A of Figure 1 so that the same comments apply. Figure 3 directly performs the comparison and shows that, although as already noted by Gätjen and Schienle, the OOS measures are generally higher than the in-sample ones, the general patterns of the IS and OOS measures are approximately identical. In panels B and C of Figure 2, there are neither significant qualitative differences in connectedness from-others and to-others between the in-sample and out-of-sample connectedness. Here qualitative means that the patterns and dynamics over time of the estimated measures are identical, even though the plotted numerical values may differ. Moreover, also in this case, the inclusion of specific deterministic components makes little difference to the empirical estimates reported.⁹

⁹ In fact, panels B and C of Figure 2 are just reported for completeness.

The key distinction that can be draw between in- and out-of-sample connectedness indices concerns the net measures, plotted in panel D of Figure 2. Differently from Figure 1, now banks can be classified in three starkly different groups:

■ Banks for which net connectedness is largely positive, UCG, ISP, BP, UBI, i.e., the largest banks;

■ Banks for which net connectedness fluctuates around 0: BMPS and MB;

■ Banks for which net connectedness is largely negative: CE, CVAL, CRG, BDB, i.e., the smallest banks in the system.

This division reflects rather closely the dimensions of the banks in our sample and confirms the systemic role of UCG, the only Italian bank and the only bank in the sample to be included continuously from 2011 to 2016 in the list of global systemically important banks (G-SIB list) published by the Financial Stability Board (FSB). However, when the time series of bootstrapped p-values that appear underneath each row of connectedness measures are taken into account, it emerges that only UCG and ISP (to some lesser extent UBI, but only after 2011) imply small p-values that allow us to reject the null of zero net connectedness.

Finally, the last three columns of Table 3 show overall, FDR-adjusted tests of the hypothesis of zero net connectedness estimated from OOS forecast errors. Differently from the case of in-sample measures, we now obtain evidence of stronger rejections of the null of zero net linkages among Italian banks. This can be seen from the fact that the reported estimates ${{\hat \pi }_{net, 0}}$ are predominantly small and below 0.10 under both VAR_C and VAR_CT (this occurs in the case of UCG, ISP, UBI, CVAL, and BDB) and that the computed $p_{net}^{FDR}$ is large and actually in excess of 0.1 especially for estimated computed from VAR_CT (this is the case of UCG, ISP, UBI, MB, and BDB). In overall terms, there are little doubts left on the non-zero net connectedness of UCG, ISP, UBI—as "exporters" of volatility to the Italian banking system—and BDB—as an "importer" of risk and instability—when OOS measures are employed.

Figure 4 closes this section by investigating one special and rather interesting case, the network connectedness of Banca Monte dei Paschi di Siena in Italian banking system. We devote our attention to such a case both because interesting per se, given the notoriety of the bank and its difficult balance sheet conditions emerged after the financial crisis, and because the empirical findings in Table 3 and in Figures 1–2 lead to an apparent paradox. Indeed, despite being probably the most debated and feared among the large-size Italian banks, BMPS reveals a pattern of estimated connectedness that is far from explosive and net connectedness that in general oscillates around zero. Figure 4 shows the in-sample and OOS connectedness measures in plots that also report the major events that have affected the stock market valuation and the realized volatility of BMPS. The first plot reveals that even though, in Tables 2 and 3 we have failed to report in overall terms any major differences between in-sample and OOS estimates, in a few individual cases, such differences may show up. In the last two panels of the figure, it turns out that while OOS connectedness tends to be higher than the in-sample measure, such a difference is particularly strong in the case of connectedness to-others and during the most difficult period, 2008–2012, before the Italian government's interventions in February 2013. Such departures yield in the first panel of Figure 4 a plot of estimated net connectedness that is drastically different under the in-sample vs. the OOS measures. Although not in the massive proportions that one may expect, according to OOS estimates, BMPS has been a net export of systemic risks between 2009 and 2012 and again in late 2016. This contrasts with the evidence arising from in-sample estimates.

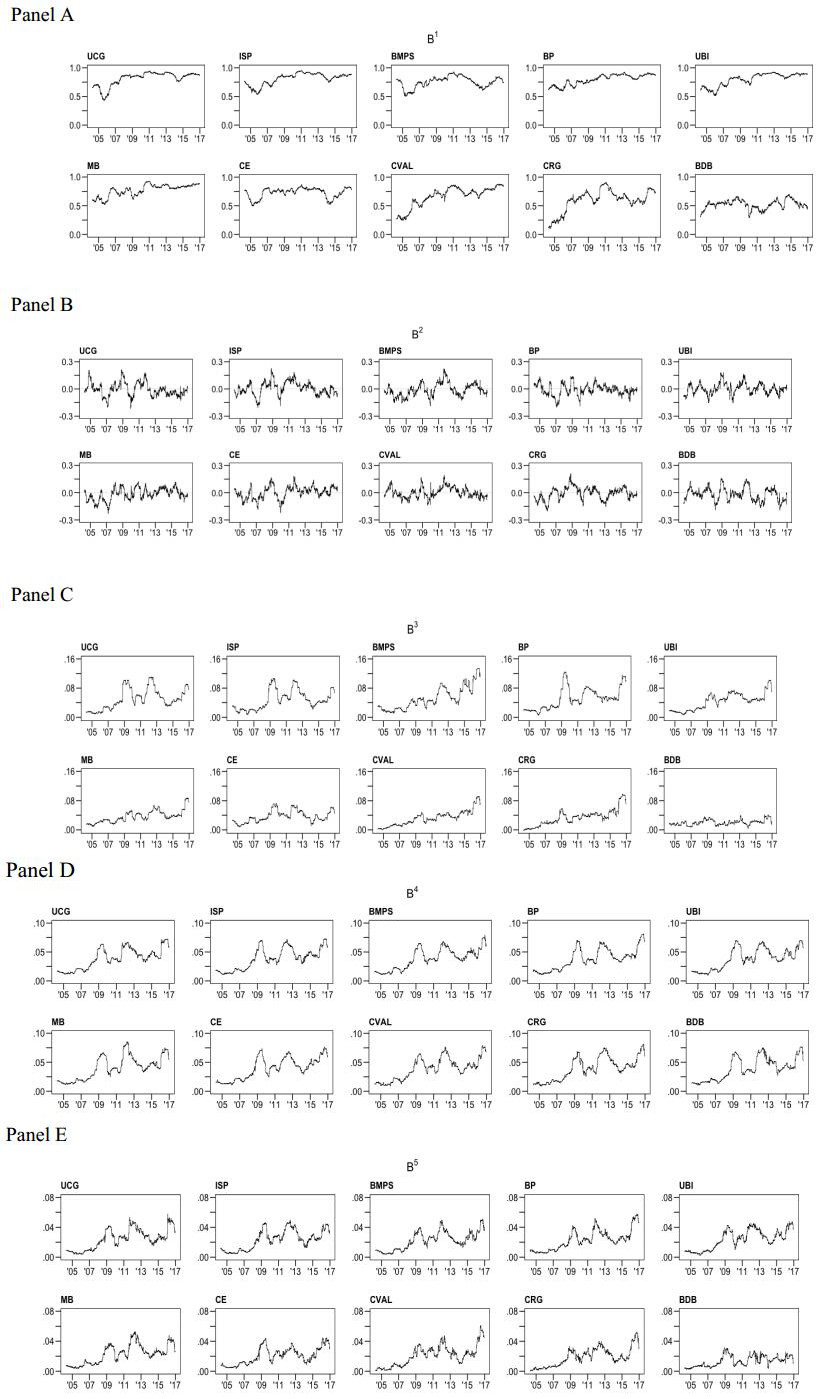
The figure shows the time series of the five benchmarks for each bank in our sample. Panel A plots $B_{j, t}^1 = \hat \rho \left({{R_{mkt, t}}, {R_{j, t}}} \right)$, panel B shows $B_{j, t}^2 = \hat \rho \left({{R_{mkt, t}}, {R_{j, t - H}}} \right)$, panel C shows $B_{j, t}^3 = ME{S_{\alpha, j, t}}$, panel D shows $B_{j, t}^4 = CoVaR_{\alpha, t}^{mkt|j}$, and panel E is devoted to $B_{j, t}^5 = {\rm{\Delta }}CoVaR_{\alpha, t}^{mkt|j}$.

---

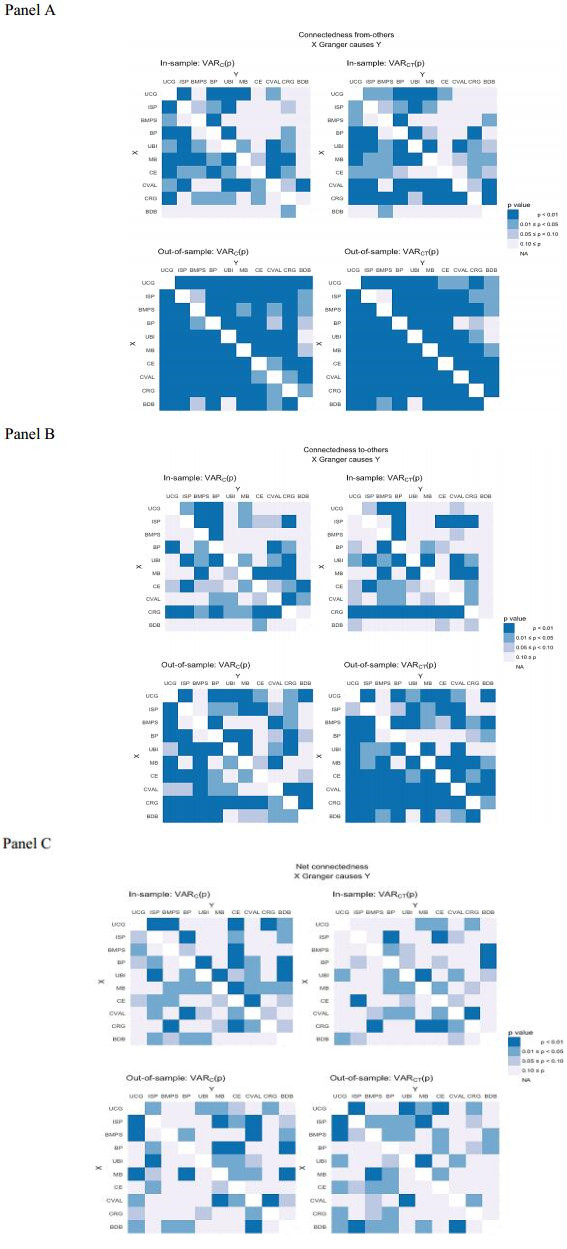
4.3. Comparison and causality links between in- and out-of-sample connectedness measures

In this section we therefore go at the heart of our research question: Does it matter whether the network connectedness estimates are computed on the basis of standard, in-sample variance decompositions vs. a more careful scheme that separates in-sample window estimation from OOS calculation of forecast errors? On the one hand, Table 3 and to a larger extent Figures 1 and 2 have provided a largely negative answer. Even though occasional departures may be detected, as far as gross connectedness to- and from-other are concerned, the differences are modest and never qualitatively (i.e., economically) important. At worst, one can detect a few differences in the mean and dynamics of the net connectedness measure. However, whether this may represent key information in terms of risk management, portfolio decisions, or system risk regulation and control (see Diebold and Yilmaz, 2015) is not obvious ex-ante. In our application, both in-sample and OOS measures suggest that there is a considerable degree of connectedness among Italian banks, around 0.67 as of the end of the sample. On the contrary, in net terms, it remains hard to isolate which banks (with the obvious exception of the systemically large UCG, ISP, and possibly UBI) are net exporters of risk using in-sample measures, while the OOS measures provide a starker answer that is supported by considerable statistical significance.

However, even though their average level, statistical significance, or dynamics over time may fail to be starkly different, there is another way through which the difference between in-sample and OOS estimation may matter: It remains possible that one measure may reveal a superior degree of predictability of some measures based on the past of others, that we interpret as an indication that a bank may react to the arrival of new information more promptly than the others do. Therefore, in Figure 5, we have performed standard VAR-based Granger causality tests.¹⁰ In panels A through C, we analyze the direct relationship between individual banks. The in-sample and OOS measures reveal starkly different pictures. In the OOS case and especially from the gross to- and from-others measures, two-way causality dominates; this means that most indices do forecast most of the others and contribute to a view of the Italian banking system as a one with widespread and complex linkages in which all or most banks are closely tied to one another. However, especially in the case of connectedness from-others, the in-sample estimates reveal in the heat maps a prevalence of one-way causality relationships (darker colors below the main diagonal and clear color above, in the corresponding square). For instance, an increase in the connectedness from-others of UCG and ISP forecast that similar measures for the smallest Italian banks are about to increase as well after a few days, but the opposite is not true. Therefore, if they were validated as superior, in a few supervisory applications, standard in-sample estimates of gross connectedness from- may prove more informative than the OOS ones. However, we must caution a Reader on the fact that in panel C of Figure 6, such differences are almost completely lost and for most pairs there is no linear causality relationship emerging from either in-sample or OOS network measures, i.e., in both cases no banks become today a net importer/exporter of risk may be used to forecast whether the same fate will be followed by one or more other banks in subsequent periods.

¹⁰ Importantly, in the figure, the order of the testing VAR p is chosen according to the AIC. We test using standard Wald statistics the null hypotheses that for each possible pair of banks either the in-sample connectedness fails to predict the OOS measure or that OOS connectedness fails to predict the in-sample measure.

The figure shows the time series of the five benchmarks for each bank in our sample. Panel A plots $B_{j, t}^1 = \hat \rho \left({{R_{mkt, t}}, {R_{j, t}}} \right)$, Panel B shows $B_{j, t}^2 = \hat \rho \left({{R_{mkt, t}}, {R_{j, t - H}}} \right)$, Panel C shows $B_{j, t}^3 = ME{S_{\alpha, j, t}}$, Panel D shows $B_{j, t}^4 = CoVaR_{\alpha, t}^{mkt|j}$, and Panel E is devoted to $B_{j, t}^5 = {\rm{\Delta }}CoVaR_{\alpha, t}^{mkt|j}$.

The figure shows in detail the estimated connectedness from-others, to-others and net of Banca Monte dei Paschi di Siena (MPS). To save space, only the measure computed under the VAR_C specification is presented. The shaded areas highlight the quarters of recession of the Italian economy. The vertical dotted lines mark events which were relevant to Banca MPS:

1- Nov. 2007: MPS announces the acquisition of Banca Antonveneta for €6.6 bln.

2- Mar. 2010: MPS reports a 76% drop in net profits in 2009 caused by the impact of the financial crisis.

3- Dec. 2011: The European Banking Authority reports Banca MPS's capital shortfall for €3.3 bln.

4- Mar. 2012: MPS discloses a loss of €4.7 bln in 2011 due to the re-assessment of goodwill originated from past deals, including Antonveneta.

5- Feb. 2013: The Italian government underwrites €4.07 bln worth of bond issued by Banca MPS. One month later, the bank reveals losses of €730 mln and €3.2 bln which originated from its exposure to derivatives and Italian bonds, respectively.

6- Mar. 2014: Banca MPS reports a loss of €1.44 bln in 2013 due to its stock of NPLs.

7- Oct. 2014: The banking stress test conducted by the European Banking Authority revels that MPS is the least capitalized institute between the ones under analysis.

8- Jul. 2016: A stress test reports that BPS would be the only bank with negative CET1 ratio in the occurrence of the adverse scenario; the bank announce a recapitalization of €5 bln and the securitization and sale of €9.2 bln non-performing loans.

9- Dec. 2016: After that the issue of €5 bln new shares fails, Banca MPS invokes a precautionary recapitalization from the Italian Government of €8.1 bln.

---

4.4. Comparison with the benchmarks

We compute the benchmarks as defined in 28–32, and 37 after setting ${T_C} = 200\;{\rm{days}}$ and $\alpha = 0.05$. Figure 6 shows the five benchmarks computed for each bank in our sample. In panel A, correlations with the volatility of the sector market portfolio are generally slowly increasing over time, with a local maximum at around 0.75 between 2009 and 2011 and subsequent modest decline between 2012 and 2014. However, after 2015, for many banks the increase in pairwise correlations with the banking sector resumes and a few banks have reached correlations in excess of 0.8 by the end of the sample (e.g., BP, UBI, and MD).¹¹ However, panel B shows that no bank's volatility consistently predicts subsequent bank sector volatility, in spite of a few spikes in $\hat \rho \left({{R_{j, t - H}}, {R_{mkt, t}}} \right)$ for UCG, ISP, and UBI between 2008 and 2012. In panel C, we note that the dynamics of MES classifies banks in three groups: Those banks with no obvious trend in the measure but visible spikes in the worst crisis periods in 2009 and 2011–2012 (UCG, ISP, and BP), banks with an upward trend in MES (BMPS, UBI, MD, CVAL, and CRG), and banks with approximately constant and generally low MES (CE and BDB, that in fact have almost zero MES). Interestingly enough, all pictures describing the rolling window dynamics of CoVaR in panel D are strikingly similar, and display a visible upward trend with spikes in correspondence to 2009, 2012–2013, and 2016. The same comment applies to the change in CoVaR in panel E, even though the picture for Banco Desio shows a constant and almost nil change in CoVaR, $CoVaR_{\alpha, t}^{mkt|j} - CoVaR_{\alpha, t}^{mkt|Med\left(j \right)}$.

¹¹ Of course, it is to be expected that Unicredit and Intesa San Paolo ought to display correlations with the banking sector in excess of 0.8, given their sheer size and weight in the sector.

The figure shows the results of the Granger causality test between connectedness measures. In panels A–C, we analyze the direct relationship between individual banks. Given the connectedness measures ${C_{i, t}}$ and ${C_{j, t}}$ for banks i and j, we estimate the VAR(p) model:

$\left[ {\begin{array}{*{20}{c}} {{C_{i, t}}}\\ {{C_{j, t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{A_{11}}\left(L \right)}&{{A_{12}}\left(L \right)}\\ {{A_{21}}\left(L \right)}&{{A_{22}}\left(L \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{C_{i, t - 1}}}\\ {{C_{j, t - 1}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\varepsilon _{i, t}}}\\ {{\varepsilon _{j, t}}} \end{array}} \right]$

Where the order p is chosen according to the AIC. We test the null hypothesis ${H_0}:{A_{12}}\left(L \right) = 0$ against ${H_1}:{A_{12}}\left(L \right) \ne 0$ using the Wald statistic of the estimated coefficients ${{\hat A}_{12}}\left(L \right)$. We repeat the test for each pair $i \ne j$ and for each specification of the connectedness measure. The p-values of the tests are reported in panels A–C, respectively, for the connectedness from-others, to-others and net. Because we are testing N null hypotheses for any given connectedness specification ($N = 10$), the significance levels $\alpha$ are divided by N, so that the probability of committing at least one type Ⅰ error is smaller than $\alpha$, according to a Bonferroni's inequality.

In Table 4, we proceed to compute the Spearman's rank correlation between the various, in- and out-of-sample estimated connectedness measures and the benchmarks. The rank correlation coefficients and the p-values of the corresponding no-correlation hypothesis tests are reported in Table 4 (under each coefficient, the p-value of the one-sided test of the corresponding null hypothesis ${\rm{ \mathsf{ ρ} }}_{ \star, {\rm{k}}, {\rm{j}}}^{\rm{S}} = 0$ is reported in brackets). In general, especially in panels A, C, D, and E, we can reject the null hypothesis at 1% significance level for the connectedness from-others indicators for almost all banks in our sample.¹² Although the result is weaker, we can draw the same conclusion with reference to the connectedness to-others. Given the established trustworthiness of the benchmarks, in particular of MES, CoVaR and ΔCoVaR, in measuring the interdependence between the whole banking system and individual banks, such a statistically significant rank correlation suggests that the connectedness from-others and to-others is able to reflect the evolution of the same underlying interconnection across time, as in Diebold and Yilmaz (2014). Although the correlation is estimated to be lower for the smallest bank in our sample, in particular for BDB, it is still significant at 1% level even though the associated null hypothesis of absence of connectedness cannot be rejected for the majority of days in our sample. Importantly, in all panels of Table 4 we fail to detect any meaningful differences between the rank correlations derived from the in-sample vs. the OOS connectedness measures, another result fully consistent with Section 5.3 above.

¹² In panel B, concerning the predictive power of the volatility of each bank for market volatility, we find rank correlations with estimated connectedness measures that are lower than in other panels, but generally positive. The little predictability that we manage to capture, is positively associated with connectedness. In particular the rank correlations are all positive and significant for the measures estimated from the VAR_C model and in the case of connectedness from-others.

As for the net connectedness estimates, the correlation against the benchmarks is lower than the one of the connectedness from-others and to-others. The null hypothesis can always be rejected at 1% significance level against all benchmarks, with the limited exception of $B_{j, t}^2 = \rho \left({{R_{mkt, t}}, {R_{j, t - H}}} \right)$ in panel B, in the case of UCG, ISP, BP and UBI, i.e., the four largest, not nationalized banks. In general, the null hypothesis cannot be rejected against all benchmarks for the other banks. This is the same subset of banks we found previously when dividing the cross-sectional sample according to the predominant sign of the OOS net connectedness or according to the significance of net connectedness, both in-sample and out-of-sample. This outcome suggests that net-connectedness can be relied upon when it is significant, which can be inferred by the sign of OOS connectedness. This is in fact the only profile according to which we manage to report in this paper an economically meaningful difference between in-sample and OOS connectedness measures, i.e., the meaning and association with benchmarks of net estimated connectedness.

---

5. Conclusions

In this paper, we have used modern methods that exploit variance decompositions from standard (rolling window) estimates of VAR(p) models to obtain estimates of network connectedness and distances among nodes. In particular, we have compared the empirical plausibility and results derived under two alternative approaches: To base the decompositions on in-sample forecast errors as recommended by Diebold and Yilmaz(2012, 2014, 2016) or on out-of-sample forecast errors derived from a separation between estimation and forecast evaluation window. In the process, we also derive novel empirical results on the level and structure of network connectedness and systemic risk of the Italian banking system.

Our results are twofold. Under a methodological perspective, it seems that in-sample and OOS yield similar results for what concerns gross connectedness among banks. However, when it comes to estimate net-connectedness, that is, to determinate whether a bank is either a net importer or exporter of volatility to the system, in-sample measures fail to provide significant evidence of net-connectedness. On the contrary, OOS measures allow us to identify a number of banks that are net-exporters of volatility (UCG, ISP, BP, and UBI) and banks that are net-importers (CE, CVAL, CRG, BDB). This has implications for the nature of the Italian banking system: Although there is an undisputable evidence of gross-connectedness that emerges independently from the measures that we use, it is less obvious to identify which banks are influencing the others. In other words, it may seem that all banks influence and are influenced by all other banks, creating an approximately symmetric and compact system. However, when OOS measures are adopted, it appears evident that large banks (such as UCG and ISP) are net-exporters of volatility shocks, while smaller banks are net-importers.

As it is often the case with applied studies, there are a number of parameter and methodological selections that it may be interesting to experiment with, adopting solutions that differ from the ones followed in this paper. For instance, the implementation of an OOS variance decomposition implies balancing a training/estimation sample with an OOS assessment period that we have simply kept fixed to a reasonable as well as conventional choice in our work. However, different choices could and should be explored. Additionally, it would be useful to develop a framework to proceed to a rigorous form of back-testing of the different methodologies that however would require the definition of one or more compelling loss functions to perform the evaluation.

---

Conflict of interest

The authors declare no conflict of interest.

---

Supplementaries

---

Appendix A. Bootstrapping p-values for in-sample variance decomposition connectedness measures

The bootstrap consists of the following steps:

1. For a given set of observations $\left\{ {{\mathit{\boldsymbol{x}}_t}} \right\}_{t = \tau - {T_C} + 1}^\tau$, corresponding to a single rolling window, we estimate 5 under $H_0^{IS}$:

${\mathit{\boldsymbol{x}}_t} = \mathop \sum_{i = 1}^p \mathit{\boldsymbol{A}}_i^0{\mathit{\boldsymbol{x}}_{t - i}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_t} + {\mathit{\boldsymbol{\varepsilon }}_t}$

(A1)

Where $\mathit{\boldsymbol{A}}_i^0$ is restricted to be a diagonal matrix.

2. Using the estimated coefficients $\mathit{\boldsymbol{\hat A}}_i^0$ and ${\mathit{\boldsymbol{\hat B}}}$, we calculate the residual series:

${{\mathit{\boldsymbol{\hat e}}}_t} = {\mathit{\boldsymbol{x}}_t} - \mathop \sum_{i = 1}^p \mathit{\boldsymbol{\hat A}}_i^0{\mathit{\boldsymbol{x}}_{t - i}} + \mathit{\boldsymbol{\hat B}}{\mathit{\boldsymbol{w}}_t}$

(A2)

With $t = \tau - {T_C} + p + 1, \ldots, \tau .$ From these vector residuals $\left\{ {{{\mathit{\boldsymbol{\hat e}}}_t}} \right\}_{t = \tau - {T_C} + p + 1}^\tau$ we extract the series of residuals of the jth variable $\left\{ {{{\hat e}_{j, t}}} \right\}_{t = \tau - {T_C} + p + 1}^\tau$.

3. We proceed by rescaling the residuals $\left\{ {{{\hat e}_{j, t}}} \right\}_{t = \tau - {T_C} + p + 1}^\tau$ so that their sample variance matches the value of the unbiased estimator for $E\left({\varepsilon _t^2} \right)$:

${{\ddot e}_{j, t}} = \sqrt {\frac{{{T_C} - p}}{{{T_C} - p - K}}} {{\hat e}_{j, t}}$

(A3)

Where $K = p + 1$ for the VAR_C(p) and $K = p + 2$ for the VAR_CT(p).

4. From the jth set of rescaled residuals $\left\{ {{{\ddot e}_{j, t}}} \right\}_{t = \tau - {T_C} + p + 1}^\tau$, we draw with replacement M independent series $\left\{ {\ddot e_{m, j, t}^*} \right\}$ of length ${T_c} - p$ with $m = 1, \ldots, M$.

5. For each $m = 1, \ldots, M$, the series $\left\{ {\ddot e_{h, j, t}^*} \right\}$ are used as random innovations to generate a new, bootstrapped stochastic process through the recursion:

$\mathit{\boldsymbol{x}}_{h, t}^* = \mathop \sum_{i = 1}^p \mathit{\boldsymbol{\hat A}}_i^0\mathit{\boldsymbol{x}}_{h, t - 1}^* + \mathit{\boldsymbol{\hat B}}{\mathit{\boldsymbol{w}}_t} + {\left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\ddot e_{h, 1, t}^*}&{\ddot e_{h, 2, t}^*} \end{array}}&{\begin{array}{*{20}{c}} \cdots &{\ddot e_{h, N, t}^*} \end{array}} \end{array}} \right]'}$

(A4)

Which mimics 15.

6. Each series $\left\{ {\mathit{\boldsymbol{x}}_{m, t}^*} \right\}_{t = \tau - {T_C} + 1}^\tau$ is now used in place of $\left\{ {{\mathit{\boldsymbol{x}}_t}} \right\}_{t = \tau - {T_C} + 1}^\tau$ in 5–9 to obtain a set of M variance decomposition matrices under $H_0^{IS}, \tilde D_{m, \tau }^{0, IS},$ and M connectedness measures under $H_0^{IS},$ $C_{ \star, m, \tau }^{0, IS}$, as defined in 1–4.¹³

¹³ $\star$ is the placeholder for one of the four connectedness measures, FROM, TO, NET or TOTAL.

7. Given the M connectedness measures $C_{ \star m, \tau }^{0, IS}$ under $H_0^{IS}$ and the connectedness measure $C_{ \star, \tau }^{IS}$, the bootstrap p-value for an upper tail test is then:

$p_{ \star, \tau }^{IS} = \frac{1}{M}\mathop \sum_{m = 1}^M I\left({C_{ \star, m, \tau }^{0, IS} > C_{ \star, \tau }^{IS}} \right)$

(A5)

Where $I\left(\cdot \right)$ is an indicator function that takes a value of 1 if the condition $\left({C_{ \star, m, \tau }^{0, IS} > C_{ \star, \tau }^{IS}} \right)$ holds and 0 otherwise. We reject $H_0^{IS}$ if $p_{ \star, \tau }^{IS} < \alpha$, where $\alpha$ is the chosen significance level of the test.

---

Appendix B. Bootstrapping p-values for OOS variance decomposition connectedness measures

The bootstrap consists of the following steps:

1. For a given set of observations $\left\{ {{x_t}} \right\}_{t = \tau - {T_M} + 1}^\tau$ corresponding to the first rolling window of length ${T_M}$, we estimate 5 under $H_0^{OOS}$:

${\mathit{\boldsymbol{x}}_t} = \mathop \sum_{i = 1}^p \mathit{\boldsymbol{A}}_i^0{\mathit{\boldsymbol{x}}_{t - i}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{w}}_t} + {\mathit{\boldsymbol{\varepsilon }}_t}$

(B1)

Where $\mathit{\boldsymbol{A}}_i^0$ is restricted to be diagonal.

2. Using the estimated coefficients $\mathit{\boldsymbol{\hat A}}_i^0$ and ${\mathit{\boldsymbol{\hat B}}}$, we calculate the minimum MSE forecast $\mathit{\boldsymbol{\hat x}}_{\tau + H|\tau }^0$ under $H_0^{OOS}$ and the corresponding out-of-sample forecast error under $H_0^{OOS}$:

$\mathit{\boldsymbol{\hat e}}_{\tau + H}^{0, OOS} = {\mathit{\boldsymbol{x}}_{\tau + H}} - \mathit{\boldsymbol{\hat x}}_{\tau + H|\tau }^0$

(B2)

3. For a given set of out-of-sample forecast errors under $H_0^{OOS}$ $\left\{ {\mathit{\boldsymbol{\hat e}}_t^{0, OOS}} \right\}_{t = \tau - {T_C} + 1}^\tau$, corresponding to the rolling window of length ${T_C}$, we extract the set of out-of-sample forecast errors of the jth variable $\left\{ {\mathit{\boldsymbol{\hat e}}_{j, t}^{0, OOS}} \right\}_{t = \tau - {T_C} + 1}^\tau$. From this set, we draw with replacement M independent series $\left\{ {\mathit{\boldsymbol{\hat e}}_{m, j, t}^{*, OOS}} \right\}$ of length ${T_c}$ with $m = 1, \ldots, M$.

4. For each $m = 1, \ldots, M$, we calculate the out-of-sample H-step ahead forecast error covariance matrix under $H_0^{OOS}$ as:

${\bf{\hat \Sigma }}_{m, \tau }^{OOS} = \frac{1}{{{T_C}}}\mathop \sum_{t = \tau - {T_C} + 1}^\tau \left({\left[ {\begin{array}{*{20}{c}} {\hat e_{m, 1, t}^{*, OOS}}\\ \vdots \\ {\hat e_{m, N, t}^{*, OOS}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\hat e_{m, 1, t}^{*, OOS}}& \cdots &{\hat e_{m, N, t}^{*, OOS}} \end{array}} \right]} \right)$

(B3)

5. The resulting M matrices ${\bf{\hat \Sigma }}_{m, \tau }^{OOS}$ are used in place of ${{\bf{\Sigma }}^{OOS, H}}$ in equations 11–12 to obtain a set of M variance decomposition matrices under $H_0^{OOS}, \tilde D_{m, \tau }^{0, OOS},$ and M connectedness measures under $H_0^{OOS},$ $C_{ \star, m, \tau }^{0, OOS}$, as defined in 1–4.

6. Given the M connectedness measures $C_{ \star, m, \tau }^{0, OOS}$ under $H_0^{OOS}$ and the connectedness measure $C_{ \star, \tau }^{OOS}$, the bootstrapped p-value for the upper tail test is:

$p_{ \star, \tau }^{OOS} = \frac{1}{M}\mathop \sum_{m = 1}^M I\left({C_{ \star, m, \tau }^{0, OOS} > C_{ \star, \tau }^{OOS}} \right)$

(B4)

Where $I\left(\cdot \right)$ is the indicator function, with has value 1 if the condition $I\left({C_{ \star, m, \tau }^{0, OOS} > C_{ \star, \tau }^{OOS}} \right)$ holds and 0 otherwise. We reject $H_0^{OOS}$ if $p_{ \star, \tau }^{OOS} < \alpha$, where $\alpha$ is the significance level of the test.

---