1. Introduction
Information is a key element of financial decision-making. However, the link between information and financial activity is complex. Hamilton et al. (2007) note that, due to the rapid financial innovation, deregulation and global capital market integration, financial intermediation and market activity have realized tremendous growth and structural change throughout the globe. These developments have profound implications for the riskiness, management and performance of the global financial system. The speed of change and its impact on financial market activity has been largely the result of advancements in information and data management technology. The latter has enabled the automation and computerization of work processes and business functions, as well as the generation and rapid processing of large volumes of data that have in turn driven innovation in new financial products and strategies. The globalization and integration of financial markets has accelerated changes in financial data infrastructure, leading to a sharp increase in global interconnectedness of financial markets and institutions that mediate financial activity.
Further, following the recent financial crisis, the accurate calculation of systemic risk has become a core policy concern. Systemic risk modelling uses financial market data. The latter are relatively easy to collect, are public, and are quite objective. However, market data may not reflect the true fundamentals of the underlying financial institutions, and may lead to biased estimates of the probability of failure. This bias may be stronger when referring to the probability of network failures. Idier et al. (2013) show that market data models are not much reliable in predicting systemic risk. Fantazzini and Maggi (2013) similarly show that market data models may be good in very short-term predictions, but not in medium and long-term ones. Indeed, market prices are formed through complex interaction mechanisms that often reflect speculative behavior rather than the fundamentals of the companies to which they refer. Market models and financial network models based on market data may therefore reflect "spurious" components that could bias systemic risk estimation. This weakness of the market suggests the need to enrich financial market data with data coming from other, complementary, sources. Evaluation criteria for the riskiness of financial institutions include not only market prices but also credit ratings, reports of qualified financial analysts and opinions of influential media, among others. Thus, data capturing diverse signals almost in real time, offer the opportunity to extract new useful evaluation information that can complement market prices and substitute market information when not available (e.g. unlisted financial institutions, shadow banking, etc.).
These developments have revealed the inadequacy of traditional risk identification methods and of functional supervision by sector or institution as well as raised the importance of the effective monitoring and regulating of the stability of the financial system as a whole. Policy analysis has accordingly moved to a new framework that focuses on risks to the system as a whole and tends to analyze the financial system as a complex adaptive system. Drawing on Arthur(1995, 1999), the concept and analysis of complex adaptive systems is increasingly used to study complex phenomena in many research disciplines. Farmer et al. (2012) note that the analysis of complex systems uses techniques, which are different from those used in conventional economic theory, such as optimization under constraint. The new techniques include network analysis, agent-based modelling, non-linear dynamics, catastrophe theory and the theory of critical phenomena, as well as data mining. In particular, agent-based modelling conceives of the financial system as made up of interacting individual agents (people, firms, regulators, governments), each with the capacity to act with purpose and intent, each of which is acting in the context of networks in which the fundamental behavior of the agent is not fixed, but evolves in response to the behavior of others. Miller and Page (2007) note that the use of computational models as a primary means for exploring the financial system complexity is important for various reasons. First, such models embrace systems characterized by dynamics, heterogeneity, and interacting components and are therefore suited for complexity analysis. Second, they require clarifications about how they can be used to study socioeconomic outcomes and therefore need to be further advanced. Third, given existing trends in the speed and ease of use of computation and the emergence of big data, computation models will become a predominant means by which to explore the world. Anand et al. (2012) argue that the challenge financial regulators are facing today in adopting computational models and frameworks to improve the understanding of risks to the financial system as a whole, is that traditional financial analysis has typically been based on an individual institution, sector, geographical location or some other partial level. That has led to the development of regulatory definitions, tools, and approaches, which are best in analyzing outcomes when studying at that partial level but not at the financial system as a whole. As instruments become increasingly complex and institutions and markets become increasingly interconnected, this segmented approach cannot provide the concepts and tools for supporting analysis of financial markets as an integrated complex network system. Haldane (2009) notes that risk measurement in financial institutions and systems has been idiosyncratic. Risks have been evaluated only by type and by institution. However, in a network, this individual node-focused approach gives little sense of risks across institutions and much less to the overall system comprising many networks, which are also expanding.
Based on these developments, Mertzanis(2013, 2014a) notes that risk management practice today has to operate within a complex financial environment, that includes complex instruments, processes, institutions and systems. Following financial innovation and changing demand patterns, financial instruments have evolved to include complex and opaque products traded in less transparent market environments. Financial behavior patterns are inadequately approximated by normal distributions thus restricting predictability. The links and interactions among financial institutions and between them and the financial system as a whole are complex and instrumental in determining the system's behavior that feeds back on the performance of institutions. The elucidation of complex instrument valuation, information generation dynamic processes, and system-wide interactions among market actors globally could allow financial institutions to respond more efficiently to events that not only affect their own financial positions but also cause feedbacks between market actions and asset valuation thus affecting performance. Complexity analysis can address these issues and inform risk management practice. In this respect, the quality of information, the integration of diverse and complementary signals and the management efficiency of all that data and information are key challenges in this process. Lin et al. (2018) provide some relevant empirical evidence of different measures of systemic risk under complexity conditions.
The purpose of this paper is to explore how complexity analysis can be used to inform the management of financial risks in modern complex financial environments characterized by system-wide interconnections that give rise to big data. Complexity characterizes financial instruments, financial processes and financial systems. Each type of complexity is examined and the implications for financial risk management are explored. Then, the paper draws the implications of financial complexity for big data management and introduces the global legal identifier initiative designed to deal with granularity and comparability of financial big data globally. The paper aims at highlighting the link between complexity in finance and big data challenges and provide a background for understanding the legal entity identifier initiative used to manage the association. While the merits and application of complexity theory to finance are still a matter of debate, complexity analysis could contribute to the formation of a coherent body of propositions that are capable of better approximating reality in financial systems, i.e. explain the stylized facts in finance and manage financial system risk. In this respect, the proper treatment of big data is essential to this endeavor.
In what follows, section 2 analyzes the nature of complexity in finance, section 3 analyses the implications of complexity in finance for risk management, section 4 outlines the link between complexity in finance and big data and finally section 5 concludes the paper.
2. Complexity in financial activity
If complexity analysis is to be useful in understanding financial behavior, the question arises as to whether the financial system is a complex system and its behavior can be depicted by evolutionary science. Arthur(1995, 1999) argues that the financial system is a complex system in at least five respects: financial markets are open, dynamic systems, far from being in equilibrium; financial activity actors are made up of heterogeneous agents, lacking perfect foresight, yet able to learn and adapt over time; agents interact through various more or less robust financial networks; macro-financial patterns emerge from micro-financial behaviors and interactions; and evolutionary processes create novelty generating growing order and complexity over time. Complexity is often loosely defined, but in all respects is meant to convey a difficulty to understand or apprehend and thus to predict financial actions and outcomes based on the use of simplistic linear functions. The relevant literature has broadly identified three dimensions of complexity in finance: financial instrument complexity, financial process complexity and financial system complexity. These dimensions of complexity interact with each other in accordance with prevalent market structures, agent actions and models used. Each dimension is briefly analyzed below.
2.1. Complex financial instruments
The first dimension of financial complexity refers to financial instruments and their pricing. Complex financial instruments, such as asset-backed securities, collateralized debt obligations (CDOs) and credit default swaps, have attracted much of the blame for the recent crisis. The complexity and the interconnections—the long chains of claims embodied in the financial engineering, re-packaging, and synthetic derivatives make it almost impossible for people to understand and price risks. The chains of borrowing and lending make it difficult to trace interdependencies among counterparties and with respect to the amount and character of the collateral securing liabilities. This is a problem with respect not only to the underlying assets, but also to the various instruments used for refinancing along the chain, such as repurchase agreements and securities lending. Under these circumstances, it is not surprising that risk is not well priced. Christophers (2009) notes that, while these instruments are not overtly complex themselves, the methods for pricing them almost certainly are. The substantial difficulty in pricing complex financial instruments and determined transactions on them, even when buyers know relevant information and use simple models of asset pricing, goes beyond the asymmetric information problem in financial markets. Regardless of the sophistication of financial agents, in such circumstances rationality cannot be assumed. Understanding complex financial instruments and their impact on financial behavior at both the micro- and macro-level requires comprehensible pricing mechanisms and investment strategies, both of which today rely on big data collection, management and analysis. The increasingly complex chain of tranching and distributing risks that characterizes the structure of complex instruments makes the derivation of fundamental values and risk profiles of underlying assets hard or impossible to reconstruct even by sophisticated investors. Complex instruments deepen the intricate links among assets and counterparties thus concealing agency costs and obscuring the underlying financial investment processes. Further, Arora et al. (2009) note that, since the value of complex financial instruments depends on the complex interaction of numerous attributes of their constituent elements, the issuer can easily tamper such instruments without an investor or risk manager being able to detect it within a reasonable amount of time. Each new complex instrument can be an opportunity for mispricing to the favor of the issuer. Designers of financial products tend to rely on computational intractability to disguise their information via suitable cherry picking. Tett (2008) notes that higher complexity and lower transparency typically enhance profit margins and therefore provide the issuer the incentive to keep the innovation cycle running.
Outstanding exposures on complex financial instruments have potential system-wide risk implications. Such instruments contribute to systemic risk in two ways. First, the imprecise valuation of riskiness of complex instruments complicates both internal risk management and the evaluation of aggregate exposures. A concentrated position or a series of counterparty relationships pose the risk of joint failures if market participants and regulators fail to understand and accurately value these instruments. Second, the imprecise valuation of complex instruments can exacerbate procyclicality. Market booms are characterized by financial innovations, which tend to create hidden, underpriced risks. Institutions feel confident to experiment, creating new, untested instruments that are difficult to understand and value. Investors tend to be highly optimistic about future economic conditions without seriously considering the possible risks when markets deteriorate; institutions have little incentive to convince them otherwise. However, as the boom begins to wane, the unseen risks materialize causing a deepening of the retrenchment that is already underway. Although financial innovation is a source of progress, it can also become a source of procyclicality that exacerbates system-wide risk.
In order to deal with these problems, financial intermediaries must report adequate information on the issuance of such complex instruments and report executed cash and derivative transactions without delay in order to properly match buyer and seller, including information on the size, type, counterparty involved, and reason for the trade.
2.2. Complex financial processes
The second dimension of financial complexity refers to financial processes generating information on market outcomes. Observed financial time series in many markets over several decades have exhibited some puzzling empirical regularities (stylized facts) which proved difficult to model. Stylized facts are universal regularities, independent of time, place and composition details, and they are taken as benchmarks for theory testing. Simon (1955), Shleifer (2000) and Keim (2008) show that the puzzling statistical properties (anomalies) of financial time-series remain a puzzle for standard financial theory. These puzzles imply reduced predictability of financial returns. Cont (2001), Bouchaud and Potters (2003) and Sornette (2003), among others, argue that the most important stylized facts in finance which are relevant to complexity analysis include: (a) fat tails: the distribution of returns of financial assets, evaluated at high frequencies, exhibits fourth moments (kurtosis) that are anomalously large when superimposed over a normal (Gaussian) probability distribution. The latter is bell-shaped and assigns greater probability to events at the center (higher peaks) than at the extreme parts (narrow tails). Observed time-series of financial returns display a significantly larger number of extreme events than a Gaussian process would predict. The standard theory of finance cannot explain fat tails as it relies on the normal distribution. This implies that massive fluctuations (disruptions or financial crashes) are assigned a diminishing small probability and therefore cannot be adequately predicted. (b) Volatility clustering: periods of intense fluctuations and mild fluctuations of financial returns tend to cluster together: Big price changes of either sign follow big price changes, and little ones of either sign follow little ones (conditional heteroscedasticity of returns). The standard theory of finance cannot explain volatility clustering for the underlying Gaussian process of time-series generation that predicts a uniform time distribution of both large and small fluctuations in returns. (c) Volatility persistence (long memory): financial returns are interdependent over time following a nonlinear pattern. This means that return volatility exhibits slowly decaying autocorrelation rather than a quick decay to zero as the efficient market hypothesis would predict and the Brownian motion model would explain. (d) Interaction of volatility clustering and persistence: volatility persistence is related to volatility clustering. The clustering itself generates excess volatility (fat tails). Explaining the clustering and long memory most likely constitutes an explanation of the fat tails. Overall, financial return volatility changes by too much, too often, and with too much order to fit the geometric Brownian motion model used by the standard finance theory. The latter cannot explain the quantity and frequency of large crashes that have been witnessed in the recent decades because it assigns lower probabilities to extreme events. Because of the clustering and interdependence, time series of financial returns exhibit too much predictability and therefore the relevant data cannot be assumed to be generated through a random walk process. (e) Leverage effect: past stock returns are negatively correlated with stock price volatility, that is stock price volatility tends to increase when stock prices drop, exhibiting negative skewness. As a company's stock price declines, it becomes more highly leveraged given a fixed level of debt outstanding, and this increase in leverage induces a higher equity-return volatility. (f) Increasing downside correlations: cross correlations increase in high volatility market conditions, in particular when prices drop significantly, without assuming that financial returns are time-dependent.
In order to explain the puzzling stylized facts, some financial economists have used empirical models based on big data without adequate theoretical grounding. The purpose of using big data is to replicate the statistical properties of observed patterns, especially in abnormal market conditions, which accord well with observed financial patterns. However, financial information is mostly discrete in nature and researchers have used high-frequency data in an effort to explain stylized facts. To obtain better explanation, diverse forms of big financial data are used. These include varying forms of velocity (batch vs. streaming data), variety (structured vs. unstructured), volume (terabytes) and veracity (uncertain vs. certain information). Different processing models are developed to deal with such data requirements.
2.3. Complex financial systems
The third dimension of financial complexity refers to the structure and behavior of the financial system as a whole. The financial crisis has highlighted the need to look at the links and connections between financial institutions and markets and the financial system as a whole. Failure of certain institutions and/or major disruption in certain markets can rapidly spill over to other institutions or markets and eventually to the whole financial system. Brunnermeier et al. (2008) and the IMF (2009) note that remote triggering event, such as a financial institution failure or a market disruption, can cause a widespread disruption of the financial system as a whole, creating significant problems in otherwise viable institutions or markets.
The financial system may prove more or less resilient to contagion depending on the nature of major triggers and prevalent channels of contagion. The crisis has shown that an apparently robust financial system may in fact become fragile. This results from the large number of interconnections within the financial system that serve as shock-amplifiers rather than shock absorbers. Financial institutions, linked through the interbank market, payment systems, monoline insurers and custodian banks, belong to financial networks with strong degree of interconnectivity and therefore systemically important. Understanding network structures is crucial for the identification of systemically important institutions and markets. The resilience of the financial system as a whole depends on proper maintaining of individual institutions' liquidity buffers and capital reserves as well as on controlling large exposures and addressing interdependencies. A particular financial institution might not only be critical to the normal functioning of financial markets or infrastructures because other institutions are financially exposed to it, but also because other market agents rely on the continued provision of its services which will not be forthcoming. Thus, the impact of a failure of a given institution or market or network also hinges on the ability of the financial infrastructure to support its resolution and to facilitate the orderly unwinding of financial exposures.
Haldane (2009) stresses that modern financial systems are characterized by complexity and homogeneity. Complexity means that the financial system is characterized by an increasingly knotted and uneven interconnectivity; more financial institutions do more business deals with more counterparties on a global scale. Homogeneity means that the financial system becomes more adaptive since behavior is driven by optimizing agents who herd and blindly jump on the next big opportunity so long as their peers are profiting without regard to the negative impact of their move on the system as a whole. Being adaptive means converging: financial institution balance sheets grew all alike; their risk models were more and more assimilated and the associated risk management strategies grew alike; strategic behavior grew alike; financial regulation grew alike through unified rulebooks regarding market operations characterized by free mobility of financial capital. Financial institutions looked alike and responded alike. Most market participants have instant electronic access to risk-return data for financial assets worldwide out of Bloomberg as everyone else. Diversification strategies by individual firms generated a lack of diversity across the system as a whole. The common pursuit of return and the uniform risk management practices explain the reduction in diversity in the financial sector. Financial institutions were racing for return on equity, which led them to pursue high-yield activities. The result was that business strategies were replicated across the financial sector. Simultaneously, risk management models became homogenous, in part because credit ratings were hardwired into regulation and Basel II provided the same rules for everyone. The consequence was a highly homogenous financial system that was less resistant to aggregate shocks, the same as ecosystems where diversity is lower. Markets segmentation is disappearing; investment behavior becomes more and more alike decided by ever-larger pools of institutional players worldwide.
The combination of complexity and homogeneity of a financial system causes fragility and instability. In complex financial systems, scaling up risks may result in building up error cascades. The reason is cross-contamination. As losses build up, links and interconnections serve as shock amplifiers, not shock absorbers. Persaud (2000) notes that, while the system is mostly self-repairing, it also exhibits a knife-edge property, which under growing homogeneity and complexity bears the danger of collapse. Financial institutions are interconnected, making them ideal candidates for risk contamination. The biggest, most complex and best-connected ones are systemically important with a high capacity to infect counterparties.
Complexity and homogeneity in market behavior undermine the stability of the financial system. While market agents start by exhibiting heterogeneous behavior, exogenous shocks may eventually drive them to homogenous reaction. In this regard, risk is amplified endogenously and the initially robust financial system turns out to become fragile. The Warwick Commission (2010) stresses that the endogeneity of risk and the rising system fragility are the result of the following factors: the increasing reliance of asset valuation and risk assessment on market prices (mark-to-market valuation); the extensive reliance of funding on leverage; and the tendency of regulators and practitioners to consider risk as one thing, to be treated the same way and measured as the volatility of short-term prices. However, risk is not one thing alone, there are different types of risk: credit risk, counterparty risk, liquidity risk and market risk, mutually distinct and interacting with each other. Different types of risk should be hedged differently. Credit risks are best hedged by finding uncorrelated or negatively correlated credits. Liquidity risks are best hedged across time: the more time you have before you have to sell an asset, the more you can hold assets that are hard to sell quickly. Market risks, like equity values, are best hedged using a combination of time and diversification.
Schleifer and Vishny (1997) and Gromb and Vayanos (2010) argue that today the risk-return trade-off is more easily observed but less easily explored. Stabilizing arbitrage opportunities tend to vanish. Based on the wealth of information readily accessible by everyone, financial assets that appear to offer a slightly higher return than past risk trade-off patterns are identified almost simultaneously by all interested traders. Everyone rushes in at the same time and the asset quickly becomes overvalued, leading to an increase in volatility, which in turn raises the risk profile of the asset, directing risk models to confirm the rise in volatility, thereby inducing everyone to sell, with the result of creating more volatility.
Persaud (2003) notes that the tendency toward the cliff edge is stronger when the homogenizing behavior of markets is coupled with strategic behavior. Strategic behavior can be understood by reference to Keynes's example of beauty contest: market behavior is driven by what investors think about average market beliefs on average market beliefs and so on. Traditional risk models do not capture strategic behavior, since risk calculations are based on Black-Scholes-Merton arbitrage-driven models of asset pricing which treat individual investment behavior as an independent atomistic activity, that is being unrelated to the actions of others. Allen et al. (2006) argue that, once strategic behavior is taken into account, asset prices can then be shown to deviate significantly from competitive market prices.
Complexity and homogeneity make inherent risk-return characteristics of financial assets difficult to infer. As a result, an investor cannot credibly estimate, based on optimization of the mean-variance relationship, the probability of loss of an investment. Risk is not a statistical but a behavioral metric. Thus, professional risk management cannot be driven by personal and detached views of market conditions in an effort to locate assets with better risk-return characteristics. The emphasis must be shifted to network behavior. In this case, the key questions are: (i) which network architectures are resilient to endogenous and exogenous shocks; (ii) how incentive structures lead the financial system into its current network architecture; (iii) how simple indicators and stress-tests can anticipate systemic distress; and (iv) what policies can modify incentives and lead the financial system into more shock resilient architectures? Big data analysis is key in answering these questions.
3. Complexity and financial risk management
3.1. Managing complex financial instruments
Financial innovation can provide flexibility in financial markets under two conditions: (a) underlying assets must have appropriate quality with sufficient historical records of defaults and a lucent relationship to macroeconomic developments; and (b) complex reengineering structures must be avoided for they lead to more opaqueness and vulnerability to macro shocks and therefore to ambiguity in pricing. Transparency about complex instruments and structures is crucial. However, for some instruments, disclosed information, even if kept up with market needs, would have been futile since instruments are so complex that the required information to appropriately monitor and price risks may be overwhelmingly large. Excessive information overload may limit the effectiveness of disclosure. This possibility points to a need for controlling complexity and for encouraging appropriate design of disclosure through a good summary of properties and clarity about the assumptions in valuation.
Further, disclosed positions must adhere to consistent standards of information aggregation. Complex instruments are bought and sold in different private markets characterized by varying information. In stressed situations, the undisclosed positions of risky complex instruments raise counterparty risk and ambiguity with regard to the trading volume deteriorating liquidity, particularly in over-the-counter markets. In the respect, three core policy issues arise, relating to the proper content, extent, and manner of information disclosure. Proper identification of significant information is required. Disclosure rules must produce information that is adequate and suitable for generating synthetic risk indicators, based on quantitative metrics that are robust, objective and backward verifiable. Transparency concerns must focus not only on the generation of information per se but also on its use through standardized risk representation and cost profiling for proper monitoring of markets and proper allocation of regulatory oversight. The traditional identification of financial risks seems inadequate in allowing informed investment decisions and effective risk management in a context where the integration of financial markets, instruments and participants often makes it difficult to separately analyze different financial risks. Thus, the focus should instead be on measuring and monitoring of the overall (rather than idiosyncratic) synthetic risk profile of complex instruments.
However, identifying the content of information is not enough. The timely and proper collection of information about complex financial instruments and the proper release of aggregate information are important. Both whether and how public information is released matters. Morris and Shin (2002) show that disseminating public information may increase or decrease social welfare depending on agents' access to information, strategic complementarities in decision-making and heterogeneous beliefs. The release of public information is beneficial only if it is sufficiently accurate and comprehensible.
3.2. Managing complex financial processes
Analytical models that strive to predict the dynamics of complex processes often include a term representing a random (stochastic) factor. In order to explain stylized facts in financial markets, models deploy random terms within an analytical structure involving fundamentals, exogenous rules/constraints, equations, and interactions. Sprott (2003) shows that the processes used to reproduce the stylized facts are divided into static and dynamic ones. The dynamic ones are further divided into deterministic and non-deterministic ones. Deterministic processes behave according to specified rules or equations that determine the next state of the process based on the current state of the process. For instance, a rule might be to always buy/sell all financial assets included in your portfolio only when all your interacting traders are buying/selling their financial assets: if this rule and the current state of uncertainty in the market are known, then the next state of market uncertainty can be predicted and the suitable risk management practice identified. Non-deterministic processes exhibit state independence—the same set of parameter values and initial conditions lead to different outcomes across states (confidence interval with a most-likely point estimate). Nothing in the course of the process at time one will determine its course at time two. This state independence is generally known as randomness. Non-deterministic dynamic processes can assume either a mild (Brownian) or a wild (Mandelbrot-like) motion. Mandelbrot (1997) shows that the use of Brownian dynamics in finance has not produced a clear structure or pattern of behavior of financial returns, making the latter rather unpredictable.
The importance of deterministic vs. non-deterministic dynamics for financial systems can be assessed by their ability to generate predictability and their capacity to generate complex forms and patterns. Modeling financial behavior has largely relied on linear mathematics with the addition of stochastic terms, that is, by utilizing some linearity with some mild Brownian randomness. Mandelbrot (1997) notes that actual financial behavior may be better understood by the use of nonlinear chaotic system analysis with a dash of wild randomness possessing a fractal quality and adhering to power-law distributions. The wild Brownian distribution exhibits both infinite variance and some dependence (long memory) of returns.
The relative merits of the different dynamic processes in approximating actual financial outcomes depend on whether financial systems are complex systems properly defined. The issue has been of particular interest to physicists. Borland (2005), Stanley et al. (2001) and Johnson et al. (2003) argue, among others, that the behavior of financial markets is one of the most vivid examples of complex system dynamics. Financial market processes are assumed to follow power laws observed in nature. It is still debatable whether the theory of critical phenomena and power laws can provide a universal mechanism for explaining the stylized facts in finance under different conditions. Nonetheless, Chakrabarti and Chakraborti (2010) note that alternative models have emerged that generate probability distributions that better approximate the stylized facts than does the normal (Gaussian) one used in standard risk management models. These models are a promising avenue for exploration by risk management practitioners. They are all data-intensive models.
3.3. Managing complex financial systems
The management of complex financial systems requires the understanding of two key elements: network topology and endogenous risk. Focusing on the role of networks, Latora and Marchiori (2004) argue that the understanding of how complexity affects the behavior of the financial system requires the understanding not only of dynamic behavior but also of the structure of links and interconnections among financial institutions and markets. Complex systems research needs to consider the structural features (topology) of financial networks rather than merely focus on the specific form of the nonlinear interactions between individual subunits. Soramäki et al. (2007) argue that network analysis can be effectively used to analyze financial behavior of interconnected institutions and markets in a complex financial system. Financial networks consist of a collections of nodes (financial institutions) and links between nodes (credit and financial relationships: assets and liabilities) affecting the attributes of the nodes (i.e. an institution's balance sheets is affected by existing links with other institutions), and the structure of the links affects the performance of the financial system as a whole. Network analysis looks at the structure of the links and the manner in which the structure affects the performance of the financial system as a whole. It includes three main areas of concern: the structural properties of a network (distribution of node degrees, diameter of the graph) to produce the appropriate graphs for the various domains in finance (different financial systems); the calculation of measurable quantity of flows within the network (financial asset/liability transfers); and the dynamical properties of network structure. The generation of actual data pattern depends on both the graph structure and the algorithm used for manipulating the graph. Haldane (2009), the ECB (2010) and Caballero and Simsek (2009) argue that direct and indirect interlinkages and contagion dynamics among financial institutions, as well as between institutions, markets and infrastructures, can be influenced by three important network characteristics: the degree of connectivity, the degree of concentration, and the size of exposures. The strength of the various shock amplification mechanisms in the web of financial connections depends on the size of aggregate macroeconomic shocks, asset price volatility, liquidity risk and financial leverage. Moreover, network analysis can be used to simulate the effect of credit and funding shocks on financial stability by taking into account not only direct balance sheet exposures but also the impact of contingent claims and credit risk transfer techniques. Overall, complexity is manifested through four mechanisms: connectivity, feedback, uncertainty and innovation. Within a certain range, connections help absorb shocks, but beyond that range connections are shock amplifiers. Connected networks exhibit long tails in the degree distribution, which is the distribution of the number of links per node. Long-tailed distributions are more robust to random disturbances, but more susceptible to targeted attacks. In particular, if a large financial institution is subject to stress, the effects are more likely to spread through the network. Uncertainty about the network structure has pricing implications, which increase with the expanded dimensionality of the network. Thus, modern risk management should strive to integrate financial network characteristics in the analysis.
Moreover, the conception of risk in the financial system needs to change. The standard risk management model divides risk into idiosyncratic and deterministic components. Within this model, markets are assumed to operate efficiently—i.e. they operate based on a law of conservation of risk. The latter states that financial institutions are efficiently allocating risk throughout the system, and risk is neither created nor destroyed but merely shuffled around. In fact, risk follows a dynamic process in which it is destroyed and created in the course of trading activity. Shifting risk may allow for more efficiency in terms of costs to market agents, but what may be lacking in standard risk models is the notion that system-wide risk is more than the sum of its idiosyncratic parts, thus justifying its complex nature.
Financial markets today represent an environment in which traders react to what is happening around them and their reactions shape the realized outcomes. Shin (2008) notes that, whenever there is a conjunction of both participants (traders) reacting to their environment (markets) and participants actions affecting their environment, risk is endogenous A sudden, exogenously-caused drop in asset prices brings traders closer to their trading limits thereby forcing them to sell, which sets off further downward pressure on asset prices, causing a new round of selling and so on. The downward spiral in asset prices is endogenous, generated within the financial system. Any market-sensitive management of risk will consequently have destabilizing effects. Persaud (2008) further notes that financial crashes and collapses are not random or deterministic events, nor can they generally be depicted by Markov approximations. Financial crashes are not once in thousand-year events as standard value-at-risk measures would predict, but occur every five-six years during the last three decades. They always follow historically specific, man-made financial booms, which occur because people are making investments that they believe to be "safe" but instead lead to hidden risks, often coupled with excessive leverage, made possible by prevalent monetary conditions. The management of risk of a crisis presupposes the management of the preceding financial boom. The credit mistakes that lead to crashes are not made in the crash, but during the preceding booms. The fundamental problem of crashes is that risks are underestimated in the boom and overestimated in the crash in a cumulative manner. This is not simply a result of investor irrationality but rather an inherent future of how financial systems function.
If the underlying uncertainty facing a trader were exogenous, modeling financial risk may be akin to a gambler facing a spin of a roulette wheel, where the bets are placed by him/her and other gamblers do not affect the outcome of the spin. Current risk management practices presuppose a roulette view of uncertainty, whereby the roulette has a large number of outcomes with different probabilities. As long as these probabilities are unaffected by the other gamblers' actions, the prediction of these outcomes and their respected probabilities can result from applying sophisticated statistical techniques to past outcomes. Current risk management responds by applying more and more refined and sophisticated statistical techniques for tracking the non-linear payoff structures arising from derivative instruments. However, to the extent that the stochastic (random) process assumed to govern asset price reactions depends on what other traders do, the prediction of possible outcomes cannot be made. The uncertainty facing traders is endogenous and depends on the actions of all market participants.
Accordingly, endogenous risk is not compatible with the law of conservation of risk whereby the total inflow of risk in a financial system must equal the total outflow of risk from the system, plus the change in the risk contained within the system. Endogenous risk means that, under certain conditions, financial risk can be created internally and amplified and not merely transferred from one form or person to another.
The endogeneity of risk should alert regulators and risk management practitioners into modifying existing measures of risk to make them more robust as well as using stress-testing and back-testing techniques. Regulators are moving into the adoption of a macro-prudential approach to the financial system regulation. Both regulators and risk practitioners must require financial institutions to revise and revalidate their risk models to include scenarios previously considered extreme or unexpected in their normal risk calculations. Artzner et al. (1999) argue that risk management practitioners need to produce coherent measures or risk. Mertzanis (2013) shows that Conditional VaR (CoVaR), extreme value, expected shortfall, expected regret and maximum drawdown are some alternative measures of financial risk devised to account for risk endogeneity and the interdependencies between financial institutions and the financial system. However, their implementation in risk management practice is awaiting and their efficiency remains to be proved. They are all data-intensive models.
4. Complexity and big data in finance
The management of risk of complex financial instruments, processes and systems requires that information and data is not only of high quality but also devoid of problems of fragmentation, incompleteness, and insufficient granularity of definitions and standards. Farmer et al. (2012) argue that most current data collection in economics is produced for econometric and dynamic stochastic general equilibrium modelling. These require aggregate data such as macroeconomic indicators from national accounts. In contrast, complexity- and agent-based modelling is best done with finer grained data, such as trades in financial markets with identity information, firm transactions, credit networks, transactions by individual consumers, and electronic text from the internet, etc. While some of these data is already collected in piecemeal form, much of it is never collected.
Current practice amounts to collecting data for a particular need or function. This is a reasonable approach when dealing with isolated instruments, markets or locations. However, it is not that useful when dealing with powerful interdependencies and interconnections between such instruments, institutions and markets in the financial system as well as the need to consider the behavior and risks to the financial network as a whole. All institutions can issue and trade all financial instruments in all markets, regulated and over-the-counter (OTC) ones, cleared and settled in all post-trade infrastructures. Further, both regulated and OTC derivatives derive their value from the underlying asset. An attempt to capture developments in OTC derivative products in isolation without linking them to the underlying position would not provide an analyst or risk manager with the full picture. A comprehensive analysis of derivative market risks needs to take account of entities holding both derivatives and cash positions in order to evaluate the impact of potential shocks.
Increasing the focus on complex instruments, processes and markets together is key to understand and deal with system-wide risks. Accordingly, macroprudential policy development requires changes in not only models, tools and framework used by regulators and financial stability authorities, but also crucially in the financial data infrastructure needed to support and implement analysis of the system-wide network. If regulators want to effectively assess the interconnectedness, interdependency and endogeneity of financial risks inherent in the globally integrated financial systems, they need to implement new approaches to financial data and its management based on the uniform definition and standardization of the key elements whether referencing an instrument, a contract, an entity/counterparty, a market, etc. These elements form the building blocks that jointly allow flexible data aggregation to support multiple objectives.
4.1. The nature of big data in finance
Financial intermediaries need to gain a better understanding of customers and their transactions in order to provide effective and differentiated services. Given that the amount of data grows, data collection occurs more frequently and data variety becomes more complex, both of which pose challenges on efficient data management. Today, these data sources broadly include: (a) traditional enterprise data from operational systems related to customer touch points, such as ATMs, call centers, web-based and mobile sources, branches/brokerage units, mortgage units, credit cards, debt including student and auto loans, volatility measures that impact client portfolios; (b) financial business forecasts from various sources, such as news, industry data, trading data, regulatory data, insolvency data, analyst reports (internal and competing intermediaries) and alerts about events (news, blogs, twitter and other messaging feeds); and (c) other sources of data, such as advertising response and social media data. However, for financial stability purposes additional types of data are needed, relating to the specifics of financial contracts, risk factors, counterparties, and system-wide behavior. As the rate that this data is generated increases, consumers of financial services and business analysts who crave such data rapidly use it. Information discovery tools enable them to rapidly combine various data sets leading to better insight. They often want more data to be ingested at higher rates and stored longer, and want to analyze the growing data volumes faster. Big data solutions help financial services institutions respond to these requirements.
Exploiting these data resources for financial stability analysis requires novel approaches to data management and statistical methods. These challenges could arise in the most inconvenient circumstances, such as in the midst of a financial crisis. Bier (2009) argues that the potential uses of big data apply to routine situational awareness, as well as occasional spike loads on analytical resources during episodes of market stress. An effective response requires an appreciation of the underlying forces at work. Experience in numerous activity sectors shows that the transition point, at which scalability begins to bind, is likely to arise in one of four general directions, often referred to as the four Vs of big data: volume, velocity, variety and veracity. First, volume refers to the simple size (in bytes) of a dataset, which can place a strain on storage and computational resources. Varian (2014) notes that modern financial datasets often outstrip the query-processing capacity of relational databases such as structured query language (SQL), creating a market for so-called NoSQL tools. In some cases, one can attenuate this burden through data aggregation or compression. AICPA (2015) shows that one example of a financial monitoring task that will experience significant increases in data volumes relative to legacy practice, is the move toward data-centric audit analytics for forensic analysis of financial accounting records. Traditional financial control tests are fundamentally different from those required for effective detection and monitoring of fraud, bribery, and corruption in conditions of increased financial complexity. Effective monitoring and oversight of complex institutions and markets requires the integration of forensic data analytic techniques that incorporate big data concepts across multiple data sources, third-party watch lists, transactional data, text mining, and even social media and email to prioritize and isolate areas of risk or abusive activity. Integrating forensic data analytics into a robust anti-fraud program or investigative process enables regulators, compliance officers and audit executives to ask questions of their data that go beyond traditional rules-based tests or random sampling that may miss important information or generate large amounts of false positive results.
Second, velocity refers to the rate at which data arrive, which can strain network bandwidth and stream analytics. O'Hara (2015) notes that this is especially important in high-frequency data analysis. Berman (2015) further stresses the importance of real-time monitoring of high-frequency data streams during a flash crash. High-frequency trading firms deliver quote and transaction messages at the technical limits of network latency, creating a significant throughput burden for any downstream process. Third, variety refers to the diversity of forms or structures of data arriving from different sources, which can strain data integration processes. Halevy et al. (2006) note that this applies to the integration of legacy systems after a bank merger as well as in the process of system-wide financial integration. Rosenthal and Seligman (2011) stress the importance of aligning and synchronizing legal entity identification schemes across a wide variety of independently managed datasets. For example, without coordination, the alignment of identifier registries across n bank branches requires n2-n mappings between them. Fourth, veracity refers to the possibility that an elevated error rate in the data can strain data validation, data integrity, and data curation processes. Dong and Srivastava (2013) show that maintaining data quality for detailed and granular portfolio data in bank stress tests requires data integrity to be assessed by reconciling (matching) data points against each other and therefore the veracity burden can rise exponentially with data volumes. Chen et al. (2018) propose a dynamic and coherent quality measure of the extent to which conveyed big data information interacts efficiently with the integrated system to achieve desired performance. Further, Sun et al.(2012, 2015) devise an optimal wavelet algorithm for decomposing the systematic pattern from noise of big financial data to better capture noise in microstructure analysis. Financial stability supervisors must properly deal with all four big data scalability problems.
4.2. Standardization and aggregation of big data in finance
Financial regulators gain understanding of data they process by deploying data standards and identifiers, which play a crucial role in enabling data collection, validation and organization. A large variety of financial data standards exists that apply to the financial sector activity and intermediaries. They are presented on the Table 1 below. While classification of data standards and initiatives may be subject to experts' perceptions, the standards map below demonstrates the heterogeneity of standardization efforts, often competing mutually across a variety of financial instruments, counterparties or other fields of interest.
Table 1. Standardization of financial data.
| Abbreviation |
Full name |
Purpose |
| ACORD |
ACORD Data Standards and Framework |
Data standards for life and annuity property and casualty and for Global Reinsurance & Large Commercial. Claims and settlements messages. |
| ACTUS |
ACTUS Financial Research Foundation |
Data and algorithmic standard aiming to break down the diversity in financial instruments into a manageable number of cash flow patterns. |
| CCS |
Clearing and connectivity standard |
Clearing of OTS transactions. |
| DPM |
Data Point Model |
Multidimensional data modeling. |
| FIBO |
Financial Industry Business Ontology |
Define financial industry terms, definitions and synonyms using RDF/OWL and UML. |
| FIRO |
Financial Industry Regulatory Ontology |
Ontology for description of financial services regulatory domain |
| FIX Protocol |
FIX Protocol |
Protocol for international real-time exchange of information related to the securities transactions and markets. |
| FPML |
Financial Product Markup Language |
Business information exchange standard for electronic dealing and processing of financial derivatives instruments. |
| Genericode |
Generic Code |
Generic code list representation. |
| IFX |
Interactive Financial eXchange |
Interoperability of systems seeking to exchange financial information internally and externally. |
| ISIN |
International Securities Identification Number |
Unique international identification of securities. |
| ISO 20022 |
Universal financial industry message scheme |
Universal financial industry message scheme. |
| LEI |
Legal Entity Identifier |
Standard for identification of business entities and transactions. |
| MDDL |
Market Data Definition Language |
Standard to describe financial instruments, corporate events and market related indicators. |
| MISMO |
Mortgage Industry Standards Maintenance Organization |
Data standards that cover the entire mortgage life cycle. |
| RIXML |
Research Information Exchange Markup Language |
Language for description of investment research documents and other research. |
| XBRL |
eXtensible Business Reporting Language |
An XML-based language for expressing semantic meaning commonly required in business financial reporting. |
| SDMX |
Statistical Data and Metadata eXchange |
An international initiative that aims at standardising and modernising the mechanisms and processes for the exchange of statistical data and metadata among international organizations and their member countries. |
| Source: the Frankfurt Group Technical Workshop (FGTW) on Data Standards Interoperability; author's addition following a reviewer's suggestion. |
The above classification should not be understood as canonical but rather an initial categorization of the key purpose or origin of the specific data standardization. Nevertheless, the real-world application of various standards crosses boundaries indicated by original intents. For instance, SDMX and XBRL are used to collect highly granular data in a number of regulatory projects. Similarly, granular data standards are increasingly coupled with aggregation mechanisms, in order to reflect aggregated indicators, cubes or groups of data. Several initiatives are under way to describe details of financial instruments and transactions through an advanced blending of ontological descriptions with elements of existing standards and identifiers. An important such initiative is the global legal entity identifier initiative deployed for financial stability purposes, to which we turn next.
4.3. The global legal entity identifier initiative
The required standardization of data has realized considerable progress in the recent years through the development of a Global Legal Entity Identifier (LEI) system. The latter sets out to provide a standardized unique identification basis for financial instruments and counterparties to financial transactions. The idea behind the introduction of the LEI is to uniquely identify all parties to financial transactions across the globe by assigning each of them a distinct code that conforms to an international standard ISO 17442:2012. Initially, that standardization is tied to key reference data for the entity, which includes basic elements such as name and address. Then, the reference data will be supplemented by more complex information on corporate hierarchical relationships addressing various questions, e.g. the identification of whether the counterparty is a member of a broader financial group.
The reference data must be produced and maintained in high quality, be freely and continuously available to users in the global regulatory community, the financial industry, and beyond. The LEI provides an essential building block that is necessary to engineer improvements in data quality and data aggregation. It offers multiple benefits to the regulatory community and to financial firms themselves, by allowing their internal systems to operate more effectively and enhancing their capability to identify and manage internal risks. Financial contracts, trades and risk positions can be reliably assigned to legal entities, delivering precision and clarity that facilitates risk assessment and management.
Despite its simplicity and obvious benefits, the financial industry has a long way to go in overcoming the collective action and first mover problems that challenge the development of common identification networks of this type. Finance lags behind other industries that have successfully introduced high quality entity identification systems, such as the chemicals industry, consumer goods distribution industry and entertainment industry to name a few.
The global LEI system for the finance sector is necessary for effective monitoring and supervision in order to address market failures. Standardization of the financial transactions identification systems will economize on conversion and other costs of participant entities and aid cross-verification. Moreover, as with other network goods, e.g. telecommunication services, the benefits of introduction of a common LEI system to each user increase with a higher overall usage of the system. It is hard for individual firms to capture the benefits from the common system as these accrue collectively. So left to the private market alone, there may be insufficient incentive for firms to introduce a common system despite the collective benefits. However, regulatory intervention encouraging or mandating the use of a standardized identification system can help to overcome such hurdles and deliver the public good benefits to all users.
Given the benefits offered by the introduction of a common entity identification system, the G20 tasked the Financial Stability Board (FSB) in November 2011 to lead the co-ordination of international regulatory work and to deliver concrete recommendations on the LEI system by June 2012. As often the case is, however, turning the simple concept and idea into a concrete policy result is not quite as simple as it might first appear. For example, although there are a number of strong, common interests between the public sector and the private sector in the introduction of a global LEI system, there are also a number of areas where interests and incentives are not fully aligned. Mandatory regulatory use of such a system would provide substantial power to the providers of the financial system. This could work against the fundamental public interest. The mandate provided by the G20 to the FSB emphasized the need to prepare recommendations for a governance framework that protects the public interest, such as preventing abuse of monopoly positions by emphasizing that the global LEI system is not- for- profit, ensuring open access, and maintaining high quality reference data.
In accordance with the BIS (2013) high-level principles, the global LEI system should:
- uniquely identify participants to financial transactions;
- meet the requirements of the global regulatory community for accurate, consistent and unique entity identification;
- be designed in a manner that provides benefits to financial market participants;
- be flexible to provide the capability for the system to expand, evolve, and adapt to accommodate innovations in financial markets;
- not be locked-in with a particular service provider for any key system functions or processes, allowing for competition on both global and local levels where appropriate;
- support a high degree of federation and local implementation under agreed and implemented common standards;
- meet evolving requirements of both the regulatory community and industry participants in terms of information content, scope of coverage, timeliness and availability;
- be properly supervised so as the responsibility of upholding the governance principles and oversight of the global LEI system functioning to serve the public interest;
- be supervised so as the mission, role and responsibilities of the supervisory authority be properly specified;
- provide for open participation to all authorities subscribing to the High Level Principles and to the objectives and commitments;
- be properly supervised so as the mission and role to ensure the application of uniform global operational standards and protocols rests with clear authority to act as the operational arm of the global LEI system;
- have a balanced governance representation of industry participants from different geographic areas and sectors of economy;
- allow the centralization of local LEI functions which are deemed not required;
- promote the provision of accurate LEI reference data at the local level from LEI registrants and ensure global uniqueness of the registrants; and
- incorporate any global universal intellectual property rights.
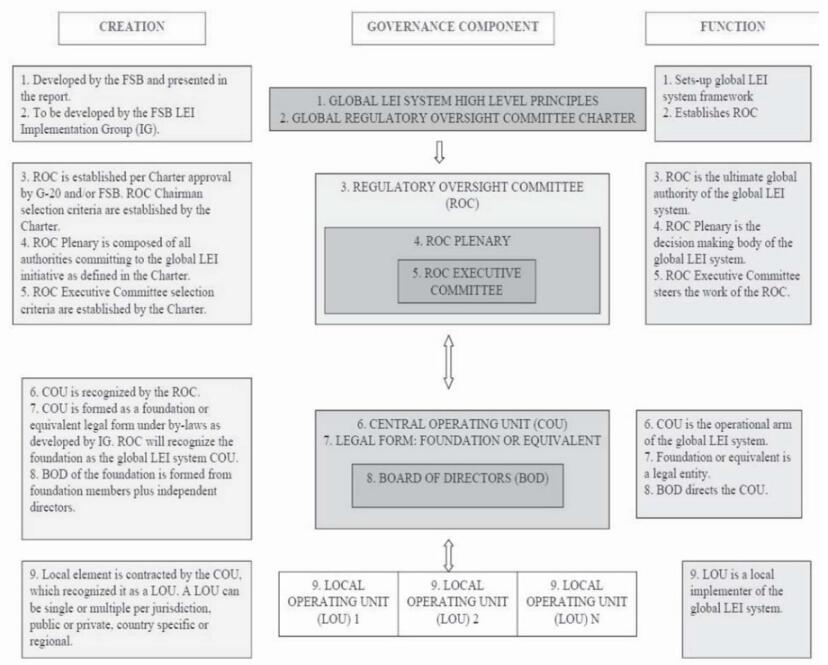
The broad framework set out by the FSB(2011, 2012) for the global LEI system is based on a federated model that includes three tiers of development: The first tier is the Regulatory Oversight Committee (ROC), which has ultimate responsibility for the governance of the system in the broad public interest. The second tier is the Global LEI Foundation operating the central operating unit (COU) that provides the operational arm of the system. It has responsibility for ensuring uniqueness of the LEI and that the system appears logically seamless to users regarding access. The third tier is provided by the federated local operating units (LOUs). These would undertake local registration and validation and would provide additional local flexibility to address issues such as local languages and character sets, as well as local privacy and confidentiality considerations. Where available and feasible, such LOUs would draw on existing local infrastructure. Good progress has been made in recent months in taking the LEI initiative forward. Figure 1 presents the basic structure of the global LEI system.
4.4. Classification of financial instruments and transactions
There has been substantial progress in the global initiative to standardize the identification of entities in a universally acceptable manner through the LEI. However, the regulatory community has not yet addressed the broader and more complex question of the standardization of the depiction of financial products/instruments/contracts across markets and locations adequately. The application of network system analysis requires the standardization of financial data at the granular level for both entities and other key elements. That is important to provide consistency and flexibility to the raw information, supporting granular analysis as well as facilitating the aggregation of information globally. Achieving uniform representation and classification of financial instruments is an important and necessary step to use computational techniques for complex financial system analysis.
There is an abundance of approaches and methods to represent financial products and contracts. Some are specific to particular sectors or locations; different vendors, regulators or firms have designed others for a particular narrow purpose within either the business or regulatory community. In the joint Committee on Payment and Settlement Systems (CPSS) and the International Organization of Securities Commissions (IOSCO) report (2012) on OTC derivatives record-keeping and reporting requirements, the concept of product identification was introduced in the form of a common system of product classification. While the report focused on the OTC derivatives markets, it emphasized the vital importance of taking a wider view. Brammertz et al. (2009) propose an approach to the integration of financial big data that helps accomplish a broad systemic network analysis of both the risks and robustness of the individual elements of the financial network as well as of the network itself. They define four input elements: (1) financial contracts; (2) risk factors; (3) counterparties; (4) behavioral elements. They explain that the standardization and uniform representation of those elements will allow both financial intermediaries and regulators to be able to assess and predict adverse events in the financial system. Flood et al. (2013) also argued that collecting contractual terms and conditions in both the financial industry and the regulators are a prerequisite to forward-looking cash-flow and risk analysis. Contracts are also a key ingredient for mapping the network of contractual relationships for systemic modelling. Measuring the edges (e.g. financial contracts) in the counterparty network graph requires much more detail about those contracts than is the case under traditional firm-focused accounting systems. Lo (2009) provided another approach regarding representation and standardization of financial contracts. Other approached are proposed too, and the debate continues.
The new tools being created to handle the increased amount of data accompanying greater financial market transparency could have the potential to reshape financial markets. We are currently in the infancy of these changes and creating the LEI system is one of the first necessary steps. While the initial driver is to facilitate regulatory reporting, its potential for reshaping the way in which data is used is greater than reporting. Recognizing the potential of these regulatory changes is key to making imaginative use of the data, which in turn could be an important factor in longer-term competitive advantage in the markets that the data describe.
4.5. Remaining challenges and policy responses
The recognition of the role of big data volume and standardization in financial services requires the launching of a policy process on a global scale to prevent any potential future consumer detriment from the increasing use of big data. This policy process should answer questions regarding: (a) the implications of big data algorithms for financial services utility and stability; (b) the impact on different groups of consumers including implications for financial access/exclusion, behavior and decision-making ability; (c) the implications for data protection, conduct, competition, and regulation; and (d) the optimal redistribution along the value chain of efficiency gains, economies of scale, and other benefits.
Further, proper governance rules should be defined for all actors providing personal data to financial service providers. These rules should prescribe that decisions about the use of data and the extent to which risk is mutualized or socialized is a collective decision by all interested stakeholders (public authorities, financial services providers, consumers, data protection authorities). Stakeholders need to decide about the proportionality of using personal data. The impact of big data and the importance of ethical use of data, however, goes much beyond the scope of financial services alone.
Moreover, the issue of cyber-security should be effectively dealt with by stakeholders, drawing on the opportunities offered by Open Source software and solutions regarding data storage of online and offline data in conventional and "cloud" venues, data encryption for sensitive information such as credit scores, and data authentication.
Finally, initiatives are needed which make big data analytics work in the interest of financial consumers (depositors, investors, policyholders). For instance, consumers could use big data analytics of their investing patterns to predict future investments, providing them advice on how to manage their budgets and risk-return tradeoffs more efficiently. Algorithms could search on behalf of financial consumers for the "best" deal in a matter of seconds, evaluate personal risk-taking capacity based on their financial situation and the assorted price they should "expect" to pay, helping them evaluate whether given offers are fair or purposefully overpriced. In this respect, careful reflection needs to be given to consumer information, consumer control and consumer consent in the digital world, as applied to big data. The answers to these challenges have not been adequately provided.
5. Conclusions
Financial stability analysis and supervision policy should strive to identify and address new sources of financial risk, and focus more on diversity and heterogeneity and less on mere diversification. Policy makers and practitioners need to take both a micro and macro view of financial risk. Instead of focusing on idiosyncratic risk alone, they should concentrate on accurate price discovery for complex instruments, realistic financial information generation processes and system-wide risk materializing within complex financial networks.
As financial markets satisfy reasonable criteria of being considered complex adaptive systems, complexity analysis can make a useful contribution. However, the methodological suitability of complexity theory for financial systems and by extension for financial risk management is still debatable. Alternative models drawn from the natural sciences and evolutionary theory are proposed. The effectiveness of these models and monitoring approaches rests crucially on the quality and standardization of big data that today characterized financial activity throughout the globe. Considerable progress is made over the recent years in the development of a key element of such standardization, the global LEI system. The latter aims to uniquely identify parties to financial transactions across the globe. While this is a necessary and important first step, it is only one-step towards a strong, flexible and adaptable global data infrastructure conducive to financial stability policy. The next step, likely to be more challenging not only in terms of complexity but also in terms of the duration of implementation, is the standardization and global acceptance of a uniform representation of financial instruments across different financial markets. This poses considerable challenges for big data infrastructures. Progress in this area will not be easy, for it requires worldwide commitment. However, such progress is important for improving the understanding of emerging system-wide risks.
The persistence of a sectoral approach to the representation of products and instruments, be it in the cash market, OTC derivatives, fixed income, alternative instruments, etc. tends to support a fragmented view that provides inaccurate and misleading signals on emerging risks to the system as a whole. Instead, a system-wide approach is needed, which crucially rests on high-quality big data management. Removing barriers to the provision of high quality, granular and consistent data emerges as an important policy goal to support the development of analytical approaches needed to understand and evaluate the complex financial system of the 21st century.
Acknowledgments
Comments and suggestions by two reviewers and the editor are gratefully acknowledged. The usual disclaimer apply.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: