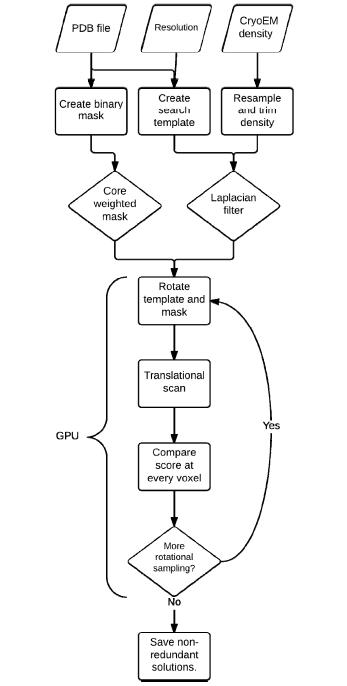
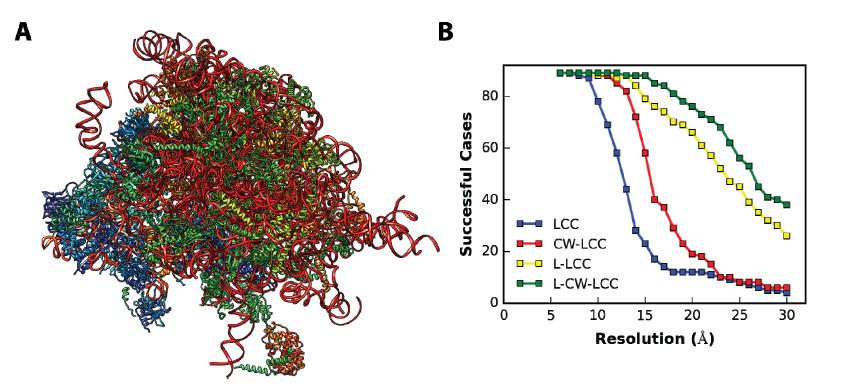
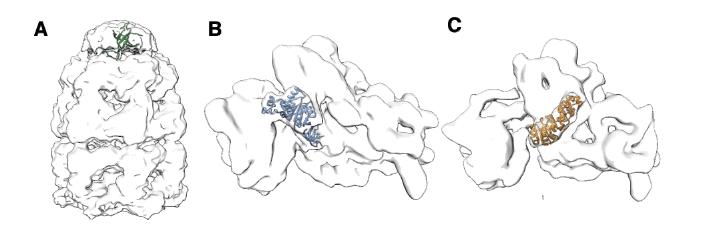
Cryo-EM is a rapidly developing method to investigate the three dimensional structure of large macromolecular complexes. In spite of all the advances in the field, the resolution of most cryo-EM density maps is too low for de novo model building. Therefore, the data are often complemented by fitting high-resolution subunits in the density to allow for an atomic interpretation. Typically, the first step in the modeling process is placing the subunits in the density as a rigid body. An objective method for automatic placement is full-exhaustive six dimensional cross correlation search between the model and the cryo-EM data, where the three translational and three rotational degrees of freedom are systematically sampled. In this article we present PowerFit, a Python package and program for fast and sensitive rigid body fitting. We introduce a novel, more sensitive scoring function, the core-weighted local cross correlation, and show how it can be calculated using FFTs for fast translational cross correlation scans. We further improved the search algorithm by using optimized rotational sets to reduce rotational redundancy and by limiting the cryo-EM data size through resampling and trimming the density. We demonstrate the superior scoring sensitivity of our scoring function on simulated data of the 80S D. melanogaster ribosome and on experimental data for four different cases. Through these advances, a fine-grained rotational search can now be performed within minutes on a CPU and seconds on a GPU. PowerFit is free software and can be downloaded from https://github.com/haddocking/powerfit.
1.
Introduction
Parameter sensitivity analysis is a useful tool for elucidating the dynamics of biological processes, optimally designing biological experiments, and investigating the identifiability of model parameters. It is particularly important in the context of reaction networks describing the time-evolution of populations of molecular species that interact with each other through a set of reactions. These biochemical reaction networks, which are used to describe signalling, regulation and development processes in molecular biology, often involve a large number of non-linear interactions parameterised with an even larger number of parameters (e.g. reaction rate constants and reaction thresholds). Sensitivity analysis in this context can be used to unravel the network complexities by identifying the key parameters and the corresponding reactions that drive the most fundamental aspects of the network. Sensitivity analysis can also be used to optimally design experiments, for example by selecting the variables, time-points and number of replicates to be observed in order to achieve maximum parameter sensitivity. Similarly, it is a useful tool for examining the identifiability of model parameters for a given set of observations.
Early results in sensitivity analysis of biochemical reaction networks were derived using deterministic (i.e. non-stochastic) models [1,2,3]. However, the technological innovations that allowed for observing molecular species at the single cell level and over time emphasised the need to account for the intrinsic stochasticity of reaction networks in molecular biology [4,5,6]. Progress has been made in estimating sensitivities of summary measures of the probability distribution of reaction networks (e.g. expectation of a key molecular population at its expected peak time) using finite difference and other methods (e.g. [7,8,9,10,11,12]).
These methods use the Stochastic Simulation Algorithm (SSA) [13] to simulate sample paths of the so-called master equation describing the evolution of the probability distribution $ P $ of the interacting molecular populations over time. However, the SSA, which simulates every single reaction occurrence, is computationally expensive for large and complex networks and especially those networks where reactions occur across well-separated time-scales.
Sensitivity analysis that uses the full probability distributions, rather than their summary measures, is computationally infeasible unless a suitable approximation of the master equation is used. The Linear Noise Approximation (LNA) is a systematic stochastic approximation of the master equation in terms of the system size. The system size, $ \Omega $, is a scale parameter that is inversely proportional to the levels of stochasticity of the evolving molecular populations, i.e. the size of fluctuations is small for large $ \Omega $ [14]. The key advantage of the LNA, over approximations such as tau-leaping [15] and Langevin or diffusion approximations [16], is that LNA provides analytical expressions for the probability distribution, $ P $, of the interacting molecular populations, which are Multivariate Normal. This implies that the LNA can be much faster than other approximations in terms of simulation and parameter estimation but also that quantities such as the Kullback-Leibler (KL) divergence and the Fisher Information can be computed. The LNA has been used for simulation [17,18], parameter estimation [19,20,21,22] and sensitivity analysis [23].
The LNA has been shown to be inaccurate for simulating noisy oscillations [17,24,25,26,27]. Oscillatory dynamics commonly arise in biology, epidemiology, engineering and beyond with numerous examples including the circadian clock, NF-$ \kappa $B signalling, cardiac rhythms, and predator-prey systems. We have recently developed (see [27]) an approximation, called phase corrected LNA (pcLNA), that corrects the standard LNA to give fast and accurate long-time stochastic simulations for oscillations. The probability distributions derived using pcLNA are Multivariate Normal with mean vector and covariance matrix that have similar expressions to the standard LNA and therefore computation of the KL divergence and the Fisher Information Matrix, which enables a parameter sensitivity analysis, is computationally feasible.
This article develops a general theory of parameter sensitivity analysis. It uses the Kullback-Leibler divergence and the Fisher Information Matrix to study the sensitivity of the probability distribution, $ P_{{\mathit{\boldsymbol{\theta}}}} $, of a stochastic process, $ \mathbf{Y} = \{Y(t), t\geq 0\} $, to changes of the parameter vector $ {{\mathit{\boldsymbol{\theta}}}} $. It is a local analysis in the sense that we study changes of the parameter vector $ {{\mathit{\boldsymbol{\theta}}}}' = {{\mathit{\boldsymbol{\theta}}}}+\delta{{\mathit{\boldsymbol{\theta}}}} $, where $ O(\|\delta{{\mathit{\boldsymbol{\theta}}}}\|^3) $ are negligible. It is, on the other hand, complete in the sense that the sensitivity of the probability distribution, rather than summaries of the probability distribution, are analysed. It extends the theory of sensitivity analysis developed earlier in [23,27,28], by (ⅰ) deriving a matrix for studying the parameter sensitivity of any stochastic process of which the Fisher information matrix can be computed, possibly even by rudimentary approximations, (ⅱ) deriving a complete method for studying the sensitivity of the joint probability distribution of any sample path of a multivariate Gaussian stochastic processes to changes in parameter values, (ⅲ) describing the application of this theory to oscillatory networks approximated by pcLNA and showing how to use it for experimental design, for studying parameter identifiability and for comparing deterministic to stochastic models.
The paper proceeds as follows. In section 2 we develop a general theory of parameter sensitivity analysis of the probability distributions of sample paths of stochastic processes. We also consider the case of multivariate Gaussian stochastic process. In section 3 we describe reaction networks and the master equation and in section 4 the LNA and pcLNA approximations. In section 5 we provide an illustrative example of our methods using the Brusselator system [29]. Our approach is then applied in section 6 to the sensitivity analysis of the Drosophila circadian clock developed in [30]. Section 7 provides a discussion of the results, while details of the Drosophila circadian clock model [30] are provided in Supplement A.
2.
Parameter sensitivity analysis
Let $ \mathbf{Y} = \{Y(t), \, t \geq 0 \} $ be a stochastic process defined on a probability space $ (\Omega, \mathcal{F}, P_\theta) $ of which the probability distribution $ P_\theta $ depends on a parameter $ {{\mathit{\boldsymbol{\theta}}}} = (\theta_1, \dots, \theta_k)^T\in \Theta \subset \mathbb{ R}^k $. We wish to study how the probability distribution of sample paths, $ Y(t_1), \dots, Y(t_n) $, for $ 0\leq t_1 < \dots < t_n < \infty $, is affected by changes in the value of $ {{\mathit{\boldsymbol{\theta}}}} $. For this purpose, we introduce the Fisher Information Matrix (FIM).
We first define the log-likelihood function $ \ell({{\mathit{\boldsymbol{\theta}}}}; y) = \log p_{{\mathit{\boldsymbol{\theta}}}}(y) $ where $ p_{{\mathit{\boldsymbol{\theta}}}}(y) $ is the probability density (or mass) function of a sample path $ y $ of $ \mathbf{Y} $. The FIM, $ \mathcal{I}({{\mathit{\boldsymbol{\theta}}}}) $, is a symmetric positive-(semi)definite $ k\times k $ matrix with entries
Here $ \mathbb{E}_{P_{{\mathit{\boldsymbol{\theta}}}}} $ denotes the expectation function under the probability distribution $ P_{{\mathit{\boldsymbol{\theta}}}} $, $ \partial_i $ the partial derivative with respect to $ \theta_i $ evaluated at $ {{\mathit{\boldsymbol{\theta}}}} $ and $ \partial^2_{ij} $ the corresponding second order derivative. The FIM is therefore the negative of the expected curvature of $ \ell({{\mathit{\boldsymbol{\theta}}}}; y) \in \mathbb{C}^2(\Theta) $. For $ k = 1 $ and convex $ \ell({{\mathit{\boldsymbol{\theta}}}}; y) $, the FIM, $ \mathcal{I}(\hat{{{\mathit{\boldsymbol{\theta}}}}}) $, measures the expected "peakedness" of the likelihood at its maximum value $ \ell(\hat{{{\mathit{\boldsymbol{\theta}}}}}; y) $.
The Fisher information matrix is related to the Kullback-Leibler (KL) divergence between two probability distributions $ P_{{{\mathit{\boldsymbol{\theta}}}}+\delta {{\mathit{\boldsymbol{\theta}}}}} $ and $ P_{{{\mathit{\boldsymbol{\theta}}}}} $. For two probability distributions $ P $ and $ Q $ with density functions $ p(y) $ and $ q(y) $, $ y \in \mathcal{Y} $, the KL divergence is
That is, the KL divergence $ D_\text{KL}(P\|Q) $ is the expected value of the logarithm of the likelihood ratio $ \log p(y)/q(y) $ with the expectation taken with respect to $ P $ and the usual conventions when $ p(y) = 0 $ or $ q(y) = 0 $. An analogous definition of KL divergence applies for discrete probability distributions.
If $ P = P_{{{\mathit{\boldsymbol{\theta}}}}+\delta{{\mathit{\boldsymbol{\theta}}}}} $ and $ Q = P_{{{\mathit{\boldsymbol{\theta}}}}} $, then (see [31]),
That is, the FIM is the hessian matrix of the above KL divergence at $ {{\mathit{\boldsymbol{\theta}}}} \in \Theta $ (the tangent of $ D_\text{KL} $ at $ \delta{{\mathit{\boldsymbol{\theta}}}} = \mathbf{0}_k $ is $ 0 $).
If the Fisher information matrix $ \mathcal{I} = \mathcal{I} ({{\mathit{\boldsymbol{\theta}}}}) $, $ {{\mathit{\boldsymbol{\theta}}}} \in \Theta $, is positive definite, it defines a Riemannian metric over the statistical manifold of probability distributions $ \{P_{{\mathit{\boldsymbol{\theta}}}}, {{\mathit{\boldsymbol{\theta}}}} \in \Theta \} $ by the inner product of two probability distributions $ P_{{{\mathit{\boldsymbol{\theta}}}}+\delta{{\mathit{\boldsymbol{\theta}}}}} $ and $ P_{{{\mathit{\boldsymbol{\theta}}}}+\delta{{\mathit{\boldsymbol{\theta}}}}'} $ in the tangent space of the manifold at $ {{\mathit{\boldsymbol{\theta}}}} $
with the FI metric
This FI metric is related to the KL divergence by
The FIM can therefore be used to locally (i.e. when $ \text{O}(||\delta{{\mathit{\boldsymbol{\theta}}}} ||^3)\approx 0 $) measure the change in probability distribution $ P_{{\mathit{\boldsymbol{\theta}}}} \to P_{{{\mathit{\boldsymbol{\theta}}}} + \delta{{\mathit{\boldsymbol{\theta}}}}} $ for a change in parameter values $ {{\mathit{\boldsymbol{\theta}}}} \to {{\mathit{\boldsymbol{\theta}}}} + \delta{{\mathit{\boldsymbol{\theta}}}} $.
2.1. The sensitivity matrix
Because the FIM $ \mathcal{I} = \mathcal{I}({{\mathit{\boldsymbol{\theta}}}}) $ is symmetric and positive semi-definite, its Singular Value Decomposition (SVD) is of the form $ VD^2V^T $ where $ V $ is orthogonal and $ D $ is diagonal with entries $ \sigma_1\geq \cdots \geq\sigma_k \geq 0 $. It can therefore be decomposed to $ \mathcal{I} = \underline{\mathbf{s}}^T\underline{\mathbf{s}} $ with the matrix $ \underline{\mathbf{s}} = \underline{\mathbf{s}}({{\mathit{\boldsymbol{\theta}}}}) = DV^T $ and the KL divergence
The length, $ \|\, \underline{\mathbf{s}}_j\, \|^2 $, of the column $ \underline{\mathbf{s}}_j = (\underline{\mathbf{s}}_{1j}, \dots, \underline{\mathbf{s}}_{kj})^T $ of $ \underline{\mathbf{s}} $, measures the effects of a single unit change of the $ j $-th parameter $ \theta_j $ to the distribution $ P_{{\mathit{\boldsymbol{\theta}}}} $, $ j = 1, \dots, k $. It can therefore be used to study the sensitivity of $ P_{{\mathit{\boldsymbol{\theta}}}} $ to changes in the parameter values.
Note that no assumptions for the probability distribution, $ P_{{\mathit{\boldsymbol{\theta}}}} $, are made so far. We next explain the role of the matrix $ \underline{\mathbf{s}} $ as a sensitivity matrix in the important case of multivariate Gaussian stochastic processes where analytical expressions for the FIM of probability distributions of sample paths are available.
2.2. Sensitivity analysis for multivariate Gaussian stochastic processes
We consider the case where $ \mathbf{Y} = \{Y(t), t\geq 0\} $ is an $ m $-dimensional Gaussian stochastic process. That is, for $ t\geq 0 $, $ Y(t) = (Y_1(t), \dots, Y_m(t))^T\in \mathbb{ R}^m $ with the joint probability distribution of sample paths $ Y(t_1), Y(t_2), \dots, Y(t_n) $ being the multivariate normal $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $, with mean vector $ \mu = \mu(t_1, \dots, t_n; {{\mathit{\boldsymbol{\theta}}}}) = \mu({{\mathit{\boldsymbol{\theta}}}}) $ and covariance matrix $ \Sigma = \Sigma(t_1, \dots, t_n; {{\mathit{\boldsymbol{\theta}}}}) = \Sigma({{\mathit{\boldsymbol{\theta}}}}) $ depending on $ {{\mathit{\boldsymbol{\theta}}}} $. In this case, the entries of the FIM are
where all derivatives are taken at $ {{\mathit{\boldsymbol{\theta}}}} $. This can also be written using the vec notation [32] as
Now consider the $ N \times k $ matrix ($ N = (m\cdot n)+(m\cdot n)^2 $)
which is the linearisation matrix of the mapping $ {{\mathit{\boldsymbol{\theta}}}} \mapsto (\mu({{\mathit{\boldsymbol{\theta}}}}), \text{vec}\Sigma({{\mathit{\boldsymbol{\theta}}}})) $ at $ {{\mathit{\boldsymbol{\theta}}}} $. That is, if we let $ \delta\mu = (\delta\mu_i) $ and $ \delta \Sigma = (\delta\Sigma_{ij}) $, with $ \delta\mu_i = \mu_i({{\mathit{\boldsymbol{\theta}}}} + \delta{{\mathit{\boldsymbol{\theta}}}}) - \mu_i({{\mathit{\boldsymbol{\theta}}}}) $ and $ \delta\Sigma_{ij} = \Sigma_{ij}({{\mathit{\boldsymbol{\theta}}}} + \delta{{\mathit{\boldsymbol{\theta}}}}) - \Sigma_{ij}({{\mathit{\boldsymbol{\theta}}}}) $, then
If we also define the matrix $ \mathcal{F} $ as the Cholesky decomposition of the block diagonal positive-definite matrix
then we can write the Fisher information in (2.1) as
Therefore, $ \mathcal{F}\!\mathcal{L} $ is a linear map from $ {{\mathit{\boldsymbol{\theta}}}} $ to $ \mathbb{R}^{N} $ which sends the $ \langle \cdot, \cdot \rangle_{{{\mathit{\boldsymbol{\theta}}}}} $ metric to the standard one in $ \mathbb{R}^{N} $,
and relates the FI metric in $ \Theta $ to the standard one in $ \mathbb{ R}^{N} $,
The matrix $ \underline{\mathbf{s}} $ characterises sensitivity
The sensitivity of the probability distribution $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $ to changes $ \delta{{\mathit{\boldsymbol{\theta}}}} $ in $ {{\mathit{\boldsymbol{\theta}}}} $ can therefore be studied using the vector $ \mathcal{F}\!\mathcal{L}\, \delta{{\mathit{\boldsymbol{\theta}}}} $. Equation (2.3) shows that
We now consider the (thin) SVD of the $ N\times k $ matrix $ \mathcal{F}\!\mathcal{L} $, $ \mathcal{F}\!\mathcal{L} = WDV^T $, where $ W = [W_1 \cdots W_k] $ is an $ N\times k $ column-orthogonal matrix, $ D $ a $ k\times k $ diagonal matrix with entries of the main diagonal the singular values $ \sigma_1\geq \dots \geq \sigma_k $, and $ V = [V_1 \cdots V_k] $ a $ k\times k $ orthogonal matrix. Because $ \mathcal{I} = (\mathcal{F}\!\mathcal{L})^T \mathcal{F}\!\mathcal{L} $, the eigenvalues of $ \mathcal{I} $ are $ \sigma_1^2\geq \dots \geq \sigma^2_k\geq 0 $, and $ V_i $, $ i = 1, \dots, k $, are the corresponding eigenvectors.
The $ N\times 1 $ orthogonal column vectors $ W_i $ of $ W $ and the $ k\times 1 $ eigenvectors $ V_i $ of $ \mathcal{I} $, satisfy the equation $ \mathcal{F}\!\mathcal{L} V_i = \sigma_i W_i, $ and if we define $ U_i = \mathcal{F} ^{-1}W_i $, $ i = 1, 2, \dots, s $ then
where the $ N $-dimensional vectors $ U_i $ can be written as $ U_i = (U_i^{\mu}, U_i^{\Sigma})' $ to reflect the correspondence of each of its first $ m\cdot n $ entries to the $ (m\cdot n) $-dimensional mean vector $ \mu $ and the last $ (m\cdot n)^2 $ entries to the covariance matrix $ \Sigma $.
By (2.4), and using that $ \delta{{\mathit{\boldsymbol{\theta}}}} = \sum_i (V_i^T\delta{{\mathit{\boldsymbol{\theta}}}})V_i $, up to terms that are $ \text{O}(\| \delta{{\mathit{\boldsymbol{\theta}}}} \|^2) $,
Therefore,
and by (2.3),
since the $ U_i $ are orthonormal in the $ \langle\cdot, \cdot \rangle_{{{\mathit{\boldsymbol{\theta}}}}} $ metric and the coefficient of $ U_i $ in $ U\cdot\underline{\mathbf{s}}\cdot\delta{{\mathit{\boldsymbol{\theta}}}} $ is the $ i $th coordinate of $ \underline{\mathbf{s}}\cdot\delta{{\mathit{\boldsymbol{\theta}}}} $. These equations are the reason we call $ \underline{\mathbf{s}} = DV^T $ the sensitivity matrix.
Similarly, up to terms that are $ \text{O}(\| \delta{{\mathit{\boldsymbol{\theta}}}} \|^2) $,
i.e. $ \mathcal{F} \mathcal{L} = W\cdot \underline{\mathbf{s}} $. We can now make a few useful observations:
1. Equation (2.6) shows that the change in the probability distribution $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $ produced by a change to the value of parameter $ {{\mathit{\boldsymbol{\theta}}}} \to {{\mathit{\boldsymbol{\theta}}}}+ \delta{{\mathit{\boldsymbol{\theta}}}} $, according to the FI metric, is a weighted sum of the vectors $ W_i = \mathcal{F} ({U_i^{\mu}}^T, {U_i^{\Sigma}}^T)^T $ with weights-coefficients $ \sigma_j V_j^T\delta{{\mathit{\boldsymbol{\theta}}}} = \sum_j \underline{\mathbf{s}}_{ij}\delta \theta_j $. The change in the probability distribution is reflected to the mean through the $ U_j^{\mu} $ directions and the covariance matrix through the $ U_j^{\Sigma} $ directions.
2. The coefficients $ \sigma_j V_j^T\delta{{\mathit{\boldsymbol{\theta}}}} $ are proportional to the singular values $ \sigma_j $ and the inner products $ V_j^T\delta{{\mathit{\boldsymbol{\theta}}}} $. The latter are the coordinates of $ \delta{{\mathit{\boldsymbol{\theta}}}} $ in the orthonormal basis of $ \Theta $ defined by the columns of the matrix $ V $. Therefore, because the singular values are chosen in non-increasing order, i.e. $ \sigma_1\geq \dots \geq \sigma_k $, the largest change in the probability distribution, subject to fixed $ \| \delta{{\mathit{\boldsymbol{\theta}}}} \| $, occurs when the change $ \delta{{\mathit{\boldsymbol{\theta}}}} $ is parallel to $ V_1 $ that corresponds to the largest singular value $ \sigma_1 $. If the singular values decay fast, there are only a few directions of the signal space that can produce a relatively large change in the $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $ distribution (subject to fixed $ \| \delta{{\mathit{\boldsymbol{\theta}}}} \| $).
3. Furthermore, the overall contribution of each coordinate $ \delta \theta_i $ of $ \delta{{\mathit{\boldsymbol{\theta}}}} $ in the change of the probability distribution is measured, according to the FI metric, by $ \sum_{j = 1}^k W_j \underline{\mathbf{s}}_{ij} = W\underline{\mathbf{s}}_i $. That is, if $ \delta{{\mathit{\boldsymbol{\theta}}}} = \epsilon e_i $ with $ e_i\in \mathbb{ R}^k $ the usual unit vector with only non-zero entry $ e_{ii} = 1 $ and constant $ \epsilon\in \mathbb{ R} $, then the corresponding change in the probability distribution $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $ according to the FI metric is
Because of the definition of $ \underline{\mathbf{s}} $ through the SVD, the sensitivity matrix $ \underline{\mathbf{s }}$ is optimal for capturing as much sensitivity as possible in the low order principal components of $ (\delta \mu, \delta \text{vec}(\Sigma))^T $. That is, for any (sensitivity) matrix $ \underline{\mathbf{s}}' $ which for some orthogonal matrix $ U' $ satisfies
the sensitivity matrix $ \underline{\mathbf{s}} $ satisfies the following inequalities for all $ \ell < k $,
i.e. among all such sensitivity matrices $ \underline{\mathbf{s}} $ squeezes as much of the sensitivity effect as possible into the lower $ i $ components.
For the above reasons, we call $ \underline{\mathbf{s}}_{ij} $, for $ j = 1, \dots, k $, principal coefficients of sensitivity of $ \mathrm{MVN}(\mu({{\mathit{\boldsymbol{\theta}}}}), \Sigma({{\mathit{\boldsymbol{\theta}}}})) $ to changes in the $ i $th component of the signal $ S_i $, $ i = 1, \dots, k $.
In the following section, we examine a particular case in which such sensitivity analysis is relevant. These are the reaction networks used to describe cellular processes such as signalling, regulation and development in molecular biology.
3.
Reaction networks
A system of multiple different molecular populations, $ M_1, M_2, \dots, M_m $ has state vector, $ Y(t) = (Y_1(t), \ldots, Y_m(t))^T $ where $ Y_i(t) $, $ i = 1, \ldots, m $, denotes the number of $ M_i $ molecules at time $ t $. These molecules undergo reactions $ R_j $, $ j = 1, \dots, r $, where $ Y(t) $ jumps to a new state $ Y(t) + \nu_j $, with $ \nu_j = (\nu_{1j}, \dots, \nu_{mj})^T \in \mathbb{Z}^m $ the stoichiometric vectors of the reactions. Each reaction occurs with intensity that depends on the current state of the network. If the current state is $ Y(t) = y $, the probability of a single $ R_j $ reaction occurring in $ [t, t+dt) $ is $ w_j(y)\, dt + o(dt) $, while the probability of no $ R_j $ reaction in $ [t, t+dt) $ is $ 1 - w_j(y)\, dt + o(dt) $. Here $ \lim_{dt\to 0} o(dt)/dt = 0 $.
The Kolmogorov forward equation that describes the time-evolution of the probability distribution, $ P(y, t) = P(Y(t) = y) $, of the stochastic process $ \mathbf{Y} = \{Y(t), t\geq 0\} $ is then
The Kolmogorov equation is often referred as (chemical) master equation.
The master equation can rarely be solved analytically and therefore the focus has been on simulation of sample paths of $ \mathbf{Y} $. The so-called Stochastic Simulation algorithm (SSA) [13] exactly simulates the sample path $ Y(t) $, $ t\in [0, T] $, for a given initial state $ Y(0) $, by generating all reactions that occur in $ [0, T] $. SSA quickly becomes slow as the complexity of the network rises.
Furthermore, computation of the likelihood of sample paths of $ \mathbf{Y} $ as well as quantities such as the KL divergence and the FIM is extremely expensive and require some form of approximation.
4.
Linear noise approximation
In this section, we focus on the Linear Noise Approximation (LNA), using which we can compute the likelihood of sample paths, the KL divergence and FIM and therefore perform the sensitivity analysis described in section 2.
4.1. System size
It is common in studying stochastic systems to introduce a system size parameter $ \Omega $ which is a parameter that occurs in the intensities of the reactions $ w_j(Y(t)) $. The precise description of this parameter depends on the system. In population models it might be considered to be of the same order of magnitude as the total population size while in molecular biology a natural choice is to use molar concentrations and therefore regard $ \Omega $ as Avogadro's number in the appropriate molar units (e.g. nM$ ^{-1} $) multiplied by the volume of the reacting solution (e.g. the cell) in appropriate units (e.g. in litres (L)). In the circadian clock system that we consider in section 6, it has units L/$ \mu $M.
The system size governs the size of the state fluctuations and therefore the size of the jumps. Larger system sizes generally imply relatively smaller fluctuations and vice versa. In a certain sense the system size parameter is just a mathematical convenience to control the overall levels of stochasticity and to enable the study of the dependence of stochastic fluctuations upon system size.
While having a system size parameter is not necessary to apply our methods, it allows one to study the dependence of stochastic fluctuations upon system size and to calculate the deterministic equations that describe the evolution of the concentration vector $ X(t) = Y(t)/\Omega $ in the limit of $ \Omega \to\infty $ (see next section). A sufficient condition to derive this limit is that the intensities $ w_j(Y(t)) $ depend upon $ \Omega $ (cf. [14,36,37]) as
where $ {u}_j(x) $ the macroscopic ($ \Omega \to \infty $) rates, derived next, that generally depend on the concentration vector $ x = x(t) $. The condition is very general and applies to all common reaction types encountered in the biochemical context.
4.2. LNA derivation
The time-evolution of the stochastic process $ \mathbf{Y} $ can be described using the random time change representation (RTC) [35]
with $ Z_j $ being independent unit Poisson processes corresponding to reaction $ R_j $*. The term $ Z_j \left(\int_0^t w_j(Y(s)) ds \right) $ in (4.1) counts the number of $ R_j $ reactions that happened in $ [0, t) $.
*If $ Z(t) $ is a unit Poisson process then it is a Poisson process with rate $ 1 $ (see properties of Poisson process) and $ Z(\lambda t) $ is a Poisson process with rate $ \lambda $.
Using the condition (4.1) we can re-write the infinitesimal RTC equation in (4.1) in terms of $ X(t) = Y(t)/\Omega $ as
If we also define $ x(t) $ as the limit in probability of $ X(t) $, i.e. $ X(t)\stackrel{P}{\to} x(t) $, as $ \Omega \to \infty $, we can use the law of large numbers (LLN) to derive the limit of equation (4.2), as $ \Omega \to \infty $,
Equivalently, this can be written as the macroscopic rate equation
We now define the LNA ansantz [14,36,37] that describes the relation between the stochastic process $ X(t) $ and the deterministic solution of the system $ x(t) $ with their difference, scaled by $ \Omega $, being a stochastic process, $ \{\xi(t), t\geq 0\} $, describing the noise around $ x(t) $. That is,
The LNA ansantz implies that
where
and
Therefore for sufficiently large values of $ \Omega $, the time-evolution of $ \{\xi(t), t\geq 0\} $ can be described by the linear Stochastic Differential equation (in the Itô sense)
or, in matrix form,
where $ J = J(x) $ the Jacobian matrix of (4.3), $ E = E(x) = S\text{diag}\left(\!\sqrt{u_1(x)}, \dots, \sqrt{u_r(x)}\right) $ the product of the stoichiometry matrix $ S = [\nu_1 \cdots \nu_r] $, and the square root of the diagonal matrix $ \text{diag}(u_1(x), \dots, u_m(x)) $, and $ W_t $ a Wiener process.
This linear SDE has a solution that can be written as
where, $ C(0, t) $ the fundamental matrix of (4.3), which is the solution of the initial value problem
and the symmetric positive-definite matrix $ V(0, t) $ is the solution of the initial value problem
The above representation implies that by solving the initial value problems in (4.3), (4.4) and (4.5) one can easily derive the probability distribution of $ \xi(t) $ for any given initial state $ \xi(0) = \xi_0 $. In particular, the probability distribution
and therefore
where here $ X(0) = x(0)+ \Omega^{-1/2}\xi(0) $.
It can also be shown that the joint probability distribution of sample paths $ (X(t_1), X(t_2), \dots, X(t_n)\, |\, X(0)\sim \mathrm{MVN}(\mu_0, \Sigma_0)) $, under the LNA, is also MVN with mean
and precision matrix (inverse of variance matrix) $ \Omega A_{1:k} $ where $ A_{1:k} $ is the block tridiagonal matrix
Here we used the notation $ C_{i, i+1} = C(t_i, t_{i+1}) $, $ V_{i, i+1} = V(t_i, t_{i+1}) $, and $ V_1 = V_{0, 1} + C_{0, 1}S_0V_{0, 1}^T $.
The above results make LNA hugely faster in simulation compared to SSA, but perhaps more importantly make feasible the computation of the likelihood function of sample paths and associated quantities such as the FIM.
However, the important question arises on whether the LNA is an accurate approximation of the master equation for finite $ \Omega $. The answer relates to the structure of the reaction network [18,39]. For example, LNA has been found to be accurate for networks involving intensity functions that are up to first order polynomials of the reactants concentrations [40]. The LNA is also very accurate for long-time approximation of reaction networks with a single stable fixed point, while it is inaccurate for long-time approximation of multi-stable networks (see e.g. [39]).
4.3. LNA for biological oscillators
Furthermore, the LNA is inaccurate for long-time approximation of reaction networks with oscillatory dynamics. This failure of the LNA was extensively studied for those oscillatory networks where in the $ \Omega\to\infty $ limit, the ode in (4.3) has a periodic solution, $ \gamma $, given by $ x = g(t) $ with $ g(t) = g(t+T) $, for some $ T > 0 $ [17,24,25,26]. In a nutshell, this failure of the LNA is due to that, for finite $ \Omega $, the stochastic sample paths, $ Y(t) $, $ t\geq 0 $, of the master equation increasingly spread in the tangental direction of $ g(t) $ (i.e. parallel to $ F(g(t)) $) as time grows. This is in contrast to the variance of $ Y(t) $, $ t\geq 0 $, in the direction transversal to $ \gamma $, which quickly converge to a fixed value. The increasing tangental variability results in the phase of $ Y(t) $, $ t\geq 0 $, increasingly drifting from the phase of the deterministic solution $ g(t) $. Therefore, the LNA predictions, which have the same phase as $ g(t) $, are increasingly out of phase with $ Y(t) $, $ t\geq 0 $ [17,24,25,26,27].
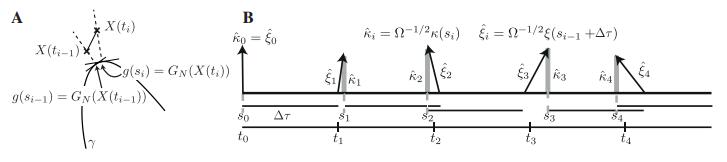
We have recently developed (see [27]) a modification of the standard LNA for oscillatory networks, called phase corrected LNA or pcLNA, that corrects for the phase drifts. We first define the section, $ \mathcal{S}_{x} $, for $ x \in \gamma $, which is an $ (m-1) $-dimensional linear hyperplane with $ x\in \mathcal{S}_{x} $ and transversal to the tangent vector, $ F(x) $. A particular example is the hyperplane normal to $ \gamma $ at $ x $, i.e. for any $ u\in \mathcal{S}_{x} $, $ u \perp F(x) $. Then the mapping $ G $ of a neighbourhood of $ \gamma $ onto $ \gamma $ is such that if $ u\in\mathcal{S}_{x} $ then $ G(u) = x\in\gamma $. We use $ G $ to map the stochastic sample path $ X(t) $, $ t\geq 0 $, to the periodic solution $ g(t) $. The pcLNA anstantz is
Here $ \kappa(t) $ lies on the transversal section $ \mathcal{S}_{G(X(t))} $ and therefore, unlike $ \xi(t) $ in the standard LNA ansantz, is unaffected by the increasing tangental variance.
The pcLNA can be used for fast and accurate long-time simulation of sample paths of oscillatory networks. The simulation algorithm (see Figure 1) proceeds as the standard LNA except that after deriving $ X(t) $ an extra step is added to find $ G(X(t)) $ and subsequently $ \kappa(t) = \Omega^{1/2}(X(t)-G(X(t))) $ to replace $ x(t) $ and $ \xi(t) $, respectively, before progressing with another LNA step. The key point here is that $ G(X(t)) = g(s) \in \gamma $ for some $ s\in [0, T] $ and therefore the same solutions of the ode's in (4.3), (4.4), (4.5) are used in all simulations. The same principle can be used for parameter estimation using the corresponding Kalman filter (see [27]).
The probability distributions on the transversal section derived under the LNA converge to a fixed point probability distribution and are shown to be almost indistinguishable from SSA simulations even for relatively low $ \Omega $ (for the Drosophila circadian clock [30] for $ \Omega\geq 300 $, see also [26,27]). They can be used to analyse the network at specific important phases of the network, e.g. peaks of the key protein in the network, but also the overall dynamics if joint probability distributions of a large number of phases are considered.
We can derive the joint probability distribution of a sample path $ Q_{x_1}, \dots, Q_{x_n} $ of points on the transversal sections $ \mathcal{S}_{x_i} $, $ i = 1, \dots, n $, respectively, where $ x_i = g(t_i) $, $ 0 < t_1 < \dots < t_n $, for initial condition $ X(0)\sim MVN(\mu_0, \Sigma_0) $. This is
where $ \mu_{x_{1:n}} $ and $ A_{x_{1:n}} $ are of the same form with $ \mu_{1:n} $ in (4.6) and $ A_{1:n} $ in (4.7) respectively. However, $ \mu(t_i) $, $ C_{i-1, i} $, and $ V_{i-1, i} $ are replaced by their projections on the transversal section $ \mathcal{S}_{x_i} $. For normal transversal sections, this can be easily derived by first deriving (e.g. using Gram-Schmidt process) an orthogonal matrix $ R = [R_{1} \; R_{2}] $ that has first column, $ R_1 $, parallel to the tangent vector $ F(x_i) $, for $ i = 1, \dots, n $, and replacing $ \mu(t_i) $ with $ R_{2}^T\mu(t_i) $, $ C_{i-1, i} $ with $ R_{2}^TC_{i-1, i} R_{2} $ and $ V_{i-1, i} $ with $ R_{2}^T V_{i-1, i} R_{2} $. For convenience, we henceforth call the probability distributions under the LNA on the transversal sections of given phases in (4.8) as pcLNA distributions.
5.
Parameter sensitivity analysis for the Brusselator model
In this section, we provide an illustrative example of our approach using the two-dimensional Brusselator model described by the ODE system
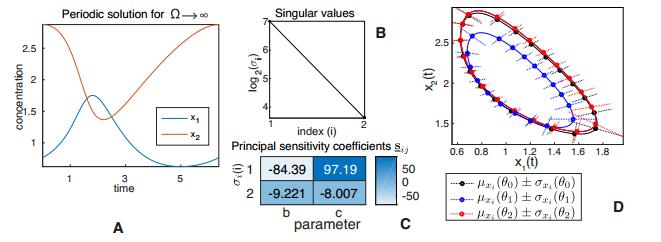
The system has a single fixed point, $ x^* = (1, b/c)' $, that is stable for $ b < 1+c $, while a unique stable periodic solution, $ x(t) = (x_1(t), x_2(t))' $, exists for $ b > 1+c $ (see Figure 2). We have previously shown that pcLNA probability distributions are almost indistinguishable to SSA empirical probability distributions of this network for $ \Omega\geq 1000 $ [27]. We now use the pcLNA joint probability distributions for $ b = 2.2 $, $ c = 1 $, at phases/times, $ t = 0.25, 0.5, \dots, 6 $, for $ \Omega = 1000 $ to analyse the parameter sensitivities of the model.
As we can see in Figure 2(B), the first singular value of the FIM is substantially larger (about $ 2^{3.25}\approx 10 $ times) than the second singular value. The large first principal sensitivity coefficients for both parameters reveal that the pcLNA probability distributions are sensitive to changes in both parameter values (see Figure 2(C)). Furthermore, the first singular value corresponds to changes that move the two parameters in opposite directions. That is, the principal sensitivity coefficients $ \underline{\mathbf{s}}_{11}, \underline{\mathbf{s}}_{12} $ and similarly the eigenvector $ V_1 = (V_{11}, V_{21})' $ of the FIM corresponding to the first singular value $ \sigma_1 $ are such that $ \underline{\mathbf{s}}_{11}\cdot\underline{\mathbf{s}}_{12} < 0 $ and $ V_{11}\cdot V_{21} < 0 $. Therefore changes of the parameter value $ \theta_0 = (2.2, 1)' $ in the $ V_1 $ direction, i.e. $ \theta_1 = \theta_0 + \delta V_1 $, $ \delta \neq 0 $, result in a relatively large fixed-point translocation and, as shown in Figure 2(D), a large change in the deterministic solution and pcLNA probability distributions. On contrary, the principal sensitivity coefficients $ \underline{\mathbf{s}}_{21}, \underline{\mathbf{s}}_{22} $ and therefore the eigenvector $ V_2 = (V_{21}, V_{22})' $ corresponding to the second singular value $ \sigma_2 $ are such that $ \underline{\mathbf{s}}_{21}\cdot\underline{\mathbf{s}}_{22} > 0 $ and $ V_{21}\cdot V_{22} > 0 $. Therefore, a change in parameter values, $ \theta_2 = \theta_0 + \delta V_2 $, result in much smaller changes in the deterministic solution and pcLNA probability distributions (see Figure 2(D)).
6.
Parameter sensitivity analysis of the Drosophila circadian clock
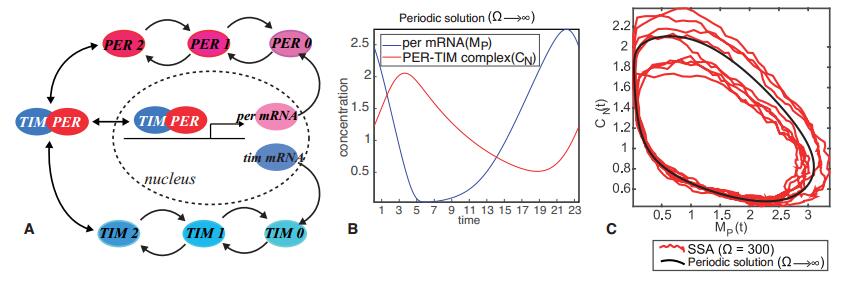
In this section, we will perform a sensitivity analysis of the reaction network of the Drosophila circadian clock in [30]. The network involves two proteins PER(iod) and TIM(eless), that can be reversely phosphorylated twice to $ P_1 $, $ T_1 $ and $ P_2 $, $ T_2 $, respectively, with the twice phosphorylated forms able to form a dimer complex, $ C $, that can translocate to the nucleus, $ C_N $, and repress the transcription of PER and TIM mRNA, $ M_P $ and $ M_T $, respectively (see Figure 3 and Supplementary A).
The network involves $ r = 30 $ reactions parameterised by $ k = 38 $ parameters. These include (see also Table 2) the constants of each reaction and the half-max constants, say $ c_1 $, for enzymatic reactions with macroscopic rates either of Michaelis-Menten form, i.e. $ c_2x_i/(c_1+x_i) $, or Hill form, i.e. $ c_2x_i^h/(c_1^h+x_i^h) $. Parameter sensitivity analysis attempts to unravel the complexities of the network dynamics.
The macroscopic rate equations have periodic solutions. Gonze et al. [30] studied the stochastic version of the network using SSA simulations in various system sizes. We have previously shown (see [27]) that pcLNA probability distributions accurately approximate empirical distributions derived using SSA simulations for $ \Omega\geq 300 $. We now use the pcLNA distributions for parameter sensitivity analysis.
We first compute the FIM and the corresponding singular values $ \sigma_i $ and principal sensitivity coefficients $ \underline{\mathbf{s}}_{ij} $ of the pcLNA distributions at phases/time-points $ t = 1, 3, \dots, 23 $ (period $ T\approx 24 $). The system size is set to $ \Omega = 300 $. For comparisons, we also compute the FIM under:
(a) the ordinary least squares (OLS) approximation with mean the deterministic model, i.e. $ X(t)\sim \mathrm{MVN}(x(t), eI_{mn}) $. Then, the (ij)-th entry of the FIM is $ e^{-1}\partial_i \mu^T \partial_j \mu $,
(b) the pcLNA but assuming that $ \partial \Sigma = 0 $. This is a weighted least squares (WLS) approximation with the weights arising from the pcLNA method, assumed to be constant to $ {{\mathit{\boldsymbol{\theta}}}} $. Then, the (ij)-th entry of the FIM is $ (\partial_i \mu)^T \Sigma^{-1} (\partial_j \mu) $.
(c) the pcLNA but assuming that $ \partial \mu = 0 $. Then, the (ij)-th entry of the FIM is $ \frac{1}{2}\text{tr}(\Sigma^{-1}(\partial_i \Sigma) \Sigma^{-1} (\partial_j \Sigma)) $.
Here, $ \mu $ and $ \Sigma $ are equal to $ \mu_{x_{1:n}} $ and $ (\Omega A_{x_{1:n}})^{-1} $ as in (4.8). The choice of the constant $ e $ in the OLS approximation is arbitrary and therefore, for the purpose of comparisons, it is chosen so that the first singular value, $ \sigma_1 $, of the corresponding FIM is equal to $ \sigma_1 $ derived under the pcLNA. The model (c) is simply used to allow an investigation of the sensitivities of the covariance matrix of pcLNA.
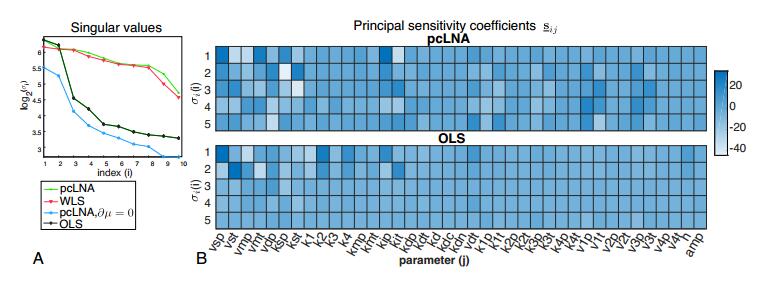
The ten largest singular values, $ \sigma_1\geq \dots \geq \sigma_{10} $ ($ k = 34 $) for each of these models are displayed in Figure 4(A). As we can see, while $ \sigma_1, \sigma_2 $ take similar values for the OLS approximation and pcLNA, the values of $ \sigma_i $, $ i\geq 3 $, for OLS drop much faster than those of the pcLNA method. This indicates that pcLNA contains much more information than the deterministic model. Most of this extra information in pcLNA is because of the use of the variance matrix $ A_{x_{1:n}} $ that provides more accurate scaling than the identity matrix. This is suggested by that the singular values of the WLS model are very close to those of the pcLNA model.
However, the first singular value, $ \sigma_1 $, of the WLS approximation is substantially lower than $ \sigma_1 $ in pcLNA and this is due to the parameter sensitivity of the covariance matrix. The $ \sigma_i $ values for approximation in (c) are much lower than pcLNA and WLS, but this largely depends on the system size. For smaller system size, the singular values of the WLS become smaller and of approximation (c) larger. Overall, this result indicates that using pcLNA over WLS and OLS approximations substantially improves parameter sensitivities.
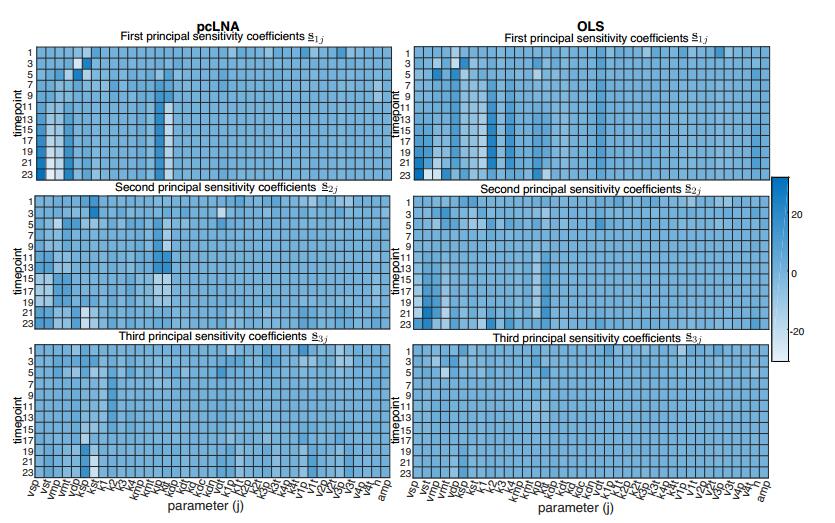
In addition to overall comparisons between parameter sensitivity of different models, we can use the principal sensitivity coefficients to investigate the sensitivities of the model to each parameter. As we can see in Figure 4(B), the change in parameter values that has the greatest effect on the pcLNA probability distributions (see $ \underline{\mathbf{s}}_{1j} $ in first row) is the one that changes a small selection of parameters of PER and TIM in opposite directions. In particular, the model is most sensitive to opposite sign changes of the mRNA transcription parameters $ vsp $ and $ vst $, the mRNA degradation parameters $ vmp $ and $ vmt $ and the half-max constants $ kip $, $ kit $ for the repression of transcription, and the translation parameters $ ksp $ and $ kst $. Furthermore, while there is some agreement between pcLNA and OLS models on the most influential parameters, OLS fails to capture sensitivity to a large number of parameters (e.g. the translation, ksp and kst, and phosphorylation, v1p and v1t, reaction constants).
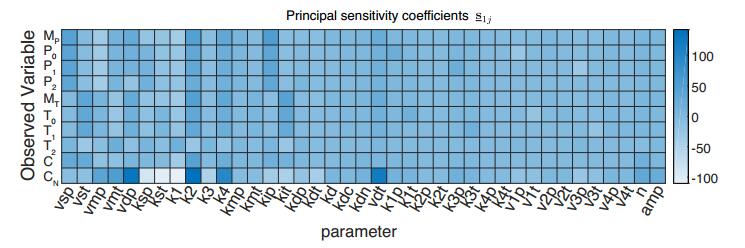
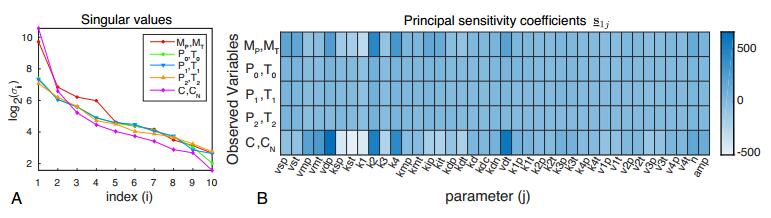
We next look at the parameter sensitivities of the marginal probability distributions of each variable of the network separately. This will be the observed sensitivities if only one variable, say $ X_i $, of the network is observed. For this computation, we eliminate the appropriate entries of $ \mu $ and $ \Sigma $ and the corresponding partial derivatives and consider only the terms that correspond to $ X_i $. We see in Figure 5 that there are substantial variations in the values of $ \underline{\mathbf{s}}_{1j} $ for the different variables. As expected, the variables of PER (TIM) are most sensitive to parameters related to reactions affecting PER (TIM), but sensitivities to some other parameters are also high. We also see that the variable that gives the largest sensitivities is the dimer complex $ C_N $, which is the transcription factor and therefore the regulatory variable of the network.
We then look in the parameter sensitivities of joint probability distributions of couples of variables of the network. In particular, we assume that either the mRNA levels, un-phosphorylated proteins, once phosphorylated proteins, twice phosphorylated proteins or dimer complexes are observed. This analysis is particularly relevant in experimental design when deciding at which of those levels a process should be observed to give the highest parameter sensitivities. We see in Figure 6(B) that there are considerable differences in sensitivity values with the biggest values observed at the level of the transcription factor ($ C $, $ C_N $), followed by mRNA ($ M_P $, $ M_T $). The differences are more prominent for the first singular value (see Figure 6(A)), which is at least $ 2^3 $ times larger than the rest of the eigenvalues.
We also investigate an important question arising in experimental design and this is the choice of time-points to take observations or to apply perturbations to the network. We compute the parameter sensitivities of the joint probability distributions of the variables of the network for the selected time-points. We first see in Figure 7 that there is considerable variation in the values of $ \underline{\mathbf{s}}_{ij} $ at each time-point. The pcLNA probability distributions are increasingly sensitive to the transcription ($ vsp $, $ vst $) and degradation ($ vmp $ and $ vmt $) parameters for the time $ t\in [11,23] $ where PER and TIM mRNA concentrations are expected to increase (see Figure 3). On contrary, the pcLNA probability distributions are less sensitive to those parameters at the times of mRNA decay. Furthermore, there is a sharp increase in sensitivity to the half-max constants for the repression of PER and TIM mRNA transcription ($ kip, kit $) around the time $ t \in [9,11] $, where the transcription factor $ C_N $ crosses these values. Many of those sensitivities are not captured by the OLS model dispayed in Figure 7, which is overall less sensitive to parameter sensitivities. The deterministic nature of the OLS model is reflected here in the sense that the model appears to be sensitive to parameter changes only in specific time-points rather than time-intervals. For example, the OLS model is very sensitive to the transcription parameters $ vsp $, $ vst $ at time $ t = 23 $ only.
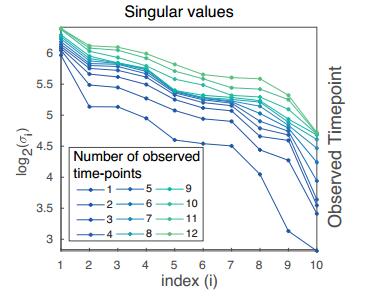
Finally, we investigate another important question regarding the number of time-points to be observed. As we can see in Figure 8, there is a great increase in the singular values of the FIM of pcLNA probability distributions as more time-points are observed. The increase in the value of $ \sigma_i $, when more time-points are observed, is larger for larger $ i $. For example, the value of $ \sigma_1 $ when 12 time-points are observed is approximately $ \sqrt{2}\approx 1.41 $ times larger than $ \sigma_1 $ when only one time-point is observed, whereas the corresponding increase in the value of $ \sigma_{10} $ is approximately twice as large ($ \approx 2\!\sqrt{2} $).
7.
Discussion
As greater understanding of biological processes leads to more complex network structures and more informative models, there is a need for further improving the methodology for analysing various salient aspects of those models. Moreover, as those models involve an increasing number of parameters, there is a need for systematic studies identifying those parameters and reactions that are most important for the given network and can be estimated from data. And as biotechnological innovation provide great opportunities for experimental data of better quality and greater quantity, there is a need for appropriate experimental design tools in order to optimise the collected information. This paper is an effort towards this direction.
The developed theory enables a study of the effects of parameter value changes to the probability distributions of sample paths of stochastic process. It applies directly to the changes in the relevant probability distribution and does not depend upon the choice of specific observables. It identifies the directions of the parameter space in which these probability distribution are most sensitive to perturbations in their parameter values. When the study considers only marginal, rather than full, probability distributions of subsets of variables or time-points, then the outcomes change substantially. This highlights that different observations capture different aspects of the network dynamics and this outcome has to be carefully considered in designing experiments and estimating parameters.
Acknowledgments
This research was funded by the BBSRC Grant BB/K003097/1 (Systems Biology Analysis of Biological Timers and Inflammation) and the EPSRC Grant EP/P019811/1 (Mathematical Foundations of Information and Decisions in Dynamic Cell Signalling). DAR was also supported by funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement n$ ^o $ 305564. BBSRC website: www.bbsrc.ac.uk EPSRC website: www.epsrc.ac.uk Seventh Framework Programme (FP7) website: cordis.europa.eu/fp7/ home_en.html. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Conflict of interest
The authors declare there is no conflict of interest.
Supplementary A
Drosophila circadian clock
The variables of the network describing the time-evolution of the Drosophila circadian clock in [30] along with the initial conditions (in nanomolar concentrations) used in our implementation are provided in Table 1. The parameter values used to derive the ODE solution of the system are provided in Table 2. The ODE system for the Drosophila circadian clock is given in Table 3. The intensity functions of the master equation are provided in Table 1 of [30].









 DownLoad:
DownLoad: