Periodically forced discrete-time SIS epidemic model with disease induced mortality

1.   Introduction

With the growth of China's transportation industry, the construction of highway tunnel has also ushered in a period of rapid development. According to the data released by the Ministry of Transport of the People's Republic of China, as of the end of 2019, the number of highway tunnels in China was 19, 067, with an increase of 7.5% compared with that in 2018, and the total length of tunnels reached 18.9666 million meters, with an increase of 10.04% compared with that in 2018. With the vigorous construction of the tunnel, people gradually found that due to the complexity and particularity of tunnel engineering, under the single or coupled action of the corrosive substances contained in the environment and groundwater, a considerable number of TLS have different degrees of damage, which seriously affects the durability of TLS and adversely affects the overall safety and service life of the tunnel. Because the tunnel is a concealed project, various uncertain factors will affect the durability of the lining, and now highway tunnels are developing towards large section and deep buried, complicated geological conditions, harsh climate environment, and corrosive groundwater penetration, etc., it will lead to LS cause by concrete carbonization, steel corrosion, lining surface cracking and other problems ^[1]. It is of great significance to evaluate the durability of the highway TLS reasonably, determine the durability grade of the TLS, and take corresponding technical measures to improve it in time.

Statistics from 2005 show that the total number of tunnels in China with serious water leakage, severe corrosion and cracking of the lining, deformation and damage of the inverted arch has reached 4587, accounting for about 60% of the total number of tunnels in operation ^[2]. At the end of 2000, a survey by the Ministry of Railways of Japanese showed that 70% of the total number of tunnels in the country had lining cracks, and 30% had foundation subsidence, leakage and bottom heave ^[3]. In European and American countries, after tunnels were built and put into use, due to concrete aging, frost damage, and corrosive substances and other reasons, many tunnels are gradually deteriorating, which affect the overall durability ^[4]. N. Burgess et al. ^[5] investigated the lining cracks and sulfate erosion in the tunnels of the north-south line of London Old Street Station from 1945 to 1960, and proposed the use of larger diameter acid-resistant pipe sheets made of stainless steel to replace cast iron pipe sheets, which eventually took 6 years to renovate and cost 15 million pounds. In summary, the durability of the TLS is gradually declining due to the deterioration of internal materials and the impact of a variety of factors in the external environment, and the number of durability damage costs for maintenance is huge, timely and reasonable evaluation of the durability of the LS, take the necessary technical measures to improve can save costs as well as extend the overall life of the tunnel.

With regard to evaluation methods, the methods currently commonly used in other fields are AHP (analytic hierarchy process)-cloud model ^[6], AHP-TOPSIS (technique for order preference by similarity to ideal solution) ^[7], AHP-EM (entropy method) ^[8] etc. Many scholars have applied relevant evaluation methods in the field of tunnels, and some research results have been achieved. Hoang Nguyen et al. ^[9] proposed a method based on particle swarm optimization and artificial neural network to evaluate the stability of tunnels and underground space roads, and used examples to verify that its accuracy is better than support vector machine, hybrid neural-fuzzy inference system, multiple linear regression, classification and regression tree and conditional inference tree methods. Zhang ^[10] and Mao ^[11] used Fuzzy Analytic Hierarchy (F-AHP) to evaluate the health of the tunnel and sudden surge water risk grade respectively, Zhang mainly by fusing different types of data from multiple sensors into the shield tunnel health grade score, combined with F-AHP for evaluation. Mao, on the other hand, combined with the natural geography, geological conditions, hydrogeological conditions and design and construction plan of a tunnel tunnel site area to get the factors of tunnel sudden surge water risk and establish a hierarchical structure model to achieve the evaluation. An et al. ^[12] created an extension evaluation model for tunnel collapse risk by using the simple correlation function method to calculate the index weights, and applied the evaluation model to the risk assessment of actual tunnel cases. Zhai et al. ^[13] used AHP and Entropy Weight (EW) to determine the comprehensive weight of the each evaluation index, and used the uncertainty measurement theory to determine the multi-index comprehensive evaluation vector of the research object, and determine the grade of tunnel collapse risk probability according to the principle of maximum affiliation, and use an example to verify that the evaluation result of this evaluation method is basically consistent with the real conditions. Regarding the evaluation of the durability of the TLS, Liu et al. ^[14] used the extended finite element method (XFEM) to simulate a tunnel lining in Hunan, China, and obtained the LS safety factor based on the maximum tensile strain and damage area safety factor calculated by XFEM. It is found that the minimum safety factor in the right vault area of the tunnel lining was 1.77, combined with the "Railway Tunnel Design Code", the compressive strength control safety factor (K1) should not be less than 2.0, and the tensile strength control safety factor (K2) should be greater than 2.4. The safety evaluation of the LS shows that the LS is unsafe, and the flawed cross section is considered to be a safety problem for the operating tunnel, it is believed that the defective section constitutes a hidden safety hazard to the operating tunnel, and the final simulation results are basically consistent with the actual lining damage form. Ye et al. ^[15] used transient electromagnetic radar (TER) to detect the lining thickness and voids deficiency behind the tunnel composite lining, and determined the contact state between the composite lining and the surrounding rock through the change in apparent resistivity, thereby to evaluate the durability of the tunnel composite lining. Ren et al. ^[16] used cloud model theory to evaluate the durability condition of mountain tunnel linings, applied the backward cloud generator principle to generate the index CM, and further used the improved EW-AHP comprehensive weighting method to determine the index weights, calculated the CM at each layer from index layer to target layer, and verified the rationality of the method by examples. Wu et al. ^[17] analyzed the causes of cracks in tunnel segment structures and their influence on the durability of segment structures, and evaluated the influence of the width, length, direction and density of cracks on the durability of segment structures by using the fuzzy set theory. Guo et al. ^[18] proposed an existing TLS disease evaluation method based on the AHP-Extenics model. This method used the AHP to establish an index system of the existing TLS disease formation factors, and used expert scoring method to determine the disease evaluation index weight, and then used the correlation function to perform extension calculation on the disease evaluation index and weight, and finally get the existing TLS disease evaluation grade. Zhang et al. ^[19] believe that chloride and carbon penetration are the most common durability problems in tunnels, which can affect the strength of reinforced concrete in TLS. Based on experimental tests, they developed a procedure to evaluate the concrete strength of tunnel lining under corrosive conditions to indirectly evaluate the durability of the LS, which includes three main steps: bonding strength, cracking and specimen performance. It is verified by other scholars' experimental data, and the result show that the method is more accurate. Zhu et al. ^[20] proposed a variable fuzzy comprehensive evaluation method for the durability of TLS, which first determines the relative affiliation matrix of the eigenvalues of the evaluation target index to each grade, and then applies the variable fuzzy optimization model to solve the comprehensive relative affiliation of the grade. The relative degree of membership is finally applied to make a comprehensive evaluation of the evaluation object using the grade characteristic value equation, and finally the tunnel engineering durability grade evaluation is realized. The durability of the TLS plays an essential role in maintaining the overall loading capacity, safety and stability of the tunnel, but there are many factors that affect the durability of the TLS, due to the lack of information on the overall durability of the tunnel lining and the complexity of the materials used in the lining construction, the uncertainty of the division of indicators makes many factors have the characteristics of uncertainty such as ambiguity and randomness. Although many scholars have put forward many methods and measures for tunnel durability evaluation, but in general, the ambiguity and randomness of the TLS durability evaluation index itself is not considered enough, it is difficult to establish a mapping relationship between quantified evaluation indicators and qualitative durability grades, etc. Because the durability evaluation index of TLS has the characteristics of fuzziness and randomness, the general method is difficult to solve the fuzziness and randomness of the evaluation index, and most of the durability status is basically qualitative description, because different decision makers have different characteristics such as their knowledge reserves and engineering experience and often makes fuzzy evaluations such as "best, good, and general", which is not conducive to truly grasping the durability of tunnel lining. It is urgent to propose a scientific and reasonable method to map qualitative language to quantitative data. CM is an uncertainty transformation model, which realizes the mutual conversion from qualitative concepts to quantitative values, and in the process of transformation of the two can reflect the randomness and ambiguity of describing things at the same time, and constitute the mapping relationship between qualitative and quantitative, and thus can be used to describe the fuzzy and uncertainty problem, can be well applied to evaluation of uncertain systems ^[21]. In addition, for weight calculation, mostly based on subjective weight assignment method, such as expert scoring method, such methods take human subjectivity into consideration. The simple correlation function method is objective and easy to calculate, and can be used for weight calculation.

In summary, in order to eliminate the shortcomings of the existing evaluation methods, this paper proposes a TLS durability evaluation method to determine the actual durability state of the LS. The significant advantage of this method is that it takes into account the actual damage state of the LS, instead of being obtained directly by experts scoring based on experience. The evaluation process reflects the fuzziness and randomness of the evaluation index, and achieves objective weighting. At the same time, the AHP-Extenics method is combined to evaluate the durability of the highway TLS, and the results of the comparative study showed that the method is more reasonable.

The main contributions of this paper are:

(i) A more systematic evaluation method is proposed to evaluate the durability of highway TLS. The advantage of this method is to consider the fuzziness and uncertainty of each durability evaluation index, transforms the fuzziness and randomness of the index into specific relationships and values, and converts the qualitative concepts of the evaluation index into quantitative values, and realizes the conversion between the durability damage degree and durability grade, which is convenient for accurately determine the durability of the LS, and its accuracy rate is relatively high.

(ii) A relatively simple method of objective weight assignment is applied, namely SCF, which can significantly reduce the influence of human subjectivity and make the weight of each evaluation index objective and science.

(iii) The method proposed in this paper effectively considers the actual damage state of the LS, can analyze the relevant durability index test data of the LS, and links the test sample data of the index with the standard values of each index in each durability grade interval, so as to achieve scientific and objective evaluation.

(iv) A application study is conducted through real engineering project cases, and the comparative study is made with AHP-Extenics, which verified the feasibility and rationality of the method, and provide a reference basis for the durability evaluation of similar projects in the future.

The structural composition of each part of this paper is as listed below. Section 2 describes the specific introduction of each method used in this study. Section 3 presents the specific evaluation process of the evaluation method. Section 4 carries out application and comparative research in combination with actual engineering projects. Section 5 is the conclusions and discussion.

2.   Methods

2.1.   Cloud model (CM)

CM is a transformation model between qualitative concepts and quantitative values proposed by academician Deyi Li on the basis of traditional fuzzy set theory and probability statistics, which can reveal the inherent correlation of randomness and ambiguity of things ^[22,23], and is used to study the problem of uncertainty. It has been applied in river health evaluation, internet of things system performance evaluation, and urban rail transit operation safety evaluation ^[24,25,26]. At present, the distribution forms of cloud theory have developed as triangular cloud, rectangular cloud, trapezoidal cloud, normal cloud, etc. Among them, the normal CM is commonly used due to its unique mathematical properties and universality ^[27].

2.1.1.   Normal cloud definition

Definition of normal cloud: Let U is a quantitative domain represented by an exact value, and C is a qualitative concept on U. If the quantitative value x ∈U, and x is a random realization of the qualitative concept C, if it satisfies: x~N (E_x , E_n ' ²), where E_n'²~N(E_n , H_e²), and the affiliation to C satisfies:

Where, E_x is the expected value, E_n is the entropy value, H_e is the super entropy.

2.1.2.   Cloud model digital features

Let U is a one-dimensional quantitative domain represented by exact values, V is a qualitative concept on domain U, x is a realization of a random variable X defined on U, and the degree of membership of x to V, $ {\mu _V}(x) \in [0, 1] $ is a random variable with a stable tendency, then the distribution of X in domain U is called a one-dimensional cloud, each x is called a cloud drop ^[28]. The one-dimensional CM is represented by three digital features: expected value E_x, entropy E_n and super entropy H_e. Digital features can reflect the qualitative features of things in a quantitative form, completing the model conversion between qualitative and quantitative concepts. The expected value of the numerical feature is expressed as the central value of the qualitative concepts in the quantitative domain, which is the point of the most qualitative concepts in the domain space; Entropy reflects the fuzziness of qualitative concepts and the range of cloud drops, which are determined by the fuzzinessand randomness of qualitative concepts, and the larger the value, the greater the fuzziness and randomness; Super entropy can measure the degree of dispersion of cloud drops, and the greater the super entropy, the greater the uncertainty of cloud drops.

2.1.3.   Cloud generators

Cloud generators act as converters that transform qualitatively and quantitatively into each other. Cloud generators ^[29] are divided into 3 types: (1) Convert qualitative to quantitative forward cloud generator (FCG), that is, generate quantitative cloud drops x_i and membership $ {\mu _i} $ through cloud $ C({E}_{x}, {E}_{n}, {H}_{e}) $; (2) The backward cloud generator (BCG) that converts from quantitative to qualitative, that is, analyzes through accurate $ Drop{\rm{(}}{x_i}{\rm{)}} $ conversion to qualitative concept $ C({E}_{x}, {E}_{n}, {H}_{e}) $. (3) X cloud generator and Y cloud generator form a special conditional cloud generator, that is, known $ C({E}_{x}, {E}_{n}, {H}_{e}) $ and specific conditions X or Y are used to calculate the degree of certainty.

2.2.   Matter-element Extension (MEE) and simple correlation function (SCF) method

Extenics theory was first created as a new discipline by Cai Wen and other scholars from Guangdong University of Technology, which adopts a formal model to study the possibility of expansion of things and the laws and methods of pioneering innovation, and is widely used in multi-objective comprehensive judgment problems. It mainly divides into matter-element theory, extension set theory and extension logic. The matter-element theory has great advantages in solving the uncertainty and ambiguity of things ^[30]. The main process of the matter-element theory is to determine the classical domain, the section domain and the matter-element to be evaluated.

The matter element is usually represented by the name of the thing (N), the characteristic of the thing (C) and its characteristic value (V). The matter element of a certain thing can be recorded as: R = (N, C, V). Let the matter element be:

Where, R_j —the classical domain matter element matrix composed of the characteristic C of the j -th evaluation grade N_j and the value range of the characteristic C, j = 1, 2, …, m.

N_j —The j -th evaluation grade divided;

c_i —The i -th evaluation index, i = 1, 2, …, n;

$ {V_{ij}}{\rm{ = }}\left\langle {{a_{ij}}, {b_{ij}}} \right\rangle $ —The range of the quantity value the i -th index c_i of the j -th evaluation grade N_j. That is, the data range of each evaluation grade corresponding to the evaluation index is the classic domain; $ {a_{ij}} $ is the lower limit of the quantity of the i -th index c_i, and b_ij is the upper limit of the quantity of the i -th index index c_i.

The section domain is:

Where, P —Something to be evaluated;

R_P —A matrix of section domain elements consisting of the characteristic C of the thing to be evaluated, P, and all of its evaluation grades, and the range of quantitative values of the characteristic C;

$ {V_{ip}} = \left\langle {{a_{ip}}, {b_{ip}}} \right\rangle $ —It is range that P measures with respect to c_i, that is the section domain of P. a_ip is the minimum value of the lower limit of the i -th index c_i in all evaluations, and b_ip is the maximum value of the upper limit of the i -th feature C in all evaluations, and $ {V_{ij}} \subset {V_{ip}}{}(i = 1, 2, \cdots, n;{}j = 1, 2, \cdots, m) $.

Determine the matter element to be evaluated (use the collected statistical data or analysis result as matter element R):

Where, P —Something to be evaluated;

$ {v_i} $ —P about the range of quantitative values of evaluation index c_i, which is the specific index data of the object to be evaluated.

SCF is a method to objectively determine the weight, and the calculation process ^[31] is as follows:

Where, r_ij represents the correlation of the i -th index and the j -th evaluation grade; v_i represents the sample value of the i -th index; V_ij represents the value range of the i -th index corresponding to the j -th evaluation grade in the classical domain; and i = 1, 2, …, n; j = 1, 2, …, m.

If $ {v}_{i}\in {V}_{ip}, (i = 1, 2, \cdots, n) $, then $ {r}_{i{j}_{max}}({v}_{i}, {V}_{ij}) = \underset{j\in (1, 2, \cdots, m)}{max}\left\{{r}_{ij}({v}_{i}, {V}_{ij})\right\} $

If the evaluation grade j of the evaluation index i of the object P to be evaluated is larger, and the weight assigned by the index is greater, then take:

Among them, j_max —represents the evaluation grade into which the sample value of index i in the element to be evaluated falls, and the larger of the value, the more restrictive the index is to treat the matter, when $ {r_{i{j_{\max }}}} = {r_{im}} $, $ {j_{\max }} = \max \left\{ m \right\} $.

If the evaluation grade j of the evaluation index i of the object P to be evaluated is larger, the weight assigned by the index is smaller, taking:

Among them, m —represents the number of categories divided for each index, when $ {r_{i{j_{\max }}}} = {r_{im}} $, $ {j_{\max }} = \min \left\{ m \right\} $.

Then the weight of index c_i is

Among them, w_i —the normalized value of the i -th evaluation index weight.

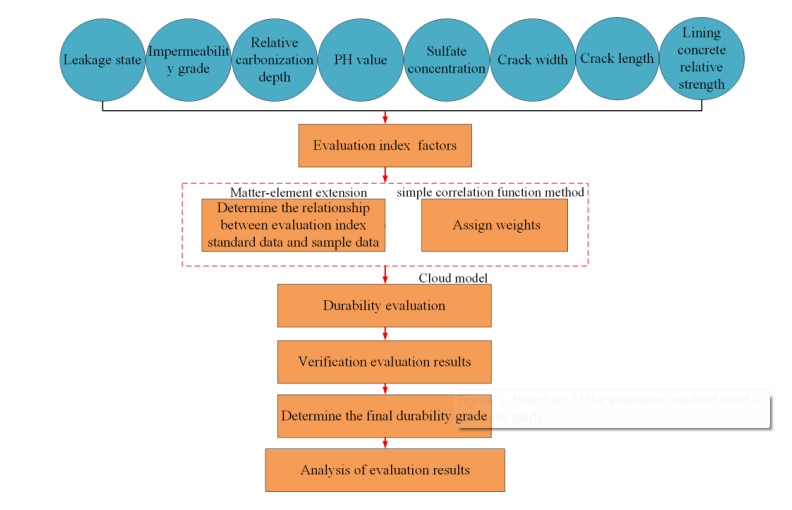
3.   Evaluation process of durability

(i) According to the causes and influencing factors of the durability damage of highway TLS, the corresponding indicators are screened out, and the durability evaluation index system of highway TLS is established.

(ii) Based on the MEE, determine the classic domain, section domain, and the matter-element to be evaluated, determine the relationship between the standard data of the evaluation index and the measured sample data of the object to be evaluated, SCF is introduced to objectively calculate the determined index data to obtain the weight of each index.

(iii) The divided highway TLS durability evaluation grade is converted into a CM according to the golden section method to generate a durability grade evaluation classification CM, and then a forward cloud generator is used to generate cloud images by classifying cloud models.

(iv) Determine the evaluation standards that affect the durability of the highway TLS at each grade. According to the positive and negative correlation between the evaluation standard value and the durability grade, the range change method was used to process the index data to make the value distribution $ [0, 1] $, it is the same as the domain interval in the CM, which is convenient for calculation.

(v) The X condition cloud generator is used to determine the digital features of the standard CM of each evaluation index. At this time, the measured values of the sample are brought in, and the digital features of the object to be evaluated are multiplied by the weight after normalization and calculation of the digital features of the CM. The weighted average is gradually solved to the top layer to obtain the comprehensive evaluation result. According to the CM theory, it is transformed into the corresponding CM and compared with the durability grade CM. According to the principle of maximum affiliation, the final durability evaluation grade is determined.

4.   Example application

4.1.   Engineering case

To verify the rationality of the method, the relevant data of the durable disease detection of a highway tunnel lining in the literature ^[32] are selected for verification.

The tunnel is located on the G50S Shanghai-Chongqing South Line with a total length of 7.3km. The development of the landform in the tunnel site area is obviously controlled by the geological structure and formation rock, and the tunnel direction is northeast-southwest, which has the characteristics of erosion-soluble geomorphology. The tunnel groundwater is abundant, and groundwater distribution and distribution range does not have a stable state ^[33]. The tunnel opened to traffic in 2013, and a problematic section of 1756m appeared when it was in operation until 2016. The main problems include: seepage cracks, no seepage cracks, structural strength defects, etc. After the water sampling test, the sulfate ion content of the groundwater in some sections is too high, and the tunnel lining is found to be cracked during the inspection.

4.2.   Constructing a highway TLS durability evaluation index system

Combining with the existing literature and the practical situation of engineering, the factors of the durability of the highway TLS are divided into four factors: osmosis, material deterioration, lining cracks, and lining relative strength, each factor is composed of several evaluation indexes, thus establishing a three-layer index evaluation system. Users can combine other methods, such as on-site investigation, to determine each evaluation index when using this method.

4.3.   Determine the durability evaluation grade of a highway TLS

Chinese code "Code for Durability Design of Concrete Structures in Highway Engineering " (JTG T3310-2019) ^[34] takes into account the impact of environmental effects, among which environmental factors mainly include six environmental categories: carbonization, freeze-thaw cycles, chloride erosion, sulfate crystal expansion, chemical corrosion and abrasion, which are classified according to their respective environmental impact grades, they are basically divided into 3 to 4 grades. However, the code does not give a detailed classification of the durability grade of the TLS. This paper referred to the literature ^[35], and the durability of the LS is divided into 5 grades, as shown in Table 1. When using this method, users can determine the durability grade according to the evaluation object from the relevant national codes, scholars' research results, etc.

Since Table 1 is a qualitative description, coupled with the TLS is a concealed project, the construction process is complicated, and many degradation factors are synergistically coupled, and it is difficult to classify accurately, which leads to ambiguity in the classification of grades. When using the traditional quantitative analysis methods to quantify these qualitative indicators, the ambiguity of the indicators is largely ignored, causing the evaluation results to be not objective. CM theory can reflect the randomness and fuzziness of describing things at the same time, and transform the uncertainty relationship between qualitative and quantitative things, and form a mapping relationship between qualitative and quantitative, which can be used to deal with the uncertainty of fuzzy factors ^[36]. Therefore, the CM theory method is used to transform the evaluation set of TLS durability grades into a normal CM to represent it, and the golden section method is used to transform the five-grade qualitative concepts in Table 1 into a five-cloud model. The domain is $ [0, 1] $, and the steps are as follows:

Let the middle cloud be $ {C_3} $ $ ({E_{x3}}, {E_{n3}}, {H_{e3}}) $, its left and right adjacent clouds are $ {C_2} $ $ ({E_{x2}}, {E_{n2}}, {H_{e2}}) $, $ {C_4} $ $ ({E_{x4}}, {E_{n4}}, {H_{e4}}) $, as well as $ {C_1} $ $ ({E_{x1}}, {E_{n1}}, {H_{e1}}) $, $ {C_5} $ $ ({E_{x5}}, {E_{n5}}, {H_{e5}}) $.

The various cloud algorithms are as follows ^[37]:

Among them, H_e represents the uncertainty of entropy and reflects the degree of dispersion of each cloud drop. Generally, the value can be obtained by experience, here H_e3 is 0.005 ^[38]. The durability evaluation grade cloud model of TLS is obtained as shown in Table 2.

The FCG is used to generate a cloud image from the evaluation grade CM, in which the number of cloud drops is 1000, and the results are shown in Figure 6.

4.4.   Determine the durability evaluation standard of a highway TLS

According to the durability grade, it divides into 5 grades. The specific numerical interval of each grade refers to the division method of the original cited literature ^[32]. At the same time, it refers to the classification of relevant index grades by Chinese standards and related scholars ^{[39,40,41,42,43,44]}. The evaluation criteria of a certain tunnel from YK83 + 085 to YK83 + 750 are divided, as shown in Table 3. As for the interval range values of each evaluation index within different grades, users can consult relevant standards, codes, literature and so on to determine them.

4.5.   Determining the durability index weight of a highway TLS

SCF is an objective weighting method, which can be used to objectively and reasonably assign weights and determine the final result. When calculating the weight, it is important to determine the relationship between the measured sample data and the standard data of each evaluation index in each durability grade, and compare the standard value of each evaluation index with the measured sample value. Here, the relationship between the standard value of each durability index in each durability grade and the measured sample data is established by using MEE.

MEE first determines the classical domain and section domain. Before that, in order to make different evaluation indicators comparable, the range change method is used to normalize and non-dimensionalize the index data. For index numbers B₁, C₁, C₃, D₁, D₂, these factors are positively related to the durability of the LS. The larger the value, the worse the durability grade. The treatment method is: $ {X_i} = \frac{{{X_i} - {X_{i\min }}}}{{{X_{i\max }} - {X_{i\min }}}} $. For index numbers B₂, C₂, E₁, these factors have a negative correlation with the durability of the LS. The smaller the value, the worse the durability grade. The treatment method is: $ {X_i} = \frac{{{X_i}_{\max } - {X_i}}}{{{X_{i\max }} - {X_{i\min }}}} $, the range of each index grade after treatment is shown in Table 4.

Combining the MEE and the SCF to determine the weight, in this case it is:

Where, j takes 1, 2, 3, 4, 5, When j = 1, range of B₁, B₂, C₁, C₂, C₃, D₁, D₂, E₁ are (0, 0.2), (0, 0.2), (0, 0.31), (0, 0.19), (0, 0.1), (0, 0.03), (0, 0.08), (0, 0.2). The test data of each evaluation index of the tunnel is shown in Table 5 after dimensionless and normalized. After obtaining the test data of each evaluation index, the user can normalize the index data according to the above method.

SCF is used to determine the index weight. In this example, the data of Tables 4 and 5 are substituted into Eqs (2) to (8) to obtain the weight of each evaluation index, as shown in Table 6.

4.6.   Determining the overall durability grade of the LS of a highway tunnel

The X condition cloud generator is used to calculate the cloud digital features of each evaluation index, and the equation ^[45] are:

Where, $ {E}_{{x}_{{}_{ij}}}、{E}_{{n}_{ij}} $ respectively represent the expected value and entropy value of the i -th index corresponding to the j -th durability grade; x_ij represents the membership value of the i -th index corresponding to the j -th durability grade; $ {x}_{ij, 1}、{x}_{ij, 2} $ respectively represents the upper and lower boundary values of the evaluation index system standard; the super entropy $ {H_{{e_{_{ij}}}}} $ is generally obtained by experience.

After normalization and dimensionless processing of each evaluation standard data, the conditional cloud generator is used to obtain the standard CM of each evaluation index, as shown in Table 7.

After normalizing the inspection data of the TLS and calculating the digital features of the CM, the measured CM for each index is shown in Table 8.

According to the established index system for durability evaluation of a highway TLS, the index CM and index weights are calculated, and the index layer is solved layer by layer until the top layer CM is obtained, which is the comprehensive evaluation result CM. The solution process are as follows ^[16]:

The calculation results are shown in Table 9. When using this method, users can perform the corresponding calculations in accordance with the above equations, and the parameters involved in each step of the equations are explained, while the sources of the equations are cited in the literature.

The CM image is drawn with the help of MATLAB software, the procedures involved are supplemented in Appendix, which can be used directly by users, and the CM image of each evaluation index is finally obtained as:

The final evaluation result cloud model is:

According to the comprehensive evaluation cloud model shown in Figure 8, the durability grade of a tunnel lining is between grade III and grade IV, with a preference for grade IV. According to the principle of maximum affiliation, it is taken as grade IV, which is in accordance with the evaluation result of the original literature. And it is consistent with the actual situation of the project, indicating the rationality and accuracy of the method. In order to test the accuracy of this method, we extracted the evaluation results of four main influencing factors, as shown in Figure 7. According to the principle of maximum affiliation, it can be found from Figure 7 that the durability grades of indicators D and E are evaluated as IV, which is consistent with the comprehensive evaluation result. The accuracy rate reached 100%. According to the CM digital features of indicators B and C and the IV grade digital features are calculated, it is found that the accuracy rates reached 73.4% and 97.6% respectively. When combined, the accuracy rate reached 92.75%. At the same time, the result of the comprehensive evaluation also showed that related measures are needed to maintain and repair this tunnel.

4.7.   Comparative Study

In order to show the rationality and science of this method, we did a comparative study using the AHP-Extenics method. AHP is a method of multi-factor sequencing and hierarchical weights decision-making analysis. It has been used in the fields of flood risk assessment ^[46] and earthquake danger assessment ^[47]. Since AHP is essentially a method of determining weights by comparison between factors, when evaluating objects to be evaluated, it is often combined with other methods to achieve the final evaluation. Extenics can meet the requirements to achieve a comprehensive evaluation of the objects to be evaluated. Among them, the durability evaluation grades of the TLS are still divided into I, II, III, IV, V.

The main steps of AHP are: constructing a hierarchical structure model, constructing a judgment matrix, assigning weights, consistency checking, and total ranking of hierarchy. AHP-Extenics uses AHP to establish the evaluation index system and weight assignment for actual problems, and on this basis, the Extenics theory is used to construct a correlation function to calculate the correlation between evaluation index and evaluation grade, so as to evaluate the actual engineering problem intuitively.

1) Building a hierarchical structure model

The top layer of the hierarchical structure model is the target layer. Generally speaking, there is only one element, which represents the goal that the decision maker wants to achieve; Generally, there are one or several levels in the middle, which are the criterion layer or sub-criteria layer, which represent the guidelines that must be followed by various measures and programs to achieve the overall goal; The bottom layer is the plan layer or index layer, which means various plans, indicators to be selected to solve the problem. Choosing a hierarchical structure model can clearly express the complex relationship between these factors. According to the actual engineering situation, the model of the components is given in Figure 9.

2) Constructing the judgment matrix

Constructing the judgment matrix is the core of the AHP method to solve the problem. Expert scoring methods are often used to determine the basic data according to the 1-9 scale method to compare the factor indicators two by two, which can quantify the relative importance between factors. The 1-9 proportional scale ^[48] is shown in Table 10. Experts with rich tunnel construction experience are invited to score, after the scoring results are calculated by geometric mean, and the final judgment matrix of the index layer relative to the target layer was obtained as shown in Table 11.

3) Assigning weights and consistency checking

Use the square root method to find the weight of each factor. Step 1: Multiply each element by row, see formula (16); Step 2: To open the second party separately, see type (17); Step 3: to formalize the weight vector, see formula (18); step 4: calculate the maximum characteristic root of the judgment matrix, see type (19).

Use the Geometric mean method to find the weight of each factor. Step 1: Multiply each element by row to get $ {u_{ij}} $, see Eq (16); Step 2: For $ {u_{ij}} $ separately open $ n $ times to obtain $ {u_i} $, see Eq (17); Step 3: Normalize $ {u_i} $ to obtain the weights vector $ {\omega _i} $, see Eq (18); Step 4: Calculate the maximum characteristic root $ {\lambda _{max}} $ of the judgment matrix, see Eq (19).

In the equation, b_ij is the relatively important value of the i -th evaluation index relative to the j -th evaluation index, which is the value in the judgment matrix; A is the judgment matrix; $ \omega $ is the eigenvector; n is the number of elements.

In order to verify the rationality of the judgment matrix construction, it is necessary to check the consistency of the evaluation indicators. The specific calculation steps are as follows:

Step 1: Calculate the consistency index CI, see Eq (20).

where: n is the order of the matrix; $ {\lambda _{max}} $ is the maximum characteristic root of the judgment matrix;

Step 2: Calculate the consistency ratio CR, see Eq (21).

Where, RI is the average random consistency index, which can be determined by checking Table 12 ^[49].

According to the consistency criterion, when the random consistency ratio CR < 0.10, it is considered that the constructed judgment matrix meets the consistency test, otherwise, the element value should be adjusted appropriately.

It should be especially noted that the reason why this case is divided into 2 layers according to the hierarchical analysis is because the RI value is 0 when the matrix order n is 1 or 2, then n needs to be at least 3. However, as can be seen from the foregoing, there are eight evaluation indicators in total and four main durability factors cannot be divided at all, so it is divided into two layers. In this case, according to the evaluation indexes chosen for the actual project by calculating Table 11, the weights vector $ {\omega _i} $ are (0.031, 0.142, 0.084, 0.019, 0.046, 0.344, 0.267, 0.067), from Eqs (16)-(21), the maximum characteristic root $ {\lambda _{max}} $ is 8.961, CI is 0.137 and RI is 1.40. Therefore, CR is 0.098 < 0.1, so it meets the consistency requirement.

4) Hierarchical total ordering

Through the above calculation of the weights vector of evaluation indexes, the weight of each index can be obtained as (0.031, 0.142, 0.084, 0.019, 0.046, 0.344, 0.267, 0.067). After sorting, the order of the index weight from largest to smallest is: B₆, B₇, B₂, B₃, B₈, B₅, B₁, B₄. However, this is only the calculation of the weight of each evaluation index. It is necessary to compare the actual test data of each evaluation index with the value of the standard interval between the evaluation indexes in each durability grade, and finally realize the durability evaluation. Based on this, we use the extenics theory, which is different from the previous one in that the above adopts the matter element theory, which is one of the important components of the extenics theory. Here, the correlation calculation is used and the weights can be combined to achieve durability evaluation.

The matter-element theory in extenics theory has been explained above, and here is the focus on the calculation of the correlation function value of the matter-element grade of the highway TLS to be evaluated.

Where, $ {\rm{ \mathsf{ ρ} }} ({v_i}, {V_{ij}}){\rm{ = }}\left| {{v_i} - \frac{{{b_{ij}} + {a_{ij}}}}{2}} \right| - \frac{{{b_{ij}} - {a_{ij}}}}{2} $; $ \left| {{V_{ij}}} \right|{\rm{ = }}\left| {{b_{ij}} - {a_{ij}}} \right| $; $ {\rm{ \mathsf{ ρ} }} ({v_i}, {V_{iP}}){\rm{ = }}\left| {{v_i} - \frac{{{b_{iP}} + {a_{iP}}}}{2}} \right| - \frac{{{b_{iP}} - {a_{iP}}}}{2} $.

$ {K_j}(v{}_i) $ is the value of the correlation function of each evaluation index, and the meaning of each other parameter has been explained in the previous section and is not listed here.

The correlation of the durability grade j of the tunnel lining to be evaluated is as follows:

If

Then rating p belongs to grade j₀.

Let

where $ {j^*} $ is the eigenvalue of the grade variable of p. The degree of bias towards which durability grade can be observed by the $ {j^*} $ value.

The value of the durability grade range of each evaluation index and the actual test data value were normalized, and the results are shown in Table 13.

From Eq (22), the correlation function value of the durability of the TLS to be evaluated with respect to each evaluation grade can be calculated as:

According to Eq (22) and Eq (23), the correlation degree of the durability of the highway TLS with respect to the evaluation grade j is calculated as:

According to Eq (24), it can be determined that the durability evaluation grade of the TLS is j₀ = 4, that is, the durability grade of the TLS is grade IV, which is severely damaged. According to Eq (25) and Eq (26), we can obtain the variable eigenvalue of the durability grade of the LS in this case $ {j^*} $ = 3.83, which means that the durability of the TLS is biased towards grade IV, which is a severely damaged state and requires technical measures for repair.

Throughout the full text, it is found that the evaluation results of the two methods are consistent and consistent with the actual damage state of the TLS. However, the shortcomings of the traditional AHP method are also very obvious. It is difficult to ensure the science and accuracy of the results due to the uneven level of experts. Secondly, it cannot achieve the durability evaluation and focuses on the calculation of weights, and requires the comprehensive use of other methods. When combining the Extenics method calculation, the amount of calculation is not small, and its accuracy rate cannot be calculated. The comparative study highlights the rationality of the method proposed in this paper.

5.   Conclusions and discussion

In order to evaluate the durability of highway TLS, a durability evaluation method based on MEE-SCF-CM is proposed. The main conclusions are as follows:

(Ⅰ) The factors that affect the durability of highway TLS are relatively complex, with many evaluation indicators, and itself is a complex system of multi-index. Establishing a multi-layer and multi-factor index system can clarify the logical relationship between factors and indexes, so that the evaluation process is clear and traceable; Based on MEE, SCF is used to objectively assign weights and calculate weights, which can reduce the influence of human subjectivity and make the evaluation results more objective.

(Ⅱ) Use the FCG to transform the measured sample data and evaluation criteria of the object to be evaluated into a quantitative cloud model, multiplying the digital features and weights of the CM of the object to be evaluated and carrying out weighted average gradually to the top layer to obtain comprehensive evaluation result of CM. By comparing the comprehensive evaluation of CM with the durability grade of CM, the durability evaluation grade of the final TLS is determined. This method greatly reduces the uncertainty in the evaluation process, and the evaluation process is more reasonable.

(Ⅲ) The case analysis shows that the durability evaluation method based on MEE-SCF-CM reduces the subjectivity of durability evaluation of TLS, the uncertainty problems such as the ambiguity and randomness of indicators are transformed into specific relationships and values, reveals the intrinsic relationship between randomness and ambiguity, and realizes the conversion between evaluation indicators and durability grades. What's more, the evaluation result obtained is consistent with the actual situation of the project, and its accuracy reaches 92.75%. At the same time, the feasibility of the method is verified by a comparative study combined with the AHP-Extenics method.

This paper combined a case to carry out theoretical and applied research, although the final evaluation result is consistent with the actual engineering project, and the accuracy rate is relatively high. However, the method also has certain drawbacks and limitations. In summary, it can be divided into the following points:

(i) This method sometimes needs to be calculated with the help of MATLAB software, so relatively speaking the method may be a bit complicated to calculate and requires some mathematical knowledge.

(ii) Due to the low level of construction personnel and deterioration of materials used in the LS, etc., and the LS may already have durability problems during the construction period, so the limitation of this method is how to select durability evaluation indicators during the construction period or other periods and how to define the standard interval values of these indicators.

However, in general, with the quantity and length of highway tunnels in China far exceeding other countries, it is of great significance to carry out timely evaluation of the durability of highway TLS so that measures can be undertaken to repair them, which is of great significance for prolonging the overall life of the tunnels, protecting people's lives and property, saving financial resources and so on. At the same time, this also requires scholars to make efforts to enrich the evaluation methods for the durability of highway TLS. In view of the complexity of the method proposed in this paper, we next make efforts to realize programming with the help of program code, so that the calculation equation in this evaluation method does not need to be calculated artificially, which simplifies the calculation process to a certain extent, and finally realizes that only the standard values of evaluation indexes within each grade of the TLS during the construction period or operation period need to be input, and then input the sample value of each index for evaluation, according to the accuracy to determine the state of the LS, and then take relevant measures.

Acknowledgments

This work received no external funding.

Conflict of interest

The authors declare no conflict of interest.

Appendix

E_x = a (Bring in the corresponding value)

E_n = b (Bring in the corresponding value)

H_e = c (Bring in the corresponding value)

hold on

for i = 1:1000 (Specific number of cloud drops)

E_nn = randn(1)*H_e +E_n;

x(i) = randn(1)*E_nn+E_x;

y(i) = exp(-(x(i)-Ex)^2/(2*E_nn ^2));

plot(x(i), y(i), 'c*')

End

Note: 'c*'—Other colors or graphics can be selected.

r-red; g-green; b-blue; c-green; m-Magenta; y-yellow; k-black; w-white.