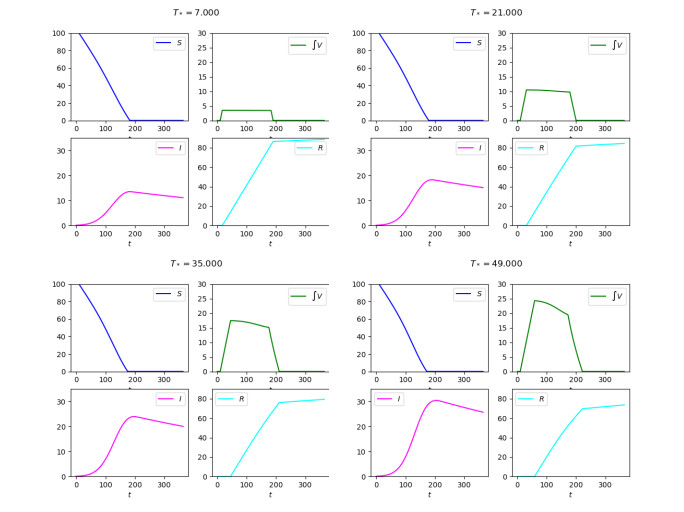
Solutions to (3)–(7)–(8) in the
Citation: Elisa Isopi, Giuseppe Legname. Pin1 and neurodegeneration: a new player for prion disorders?[J]. AIMS Molecular Science, 2015, 2(3): 311-323. doi: 10.3934/molsci.2015.3.311
| [1] | Qi Luo, Ryan Weightman, Sean T. McQuade, Mateo Díaz, Emmanuel Trélat, William Barbour, Dan Work, Samitha Samaranayake, Benedetto Piccoli . Optimization of vaccination for COVID-19 in the midst of a pandemic. Networks and Heterogeneous Media, 2022, 17(3): 443-466. doi: 10.3934/nhm.2022016 |
| [2] | Prateek Kunwar, Oleksandr Markovichenko, Monique Chyba, Yuriy Mileyko, Alice Koniges, Thomas Lee . A study of computational and conceptual complexities of compartment and agent based models. Networks and Heterogeneous Media, 2022, 17(3): 359-384. doi: 10.3934/nhm.2022011 |
| [3] | Xia Li, Chuntian Wang, Hao Li, Andrea L. Bertozzi . A martingale formulation for stochastic compartmental susceptible-infected-recovered (SIR) models to analyze finite size effects in COVID-19 case studies. Networks and Heterogeneous Media, 2022, 17(3): 311-331. doi: 10.3934/nhm.2022009 |
| [4] | Eiman, Kamal Shah, Muhammad Sarwar, Thabet Abdeljawad . On rotavirus infectious disease model using piecewise modified $ ABC $ fractional order derivative. Networks and Heterogeneous Media, 2024, 19(1): 214-234. doi: 10.3934/nhm.2024010 |
| [5] | Ryan Weightman, Temitope Akinode, Benedetto Piccoli . Optimal control of pandemics via a sociodemographic model of non-pharmaceutical interventions. Networks and Heterogeneous Media, 2024, 19(2): 500-525. doi: 10.3934/nhm.2024022 |
| [6] | Guillaume Cantin, Cristiana J. Silva, Arnaud Banos . Mathematical analysis of a hybrid model: Impacts of individual behaviors on the spreading of an epidemic. Networks and Heterogeneous Media, 2022, 17(3): 333-357. doi: 10.3934/nhm.2022010 |
| [7] | Xavier Blanc, Claude Le Bris, Frédéric Legoll, Tony Lelièvre . Beyond multiscale and multiphysics: Multimaths for model coupling. Networks and Heterogeneous Media, 2010, 5(3): 423-460. doi: 10.3934/nhm.2010.5.423 |
| [8] | Richard Carney, Monique Chyba, Taylor Klotz . Using hybrid automata to model mitigation of global disease spread via travel restriction. Networks and Heterogeneous Media, 2024, 19(1): 324-354. doi: 10.3934/nhm.2024015 |
| [9] | Yimamu Maimaiti, Zunyou Lv, Ahmadjan Muhammadhaji, Wang Zhang . Analyzing vegetation pattern formation through a time-ordered fractional vegetation-sand model: A spatiotemporal dynamic approach. Networks and Heterogeneous Media, 2024, 19(3): 1286-1308. doi: 10.3934/nhm.2024055 |
| [10] | Xia Li, Andrea L. Bertozzi, P. Jeffrey Brantingham, Yevgeniy Vorobeychik . Optimal policy for control of epidemics with constrained time intervals and region-based interactions. Networks and Heterogeneous Media, 2024, 19(2): 867-886. doi: 10.3934/nhm.2024039 |
In this paper we propose an epidemiological compartmental model where the efficacy time of vaccinations, i.e., the time a dosed individual needs to become immune, plays a key role. Furthermore, we also account for the concurrent effect of different vaccines, differing, for instance, in the time they need to provide immunization. The role of age can also be accounted for, letting vaccines' efficacy and immunization times depend on age, as well as on the choice of the vaccine type. These features are well known to be relevant in the present Covid-19 pandemic.
Compartmental models are a formidable tool in the description of a variety of real situations. The techniques above suggest a general framework able to introduce a specific dynamic evolution within compartments. In these models, each individual is considered to be of one compartment at any given time, its evolution consisting in passing from one compartment to another one, based on the structure and on the parameters of the model. In other words, the global dynamics consist in individuals entering the system (e.g., newborns), others leaving the system (e.g., casualties) and, during the evolution, passing from one compartment to another (e.g., getting ill, being vaccinated, recovering,
In the context of epidemiological models describing the spread of infectious diseases, the SIR model, named after its three compartments (Susceptible, Infected and Recovered), is the traditional prototype. This epidemic model dates back to 1927, see [16], less than a decade after the 1918 influenza pandemic. In what is probably its simplest form [22,§10.2], a prototype SIR model reads
|
$ S→I→R↓{˙S=−ρIS˙I=ρIS−(ϑ+μ)I˙R=ϑI $
|
(1) |
where
The popularity of (1) is due partly to its simplicity, which allows to describe the disease behavior by estimating a small number of parameters, and partly to its being amenable to a variety of extensions. The dynamics of the SIR epidemic model are widely considered, here we recall for instance [1,4,21,25], or [14,Chapter 6], [22,Chapter 10], and [23,§1.5.1].
The literature on SIR-type models, typically containing additional compartments, is indeed huge. For instance, SEIR and SEIRS-type models contain also the compartment E (Exposed) where infected individuals spend a latent/incubation period prior to become infective, see [12,13,18,19] and the references therein. Vaccination campaigns and effects are described in SVIR-type models which consider individuals that get vaccinated, see [9,17,20] or also the different approach in [5].
Recall also, for instance, the SIHR model proposed in [6], where infected individuals are either Infective (I) or Hospitalized (H), the former ones spreading the disease, while the latter ones being isolated, typically hospitalized or in quarantine, thus taking into account lockdown effects.
Since 2020, with the Covid-19 pandemic, the development and use of these models boomed. The need to explicitly introduce the immunization time of a vaccine and the concurrent use of different vaccines lead us to introduce a dynamics within compartments. This machinery allows to fix a priori the time an individual spends in a compartment, as in the case of the immunization time of a vaccine, see §2, allowing also this time to be age dependent, as in §3. This general framework is sufficiently flexible to account for the simultaneous adoption of different vaccines, as in model (4).
In other instances, it might be appropriate to smoothen the change of status related to the change of compartment, an example being the SEIR model as modified in §4. Indeed, pass from (15) to (16) allows to account for a somewhat continuous evolution from exposed to infective. In all these examples, key statistics, such as the basic reproduction number, are naturally extended to these new frameworks keeping their original meaning.
Worth mentioning is the recent SIDARTHE model from [11], consisting of
In §6, the SIHR model is modified to comprehend spatial (geographic) movements. The introduction of the age structure, where advisable, is in general possible, as shown in §7. These two steps, namely the introduction of space and age structures, are indeed doable in all the examples discussed.
Remark that the present framework indeed provides an extension to the current compartmental modeling habits. In fact, suitable choices of various functions or parameters allow to trivialize intra–compartmental dynamics, thus recovering known models.
Pandemic dynamics can clearly be described through many other tools. For instance, the recent work [2] proposes a multiscale approach and discusses the current kinetic literature on the subject. Cellular automata are used for instance in [10] in a probabilistic setting, still with a compartmental structure, see [10,Figure 1 (b)]. The literature also offers essays correlating pandemics to other human activities, primarily to economy, see for instance [8].
In the effective application of the models discussed below, a key issue is parameters' estimation. We defer for instance to [24] and to [27] for two entirely different approaches.
From the analytic point of view, a rigorous abstract approach to these classes of models is possible but at the cost of a quite intricate PDE based formalism, see a first attempt in [7]. Therefore, the sequel is devoted to show that intra-compartmental dynamics can both refine usual models, and also take into account new features, not captured by standard compartmental models.
The model presented in [20], here slightly modified, amounts to this extension of (1):
|
$ V↗↓↘S→I→R↓{˙S=−ρSIS−p(t,S)˙V=p(t,S)−ρVIV−ϑVV˙I=(ρSS+ρVV)I−(ϑI+μ)I˙R=ϑII+ϑVV. $
|
(2) |
Here,
Before introducing the immunization time in (2), we remark that setting
The effect of doses, as is well known, is not immediate. On the contrary, the time
|
$ V(0)→V(T∗)↗↓↘S→I→R↓{˙S=−ρSIS−p(t,S)∂tV+∂τV=−ρVIV˙I=(ρSS+∫T∗0ρVV)I−ϑI−μI˙R=ϑI+V(t,T∗)V(t,0)=p(t,S(t)). $
|
(3) |
Here, the number of individuals at time
In connection with the present Covid-19 pandemic, we remark that model (3) can be easily extended to the case of different, say
|
$ Vℓ(0)→Vℓ(Tℓ∗)ℓ=1,…,m↗↓↘S→I→R↓{˙S=−ρSIS−m∑ℓ=1pℓ(t,S)∂tVℓ+∂τVℓ=−ρVℓIVℓ˙I=(ρSS+m∑ℓ=1∫Tℓ∗0ρVℓVℓ)I−(ϑ+μ)I˙R=ϑI+m∑ℓ=1Vℓ(t,Tℓ∗)Vℓ(t,0)=pℓ(t,S(t)). $
|
(4) |
Note that, as is to be expected, according to (4) the total number of individuals is affected only by mortality, in the sense that
| $ \dfrac{\mathinner{\mathrm{d}{{\; }}}}{\mathinner{\mathrm{d}{{t}}}} \left( S (t) + \sum\limits_{\ell = 1}^m \int_0^{T_*^\ell} V_\ell (t, \tau) \, \mathinner{\mathrm{d}{\tau}} + I (t) + R (t) \right) = - \mu \, I (t) \, . $ |
A parameter often used to describe the tendency of the pandemic is the (time dependent) basic reproduction number
|
$ Ro(t)=ρSS(t)+m∑ℓ=1∫Tℓ∗0ρVℓ(τ)Vℓ(t,τ)dτϑ+μ, $
|
(5) |
so that the increasing in the infected individuals at time
|
$ ddtI(t)≷0⟺Ro(t)≷1. $
|
(6) |
The above equivalence holds also in the case of the parameters
At first sight, the numerator in the right hand side of (5) is misleading, for it apparently implies that higher values of
A direct comparison between (2) and (3), though suggestive, is inevitably highly arbitrary. Clearly,
Thus, below, to investigate the role of
1
|
$ ρS=5×10−4ϑ=1×10−3μ=1×10−4ρV(τ)=ρS√1−τT∗p(t,S)=0.5χ[10,+∞[(t)χR+(S) $
|
(7) |
and initial data
|
$ So=99.9,Vo(τ)≡0,Io=0.1,Ro=0. $
|
(8) |
We consider
Times necessary for the vaccination to provide immunity and corresponding casualties according to model (3)–(7)–(8). The initial total population is
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 0.28 | 0.32 | 0.37 | 0.43 | 0.49 | 0.56 | 0.63 | 0.70 |
The relevant differences in the diagram of the map
In Figure 1, the differences in the
The evolutions in the
The flexibility introduced by dynamics internal to the dosed (
|
$ p(t,S)=0.5χ[10,30]∪[120,+∞[(t)χR+(S). $
|
(9) |
Then, the number of casualties sharply grows with respect to the number of casualties in (3)–(7)–(8), as clearly shown when comparing Table 1 with Table 2.
Times necessary for the vaccination to provide immunity and corresponding casualties, according to model (3)–(7)–(8), in the case vaccinations are suspended as detailed in (9). The initial total population is
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 1.11 | 1.18 | 1.25 | 1.32 | 1.38 | 1.43 | 1.48 | 1.53 |
The diagrams in Figure 2 also confirm the negative effect in a suspension of the vaccination campaign.
As a further example, we consider the problem of choosing between two different vaccines. We integrate (4) with
|
$ T1∗=7ρV1(τ)=ρS√1−τT1∗p1(t,S)=ωχ[20,+∞[(t)χR+(S)T2∗=35ρV2(τ)=0.2ρS√1−τT2∗p2(t,S)=(0.5−ω)χ[20,+∞[(t)χR+(S), $
|
(10) |
with the parameter
The insertion of an intra–compartmental dynamics is not limited to ODE models. As it is well known, age differences often have a role in the spreading of diseases. Therefore, we introduce the following extension of (3):
|
$ {∂tS+∂aS=−∫R+ρ(t,a,α)I(t,α)dαS−p(t,a,S)∂tV+∂aV+∂τV=−ρVIV∂tI+∂aI=∫R+ρ(t,a,α)I(t,α)dαS+∫R+∫T∗0ρV(t,a,τ,α)V(t,α,τ)dαdτI−ϑI−μI∂tR+∂aR=ϑI+V(t,a,T∗), $
|
(11) |
Vaccination entering also as boundary datum in the evolution of the
|
$ V(t,a,0)=p(t,a,S(t,a)). $
|
(12) |
In (11)–(12), we use the same symbols as in (3), allowing the various parameters to depend also on age. For instance
System (11) needs to be supplied with initial and boundary data, such as
|
$ {S(0,a)=So(a)V(0,a,τ)=Vo(a,τ)I(0,a)=Io(a)R(0,a)=Ro(a){S(t,0)=Sb(t)V(t,0,τ)=0I(t,0)=0R(t,0)=0 $
|
(13) |
where, as it is realistic, we set to
Note that setting all data and parameters in (11)–(12)–(13) constant in
Extending the analogous property valid for system (3), note that the total number of individuals varies not only due to mortality but also due to the natality
|
$ ddt∫R+(S(t,a)+∫T∗0V(t,a,τ)dτ+I(t,a)+R(t,a))da=−∫R+μ(t,a)I(t,a)da+Sb(t). $
|
The present model realistically allows infection to be propagated across different ages. Therefore, we can only have an index
| $ \mathcal{R}_o (t) = \dfrac{ \int_{ {\mathbb{R}}_+} \int_{ {\mathbb{R}}_+} \! \left( \rho (t, \alpha, a) \, S (t, \alpha) + \int_0^{T_*} \rho_V (t, a, \tau, \alpha) \, V (t, \alpha, \tau)\mathinner{\mathrm{d}{\tau}} \right) \mathinner{\mathrm{d}{\alpha}} I (t, a) \mathinner{\mathrm{d}{{a}}} }{ \int_{ {\mathbb{R}}_+} \left( \vartheta (t, a) + \mu (t, a)\right)I (t, a) \, \mathinner{\mathrm{d}{{a}}}} $ |
we have the following extension of (6):
|
$ ddt∫R+I(t,a)da≷0⟺Ro(t)≷1. $
|
(14) |
Remark that also model (11) can easily be extended to the case of different vaccines having different full efficacy times through the introduction of different vaccinated populations
The use of model (11)–(12)–(13) allows to tackle the key issue of optimizing the use of the available vaccines on the basis of their different efficacy on different age classes.
The description provided by (1) is often too approximate. For instance, it might be necessary to distinguish between exposed (
|
$ S→E→I→R↓↓{˙S=−ρIS˙E=ρIS−(ϑE+μE+κ)E˙I=κE−(ϑI+μI)I˙R=ϑEE+ϑII, $
|
(15) |
where we introduced the term
Assume now that individuals infected at time
|
$ S→I(0)→I(τ)→→R↓{˙S=−∫R+ρ(τ)I(t,τ)dτS∂tI+∂τI=−ϑ(τ)I−μ(τ)I˙R=∫ϑ(τ)I(t,τ)dτI(t,0)=∫R+ρ(τ)I(t,τ)dτS(t). $
|
(16) |
Observe that the last line above is in fact a boundary condition, prescribing how many individuals get infected at time
Remark that the dependence of
Observe that, as is to be expected, the variation in the total number of individuals resulting from (16) is due exclusively to mortality. Indeed
|
$ ddt(S(t)+∫R+I(t,τ)dτ+R(t))=−∫R+μ(τ)I(t,τ)dτ. $
|
(17) |
Within the framework of (16), an explicit expression for the basic reproduction number
| $ \mathcal{R}_o (t) = \dfrac{\int_{ {\mathbb{R}}_+} \rho (\tau) \, I (t, \tau) \mathinner{\mathrm{d}{\tau}} \, S (t)} {\int_{ {\mathbb{R}}_+}\left( \vartheta (\tau) + \mu (\tau)\right) I (t, \tau) \mathinner{\mathrm{d}{\tau}}} $ |
and it is immediate to see that its exceeding unity is equivalent to the increase of the total number of infected individuals:
|
$ ddt(∫R+I(t,τ)dτ)≷0⟺Ro(t)≷1. $
|
(18) |
It goes without saying that suitable choices of initial data and parameters in (16) allow to recover within (16) the solutions of (1). Here we only provide a quick example of a comparison among solutions to (1), (15) and (16), with data and parameters in (1) being an average of those in (15), while the choices in (16) are an interpolation of those in (15), as detailed in (19).
|
$ (1)(15)(16)ρ=0.1ρ=0.1ρ(τ)=0.1(1−e−0.2τ)ϑ=3(ϑE,ϑI)=(7,1)ϑ(τ)={7τ<21τ≥2μ=0.5(μE,μI)=(0.1,0.9)μ(τ)=0.9−0.8e−2τκ=5So=10So=10So=10Io=6.(Eo,Io)=(1,5)Io(τ)={0.5τ∈[0,2[2.5τ∈[2,4]Ro=0Ro=0Ro=0. $
|
(19) |
Figure 4 shows sample integrations of (1), (15) and (16). In the situation considered, according to mortality, the mixed ODE–PDE system (16) can be seen in some senses in the middle between the other two classical purely ODE based compartmental models (1) and (15). Intra-compartmental dynamics can thus recover the dynamics described through standard compartmental models.

Above, the integrations of (1) and (15), below on the left that of (16) (19). The rightmost diagram on the second line displays the total number of living individuals in the three cases, showing that, with respect to mortality, the ODE–PDE model (16) can be seen in some senses in the middle between the ODE models (1) and (15)
.On the other hand, other scenarios can hardly be recovered through the use of only standard compartments. Indeed, for instance, it can be reasonable to assume that infected individuals are most infective in given time intervals after infection where, in general, these intervals depend on the specific disease under consideration. Such a situation, within Model (16), is easily described and we consider, for instance, the following choices:
|
$ ρ(τ)=ˉρte−α(t−ˉT)2 with ρ=0.1 and (i)α=1.0,ˉT=10.0,(ii)α=1.0,ˉT=4.0,(iii)α=0.25,ˉT=4.0. $
|
(20) |
The sample choices (20) differ in the time
The results are summarized in Figure 5. The differences in the evolutions prescribed by (16) corresponding to the choices (20) are very intuitive, Case

Above, from left to right, the integrations of Case
We now consider the SIDARTHE model introduced in [11]. It consists of
Populations in model (21) from [11]
.| Susceptible | healthy | can be infected | ||
| Infected | asymptomatic | infective | undetected | |
| Diagnosed | asymptomatic | infective | detected | |
| Ailing | symptomatic | infective | undetected | |
| Recognized | symptomatic | infective | detected | |
| Threatened | acutely symptomatic | infected | detected | |
| Healed | healthy | immune | ||
| Extinct |
Its block diagram and the corresponding system of ordinary differential equations read:
|
$ S→I→D↙↓↓↘H←A→R↘↑↘↓↘↓↑E←T→↓↑↓←←←←←←←{˙S=−αIS−γAS−βDS−δRS˙I=αIS+γAS+βDS+δRS−(ε+ζ+λ)I˙D=εI−(η+ρ)D˙A=ζI−(ϑ+μ+κ)A˙R=ηD+ϑA−(ν+ξ)R˙T=μA+νR−(σ+τ)T˙H=λI+ρD+κA+ξR+σT˙E=τT. $
|
(21) |
We refer to [11] for the specific meaning of each constant and for the motivations of this model.
Here, we note that both the evolutions
| (22) |
Introduce now the populations
|
$ S→I(0)→I(s)→→R(0)→R(s)→→E↘↙ ⟶H⟵ $
|
(23) |
|
$ {˙S=−∫α(s)I(t,s)dsS−∫δ(s)R(t,s)dsS∂tI+∂sI=∫α(s)I(t,s)dsS+∫δ(s)R(t,s)dsS−∫ε(s)I(t,s)ds−∫ϑ(s)I(t,s)ds∂tR+∂sR=∫ϑ(s)I(t,s)s−∫η(s)R(t,s)ds˙H=∫ε(s)Ids˙E=∫η(s)R(t,s)ds, $
|
(24) |
All integrals being computed over
Note also that in model (24) the explicit expression of the basic reproduction number is immediately at hand. Indeed, defining
| $ \mathcal{R}_o (t) = \dfrac{\int \left(\alpha(s) \, \mathcal{I} (t, s) + \delta(s) \, \mathcal{R} (t, s) \right) \mathinner{\mathrm{d}{{s}}} \, S (t)} {\int \left( {\varepsilon} (s) + \vartheta (s)\right) \mathcal{I} (t, s) \mathinner{\mathrm{d}{{s}}}} $ |
the key property (18) still holds.
As a further example of intra-compartmental dynamics we consider movements. Indeed, as a prototype for the description of the role of quarantine in the spreading of a pandemic, consider the model [6,Formula (9)]
|
$ S→I↘↓RH↗{∂tS+μSS=−ρIS∂tI+μII=ρIS−κI−ϑI∂tH+μHH=κI−ηH∂tR+μRR=ϑI+ηH, $
|
(25) |
where we used the standard notation for the
In this connection, it can be relevant to take into consideration events that provoked relevant gatherings of crowds, a well known example being the Atalanta vs. Valencia football match played in Milan (Italy) on February 19th, 2020, see [26]. To this aim, following [6], we introduce a geographical movement as follows
|
$ S(x)↺→I(x)↺↘↓R(x)↺H↗{∂tS+div(vSS)+μSS=−ρIS∂tI+div(vII)+μII=ρIS−κI−ϑI∂tH+μHH=κI−ηH∂tR+div(vRR)+μRR=ϑI+ηH. $
|
(26) |
Above, all populations are also space dependent, so that, for instance,
Introducing age structure in the SIS model [15], see also [3,Formula 10.1], we get
|
$ S⟷I{∂tS+∂aS=−ρIS+γI∂tI+∂aI=ρIS−γI. $
|
(27) |
In this model, when infected individuals recover, they get back to being susceptible at a rate governed by the, possibly age dependent, parameter
|
$ S⟶⟶I↖↙R(0)→R(T∗){∂tS+∂aS=−ρIS+R(t,a,T∗(a))∂tI+∂aI=ρIS−γI∂tR+∂aR+∂τR=0R(t,a,0)=γI(t,a). $
|
(28) |
Note however that the very simple nature of the third equation allows to rewrite (28) as a system of
|
$ {∂tS+∂aS=−ρIS+γI(t−T∗(a),a−T∗(a))∂tI+∂aI=ρIS−γI(t,a). $
|
(29) |
The form (28) is more prone to extensions than (29), since it allows to specify various evolutions of the
From the analytic point of view, we remark that (28) provides a first minimal example of a "junction" in
| [1] |
Lu KP, Hanes SD, Hunter T (1996) A human peptidyl-prolyl isomerase essential for regulation of mitosis. Nature 380: 544-547. doi: 10.1038/380544a0

|
| [2] |
Lu KP, Zhou XZ (2007) The prolyl isomerase PIN1: a pivotal new twist in phosphorylation signalling and disease. Nat Rev Mol Cell Biol 8: 904-916. doi: 10.1038/nrm2261

|
| [3] |
Liou Y-C, Sun A, Ryo A, et al. (2003) Role of the prolyl isomerase Pin1 in protecting against age-dependent neurodegeneration. Nature 424: 556-561. doi: 10.1038/nature01832

|
| [4] | Rudrabhatla P (2014) Regulation of neuronal cytoskeletal protein phosphorylation in neurodegenerative diseases. J Alzheimers Dis 41: 671-684. |
| [5] |
Hardy J, Selkoe DJ (2002) The amyloid hypothesis of Alzheimer's disease: progress and problems on the road to therapeutics. Science 297: 353-356. doi: 10.1126/science.1072994

|
| [6] |
Anderson JP, Walker DE, Goldstein JM, et al. (2006) Phosphorylation of Ser-129 is the dominant pathological modification of alpha-synuclein in familial and sporadic Lewy body disease. J Biol Chem 281: 29739-29752. doi: 10.1074/jbc.M600933200

|
| [7] |
Kardos J, Kiss B, Micsonai A, et al. (2015) Phosphorylation as conformational switch from the native to amyloid state: trp-cage as a protein aggregation model. J Phys Chem B 119: 2946-2955. doi: 10.1021/jp5124234

|
| [8] |
Grison A, Mantovani F, Comel A, et al. (2011) Ser46 phosphorylation and prolyl-isomerase Pin1-mediated isomerization of p53 are key events in p53-dependent apoptosis induced by mutant huntingtin. P Natl Acad Sci U S A 108: 17979-17984. doi: 10.1073/pnas.1106198108

|
| [9] | Rudrabhatla P, Pant HC (2010) Phosphorylation-specific peptidyl-prolyl isomerization of neuronal cytoskeletal proteins by Pin1: implications for therapeutics in neurodegeneration. J Alzheimers Dis 19: 389-403. |
| [10] | Driver JA, Zhou XZ, Lu KP (2014) Regulation of protein conformation by Pin1 offers novel disease mechanisms and therapeutic approaches in Alzheimer's disease. Discov Med 17: 93-99. |
| [11] |
Nakamura K, Greenwood A, Binder L, et al. (2012) Proline isomer-specific antibodies reveal the early pathogenic tau conformation in Alzheimer's disease. Cell 149: 232-244. doi: 10.1016/j.cell.2012.02.016

|
| [12] |
Giannopoulos PN, Robertson C, Jodoin J, et al. (2009) Phosphorylation of prion protein at serine 43 induces prion protein conformational change. J Neurosci 29: 8743-8751. doi: 10.1523/JNEUROSCI.2294-09.2009

|
| [13] |
Liou Y-C, Zhou XZ, Lu KP (2011) Prolyl isomerase Pin1 as a molecular switch to determine the fate of phosphoproteins. Trends Biochem Sci 36: 501-514. doi: 10.1016/j.tibs.2011.07.001

|
| [14] |
Bayer E, Goettsch S, Mueller JW, et al. (2003) Structural analysis of the mitotic regulator hPin1 in solution: insights into domain architecture and substrate binding. J Biol Chem 278: 26183-26193. doi: 10.1074/jbc.M300721200

|
| [15] |
Matena A, Sinnen C, van den Boom J, et al. (2013) Transient domain interactions enhance the affinity of the mitotic regulator Pin1 toward phosphorylated peptide ligands. Structure 21: 1769-1777. doi: 10.1016/j.str.2013.07.016

|
| [16] |
Vöhringer-Martinez E, Verstraelen T, Ayers PW (2014) The influence of Ser-154, Cys-113, and the phosphorylated threonine residue on the catalytic reaction mechanism of Pin1. J Phys Chem B 118: 9871-9880. doi: 10.1021/jp505638w

|
| [17] |
Pastorino L, Sun A, Lu P-J, et al. (2006) The prolyl isomerase Pin1 regulates amyloid precursor protein processing and amyloid-beta production. Nature 440: 528-534. doi: 10.1038/nature04543

|
| [18] |
Zita MM, Marchionni I, Bottos E, et al. (2007) Post-phosphorylation prolyl isomerisation of gephyrin represents a mechanism to modulate glycine receptors function. EMBO J 26: 1761-1771. doi: 10.1038/sj.emboj.7601625

|
| [19] |
Taylor JP, Hardy J, Fischbeck KH (2002) Toxic proteins in neurodegenerative disease. Science 296: 1991-1995. doi: 10.1126/science.1067122

|
| [20] |
Kim S, Nollen EA, Kitagawa K, et al. (2002) Polyglutamine protein aggregates are dynamic. Nat Cell Biol 4: 826-831. doi: 10.1038/ncb863

|
| [21] | Soto C, Estrada LD (2008) Protein misfolding and neurodegeneration. Arch Neurol 65: 184-189. |
| [22] | Tenreiro S, Eckermann K, Outeiro TF (2014) Protein phosphorylation in neurodegeneration: friend or foe? Front Mol Neurosci 7: 42. |
| [23] | Brundin P, Melki R, Kopito R (2010) Prion-like transmission of protein aggregates in neurodegenerative diseases. Nat Rev Mol Cell Biol 11: 301-307. |
| [24] |
Brettschneider J, Del Tredici K, Lee VM, et al. (2015) Spreading of pathology in neurodegenerative diseases: a focus on human studies. Nat Rev Neurosci 16: 109-120. doi: 10.1038/nrn3887

|
| [25] |
LaFerla FM (2010) Pathways linking Abeta and tau pathologies. Biochem Soc Trans 38: 993-995. doi: 10.1042/BST0380993

|
| [26] |
Iqbal K, Grundke-Iqbal I (2010) Alzheimer's disease, a multifactorial disorder seeking multitherapies. Alzheimers Dement 6: 420-424. doi: 10.1016/j.jalz.2010.04.006

|
| [27] |
Rudrabhatla P, Jaffe H, Pant HC (2011) Direct evidence of phosphorylated neuronal intermediate filament proteins in neurofibrillary tangles (NFTs): phosphoproteomics of Alzheimer's NFTs. FASEB J 25: 3896-3905. doi: 10.1096/fj.11-181297

|
| [28] |
Huang Y, Mucke L (2012) Alzheimer mechanisms and therapeutic strategies. Cell 148: 1204-1222. doi: 10.1016/j.cell.2012.02.040

|
| [29] |
Cancino GI, Miller FD, Kaplan DR (2013) p73 haploinsufficiency causes tau hyperphosphorylation and tau kinase dysregulation in mouse models of aging and Alzheimer's disease. Neurobiol Aging 34: 387-399. doi: 10.1016/j.neurobiolaging.2012.04.010

|
| [30] |
Sultana R, Boyd-Kimball D, Poon HF, et al. (2006) Oxidative modification and down-regulation of Pin1 in Alzheimer's disease hippocampus: A redox proteomics analysis. Neurobiol Aging 27: 918-925. doi: 10.1016/j.neurobiolaging.2005.05.005

|
| [31] |
Chen C-H, Li W, Sultana R, et al. (2015) Pin1 cysteine-113 oxidation inhibits its catalytic activity and cellular function in Alzheimer's disease. Neurobiol Dis 76: 13-23. doi: 10.1016/j.nbd.2014.12.027

|
| [32] |
Innes BT, Sowole MA, Gyenis L, et al. (2015) Peroxide-mediated oxidation and inhibition of the peptidyl-prolyl isomerase Pin1. Biochim Biophys Acta 1852: 905-912. doi: 10.1016/j.bbadis.2014.12.025

|
| [33] |
Binder LI, Guillozet-Bongaarts AL, Garcia-Sierra F, et al. (2005) Tau, tangles, and Alzheimer's disease. Biochim Biophys Acta 1739: 216-223. doi: 10.1016/j.bbadis.2004.08.014

|
| [34] |
Gendron TF, Petrucelli L (2009) The role of tau in neurodegeneration. Mol Neurodegener 4: 13. doi: 10.1186/1750-1326-4-13

|
| [35] |
Kimura T, Tsutsumi K, Taoka M, et al. (2013) Isomerase Pin1 stimulates dephosphorylation of tau protein at cyclin-dependent kinase (Cdk5)-dependent Alzheimer phosphorylation sites. J Biol Chem 288: 7968-7977. doi: 10.1074/jbc.M112.433326

|
| [36] |
Yotsumoto K, Saito T, Asada A, et al. (2009) Effect of Pin1 or microtubule binding on dephosphorylation of FTDP-17 mutant Tau. J Biol Chem 284: 16840-16847. doi: 10.1074/jbc.M109.003277

|
| [37] |
Smet C, Sambo A-V, Wieruszeski J-M, et al. (2004) The peptidyl prolyl cis/trans-isomerase Pin1 recognizes the phospho-Thr212-Pro213 site on Tau. Biochemistry 43: 2032-2040. doi: 10.1021/bi035479x

|
| [38] |
Wang J-Z, Zhang Y (2015) Configuration-specific immunotherapy targeting cis pThr231-Pro232 tau for Alzheimer disease. J Neurol Sci 348: 253-255. doi: 10.1016/j.jns.2014.11.011

|
| [39] |
Yuan A, Sasaki T, Rao MV, et al. (2009) Neurofilaments form a highly stable stationary cytoskeleton after reaching a critical level in axons. J Neurosci 29: 11316-11329. doi: 10.1523/JNEUROSCI.1942-09.2009

|
| [40] |
Nixon RA, Shea TB (1992) Dynamics of neuronal intermediate filaments: a developmental perspective. Cell Motil Cytoskeleton 22: 81-91. doi: 10.1002/cm.970220202

|
| [41] | Giasson BI, Mushynski WE (1997) Study of proline-directed protein kinases involved in phosphorylation of the heavy neurofilament subunit. J Neurosci 17: 9466-9472. |
| [42] | Haass C, Kaether C, Thinakaran G, et al. (2012) Trafficking and proteolytic processing of APP. Cold Spring Harb Perspect Med 2: a006270. |
| [43] | Pastorino L, Ma SL, Balastik M, et al. (2012) Alzheimer's disease-related loss of Pin1 function influences the intracellular localization and the processing of AβPP. J Alzheimers Dis 30: 277-297. |
| [44] |
Lee M-S, Kao S-C, Lemere CA, et al. (2003) APP processing is regulated by cytoplasmic phosphorylation. J Cell Biol 163: 83-95. doi: 10.1083/jcb.200301115

|
| [45] |
Ma SL, Pastorino L, Zhou XZ, et al. (2012) Prolyl isomerase Pin1 promotes amyloid precursor protein (APP) turnover by inhibiting glycogen synthase kinase-3β (GSK3β) activity: novel mechanism for Pin1 to protect against Alzheimer disease. J Biol Chem 287: 6969-6973. doi: 10.1074/jbc.C111.298596

|
| [46] |
Cisbani G, Cicchetti F (2012) An in vitro perspective on the molecular mechanisms underlying mutant huntingtin protein toxicity. Cell Death Dis 3: e382. doi: 10.1038/cddis.2012.121

|
| [47] |
Ross CA, Aylward EH, Wild EJ, et al. (2014) Huntington disease: natural history, biomarkers and prospects for therapeutics. Nat Rev Neurol 10: 204-216. doi: 10.1038/nrneurol.2014.24

|
| [48] |
Bertoni A, Giuliano P, Galgani M, et al. (2011) Early and late events induced by polyQ-expanded proteins: identification of a common pathogenic property of polYQ-expanded proteins. J Biol Chem 286: 4727-4741. doi: 10.1074/jbc.M110.156521

|
| [49] |
Bae B-I, Xu H, Igarashi S, et al. (2005) p53 mediates cellular dysfunction and behavioral abnormalities in Huntington's disease. Neuron 47: 29-41. doi: 10.1016/j.neuron.2005.06.005

|
| [50] | Sorrentino G, Comel A, Mantovani F, et al. (2014) Regulation of mitochondrial apoptosis by Pin1 in cancer and neurodegeneration. Mitochondrion 19 Pt A: 88-96. |
| [51] | Mantovani F, Zannini A, Rustighi A, et al. (2015) Interaction of p53 with prolyl isomerases: Healthy and unhealthy relationships. Biochim Biophys Acta [in press]. |
| [52] |
Sorrentino G, Mioni M, Giorgi C, et al. (2013) The prolyl-isomerase Pin1 activates the mitochondrial death program of p53. Cell Death Differ 20: 198-208. doi: 10.1038/cdd.2012.112

|
| [53] | Beitz JM (2014) Parkinson's disease: a review. Front Biosci 6: 65-74. |
| [54] |
Dauer W, Przedborski S (2003) Parkinson's disease: mechanisms and models. Neuron 39: 889-909. doi: 10.1016/S0896-6273(03)00568-3

|
| [55] | Fujiwara H, Hasegawa M, Dohmae N, et al. (2002) alpha-Synuclein is phosphorylated in synucleinopathy lesions. Nat Cell Biol 4: 160-164. |
| [56] | Sato H, Kato T, Arawaka S (2013) The role of Ser129 phosphorylation of α-synuclein in neurodegeneration of Parkinson's disease: a review of in vivo models. Rev Neurosci 24: 115-123. |
| [57] |
Ryo A, Togo T, Nakai T, et al. (2006) Prolyl-isomerase Pin1 accumulates in lewy bodies of parkinson disease and facilitates formation of alpha-synuclein inclusions. J Biol Chem 281: 4117-4125. doi: 10.1074/jbc.M507026200

|
| [58] |
Ghosh A, Saminathan H, Kanthasamy A, et al. (2013) The peptidyl-prolyl isomerase Pin1 up-regulation and proapoptotic function in dopaminergic neurons: relevance to the pathogenesis of Parkinson disease. J Biol Chem 288: 21955-21971. doi: 10.1074/jbc.M112.444224

|
| [59] |
Lee S-J, Kim D-C, Choi B-H, et al. (2006) Regulation of p53 by activated protein kinase C-delta during nitric oxide-induced dopaminergic cell death. J Biol Chem 281: 2215-2224. doi: 10.1074/jbc.M509509200

|
| [60] |
Martin LJ, Pan Y, Price AC, et al. (2006) Parkinson's disease alpha-synuclein transgenic mice develop neuronal mitochondrial degeneration and cell death. J Neurosci 26: 41-50. doi: 10.1523/JNEUROSCI.4308-05.2006

|
| [61] |
Mogi M, Kondo T, Mizuno Y, et al. (2007) p53 protein, interferon-gamma, and NF-kappaB levels are elevated in the parkinsonian brain. Neurosci Lett 414: 94-97. doi: 10.1016/j.neulet.2006.12.003

|
| [62] |
Prusiner SB (1988) Molecular structure, biology, and genetics of prions. Adv Virus Res 35: 83-136. doi: 10.1016/S0065-3527(08)60709-5

|
| [63] |
Prusiner SB (1991) Molecular biology of prion diseases. Science 252: 1515-1522. doi: 10.1126/science.1675487

|
| [64] |
Prusiner SB (1994) Molecular biology and genetics of prion diseases. Philos Trans R Soc Lond B Biol Sci 343: 447-463. doi: 10.1098/rstb.1994.0043

|
| [65] |
Prusiner SB (2001) Shattuck lecture--neurodegenerative diseases and prions. New Engl J Med 344: 1516-1526. doi: 10.1056/NEJM200105173442006

|
| [66] |
Zhou Z, Xiao G (2013) Conformational conversion of prion protein in prion diseases. Acta Biochim Biophys Sin 45: 465-476. doi: 10.1093/abbs/gmt027

|
| [67] |
Negro A, Meggio F, Bertoli A, et al. (2000) Susceptibility of the prion protein to enzymic phosphorylation. Biochem Biophys Res Commun 271: 337-341. doi: 10.1006/bbrc.2000.2628

|
| [68] |
Wang G-R, Shi S, Gao C, et al. (2010) Changes of tau profiles in brains of the hamsters infected with scrapie strains 263 K or 139 A possibly associated with the alteration of phosphate kinases. BMC Infect Dis 10: 86. doi: 10.1186/1471-2334-10-86

|
| [69] |
Schmitz M, Lüllmann K, Zafar S, et al. (2014) Association of prion protein genotype and scrapie prion protein type with cellular prion protein charge isoform profiles in cerebrospinal fluid of humans with sporadic or familial prion diseases. Neurobiol Aging 35: 1177-1188. doi: 10.1016/j.neurobiolaging.2013.11.010

|
| [70] |
Rouget R, Sharma G, LeBlanc AC (2015) Cyclin-dependent Kinase 5 Phosphorylation of Familial Prion Protein Mutants Exacerbates Conversion into Amyloid Structure. J Biol Chem 290: 5759-5771. doi: 10.1074/jbc.M114.630699

|
| [71] |
Trevitt CR, Hosszu LLP, Batchelor M, et al. (2014) N-terminal domain of prion protein directs its oligomeric association. J Biol Chem 289: 25497-25508. doi: 10.1074/jbc.M114.566588

|
| [72] |
Supattapone S, Muramoto T, Legname G, et al. (2001) Identification of two prion protein regions that modify scrapie incubation time. J Virol 75: 1408-1413. doi: 10.1128/JVI.75.3.1408-1413.2001

|
| [73] |
Frankenfield KN, Powers ET, Kelly JW (2005) Influence of the N-terminal domain on the aggregation properties of the prion protein. Protein Sci 14: 2154-2166. doi: 10.1110/ps.051434005

|
| [74] |
Uchida T, Takamiya M, Takahashi M, et al. (2003) Pin1 and Par14 peptidyl prolyl isomerase inhibitors block cell proliferation. Chem Biol 10: 15-24. doi: 10.1016/S1074-5521(02)00310-1

|
| 1. | Rinaldo M. Colombo, Mauro Garavello, Infectious Disease Spreading Fought by Multiple Vaccines Having a Prescribed Time Effect, 2023, 71, 0001-5342, 10.1007/s10441-022-09452-4 | |
| 2. | Lihong Sun, Qiang He, Yueyang Teng, Qi Zhao, Xin Yan, Xingwei Wang, A complex network-based vaccination strategy for infectious diseases, 2023, 136, 15684946, 110081, 10.1016/j.asoc.2023.110081 | |
| 3. | R.M. Colombo, M. Garavello, M. Tandy, On the coupling of well posed differential models, 2023, 232, 0362546X, 113290, 10.1016/j.na.2023.113290 | |
| 4. | Rinaldo M. Colombo, Mauro Garavello, Francesca Marcellini, Elena Rossi, 2024, Chapter 28, 978-3-031-55263-2, 325, 10.1007/978-3-031-55264-9_28 |
Times necessary for the vaccination to provide immunity and corresponding casualties according to model (3)–(7)–(8). The initial total population is
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 0.28 | 0.32 | 0.37 | 0.43 | 0.49 | 0.56 | 0.63 | 0.70 |
Times necessary for the vaccination to provide immunity and corresponding casualties, according to model (3)–(7)–(8), in the case vaccinations are suspended as detailed in (9). The initial total population is
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 1.11 | 1.18 | 1.25 | 1.32 | 1.38 | 1.43 | 1.48 | 1.53 |
Populations in model (21) from [11]
.| Susceptible | healthy | can be infected | ||
| Infected | asymptomatic | infective | undetected | |
| Diagnosed | asymptomatic | infective | detected | |
| Ailing | symptomatic | infective | undetected | |
| Recognized | symptomatic | infective | detected | |
| Threatened | acutely symptomatic | infected | detected | |
| Healed | healthy | immune | ||
| Extinct |
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 0.28 | 0.32 | 0.37 | 0.43 | 0.49 | 0.56 | 0.63 | 0.70 |
| 1 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | |
| Deaths: | 1.11 | 1.18 | 1.25 | 1.32 | 1.38 | 1.43 | 1.48 | 1.53 |
| Susceptible | healthy | can be infected | ||
| Infected | asymptomatic | infective | undetected | |
| Diagnosed | asymptomatic | infective | detected | |
| Ailing | symptomatic | infective | undetected | |
| Recognized | symptomatic | infective | detected | |
| Threatened | acutely symptomatic | infected | detected | |
| Healed | healthy | immune | ||
| Extinct |