1. Introduction
The environment in the context of medicine and public health usually refers to air and water pollutants, and contaminants in food, such as heavy metals and pesticide residues. The environment encompasses much more than this, however. We include nutrients, noise, occupation, psychosocial environment, social economic status and education as well as drugs, food, and additives, known collectively as the exposome [1,2]. Determining how the environment relates to common complex diseases is not always so straightforward as we have come to accept from classical toxicology studies of single toxicant interactions with our genes. Understanding the exposure pathway is one of the large gaps in trying to understand disease etiology. We are exposed to approximately 100, 000 different chemicals in our daily lives [3]. The social environment is also an important part of the disease pathway resulting from chemical exposure. For example, stress can play an important exacerbating role in environmentally determined diseases. The biology associated with social aspects is often not taken into account when looking for environment gene interactions. The exposome considers social environment as one aspect of the pathway to disease. Wild defines three aspects of the exposome, General external environment, internal environment, and the specific external environment [2]. The general external environment includes social capital, education, social economic status, and where you live. The internal environment is comprised of metabolism, endogenous hormones, microbial flora, physical activity, and oxidative stress. The specific external environment includes chemical pollutants; infectious agents and life style exposures, such as alcohol and tobacco use [2]. Therefore, the paradigm of exposure → physiological change → disease, while still true is more complex than previously thought. For example, Exposure to persistent organic pollutants has been associated with specific cancers, and other common complex diseases, including asthma and diabetes [4,5,6,7,8]. However, the process is not a linear one because the exposure domain is complex, the changes in gene expression are multifactorial, and there is multi channel communications among the parts. In this review, we look at some of the advances in biomedical sciences that we think could get a conversation started about how we can apply these approaches to public health to understand mechanisms of common diseases originate.
2. Common complex diseases
Almost all chronic conditions involve a genetic component. Some of those diseases are mono genic, including sickle cell anemia and cystic fibrosis [9,10]. The global annual death count is about 58 million [11]. Approximately 10 million of these deaths are from infectious diseases; 35 million deaths result from non-communicable diseases and injuries. Of these, approximately 30 million are related to the environment, broadly defined. The so-called big four common complex diseases that have modifiable or environmental risk factors are: cardiovascular diseases, diabetes, chronic respiratory diseases and various cancers [11]. We define the diseases as those that affect a large number of the global population, are non-communicable, are multigenic, and involve environmental factors and lifestyle. Considerable effort has been expended to develop and produce drugs to mitigate the effects of these diseases, but because of their complex nature, little progress has been made to prevent them. This is because of incomplete data and the complex nature of these diseases.
Some people have referred to these diseases as "Wicked Problems"[12], because it is difficult, or impossible to find solutions using current approaches in which problems are defined, analyzed, and solved in sequential steps [12]. To study complex common disease, we need to use a transdisciplinary approach, which is defined as research conducted by investigators from different disciplines working jointly to create new conceptual, theoretical, methodological, and translational innovations that integrate and move beyond discipline-specific approaches to address a common problem [13]. This approach is different from multidisciplinary or interdisciplinary research. In the multidisciplinary approach, researchers from different disciplines work independently or sequentially, from their own disciplinary-specific perspective, to address a common problem. In interdisciplinary research, investigators work jointly, but from each of their respective disciplinary perspectives, to address a common problem [14,15,16].
The term "translational research" has become the unquestioned under pinning of current approaches to therapeutics. However, this concept involves a linear approach, which is not well suited to understanding complex diseases. Pitfalls associated with this approach were addressed by Samuel Broder, a former head of the National Cancer Institute, where he warned, "if you had demanded that the NIH solve the problem of polio not through independent, investigator-driven discovery research, but by means of a centrally directed program, the odds are very strong that you would get the very best iron lungs in the world but you wouldn't get the vaccine that eradicated polio".
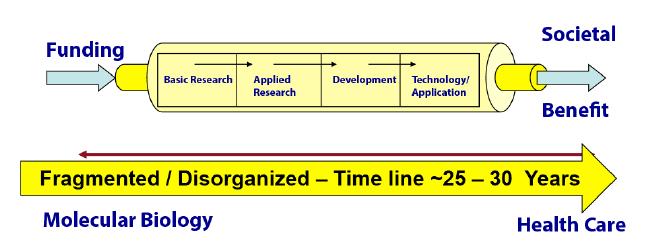
One reason for the inefficiency of the linear translational approach is that communication between basic and applied scientists, engineers, and practitioners doesn't happen on a regular basis (Figure 1) [17]. This is because they commonly attend different seminars and meetings, and read different journals [18]. The result is a fragmented system that may take many years to achieve results that are costly and are often mixed. Some important science may be lost in "translation.?However, when scientists work in transdisciplinary teams, a free transfer of information can be obtained.
Linear research has been the structure of scientific research since the end of World War II. A new model was proposed by Donald Stokes in 1997 [17]. He divided science into four quadrants, relating relevance to knowledge generation vs. consideration for immediate use (Figure 2) [17]. Pure basic science that leads to knowledge for knowledge sake is the Planck Quadrant; other examples could be Niels Bohr or Marie Curie. The quadrant for immediate application without an increase in basic knowledge is assigned to Thomas Edison, where it is said that if one of his employees wanted to study the mechanism by which one of the inventions worked, he would be fired [19]. A third quadrant doesn't add to basic knowledge, and doesn't generally produce useful applications and is left blank. The fourth quadrant was designated as Pasteur's quadrant, which used basic science to obtain knowledge for immediate use. Pasteur's research philosophy was to use basic science to tackle applied problems. Thus, the Pasteur Quadrant is also called use-inspired science. Stokes suggests tha
t this is a more efficient model of using science to solve complex problems than the linear approach currently suggested by the translational science model. It also suggests a model that incorporates transdisciplinary approaches to tackle modern problems of disease prevention.
There are many examples of how work in the Pasteur Quadrant and transdisciplinary approaches leads to new insights in basic science, and has an impact on important biological problems. Protein energy malnutrition (PEM) is an important health problem globally [20]. Finding a practical solution to this problem required a transdisciplinary team of scientists, including, molecular biochemists, nutritionists, dieticians, food technologists, water chemists and sanitation engineers, social scientists, and economists to modernize thinking about diets and the roles of the many factors play in undernutrition in humans [21]. PEM results in a cascade of events that cannot be solved merely by consuming of available foods. As a result, new types of food, called functional foods, were developed to mitigate severe PEM [22]. An extension of this approach of work in the Pasteur Quadrant is research being carried out in the area of survival of premature children in middle-income countries, which brings to bear expertise in social science, economics, medicine and basic science to increase survivability and quality of life for those infants that survive [23].
Limb prosthetics is another good example of research in the Pasteur Quadrant. The study of the gait of walkers on artificial limbs advanced the understanding of mechanisms of human walking and at the same time led to improved designs for artificial limbs [24]. Use-inspired study of the technology of leg prostheses led to new technologies for limbs and to new understanding of walking processes [25].
Research on the relation between Helicobacter pylori and gastrointestinal disease is a perfect example of work in the Pasteur Quadrant of science [26,27]. The research resulted in the award of the Nobel Prize in physiology or medicine to Barry Marshall, and J. Robin Warren in 2005 for "for their discovery of the bacterium Helicobacter pylori and its role in gastritis and peptic ulcer disease, " [28]. They developed new treatments for the infection and diagnostic tests, which allowed the hypothesis that H. pylori was the cause of ulcerative disease and ultimately gastrointestinal cancers to be evaluated and put into practice. After 1994, Helicobacter was generally accepted as the cause of most gastroduodenal diseases including peptic ulcer and gastric cancer. As a result of the research by Marshall and Warren, greater understanding of the underlying causes of disease and treatment is now a simple procedure and stomach surgery has become less often needed [26,27,29,30,31].
Common complex diseases are by their very nature difficult to tease apart because there is no single identifiable cause as there is for an infectious disease. For this reason transdisciplinary teams of scientists are needed to work within the Pasteur Quadrant if we are going to make any inroads in identifying environmental causes, or cures for these diseases. Common complex diseasesare caused by interactions among genes and environment factors. Multiple genes are involved in these diseases thus it was necessary to develop new techniques to screen for the genes that were involved in the etiology of these diseases [32].
3. Genomics
One of the greatest accomplishments of the 20th-21st centuries was the sequencing of the human genome. With the announcement of the sequencing of the human genome in 2000, new fields of genomics, transcriptomics, proteomics, and metabolomics were born. The promise of the Genomics Era was that we would quickly be able to determine the causes of human diseases. Craig Venter stated that sequencing the genome didn't teach us much about biology [33]. The healthy phenotype of a human is not determined solely by our gene make up. Venter and others quickly recognized that the environment is interacting with our genome, which results in a healthy or sick phenotype [33]. The question is how does the environment interact with our genome.
The environment interacts with the human genome by several mechanisms. Mutations were recognized in carcinogenesis and teratogenesis many years ago [34,35]. Classically, mutations were thought to be the only way in which environmental agents could interact with our genes to alter health phenotypes. This concept followed from classical Mendelian genetics showing phenotypic traits resulting from environmental exposures is heritable [36]. It was long thought that change from healthy to disease phenotype after environmental exposure was caused by mutations of the genome. This followed from the emerging knowledge of DNA helical structure [33], and from the Central Dogma of Biology put forth by Francis Crick in the 1950s [37,38]. These ideas were useful in considering cancer as the end-point for environment interaction with our genes [39]. However, for most common complex diseases, this concept is not sufficient. The remaining question is how does the environment interact with our genomes to change from healthy to disease phenotypes seen in common complex diseases.
The science of genomics was a great advance in identifying genes that might be involved in environmentally determined diseases, and led to the fields of pharmacogenomics and toxicogenomics but was insufficient on its own to explain diseases. The development of other fields including transcriptomics, proteomics, and metabolomics, and bioinformatics, which could be used to determine physiological changes from gene-environment expression had to be developed to fill in pieces of the puzzle [40]. Exposure to environmental agents is associated with changes in DNA methylation and gene expression profiles that can contribute to increased complex common disease susceptibility. Environmental factors have been associated with changes in gene expression via alterations in methylation or acetylation patterns of DNA or histones, which is the study of epigenomics [41].
4. Epigenomics
Epigenomic control of gene expression programs is essential for normal organismal development and cellular function [42]. However, in the presence of environmental agents, epigenomic control of gene expression may change, resulting in disease. Reports of nonmendelian transgenerational epigenetic inheritance, i.e., the inheritance of traits not determined by the DNA sequence (or mutation), are appearing more frequently in the literature. The idea that the environment could cause an inheritable change in phenotype without mutations was controversial [43], but it is now becoming accepted that epigenetic regulation of gene expression across generations without mutation occurs widely in mammalian and other systems [44,45]. Epigenetic gene expression can be driven through ligand-activated intracellular transcription factors, or through modification of other signal transduction pathways.
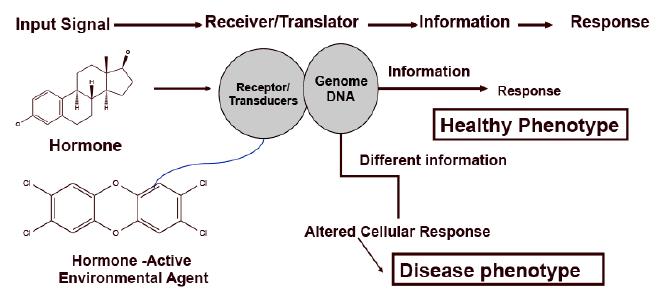
When an environmental ligand binds to an intracellular receptor, the receptor-ligand complex binds to specific sites on DNA (called response elements) and modulates gene expression in the absence of a mutation (Figure 3) [46,47,48]. This is one mechanism by which the external environment may alter intracellular signaling systems and serves as an initial step in developmental changes [49] and early steps in complex diseases, such as diabetes, an example is early exposure to bisphenol-A and its link to insulin production [50,51,52].
There is a large body of accumulating data suggesting the environment plays an important role in the onset of type II diabetes. This may especially be so for early onset of the disease in people 20 years of age and younger. Type II diabetes is commonly known as adult onset diabetes mellitus, because most cases occur in older adults. Now however the onset of diabetes in the population is occurring at earlier ages. It is estimated that approximately 208, 000 Americans under age 20 have diabetes, approximately 5, 000 present with Type II diabetes [53]. It is now a well-established notion that the early-life period is a critical window of development and that environmental exposures exert an influence during this period can "developmentally prime" the metabolic status of the adult [54,55].
Type II diabetes mellitus is a polygenic disease, characterized by insulin resistance and pancreatic inability to increase beta cell function and mass to meet the demands of insulin resistance. Endocrine disrupting chemicals (EDCs) have recently come under scrutiny as possible "obesogens" through their interaction with nuclear receptors. Peroxisome proliferator-activated receptor gamma (PPARγ), a receptor with well-known down-stream lipid metabolism functions, is a receptor of particular interest [56]. PPARγ is responsible for adipocyte differentiation, glucose and insulin hemostasis, cholesterol metabolism, fatty acid transport, and lipogenesis [57,58]. To ensure that extraneous adipocyte formation and growth does not occur, the body closely regulates endogenous chemicals that activate PPARγ. Activation of this intracellular receptor by an exogenous chemical such as an endocrine disrupting chemical (EDC) could have serious consequences in adipocyteformation and obesity, thus the term "obesogen" was coined [59].
Recent data suggest that two ligand activated transcription factors (nuclear receptors), estrogen receptor-a (ER-α) and glucocorticoid receptor-a (GR-α) interact with EDC's to activate PPARγ [60]. Both of these receptors are upstream of PPARγ, however Bisphenol-A, a well-known EDC, also activates PPARγ directly [61]. Each of these activation schemes may potentially lead to downstream adipocyte formation and alteration of lipid metabolism. Continual increases in each of these processes may put an individual at risk for developing a metabolic disorder like type II diabetes.
The estrogen receptor alpha regulates adipocyte hypertrophy and hyperplasia as well as the remodeling of lipid tissues [59]. Known obesogenic EDC's like BPA are ER-α agonists and can alter adipogenesis [61,62]. A possible biological mechanism that could explain this observation is PPARγ activation through ER-α. ER-α modulates PPARγ coactivator 1 (PGC1-alpha). As the name suggests PGC1-a activates PPARγ, leading to adipocyte differentiation and altered lipid transport and metabolism [63,64]. Additionally, PGC1-a activation has been shown to induce insulin resistance through PPARα, a disorder that is often linked to obesity and a risk factor for type II diabetes [65].
Another mechanism of PPARγ activation that has been of interest lately occurs through the glucocorticoid receptor. GCR-a is activated by EDC's like BPA [66]. GCR-a results in activation of CCAAT/enhancer binding protein alpha (C/EBP-a) [67]. C/EBP-a in turn, activates PPARγ [68]. Studies have shown that activation of GCR-a can cause adipocyte differentiation in vitro, suggesting that a similar mechanism may occur in vivo [69]. EDC's like BPA have been shown to cause adipogenesis in vitro [61]. Further investigation into the mechanism of adipogenesis showed BPA is also a direct PPARγ activator. X-ray crystallography structures of PPARγ bound to BPA confirmed that BPA is an agonist for PPARg [61]. PPARγ's binding site is relatively large and non-specific, allowing a wide range of endogenous chemicals and exogenous chemicals to bind. Interestingly, BPA is not structurally similar to PPARγ's known endogenous agonists [61]. Consequently, many EDC's, as shown by the case of BPA, have the potential to be agonists of PPARγ, and thus could act as obesogens.
Halogenated BPA derivatives have 10 to 100 times greater binding affinity to PPARγ than BPA itself [61]. This finding is especially troublesome as many wastewater treatment systems use a halogen, chlorine, to kill pathogens in their effluent. High concentrations of chlorine may chlorinate EDC's like BPA, creating halogenated EDC's that have a much greater binding affinity for PPARγ [70,71]. Similarly, water treatment plants often use chlorine as their secondary disinfectant, leaving enough chlorine in the water to prevent pathogen growth while the treated water is piped to commercial and residential areas. EDC's like BPA have been found in numerous streams and other bodies of water used as drinking water sources, creating the potential for the formation of halogenated BPA's and other EDC's [72,73,74]. In this case, the halogenated compounds have the potential to be formed directly in drinking water, exposing people to potentially potent obesogens.
Changing of expression of specific genes is not an isolated event. It has been recognized for some time that pleotropic effects occur even after a single exposure to an environmental agent [75]. Thus, it was apparent that there was much cross communication between and among cellular components and that environmental modification of cellular physiology does not occur in isolation. Many genes, proteins, and metabolites communicate with one another in the cell, and that disruption may lead to a disease state.
5. Systems Biology
Atomic and molecular interactions lead to cellular and tissue networking and physiology that in turn leads to organ level communication and networking and physiology with an outcome on the entire organism, be it health or disease states [76]. The environment, including psychosocial, food, and pollutants can interact with the human genome to result in a cascade of effects [77,78]. When we talk about the systems view of life, we are implying that we are looking at an organism in its totality of mutual interactions. A perturbation anywhere in the system will cause a change everywhere (Christopher McLachlan, personal communication).
In biomedical models, health is defined as the absence of disease, and disease as the malfunctioning of biological mechanisms. Based on the systems view of life it is impossible to give a precise definition of health. We are all aware that health and illness is a spectrum. Health is a subjective experience whose quality can be known intuitively but can never be exhaustively described quantitatively. Health is a state of well-being that arises when the organism functions in a certain way. We know people who appear healthy, but who have an unexpressed initiated disease. Similarly, people who have a chronic condition may be able to perform work duties as if they were well. The systems view of life leads us to see health as a process, and as a multidimensional and multilevel phenomenon. To improve public health, it is necessary to gain a greater understanding of the complex adaptive systems involved in both causing and solving public health problems. When we think of environmental exposure and systems approaches, we take into account the multiple pathways activated by the exposure. These involve gene-gene, gene-protein, protein-protein, and protein-metabolite and metabolite-metabolite interactions to form a network of dynamic interactive species [79]. The evolution of new sciences of genomics, transcriptomics, proteomics, and metalolomics, to mention a few led to the recognition that computer sciences must be involved to tease out the mounds of data.
To be able to study these complex interactions, we need strong computational capacity [77]. Using genomic scans of single nucleotide polymorphism (SNP) expressions is a first step to identify susceptibility of a person to developing a disease [80]. An instance of this application is a recent study that showed some rare variants in PPARG are associated with enhanced risk of developing diabetes Type II [81]. So genomic scans together with epigenomic scans are both needed to gain insight into common complex diseases. We also need to develop models and projections, using various analytical approaches e.g., informatics, big-data, agent-based modeling, system-dynamics modeling using data from the exposome and systems biology studies. To improve strategic decision-making we will soon have access to inexpensive gene expression analysis with a thousand-dollar chip that will be used for personalized health investigations [82,83,84]. However, to gain more insight into risks for complex common diseases, epigenomic scans that assess changes in epigenetic regulation of gene expression after an environmental insult are necessary [85]. The current technology is advancing [86,87], but is primarily laboratory based. Epigenomic analysis can be a valuable asset in public health if we can get it into the hands of practitioners, so we need to enlist engineers and technologists to develop methods that will simplify and reduce the cost of the analyses, so they can be applied to studies of exposed populations. Together these tools will be very valuable at understanding how environmental exposures alter gene expression, and will be useful in preventing long-term effects of environment gene interactions.
6. Conclusion
Advances in genomics and epigenomics will lay the groundwork for an era of personalized health for many common complex conditions. The current "one-size-fits-all? approach to health will go away as practitioners increasingly adopt strategies tailored to an individual's unique genetic makeup, lifestyle, and environment. Transdisciplinary teams implementing advances in biomedical science such as exposome, genomics, epigenomics, and systems biology, will provide people with personalized information about their individual disease risk and information of how to prevent or reduce their risk of developing conditions such as diabetes, heart disease, and cancer.
Environment wide association studies (EWAS) have been carried out for Type 2 Diabetes [88]. These types of studies have promise for finding the environmental factors associated with complex common diseases in general. Taken together with genome-wide association study (GWAS), EWAS has yielded important information on susceptibility genes and possible environmental factors [89,90]. These are important hints to understanding genomics and environmental factors, however, they do not give the full picture [91]. Initial attempts of bringing exposure and disease genes is being made at the Comparative Toxicogenomics Database site (CTD, http://ctd.mdibl.org/) [92], however more attention should be focused on epigenetic studies to complete the picture.
Conflict of Interest
The authors declare that there are no conflicts of interest related to this study.









 DownLoad:
DownLoad: