Dynamics of an SEIR model with media coverage mediated nonlinear infectious force

1.   Introduction

The spread of infectious diseases is a serious threat to human life and health, and the number of deaths due to infectious diseases accounts for a quarter of the total deaths worldwide every year ^[1]. When an emerging infectious disease occurs, a vaccine or effective drugs to treat the disease cannot be developed in time. This makes it very challenging to control the spread of the disease in both temporal and spatial dimensions, especially in some low- and middle-income countries, where medical resources are not fully guaranteed. Therefore, reducing the rate of disease transmission has become one of the most direct and effective means of prevention and control. At the beginning of the epidemic, in order to prevent the spread of the disease, lockdown, static management at home, quarantine treatment and other measures are taken to control the spread of the disease. In the era of rapid development of information technology, media coverage plays an important role in the spread and control of infectious diseases. Media coverage may change people's understanding of emerging infectious diseases and influence people's attitudes and behaviors during the outbreak of infectious diseases. Simultaneously, it may warn people to reduce unnecessary contact with others and reduce the transmission rate ^[2].

Mathematical modeling has become an essential tool to better understand the impacts of media coverage on the spread and control of infectious diseases. In this regard, there are three main approaches addressing the influences of media awareness on the spread of infectious diseases. One approach is to introduce a reduction factor on the transmission rate. For example, in ^[3,4], functions $f\left(E, I, H \right) = {{e}^{-{{\alpha }_{1}}E-{{\alpha }_{2}}I-{{\alpha }_{3}}H}}$ and $f(I) = \dfrac{k}{(1+a{{I}^{2}})}$ were respectively used to reflect the effective transmission rate affected by media coverage. Cui et al. ^[5] used the nonlinear incidence of form ${{\mu }_{1}}-{{\mu }_{2}}f(I)$ to express the influence of media coverage and education in the process of infectious disease transmission. Another different form of incidence function, $({\beta _1} - {\beta _2}f(I))SI$, was used in Cui and Wu ^[6]. The second approach is to introduce a new independent compartment $M(t)$ to represent the disease information level related to media coverage ^{[7,8,9,10,11]}. Xing et al. ^[12] added an independent compartment $M(t)$, and $\dfrac{M}{1+kM}\beta f(S)I$ was used to represent the effective contact rate of diseases under the influence of media coverage. Yan et al. ^[13] described the dynamic impact of media reports on the population as $f(M, p) = {{e}^{-pM}},$ and $p$ was a positive constant that changes with the number of hospital notifications. The third approach divides the population into conscious and unconscious groups, assuming the individuals in the unconscious group can be converted to the conscious compartment due to media coverage ^[14,15]. For instance, Latifah et al. ^[16] considered the level of human awareness of the existence of certain diseases, and proposed an SIS-M mathematical model. In their model, the susceptibles were divided into unconscious predisposition $S_{n}$ and conscious susceptibles $S_{a}$, and the independent compartment $M$ was added to represent the level of consciousness of the population. The unconscious susceptible compartment may be transferred to the conscious susceptible compartment through media coverage, and a certain proportion of conscious susceptibles who lose their disease consciousness would return to the unconscious susceptible compartment. Agaba et al. ^[17] analyzed an SIRS model, which divided susceptible $(S)$, infected $(I)$ and recovered $(R)$ into conscious and unconscious populations, and considered the behavioral changes of simultaneous transmission of consciousness in the population.

In the above mentioned papers, either the exposed compartment was not included or the individuals in the exposed compartment were assumed to be not infectious. Given that some exposed individuals also have the ability to infect susceptibles, in this paper, we propose an SEIR model which assumes transmission of disease for both exposed and infectious compartments, and incorporates a novel nonlinear incidence force mediated by media coverage. We will present our model in Section 2 and study its dynamics in Section 3.

2.   Model formulation

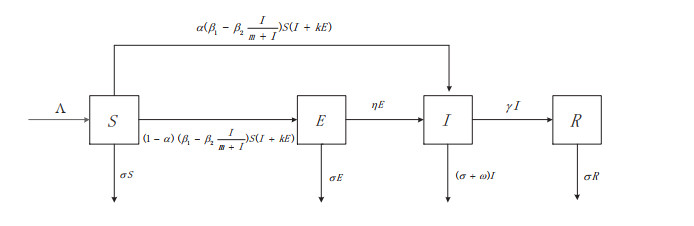
Based on the stages of the disease, we divide the population into $4$ disjoint compartments, namely, Susceptible $(S)$, Exposed $(E)$, Infective $(I)$ and Recovered $(R)$ compartments. Let $S(t)$, $E(t)$, $I(t)$ and $R(t)$ denote, respectively, the associated population sizes at time $t$. Then, the total population size at time $t$ is $N(t) = S(t)+E(t)+I(t)+R(t)$.

Let $\Lambda > 0$ be recruitment and assume all newly recruited individuals are susceptible. Let $\sigma > 0$, $\omega\geq 0$, $\eta > 0$ and $\gamma > 0$ be the natural death rate, disease-induced death rate, progression rate from exposed compartment to infective compartment, and recovery rate from infective compartment, respectively. We assume that the exposed individuals also have the ability to infect susceptibles (with a reduced rate measured by $k\in(0, 1)$) and the infection force is of the form, $({{\beta }_{1}}-{{\beta }_{2}}\frac{I}{m+I})S(I+kE)$. Here, $\beta_{1}$ represents the transmission rate of disease not affected by media coverage, $\beta_{2} < \beta_1$ is the maximum reduction rate of disease transmission rate caused by media coverage, and $m$ is the half-saturation constant. The impact of media coverage on the reduction of transmission rate is quantified by the function $g(I) = \dfrac{I}{{m + I}}$. We also assume that after contacting exposed and infective individuals, the susceptibles who become infected enter the exposed compartment with the proportion of $1-\alpha$ and infective compartment with the proportion of $\alpha$. Recovered individuals are assumed to gain permanent immunity.

The above assumptions allow us to describe our model by the following system of differential equations:

The flow chart of our model is presented in Figure 1, and the associated initial condition is given as

3.   Model analysis: Basic reproduction number and threshold dynamics

Our first result presented below shows that our model is well posed.

Theorem 3.1. Consider model (2.1) with initial condition given in (2.2). There exists a unique solution $(S(t), E(t), I(t), R(t))$, which remains nonnegative and is bounded satisfying

Moreover, the set $\Gamma$ is attracting and is positively invariant, where

Proof. Note that the vector field, defined by the right hand side of model (2.1), is smooth in $\mathbb{R}^4_+$. Thus, with any initial condition given in (2.2), model (2.1) admits a unique solution.

It follows from (2.1) that

This shows that the vector field is oriented inward from the plane boundaries, starting from a nonnegative cone. Hence, $\mathbb{R}^4_+$ is positively invariant. That is, the unique solution through $(S_0, E_0, I_0, R_0)\in \mathbb{R}^4_+$ remains nonnegative for $t > 0$.

Note that the total population $N(t) = S(t) + E(t) + I(t) + R(t)$ satisfies

which yields

Therefore,

Moreover, the set $\Gamma$ is attracting and is positively invariant.

Obviously, model (2.1) always admits a disease-free equilibrium (DFE), ${P_0} = (\frac{\Lambda }{\sigma}, 0, 0, 0)$. Linearizing model (2.1) at the DFE and using the next generation matrix method, we find that the basic reproduction number, $\mathcal{R}_0$, is given by

with

and

Theorem 3.2. The DFE $P_0$ is globally asymptotically stable if $\mathcal{R}_0 < 1$, and is unstable if $\mathcal{R}_0 > 1.$

Proof. It follows from ^[18] that the DFE $P_0$ is locally asymptotically stable if $\mathcal{R}_0 < 1$ and is unstable if $\mathcal{R}_0 > 1$. We only need to show that $P_0$ is globally attractive if $\mathcal{R}_0 < 1$.

It follows from Theorem 3.1 that

Thus, for sufficiently small real number $\epsilon > 0$, there exists $T_1 > 0$ such that $S(t) < \frac{\Lambda}{\sigma}+\epsilon.$

By the nonnegativity of solution, from the second and the third equations of model (2.1), we have

where $F$ and $V$ are given in (3.3) and (3.4), respectively.

Note that, from ^[18], we see that $\mathcal{R}_0 < 1$ implies that all eigenvalues of $F-V$ have negative real parts. Thus, for sufficiently small $\epsilon > 0$, all eigenvalues of $F-V + \frac{\epsilon}{\bar{S}} F$ also have negative real parts. Consequently, the unique equilibrium, $(0, 0)$, of the following linear system

is globally asymptotically stable. That is,

By a comparison, we obtain that

Therefore, by the theory of asymptotically autonomous systems ^[19], the DFE is globally asymptotically stable if $\mathcal{R}_0 < 1$.

Theorem 3.2 indicates that the disease dies out if the basic reproduction number $\mathcal{R}_0 < 1$. Next, we see if there will be an endemic equilibrium if $\mathcal{R}_0 > 1$. Note that an endemic equilibrium ${P^*} = ({S^*}, {E^*}, {I^*}, {R^*})$ exists if the following system has a positive solution.

From the last equation of (3.7), we get

From the second and the third equations of (3.7), we can express $E$ in terms of $I$ as follows:

Adding the first three equations of (3.7) together, we get

Substituting (3.10) and (3.11) into the third equation of (3.7), we get

where

If ${\mathcal R_0} > 1$, then ${a_0} > 0$. This implies that Eq (3.11) has a unique positive root, ${I^*}$, with

Plugging ${I^*}$ into Eqs (3.8)–(3.10), we can obtain $R^* > 0$, $E^* > 0$ and $S^*$, respectively. From the second equation of (3.7), we see that $S^* > 0$ as long as $I^* > 0$. Thus, model (2.1) admits a unique endemic equilibrium ${P^*}$ if ${\mathcal R_0} > 1$.

Let

and set

and

Theorem 3.3. If $\mathcal R_0 > 1$, then there is a unique endemic equilibrium ${P^*} = ({S^*}, {E^*}, {I^*}, {R^*})$, which is locally asymptotically stable provided that the following conditions hold simultaneously:

Proof. The Jacobian matrix of model (2.1) at ${P^*} = ({S^*}, {E^*}, {I^*}, {R^*})$ is

Thus, the corresponding characteristic equation at ${P^*}$ is given by

Obviously, there exists always a negative eigenvalue, $\lambda = - \sigma$, and other roots need to be determined by the Routh-Hurwitz criterion. A necessary and sufficient condition for $P^{*}$ to be locally asymptotically stable is ${D_2} > 0, {D_0} > 0, {D_1}{D_2} > {D_0}$.

We next discuss the global stability of the endemic equilibrium. Since the first three equations of model (2.1) are independent of $R$, we only need to consider the following subsystem of (2.1).

Lemma 3.4. (Global asymptotic stability theorem ^[20]) Let $D \subset \bf{R^n}$ be an open set, and let $x \mapsto P(x) \in \bf{R^n}$ be a ${C^1}$ function defined in $D$. We consider the differential equation

Let $x(t, {x_0})$ be the solution of Eq (3.15) satisfying the initial value $x(0, {x_0}) = {x_0}$. Assume the following.

(i) $D$ is simply connected.

(ii) There exists a compact attractive subset $K \subset D$.

(iii) There is a unique equilibrium $x \in D$ for Eq (3.15).

Furthermore, we suppose ${P^{ - 1}}(x)$ exists, and it is continuous when $x \in K$. Define

where $B = {P_f}{P^{ - 1}} + P\dfrac{{\partial {f^{[2]}}}}{{\partial x}}{P^{ - 1}}$, and the matrix $P_{f}$ is the derivative of $P{(x)}$ along the $f$ direction. $\mu (B)$ is the Lozinskil measure of the matrix, and $\mu (B) = \mathop {\lim }\limits_{h \to {0^ + }} \dfrac{{\left\| {I + hB} \right\| - 1}}{h}$.

Suppose that (i)–(iii) hold, and $q < 0$ is satisfied. Then, the only equilibrium point of Eq (3.15) is globally asymptotically stable.

Theorem 3.5. If $\mathcal R_0 > 1$, and $\frac{{\sigma (\sigma + \omega + \gamma)}}{{\alpha \Lambda }} < h(I) < \frac{{\sigma (2\sigma + \eta)}}{{\left({1 - \alpha } \right)k\Lambda }}$, and ${\beta _1}{(m + I)^2} > {\beta _2}(2mI + {I^2} + mkE)$, then the endemic equilibrium of model (3.14) is globally asymptotically stable.

Proof. Theorem 3.5 is proved by Lemma 3.4. The existence of attractive compact sets inside $\Gamma$ is equivalent to proving that the model (3.14) is uniformly persistent ^[6]. According to Theorem 3.2, when $\mathcal R_0 > 1$, ${\bar P_0}$ is unstable. Because $\Gamma$ is the positive invariant set of model (3.14), there is always a unique disease-free equilibrium point $\partial \Gamma$, the boundary of $\Gamma$. Therefore, model (3.14) is consistent and persistent, and (i) is proved. The model (3.14) has a unique endemic equilibrium point, and (ii) is satisfied. The Jacobian matrix of model (3.14) is

The second additive composition matrix corresponding to matrix $J$ is

Let $P(x) = P(S, E, I) = diag(1, \dfrac{E}{I}, \dfrac{E}{I})$, ${P_f}{P^{ - 1}} = diag(0, \dfrac{{E'}}{E} - \dfrac{{I'}}{I}, \dfrac{{E'}}{E} - \dfrac{{I'}}{I})$. Matrix $B = {P_f}{P^{ - 1}} + P{J^{[2]}}{P^{ - 1}}$ can be written as a block matrix

where

Let $(u, v, w)$ represent the vector in ${\mathbb R^3} \cong {\mathbb R^{\left({ 3 \atop 2 s} \right)}}$, and $\left\| \cdot \right\|$ is defined as $\left\| {(u, v, w)} \right\| = \max \{ \left| u \right|, \left| {v + w} \right|\}$. Using the valuation method, we get $\mu (B) \le \sup \{ {g_1}, {g_2}\}$, where ${g_1} = {\mu _1}({B_{11}}) + \left| {{B_{12}}} \right|, {g_2} = {\mu _1}({B_{22}}) + \left| {{B_{21}}} \right|$, $\left| {{B_{12}}} \right|$ and $\left| {{B_{21}}} \right|$ are the norms of the matrix with respect to the norm of the $l_1$ vector, ${\mu _1}$ is the Lozinkil measure with respect to the $l_1$ vector norm.

The absolute value of each column of off-diagonal matrix of determinant $B_{22}$ is added to the corresponding diagonal elements to obtain

Let

Taking the maximum value of two diagonal elements of ${B_{22}}^\prime$, that is, ${\mu _1}({B_{22}})$, then, ${\mu _1}({B_{22}}) = \max \{ X, Y\}$. Therefore, we have

According to the last two equations of model (3.14), the following equation can be obtained:

Substitute in (3.16) and (3.17) to get

If $\max \left\{ {\eta + \alpha h(I)kS, \alpha h(I)(I + kE)} \right\} = \eta + \alpha h(I)kS,$ then $\max \{ X, Y\} = X$, $\left| {{B_{21}}} \right| = \frac{E}{I}(\eta + \alpha h(I)kS),$ and

If $\max \left\{ {\eta + \alpha h(I)kS, \alpha h(I)(I + kE)} \right\} = \alpha h(I)(I + kE),$ then $\max \{ X, Y\} = Y$, $\left| {{B_{21}}} \right| = \frac{E}{I}\alpha h(I)(I + kE),$ and

In addition, ${g_2} = \sup \{ {g_2}^\prime, {g_2}^{\prime \prime }\}$. When $\mathcal R_0 > 1$, $\frac{{\sigma (\sigma + \omega + \gamma)}}{{\alpha \Lambda }} < h(I) < \frac{{\sigma (2\sigma + \eta)}}{{\left({1 - \alpha } \right)k\Lambda }}$, and ${\beta _1}{(m + I)^2} > {\beta _2}(2mI + {I^2} + mkE),$

So, we can get $q = \mathop {\lim }\limits_{t \to \infty } \mathop {\sup }\limits_{{x_o} \in K} \frac{1}{t}\int_0^t {\mu \left({B(x(s, {x_0}))} \right)} dt < 0$. According to Lemma 3.4, the endemic equilibrium of system (3.14) is globally asymptotically stable.

Theorem 3.6. When $\mathcal R_0 > 1$, and $\frac{{\sigma (\sigma + \omega + \gamma)}}{{\alpha \Lambda }} < h(I) < \frac{{\sigma (2\sigma + \eta)}}{{\left({1 - \alpha } \right)k\Lambda }}$ and ${\beta _1}{(m + I)^2} > {\beta _2}(2mI + {I^2} + mkE)$ are satisfied, the endemic equilibrium $P^*$ of model (2.1) is globally asymptotically stable.

Proof. According to Theorem 3.5, when $t \to \infty$, $(S, E, I) \to ({S^*}, {E^*}, {I^*})$. We have the limit subsystem of model (2.1):

We can solve it directly to get $R = c{e^{ - \sigma t}} + {e^{ - \sigma t}}\int \gamma {I^*}{e^{\sigma t}}dt$. (c is an arbitrary constant). When $t \to \infty$, $R(t) \to \dfrac{\gamma {I^*}}{{\sigma}} = {R^*}$. Therefore, the endemic equilibrium of model (2.1) is globally asymptotically stable.

4.   Sensitivity analysis

Note that the basic reproduction number $\mathcal{R}_{0}$ is the threshold determining the disease dynamics. It is of great interest to explore how model parameters affect $\mathcal{R}_{0}$. Therefore, in this section, we carry out sensitivity analysis by using the method described in ^[21].

Definition 4.1. The normalized forward sensitivity index of a variable $u$ to a parameter $q$ is defined as

We summarize the computed sensitivity indices of $\mathcal R_0$ to several important model parameters in Table 1 and present them in Figure 2.

Sensitivity indices shown in Table 1 indicate that increasing the recruitment, $\Lambda$, by $1%$ will increase the basic reproduction number $\mathcal{R}_0$ by $1%$. Increasing the transmission rate, $\beta_1$, by $1%$ will also increase the basic reproduction number $\mathcal{R}_0$ by $1%$. Sensitivity indices in Table 1 show that $\Lambda$, $\beta_1$ and $k$ have positive effects on $\mathcal R_0$, while other parameters ($\alpha, \sigma, \eta, \omega, \gamma$) all have negative effects on $\mathcal R_0$. For instance, increasing the recovery rate, $\gamma$, by $1%$, will lower the basic reproduction number $\mathcal R_0$ by $0.684921%$. Table 1 also shows that $\Lambda$, $\beta _{1}$, $\sigma$ and $\gamma$ are the most important parameters affecting the basic reproduction number $\mathcal R_0$. In practice, control measures should therefore focus on lowering the disease transmission rate $\beta_1$, and increasing the recovery rate $\gamma$.

5.   Numerical simulations

According to the expression of basic reproduction number, we analyze the change of $\mathcal R_0$ when some parameters change.

The contour plots of the basic reproduction number $\mathcal R_0$ with respect to parameters $\Lambda \; vs.\; {\beta _1}, {\beta _1}\; vs.\; \gamma, {\beta _1}\; vs.\; k$ are presented in Figure 3. When other parameters are fixed, as shown in Figure 3, $\mathcal R_0$ increases as $\Lambda$ and/or $\beta _{1}$ increases, while $\mathcal R_0$ decreases if $\beta _{1}$ decreases and/or $\gamma$ increases. This is consistent with the sensitivity analysis presented in Table 1.

Take $m$ = 40, 100, ${{\beta }_{1}} = 0.027$, ${{\beta }_{2}} = 0.01$ with other parameters given in Table 1. We see that ${\mathcal R_0} = 0.6203 < 1$. Numerical simulation presented in Figure 4 confirms that the DFE, ${{P}_{0}} = (6.25, 0, 0, 0)$, is globally asymptotically stable, and the disease dies out. Now, we increase $\beta_{1}$ to $0.08$ so that ${\mathcal R_0} = 1.8380 > 1$, and the numerical simulation presented in Figure 5 shows that the solution approaches the endemic equilibrium, ${{P}^{*}} = (3.4004, 0.2007, 0.1214, 2.5047)$.

If $\mathcal R_0 > 1$, the disease becomes endemic. Taking different sets of initial values, Figure 6 indicates that the endemic equilibrium ${{P} ^ {*}}$ is globally asymptotically stable.

It follows from the expression of $\mathcal{R}_0$ that media coverage related parameters $\beta_2$ and $m$ do not affect the basic reproduction number. However, both $\beta_2$ and $m$ have impacts on the endemic equilibrium level.

Take $\beta_{1} = 0.08$, $m = 0.1$. Set ${{\beta }_{2}}$ as $0.06, 0.03, 0.01, 0$, respectively, and other parameters are the same as those in Table 1. Figure 7 presents the time courses of infected population $I(t)$ under different values of $\beta_{2}$ (assuming the same initial value), showing that as $\beta_2$ increases, the infected population decreases.

Similarly, we can explore the impact of $m$ on the spread of disease. Let ${{\beta} _ {1}} = 0.08, {{\beta} _ {2}} = 0.06$ and $m$ be $100, 10, 1, 0$, respectively. Numerical solutions shown in Figure 8 show that the smaller the half-saturation constant $m$ is, the faster the number of infected individuals decreases, with fewer infected individuals.

6.   Summary

In this paper, we considered an SEIR model with media coverage mediated nonlinear infection force. Using the next generation matrix method, we identified the basic reproduction number $\mathcal R_0$. Similar to many other disease models, our model also exhibits threshold dynamics in the sense that the disease dies out if the basic reproduction number is less than one, and the disease is endemic if the basic reproduction number is greater than one.

If $\mathcal{R}_0 < 1$, the disease free equilibrium has been shown to be globally asymptotically stable, which was achieved by using the comparison method. If $\mathcal{R}_0 > 1$, a global stability result of the endemic equilibrium has been established by using the second additive composite matrix method.

We also performed (local) sensitivity analysis of $\mathcal{R}_0$ to disease parameters, and we found that parameters $\Lambda$, $\beta_1$ and $k$ have positive effects on the increase of $\mathcal R_0$, while other parameters, $\alpha, \sigma, \eta, \omega, \gamma$, all have negative effects on $\mathcal R_0$. Of all related parameters, $\Lambda$, $\beta _{1}$, $\sigma$ and $\gamma$ are the most important parameters affecting the basic reproduction number $\mathcal R_0$. However, practical control measures should focus on lowering the disease transmission rate $\beta_1$, and increasing the recovery rate $\gamma$.

Numerical simulations were carried out to illustrate our theoretical results and to explore how the basic reproduction number $\mathcal R_0$ depends on disease parameters. In our model, the media coverage related parameters $\beta_2$ and $m$ have no impacts on the basic reproduction number, but they do affect the endemic equilibrium level: A larger $\beta_2$ and smaller $m$ will be beneficial to lowering the endemic level of disease. This suggests that if the disease persists and becomes endemic, proper media coverage resulting in public awareness of the disease would lower the endemic level.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Major Project of Science Research Fund of Hunan Provincial Education Department (No: 22A0368) and the Scientific Research Fund of Jishou University (No: Jdy22005).

Conflict of interest

The authors declare that they have no competing interests.

Authors' contributions

J. Xie and H. Guo conceived of the studies, and drafted the manuscript. M. Zhang participated in the discussion. All authors read and approved the final manuscript.