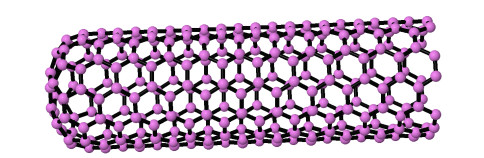
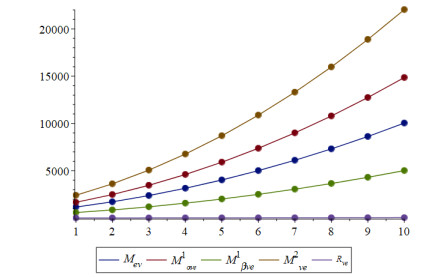
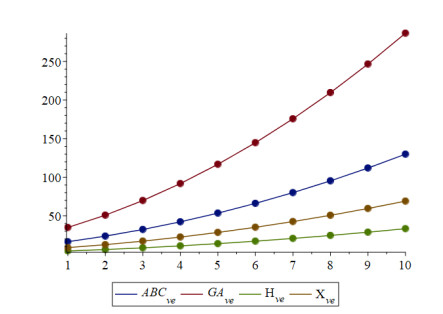
|
[1]
|
S. Iijima, Helical microtubules of graphitic carbon, Nature, 354 (1991), 56–58. https://doi.org/10.1038/354056a0 doi: 10.1038/354056a0

|
|
[2]
|
M. F. Thorpe, D. Tománek, R. J. Enbody, Science and Application of Nanotubes, Springer, 2002.
|
|
[3]
|
U. Kuhlmann, H. Jantoljak, N. Pfander, P. Bernier, C. Journet, C. Thomsen, Infrared active phonons in single-walled carbon nanotubes, Chem. Phys. Lett., 294 (1998), 237–240. https://doi.org/10.1016/S0009-2614(98)00845-8 doi: 10.1016/S0009-2614(98)00845-8

|
|
[4]
|
P. Mlynarska, S. Tomczewski, A. Pakuła, G. Wróblewski, M. Sloma, L. Salbut, Detection of subsurface defects and measurement of thickness of screen layers made of graphene and carbon nanotubes with application of full-field optical coherence tomography in linnik configuration, in Optical Manufacturing and Testing XI, 9575 (2015), 246–251. https://doi.org/10.1117/12.2188640
|
|
[5]
|
J. Tang, Y. Wang, S. Cheng, P. Yu, K. Huang, C. Yuan, Applications of single-walled carbon nanotubes and type-II quantum dots in photovoltaics and passive mode-locking saturable absorbers, in Carbon Nanotubes, Graphene, and Associated Devices V, 8462 (2012), 108–119. https://doi.org/10.1117/12.928211
|
|
[6]
|
P. Li, W. Xue, Dielectrophoretic assembly of organized carbon nanotubes and thin films, in ASME International Mechanical Engineering Congress and Exposition, 44496 (2010), 49–54. https://doi.org/10.1115/IMECE2010-37441
|
|
[7]
|
R. P. Raffaelle, B. Landi, T. Gennett, R. S. Morris, B. Dixon, P. Lamarre, Fuel cell applications of single wall carbon nanotubes, in International Conference on Fuel Cell Science, Engineering and Technology, 36681 (2003), 121–128. https://doi.org/10.1115/FUELCELL2003-1708
|
|
[8]
|
S. A. Bakar, S. Muhamad, A. A. Aziz, N. A. Asli, M. Mohammad, M. S. Shamsudin, et al., CVD growth of carbon nanotubes from palm oil precursor, in 2012 IEEE Symposium on Business, Engineering and Industrial Applications, IEEE, (2012), 377–381. https://doi.org/10.1109/ISBEIA.2012.6422908
|
|
[9]
|
E. V. Antoniadou, B. G. Cousins, A. M. Seifalian, Development of conductive polymer with carbon nanotubes for regenerative medicine applications, in 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, IEEE, (2010), 815–818. https://doi.org/10.1109/IEMBS.2010.5626760
|
|
[10]
|
R. Sen, T. Kocab, J. Black, J. McDermott, S. K. Pal, S. Buffat, et al., Engineering nanomaterials and nanostructures for electronic applications: A case study of carbon nanotubes for memory devices, in 2020 4th IEEE Electron Devices Technology & Manufacturing Conference (EDTM), IEEE, (2020). https://doi.org/10.1109/EDTM47692.2020.9117911
|
|
[11]
|
C. A. C. Abdullah, E. L. Albert, Carbon nanotubes as biological transporters and tissue-engineering scaffolds, in Synthesis, Technology and Applications of Carbon Nanomaterials, Elsevier, (2019), 135–156. https://doi.org/10.1016/B978-0-12-815757-2.00006-1
|
|
[12]
|
N. Mamidi, Cytotoxicity evaluation of carbon nanotubes for biomedical and tissue engineering applications, in Perspective of Carbon Nanotubes, IntechOpen, 2019.
|
|
[13]
|
M. K. Assadi, H. Hanaei, Transparent carbon nanotubes (CNTs) as antireflection and self-cleaning solar cell coating, in Engineering Applications of Nanotechnology, Springer, Cham, (2017), 101–114. https://doi.org/10.1007/978-3-319-29761-3_4
|
|
[14]
|
P. J. Britto, K. S. V. Santhanam, A. Rubio, J. A. Alonso, P. M. Ajayan, Improved charge transfer at carbon nanotube electrodes, Adv. Mater., 11 (1999), 154–157. https://doi.org/10.1002/(SICI)1521-4095(199902)11:2<154::AID-ADMA154>3.0.CO;2-B doi: 10.1002/(SICI)1521-4095(199902)11:2<154::AID-ADMA154>3.0.CO;2-B

|
|
[15]
|
G. A. Rivas, M. D. Rubianes, M. C. Rodríguez, N. F. Ferreyra, G. L. Luque, M. L. Pedano, et al., Carbon nanotubes for electrochemical biosensing, Talanta, 74 (2007), 291–307. https://doi.org/10.1016/j.talanta.2007.10.013 doi: 10.1016/j.talanta.2007.10.013

|
|
[16]
|
A. J. S. Ahammad, J. J. Lee, Md. A. Rahman, Electrochemical sensors based on carbon nanotubes, Sensors, 9 (2009), 2289–2319. https://doi.org/10.3390/s90402289 doi: 10.3390/s90402289

|
|
[17]
|
A. N. Ribeiro, N. S. Ferreira. Systematic study of the physical origin of ferromagnetism in CeO2- nanoparticles, Phys. Rev. B, 95 (2017), 144430. https://doi.org/10.1103/PhysRevB.95.144430 doi: 10.1103/PhysRevB.95.144430

|
|
[18]
|
E. N. Tseng, Y. T. Hsiao, Y. C. Chen, S. Y. Chen, A. Gloter, J. M. Song, Magnetism and plasmonic performance of mesoscopic hollow ceria spheres decorated with silver nanoparticles, Nanoscale, 11 (2019), 3574–3582. https://doi.org/10.1039/C8NR09636H doi: 10.1039/C8NR09636H

|
|
[19]
|
S. A. Holgate, Understanding Solid State Physics, CRC Press, 2009.
|
|
[20]
|
H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl, R. E. Smalley, C60: Buckminsterfullerene, Nature, 318 (1985), 162–163. https://doi.org/10.1038/318162a0 doi: 10.1038/318162a0

|
|
[21]
|
A. Younis, D. Chu, S. Li, Cerium oxide nanostructures and their applications, in Functionalized Nanomaterials, InTech, 2016.
|
|
[22]
|
S. T. R. Naqvi, B. Shirinfar, S. Majeed, M. N. Haq, D. Hussain, T. Iqbal, et al., Synthesis, design and sensing applications of nanostructured ceria-based materials, Analyst., 143 (2018), 5610–5628. https://doi.org/10.1039/c8an01268g doi: 10.1039/c8an01268g

|
|
[23]
|
A. Dhall, W. Self, Cerium oxide nanoparticles: A brief review of their synthesis methods and biomedical applications, Antioxidants, 7 (2018), 97. https://doi.org/10.3390/antiox7080097 doi: 10.3390/antiox7080097

|
|
[24]
|
S. Borgmann, A. Schulte, S. Neugebauer, W. Schuhmann, Amperometric biosensors, in Advances in Electrochemical Sciences and Engineering, (2012), 1–83.
|
|
[25]
|
E. N. Primo, F. Gutiérrez, M. D. Rubianes, N. F. Ferreyra, M. C. Rodríguez, M. L. Pedano, et al., Electrochemistry in one dimension: Applications of carbon nanotubes, in Advances in Electrochemical Sciences and Engineering, 2015 (2015), 83–120. https://doi.org/10.1002/9783527697489.ch3
|
|
[26]
|
H. Wiener, Structural determination of paraffin boiling points, J. Am. Chem. Soc., 69 (1947), 17–20. https://doi.org/10.1021/ja01193a005 doi: 10.1021/ja01193a005

|
|
[27]
|
S. B. Chen, A. Rauf, M. Ishtiaq, M. Naeem, A. Aslam, On ve-degree- and ev-degree-based topological properties of crystallographic structure of cuprite Cu2o, Open Chem., 19 (2021), 576–5851. https://doi.org/10.1515/chem-2021-0051 doi: 10.1515/chem-2021-0051

|
|
[28]
|
S. Ediz, A new tool for QSPR researches: ev-degree randić index, Celal Bayar Univ. J. Sci., 13 (2017), 615–618. https://doi.org/10.1177/1559827617729634 doi: 10.1177/1559827617729634

|
|
[29]
|
S. Ediz, On ve-degree molecular topological properties of silicate and oxygen networks, Int. J. Comput. Sci. Math., 9 (2018). https://doi.org/10.1504/ijcsm.2018.10011733
|
|
[30]
|
B. Sahin, S. Ediz, On ev-degree and ve-degree topological indices, Iran. J. Math. Chem., 9 (2018).
|
|
[31]
|
M. Chellali, T. W. Haynes, S. T. Hedetniemi, T. M. Lewis, On ve-degrees and ev-degrees in graphs, Discrete Math., 340 (2007), 31–38. https://doi.org/10.4028/www.scientific.net/KEM.340-341.31 doi: 10.4028/www.scientific.net/KEM.340-341.31

|
|
[32]
|
M. F. Nadeem, M. Azeem, I. Farman, Comparative study of topological indices for capped and uncapped carbon nanotubes, Polycyclic Aromat. Compd., 2021 (2021), 1–18. https://doi.org/10.1080/10406638.2021.1903952 doi: 10.1080/10406638.2021.1903952

|
|
[33]
|
M. F. Nadeem, M. Azeem, H. M. A.Siddiqui, Comparative study of zagreb indices for capped, semi-capped, and uncapped carbon nanotubes, Polycyclic Aromat. Compd., 2021 (2021), 1–18. https://doi.org/10.1080/10406638.2021.1890625 doi: 10.1080/10406638.2021.1890625

|
|
[34]
|
M. F. Nadeem, M. Imran, H. M. A. Siddiqui, M. Azeem, A. Khalil, Y. Ali, Topological aspects of metal-organic structure with the help of underlying networks, Arabian J. Chem., 14 (2021), 103157. https://doi.org/10.1016/j.arabjc.2021.103157 doi: 10.1016/j.arabjc.2021.103157

|
|
[35]
|
W. Gao, M. R. Farahani, Degree-based indices computation for special chemical molecular structures using edge dividing method, Appl. Math. Nonlinear Sci., 1 (2016), 99–122. https://doi.org/10.21042/AMNS.2016.1.00009 doi: 10.21042/AMNS.2016.1.00009

|
|
[36]
|
S. Hayat, M. A. Malik, M. Imran, Computing topological indices of honeycomb derived networks, Rom. J. Inf. Sci. Technol., 18 (2015), 144–165. https://doi.org/10.1525/nr.2015.18.3.144 doi: 10.1525/nr.2015.18.3.144

|
|
[37]
|
A. Ahmad, Computation of certain topological properties of para-line graph of honeycomb networks and graphene, Discrete Math. Algorithms Appl., 9 (2017), 1750064. https://doi.org/10.1142/S1793830917500641 doi: 10.1142/S1793830917500641

|
|
[38]
|
A. N. A. Koam, A. Ahmad, M. F. Nadeem, Comparative study of valency-based topological descriptor for hexagon star network, Comput. Syst. Sci. Eng., 36 (2021), 293–306. https://doi.org/10.32604/csse.2021.014896 doi: 10.32604/csse.2021.014896

|
|
[39]
|
A. N. A. Koam, A. Ahmad, A. A. H. Ahmadini, Computation of vertex-edge degree based topological descriptors for hex-derived network, IEEE Access, 9 (2021), 82989–83001. https://doi.org/10.1109/ACCESS.2021.3086451
|
|
[40]
|
A. Ahmad, R. Hasni, K. Elahi, M. A. Asim, Polynomials of degree-based indices for swapped networks modeled by optical transpose interconnection system, IEEE Access, 8 (2020), 214293–214299. https://doi.org/10.1109/ACCESS.2020.3039298
|
|
[41]
|
A. Shabbir, M. F. Nadeem, S. Mukhtar, A. Raza, On edge version of some degree-based topological indices of HAC5c7 [p, q] and VC5c7[p, q] nanotubes, Polycyclic Aromat. Compd., (2020), 1–17. https://doi.org/10.1080/10406638.2020.1753220
|
|
[42]
|
N. Zahra, M. Ibrahim, M. K. Siddiqui, On topological indices for swapped networks modeled by optical transpose interconnection system, IEEE Access, 8 (2020), 200091–200099. https://doi.org/10.1109/ACCESS.2020.3034439
|
|
[43]
|
B. Horoldagva, K. C. Das, T. A. Selenge, On ve-degree and ev-degree of graphs, Discrete Optim., 31 (2019), 1–7. https://doi.org/10.1016/j.disopt.2018.07.002 doi: 10.1016/j.disopt.2018.07.002

|
|
[44]
|
J. Zhang, M. K. Siddiqui, A. Rauf, M. Ishtiaq, On ve-degree and ev-degree based topological properties of single walled titanium dioxide nanotube, J. Cluster Sci., 32 (2020), 821–832. https://doi.org/10.1007/s10876-020-01842-3 doi: 10.1007/s10876-020-01842-3

|
|
[45]
|
F. A. Abolaban, A. Ahmad, M. A. Asim, Computation of vertex-edge degree based topological descriptors for metal trihalides network, IEEE Access, 9 (2021), 65330–65339. https://doi.org/10.1109/ACCESS.2021.3076036
|
|
[46]
|
E. A. Refaee, A. Ahmad, A study of hexagon star network with vertex-edge-based topological descriptors, Complexity, 2021 (2021), 9911308. https://doi.org/10.1155/2021/9911308 doi: 10.1155/2021/9911308

|
|
[47]
|
H. Raza, M. Waheed, M. K. Jamil, M. Azeem, Structures devised by the generalizations of two graph operations and their topological descriptors, Main Group Met. Chem., 45 (2022), 44–56. https://doi.org/10.1515/mgmc-2022-0006 doi: 10.1515/mgmc-2022-0006

|
|
[48]
|
A. N. A. H. Ahmad, A. Ahmad, M. Azeem, Computation of edge- and vertex-degree-based topological indices for tetrahedral sheets of clay minerals, Main Group Met. Chem., 45 (2022), 26–34. https://doi.org/10.1515/mgmc-2022-0007 doi: 10.1515/mgmc-2022-0007

|
|
[49]
|
A. Ahmad, Vertex-degree based eccentric topological descriptors of zero divisor graph of commutative rings, Online J. Anal. Comb., 15 (2020), 1–10.
|
|
[50]
|
A. Ahmad, On the degree based topological indices of benzene ring embedded in p-type-surface in 2d network, Hacettepe J. Math. Stat., 47 (2018), 9–18.
|
|
[51]
|
A. Ahmad, K. Elahi, R. Hasni, M. F. Nadeem, Computing the degree based topological indices of line graph of benzene ring embedded in p-type-surface in 2d network, J. Inf. Optim. Sci., 40 (2019), 1511–1528. https://doi.org/10.1017/S0144686X19000138 doi: 10.1017/S0144686X19000138

|
|
[52]
|
A. N. A. Koam, A. Ahmad, M. A. Asim, M. Azeem, Computation of vertex and edge resolvability of benzenoid tripod structure, J. King Saud Univ. Sci., 34 (2022), 102208. https://doi.org/10.1016/j.jksus.2022.102208 doi: 10.1016/j.jksus.2022.102208

|
|
[53]
|
A. N. A. Koam, A. Ahmad, M. Azeem, A. Khalil, M. F. Nadeem, On adjacency metric dimension of some families of graph, J. Funct. Spaces, 2022 (2022), 6906316. https://doi.org/10.1155/2022/6906316 doi: 10.1155/2022/6906316

|
|
[54]
|
S. Hameed, M. K. Jamil, M. Waheed, M. Azeem, S. Swaray, Two complex graph operations and their exact formulations on topological properties, Complexity, 2022 (2022), 1–15. https://doi.org/10.1155/2022/6331366 doi: 10.1155/2022/6331366

|
|
[55]
|
M. Azeem, M. Imran, M. F. Nadeem, Sharp bounds on partition dimension of hexagonal möbius ladder, J. King Saud Univ. Sci., 34 (2022), 101779. https://doi.org/10.1016/j.jksus.2021.101779 doi: 10.1016/j.jksus.2021.101779

|
|
[56]
|
W. Wu, C. Zhang, W. Lin, Q. Chen, X. Guo, Y. Qian, et al., Quantitative structure-property relationship (QSPR) modeling of drug-loaded polymeric micelles via genetic function approximation, PLOS One, 10 (2015), e0119575. https://doi.org/10.1371/journal.pone.0119575
|
|
[57]
|
X. Zhang, A. Raza, A. Fahad, M. K. Jamil, M. A. Chaudhry, Z. Iqbal, On face index of silicon carbides, Discrete Dyn. Nat. Soc., 2020 (2020), 6048438. https://doi.org/10.1155/2020/6048438 doi: 10.1155/2020/6048438

|
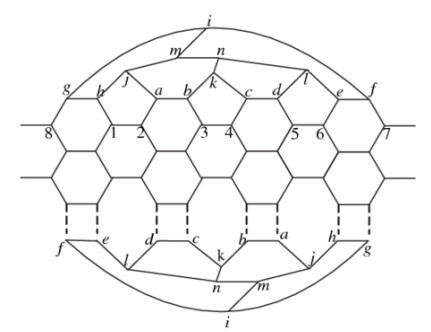









 DownLoad:
DownLoad: