Adaptive decision support model for sustainable transport system using fuzzy AHP and dynamical Dijkstra simulations

1.   Introduction

With the rapid growth of population and urbanization, each year thousands of new roads, subways and many other types of transportation lines are built in the world. How to ensure the new transportation projects could satisfy our requirements in a long term is a worldwide concerned problem. Currently, many countries have reached a consensus that sustainable transportation is the right solution.

Sustainable transportation can be referred to a type of transportation that allows the movement of goods and people by modalities that are sustainable from social, economic, and environmental perspectives ^[1]. Therefore, many factors should be taken in to considerations when a new transportation project is proposed. For example, its impact on the environments, the possible number of passengers, the cost and etc. And all these factors affecting the transportation sustainability should be considered when we make decisions for the project.

Multi-criteria decision making (MCDM) is a widely utilized approach for making rational decisions based on multiple factors and alternatives. It allows for comparison of alternatives to select the one with the highest overall utility. Before the construction of public traffic projects, MCDM is usually applied to select appropriate plans with contradictory objectives and factors of sustainability ^[2]. For example, Zhou ^[3] proposed a coupling evaluation index model of urban spatial structure and public transport system to determine the weight of the index. Madhushree ^[4] applied an improved genetic algorithm to ship routing and scheduling problems, aiming at minimizing the risk and cost to achieve sustainable ship routing in an uncertain environment. Cam and Sezen ^[5] proposed a linear programming model for vehicle routing problem using a customized objective function to minimize the idle time of passenger station vehicles. Aslan and Yazici ^[6] improved the classical A-star algorithm to enable it to simultaneously plan routes for multiple start and end nodes. Surnin ^[7] conducted real-time evaluation of urban traffic conditions using big data analysis based on neural networks. In the route planning platform proposed by Ismael ^[8], the long and short-term memory model was employed to predict the traffic situation, which was in turn put into a route planner to construct an optimal green route. In addition to the above methods, analytic hierarchy process (AHP) is a well-known robust MCDM method to make decision for complex problems ^[9,10]. AHP incorporates the expert knowledge through a structured framework for organizing and analyzing complex and crucial decision problems. It carries out a pairwise comparative analysis between the alternatives and some criteria to achieve a specified goal, and selects the most suitable alternative by ranking the alternatives with respect to each of the criteria. The AHP approach has been successfully applied in many areas, including transport engineering, construction engineering, and etc. ^[11,12,13].

Public participation in decision making is a crucial issue, as the implementations will only be practical if they meet the requirement of citizens' travels. The subjective judgments based on the preference of decision-participants have a significant influence on the results. Therefore, avoiding the uncertainty and vagueness involved in the public evaluators' judgments becomes a crucial objective of decision makers. In fact, most of the decisions that address transportation are made under vague and uncertain situations.

However, the traditional AHP method does not take into account the uncertainty associated with the mapping of human judgment to a number by natural language ^[14]. The ranking of the AHP is somewhat imprecise. Moreover, the dependencies between variables of the AHP usually result in some inconsistencies in the weighting of criteria ^[15]. Thus it is considered to be inadequate when addressing uncertainty and impreciseness.

To solve the decision making problems under uncertainty and improve the decision quality of AHP, it is often integrated with other models ^[16,17], which are capable of dealing with ambiguous issues. For example, the sensitivity and uncertainty analyses are statistically evaluated and integrated with the AHP by using the Monte Carlo simulation (MCS) ^[18]. Frequency Ratio (FR) assessment model and spatial multi-criteria evaluation (SMCE) model are combined with knowledge-driven AHP models to make decisions for a sustainable planning of mitigations ^[19]. To augment the AHP model, both the MCS and FR methods require an inventory dataset, which is usually not available for all decision problems. Duleba ^[10] examined Pareto-optimality on real data pairwise comparison matrices gained from a public transport AHP survey. They proposed that conducting Pareto optimality test on real pairwise comparison data can be successful in a sense that non-Pareto optimal weight vector could be detected in the AHP structure.

Obviously, the fuzzy theory is superior in most of the MCDM applications as it is capable of representing vague measures within mathematical operators to make decisions in the fuzzy domain. Thus, currently, most of the researchers are inclined to integrate fuzzy theories with the hierarchical decision models ^{[20,21,22,23]}, such as FAHP, fuzzy-TOPSIS to overcome the uncertain problems in decision making process. Buran ^[24] applied Fuzzy Analytic Hierarchy Process (F-AHP) to evaluate the business model, and extended the model to incorporate intuitive fuzzy sets (IFS) and spherical fuzzy sets. Wątrobski ^[25] used PROMETHEE Ⅱ and fuzzy TOPSIS to evaluate electric vans for city logistics applications. Ha et al. ^[26] used the AHP method integrated with fuzzy-TOPSIS. Yavuz ^[27] developed a Hierarchical Hesitant Fuzzy Linguistic model to evaluate alternative fuel heavy duty vehicles. Tuzkaya ^[28] developed an approach based on the concept of fuzzy AHP and the method of PROMETHEE Ⅰ and Ⅱ to evaluate the most environmental friendly way of transportation in the Marmara region, Turkey while considering all the concerned stakeholders. Awasthi ^[29] introduced a model based on affinity diagram, AHP and TOPSIS for sustainable city logistics planning under fuzzy uncertainty.

Despite all the efforts to model the uncertainty of a sustainable transportation evaluation problem in AHP methods, most of them were still hard to test applicability of the final decisions. Especially when we take the variable factors into consideration, such as the population size, the variation of transportation cost. Unfortunately, many decision models give decision opinions without evaluation with these variable factors and the test of the project's sustainability. Thus with regard to the sustainable evaluation of new constructed transportation lines, we cannot ensure the decisions made by fuzzy MCDM are compatible with the real situations in the near future.

In this study we concerned about the optimization of decisions for the transportation projects. Obviously, the Dijkstra simulation is suitable to simulate the passengers' transport behaviors and make a response to the decision makers based on the simulation results. In order to support consensual decision making concerning sustainable transport development, a fuzzy AHP decision model is proposed to working with a dynamical Dijkstra simulation model, which is designed to mimic the dynamical behavior of the transportation lines built based on the decision results and test whether the decision is sustainable through the mimic results. The fuzzy AHP and dynamical Dijkstra models are built from the aspect of different stakeholder groups: passengers and the local governance. It is believed that only the requirement of both the users (passengers) and providers (local governance) are simultaneously satisfied, the transportation can be sustainable. Once the result of dynamical Dijkstra demonstrated that the transportation is not sustainable, and then the pairwise comparison matrix of fuzzy AHP along with the important factors(control parameters) of the transportation systems will be automatically adjusted based on the responded results, and then begin a new round of dynamical Dijkstra simulation until the result is sustainable or clearly demonstrated that the sustainable transportation with current plans is impractical even with optimized parameters, and the plans should be changed fundamentally. To the best of our knowledge, the initial work here is the first to apply dynamical Dijkstra algorithm to working with the transportation plans based on fuzzy AHP; consequently, the test result can provide effective means for the validation of the decisions for sustainable transportation.

The main contributions of this paper include:

1) A dynamical Dijkstra simulation model is proposed to simulate the real traffic flows, and test the sustainability of the transportation systems. In the model, the cost (including physical distance, money cost, time cost, mental comfortable, and etc.) of the road connections is dynamically updated according to the change of the passenger flows. Thus, our model is more similar with the real situations than the traditional static Dijkstra algorithm which just concerns static physical distances.

2) The dynamic Dijkstra model is combined with Fuzzy Analytic Hierarchy Process for the first time. The combination ensures that the consensus creation is not only based on the FAHP decision making process but also on the response from the simulated execution of the decisions by dynamical Dijkstra. Such that, the decisions of the FAHP is tested by the dynamical Dijkstra to make a response, and then decision can be fine-tuned until consensus are created among different stakeholder participants.

3) Empirical analysis of the proposed model is carried out, the results demonstrated that the our model not only considers different criteria to realize the integrated decision of traffic planning, but also continuously optimizes the planning to make traffic more sustainable

The rest of this paper is organized as follows: Section 2 introduces the overall methodology. Sections 3 and 4 respectively discusses the fuzzy AHP and Dynamic Dijkstra simulations applied to sustainable transportation. In Section 5, the proposed methodology is empirically analyzed. Finally, conclusions and future scope are presented in Section 6.

2.   Overall methodology

In our model, there are two directly involved groups including: regular passengers (users) and constructors (providers). The two groups' requirements must be simultaneously satisfied; otherwise the transport project definitely cannot be sustainable. For example, if a newly built road is too congestion, or charge too much tolls, then nearly no passengers will travel on the road; on the contrary, if the revenues of the road cannot afford the cost of the constructions and maintaining, then the project will be also unstainable. To simplify the discussion, we just take passengers and constructors into our model, but more roles can be incorporated to make a comprehensive discussion, such as the environment protester, non-passengers, and even the laws and competition lines.

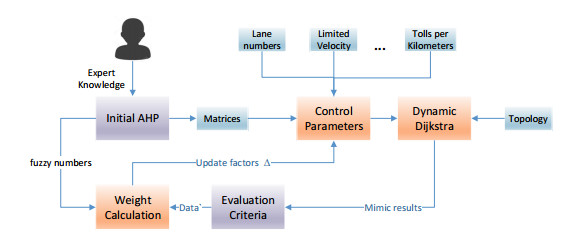
We incorporated the fuzzy AHP as a central part of MCDA and used this approach along with dynamical Dijkstra simulations. As shown in Figure 1 these two parts constitute a response-and-control system. The overall methodology of this study is as follows: firstly, FAHP is built based on the linguistic variables of experts and obtaining the final fuzzy weight scores for all groups, and then the weight of different criteria of FAHP is obtained based on the pairwise comparison matrices. The road control parameters of transportations are estimated based on the weights. After that, the control parameters are input into a dynamical Dijkstra model, which simulated the planned transportation system, to mimic the running of the system. Finally, after the simulations, the simulated results are evaluated by a group of criteria and the FAHP matrix along with the control parameters are adjusted according to the evaluation results. The adjustable parameters include lane numbers, limited velocity, tolls and etc. After the updating, a new round of response-and-control is issued until the requirements of each group are satisfied.

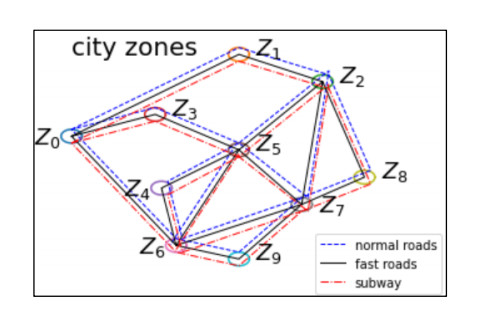
This study aims to design a new decision model for sustainable transport supply project based on the response-and-control between FAHP's decisions and dynamical Dijkstra's simulations. For this, a case study in Figure 2 is chosen. For easy of discussion, a virtual city with 10 zones are used throughout this paper. In the figure, Z_i represents the i-th zone of the city and the zones can be connected by three different types of lines: subway, normal road and fast road. Noted that, there can be multiple lines connecting any pair of zones or can be no lines at all. The service quality and the revenues are two important criteria to test the sustainable of the transportation project. And the criteria is affected by many factors, some of which are adjustable including high speed limit, number of lanes, road quality. In Section 4, these factors are input into a dynamical Dijkstra model as adjustable parameters to generate a response for the updating of themselves and the FAHP's pairwise comparison matrices.

3.   Fuzzy AHP

Fuzzy AHP (FAHP) is a combination of the AHP method with the Fuzzy concept approach. It is a synthetic model that is centered on fuzzy logic and introduce the multi-criteria decision making (MCDM) method to assess the quality of the alternatives. On the one hand, analytic hierarchy process (AHP) is widely used in MCDM as it can solve the unstructured problems and sort out the stakeholders' preferences into structured hierarchies ^[30]. On the other hand, the possibility of uncertainty between factors can be evaluated using fuzzy logic, which deals with uncertainty and imprecise problems more sophisticatedly. Integrating fuzzy theory with AHP provides a synthetic method to eliminate the ambiguity between the border of two criteria and the inconsistency of linguistic and numerable criteria and support decision-makers to give interval judgements ^[31]. Currently, most of the geographic phenomena tend to be described by vague terms, and the fuzzy theory is widely integrated with different MCDA for solving the spatial problems ^[32].

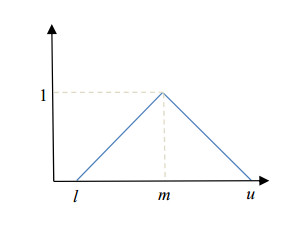
The expert's assessment greatly influences the calculation of the Analytic Hierarchy Process (AHP) method to obtain a priority scale. The assessments are the primary source to weigh the criteria based on their importance regarding the spatial problem ^[21,25]. Originally, the assessments are qualitatively expressed by imprecise linguistic variables. In the paper, Fuzzy-AHP is used to overcome the uncertainty of linguistic data involved in determining preferences for the assessment of transportation criteria. As shown in Table 1, a fuzzy set comprised triangular fuzzy numbers is designed to quantify the linguistic assessment using respective membership function shown in Figure 3.

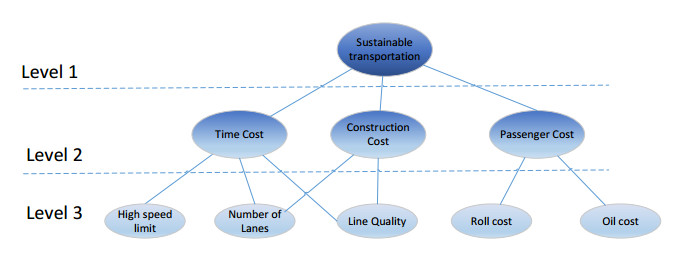
To get a more flexible pairwise comparison value in AHP, the triangular fuzzy number approach is used in FAHP, which firstly creates a hierarchical structure of the alternatives of transportation plans, and then determines the pairwise comparisons matrix of the stakeholders (passengers and constructors) with a triangular fuzzy number scale. As shown in Figure 4, the hierarchical structural model has been integrated and employed for elaborating the public transport situation.

After that, the pairwise comparison matrices of the AHP are reproduced by the fuzzy numbers in Table 1 to deal with the vague linguistic terms of experts. Accordingly, the experts' assessments and pairwise comparisons with regard to the criteria in the hierarchical tree in Figure 4 are expressed by triangular fuzzy numbers. Take the target 'Sustainable Transportation' in level 1 as an example, there are three sub-criteria: 'Time cost', 'Construction Cost' and 'Oil Cost', the experts compare the relative importance of them with regard to the target. Compared with 'Construction Cost', if the 'Time Cost' is supposed to be very important, and it is as same import as 'Passenger Cost', the first line of the comparison matrix will be [(111), (6, 7, 8), (1, 1, 1)], according to the symmetrical characteristic of matrix, the second and third lines of the matrix are [(1/8, 1/7, 1/6), (111), (1/8, 1/7, 1/6)], [(111), (6, 7, 8), (111)]. In the same way, we can get the pairwise comparison matrices of each level with the fuzzy numbers as defined in Eq (1).

where the element in the matrix satisfy the inverse rule that if a_ij = (l_ij, m_ij, u_ij), then a_ij^-1 = (1/l_ij, 1/m_ij, 1/ u_ij) for i, j = 1, 2…n and i ≠ j, l_ij, m_ij and u_ij are the first to third components in the fuzzy number a_ij.

After all elements are defined by the triangular fuzzy numbers, the initial weight of the three criteria 'Time cost', 'Construction Cost' and 'Oil Cost' are calculated by the following Eq (2).

where n is the number of criteria and $\otimes$ is extended operations of two fuzzy triangular numbers: (l₁, m₁, u₁)$\otimes$ (l₂, m₂, u₂) = (l₁ l₂, m₁ m₂, u₁ u₂). a_ij = (l_ij, m_ij, u_ij), is the triangular fuzzy numbers in the pairwise matrices. The summations in Eq (2) are calculated by Eqs (3) and (4).

Let S₁ = (l₁, m₁, u₁), S₂ = (l₂, m₂, u₂), S₃ = (l₃, m₃, u₃) represent the initial fuzzy weight of the three criteria, to get the final weight of the criteria by defuzzification, then the 'degree of possibility' S_i in comparison with S_j was defined as in Eq (5).

Then the probability that a triangular number Si is bigger than the other fuzzy number S₁, S₂, …, S_n is defined in Eq (6).

Equation (7) is utilized to calculate the final weight of criteria in the paired comparative matrices,

Accordingly, the normalized vector is defined in following

And the final weight vector of the criteria in level 2 is calculated through the normalization of Eq (8), as defined in Eq (9)

where W_sum = W (S₁) + W (S₂) +… W (S_n). In the same way, we can calculate the weight of criteria in level 3 with regard to each criteria in the higher level.

Usually, the matrix is tested to be consistent through an extended CR test using interval pairwise comparison matrices. However, even the matrix is consistent and reliable based on the consensus of experts. We cannot afford to ignore the trues that the transport is sustainable only if the construction is economical and can satisfy the passengers' requirements, which permanently changes as time goes by. For example, the number of passengers gradually increases or decreases along with the population size in a city. Therefore, even the matrix is consistent and the weight in Eq (9) is suitable for current situation, but in the near future, the transportation system construction based on the weighting results may be inconsistent with the social economic and populations.

4.   Dynamic Dijkstra simulations for solving preference path problem

The consensus among the stakeholders in different interest groups (users and constructors) is much important for the sustainability of transport systems. However, even consensus is reached between stakeholders at the current time, how it would be possible to obtain more knowledge on the violations or considerations of different interests of the involved groups in the future. Sustainability aspect requires this knowledge in order to avoid the opposition of one involved group or another ^[21]. A variety of methods have been successfully integrated with knowledge-based models for optimization of the model for transportation improvement projects. However, all the decision methods give the final decision based on current input of factors, which may be totally different as the social context changed and the transportation system built based on the decisions is outdated and unsustainable.

In this section, we proposed to combine the FAHP with dynamic the Dijkstra simulation for supporting consensual decision making concerning sustainability in urban transport development. To ensure the Dijkstra simulations can dynamically reflect the passengers' travel situations, we periodically recount the number of passengers and update the distance matrix of Dijkstra according to the newest traffic situations, and finally the time cost, transportation expenses, and revenues are periodically counted to judge the sustainability of the transportation system. It should be noted that the distance is not only evaluated based on the original physical distances, but also based on the time cost, tolls, road quality to reflect the passengers routing selection preference.

4.1.   Basic definition

First of all, we give the basic notations related to dynamical Dijkstra. Let G = (V, E, C) be a simple undirected graph, where V and E are the sets of vertices and edges, respectively, Let e = (u, v) e ∈ E in the graph is assigned with a cost C(u, v), and C is a function from E to the set of non-negative real numbers, it gives the cost of the corresponding edges. Each vertex v represents a city zone in the 'virtual city' in Figure 2 and it contains some auxiliary information, including the predicted shortest distance from v to a given source vertex s and the number of passengers in zone v.

4.2.   Dynamical evaluations

Obviously, the changes of some factors affect the sustainability of transportations, including user number, charge, time cost and etc. The changes increase the uncertainty around the decisions influencing the shift towards sustainable transport due to financial, social, and technical uncertainties. Therefore, taken these variable factors into consideration and further, to examine the plans from the development decision point of view, the decision results from FAHP may be improper for the situations in the further.

As defined in Eq (10), the dynamical updating of the cost matrix Cos is realized by recounting the number of traveler n_ij between zone i and j, the velocity v_ij between the zones, and the line quality QoS_ij.

where L_ij is the original physical distance between zone_i and zone_j, U_cost and U_comf represent the cost and mental comfortable of the passengers per kilometer, which can be estimated according the experience, and ${\varpi }_{i}$ is the corresponding weight, v_ij is the velocity between zone_i and zone_j, which is estimated by Eq (11)

where HsL is the high speed limit, QoS_ij∈(0, 10] is the level of construction quality, n_ij is the number of passengers between zone_i and zone_j, N_ij is the maximum allowed number of passengers on the line connected zone_i and zone_j, and it is estimated by Eq (12)

where IoV is the interval between vehicles, Cov is the capacity of each vehicle.

After that, the shortest path for each passenger's routing is selected, and accordingly n_ij is updating, i, j ∈{1, 2, …, m}, m is the number of zones and then begin a new round of simulations.

4.3.   Dynamic Dijkstra Simulations

The proposed algorithm is a modification of the standard Dijkstra's algorithm, such that the distances in the graph are changeable and any distance variation can immediately affect the following passengers' nearest path selection. The algorithm accommodates the distance change and the number of passengers in each zone to find the shortest path for each passenger.

For the dynamic shortest path problem, we consider that the travel cost Cos changes according to the distance and number of travelers on each edge, so does the velocity v_ij and time cost L_ij/v_ij. Therefore, before the searching process of the shortest path in steps 4 and 5, the cost of each edge is firstly updated. Then, the nearest unvisited zone k to the starting point s is found, accordingly the distance matrix Dis is updated by comparisons between Dis_i and Dis_k + Cos_ki in step 4. As we aim to found the shortest path from s to e, the visited zone on the path should be conserved, so the matrix midpath is utilized to rebuild the path in step5. It should be noted that, sometimes, we may fail to found the path in step 4, that's because the edges connecting the zones from s to e may be congested, which simulated the scenarios that there are too many passengers on the lines resulting the velocity tends to zero.

4.4.   Response control

After all the simulated passengers have reached the destinations, the transportation system's sustainability is judged under a group of criteria, and then feedback the results to FAHP to update its comparison matrices as well as the control factors.

Let λ_m and λ_t represent the expected higher bound of average money and time cost of passengers per kilometer. λ_f and λ_r denote the allowed failed time of searing shortest path by dynamic Dijkstra and revenue of the transportation system per M travelers.

If avgMoncost - λ_m = Δ_m > 0, it means the money cost is too high for the travelers, then the weight of the passenger cost in the matrix of level defined by Eq (1) should be increased, accordingly the other two criteria construction cost and time cost should be decrease to keep consistence of the matrix. The change of the matrix in Eq (1) is defined in Eq (13).

where $\mathrm{A}\left[3\right]\left[i\right] = ({l}_{3i}, {m}_{3i}, {u}_{3i})$ represents the fuzzy comparison important of passenger cost to the other two criteria: time cost and construction cost, and $\mathrm{A}\left[i\right]\left[3\right]$ is the reverse comparison important

In the same way, if avgTimecost > λ_t or TotalMonCost < λ_r the matrix should be adjust by Eqs (14) and (15) respectively.

Accordingly, the matrices of level 2 for the criteria: high speed limit, number of lanes, line quality, rolls and oil cost in Figure 4 are also adjusted in the same manner.

The key control parameters affecting the transportation simulation result of the dynamical Ddijkstra should also be updated along with the adjusting of the matrices, including high speed limit, number of lanes, line quality, roll and oil cost.

Suppose:

1) The weight of time cost, construction cost and passenger cost for 'sustainable transportation' in level 1 of the FAHP in Figure 4 is ω₁, ω₂, ω₃, respectively.

2) The weight of high speed limit, number of lanes, and line quality for time cost in level 2 of the FAHP in Figure 4 is ω₁₁, ω₂₁, ω₃₁, respectively.

3) The weight of number of lanes, line quality for construction cost in level 2 of the FAHP in Figure 4 is ω₁₂, ω₂₂, respectively.

4) The weight of passenger cost, roll cost oil cost for passenger cost in level 2 of the FAHP in Figure 4 is ω₁₃, ω₂₃, respectively.

When avgMoncost-λm = Δ_m > 0, avgTimecost-λ_t = Δ_t > 0 or TotalMonCost-λ_r = Δ_r < 0, which means the money cost, time cost or revenues cannot satisfy the requirement of passengers or constructors, thus the transportation cannot be sustainable, thus not only the comparison matrix, but also the control parameters related to the criteria in level 2 should be updated. For example, when Δ_t > 0, the parameters: high speed limit P₁, number of lanes P₂, line quality P₃ for construction cost in level 2 is adjusted as shown in Eq (16)

$\eta$ represents the learning rate. Similarly, when Δ_r < 0, the parameters: number of lanes P₁, line quality P₂ for construction cost in leve2 is adjusted as shown in Eq (17)

When Δ_m > 0, it means the parameters: roll cost P₁ and oil cost P₂ affecting 'passenger cost' is adjusted as shown in Eq (18).

5.   Empirical analysis

In this section, the proposed algorithm is empirically analyzed. The transportation system connecting the 10 zones shown in Figure 2, and the alternative lines include: normal road, fast road and subway. The parameters affecting the transportation service quality and revenues are shown in Table 2.

Firstly, the empirical fuzzy AHP matrices are given. ST is the matrix for level 1 'sustainable transportation', and the matrices for 'time cost', 'construction cost' and 'passenger cost', TC, CC and PC are shown in the following.

To simulate a scenario that from the beginning of a day, usually 7 o'clock, the number of passengers slowly increases among different zones. Suppose there are M∈[1000,100000] travelers uniformly distributed in the 10 zones in Figure 2, and 80% of them travel to the directly connected neighbor zones, and the others travel to the targets crossing multiple zones, which is similar to the real situation that most of the time, people working and living in a small area, and do not need to travel across the city. As the subway has more capacity of passengers, in the simulations, the number of passengers on subway is 10 times than that on the other two lines. In the first round of simulations, the traffic parameters are constant, which means the factors: lane numbers, high speed limit and toll fees are all the same during the experiment.

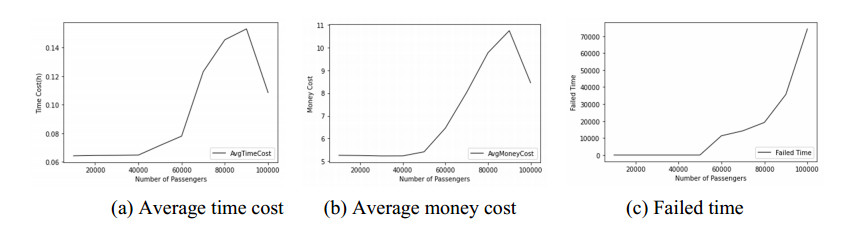
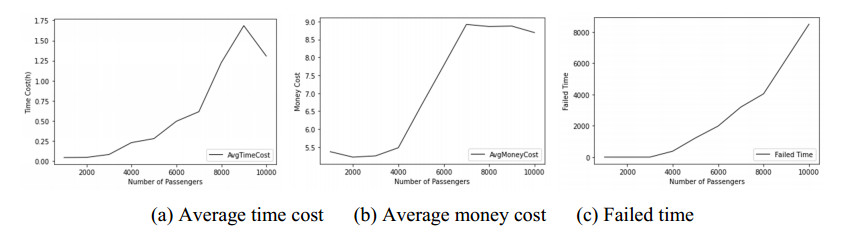
The passengers' average time cost, average fare toll cost and failed number to select a reachable line to the target zones are shown in Figures 5–7. From the figures we can see that, for the three different lines, the travelers' average time cost and failed number basically increases with the number of passengers, and the average money cost firstly fluctuates as the increasing of the passengers, but it increases in a whole. That's because when there are too many passengers, some lines become overwhelmed, and the new arrivers have to select longer path to their destinations, which cost more time and money. As for the average money cost of passengers on the subway, it decreased at the end of the simulations. As shown in Figure 5(c), there are too many users failed to select a reachable routing line to the target when the passenger number surpassed 80,000, and at this moment their money cost is not counted, thus the average cost become less. It can be seen that for fast road and normal road, near half of the passengers failed to reach their destinations when the number of passengers surpassed 4000. Therefore, the lines should incorporate more lanes to improve traffic capability. From the results we can see, if the control factors of traffics are not adjusted according to the real transportations, the system cannot be sustainable, since it failed to provide users fast and relatively cheap transportations. On the other hand, if the toll fees can not compensate the construction cost or maintain fees of the transportation system, it will also fail to be sustainable.

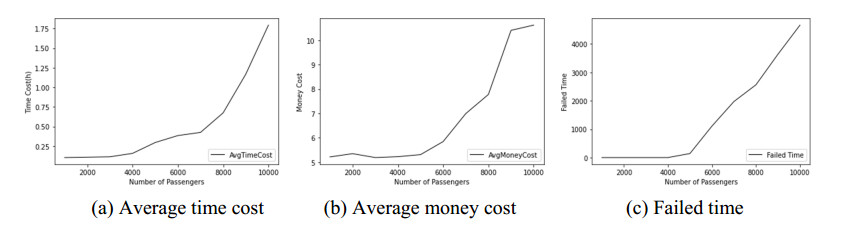
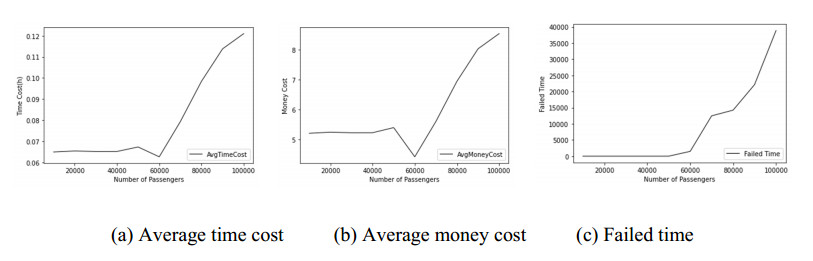
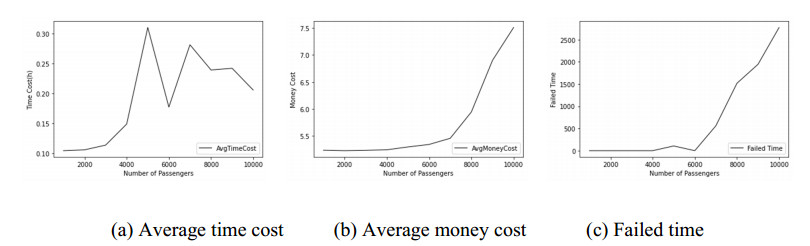
In the second round of simulations, every 10 percent of the progress, the pairwise comparison matrix of the FAHP and the control parameters are iteratively adjusted according to the simulation result of the dynamical Dijkstra. And the results are shown in Figures 8–10.

From the results we can see that, the time cost, money cost and failed time periodically decreased as a result of the updating of the control parameters. The results demonstrated the effectiveness of the combined model of FAHP and dynamical Dijkstra. By the Comparison of the failed number in Figures 5(c) to 10(c), we can see that, obviously in Figures 5(c), 6(c) and 7(c) the failed number of arriving the destinations continually increases with the passengers' number, as the pairwise comparison matrices and control parameters are fixed, and when the population increased, the original optimized transportation system becomes unsuitable for the requirements of travelers and constructors, thus it is not sustainable. On the contrary, from Figures 8–10, we can see that, the cost of passengers and the failed numbers firstly increase at the beginning of a short period, and then they all decreased after the adjustment of the FAHP matrices and parameters. However, we also noted that, although the matrices and parameters are periodically adjusted, as the continually increase of passenger number, the cost and failed times still increase on the whole, that's because the traffic capacity must match with the passenger numbers. Once the transportation burden exceeds its maximum capacity, the system will definitely failed to provide transportation service for passengers.

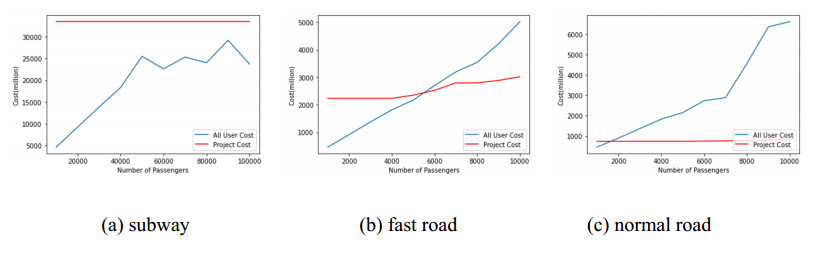
Furthermore, if all of the project revenue (user cost) cannot compensate the project cost, the transportation still unsustainable. As shown in Figure 11(a), the revenues of the subway are always lower than the construction cost. In this situation, the constructor as well as the maintainers has to abandon the transportation system. From the figures we can see that, the revenue of normal roads is easier to surpass the cost than the others, that's because in our simulation scenarios, its construction cost is much lower than the others. As for the subway, although the capacity is higher which means it is capable of providing transportation services for more passengers, however, it is built with enormous cost while the subway toll is the cheapest one. Furthermore, the real number of users is not far more than the other two types of lines: fast road and normal road, resulting in its revenues cannot compensate the construction cost, and failed to be sustainable for a long time.

To avoid the failures, we need to build cheap lanes, increase the burden (toll, tax, oil cost, etc.) of passengers or raise the bound of the high speed, which may not be applicable, as we also must take the passengers' affordability and security factors into considerations. Therefore, we believe that our research proposed a new way to test the transportation plans whether it is sustainable, especially suitable for the scenarios that the traveler number continuously change. Furthermore, to ensure the sustainable, we need to carefully taken all the factors, including both the current and future number of citizens, roll and time cost of passengers, revenues of constructors, environment protections and etc., into considerations to make sure both the users and constructions can get consensus for a long period.

6.   Conclusions

In modern transportation plan decision, it is important to satisfy the involved groups' requirement to ensure a sustainable result. In case this criterion is violated due to the increase of population size, oil cost or other impact factors, the development and sustainable will be less than expected due to the resistance of one group or another. In this paper, we proposed a combined decision make model for the transportation project plan, on the one hand, it takes the experts' knowledge into the decision process through a fuzzy Multi-Criteria Decision-Making model FAHP, which is more suitable for the anthropological mode of human thinking directly based on the linguistic variables using fuzzy numbers. On the other hand, the decision matrices along with the transportation control parameters are put into a dynamical Dijkstra simulation model to test the plans and response to FAHP to realize iteratively adjustment of the plans. Different scenarios are designed to test the proposed model, and the results demonstrated that our model not only take different criteria into consideration to realize a fusion decision for the transportation plan, but it also continually optimize the plan to make the transportation more sustainable. To the best of our known, our model is the first one to take the variation of impacting factors into the MCDM decision process to ensure a sustainable plan for the transportation lines.

Overall, with the development of new urbanization, green, intelligent and sharing are becoming the focus and breakthrough of sustainable transportation development. In the future, more criteria of FAHP, which impacting the environment, road constructions, operations, matins will be taken into considerations, and some more sophisticated methodology can be applied to iteratively test the decision plans.

Acknowledgments

This work was supported by the National Key Research and Development Program of China (020YFB1805405, 2019QY0800), the Natural Science Foundation of China (61872255, U19A2068), Sichuan Science and Technology Program under Grant 2022YFG0171, Fundamental Research Funds for the Central Universities 2021SCU12136.

Conflict of interest

The authors declare there is no conflict of interest.