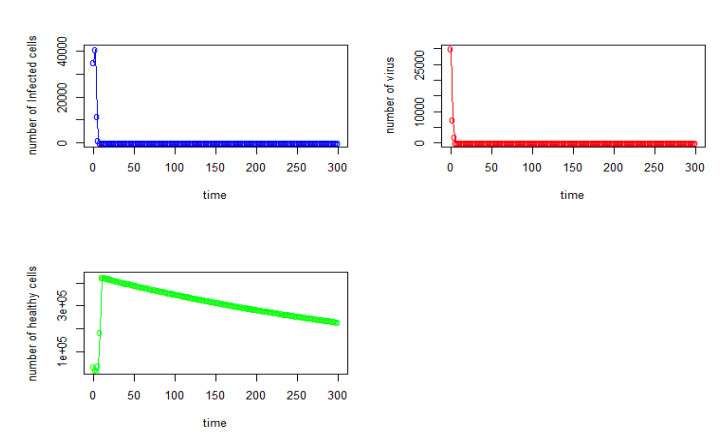
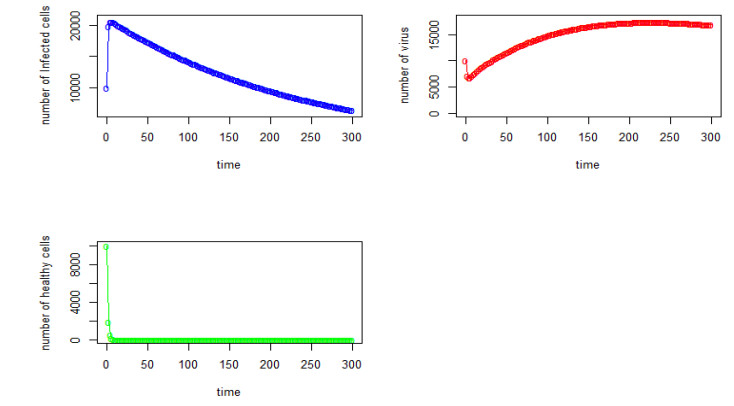
|
[1]
|
Available online: https://patch.com/new-jersey/oceancity/nj-coronavirus-update-gov-murphy-considers-curfew-31-new-cases (accessed on16 March 2020).
|
|
[2]
|
Available online: https://www.osha.gov/SLTC/covid-19/medicalinformation.html (accessed on.17 March 2020).
|
|
[3]
|
Centers for Disease Control and Prevention, https://www.cdc.gov/coronavirus/2019-ncov/prevent-getting-sick/social-distancing.html (accessed on 8 April 2020)
|
|
[4]
|
H. Pham, On estimating the number of deaths related to Covid-19, Mathematics, 8 (2020), 655. https://doi.org/10.3390/math8050655 doi: 10.3390/math8050655

|
|
[5]
|
Worldometers, 2022 (accessed on April 1, 2022).
|
|
[6]
|
https://www.worldometers.info/coronavirus/?utm_campaign = homeAdvegas1?#countries
|
|
[7]
|
World Health Organization, https://covid19.who.int/ (accessed on April 1, 2022).
|
|
[8]
|
H. Pham, Estimating the COVID-19 death toll by considering the time-dependent effects of various pandemic restrictions, Mathematics, 8 (2020), 1628. https://doi.org/10.3390/math8091628 doi: 10.3390/math8091628

|
|
[9]
|
A. W. H. Chin, J. T. S. Chu, M. R. A. Perera, K. P. Y. Hui, H. L. Yen, M. C. W. Chan, et al., Stability of SARS-CoV-2 in different environmental conditions, Lancet Microbe, 1 (2020), 1. https://doi.org/10.1016/S2666-5247(20)30003-3 doi: 10.1016/S2666-5247(20)30003-3

|
|
[10]
|
E. Dong, H. Du, L. Gardner, An interactive web-based dashboard to track COVID-19 in real time, Lancet Infect. Dis. 20 (2020), 533-534. https://doi.org/10.1016/S1473-3099(20)30120-1 doi: 10.1016/S1473-3099(20)30120-1

|
|
[11]
|
K. Prem, Y. Liu, T. W. Russell, A. J. Kucharski, R. M. Eggo, N. Davies, et al., The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: A modelling study, Lancet Public Health, 20 (2020), e261-e270. https://doi.org/10.1016/S2468-2667(20)30073-6 doi: 10.1016/S2468-2667(20)30073-6

|
|
[12]
|
G. Sebastiani, M. Massa, E. Riboli, Covid-19 epidemic in Italy: Evolution, projections and impact of government measures, Eur. J. Epidemiol., 35 (2020), 341-345. https://doi.org/10.1007/s10654-020-00631-6 doi: 10.1007/s10654-020-00631-6

|
|
[13]
|
G. Onder, G. Rezza, S. Brusaferro, Case-Fatality rate and characteristics of patients dying in relation to COVID-19 in Italy, JAMA, 20 (2020), 1775-1776. https://doi.org/10.1001/jama.2020.4683 doi: 10.1001/jama.2020.4683

|
|
[14]
|
D. D. Rajgor, M. H. Lee, S. Archuleta, N. Bagdasarian, S. C. Quek, The many estimates of the COVID-19 case fatality rate, Lancet Infect. Dis., 20 (2020), 776-777. https://doi.org/10.1016/S1473-3099(20)30244-9 doi: 10.1016/S1473-3099(20)30244-9

|
|
[15]
|
A. J. Kucharski, T. W. Russell, C. Diamond, Y. Liu, J. Edmunds, S. Funk, et al., Early dynamics of transmission and control of COVID-19: A mathematical modelling study, Lancet Infect. Dis., 20 (2020), 553-558. https://doi.org/10.1016/S1473-3099(20)30144-4 doi: 10.1016/S1473-3099(20)30144-4

|
|
[16]
|
X. Wang, Y. Zhang, F. Fang, Role of vitamin D in COVID-19 infections and deaths, J. Evid. Based Med., 14 (2021), 5-6. https://doi.org/10.1111/jebm.12421 doi: 10.1111/jebm.12421

|
|
[17]
|
E. D. Gorham, C. F. Garland, F. C. Garland, W. B. Grant, S. B. Mohr, M. Lipkin, et al., Optimal vitamin D status for colorectal cancer prevention: A quantitative meta analysis, Am. J. Prev. Med., 32 (2007), 210-216. https://doi.org/10.1016/j.amepre.2006.11.004 doi: 10.1016/j.amepre.2006.11.004

|
|
[18]
|
A. G. Pittas, S. S. Harris, P. C. Stark, H. B. Dawson, The effects of calcium and vitamin D supplementation on blood glucose and markers of inflammation in nondiabetic adults, Diabetes Care, 30 (2007), 980-986. https://doi.org/10.2337/dc06-1994 doi: 10.2337/dc06-1994

|
|
[19]
|
M. Urashima, T. Segawa, M. Okazaki, M. Kurihara, Y. Wada, H. Ida, Randomized trial of vitamin D supplementation to prevent seasonal influenza A in schoolchildren, Am. J. Clin. Nutr., 91 (2010), 1255-1260. https://doi.org/10.3945/ajcn.2009.29094 doi: 10.3945/ajcn.2009.29094

|
|
[20]
|
H. Pham, D. H. Pham, A novel generalized logistic dependent model to predict the presence of breast cancer based on biomarkers, Concurr. Comput. Pract. Exper., 32 (2020), 1. https://doi.org/10.1002/cpe.5467 doi: 10.1002/cpe.5467

|
|
[21]
|
V. Verhoeven, K. Vanpuyenbroeck, M. Lopez-Hartmann, J. Wens, R. Remmen, Walk on the sunny side of life—epidemiology of hypovitaminosis D and mental health in elderly nursing home residents, J. Nutr. Health Aging, 16 (2012), 417-420. https://doi.org/10.1007/s12603-011-0361-5 doi: 10.1007/s12603-011-0361-5

|
|
[22]
|
D. Boersma, O. Demontiero, A. Z. Mohtasham, S. Hassan, H. Suarez, D. Geisinger, et al., Vitamin D status in relation to postural stability in the elderly, J. Nutr. Health Aging, 16 (2012), 270-275. https://doi.org/10.1007/s12603-011-0345-5 doi: 10.1007/s12603-011-0345-5

|
|
[23]
|
N. Charoenngam, M. F. Holick, Immunologic effects of vitamin D on human health and disease, Nutrients, 12 (2020), 2097. https://doi.org/10.3390/nu12072097 doi: 10.3390/nu12072097

|
|
[24]
|
A. R. Martineau, D. A. Jolliffe, L. Greenberg, J. F. Aloia, P. Bergman, G. Dubnov-Raz, Vitamin D supplementation to prevent acute respiratory infections: Individual participant data meta-analysis, Health Technol. Assess., 23 (2019), 23020. https://doi.org/10.3310/hta23020 doi: 10.3310/hta23020

|
|
[25]
|
C. E. Hayes, J. M. Ntambi, Multiple sclerosis: Lipids, Lymphocytes, and vitamin D, Immunometabolism, 10 (2020), 19.
|
|
[26]
|
K. de Haan, A. B. J. Groeneveld, H. R. H. de Geus, M. Egal, A. Struijs, Vitamin D deficiency as a risk factor for infection, sepsisand mortality in the critically ill: Systematic review and meta-analysis, Crit. Care, 66 (2014), 6604. https://doi.org/10.1186/s13054-014-0660-4 doi: 10.1186/s13054-014-0660-4

|
|
[27]
|
A. Braun, D. Chang, K. Mahadevappa, F. K. Gibbons, Y. Liu, E. Giovannucci, Association of low serum 25-hydroxyvitamin D levels and mortality in the critically ill, Crit. Care Med., 39 (2011), 671. https://doi.org/10.1097/CCM.0b013e318206ccdf doi: 10.1097/CCM.0b013e318206ccdf

|
|
[28]
|
P. Autier, M. Boniol, C. Pizot, P. Mullie, Vitamin D status and ill health: A systematic review, Lancet Diabetes Endocrinol., 2 (2014) 76. https://doi.org/10.1016/S2213-8587(13)70165-7 doi: 10.1016/S2213-8587(13)70165-7

|
|
[29]
|
Y. F. Zhou, B. A. Luo, L. L. Qin, The association between vitamin D deficiency and community-acquired pneumonia, Medicine, 98 (2019), e17252. https://doi.org/10.1097/MD.0000000000017252 doi: 10.1097/MD.0000000000017252

|
|
[30]
|
E. C. Goodall, A. C. Granados, K. Luinstra, E. Pullenayegum, B. L. Coleman, M. Loeb, Vitamin D3 and gargling for the prevention of upper respiratory tract infections: A randomized controlled trial, BMC Infect. Dis., 11 (2014), 14273. https://doi.org/10.1186/1471-2334-14-273 doi: 10.1186/1471-2334-14-273

|
|
[31]
|
A. S. Vanherwegen, C. Gysemans, C. Mathieu, Regulation of immune function by vitamin D and its use in diseases of immunity, Endocrinol. Metab. Clin. N. Am., 46 (2017), 1061. https://doi.org/10.1016/j.ecl.2017.07.010 doi: 10.1016/j.ecl.2017.07.010

|
|
[32]
|
C. Greiller, A. Martineau, Modulation of the immune response to respiratory viruses by vitamin D, Nutrients, 7 (2015), 4240-4270. https://doi.org/10.3390/nu7064240 doi: 10.3390/nu7064240

|
|
[33]
|
M. T. Zdrenghea, H. Makrinioti, C. Bagacean, A. Bush, S. L. Johnston, L.A. Stanciu, Vitamin D modulation of innate immune responses to respiratory viral infections, Rev. Med. Virol., 27 (2016), e1909. https://doi.org/10.1002/rmv.1909 doi: 10.1002/rmv.1909

|
|
[34]
|
J. R. Sabetta, P. DePetrillo, R. J. Cipriani, J. Smardin, L. A. Burns, M. L. Landry, Serum 25-hydroxyvitamin d and the incidence of acute viral respiratory tract infections in healthy adults, PLoS One, 5 (2010), e11088. https://doi.org/10.1371/journal.pone.0011088 doi: 10.1371/journal.pone.0011088

|
|
[35]
|
T. R. Ingham, B. Jones, C. A. Camargo, J. Kirman, A. C. Dowell, J. Crane, Association of vitamin D deficiency with severity of acute respiratory infection: A case-control study in New Zealand children, Eur. Respir. J. Eur. Respir. Soc., 44 (2014), 124.
|
|
[36]
|
C. FGunville, P. MMourani, A. AGinde, The role of vitamin D in prevention and treatment of infection, Inflamm. Allergy-DrugTargets, 12 (2013), 239-245. https://doi.org/10.2174/18715281113129990046 doi: 10.2174/18715281113129990046

|
|
[37]
|
A. L. Khoo, L. Chai, H. Koenen, I. Joosten, M. Netea, A. van der Ven, Translating the role of vitamin D3 in infectious diseases, Crit. Rev. Microbiol., 38 (2012), 122. https://doi.org/10.3109/1040841X.2011.622716 doi: 10.3109/1040841X.2011.622716

|
|
[38]
|
R. Taha, S. Abureesh, S. Alghamdi, R. Y. Hassan, M. M. Cheikh, R. A. Bagabir, The relationship between vitamin D and infections including COVID-19: Any hopes? Int. J. Gen. Med., 14 (2021), 3849. https://doi.org/10.2147/IJGM.S317421 doi: 10.2147/IJGM.S317421

|
|
[39]
|
A. R. Martineau, D. A. Jolliffe, R. L. Hooper, L. Greenberg, J. F. Aloia, P. Bergman, Vitamin D supplementation to prevent acute respiratory tract infections: Systematic review and meta-analysis of individual participant data, BMJ, 65 (2017), 6583. https://doi.org/10.1136/bmj.i6583 doi: 10.1136/bmj.i6583

|
|
[40]
|
R. C. A. Dancer, D. Parekh, S. Lax, V. D'Souza, S. Zheng, C. R. Bassford, Vitamin D deficiency contributes directly to the acute respiratory distress syndrome (ARDS), Thorax BMJ, 70 (2015), 617. https://doi.org/10.1136/thoraxjnl-2014-206680 doi: 10.1136/thoraxjnl-2014-206680

|
|
[41]
|
D. R. Thickett, T. Moromizato, A. A. Litonjua, K. Amrein, S. A. Quraishi, K. A. Lee-Sarwar, Association between prehospital vitamin D status and incident acute respiratory failure in critically ill patients: A retrospective cohort study, BMJ Open Respir. Res., 2 (2015), e74. https://doi.org/10.1136/bmjresp-2014-000074 doi: 10.1136/bmjresp-2014-000074

|
|
[42]
|
M. T. Cantorna, B. D. Mahon, D-hormone and the immune system, J. Rheumatol. Suppl., 76 (2005), 11-20.
|
|
[43]
|
A. Antico, M. Tampoia, R. Tozzoli, N. Bizzaro, Can supplementation with vitamin D reduce the risk or modify the course of autoimmune diseases? A systematic review of the literature, Autoimmun. Rev., 12 (2012), 127. https://doi.org/10.1016/j.autrev.2012.07.007 doi: 10.1016/j.autrev.2012.07.007

|
|
[44]
|
T. Michigami, O. Rickets, Consensus on vitamin D deficiency and insufficiency in children, Clin. Calcium., 28 (2018), 1307-1311.
|
|
[45]
|
W. Grant, H. Lahore, S. McDonnell, C. Baggerly, C. French, J. Aliano, Evidence that vitamin D supplementation could reduce risk of influenza and COVID-19 infections and deaths, Nutrients, 12 (2020), 988. https://doi.org/10.3390/nu12040988 doi: 10.3390/nu12040988

|
|
[46]
|
P. A. Danai, S. Sinha, M. Moss, M. J. Haber, G. S. Martin, Seasonal variation in the epidemiology of sepsis, Crit. Care Med., 35 (2007), 410-415. https://doi.org/10.1097/01.CCM.0000253405.17038.43 doi: 10.1097/01.CCM.0000253405.17038.43

|
|
[47]
|
W. B. Grant, Variations in vitamin D production could possibly explain the seasonality of childhood respiratory infections in Hawaii, Pediatr. Infect. Dis. J., 27 (2008), 853. https://doi.org/10.1097/INF.0b013e3181817bc1 doi: 10.1097/INF.0b013e3181817bc1

|
|
[48]
|
J. J. Cannell, R. Vieth, J. Umhau, M. Holick, W. Grant, S. Madronich, et al., Epidemic influenza and vitamin D, Epidemiol. Infect., 134 (2006), 1129-1140. https://doi.org/10.1017/S0950268806007175 doi: 10.1017/S0950268806007175

|
|
[49]
|
V. Dimitrov, C. Barbier, A. Ismailova, Y. Wang, K. Dmowski, R. Salehi-Tabar, et al., Vitamin D-regulated gene expression profiles: species-specificity and cell-specific effects on metabolism and immunity, Endocrinology, 162 (2021), 218. https://doi.org/10.1210/endocr/bqaa218 doi: 10.1210/endocr/bqaa218

|
|
[50]
|
M. Olliver, L. Spelmink, J. Hiew, U. Meyer-Hoffert, B. Henriques-Normark, P. Bergman, Immunomodulatory effects of vitamin D on innate and adaptive immune responses to Streptococcus pneumoniae, J. Infect. Dis., 208 (2013), 1474-1481. https://doi.org/10.1093/infdis/jit355 doi: 10.1093/infdis/jit355

|
|
[51]
|
S. Maggini, E. S. Wintergerst, S. Beveridge, D. H. Hornig, Selected vitamins and trace elements support immune function by strengthening epithelial barriers and cellular and humoral immune responses, Br. J. Nut., 98 (2007), S29-S35. https://doi.org/10.1017/S0007114507832971 doi: 10.1017/S0007114507832971

|
|
[52]
|
W. B. Grant, H. Lahore, S. L. McDonnell, C. A. Baggerly, C. B. French, J. L. Aliano, et al., Evidence that vitamin D supplementation could reduce risk of influenza and COVID-19 infections and deaths, Nutrients, 12 (2020), 988. https://doi.org/10.3390/nu12040988 doi: 10.3390/nu12040988

|
|
[53]
|
S. Piumika, T. J. Dhanushya, K. Neil, J. Ranil, Impact of vitamin D deficiency on COVID-19, Clin. Nutr. ESPEN, 44 (2021), 372-378. https://doi.org/10.1016/j.clnesp.2021.05.011 doi: 10.1016/j.clnesp.2021.05.011

|
|
[54]
|
E. Laird, R. A. Kenny, Vitamin D deficiency in Ireland-implications for COVID-19. Results from the Irish Longitudinal Study on Ageing (TILDA), April 2020. https://doi.org/10.38018/TildaRe.2020-05
|
|
[55]
|
D. P. Richardson, J. A. Lovegrove, Nutritional status of micronutrients as a possible and modifiable risk factor for COVID-19: A UK perspective, Br. J. Nutr., 125 (2021), 678-684. https://doi.org/10.1017/S000711452000330X doi: 10.1017/S000711452000330X

|
|
[56]
|
M. Ebadi, A. J. Montano-Loza, Perspective: Improving vitamin D status in the management of COVID-19, Eur. J. Clin. Nutr., 74 (2020), 856-859. https://doi.org/10.1038/s41430-020-0661-0 doi: 10.1038/s41430-020-0661-0

|
|
[57]
|
W. B. Grant, H. Lahore, S. L. McDonnell, C. A. Baggerly, C. B. French, J. L. Aliano, et al., Evidence that vitamin D supplementation could reduce risk of influenza and COVID-19 infections and deaths, Nutrients, 12 (2020), 988. https://doi.org/10.3390/nu12040988 doi: 10.3390/nu12040988

|
|
[58]
|
D. M. McCartney, D. G. Byrne, Optimisation of vitamin D status for enhanced Immuno-protection against Covid-19, Ir. Med. J., 113 (2020), 58.
|
|
[59]
|
M. Di Rosa, M. Malaguarnera, F. Nicoletti, L. Malaguarnera, Vitamin D3: A helpful immuno-modulator. Immunology, 134 (2020), 123-139. https://doi.org/10.1111/j.1365-2567.2011.03482.x doi: 10.1111/j.1365-2567.2011.03482.x

|
|
[60]
|
J. Zhong, J. Tang, C. Ye, L. Dong, The immunology of COVID-19: Is immune modulation an option for treatment? Lancet Rheumatol., 2 (2020), e428-e436. https://doi.org/10.1016/S2665-9913(20)30120-X doi: 10.1016/S2665-9913(20)30120-X

|
|
[61]
|
A. Panarese, E. Shahini, Covid-19, and vitamin D, Aliment. Pharmacol. Ther., 51 (2020), 993. https://doi.org/10.1111/apt.15752 doi: 10.1111/apt.15752

|
|
[62]
|
G. Grasselli, T. Tonetti, A. Protti, T. Langer, M. Girardis, G. Bellani, et al., Pathophysiology of COVID-19-associated acute respiratory distress syndrome: A multicentre prospective observational study, Lancet Respir. Med., 8 (2020), 1201-1208. https://doi.org/10.1016/S2213-2600(20)30370-2 doi: 10.1016/S2213-2600(20)30370-2

|
|
[63]
|
A. A. Ginde, J. M. Mansbach, C. A. Camargo, Association between serum 25-hydroxyvitamin D level and upper respiratory tract infection in the Third National Health and Nutrition Examination Survey, Arch. Int. Med., 169 (2009), 384-390. https://doi.org/10.1001/archinternmed.2008.560 doi: 10.1001/archinternmed.2008.560

|
|
[64]
|
D. A. Jolliffe, C. J. Griffiths, A. R. Martineau, Vitamin D in the prevention of acute respiratory infection: Systematic review of clinical studies, J. Steroid Biochem. Mol. Biol., 136 (2020), 321-329. https://doi.org/10.1016/j.jsbmb.2012.11.017 doi: 10.1016/j.jsbmb.2012.11.017

|
|
[65]
|
D. Prantas, S. Nandeeta, O. A. Bright, E. H. John, P. Prince, M. Aliu, et al., Effect of vitamin D deficiency on COVID-19 status: A systematic review, COVID, 1 (2021), 97-104. https://doi.org/10.3390/covid1010008 doi: 10.3390/covid1010008

|
|
[66]
|
A. Radujkovic, T. Hippchen, S. Tiwari-Heckler, S. Dreher, M. Boxberger, U. Merle, Vitamin D deficiency and outcome of COVID-19 patients, Nutrients, 12 (2020), 2757. https://doi.org/10.3390/nu12092757 doi: 10.3390/nu12092757

|
|
[67]
|
D. O. Meltzer, T. J. Best, H. Zhang, T. Vokes, V. Arora, J. Solway, Association of vitamin D status and other clinical characteristics with COVID-19 test results, JAMA Netw. Open, 3 (2020), e2019722. https://doi.org/10.1001/jamanetworkopen.2020.19722 doi: 10.1001/jamanetworkopen.2020.19722

|
|
[68]
|
C. E. Hastie, D. F. Mackay, F. Ho, C. A. Celis-Morales, S. V. Katikireddi, C. L. Niedzwiedz, et al., Vitamin D concentrations and COVID-19 infection in UK Biobank, Diabetes Metab. Syndr. Clin. Res. Rev., 14 (2020), 561-565. https://doi.org/10.1016/j.dsx.2020.04.050 doi: 10.1016/j.dsx.2020.04.050

|
|
[69]
|
A. Abrishami, N. Dalili, P. M. Torbati, R. Asgari, M. Arab-Ahmadi, B. Behnam, et al., Possible association of vitamin D status with lung involvement and outcome in patients with COVID-19: A retrospective study, Eur. J. Nutr., 60 (2020), 2249-2257. https://doi.org/10.1007/s00394-020-02411-0 doi: 10.1007/s00394-020-02411-0

|
|
[70]
|
V. Baktash, T. Hosack, N. Patel, S. Shah, P. Kandiah, K. Van den Abbeele, et al., Vitamin D status and outcomes for hospitalised older patients with COVID-19, Postgrad. Med. J., 2 (2020), 1-6. https://doi.org/10.1136/postgradmedj-2020-138712 doi: 10.1136/postgradmedj-2020-138712

|
|
[71]
|
Z. Maghbooli, M. A. Sahraian, M. Ebrahimi, M. Pazoki, M. Kafan, S. Tabriz, et al., Vitamin D sufficiency, a serum 25-hydroxyvitamin D at least 30 ng/mL reduced risk for adverse clinical outcomes in patients with COVID-19 infection, PLoS One, 15 (2020), e0239799. https://doi.org/10.1371/journal.pone.0239799 doi: 10.1371/journal.pone.0239799

|
|
[72]
|
K. Ye, F. Tang, X. Liao, B. A. Shaw, M. Deng, G. Huang, et al., Does serum vitamin D level affect COVID-19 infection and its severity? A case-control study, J. Am. Coll. Nutr., (2020), 1-8. https://doi.org/10.1080/07315724.2020.1826005 doi: 10.1080/07315724.2020.1826005

|
|
[73]
|
P. Bergman, A. C. Norlin, S. Hansen, R. S. Rekha, B. Agerberth, L. Björkhem-Bergman, et al., Vitamin D3 supplementation in patients with frequent respiratory tract infections: A randomised and double-blind intervention study, BMJ Open, 2 (2012), e001663. https://doi.org/10.1136/bmjopen-2012-001663 doi: 10.1136/bmjopen-2012-001663

|
|
[74]
|
A. R. Martineau, N. G. Forouhi, Vitamin D for COVID-19: A case to answer? Lancet Diabetes Endocrinol, 8 (2020), 735-736. https://doi.org/10.1016/S2213-8587(20)30268-0 doi: 10.1016/S2213-8587(20)30268-0

|
|
[75]
|
N. Ali, Role of vitamin D in preventing of COVID-19 infection, progression and severity, J. Infect. Public Health, 13 (2020), 1373-1380. https://doi.org/10.1016/j.jiph.2020.06.021 doi: 10.1016/j.jiph.2020.06.021

|
|
[76]
|
P. C. Ilie, S. Stefanescu, L. Smith, The role of vitamin D in the prevention of coronavirus disease 2019 infection and mortality, Aging Clin. Exp. Res., 32 (2020), 1195-1198. https://doi.org/10.1007/s40520-020-01570-8 doi: 10.1007/s40520-020-01570-8

|
|
[77]
|
S. Walrand, Autumn COVID-19 surge dates in Europe correlated to latitudes, not to temperature-humidity, pointing to vitamin D as contributing factor, Sci. Rep., 11 (2021), 1981. https://doi.org/10.1038/s41598-021-81419-w doi: 10.1038/s41598-021-81419-w

|
|
[78]
|
E. Klingberg, G. Oleröd, J. Konar, M. Petzold, O. Hammarsten, Seasonal variations in serum 25-hydroxy vitamin D levels in a Swedish cohort, Endocrine, 49 (2015), 800-808. https://doi.org/10.1007/s12020-015-0548-3 doi: 10.1007/s12020-015-0548-3

|
|
[79]
|
Institute of Medicine. Dietary reference intakes for calcium and vitamin D. Washington, DC: The National Academies Press, 2011.
|
|
[80]
|
M. F. Holick N. C. Binkley, H. A. Bischoff-Ferrari, C. M. Gordon, D. A. Hanley, R. P. Heaney, et al., Evaluation, treatment, and prevention of vitamin D deficiency: An Endocrine Society Clinical Practice Guideline, J. Clin. Endocrinol. Metab., 96 (2011), 1911-1130. https://doi.org/10.1210/jc.2011-0385 doi: 10.1210/jc.2011-0385

|
|
[81]
|
D. E. Roth, P. Martz, R. Yeo, C. Prosser, M. Bell, A. B. Jones, Are national vitamin D guidelines sufficient to maintain adequate blood levels in children? Can. J. Public Health, 96 (2005), 443-449. https://doi.org/10.1007/BF03405185 doi: 10.1007/BF03405185

|
|
[82]
|
D. Rucker, J. A. Allan, G. H. Fick, D. A. Hanley, Vitamin D insufficiency in a population of healthy western Canadians, CMAJ, 166 (2002), 1517-1524.
|
|
[83]
|
R. Vieth, D. E. Cole, G. A. Hawker, H. M. Trang, L. A. Rubin, Winter time vitamin D insufficiency is common in young Canadian women, and their vitamin D intake does not prevent it, Eur. J. Clin. Nutr., 55 (2001), 1091-1097. https://doi.org/10.1038/sj.ejcn. 1601275 doi: 10.1038/sj.ejcn.1601275

|
|
[84]
|
R. P. Heaney, K. M. Davies, T. C. Chen, M. F. Holick, M. J. Barger-Lux, Human serum 25-hydroxycholecalciferol response to extended oral dosing with cholecalciferol, Am. J. Clin. Nutr., 77 (2003), 204-210. https://doi.org/10.1093/ajcn/77.1.204 doi: 10.1093/ajcn/77.1.204

|
|
[85]
|
J. N. Hathcock, A. Shao, R. Vieth, R. Heaney, Risk assessment for vitamin D, Am. J. Clin. Nutr., 85 (2007), 6-18. https://doi.org/10. 1093/ajcn/85.1.6 doi: 10.1093/ajcn/85.1.6

|
|
[86]
|
M. Pfeifer, B. Begerow, H. W. Minne, C. Abrams, D. Nachtigall, C. Hansen, Effects of a short-term vitamin D and calcium supplementation on body sway and secondary hyperparathyroidism in elderly women, J. Bone Miner Res., 15 (2000), 1113-1118. https://doi.org/10.1359/jbmr.2000.15.6.1113 doi: 10.1359/jbmr.2000.15.6.1113

|
|
[87]
|
Medicine Io, Dietary reference intakes for calcium, phosphorus, magnesium, vitamin D, and fluoride. The Washington, DC: National Academies Press, 1997.
|
|
[88]
|
J. F. Aloia, M. Patel, R. DiMaano, M. Li-Ng, S. A. Talwar, M. Mikhail, et al., Vitamin D intake to attain a desired serum 25- hydroxyvitamin D concentration, Am. J. Clin. Nutr., 87 (2008), 1952-1958. https://doi.org/10.1093/ajcn/87.6.1952 doi: 10.1093/ajcn/87.6.1952

|
|
[89]
|
A. C. Ross, J. E. Manson, S. A. Abrams, J. F. Aloia, P. M. Brannon, S. K. Clinton, et al., The 2011 report on dietary reference intakes for calcium and vitamin D from the institute of medicine: what clinicians need to know, J. Clin. Endocrinol. Metab., 96 (2011), 53-58. https://doi.org/10.1016/j.jada.2011.01.004 doi: 10.1016/j.jada.2011.01.004

|
|
[90]
|
EFSA Panel on Dietetic Products N, Allergies. Scientific opinion on the tolerable upper intake level of vitamin D, EFSA J., 10 (2012), 2813. https://doi.org/10.2903/j.efsa.2012.2813
|
|
[91]
|
D. A. Hanley, A. Cranney, G. Jones, S. J. Whiting, W. D. Leslie, D. E. Cole, et al., Vitamin D in adult health and disease: A review and guideline statement from Osteoporosis Canada, CMAJ, 182 (2010), E610-E618. https://doi.org/10.1503/cmaj.080663 doi: 10.1503/cmaj.080663

|
|
[92]
|
S. M. Pietras, B. K. Obayan, M. H. Cai, M. F. Holick, Vitamin D2 treatment for vitamin D deficiency and insufficiency for up to 6 Years, JAMA Intern. Med., 169 (2009), 1806-1818. https://doi.org/10. 1001/archinternmed.2009.361 doi: 10.1001/archinternmed.2009.361

|
|
[93]
|
S. L. McDonnell, C. A. Baggerly, C. B. French, L. L. Baggerly, C. F. Garland, E. D. Gorham, et al., Breast cancer risk markedly lower with serum 25-hydroxyvitamin D concentrations ≥60 vs < 20 ng/ml (150 vs 50 nmol/L): Pooled analysis of two randomized trials and a prospective cohort, PLoS One, 13 (2018), e0199265. https://doi.org/10.1371/journal.pone.0199265 doi: 10.1371/journal.pone.0199265

|
|
[94]
|
J. M. Madden, L. Murphy, L. Zgaga, K. K. Bennett, De novo vitamin D supplement use post-diagnosis is associated with breast cancer survival, Breast Cancer Res. Treat., 172 (2018), 179-90. https://doi.org/10.1007/s10549-018-4896-6 doi: 10.1007/s10549-018-4896-6

|
|
[95]
|
N. Mirhosseini, H. Vatanparast, S. M. Kimball, The association between Serum 25(OH)D status and blood pressure in participants of a community-based program taking vitamin D supplements, Nutrients, 9 (2017), 1244. https://doi.org/10.3390/nu9111244 doi: 10.3390/nu9111244

|
|
[96]
|
A. Rusińska, P. Płudowski, M. Walczak, M. K. Borszewska-Kornacka, A. Bossowski, D. Chlebna-Sokół, et al., Vitamin D supplementation guidelines for general population and groups at risk of vitamin D deficiency in poland—recommendations of the polish society of pediatric endocrinology and diabetes and the expert panel with participation of national specialist consultants and representatives of scientific societies, Front. Endocrinol., 9 (2018). https://doi.org/10.3389/fendo.2018.00246 doi: 10.3389/fendo.2018.00246

|
|
[97]
|
K. Amrein, M. Scherkl, M. Hoffmann, S. Neuwersch-Sommeregger, M. Köstenberger, A. Tmava Berisha, et al., Vitamin D deficiency 2.0: An update on the current status worldwide, European J. Clin. Nutr., 74 (2020), 1498-1513. https://doi.org/10.1038/s41430-020-0558-y doi: 10.1038/s41430-020-0558-y

|
|
[98]
|
N. Charoenngam, M. F. Holick, Immunologic effects of vitamin d on human health and disease, Nutrients, 12 (2020), 1-28. https://doi.org/10.3390/nu12072097 doi: 10.3390/nu12072097

|
|
[99]
|
M. Chakhtoura, M. Rahme, N. Chamoun, G. El-Hajj Fuleihan, Vitamin D in the Middle East and North Africa, Bone Rep., 8 (2018), 135-146. https://doi.org/10.1016/j.bonr.2018.03.004 doi: 10.1016/j.bonr.2018.03.004

|
|
[100]
|
A. Batieha, Y. Khader, H. Jaddou, D. Hyassat, Z. Batieha, M. Khateeb, et al., Vitamin D status in Jordan: dress style and gender discrepancies, Ann. Nutr. Metab., 58 (2011), 10-18. https://doi.org/10.1159/000323097 doi: 10.1159/000323097

|
|
[101]
|
P. Bergman, A. U. Lindh, L. Björkhem-Bergman, J. D. Lindh, Vitamin D and respiratory tract infections: A systematic review and meta-analysis of randomized controlled trials, PLoS One, 8 (2013), e65835. https://doi.org/10.1371/journal.pone.0065835 doi: 10.1371/journal.pone.0065835

|
|
[102]
|
D. A. Jolliffe, C. A. Camargo, J. D. Sluyter, M. Aglipay, J. F. Aloia, D. Ganmaa, et al., Vitamin D supplementation to prevent acute respiratory infections: A systematic review and meta-analysis of aggregate data from randomised controlled trials, Lancet Diab. Endocrinol., 9 (2021), 276-292. https://doi.org/10.1136/thorax-2020-BTSabstracts.105 doi: 10.1136/thorax-2020-BTSabstracts.105

|
|
[103]
|
J. M. Rhodes, S. Subramanian, E. Laird, G. Griffig, R. A. Kenny, Perspective: Vitamin D deficiency and COVID-19 severity—plausibly linked by latitude, ethnicity, impacts on cytokines, ACE2 and thrombosis, J. Intern. Med., 289 (2021), 97-115. https://doi.org/10.1111/joim.13149 doi: 10.1111/joim.13149

|
|
[104]
|
D. O. Meltzer, T. J. Best, H. Zhang, T. Vokes, V. Arora, J. Solway, Association of vitamin D status and other clinical characteristics with COVID-19 test results, JAMA Netw. Open., 3 (2020), e2019722. https://doi.org/10.1001/jamanetworkopen.2020.19722 doi: 10.1001/jamanetworkopen.2020.19722

|
|
[105]
|
E. Merzon, D. Tworowski, A. Gorohovski, S. Vinker, A. G. Cohen, I. Green, et al., Low plasma 25(OH) vitamin D level is associated with increased risk of COVID-19 infection: An Israeli population-based study, FEBS J., 287 (2020), 3693-3702. https://doi.org/10.1111/febs.15495 doi: 10.1111/febs.15495

|
|
[106]
|
A. Jain, R. Chaurasia, N. S. Sengar, M. Singh, S. Mahor, S, Narain, Analysis of vitamin D level among asymptomatic and critically ill COVID-19 patients and its correlation with inflammatory markers, Sci. Rep., 10 (2020), 20191. https://doi.org/10.1038/s41598-020-77093-z doi: 10.1038/s41598-020-77093-z

|
|
[107]
|
D. De Smet, K. De Smet, P. Herroelen, S. Gryspeerdt, G. A. Martens, Vitamin D deficiency as risk factor for severe COVID-19: A convergence of two pandemics, medRxiv, (2020). https://doi.org/10.1101/2020.05.01.20079376
|
|
[108]
|
R. L. Schleicher, M. R. Sternberg, A. C. Looker, E. A. Yetley, D. A. Lacher, C. T. Sempos, et al., National estimates of serum total 25-Hydroxyvitamin D and metabolite concentrations measured by liquid chromatography-Tandem mass spectrometry in the US population during 2007-2010, J. Nutr., 146 (2016), 1051-1061.https://doi.org/10.3945/jn.115.227728 doi: 10.3945/jn.115.227728

|
|
[109]
|
K. Sarafin, R. Durazo-Arvizu, L. Tian, K. W. Phinney, S. Tai, J. E. Camara, et al., Standardizing 25-hydroxyvitamin D values from the Canadian health measures survey, Am. J. Clin. Nutr., 102 (2015), 1044-1050. https://doi.org/10.3945/ajcn.114.103689 doi: 10.3945/ajcn.114.103689

|
|
[110]
|
K. D. Cashman, K. G. Dowling, Z. Škrabáková, M. Gonzalez-Gross, J. Valtueña, S. De Henauw, et al., Vitamin D deficiency in Europe: pandemic? Am. J. Clin. Nutr., 103 (2016), 1033-1044. https://doi.org/ 10.3945/ajcn.115.120873 doi: 10.3945/ajcn.115.120873

|
|
[111]
|
K. D. Cashman, Vitamin D deficiency: Defining, prevalence, causes, and strategies of addressing, Calcif. Tissue Int., (2019). https://doi.org/10.1007/s00223-019-00559-4 doi: 10.1007/s00223-019-00559-4

|
|
[112]
|
H. Pham, Modeling U.S. mortality and risk-cost optimization on life expectancy, IEEE Trans. Reliabil., 60 (2011), 125-133. https://doi.org/10.1109/TR.2010.2103990 doi: 10.1109/TR.2010.2103990

|
|
[113]
|
A. A. Dror, N. Morozov, A. Daoud, Y. Namir, O. Yakir, Y. Shachar, et al., Pre-infection 25-hydroxyvitamin D3 levels and association with severity of COVID-19 illness, PLoS One, 17 (2022), e0263069. https://doi.org/10.1371/journal.pone.0263069 doi: 10.1371/journal.pone.0263069

|
|
[114]
|
J. Ng, Y. R. Stovezky, D. J. Brenner, S. C. Formenti, I. Shuryak, Development of a model to estimate the association between delay in cancer treatment and local tumor control and risk of metastates, JAMA Netw. Open, 4 (2021), 1-10. https://doi.org/10.1001/jamanetworkopen.2020.34065 doi: 10.1001/jamanetworkopen.2020.34065

|
|
[115]
|
A. Talkington, R. Durrett, Estimating tumor growth rates in vivo, Bull. Math. Biol., 77 (2015), 1934-1954. https://doi.org/10.1007/s11538-015-0110-8 doi: 10.1007/s11538-015-0110-8

|
|
[116]
|
C. Vaghi, A. Rodallec, R. Fanciullino, J. Ciccolini, J. P. Mochel, M. Mastri, Population modeling of tumor growth curves and the reduced Gompertz model improve prediction of the age of experimental tumors, PLoS Comput. Biol., 16 (2020), e1007178. https://doi.org/10.1371/journal.pcbi.1007178 doi: 10.1371/journal.pcbi.1007178

|
|
[117]
|
D. J. Yin, A. R. Moes, J. G. C. van Hasselt, J. J. Swen, H. J. Guchelaar, A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors, CPTPharmacomet. Syst. Pharmacol., 8 (2019), 720-737. https://doi.org/10.1002/psp4.12450 doi: 10.1002/psp4.12450

|
|
[118]
|
T. L. Jackson, H. M. A. Byrne, A mathematical model to study the effects of drug resistance and vasculature on the response of solid tumors to chemotherapy, Math. Biosci., 104 (2000), 17-38. https://doi.org/10.1016/S0025-5564(99)00062-0 doi: 10.1016/S0025-5564(99)00062-0

|
|
[119]
|
C. E. Meacham, S. J. Morrison, Tumour heterogeneity and cancer cell plasticity, Nature, 501 (2013), 328-337. https://doi.org/10.1038/nature12624 doi: 10.1038/nature12624

|
|
[120]
|
X. Sun, J. Bao, Y. Z. Shao, Mathematical modeling of therapy-induced cancer drug resistance: Connecting cancer mechanisms to population survival rates, Sci. Rep., 6 (2016) 22498. https://doi.org/10.1038/srep22498 doi: 10.1038/srep22498

|
|
[121]
|
K. Taniguchi, J. Okami, K. Kodama, M. Higashiyama, K. Kato, Intratumor heterogeneity of epidermal growth factor receptor mutations in lung cancer and its correlation to the response to gefitinib, Cancer Sci., 99 (2008), 929-935. https://doi.org/10.1111/j.1349-7006.2008.00782.x doi: 10.1111/j.1349-7006.2008.00782.x

|
|
[122]
|
E. R. Lestari, H. Arifah, Dynamics of a mathematical model of cancer cells with chemotherapy, J. Phys. Conf. Ser., 1320 (2019), 1-8. https://doi.org/10.1088/1742-6596/1320/1/012026 doi: 10.1088/1742-6596/1320/1/012026

|
|
[123]
|
H. Pham, A dynamic model of multiple time-delay interactions between the virus-infected cells and body's immune system with autoimmune diseases, Axioms, 10 (2021), 216. https://doi.org/10.3390/axioms10030216 doi: 10.3390/axioms10030216

|
|
[124]
|
H. Pham, Mathematical modeling the time-delay interactions between tumor viruses and the immune system with the effects of chemotherapy and autoimmune Diseases, Mathematics, 10 (2022), 756. https://doi.org/10.3390/math10050756 doi: 10.3390/math10050756

|









 DownLoad:
DownLoad: