Search Advanced

Mathematical Biosciences and Engineering

2020, Volume 17, Issue 5: 5414-5431. doi: 10.3934/mbe.2020292
Previous Article Next Article
Review Special Issues

Review of conformal cooling system design and additive manufacturing for injection molds

  • 1.
    Center for Advanced Jet Engineering Technologies (CaJET), School of Mechanical Engineering, Shandong University, Jinan 250061, China
  • 2.
    Key Laboratory of High-efficiency and Clean Mechanical Manufacture at Shandong University, Ministry of Education, Jinan 250061, China
  • 3.
    National Demonstration Center for Experimental Mechanical Engineering Education at Shandong University, Jinan 250061, China
  • 4.
    School of Civil Engineering and Architecture, University of Jinan, Jinan 250022, China
  • Received: 27 May 2020 Accepted: 16 July 2020 Published: 12 August 2020

  • This paper points out the significance of cooling in injection molding and briefly reviews the development of cooling systems. The focus of this survey is on the physical model, development, and optimization of conformal cooling systems which have curved cooling circuits following the shape of mold cavity. Compared with traditional cooling systems, conformal cooling can greatly reduce the warpage defect and shorten the cooling cycle time. The computational design methods and additive manufacturing techniques that prompt the development of conformal cooling are deeply investigated. At the end of this survey, the future perspectives for conformal cooling design and manufacturing are discussed.

    Citation: Zhihao Wei, Jiacai Wu, Nan Shi, Lei Li. Review of conformal cooling system design and additive manufacturing for injection molds[J]. Mathematical Biosciences and Engineering, 2020, 17(5): 5414-5431. doi: 10.3934/mbe.2020292

    Related Papers:

  • This paper points out the significance of cooling in injection molding and briefly reviews the development of cooling systems. The focus of this survey is on the physical model, development, and optimization of conformal cooling systems which have curved cooling circuits following the shape of mold cavity. Compared with traditional cooling systems, conformal cooling can greatly reduce the warpage defect and shorten the cooling cycle time. The computational design methods and additive manufacturing techniques that prompt the development of conformal cooling are deeply investigated. At the end of this survey, the future perspectives for conformal cooling design and manufacturing are discussed.


    加载中


    [1] P. Wang, B. Zou, S. Ding, C. Huang, Z. Shi, Y. Ma, et al., Preparation of short CF/GF reinforced PEEK composite filaments and their comprehensive properties evaluation for FDM-3D printing, Compos. Part B Eng., 198 (2020), 108175.
    [2] P. Wang, B. Zou, H. C. Xiao, S. Ding, C. Huang, Effects of printing parameters of fused deposition modeling on mechanical properties, surface quality, and microstructure of PEEK, J. Mater. Process. Technol., 271 (2019), 62-74.
    [3] J. K. Liu, Y. S. Ma, J. Y. Fu, K. Duke, A novel CACD/CAD/CAE integrated design framework for fiber-reinforced plastic parts, Adv. Eng. Software, 87 (2015), 13-29.
    [4] E. Vojnova, The benefits of a conforming cooling systems the molds in injection moulding process, Procedia Eng., 149 (2016), 535-543.
    [5] Y. Wang, K. M. Yu, C. C. L. Wang, Y. Zhang, Automatic design of conformal cooling circuits for rapid tooling, Comput. Aided Des., 43 (2011), 1001-1010.
    [6] L. Li, Y. F. Zheng, M. L. Yang, J. Leng, Z. Cheng, Y. Xie, et al., A survey of feature modeling methods: Historical evolution and new development, Rob. Comput. Integr. Manuf., 61 (2020), 101851.
    [7] M. Bendsøe, O. Sigmund, Topology Optimization: Theory, Method and Applications, Berllin, Heidelberg, Springer, 2003.
    [8] J. K. Liu, A. T. Gaynor, S. K. Chen, Z. Kang, K. Suresh, A. Takezawa, et al., Current and future trends in topology optimization for additive manufacturing, Struct. Multidiscip. Optim., 57 (2018), 2457-2483.
    [9] Z. Li, X. Y. Wang, J. F. Gu, S. Ruan, C. Shen, Y. Lyu, et al., Topology Optimization for the Design of Conformal Cooling System in Thin-wall Injection Molding Based on BEM, Int. J. Adv. Manuf. Technol., 94 (2018), 1041-1059.
    [10] T. Wu, A. Tovar, Design for Additive Manufacturing of Conformal Cooling Channels Using Thermal-Fluid Topology Optimization and Application in Injection Molds, Proceedings of the Asme International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2018.
    [11] L. Meng, W. H. Zhang, D. L. Quan, G. Shi, L. Tang, Y. Hou, From Topology Optimization Design to Additive Manufacturing: Today's Success and Tomorrow's Roadmap, Arch. Comput. Methods Eng., 27 (2020), 805-830.
    [12] J. Q. Huang, Q. Chen, H. Jiang, B. Zou, L. Li, J. Liu, et al., A survey of design methods for material extrusion polymer 3D printing, Virtual Phys. Prototyping, 15 (2020), 148-162.
    [13] J. K. Liu, Y. S. Ma, A survey of manufacturing oriented topology optimization methods, Adv. Eng. Software, 100 (2016), 161-175.
    [14] D. Brackett, I. Ashcroft, R. Hague, Topology optimization for additive manufacturing, 22nd Annual International Solid Freeform Fabrication Symposium-An Additive Manufacturing Conference, 2011.
    [15] J. Y. Fu, Y. S. Ma, A method to predict early-ejected plastic part air-cooling behavior towards quality mold design and less molding cycle time, Rob. Comput. Integr. Manuf., 56 (2019), 66-74.
    [16] J. Y. Fu, Y. S. Ma, Computer-aided engineering analysis for early-ejected plastic part dimension prediction and quality assurance, Int. J. Adv. Manuf. Technol., 98 (2018), 2389-2399.
    [17] H. M. Zhou, D. Q. Li, Mold cooling simulation of the pressing process in TV panel production, Simul. Modell. Pract. Theory, 13 (2005), 273-285.
    [18] S. J. Park, T. H. Kwon, Optimal cooling system design for the injection molding process, Polym. Eng. Sci., 38 (1998), 1450-1462.
    [19] E. Sachs, E. Wylonis, S. Allen, M. Cima, H. Guo, Production of injection molding tooling with conformal cooling channels using the three dimensional printing process, Polym. Eng. Sci., 40 (2000), 1232-1247.
    [20] A. S. Sachs, S. Allen, H. Guo, J. Banos, M. Cima, J. Serdy, et al., Progress on tooling by 3D printing; conformal cooling, dimensional control, surface finish and hardness, Proceedings of the Eighth Annual Solid Freeform Fabrication Symposium, 1997.
    [21] G. Venkatesh, Y. R. Kumar, G. Raghavendra, Comparison of Straight Line to Conformal Cooling Channel in Injection Molding, Mater. Today Proc., 4 (2017), 1167-1173.
    [22] C. T. Lu, G. S. Chen, S. C. Tseng, Effectiveness of Conformal Cooling for a V-Shaped Plate and its Influence on Warpage: 2017 International Conference on Information, Communication and Engineering (ICICE), 2017.
    [23] M. Mazur, P. Brincat, M. Leary, M. Brandt, Numerical and experimental evaluation of a conformally cooled H13 steel injection mould manufactured with selective laser melting, Int. J. Adv. Manuf. Technol., 93 (2017), 881-900.
    [24] M. Khan, S. Afaq, N. Khan, S. Ahmad, Cycle Time Reduction in Injection Molding Process by Selection of Robust Cooling Channel Design, ISRN Mech. Eng., 2014 (2014), 968484.
    [25] A. B. M. Saifullah, S. H. Masood, I. Sbarski, New Cooling Channel Design for Injection Moulding, World Congress on Engineering, 2009.
    [26] Z. Shayfull, S. Sharif, A. M. Zain, R. M. Saad, M. A. Fairuz, Milled Groove Square Shape Conformal Cooling Channels in Injection Molding Process, Mater. Manuf. Processes, 28 (2013), 884-891.
    [27] S. Z. A. Rahim, S. Sharif, A. M. Zain, S. M. Nasir, R. M. Saad, Improving the Quality and Productivity of Molded Parts with a New Design of Conformal Cooling Channels for the Injection Molding Process, Adv. Polym. Technol., 35 (2016).
    [28] M. Kamarudin, M. S. Wahab, M. Batcha, Z. Shayfull, A. A. Raus, A. Ahmed, Cycle time improvement for plastic injection moulding process by sub groove modification in conformal cooling channel, AIP Conference Proceedings, 1885 (2017), 020176.
    [29] A. J. Norwood, P. M. Dickens, R. C. Soar, R. Harris, G. Gibbons, R. Hansell, Analysis of cooling channels performance, Int. J. Comput. Integr. Manuf., 17 (2004), 669-678.
    [30] Y. Wang, K. M. Yu, C. C. L. Wang, Spiral and conformal cooling in plastic injection molding, Comput. Aided Des., 63 (2015), 1-11.
    [31] H. S. Park, N. H. Pham, Design of Conformal Cooling Channels for an Automotive Part, Int. J. Automot. Technol., 10 (2009), 87-93.
    [32] F. H. Hsu, K. Wang, C. T. Huang, R. Y. Chang, Investigation on conformal cooling system design in injection molding, Adv. Prod. Eng. Manage., 8 (2013), 107-115.
    [33] K. M. Au, K. M. Yu, W. K. Chiu, Visibility-based conformal cooling channel generation for rapid tooling, Comput. Aided Des., 43 (2011), 356-373.
    [34] K. M. Au, K. M. Yu, Variable Distance Adjustment for Conformal Cooling Channel Design in Rapid Tool, J. Manuf. Sci. Eng. Trans. Asme, 136 (2014), 044501.
    [35] A. B. M. Saifullah, S. H. Masood, I. Sbarski, Thermal-structural analysis of bi-metallic conformal cooling for injection moulds, Int. J. Adv. Manuf Technol., 62 (2012), 123-133.
    [36] B. Zink, F. Szabo, I. Hatos, A. Suplicz, N. K. Kovács, H. Hargitai, et al., Enhanced Injection Molding Simulation of Advanced Injection Molds, Polymers, 9 (2017), 77.
    [37] K. Eiamsa-Ard, K. Wannissorn, Conformal bubbler cooling for molds by metal deposition process, Comput. Aided Des., 69 (2015), 126-133.
    [38] K. M. Au, K. M. Yu, A scaffolding architecture for conformal cooling design in rapid plastic injection moulding, Int. J. Adv. Manuf. Technol., 34 (2007), 496-515.
    [39] K. M. Au, K. M. Yu, Modeling of multi-connected porous passageway for mould cooling, Comput. Aided Des., 43 (2011), 989-1000.
    [40] Y. Tang, Z. Gao, Y. Zhao, Design of Conformal Porous Structures for the Cooling System of an Injection Mold Fabricated by Additive Manufacturing Process, J. Mech. Des., 141 (2019), 101702.
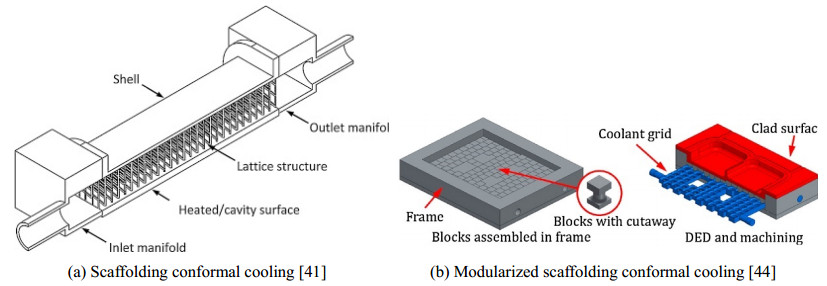
    [41] H. Brooks, K. Brigden, Design of conformal cooling layers with self-supporting lattices for additively manufactured tooling, Addit. Manuf., 11 (2016), 16-22.
    [42] F. Marin, J. R. de Miranda, A. F. de Souza, Study of the design of cooling channels for polymers injection molds, Polym. Eng. Sci., 58 (2018), 552-559.
    [43] L. Cheng, J. K. Liu, X. Liang, A. C. To, Coupling lattice structure topology optimization with designdependent feature evolution for additive manufactured heat conduction design, Comput. Methods Appl. Mech. Eng., 332 (2018), 408-439.
    [44] M. Soshi, J. Ring, C. Young, Y. Oda, M. Mori, Innovative grid molding and cooling using an additive and subtractive hybrid CNC machine tool, Cirp Ann., 66 (2017), 401-404.
    [45] X. H. Ding, K. Yamazaki, Constructal design of cooling channel in heat transfer system by utilizing optimality of branch systems in nature, J. Heat Transfer Trans. Asme, 129 (2007), 245-255.
    [46] J. H. Choi, J. S. Kim, E. S. Han, H. P. Park, B. O. Rhee, Study on an Optimized Configuration of Conformal Cooling Channel by Branching Law, Proceedings of the Asme 12th Biennial Conference on Engineering Systems Design and Analysis, 2014.
    [47] P. Hu, B. He, L. Ying, Numerical investigation on cooling performance of hot stamping tool with various channel designs, Appl. Therm. Eng., 96 (2016), 338-351.
    [48] S. A. Jahan, H. El-Mounayri, Optimal Conformal Cooling Channels in 3D Printed Dies for Plastic Injection Molding, Procedia Manuf., 5 (2016), 888-900.
    [49] S. A. Jahan, T. Wu, Y. Zhang, et al., Thermo-mechanical design optimization of conformal cooling channels using design of experiments approach, Procedia Manuf., 10 (2017), 898-911.
    [50] L. Li, Z. R. Cheng, C. F. Lange, CFD-Based Optimization of Fluid Flow Product Aided by Artificial Intelligence and Design Space Validation, Math. Probl. Eng., 2018 (2018), 8465020.
    [51] B. He, L. Ying, X. D. Li, P. Hu, Optimal design of longitudinal conformal cooling channels in hot stamping tools, Appl. Therm. Eng., 106 (2016), 1176-1189.
    [52] G. Venkatesh, Y. Kumar, Thermal Analysis for Conformal Cooling Channel, Mater. Today Proc., 4 (2017), 2592-2598.
    [53] M. H. M. Hazwan, Z. Shayfull1, S. Sharif, S. M. Nasir, M. M. Rashidi, Warpage optimisation on the moulded part with straight-drilled and MGSS conformal cooling channels using response surface methodology (RSM), AIP Conference Proceedings, 2017.
    [54] M. Hazwan, S. Z. Abd. Rahim, S. Sharif, M. Saad, Warpage Optimisation on the Moulded Part with Conformal Cooling Channels using Response Surface Methodology (RSM) and Glowworm Swarm Optimisation (GSO), AIP Conference Proceedings, 2017.
    [55] S. Z. A. R. M. Hazwan, S. Sharif, M.N. Mat Saad, M. Rashidi, Warpage optimisation on the moulded part with conformal cooling channels using response surface methodology (RSM) and genetic algorithm (GA) optimisation approaches, AIP Conference Proceedings, 2017.
    [56] M. Hazwan, Z. Shayfull1, S. Sharif, S. M. Nasir, M. M. Rashidi, Warpage Optimisation on the Moulded Part using Response Surface Methodology (RSM) and Glowworm Swarm Optimisation (GSO), MATEC Web of Conferences, 2017.
    [57] M. H. M. Hazwan, Z. Shayfull1, S. Sharif, N. Zainal, S. M. Nasir, Optimisation of warpage on plastic injection moulding part with MGSS conformal cooling channels moulds using response surface methodology (RSM): AIP Conference Proceedings. 2017.
    [58] X. P. Dang, H. S. Park, Design of U-shape Milled Groove Conformal Cooling Channels for Plastic Injection Mold, Int. J. Precis. Eng. Manuf., 12 (2011), 73-84.
    [59] S. Kitayama, H. Miyakawa, M. Takano, S. Aiba, Multi-objective optimization of injection molding process parameters for short cycle time and warpage reduction using conformal cooling channel, Int. J. Adv. Manuf. Technol., 88 (2017), 1735-1744.
    [60] J. M. Mercado-Colmenero, C. Martin-Donate, M. Rodriguez-Santiago, F. Moral-Pulido, M. A. Rubio-Paramio, A new conformal cooling lattice design procedure for injection molding applications based on expert algorithms, Int. J. Adv. Manuf. Technol., 102 (2019), 1719-1746.
    [61] J. M. Mercado-Colmenero, M. A. Rubio-Paramio, J. D. Marquez-Sevillano, C. Martin-Donate, A new method for the automated design of cooling systems in injection molds, Comput. Aided Des., 104 (2018), 60-86.
    [62] A. Agazzi, V. Sobotka, R. LeGoff, Y. Jarny, Uniform cooling and part warpage reduction in injection molding thanks to the design of an effective cooling system, Key Eng. Mater., 554-557 (2013), 1611-1618.
    [63] A. Agazzi, V. S. Otka, R. LeGoff, Y. Jarnya, Optimal cooling design in injection moulding process-A new approach based on morphological surfaces, Appl. Therm. Eng., 52 (2013), 170-178.
    [64] X. Wang, P. Zhang, S. Ludwick, E. Belski, A. C. To, Natural Frequency Optimization of 3D Printed Variable-Density Honeycomb Structure via a Homogenization-Based Approach, Addit. Manuf., 20 (2017), 189-198.
    [65] P. Zhang, J. Toman, Y. Yu, E. Biyikli, M. Kirca, M. Chmielus, et al., Efficient Design-Optimization of Variable-Density Hexagonal Cellular Structure by Additive Manufacturing: Theory and Validation, J. Manuf. Sci. Eng., 137 (2015), 021004.
    [66] J. K. Liu, Y. F. Zheng, R. Ahmad, J. Tang, Y. Ma, Minimum length scale constraints in multi-scale topology optimisation for additive manufacturing, Virtual Phys. Prototyping, 14 (2019), 229-241.
    [67] H. C. Yu, J. Q. Huang, B. Zou, W. Shao, J. Liu, Stress-constrained shell-lattice infill structural optimisation for additive manufacturing, Virtual Phys. Prototyping, 15 (2020), 35-48.
    [68] T. Wu, K. Liu, A. Tovar, Multiphase topology optimization of lattice injection molds, Comput. Struct., 192 (2017), 71-82.
    [69] S. A. Jahan, T. Wu, Y. Zhang, H. EI-Mounayri, A. Tovar, J. Zhang, Implementation of Conformal Cooling & Topology Optimization in 3D Printed Stainless Steel Porous Structure Injection Molds, Procedia Manuf., 5 (2016), 901-915.
    [70] Q. Chen, X. Liang, D. Hayduke, J. Liu, L. Chen, J. Oskin, et al., An inherent strain based multiscale modeling framework for simulating part-scale residual deformation for direct metal laser sintering, Addit. Manuf., 28 (2019), 406-418.
    [71] Q. Chen, J. K. Liu, X. Liang, A. C. To, A level-set based continuous scanning path optimization method for reducing residual stress and deformation in metal additive manufacturing, Comput. Methods Appl. Mech. Eng., 360 (2020), 112719.
    [72] J. M. Flynn, A. Shokrani, S. T. Newman, V. Dhokia, Hybrid additive and subtractive machine tools-Research and industrial developments, Int. J. Mach. Tools Manuf., 101 (2016), 79-101.
    [73] J. Liu, Y. Zheng, Y. Ma, A. Qureshi, R. Ahmad, A Topology Optimization Method for Hybrid Subtractive-Additive Remanufacturing, Int. J. Precis. Eng. Manuf., 55 (2019), 1281-1299.
    [74] Y. Fu, B. Rolfe, L. N. S. Chiu, Y. Wang, X. Huang, K. Ghabraie, Design and experimental validation of self-supporting topologies for additive manufacturing, Virtual Phys. Prototyping, 14 (2019), 382-294.
    [75] J. Liu, H. Yu, Self-Support Topology Optimization With Horizontal Overhangs for Additive Manufacturing, J. Manuf. Sci. Eng., 142 (2020), 1-19.
    [76] T. Johnson, A. Gaynor, Three-dimensional Projection-based Topology Optimization for Prescribed-angle Self-Supporting Additively Manufactured Structures, Addit. Manuf., 24 (2018), 667-686.
    [77] J. K. Liu, A. C. To, Deposition path planning-integrated structural topology optimization for 3D additive manufacturing subject to self-support constraint, Comput. Aided Des., 91 (2017), 27-45.
    [78] A. M. Mirzendehdel, M. Behandish, S. Nelaturi, Topology optimization with accessibility constraint for multi-axis machining, Comput. Aided Des., 122 (2020), 102825.
    [79] L. Chen, T. Y. Lau, K. Tang, Manufacturability analysis and process planning for additive and subtractive hybrid manufacturing of Quasi-rotational parts with columnar features, Comput. Aided Des., 118 (2020), 102759.
    [80] J. K. Liu, H. C. Yu, Y. S. Ma, Minimum void length scale control in level set topology optimization subject to machining radii, Comput. Aided Des., 81 (2016), 70-80.
    [81] N. Morris, A. Butscher, F. Iorio, A subtractive manufacturing constraint for level set topology optimization, Struct. Multidiscip. Optim., 61 (2020), 1573-1588.
    [82] M. Langelaar, Topology optimization for multi-axis machining, Comput. Methods Appl. Mech. Eng., 351 (2019), 226-252.
    [83] J. K. Liu, Y. S. Ma, 3D level-set topology optimization: A machining feature-based approach, Struct. Multidiscip. Optim., 52 (2015), 563-582.
    [84] J. V. Carstensen, J. K. Guest, Projection-based two-phase minimum and maximum length scale control in topology optimization, Struct. Multidiscip. Optim., 58 (2018), 1845-1860.
    [85] J. K. Liu, Piecewise length scale control for topology optimization with an irregular design domain, Comput. Methods Appl. Mech. Eng., 351 (2019), 744-765.
    [86] F. W. Wang, B. S. Lazarov, O. Sigmund, On projection methods, convergence and robust formulations in topology optimization, Struct. Multidiscip. Optim., 43 (2011), 767-784.
    [87] Y. F. Zheng, J. K. Liu, R. Ahmad, A cost-driven process planning method for hybrid additive-subtractive remanufacturing, J. Manuf. Syst., 55 (2020), 248-263.
    [88] Z. C. Zhu, V. Dhokia, A. Nassehi, S. T. Newman, Investigation of part distortions as a result of hybrid manufacturing, Rob. Comput. Integr. Manuf., 37 (2016), 23-32.
    [89] J. K. Liu, Q. Chen, X. Liang, A. C. To, Manufacturing cost constrained topology optimization for additive manufacturing, Front. Mech. Eng., 14 (2019), 213-221.
    [90] J. Alexandersen, C. S. Andreasen, A Review of Topology Optimisation for Fluid-Based Problems, Fluids, 5 (2020), 29.
    [91] J. Alexandersen, O. Sigmund, K. E. Meyer, B. S. Lazarov, Design of passive coolers for light-emitting diode lamps using topology optimisation, Int. J. Heat Mass Transfer, 122 (2018), 138-149.
    [92] D. Saltzman, M. Bichnevicius, S. Lynch, T. W. Simpson, E. W. Reutzal, C. Dickman, et al., Design and evaluation of an additively manufactured aircraft heat exchanger, Appl. Therm. Eng., 138 (2018), 254-263.
    [93] H. Li, X. H. Ding, D. L. Jing, M. Xiong, F. Meng, Experimental and numerical investigation of liquid-cooled heat sinks designed by topology optimization, Int. J. Therm. Sci., 146 (2019), 106065.
    [94] S. Zeng, P. S. Lee, Topology optimization of liquid-cooled microchannel heat sinks: An experimental and numerical study, Int. J. Heat Mass Transfer, 142 (2019), 118401.
    [95] J. Haertel, G. Nellis, A Fully Developed Flow Thermofluid Model for Topology Optimization of 3D-Printed Air-Cooled Heat Exchangers, Appl. Therm. Eng., 119 (2017), 10-24.
    [96] J. H. K. Haertel, K. Engelbrecht, B. S. Lazarov, O. Sigmund, Topology optimization of a pseudo 3D thermofluid heat sink model, Int. J. Heat Mass Transfer, 121 (2018), 1073-1088.
    [97] C. B. Dilgen, S. B. Dilgen, D. R. Fuhrman, O. Sigmund, B. S. Lazarov, Topology optimization of turbulent flows, Comput. Methods Appl. Mech. Eng., 331 (2018), 363-393.
    [98] K. T. Gkaragkounis, E. M. Papoutsis-Kiachagias, K. C. Giannakoglou, The continuous adjoint method for shape optimization in Conjugate Heat Transfer problems with turbulent incompressible flows, Appl. Therm. Eng., 140 (2018), 351-362.
    [99] A. Takezawa, X. P. Zhang, M. Kitamura, Optimization of an additively manufactured functionally graded lattice structure with liquid cooling considering structural performances, Int. J. Heat Mass Transfer, 143 (2019), 118564.
  • Reader Comments
  • © 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)
通讯作者: 陈斌, bchen63@163.com
  • 1. 

    沈阳化工大学材料科学与工程学院 沈阳 110142

  1. 本站搜索
  2. 百度学术搜索
  3. 万方数据库搜索
  4. CNKI搜索
Mathematical Biosciences and Engineering
3.9

Metrics

Article views(7211) PDF downloads(690) Cited by(15)

Preview PDF
Download XML
Export Citation
Article outline

Figures and Tables

Figures(6)

Other Articles By Authors

Related pages

Tools

/

DownLoad:  Full-Size Img  PowerPoint
Return
Return

Catalog