Transmission dynamics of acute respiratory diseases in a population structured by age

1.   Introduction

Acute respiratory diseases afflict populations all over the world and represent a serious health burden in many countries ^[1]. Respiratory syncytial virus (RSV) and influenza are particularly important as the main viruses that cause mortality and morbidity worldwide on a yearly basis ^[2,3,4,5,6]. It is estimated that 8.1% of all deaths between 2003 and 2009 were caused by influenza and RSV. 7478 Moreover adults over 60 years old present the highest mortality rate caused by Acute Respiratory Infections (ARIs) ^[7]. Age and other diseases such as diabetes, hypertension and obesity, are factors that compromise the recovery of individuals affected by these class of diseases ^[8].

It is estimated that, worldwide, 5% of elders and 20% of children develop influenza type A or B each year ^[9]. Children are the main disseminators of influenza because of the high contact rate within their age class and 50% of influenza infections in elders are caused by direct contact with children ^[10], implying that social distancing between grandparents and grandchildren can be effective in reducing the risk of this population. In ^[11,12] it is shown that school closures cause a decrease in the transmission of respiratory diseases, and the return of children after vacations increases them. However, the nature of the interaction between different age groups is not completely clear. Quantifying the influence of one age group upon the others, as well as its impact on ARIs transmission dynamics, is an important issue that must be addressed.

There are several studies in the literature related to the estimation of the transmission rate in these diseases ^{[13,14,15,16,17]}. According to ^[18,19] measuring the transmission rate is one of the most important factors necessary to predict the impact caused by public health programs and establish measures to mitigate disease impact on a population.

Age structure is a main determinant of ARIs dynamics. Contact rate, the level of susceptibility as well as immunity, among other aspects, may vary depending upon age. Unfortunately, there is scarce information on the impact that different age groups have on the propagation of ARIs. Usually, different transmission rates are proposed for each group of the population, sometimes derived from a contact matrix that describes the interaction between all groups.

Our work develops an age-structured epidemiological model for the transmission of ARIs. We fit the model to a dataset of ARIs from San Luis Potosí City in Mexico and use a Bayesian inference method to estimate the main parameters in the model in order to understand the role of age in ARIs transmission. The work is organized as follows. Section 2 presents a detailed description and preliminary analysis of the data. Section 3 describes the SEIRS model for the ARIs transmission dynamics, then section 4 explains the Bayesian inference methodology used to estimate the parameters of interest. The results of the analysis are presented in Section 5. Finally, the discussion and conclusion about our findings appears in Section 6.

2.   Data exploration

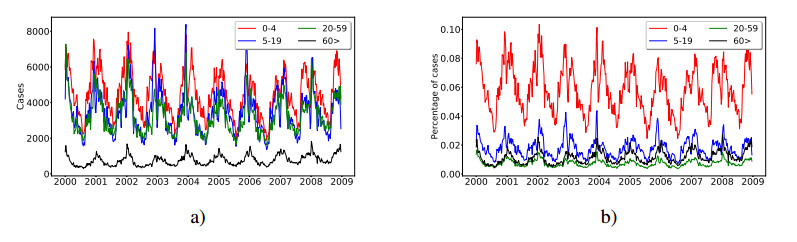
Our data consists of weekly records of confirmed ARIs cases from the General Hospital of the State of San Luis Potosi, Mexico, reported by the State Department of Epidemiology and Health Services. There are reports available from 2000 to 2010 for each of four age groups. Group 1 corresponds to children 0 to 4 years old, Group 2 consists of young children and teenagers from 5 to 19, Group 3 has adults from 20 to 59 and Group 4 includes older adults 60 years old or higher. This ARIs data complies with the standard of the International Classification of Disease, 10th Review of the World Health Organization. Our data includes respiratory infections classified with the ICD-10 codes J00- J06, J20, J2, except J02.0 and J03.0 ^[7]. The number of infected individuals per week is shown in Figure 1 a). We note that the number of cases is similar in the first three age groups. The age class with lower cases corresponds to old adults. However, if we present the data as a percentage of the total population in each age group, it can be seen that children's group (0–4) has considerably more cases while the other three groups are more similar to each other (see Figure 1 b).

Figure 1.  a) Weekly number of new ARIs cases in San Luis Potosí, Mexico, from 2000 to 2010 separated by age. b) Percentage of weekly cases with respect to the total in each age class.

DownLoad: Full-Size Img PowerPoint

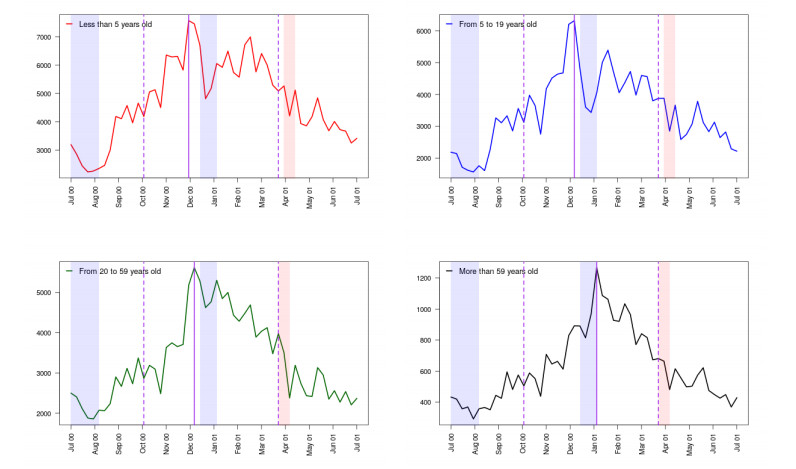
To analyze the data, we partition the time series into eight periods of one year each (52 consecutive weeks) starting from late July (30th week of 2000). Therefore, the periods are July 2000 to July 2001, July 2001 to July 2002, and so on. We do not include in our analysis data from 2008-2010 since the influenza outbreak of 2009 presents atypical characteristics when compared to the previous years. For each period we define a peak week as the calendar week with the highest number of ARIs cases. Then we identify a pre-peak period (epidemics' ascent) to start with the flu season that usually falls in early October (week 40), and a post-peak (epidemics' descent) to end with the winter season usually in late March (week 12) of the following year. Figure 2 shows data from 2000 to 2001 for each age group. The peek of the infection is indicated with a purple continuous line while the purple dashed lines represent the beginning and the end of the outbreak. The orange band indicates the two-week Easter holiday, and the purple band indicates summer and winter vacations, as read from the Mexican Public Education System (PES) calendar.

Figure 2.  Weekly number of ARIs by age group from July 2000 to June 2001. The purple continuous line indicates the peek of the infection. Purple dashed lines indicate the beginning and the end of the outbreak; orange region corresponds to the two-week Easter holidays; and purple region corresponds to the summer and winter vacations, according to the PES calendar. The data is described in the main text.

DownLoad: Full-Size Img PowerPoint

We observe that, for the school age groups (0-4 and 5-19), the first epidemic outbreak begins around the first week of August. By the end of December 2000 approximately, the number of cases decreases, to increase again two or three weeks later. These weeks coincide with the PES winter vacations (last two weeks of 2000 and the first week of 2001). For the group of older people, the peak week is the one farthest from the beginning of the rise of the epidemic compared to the same trend in other age classes.

Our data suggests that the start of vacations diminishes the incidence in school age individuals (age groups from 0 to 19 years old) and that the time when the number of infections begins to rise again is around the return to school. The opposite happens with elders, for which the start of vacations seems to be the time when they are more susceptible to ARIs. This pattern occurs in 75 % of the periods studied.

The spread of viruses and bacteria that cause ARIs is directly related to the number of contacts between individuals. Consequently, as our data suggests, it is natural to expect a decrease in cases of infection during school vacations. Other studies on similar kind of diseases ^[10,12,20] have confirmed what we observed in our data: vacation and social isolation decrease the number of new infections.

2.1.   Before and after the peak week

We calculate here some statistical measures that provide information about the risk of infection of each age group. The Relative Risk (RR) evaluates the change in the proportion of infected individuals in the population before and after the epidemic peak week relative to the total number of reported cases during the year. Following ^[8], the relative risk for age group $k$ is defined by

where the total number of cases occurring before and after the outbreak peak are denoted by $B_k$ and $A_k$, respectively. The RRs values informs about the group that has a higher risk of infection in the pre-peak time. Estimates of relative risk for each group along with their 95% confidence intervals are shown in Table 1. Technical details regarding the calculation of the confidence intervals can be found in ^[21]. We observed that the age group 5-19 tends to have greater risk before the peak while group 20-59 tends to have higher risk after the peak. The pattern is not clear for both the children and the senior adults as the pre-peak and post-peak relative risks change depending on the year.

Table 1.  Relative risk estimation and 95% confidence intervals for each age group.

	2000-2001	2001-2002	2002-2003	2003-2004	2004-2005	2005-2006	2006-2007	2007-2008
5 <	0.87	1.22	1.07	0.95	1.81	1.03	0.98	1.22
	[0.86, 0.87]	[1.21, 1.23]	[1.07, 1.08]	[0.94, 0.96]	[1.79, 1.83]	[1.02, 1.04]	[0.97, 0.99]	[1.21, 1.24]
5–19	1.11	1.07	1.06	1.18	1.25	0.96	1.35	1.17
	[1.10, 1.12]	[1.05, 1.08]	[1.05, 1.07]	[1.17, 1.19]	[1.23, 12.6]	[0.95, 0.97]	[1.33, 1.37]	[1.16, 1.19]
20–59	0.97	0.78	0.80	0.95	0.48	0.77	1.04	0.71
	[0.96, 0.98]	[0.77, 0.78]	[0.79, 0.81]	[0.94, 0.96]	[0.47, 0.49]	[0.76, 0.78]	[1.03, 1.05]	[0.71, 0.72]
≥ 60	1.78	0.76	1.16	0.83	0.50	2.39	0.37	0.78
	[1.73, 1.83]	[0.74, 0.78]	[1.14, 1.19]	[0.81, 0.85]	[0.48, 0.51]	[2.33, 2.45]	[0.36, 0.38]	[0.76, 0.80]

---

 | Show Table

DownLoad: CSV

3.   The population dynamics model

To evaluate the role of age in the transmission of ARIs, we use a multi-group SEIRS deterministic model with age structure. Multi-group models have been introduced in the literature to describe the transmission dynamics of infectious diseases in heterogeneous host populations.

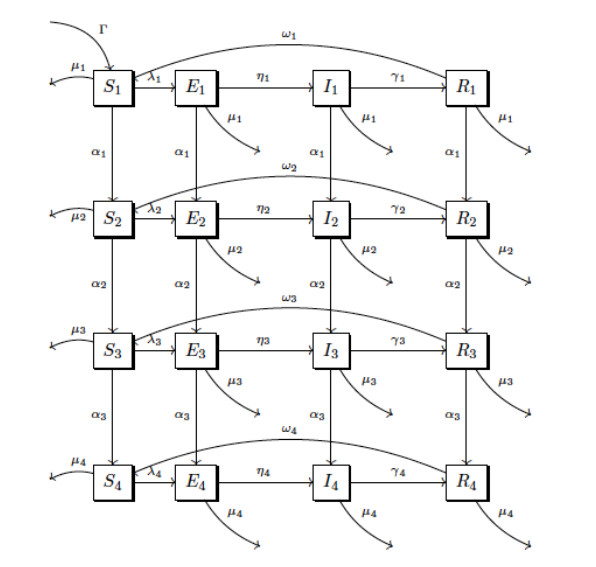
A multigroup model is formulated by dividing the population of size $N(t)$ into $m$ distinct groups. For $1 \leq k\leq m$, the $k$-th group is further partitioned into four compartments: the susceptible, latent, infectious, and recovered, whose numbers of individuals at time $t$ are denoted by $S_k (t), \, E_k(t), \, I_k (t)$ and $R_k (t)$, respectively. Individuals are born susceptible and if they are exposed and infected, then show a latency period before becoming infectious. After their recovery, they remain immune for a period of time.

The influx of individuals into the first susceptible group is given by a constant $\nu_i$, called the fertility rate. The sex-ratio is assumed to be 1:1. Within the $k$-th group, it is assumed that death occurs due to cardiovascular diseases, respiratory infections, etc. The average time in the latency state is given by $1/\eta_k$. We assume that individuals in state $I_k$ recover with a constant rate $\gamma_k$, and once recovered they remain immune (recovered compartment) to the disease during a mean time $1/\omega_k$. Let $1/\alpha_k$ be the average time that one individuals remain in age group $k$. Finally, $\lambda_k(t)$ denotes the force of the infection of group $k$ at time $t$ and it is given as

where $N_j(t) = S_j(t)+E_j(t)+I_j(t)+R_j(t)$. The function

describes seasonality in the contact rate ^[22]. The parameter $\beta_k$ is the infection risk of group $k$, or the probability that one contact made by a group $k$ individual generates a new infection. The $m\times m$-square matrix $C = (c_{jk})$ is the contact matrix and each element $c_{jk}$ represents the average number of contacts between age groups $j$ and $k$.

Our model is the following system of differential equations:

where $\Gamma = \nu_2X_2+\nu_3X_3$ is the recruitment rate with $X_2$, $X_3$ representing the number of fertile women at the beginning of the epidemic in age group 2 and 3, respectively. It is only defined for the first group of susceptible because individuals are assumed to be born healthy. Model (3.3) is represented by the diagram in Figure 3. We make the following assumptions for the parameters in model (3.3):

Figure 3.  Flow diagram for the equations that define the SEIRS model (3.3).

DownLoad: Full-Size Img PowerPoint

(ⅰ) $\Gamma, \mu_k, \gamma_k, \eta_k, \omega_k$ are positive for all $k\in \{1, 2, 3, 4\}$.

(ⅱ) $\alpha_4 = 0$.

(ⅲ) Let $\overline{\beta}_{kj} = \beta_k\cdot c_{kj}$. Here $\overline{\beta}_{kj}$ is nonnegative for all $k, \, j\in \{1, 2, ..., m\}$ and the $m\times m$-square matrix $(\overline{\beta}_{kj}), \, \, 1\leq k, j\leq m$ is irreducible.

(ⅳ) $\nu_1 = \nu_4 = 0$ since the fertile period of a woman is considered from 15 to 49 years old.

We now would like to see whether our model is able to describe our data. In order to do so, it is necessary to provide adequate values for all the parameters involved. We use a Bayesian inference approach to estimate the values of relevant parameters as described in Section 2.

4.   Bayesian inference

From the mathematical point of view, estimating the parameters of a system of differential equations is considered a non-linear inverse problem. The standard way to solve this class of problems is to use an optimization approach. The idea is to find a set of parameters that provide a solution as closer as possible to the data. A better alternative, from our perspective, is to see it as an inference problem. We use a Bayesian approach where the solution of the inverse problem is the analysis of the posterior distribution of the parameters of interest. The Bayesian framework provides a formal way to quantify uncertainty about the unknown quantities. The idea is to find the parameter set that generate solutions closer (in a probabilistic sense) to the observed data. Instead of keeping only one solution, as an optimization approach would, we consider a set of solutions.

To briefly describe the Bayesian inference methodology, some notation is needed. Let $\mathit{\boldsymbol{Y}}$ be a vector of observations (data) and let $\mathit{\boldsymbol{\theta }}$ be a vector of parameters representing the unknown quantities of interest. From the Bayesian perspective, all the unknown quantities $\mathit{\boldsymbol{\theta }}$ are considered random variables and the data $\mathit{\boldsymbol{Y}}$ is fixed. All the available knowledge regarding the unknowns is codified into a probability distribution known as prior with joint density function $\pi(\mathit{\boldsymbol{\theta }})$. The observational model, also known as the likelihood function, $\pi(\mathit{\boldsymbol{Y}}|\mathit{\boldsymbol{\theta }})$, relates the data with the unknown quantities by describing the probability of the data if the true values of the parameters were known. The prior can be combined with the likelihood through Bayes theorem as follows

Equation (4.1) is known as the posterior distribution of $\mathit{\boldsymbol{\theta }}$ given the data $\mathit{\boldsymbol{Y}}$ and represents the updated knowledge. Until further data is available, this posterior distribution contains the only relevant information. Now that we have established the basic notation used in Bayesian inference, we can describe in detail how we use this approach to infer the quantities of interest in the SEIRS model.

4.1.   Likelihood function for the SEIRS model

Our data consists of weekly reports of ARIs confirmed cases. To account for the discrete nature of these counts, it is reasonable to assume that the observations are realizations of a Poisson distribution with a time dependent mean parameter. However, prior knowledge regarding this type of diseases suggest that the variance of the data is larger than the mean, which indicates that there is over-dispersion. Therefore, a more appropriate model is the Negative Binomial distribution since it has an additional parameter that allows the variance to exceed the mean ^[21].

We have four age groups and 52 weeks for each time period. Let $Y_{ik}$ be the number of reported cases for week $i$ and age group $k$, $i = 1, 2, 3, \ldots, 52$, $k = 1, 2, 3, 4$. Then, conditional to the parameters $\mathit{\boldsymbol{\theta }}$, we assume that $Y_{ik}$ follows a Negative Binomial distribution with mean $A_{ik}(\mathit{\boldsymbol{\theta }})$ and dispersion parameter $\kappa$, where $A_{ik}(\mathit{\boldsymbol{\theta }})$ is the prevalence of the infection for week $j$ obtained from solving the SEIRS model in (3.3). Here $\mathit{\boldsymbol{\theta }}$ contains all the necessary parameters to solve the SEIRS model including, for example, demographic information such as the population size, birth and death rates, etc.

Furthermore, we assume that the observations $Y_{ik}$ are conditionally independent given the parameters, that is equivalent to say that all the dependency in the data is codified into the SEIRS model. This last assumption allows to write the likelihood function as a product of Negative Binomial probability functions, i.e.

We use the same dispersion parameter for each age group to reduce the number of parameters to estimate.

4.2.   Prior distributions

For many diseases, the parameters involved in the SEIRS model can be fixed based upon previous studies or expert knowledge. However, since ARIs is really a set of diseases, it is unreasonable to estimate a single or unique value for parameters such as recovery rates or infection risk. Therefore, it is appropriate to consider these quantities as random variables. With this idea in mind, the parameters that will then be estimated are the infection probabilities $\beta_k$, the recovery rates $\gamma_k$, the immunity rates $\omega_k$, the amplitude and phase shift of the seasonality function $\rho$ and $\phi$, and the dispersion parameter $\kappa$ of the Negative Binomial distribution. These parameters were chosen because they are considered either the most relevant or the most controversial to be fixed a priori.

Independent informative truncated Gamma priors with shape $a_{\gamma_k} = 4$ and scale $b_{\gamma_k} = 0.2$ hyper-parameters are used for the recovery rates $\gamma_k$, $k = 1, 2, 3, 4$. We consider a priori that $0.25 \leq \gamma_k \le 2$, which implies that the mean recovery time $1/\gamma_k$ must be between 0.5 and 4 weeks, which is reasonable for this class of diseases. As the support of $\gamma_k$ is bounded, we could simply use a uniform prior distribution. However, this choice would result in a very informative prior for $1/\gamma_k$. By choosing the hyper-parameters $a_{\gamma_k}$, $b_{\gamma_k}$ as above, we provide similar knowledge to both parameters. In fact, the hyper-parameters are used to guarantee that the expected value of the resulting probability distribution coincides with a reference value for the parameter of interest either taken from the literature or deduced from personal communication with experts in the field.

For the parameters $\omega_k$ a similar prior scheme as the one described above was used. Independent truncated Gamma priors with shape $a_{\omega_k} = 3$ and scale $b_{\omega_k} = 0.02$ were chosen. We assume that the immunity rate must be lower than 0.25, which results in a mean immunity time of at least 4 weeks.

Uniform(0, 1) priors were used for $\beta_k$ and $\rho$ while a Uniform$(0, 2\pi)$ was used for $\phi$. Finally, for the dispersion parameter we use a Gamma prior with $a_{\kappa} = 2$ and scale $b_{\kappa} = 0.5$. Table 2 summarizes our prior distributions.

Table 2.  Prior distributions summary. Gamma distributions were used for parameters $\kappa$, $\gamma_k$ and $\omega_k$, $k = 1, 2, 3, 4$. Uniform distribution were used for the rest of parameters.

Parameter	Expected value	Support	Prior distribution
$\gamma_k$	0.8	[0.25, 2]	Gamma, $a_{\gamma_k}=4$, $b_{\gamma_k}=0.2$
$\omega_k$	0.06	$[0.25, \infty)$	Gamma, $a_{\omega_k}=3$, $b_{\omega_k}=0.02$
$k$	1	$[0, \infty)$	Gamma, $a_{\kappa}=2$, $b_{\kappa}=0.5$
$\rho$	0.5	[0, 1]	Uniform
$\phi$	0.5	$[0, 2\pi]$	Uniform
$\beta_k$	0.5	[0, 1]	Uniform

---

 | Show Table

DownLoad: CSV

A list of all the parameters involved in the SEIRS model is shown in Table 3. For those parameters that are fixed, the table shows the values that will be used to model the data described in Section 2. These values are obtained from previous results, official statistical sites and other various sources. More details are given in later sections.

Table 3.  Parameters of the SEIRS model.

Parameter	Description	Value
$N$	Population size	772604
$\mu_k$	Death rate	$2.7\times 10^{-6}, 1.1\times 10^{-7}, 7.3\times 10^{-7}, 2.9\times 10^{-5}$
$\nu_k$	Birth rate	$6.6\times 10^{-4}, 5.3\times 10^{-4}$
$\alpha_k$	Aging rates	$1/(52\cdot4), 1/(52\cdot14), 1.0/(52\cdot39)$
$\omega_k$	Immunity rate	To be estimated
$\eta_k$	Latency rate	1
$\gamma_k$	Recovery rate	To be estimated
$C_{kj}$	Number of contacts between groups	Estimated using POLYMOD, Table 4
$\beta_k$	Probability of infection	To be estimated
$\kappa$	Dispersion parameter	To be estimated
$\lambda_k(t)$	Force of infection	Defined by (3.1)
$h(t)$	Seasonality function	Defined by (3.2)
$\rho$	Seasonality amplitude	To be estimated
$\phi$	Seasonality phase shift	To be estimated

---

 | Show Table

DownLoad: CSV

4.3.   Posterior distribution

The posterior distribution for the parameters of interest $\mathit{\boldsymbol{\theta }} = (\beta_1, \beta_2, \beta_3, \beta_4, \gamma_1, \gamma_2, \gamma_3, \gamma_4, \omega_1, \omega_2, \omega_3, \omega_4, \rho, \phi, \kappa)$ satisfies

It does not have an analytical form since the likelihood function depends on the solution of the SEIRS model, which also has no explicit solution and must be approximated numerically. In order to analyze the posterior distribution we use the t-walk, a general purpose Markov Chain Monte Carlo (MCMC) algorithm to sample from continuous probability distributions and does not require tuning ^[23]. This algorithm generates samples from the posterior distribution that can be used to estimate marginal posterior densities, mean, variance, quantiles, etc. We refer the reader to ^[24] for more details on MCMC methods.

5.   Results

In this section we fit our SEIRS model to the ARIs data described before. Instead of estimating all the parameters of interest using the data from 2000 to 2008, we analyze one year at a time. This allow us to identify important changes (if any) from one year to the other.

5.1.   Implementation details

All the analysis is performed in Python 2.7 software. In order to solve the SEIRS model, we use the numerical ordinary differential equations solver $\texttt{odeint}$ available in the $\texttt{scipy}$ package. To explore the posterior distribution we use the implementation of the t-walk available in Python. The algorithm is run for two million iterations and the first 100, 000 are discarded as burn-in. We use 4000 samples to construct estimates of the marginal posterior distributions, probability bands for the evolution of the infection, etc. We ran the algorithm starting from different initial points to be certain that each time the MCMC converges to the same posterior distribution. These initial points are generated at random from the prior distributions.

To initialize the model for the first period (July 2000 to July 2001), we assume that the number of infected $I_k(0)$ for each age group is given by the data records at week 30. This point is close to the lowest point of the infection for that year and we consider that here starts a new infection period. The number of susceptible individuals is set as $(N_k-I_k)(0)$, $k = 1, 2, 3, 4$, where $N_k$ denotes the population size for age group $k$. This data was obtained from the National Institute of Statistics and Geography (INEGI). The number of exposed $E_k(0)$ and the number of recovered $R_k(0)$ are set to 0. Although this is not ideal, the estimation algorithm corrects this initial approximation error. Once we obtain the estimates for the data of the first period, we use them to initialize the MCMC for the next period.

We fixed birth, death, aging, and latency rates as shown in table 3. Mortality rates for each age group were taken from the study conducted in ^[7]; this work analyzes the impact of pandemic influenza A(H1N1) on the mortality of a Mexican population, and obtains mortality rates for our age groups, attributed to RSV and FLU. Fertility rates were taken from a study carried out by the Mexican National Council of Population (CONAPO)^*. It is considered that the fertile population is between 15 and 49 years old. In group 2 we have a portion of this fertile population (from 15 to 19 years old), which has a rate of 69.5 births per thousand women, per year. The third group refers to the other part of the fertile population, from 20 to 49 years old, which has an average rate of 55.14 births per thousand women, per year. The aging rates are estimated from the number of weeks that individuals remain in their corresponding age group. Finally, the estimates for the number of contacts between age groups can be found in Table 4 and are based on the POLYMOD study on contact data. ^[25].

^* Approximations to the level of fertility in Mexico 1990-2014.

Table 4.  Contact matrix $C$ estimated using the data in the POLYMOD study. The entries refer to the mean number of contacts per individual per day.

	0-4	5-19	20-59	$\geq$ 60
0-4	2.21	1.13	2.86	0.53
5-19	1.13	10.12	3.87	0.71
20-59	2.86	3.87	9.69	3.08
$\geq$ 60	0.53	0.71	3.08	2.56

---

 | Show Table

DownLoad: CSV

5.2.   The role of children in the observed dynamics

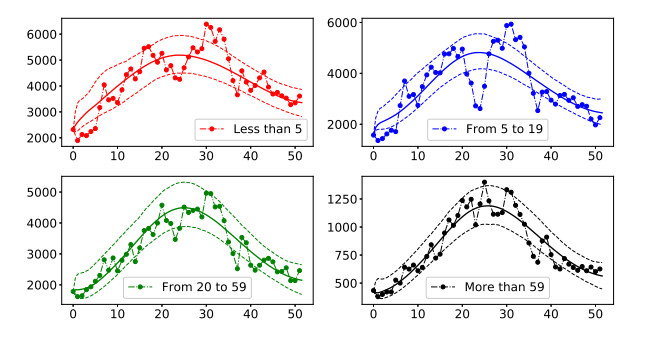
In this section we present the analysis of the period 2006-2007. Figure 4 shows the posterior median of the infection with a solid line which represents correctly the tendency of the data. The dashed lines represent 95% pointwise probability bands for the expected value of the infection at each time. There is some lack of fit especially for age group 5-19. As can be seen from the figure, the number of infections substantially decreases at the end of the year, possibly caused by the vacation period as we already have discussed. The model is unable to recover this behavior since it assumes that the number of contacts among groups remains constant.

Figure 4.  Model fit for the evolution of the infection from July 2006 to July 2007 by age group. Dotted lines represent the observed data. Solid lines are the posterior median estimates. Dashed lines represent the 95% pointwise probability bands for the expected value of the infection at each time.

DownLoad: Full-Size Img PowerPoint

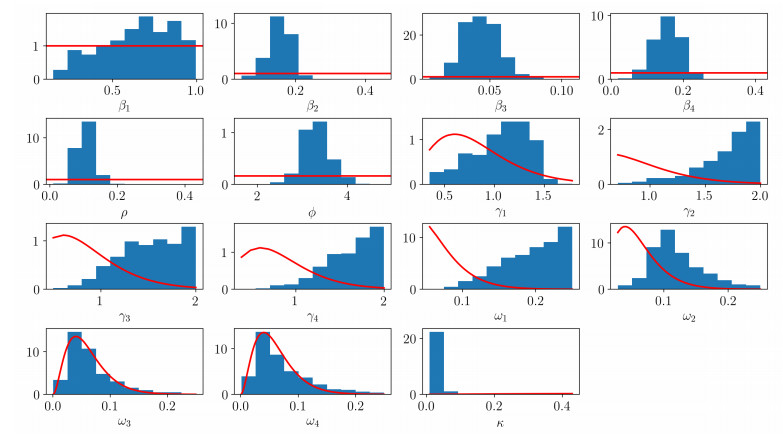
Figure 5 shows the empirical estimates of the marginal posterior distributions for all the unknown parameters and their corresponding prior distributions. It can be seen that, for most of the parameters, there is a considerable difference between their prior and their posterior distributions. For parameters $\beta_2$, $\beta_3$, $\beta_4$, $\rho$, $\phi$ and $\kappa$ the posterior distribution is clearly unimodal and with low variability. All gamma parameters (recovery rates) and $\beta_1$ (probability of infection in the group from 0-5 years old) have different posterior distributions with respect to their corresponding priors but there is considerably more variability. It seems that there is not much information in the data for parameters $\omega_3$ and $\omega_4$ as their posterior distributions are very similar to the priors. Therefore, we could simplify the model by fixing those two parameters. However, this would be difficult since, as we have mentioned before, data corresponds to a group of diseases.

Figure 5.  Parameter estimates using data from July 2006 to July 2007. Blue histograms represent the empirical estimates of the marginal posterior distributions. Red lines correspond to the prior distributions for each parameter.

DownLoad: Full-Size Img PowerPoint

To have a better understanding of the posterior estimates and the role of age in the transmission process, Table 5 shows median posterior estimates and 95% posterior probability intervals for each parameter. It can be seen that the first group is reinfected more frequently since its mean immunity time $1/\omega_1$ is the smallest among all age groups ranging from 4 to almost 10 weeks with a median of 5 weeks. Conversely, young adults have the longest immunity time as expected. In terms of the probability of infection $\beta_k$, it is clear that children from 0 to 4 years old are the most likely to be infected ($\beta _k$) and adults from 20 to 59 years old are those with less probability. Also, the recovery time is larger for children, potentially exceeding two weeks. The other three groups recover faster, typically in less than 1 week.

Table 5.  Posterior median and 95% probability intervals for all the estimated parameters for the period July 2006-July 2007.

	Low	Median	High
$\beta_1$	0.25	0.66	0.97
$\beta_2$	0.09	0.16	0.21
$\beta_3$	0.02	0.04	0.07
$\beta_4$	0.08	0.16	0.22
$1/\gamma_1$	0.68	0.92	2.17
$1/\gamma_2$	0.50	0.57	0.95
$1/\gamma_3$	0.50	0.64	1.12
$1/\gamma_4$	0.50	0.60	1.10
$1/\omega_1$	4.04	4.96	9.67
$1/\omega_2$	4.60	8.92	18.42
$1/\omega_3$	5.49	18.60	80.77
$1/\omega_4$	5.02	18.13	58.90
$\rho$	0.07	0.10	0.16
$\phi$	2.72	3.28	3.99
$\kappa$	0.02	0.03	0.07

---

 | Show Table

DownLoad: CSV

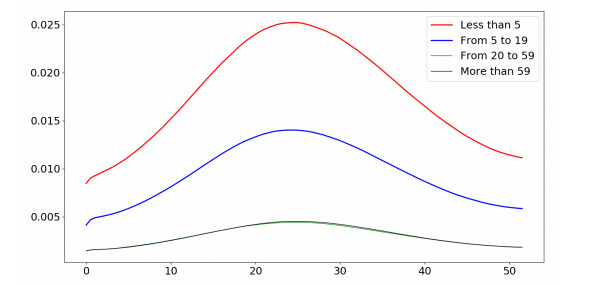
From the posterior samples we can also estimate the median force of infection for each group, which is shown in Figure 6. It is clear that children less than 4 years have the highest force of infection followed by children between 5 and 19 years old. Also, adults have the lowest values as expected.

Figure 6.  Median posterior estimate for the force of infection obtained using the data from 2006–2007, as defined in equation 3.1.

DownLoad: Full-Size Img PowerPoint

Despite the fact that older adults have the second highest probability of infection, they have a low force of infection. It is possible that this phenomenon is associated to their low participation in social activities (see contact matrix $C$ in Table 4) and their high immunity time.

For each period defined in Section 2 we performed the previous analysis. Tables 6 and ?? contains posterior median estimates and 95% probability intervals for all the parameters and all the periods analyzed in this study and can be found as supplementary material. Although numerical results present small changes in magnitude from one year to another, the patterns we observed are the same for all periods.

6.   Discussion and conclusions

The objective of this work is to understand the role of age groups in the propagation of ARIs by estimating key parameters related to the dynamics of the infections. In order to achieve this, we propose a SEIRS model and estimate parameters such as the mean recovery time, the mean immunity time and the probability of infection for each group. A Bayesian approach was chosen to perform the inference using ARIs data from San Luis Potosí, Mexico from 2000 to 2008.

For each age group we focused on four characteristics: the probability of infection ($\beta_k$), the average time that one individual remains infectious ($1 /\gamma_k$), the average time that one individual remains immune ($1/\omega_k$), and the force of infection ($\lambda_k(t)$), which can be seen as a function of the other parameters. From the estimation process, specifically Table 5 and Figure 6, we saw that children under five years old have the highest probability of infection (with a posterior median of 0.66), the lowest immunity time (around five weeks), the longest recovery time (up to two weeks) and, in general, the largest force of infection. In other words, the children's group (0-4) is more prone to get sick, it remains infectious for longer periods and it is reinfected more rapidly. All of this leads us to hypothesize that children less than 5 years old are the primary spreaders of acute respiratory infections in San Luis Potosí's population from 2000 to 2008.

On the other hand, the group of young adults (20-59) is the one that differs the most from the little children's group since the former has the lowest probability of infection (with a posterior median of 0.04), the longest immunity time (around 18 weeks), a low recovery time (up to one week) and the lowest force of infection. It means that the group of young adults does not get sick often, it remains infectious only a few days and it stays healthy for longer periods. Then, it is reasonable to conclude that the group of young adults is the one that less contributes to the spread of this class of infections. Although we are mentioning a few point estimates to compare the characteristics of these two age groups, the posterior distributions for each parameter support our claims regarding the differences among little children and young adults.

The model fits the data reasonably well, nonetheless, it is not able to predict the decrement of cases reported during the vacations period at the end of each year. A possible explanation for this behavior in the data is that the drop in the reported cases is not due to a biological aspect of the infectious process or due to a change in the circulating viruses and bacteria that cause respiratory diseases, but rather, a matter of decreasing the number of contacts among school age groups. We observed that it is a repetitive pattern each year that only seems to affect individuals that effectively reduce their activities during those three weeks of vacation. Furthermore, there is evidence that by the end of holidays ARIs records increase again. In order to estimate the effect of vacations, we need a more flexible model that could change the number of contacts between groups with time. This can be achieved, for example, by allowing matrix $C$ to change with time or to use a more flexible seasonality function. We leave this as future research.

Acknowledgments

YNA thanks CONACyT for the PhD scholarship. YNA also thanks to the Kovalevskaia Fund and the Mexican Mathematical Society for partial financial support. MS-C thanks CONACYT for the support provided through the Cátedras CONACYT program to develop this work. JXV-H acknowledges support from UNAM PAPIIT grant IN110917. The authors thank Dr. Daniel Noyola and Dr. Andreu Comas from UASLP for providing access to the San Luis Potosí data. YNA would like to thank Dr. Andreu Comas for his valuable knowledge and feedback on epidemiology.

Conflict of interest

All authors declare no conflicts of interest in this paper.

A. Supplementary material

Table 6.  Posterior median and 95% probability intervals for all the estimated parameters from 2000 to 2004.

	2000-2001				2001-2002				2002-2003				2003-2004
	Lower	Median	Upper		Lower	Median	Upper		Lower	Median	Upper		Lower	Median	Upper
$\beta_1$	0.13	0.37	0.94		0.11	0.45	0.96		0.27	0.65	0.98		0.23	0.53	0.94
$\beta_2$	0.04	0.12	0.20		0.03	0.10	0.22		0.05	0.13	0.23		0.07	0.16	0.23
$\beta_3$	0.01	0.03	0.07		0.02	0.05	0.09		0.01	0.03	0.07		0.01	0.04	0.07
$\beta_4$	0.05	0.17	0.30		0.06	0.18	0.33		0.03	0.10	0.28		0.07	0.15	0.26
$\rho$	0.01	0.08	0.20		0.08	0.13	0.22		0.05	0.11	0.17		0.08	0.11	0.16
$\phi$	1.72	2.99	5.09		2.61	3.62	4.47		2.67	3.65	4.49		3.18	3.86	4.62
$\gamma_1$	0.27	0.68	1.42		0.29	0.72	1.31		0.33	0.91	1.39		0.40	0.88	1.40
$\gamma_2$	0.49	1.32	1.94		0.39	1.06	1.94		0.44	1.34	1.94		0.88	1.64	1.99
$\gamma_3$	0.29	1.08	1.93		0.61	1.56	1.98		0.30	1.07	1.92		0.52	1.50	1.97
$\gamma_4$	0.50	1.32	1.98		0.53	1.26	1.94		0.30	0.89	1.90		0.63	1.31	1.93
$\omega_1$	0.02	0.14	0.24		0.04	0.13	0.24		0.03	0.14	0.24		0.05	0.18	0.25
$\omega_2$	0.02	0.08	0.19		0.01	0.07	0.22		0.01	0.08	0.20		0.04	0.08	0.21
$\omega_3$	0.00	0.03	0.16		0.01	0.03	0.16		0.01	0.03	0.20		0.01	0.04	0.21
$\omega_4$	0.01	0.03	0.16		0.01	0.03	0.19		0.01	0.04	0.22		0.01	0.05	0.20
$\kappa$	0.03	0.04	0.14		0.03	0.04	0.11		0.02	0.03	0.11		0.02	0.03	0.08

---

 | Show Table

DownLoad: CSV

Table 7.  Posterior median and 95% probability intervals for all the estimated parameters from 2004 to 2008.

	2004-2005				2005-2006				2006-2007				2007-2008
	Lower	Median	Upper		Lower	Median	Upper		Lower	Median	Upper		Lower	Median	Upper
$\beta_1$	0.18	0.67	0.99		0.18	0.54	0.95		0.25	0.66	0.97		0.37	0.73	0.99
$\beta_2$	0.02	0.14	0.21		0.07	0.15	0.22		0.09	0.16	0.21		0.07	0.15	0.21
$\beta_3$	0.02	0.05	0.07		0.01	0.05	0.07		0.02	0.04	0.07		0.01	0.05	0.07
$\beta_4$	0.08	0.17	0.25		0.05	0.14	0.25		0.08	0.16	0.22		0.06	0.14	0.21
$\rho$	0.07	0.11	0.16		0.08	0.11	0.14		0.07	0.10	0.16		0.06	0.10	0.14
$\phi$	2.75	3.33	4.20		3.32	3.98	4.60		2.72	3.28	3.99		2.99	3.49	4.11
$\gamma_1$	0.38	1.01	1.48		0.37	0.96	1.48		0.46	1.09	1.47		0.61	1.06	1.45
$\gamma_2$	0.34	1.56	1.99		0.96	1.69	1.98		1.06	1.76	1.99		0.90	1.68	1.99
$\gamma_3$	0.75	1.65	1.99		0.54	1.55	1.97		0.89	1.55	1.99		0.58	1.55	1.99
$\gamma_4$	0.84	1.53	1.97		0.54	1.29	1.97		0.91	1.68	1.99		0.65	1.53	1.97
$\omega_1$	0.05	0.16	0.24		0.07	0.18	0.25		0.10	0.20	0.25		0.09	0.17	0.25
$\omega_2$	0.05	0.11	0.24		0.05	0.11	0.23		0.05	0.11	0.22		0.05	0.10	0.23
$\omega_3$	0.01	0.04	0.21		0.02	0.05	0.19		0.01	0.05	0.18		0.02	0.07	0.21
$\omega_4$	0.01	0.03	0.19		0.01	0.04	0.18		0.02	0.06	0.20		0.01	0.04	0.17
$\kappa$	0.02	0.02	0.07		0.02	0.03	0.09		0.02	0.03	0.07		0.02	0.03	0.08

---

 | Show Table

DownLoad: CSV