Basic reproduction number of SEIRS model on regular lattice

1.   Introduction

The basic reproduction number, usually expressed by $\mathscr{R}_0$, is one of the most important indices of epidemic models. This quantity gives the criterion for determining whether the infectious disease can spread into the whole population or not: when $\mathscr{R}_0 > 1$ an epidemic will result from the introduction of infectious agent, whereas when $\mathscr{R}_0 < 1$ the number of infected is expected to decline (e.g., ^[1]). Therefore it is known from the threshold principle, that $\mathscr{R}_0 = 1$ gives its threshold.

This equation for theshold also coincides with the condition for the threshold between stability and instability of disease-free equilibrium, but we sometimes obtain different basic reproduction numbers even if the stability conditions for disease-free equilibrium are the same. When this happens, we can determine whether or not the infectious disease can expand, but it produces a possibility for us to make a wrong evaluation of its propagation speed.

In simplest cases, the basic reproduction number can be calculated as the ratio of newly reproduction rate of infectious individuals during the infected period of the focal infected individual. Unfortunately, however, for more complicated models, it requires some other contrivances to obtain the basic reproduction number in general.

In such situations, the most outstanding invention for obtaining $\mathscr{R}_0$ is to use next-generation matirix approach ^[2], in which $\mathscr{R}_0$ is defined as the spectral radius or dominant eigenvalue of the next-generation matrix. The computation of $\mathscr{R}_0$ by the next-generation matrix is formulated by ^[3] and ^[4] (these methods by next-generation matrix are reviewed by ^[5]). Since then, a tremendous number of studies have adopted this method to obtain $\mathscr{R}_0$, and now it has become a standard approach to finding $\mathscr{R}_0$. On the other hand, we should notice that we can only find a few examples of obtaining $\mathscr{R}_0$ in spatial epidemic models by using the next-generation model. In ^[6], $\mathscr{R}_0$ was first obtained for their infectious model on the lattice by using next-generation matrix.

The rest of this paper is organized as follows. Section 2 reviews the basic reproduction number of SIR model, which gives us the most understandable derivation and result. In Section 3, we verify the procedure for calculating the basic reproduction number by using the next-generation matrix shown in the seminal work ^[3], and we apply it to SEIRS model on a regular lattice. In Section 4, we compare our result with the previous studies so far.

2.   SIR model and its basic reproduction number $\mathscr{R}_0$

First, we concentrate on the SIR model proposed by ^[7] as one of the most fundamental epidemic models. This SIR model can be written as follows:

Here, $\rho_S, \rho_I$, and $\rho_R$ indicate the fractions of susceptible, infected and recovered individual, respectively. The infection occurs by the right-hand side (RHS) in Eq (1) or the first term of the RHS in Eq (2), which are assumed by the product of both fractions $\rho_S$ and $\rho_I$, i.e., the law of mass action. The recovery from infection randomly occurs by the second term of the RHS in Eq (2) or the RHS in Eq (3). The rates $\beta > 0$ and $\sigma > 0$ indicate the unit time of speed of infection and recovery, respectively.

To check the behavior after introduction of a small amount of infectious individuals into susceptible population, or a small disturbance around the disease-free equilibrium $(1, 0, 0)$, which is an equilibrium of the system (1)–(3), one has to determine whether the disease can invade the population or not. Thus, the linearization of Eq (2) around $(1, 0, 0)$ becomes

and defining the ratio of infectious rate during the period of infected:

then $\mathscr{R}_0 > 1$ if and only if $\beta > \sigma$.

Compared with the above result, limiting transmission of the disease only within the nearest neighboring individuals reduces the value of $\mathscr{R}_0$. Therefore, we review the derivation of $\mathscr{R}_0$ for SIR model by ^[8] (the notation in ^[8] slightly differs from the one presented below, but we can have an exact correspondence). First of all, Eq (2) corresponds to the following equation:

where $\rho_{SI}$ is the fraction of the nearest-neighboring pair $S$ and $I$, and $q_{S/I}$ is the conditional probability that the focal site has state $S$ under the condition of state $I$ in the nearest-neighbor site: $\rho_{SI} = \rho_I q_{S/I}$.

At the initial phase of an infection invading, we can write the rate of $I$ in Eq (5) as

Therefore, the basic reproduction number is defined as

and then if $\mathscr{R}_0 > 1$, then the disease can spread into population on a lattice. So we need to give the initial value of $q_{S/I}(0)$ at the neighborhood around the steady state without infectious individuals.

After the invasion of an infectious individual, the spatial structure with the dynamical steady state would be soon reached, and so it can be used as an initial condition for the variable $q_{S/I}$ to determine whether or not an infection will succeed to invade. Then we consider the dynamics of $q_{S/I}$:

where we use Eq (5) and the following relation:

in which $z$ is the number of nearest neighbors; e.g., $z = 4$ for two-dimensional square lattice and approximated $\rho_{ISI}\approx \rho_{SI}^2/\rho_S$ and $\rho_{SSI}\approx \rho_{SS}\rho_{SI}/\rho_S$ come from pair approximation ^[9] in the second equality (we explain pair approximation in the next section).

Here, setting $q_{S/S} = 1$ and $q_{I/S} = 0$ as a disease-free equilibrium, then Eq (8) becomes

and so we obtain the steady state as $q_{S/I} = 1-2/z$. Substituting this as an initial state into Eq (7) results as

which indicates that the basic reproduction number for SIR model on lattice or network by Eq (10) is less than the one for the corresponding non-spatial model by Eq (4).

Based on the above idea the basic reproduction numbers for basic epidemic models on regular lattice have been obtained by several studies ^[8,10,11]. In the next section we derive the basic reproduction number for SEIRS model, which is considered as more generalized model than SIR model, by using next-generation matrix introduced by ^[2] and studied extensively by ^[3].

3.   Definition of $\mathscr{R}_0$ for an epidemic model on the lattice by using next-generation matrix

3.1.   Next-generation matrix and $\mathscr{R}_0$

We can calculate $\mathscr{R}_0$ through the next-generation matrix by ^[3] as follows.

Consider the vector

with $x_i \ge 0 \ (i = 1, \ldots, n)$. Here $x_1, \cdots, x_m$ corresponds to $m$ population densities of infected classes. Then disease free state is defined as

The epidemic model is rewritten as

where $\mathscr{V}_i = \mathscr{V}_i^- - \mathscr{V}_i^+$. $\mathscr{F}_i, \mathscr{V}_i^+, \mathscr{V}_i^-$ are the terms corresponding to the appearance of new infections in compartment $i$, transfer of individuals into compartment $i$ by all other means, and transfer of individuals out of compartment $i$, respectively. Also, these functions $\mathscr{F}_i, \mathscr{V}_i, \mathscr{V}_i^-, \mathscr{V}_i^+$ satisfy the following conditions (A1)–(A5) with a disease free equilibrium $x_0$:

Then $\mathscr{R}_0$ is defined as the spectrum radius or dominant eigenvalue of next-generation matrix $FV^{-1}:$

where

for $1 \le i, j \le m$.

In the next subsections we use the above procedure to get $\mathscr{R}_0$'s for SEIRS epidemic model in both cases of completely mixing and only the nearest neighboring infection on regular lattice.

3.2.   $\mathscr{R}_0$ for SEIRS epidemic model for completely mixing population

In addition to the system (1)–(3) we use the notation $\rho_E, \omega, \nu$ for the fraction of exposed individuals (who are in incubation period during which the individual has been infected but is not yet infectious), the rate of natural loss of immunity, transition rate to infectious, respectively. Then, we consider the following SEIRS model:

Observe that $d\rho_S/dt+d\rho_E/dt+d\rho_I/dt+d\rho_R/dt = 0$ and each variable indicates the fraction of each state, we can assume the total sum of $\rho_S+\rho_E+\rho_I+\rho_R = 1$. Then we can choose only three variables, $\rho_S, \rho_E, \rho_I$ as independent, and so $\rho_R = 1-(\rho_S+\rho_E+\rho_I)$. Therefore, we get the following system from Eqs (11)–(14):

To express this system in non-dimensional terms, we choose new variables as follows:

Then the above system (15)–(17) is transformed as

We consider $\{\rho_E, \rho_I\}$ as population densities of infected class. Hence, when we check conditions (A1)–(A5) for this system (18)–(20), we find three cases of vectors $\mathscr{F}$ and $\mathscr{V}$ as follows:

Also, observe that the disease-free equilibrium is $(\rho_S, \rho_E, \rho_I) = (1, 0, 0)$; the matrices $F$ and $V$ are given as,

respectively. Then

respectively. Therefore, basic reproduction numbers for these matrices become

respectively. As pointed out by ^[3], we should choose $\mathscr{F}$ and $\mathscr{V}$ by appropriate epidemiological interpretation rather than mathematically. The first and the second choices give the same basic reproduction numbers, but both the second and the third include the terms of progression of infectiousness in the vector $\mathscr{F}$. Therefore, we should adopt the first choice which considers only newly infected individuals.

3.3.   $\mathscr{R}_0$ for SEIRS epidemic model for the nearest-neighboring infection

Using the same notatons in the previous sections and others, such as $\rho_{SSI}$, which indicates the fraction of the triplet $SSI$, the dynamics of SEIRS model on regular lattice is written as follows:

where $\rho_{\sigma\sigma'} = \rho_{\sigma'\sigma}$ holds due to symmetry.

Observe that by using (22)–(30),

indicates that the system (31)–(33) including spatial structure corresponds to the non-spatial model (18)–(20) in the previous subsection. And so, the system of nine equations (22)–(30) with the following relation gives the dynamics of the nearest-neighboring pairs for spatial model: $1 = \rho_S+\rho_E+\rho_I+\rho_R = (\rho_{SS}+\rho_{SE}+\rho_{SI}+\rho_{SR})+$$(\rho_{SE}+\rho_{EE}+\rho_{EI}+\rho_{ER})+ (\rho_{SI}+\rho_{EI}+\rho_{II}+\rho_{IR})+$$(\rho_{SR}+\rho_{ER}+\rho_{IR}+\rho_{RR}) = (\rho_{SS}+\rho_{EE}+\rho_{II}+\rho_{RR}) +$$2(\rho_{SE}+\rho_{SI}+\rho_{SR}+\rho_{EI}+\rho_{ER}+\rho_{IR})$, i.e., $\rho_{RR} = 1 - (\rho_{SS}+\rho_{EE}+\rho_{II}) -$$2(\rho_{SE}+\rho_{SI}+\rho_{SR}+\rho_{EI}+\rho_{ER}+\rho_{IR})$.

Unfortunately, however, the system (22)–(30) is not closed since triplet densities such as $\rho_{SSI}$ may change as time passes, whose dynamics also includes higher-order correlation functions (quartet densities) and these procedures continue forever. Therefore, we adopt an approximation called pair approximation ^[9] to this system. By pair approximation, conditional probabilities are defined:

and the effect of the site with state $\sigma$ from the site with state $\sigma''$ may be considered smaller compared with the site with state $\sigma'$ because the former is the next-nearest neighbor, but the latter is the nearest neighbor. Then we can approximate the conditional probability (34) as follows:

Using Eqs (34) and (35), we obtain

Pair approximation (36) with $\rho_S = \rho_{SS}+\rho_{SE}+\rho_{SI}+\rho_{SR}$ transforms Eqs (22)–(30) into the closed system as follows:

We consider $\{\rho_{SE}, \rho_{SI}, \rho_{EE}, \rho_{EI}, \rho_{ER}, \rho_{II}, \rho_{IR} \}$ as population densities of infected class because these variables include $E$ or $I$. When we check conditions (A1)–(A5) for the system (37)–(45) with the choice of $\mathscr{F}$ from the viewpoint of the reproduction of newly infected individuals, we can determine only one possible set of vectors $\mathscr{F}$ and $\mathscr{V}$:

and

Observe that the first and the fourth elements correspond to the changes of variables $\rho_{SS}$ and $\rho_{SR}$, respectively, and that the disease-free equilibrium is $(\rho_{SS}, \rho_{SE}, \rho_{SI}, \rho_{SR}, \rho_{EE}, \rho_{EI}, \rho_{ER}, \rho_{II}, \rho_{IR}) = (1, 0, 0, 0, 0, 0, 0, 0, 0)$,

and

Then, the next-generation matrix is

where

The characteristic equation of this next-generation matrix (46) becomes

Therefore the spectral radius of the next-generation matrix, or the basic reproduction number, for SEIRS model is

When we set $z\to\infty$ then we obtain

which corresponds to $\mathscr{R}_0$ for the standard SEIRS, SEIR, SIRS, SIR, and SIS models as Eq (4) and (21). Compared with Eq (48) and (47), epidemic breakout for the former only depends on the infectious rate $\tilde{\beta}$, on the other hand, the latter depends not only on the infectious rate but also on other parameters, progression to infectiousness $\tilde{\nu}$ and rate of the natural loss of immunity $\tilde{\omega}$.

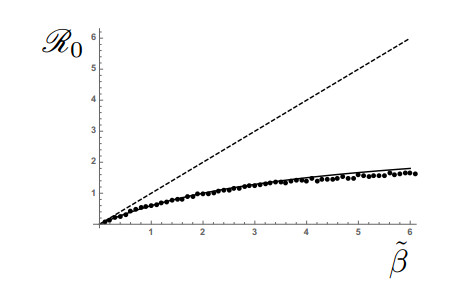
In Figure 1, we show the dependence of these three parameters on the threshold value of $\mathscr{R}_0 = 1$. We can see that critical infectious rate $\tilde{\beta}$ increases as transition rate to infectious $\tilde{\nu}$ but decreases as rate of the natural loss of immunity $\tilde{\omega}$. This is reasonable because the period during infected $1/\tilde{\nu}$ is shorter as $\tilde{\nu}$ increases, then the strength of infection should be larger to maintain the value of $\mathscr{R}_0$. On the other hand, if $\tilde{\omega}$ increases, then the number of susceptibles, to some of which the focal infected individual has not yet transmitted disease, increases, and so $\tilde{\beta}$ can be reduced for the critical $\mathscr{R}_0 = 1$.

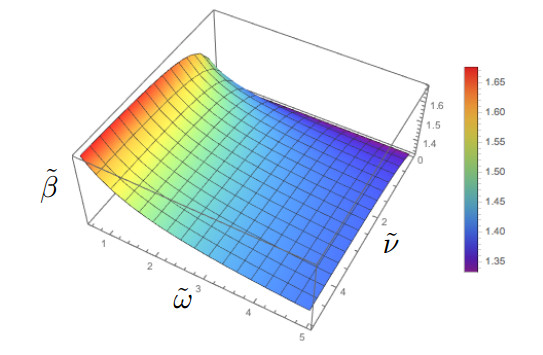
In Figure 2, we show $\mathscr{R}_0$ against $\tilde{\nu}$ and $\tilde{\omega}$ when $\tilde{\beta}\to \infty$. If the infectious rate $\tilde{\beta}$ becomes very large, then the focal infectious individual can immediately transmit the disease to all susceptibles in the nearest neighbor. Therefore the maximum number of $\mathscr{R}_0$ should not exceed the number of the nearest neighbor $z$. Indeed, we can get this extremal value as

for $\tilde\beta\to\infty$. When $\tilde\nu\to 0$ or $\tilde\omega\to 0$, Eq (49) converges to $z$ or $z-1$, respectively. When $\tilde\nu\to \infty$ or $\tilde\omega\to \infty$, Eq (49) becomes $z-\frac{1}{1+\tilde\omega}$ or $z$. Furthermore we can check that Eq (49) is greater than $z-1$ and less than $z$ by $z - \mbox{Eq (49)} = \tilde{\nu}(1+\tilde{\nu}+\tilde{\omega})/(1+\tilde{\nu})(1+\tilde{\omega})(\tilde{\nu}+\tilde{\omega}) > 0$ and $\mbox{Eq (49)} - (z-1) = \tilde{\omega}\{1+(1+\tilde{\nu})(\tilde{\nu}+\tilde{\omega})\}/(1+\tilde{\nu})(1+\tilde{\omega})(\tilde{\nu}+\tilde{\omega}) > 0$. From Figure 2 we can observe that $\mathscr{R}_0$ approaches to $z = 4$ or $z-1 = 3$ for $\tilde{\nu}\to 0$ or $\tilde{\omega}\to 0$, respectively.

3.4.   $\mathscr{R}_0$ for SEIR, SIRS, SIR, SIS epidemic models: simpler cases

We consider simpler epidemic models with reducing variables and parameters.

When R never returns to S and $\tilde{\omega}$ becomes zero, then we get SEIR model with pair approximation:

By similar calculation as SEIRS model for disease-free equilibrium, we obtain the next-generation matrix and its characteristic equation as

and

Therefore the basic reproduction number for SEIR model is

When the exposed period can be neglected and we don't need consider the state E, then we get SIRS model with pair approximation:

We can consider $\{\rho_{SI}, \rho_{II}, \rho_{IR} \}$ as population densities of infected class, and noticing that the first and the third elements correspond to the changes of variables $\rho_{SS}$ and $\rho_{SR}$, respectively, then the next-generation matrix and its characteristic equation become

and

Therefore, the basic reproduction number for SIRS model is given as

Next, we move to SIR model without the natural loss of immunity from R to S. SIR model with pair approximation is given as follows:

By similar calculation as SIRS model for disease-free equilibrium, we obtain the next-generation matrix and its characteristic equation as

and

Therefore, the basic reproduction number for SIR model is given by

The last model SIS with pair approximation is given as follows:

We can consider all the variables $\{\rho_{SI}, \rho_{II} \}$ as population densities of infected class, then the next-generation matrix and its characteristic equation become

and

Therefore, the basic reproduction number for SIS model is

3.5.   $\mathscr{R}_0$ relations between various models

Here, we consider the relationships of $\mathscr{R}_0$ among various models. If there is no natural loss of immunity, we set the model as $\tilde{\omega} \to 0$ for SEIRS model. By taking $\tilde{\omega}\to 0$ for Eq (47) $\mathscr{R}_0$ for SEIR model becomes

which coincides with Eq (50).

If the transition from E to I occurs instantaneously, i.e., the transition rate $\tilde{\nu}$ is very large, then the model can be interpreted as SIRS model. By taking the limit $\tilde{\nu}\to \infty$ for Eq (47) $\mathscr{R}_0$ for SIRS model becomes

which coincides with Eq (51).

SIR model can be obtained by taking the limit of $\tilde{\omega}\to 0$ for SIRS model (51). Therefore, $\mathscr{R}_0$ for SIR model is

which coincides with Eq (53).

SIS model can be obtained by taking the limit of $\tilde{\omega}\to\infty$ for SIRS model (51) by regarding the transition from R to S as being instantaneous. So $\mathscr{R}_0$ for SIS model is obtained as

which coincides with Eq (54).

3.6.   Comparison with Monte Carlo simulation

In this paper, we adopted an approximation to evaluate $\mathscr{R}_0$, so in order to check its accuracy, we would compare the result with the Monte Carlo simulation. To do this, we need an equation for some variable corresponding to $\mathscr{R}_0$, which increases for $\mathscr{R}_0 > 1$ but decreases for $\mathscr{R}_0 < 1$. Fortunately, we can find the variable for the SIR model, and so we explain it below.

SIR model gives the linearized equation of Eq (52) for $\rho_{SI}$ around disease free equilibrium gives

The ratio of positive term to negative one $(1-1/z)\tilde{\beta}/(1+\tilde{\beta}/z) = (z-1)\tilde{\beta}/(z+\tilde{\beta})$ coincides with $\mathscr{R}_0$ by Eq (53).

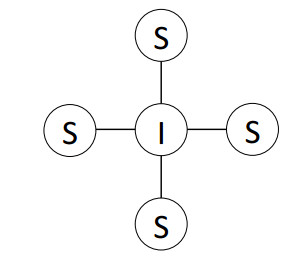
We can expect the newly produced number of S-I pairs as this quantity in Monte Carlo simulation. Let us consider one infectious individual to invade into a susceptible population on two-dimensional square lattice space $z = 4$ (Figure 3).

There are four S-I pairs, then we trace how many S-I pairs are newly produced by the direct disease transmission of this infectious to the neighboring susceptibles before changing I to R.

(ⅰ) If the transition from I to R occurs, its probability is $1/(1+\tilde{\beta})$ and no newly S-I pairs are produced.

(ⅱ) If the transition from I to R does not occur and one of four Ss is infected, its probability is $1-1/(1+\tilde{\beta})$. Then if the transition from I to R occurs, the probability becomes $\left\{1-1/(1+\tilde{\beta})\right\}\cdot 1/(1+\frac{3}{4}\tilde{\beta})$ and three S-I pairs are produced.

(ⅲ) If the transition from I to R does not occur and one of the four Ss is infected. And then if the transition from I to R does not occur and one of the three Ss is infected. Then if the transition from I to R occurs, the probability becomes $\left\{1-1/(1+\tilde{\beta})\right\}\cdot \left\{1-1/(1+\frac{3}{4}\tilde{\beta})\right\} \cdot 1/(1+\frac{2}{4}\tilde{\beta})$. $2 \times 3$ S-I pairs are produced.

(ⅳ) If the transition from I to R does not occur and one of the four Ss is infected. And if the transition from I to R does not occur and one of the three Ss is infected. And if the transition from I to R does not occur and one of two Ss is infected. Then if the transition from I to R occurs, the probability becomes $\left\{1-1/(1+\tilde{\beta})\right\}\cdot \left\{1-1/(1+\frac{3}{4}\tilde{\beta})\right\} \cdot \left\{1-1/(1+\frac{2}{4}\tilde{\beta})\right\} \cdot 1/(1+\frac{1}{4}\tilde{\beta})$. $3 \times 3$ S-I pairs are produced.

(ⅴ) At the remaining probability $\left\{1-1/(1+\tilde{\beta})\right\}\cdot \left\{1-1/(1+\frac{3}{4}\tilde{\beta})\right\} \cdot \left\{1-1/(1+\frac{2}{4}\tilde{\beta})\right\} \cdot \left\{1-1/(1+\frac{1}{4}\tilde{\beta})\right\}$, $4 \times 3$ S-I pairs are produced.

The total sum of (ⅰ)–(ⅴ) over 4 (averaged for one S-I pair) gives $3\tilde{\beta}/(4+\tilde{\beta})$, which is the case of $z = 4$ in Eq (53).

In the real simulation space there are more sites around these five sites and tertiary infections that can occur in these four Ss by the transmission from going around of secondary infections along the loop. So, the number of newly produced S-I pairs are expected to be somehow small. The results are shown in Figure 4.

Unfortunately we cannot succeed in finding a way of evaluating $\mathscr{R}_0$ by Monte Carlo simulation for other models.

4.   Discussion

We obtained the basic reproduction number for SEIRS model on the regular lattice as Eq (47) by using the next-generation matrix. Inaba ^[12] stated $\mathscr{R}_0$ is determined uniquely, but from the viewpoint of ^[13], basic reproduction number by one method may not always agree with the one by another. Here we compare it to the results of other previous studies.

Ringa and Bauch ^[11] gives a basic reproduction number for SEIRS model on the lattice as

in which ^[11] uses the different notation $n$ instead of $z$ on page 158. It has much contrast to our Eq (47), which is dependent on $\tilde{\omega}$ but Eq (56) does not include it. In addition, observe that the effects of $\tilde{\nu}$ are completely opposite between them. Therefore, they have no coincidence on the critical condition for disease outbreak. Ringa and Bauch ^[11] adopted several assumptions to derive $\mathscr{R}_0$. We cannot specify which assumption most crucially causes the differences, but it shows the need to pay attention to use additional kind of approximations.

Keeling ^[8] studied the SIR model on a network including regular lattice, and obtained the basic reproduction number as

as shown in Section 2. Equation (57) says $\mathscr R_0 = 0$ for $z = 2$ and then someone interprets it as disease cannot invade into the susceptible population for any infectious rate on one-dimensional linear lattice space. However, it is natural to consider that $\mathscr R_0$ is always positive and the threshold condition to invade into the susceptible population is $\mathscr R_0 = 1$. Equation (53) gives $0 < \mathscr R_0 = \tilde{\beta}/(2+\tilde{\beta}) < 1$ for $z = 2$, then the basic reproduction number is positive but less than the threshold one, so infectious disease fails to invade on one dimensional lattice space.

When we carefully check the derivation of Eq (10) from Eqs (8) and (9), Eq (6) can be read as

It indicates that

which coincides with Eq (53). Hence, there is no difference in the critical infectious rate for outbreak between Eqs (53) and (57). However, the former is bounded by $z-1$, where $z$ is the number of nearest neighboring individuals, but the latter is unbounded when the infectious rate $\tilde{\beta}$ goes to infinity.

Kiss et al. ^[13] distinguished two kinds of basic reproductive ratio as $R_0$, an average number of transmissions an individual causes, and $\bar{R}_0$, growth-based basic reproduction ratio. They exemplified $\bar{R}_0$ by mean-field approximation for both SIS and SIR models, i.e.,

and by pairwise approximation ( = pair approximation) for SIS

and for SIR

For SIR they also give

which coincides with Eq (58) because transmission probability before recovery is $(\tilde\beta/z)/\{(\tilde\beta/z)+1\}$ and a newly infected individual has $z-1$ susceptible neighbors. However, using Eq (55), we can interpret transition rate of S-I pair to another as $\frac{1}{z}\tilde\beta+1$ instead of $1$, then growth-based basic reproduction ratio also becomes Eq (58) but not Eq (60). Therefore, there seems no difference between the two basic reproduction numbers by ^[13] for the SIR model. Here, we use $z$ instead of their $n$.

Bauch ^[10] concentrates on SIS lattice model and gives the basic reproduction number as

in Eq (50) in ^[10], in which the author uses $Q$ and $\beta/\nu$ instead of $z$ and $\tilde{\beta}$, respectively. Equation (61) is the same as Eq (59) by ^[13]. Observe that Eq (54) and (61) have the same critical infectious rate for an outbreak. Bauch ^[10] claimed that the basic reproduction number obtained by ordinary pair approximation as in Eq (61) is unbounded when $\tilde{\beta}$ goes to infinity. And then Bauch ^[10] proposed another new approximation called "invasory pair approximation" and succeeded in obtaining a bounded $\mathscr{R}_0$ for infinite large infectious rate. Alternatively we show another form of $\mathscr{R}_0$ by ordinary pair approximation using the next-generation matrix, which satisfies boundedness for infinite large infectious rate. Invasory pair approximation, in turn, gives the value $\frac{-z-1+z^2+\sqrt{z^4+2z^3-5z^2+2z+1}}{2(z-1)}$ for $\tilde{\beta}\to\infty$, which is easily seen to be greater than an integer $z \ge 2$. On the other hand, the basic reproduction number (54) is an increasing function of $\tilde{\beta}$ and gives $z$ when $\tilde{\beta}$ goes to infinity. It seems reasonable that the possible number of newly infected individuals is less than or equal to $z$, so ordinary pair approximation is considered to give rather a good estimation than invasory pair approximation in this meaning.

In the end, we should refer to the seminal work ^[14]. Trapman ^[14] gives a formal definition of the asymptotic reproduction number and its alternative to be applicable by pair approximation. Trapman ^[14] shows an example of SIR model on a regular network whose reproduction number can be calculated exactly and can compare several $\mathscr{R}_0$'s including ^[8] and correspondence to Eq (53), which is heuristically derived in ^[14]. This approach, i.e., comparison to an exact solution, clearly shows what a better solution or an approximation is. So, we would like to propose such models with exact basic reproduction number and evaluate the results obtained by th next-generation matrix.

In this paper, we derived basic reproduction number $\mathscr{R}_0$ for SEIRS, SEIR, SIRS, SIR, SIS models on regular lattice space using the next-generation matrix approach with pair approximation. We cannot find an appropriate quantity or variable to compare these results with Monte Carlo simulation except SIR model and then, we leave it as a future problem to estimate a basic reproduction number by Monte Carlo simulation for other basic epidemic models.

Here, we consider the basic reproduction number $\mathscr{R}_0$ for fundamental epidemic models by using next-generation matrix only on a regular lattice. However, realistic epidemics may usually occur on heterogeneous networks, then we will study the effects of these spatial structures on $\mathscr{R}_0$ by next-generation matrix approach in the future.

Acknowledgements

We sincerely appreciate Prof. Akira Sasaki and Dr. Koichi Saeki for telling me an idea to use next-generation matrix approach to get basic reproduction number for epidemic models on lattice. We also thank two anonymous reviewers whose comments are very much helpful to revise our manuscript. The authors would like to thank Enago (www.enago.jp) for the English language review.

Conflict of interest

The author declares there is no conflict of interest.