Using cultural, historical, and epidemiological data to inform, calibrate, and verify model structures in agent-based simulations

1.   Introduction

The use of equation-based models to study and explain the dynamics of infectious disease epidemics has a long history extending at least to the work of Daniel Bernoulli in the 18^th century ^[1], although the vast majority of work in this area dates from the last quarter of the 20^th century to the present. Much has been learned from these models about how infectious diseases spread, are maintained, and can be controlled in human populations. However, of necessity as well as by design, equation-based models possess numerous simplifying assumptions that make them unrealistic, especially when applied to small populations. Yet throughout most of their evolutionary history, humans have lived in very small groups and have interacted with other such groups on a relatively limited basis ^[2]. One could argue that even today, most people interact regularly with only a small number of other people ^[3,4]. In such situations, random factors can have very large effects on the outcome of infectious disease spread.

Incorporation of these random influences into equation-based models is often very challenging, however, and analysis of such models is usually limited in scope. Exceptions to this include the work of Frank Ball and colleagues, who have developed a series of equation-based stochastic models that incorporate households within communities and address the issue of disease transmission within the confines of the very small groups living within individual households ^[5,6,7]. Extensive analyses have been done on these models, which have provided substantial theoretical insights into how the household/community hierarchical structure and the social clustering that occurs at the household level influences threshold behavior as well as final epidemic size. Over the last several decades computer technology has progressed to such a degree, however, that it is now possible to develop very realistic epidemic models using computer simulation techniques. These should not replace equation-based models, but, especially when the structure of the computer models is inspired by similar equation-based models, they can be used to complement and supplement the important insights derived from the analysis of more theoretical models.

A variety of computer modeling approaches are available and have been used to study the spread of infectious diseases. In this paper we focus on one of these approaches, agent-based simulation. We begin by briefly describing what an agent-based model (ABM) is and the types of problems for which agent-based modeling is most appropriate. We also examine in a general sense how the modeling process works when designing an ABM as well as how to best calibrate such a model to guarantee that it is an appropriate representation of real processes. Following this we describe an ABM that we have developed for the spread of the 1918 influenza pandemic on the island of Newfoundland. We highlight decisions that we made about how to structure the model; specific calibration methods we used, including a replication study to verify the model and assess general model behavior; and some of the results from the sensitivity analysis. To emphasize the value of using data to help guide the development of specific structures in a model and the testing of the model, we finish by illustrating how these approaches facilitate realistic experiments to address practical questions related to the transmission patterns of infectious diseases.

2.   Agent-based modeling: a complementary approach to equation-based modeling of epidemics

Agent-based models are models in which the primary unit of analysis is an "agent", an individual that has the ability to take information from the environment and use that information to make a decision about its next action ^[8]. Agents may represent individual cells, entire organisms, or even groups of organisms that act in unison (e.g. households or communities). The environment may include attributes of the physical space, like natural resources, or non-physical space, like the passage of time. Besides the agents and the environment, ABMs include a set of rules that govern the specific interactions possible between different agents or between agents and their environment. One of the key characteristics of ABMs is that these rules are often stochastic in nature, which results in highly variable outcomes across runs.

Agent-based modeling differs from equation-based approaches in important ways ^[9]. The techniques used in agent-based modeling make it relatively easy to incorporate stochasticity, which is generally present in real world processes, especially when looking at individual behaviors and small populations. Typically, modelers using an agent-based approach will build randomness into agent behavior and/or environmental conditions. Stochasticity may also play a role in parameter selection, as some modelers choose to draw parameter estimates from distributions of possible values. The element of stochasticity in ABMs can be useful for helping to understand the range of variation in model results as well as potentially real situations, given a standard set of parameters. For example, how likely is an epidemic in a human population, given the parameters of a specific disease? How likely is it that an outbreak will end without developing into an epidemic? What if the disease is caused by a more virulent pathogen strain? Is an epidemic more or less likely if certain behavioral controls are put in place? All of these are questions that ABMs can help to answer. It is important to keep in mind, however, that models of many types can be used to address these same questions—ABMs are an addition to the arsenal of modeling approaches that have contributed to our ever-increasing understanding of how infectious disease epidemics spread and influence human populations.

In an ABM, the math is implicit and, in some ways, invisible. The modeling software that most agent-based modelers use does not require complete equations that describe the likelihood of certain outcomes. Instead, a modeler designs a hypothetical world and a set of agents that have individually varying characteristics. Agents are also designed with specific rules that govern their behavior and these rules (along with any random chance that might be built in) determine the likelihood of the outcome variables. While they might not be explicitly formulated, mathematical equations usually underlie the rules upon which the model is built, however. For example, infectious disease modelers using mathematical approaches commonly base the model on an SIR process or similar construct. The population is divided according to status with respect to the disease—susceptible (S), infectious (I), or recovered (R)—and then, for example, differential equations may be used to govern the transition between these stages. ABMs used to model infectious processes generally also divide the population into these disease classes and use similar formulations to govern the transition between stages, but the underlying mathematical structures are often not obvious.

ABMs have three major advantages over equation-based modeling techniques. First, as mentioned above, they are usually stochastic in nature and allow one to incorporate as many random factors as desired in a relatively straightforward fashion. As such, ABMs are particularly useful for illustrating how small changes in behavior might influence outcomes due to the cascading effects of those changes across a population and through time. Such effects are most important when modeling individuals and small populations, because in these situations random factors can have large and unexpected impacts on model outcomes. In addition, large population size is generally an assumption of traditional equation-based modeling methods, which limits their applicability to small populations.

A second advantage of ABMs is that they have the capacity to include more complex behaviors and structures than can equation-based models, allowing them to represent the world in a much more realistic fashion. They also can use a variety of mathematical tools within the structure of the model as long as the tools can be translated properly into the computer model. Furthermore, although a model's structures are always artificial, they are often able to capture essential aspects of real behavior, which opens the door to systematic study of these behaviors. This can be especially important in studies of infectious disease epidemiology, since experimental studies of the impact of specific behaviors on the spread of human diseases are often unethical and/or impossible to conduct. In order to have confidence in the results of "experiments" using an ABM, the more complex structures that can be incorporated into a model should, however, be based on an adequate understanding of and sufficient data from real world populations.

Although it is often advantageous to build into an ABM a fair degree of complex behaviors, that increased complexity can become a problem—sometimes researchers try to make a model so realistic that the number of parameters becomes too large for the researcher to determine which parts of the model are most responsible for observed results. Because of this, carefully designed ABMs often retain many simplifying assumptions that are justified by knowledge of the situation being modeled. This ensures that the models are reasonably realistic, but that the results are interpretable.

A third advantage of ABMs relates to their analysis. Analyses of stochastic equation-based models are generally very challenging, and depending on the complexity of the model, the appropriate techniques may not exist. The data resulting from ABMs on the other hand, are usually analyzed using standard statistical procedures, and most often these are much less complex than the methods needed to analyze stochastic equation-based models.

An essential component of developing an ABM is calibration. This occurs at multiple stages of the modeling process and should begin during the earliest stages of model development, when one is first attempting to construct the specific model components. If the goal is to develop a model that adequately represents real world situations, it is absolutely essential to base the relevant model structures as much as possible on empirical data. In addition, data are used to determine the appropriate level of detail to use in formulating model components ^[10]. In addition to aiding in the development of model structures, analysis of relevant empirical data should also underlie the estimation of model parameters, though in reality, such data may be lacking and assumptions may be needed. These uses of data in the development of an ABM may not typically be thought of as calibration procedures, but in essence they involve making sure that the model adequately reflects actual data. In other words, model structures are determined by comparing them to the "standard" that is derived from analysis of empirical data, and that comparison is at the heart of any calibration process.

Calibration of an ABM also occurs during verification and validation of the model. Model validation is a process during which comparisons are made between simulated data and empirical data to make sure the model as a whole is a reasonable representation of the real situation being modeled ^[11]. Validation is explicitly concerned with the relationship between the model and the real world and involves evaluating the credibility of model processes, checking their ability to generate realistic data similar to empirical data, and assessing how well the model can predict future outcomes in a real-world situation.

Verification of a model is a process designed to check that the model is doing what it was designed to do and does not include bugs or unintended behaviors ^[11]. This process occurs for individual methods while the model is under development, and also occurs once the model is completed but before it is used in specific applications. During this stage the ways that individual methods or the entire model work are compared with (i.e., calibrated to) theoretical expectations and empirical observations of what occurs in realistic instances of those processes; the assessment is not just a mechanistic examination of whether the computer algorithms are working as intended. Graebner ^[11] suggests that two steps should be included in the verification process: a) exploring how the model works, and b) making sure that the model adequately implements the real-world situation being conceptualized. Verification is done to ensure that the model is internally consistent and adequately reflects the scenario being modeled.

One method that can be used in initial verification of an ABM is a replication analysis. The goal of such an analysis is two-fold: a) to determine the "normal" behavior of a model, and b) to determine how many runs of a model are needed in order to ensure that the average results from a set of runs reflect this "normal" model behavior. A single epidemic in the real world might not resemble the normal model behavior, but real-world epidemics should fall within the range of potential outcomes of the model if the model has been designed appropriately. In order to determine whether the simulation model outputs do, in fact, encompass potential real-world epidemics, it is essential to replicate simulation results a sufficient number of times to be able to identify characteristics of the typical output and range of potential variation in outcomes of the model. This kind of analysis is only rarely done, and there are many examples in the literature of studies that are based on averaging only a small number of runs. The problem with these kinds of results is that one or two unusual runs can markedly skew the averages and give a misleading impression of the true model behavior. Conversely, an unusual set of "good" runs can make it seem that the "fit" of the model to reality is adequate, when it actually is not. Nonetheless, a replication study does not require all results to be essentially identical. Indeed, for our analyses, a pattern was observed where a substantial number of simulations resulted in no epidemic, which is consistent with our expectations of how both the model and real instances of disease transmission should work. As another example, if a set of parameters would lead to outcomes exhibiting threshold behavior or tipping points, the replication study would produce a set of plausible outcomes that include those behaviors and would document the frequencies of such outcomes and the circumstances under which they might occur. We illustrate below how replication analysis can help determine both the normal behavior and an adequate number of replications. This important issue is also discussed on a more technical level by Lee, et al. ^[12].

An essential part of the verification process is sensitivity analysis. Sensitivity analyses serve several important functions in model design, calibration, optimization and communication. They provide insights into model processes, including emergent properties, by identifying which input variables (or interactions between variables) underlie the most variation in output and which are most stable, and by quantifying uncertainty in model outcomes associated with uncertain parameter values. Sensitivity analyses are also used to assess robustness of models in response to different parameter values or under different scenarios. Results can be used to identify aspects of models that are insensitive and thus may not need to be modeled in more detail or at all ^{[13,14,15,16,17]}.

Sensitivity analyses can be broadly divided into local and global methods. Local sensitivity analyses focus on variation around a parameter of interest; typically, "one factor at a time" strategies are used, where one parameter is varied around a reference value and all other parameters are held constant. These analyses reveal the direction of change and magnitude of impact that can be reasonably attributed to the influence of a particular parameter ^{[13,16,17,18]}. Global analyses vary multiple or all input parameters simultaneously and/or sample across the entire parameter space. These methods, for example, Bayesian and Monte Carlo approaches (including Latin hypercube sampling), can better evaluate the effects of interactions between parameters and also do not rely on assumptions of linearity and additivity, as local methods often do ^{[13,16,17,18]}. Local sensitivity analyses are more common in modeling literature, but recent critiques have focused on their shortcomings for model evaluation (e.g. ^[19]).

The selection of methods for sensitivity analysis depends on the purpose of the analyses and the nature of the system under study. Complex models with many parameters are computationally expensive, limiting the benefits or feasibility of global sensitivity analyses ^[13,15]. ten Broeke, et al. ^[17] compared the "one factor at a time" method described above, a local sensitivity analysis method, to two different global sensitivity approaches, both of which had as a goal the decomposition of the variance in model outcomes into components related to particular model parameters. The first global method they considered in their review was a model-based approach that used an ordinary least-squares regression model in the variance decomposition; the second was a model-free method based on the Sobol' method (see ten Broeke, et al. ^[17] for details on this method). The Sobol' method does not use a specific model to decompose the variance in model outcomes; bootstrapping is used to assess the accuracy of the sensitivity indices. In their comparison, ten Broeke et al. ^[17] applied all three of these methods to the same, relatively simple ABM, and determined that none of them were fully adequate, but that the "one factor at a time" method was best able to provide insights into the mechanisms and patterns resulting from the model and was the least difficult to implement. For this reason, they recommended using this method as the starting point for all simulations. We also used this method in our research, and describe some of the results from our sensitivity analyses below.

3.   An illustration of the calibration and verification of an ABM

We illustrate the calibration and verification processes using a model we have built to examine the 1918 influenza pandemic in Newfoundland and Labrador. The model has been described in full detail elsewhere ^[20,21,22], so the brief description here will focus on the elements of the model most important to the larger discussion of linking models to a real scenario. The model community of St. Anthony was chosen because of some unusual data sources that helped to illuminate the social structure of the community and allowed us to build a more realistic model. We focus most of our discussion in this paper on calibration and verification, although we present selected results below to provide some examples of how the ABM model has been used to address questions about flu transmission in small human communities.

Boero & Squazzoni ^[10] divide ABMs designed for social science questions into three major types: case-based models, typifications, and theoretical abstractions. Case-based models are those that are based on the details of a specific place at a particular time and are characterized by features that are applicable only to that place and time. Boero & Squazzoni ^[10] suggest that the goal of such models is to explain the specific situation and possibly evaluate realistic scenarios to facilitate policy-making applicable to the particular place being modeled. Typifications are designed to provide the rationale for generalizations that help explain the underlying causes of empirical phenomena. Such models are stimulated by the empirical reality used in their design, but the degree of correspondence is not as great as with case-based models. Models of the third type, theoretical abstractions, focus on general social phenomena and do not relate to specific scenarios either in time or space.

On its surface, the model that we describe here (hereafter called the "SAmort model", referring to the fact that it is the St. Anthony model with mortality), appears to be a case-based model. It concerns a specific historical context and was designed with the goal to address time- and space-based questions. However, the decision to base the model on a specific historical community was done not to explain what happened in that particular community, but to realistically capture the kinds of social activities and interactions that often characterize small, traditional human communities. Thus, our model is more like a typification, with the consequence that the results can be extended beyond the particular historical context on which the model is based.

The disease process in the SAmort model follows an SEIR epidemic model, in which agents can be in one of five disease states: Susceptible, Exposed, Infectious, Recovered, or Dead. All agents, except for a randomly-chosen first case, begin in the susceptible state. As a consequence of their daily activities, susceptible agents may come into contact with an infectious agent. If such a contact results in disease transmission, the susceptible agent enters the exposed state and stays there for a pre-determined amount of time. The exposed agent then becomes infectious and is at risk of dying over a user-specified number of ticks. Infectious agents are also able to transmit the pathogen to susceptible agents when they come into contact. If the agent survives the infectious period, it transitions to the recovered state and is immune to the disease for the rest of the simulation.

The disease parameters used in the SAmort model are single values that can be changed by the user. Because our primary questions relate to stochastic variation in patterns of interaction among individuals within the population rather than in the variation of disease-related parameters, we have assumed constant values for the disease parameters, though the model could easily be adapted to allow them to be chosen according to a user-specified probability distribution. The default values of these parameters used in the sensitivity analyses (i.e., their values when they were held constant; see Table 1 below) were set to make it easier to focus on the actual impact of the parameter(s) being tested. For example, unless it was the parameter under consideration, the transmission rate was set at 1.0 (i.e., every contact leads to a transmission), even though this value is not realistic.

Table 1.  Parameter values used in sensitivity analyses of the model.

Parameter	Value when held constant	Range when varied
Latent Period	1 day	1–7 days, increment 1 day
Infectious Period	5 days	1–10 days, increment 1 day
Population Size	503	Target of 50–500, increment 50
Transmission Probability	1.0	0.01–0.1, increment of 0.01; 0.5; 1.0
Mortality Probability	0.00025	0.00005, 0.0001, 0.00015, 0.0002, 0.00025, 0.0003, 0.00035, 0.0004, 0.00045, 0.0005, 0.001, 0.01, 0.05, 0.1, 0.4, 0.7, 1.0

---

 | Show Table

DownLoad: CSV

The SAmort model population is based on the historical population of St. Anthony, Newfoundland and Labrador. We chose this community because we were interested in modeling the pandemic in a model population that reflected a rural, non-industrial community during the early 20^th century. Models of the 1918 influenza pandemic have largely focused on large, urban populations (e.g., ^[23,24,25]) and the opportunity to examine disease dynamics in a smaller, isolated community presented an interesting challenge for exploring nuances that could help explain regional variation in outcomes.

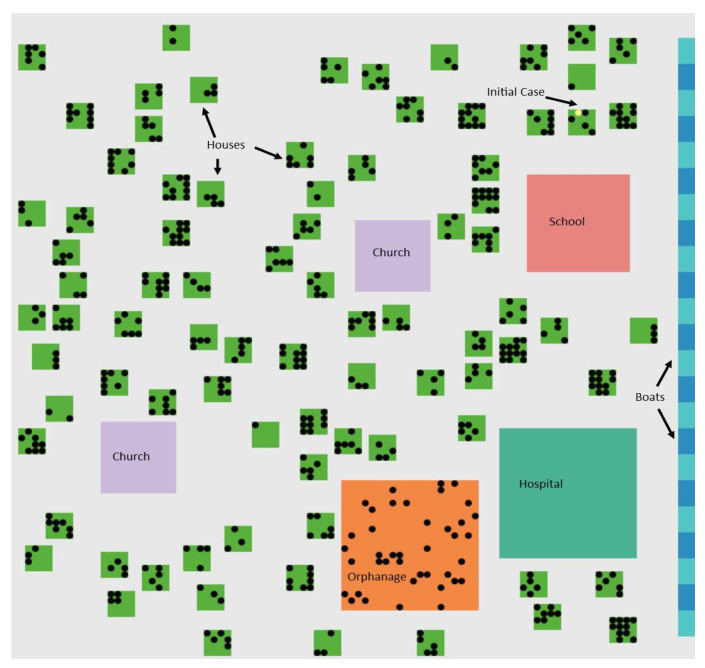
St. Anthony, a small coastal village, is located on the northernmost tip of the island of Newfoundland. In the early 20^th century, it was isolated and the main connections between it and other similar communities were via boat travel. Communities such as St. Anthony were typically small and kin-based. Local economies largely revolved around fishing or seasonal extractive activities (like logging or sealing). Most of the important economic activities were organized around patrilineal kin groups—fathers and sons or brothers typically co-owned fishing boats, while women helped process fish in shore crews. Most Newfoundland communities had few economic or occupational opportunities outside of fishing. Therefore, there was limited income and social inequality, and risk of hardship and disease was spread relatively evenly across the population ^{[26,27,28,29,30]}. Given these basic characteristics, the agent population used in the SAmort model was divided into several groups, including fishermen, fisherwomen (women who did not have dependent children), mothers, children, teachers, pastors, doctors and nurses, and selected other groups. Individuals were assigned to particular households and rules were devised to govern each type of agents' specific movements on different days of the week. Figure 1 provides a map of the community at night when everyone is at home, showing the different types of buildings and the agents assigned to each dwelling. Because fishing is the main occupational activity in the community, the map also indicates the numerous fishing boats to which specific households are assigned (two colors are distinguished only to allow visualization of particular boats).

Figure 1.  Map of the simulated community showing the different building types and the location of agents at night when all agents are at their assigned home location.

DownLoad: Full-Size Img PowerPoint

Rich family census data and ethnohistorical records provided the specific data we needed to calibrate the structures for the model population. Census data listed all members of the community by age, sex, and household, allowing us to model a realistic age and sex structure at the household and community level. Ethnographic information about Newfoundland culture and historical documents from St. Anthony during the early 20^th century were used to build the rules that governed agent behavior. Historical information included newspaper articles, government reports, telegrams, photos, diaries and memoirs, and other ephemera (e.g. ^[31,32]; the International Grenfell Association's journal Among the Deep Sea Fishers). These sources provided a sense of how the community worked, which allowed us to develop rules for agents that realistically governed typical daily activities during a week. Sex and age were important determinants of activities, so behavioral rules were largely structured according to subetaoups based on these criteria. ABMs are a natural way to incorporate these culturally specific rules. Furthermore, they allow the models to be particularistic, but the rules themselves are generalizable to a variety of populations and the models can be easily extended to other places and times.

We illustrate how the data described above can actually be translated into these rules by elaborating on how the SAmort model rules governed daily agent behavior. We first set up a daily schedule, in which each tick represented a four-hour unit of time. Every agent was assigned an age- and sex-related occupation, which they used to determine what movements and behaviors to undertake at a given time, often with some degree of probability. So, for example, at 10 a.m. on a Tuesday morning, an adult male is likely to be on his fishing boat, while his school-aged children will likely be in the school building, and his wife and preschool children may be in their home or out visiting in the community. At the end of the day, the family comes back together in the house in the evening and then disperses again the next day.

Agents move directly from point to point on the space. They choose their locations by referencing their own demographic attributes, the day of the week and time of day, and the number of available spaces in the location to which they want to move. There are no movement paths, instead individuals moving look for a single open cell in the desired location, while family groups will look for a location that has enough space for the entire group. Alternative movements are usually available for agents who cannot find space in their desired location. As the epidemic progresses, dependent children who lose their caretakers are assigned to new caretakers. The reassignment process was designed with cultural principles in mind—other caretakers within a household are identified first, and if none are available, an attempt is made to identify a close female relative in the wider community before trying to find other potential caretakers.

Though these decisions seem simple, a deep understanding of ethnographic knowledge and data derived from many different sources was essential in coming up with the daily schedule of activities. These sources are, for the most part, primary historical records created by people alive during the early 20^th century and are drawn from a number of different communities, not just St. Anthony. Through cultural, demographic, and historical research, we learned how to distribute the community into different occupational groups and how the schedules of adult men and women differed. We learned the average length of a school day and the ages at which children started and stopped attending school, and we also learned that children were likely to help with the family fishing business, especially on Saturdays. From this, we decided that children would be in school from ages 5 to 15, and that older children (≥ 10 years) would have a chance of going to the boats on Saturdays. From memoirs and letters, we learned about the lives of married women, and how they spent their days on shore as their husbands and adult sons fished. It was this information that was the basis of visiting that women do on weekdays, as well as their involvement in shore crews. From photos and maps, we were able to get a sense of the density of the community and of the particular buildings within the community. We used these to decide on the sizes of the houses, churches, and school buildings. In the calibration process, we checked how and when agents were moving on the visual map of the simulation as well as values we recorded to indicate where each agent was during a model step in order to guarantee that the timing and locations of agents' behaviors were analogous to what we had seen in historic sources. Without these background resources to guide us, we would have made decisions on all these behaviors that might have been acceptable, but would not have been calibrated well enough to reflect the reality of people in towns like St. Anthony, and thus the model would have remained more theoretical than we were aiming for.

Although it would be interesting to compare this model to an equation-based homogeneous model, designing an equation-based model that is directly comparable to the ABM is a non-trivial process and would be difficult, if not impossible. This is especially the case since, as described below, one of the interesting uses of our model involves a consideration of the interaction between the length of the latent period and the specific day an epidemic begins. Variation in latent period length is easy to incorporate into a homogeneous, equation-based model, but in a homogeneous model, variation in the start day would not affect model behavior, since the behavior of the population does not change from day to day, making it much more difficult to determine what an appropriate equation-based analog would look like.

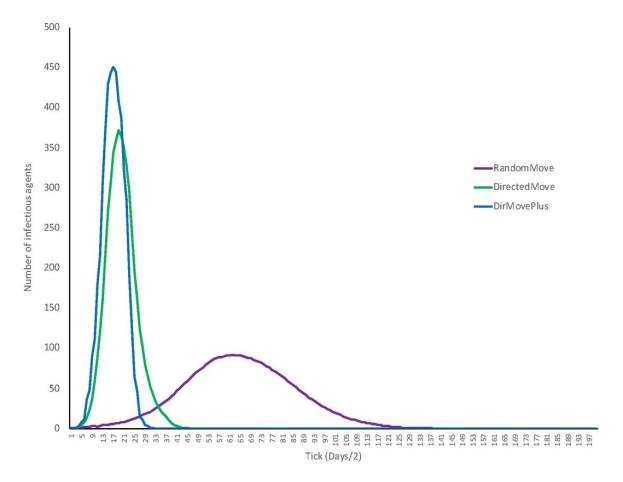
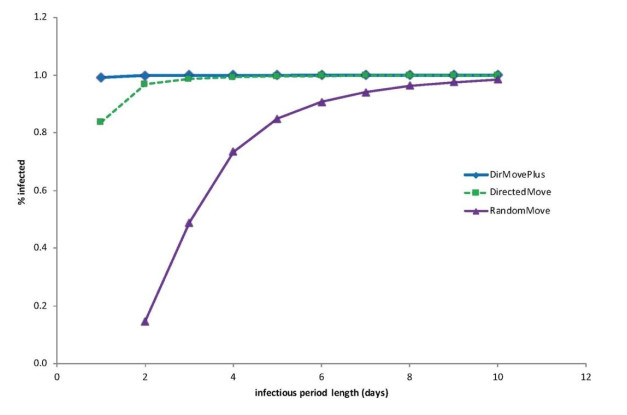
However, the model just described was developed in stages from simpler to more complex movements and interactions, with extensive analyses at each stage. A comparison of the outcomes from the analyses of these different stages provides insight into how the increasing complexity changes our understanding of disease transmission in human groups. In the earliest version, RandomMove, agents moved randomly on the space without any structured interactions. The following version, DirectedMove, included specific movements only for fishermen and schoolchildren, while all other agents moved within the home. The third version, DirMovePlus, contained full movement and is identical to the SAmort model when the mortality probability is set to zero. Comparisons of these successively more complex models (Figures 2 and 3) demonstrate that quantitatively and qualitatively different epidemics are produced with more realistic social spaces and movement, illustrating the usefulness of ABM for obtaining new insights into disease transmission. Notably, epidemics produced by the random movement model are, on average, slower and smaller than those produced by the other two versions, particularly the most complex yet realistic of the three.

Figure 2.  Epidemic curves for three different versions of an ABM of influenza transmission. See text for descriptions of each model. All models were run using the same basic parameters. Curves show the means of 100-run sets.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Final percentage infected for different lengths of the infectious period in three versions of an ABM of influenza transmission. See text for descriptions of each model. All models were run using the same basic parameters. Curves show the means of 100-run sets.

DownLoad: Full-Size Img PowerPoint

Humans do not move randomly throughout space. This model comparison clearly indicates that a random movement assumption can lead to conclusions about disease transmission that would be different if more realistic movement patterns were incorporated into the model. This is especially true when modeling small populations.

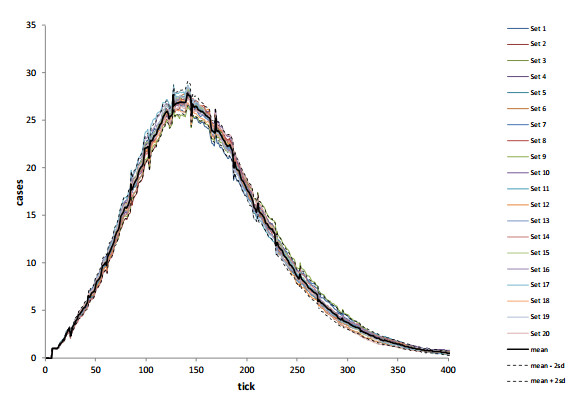
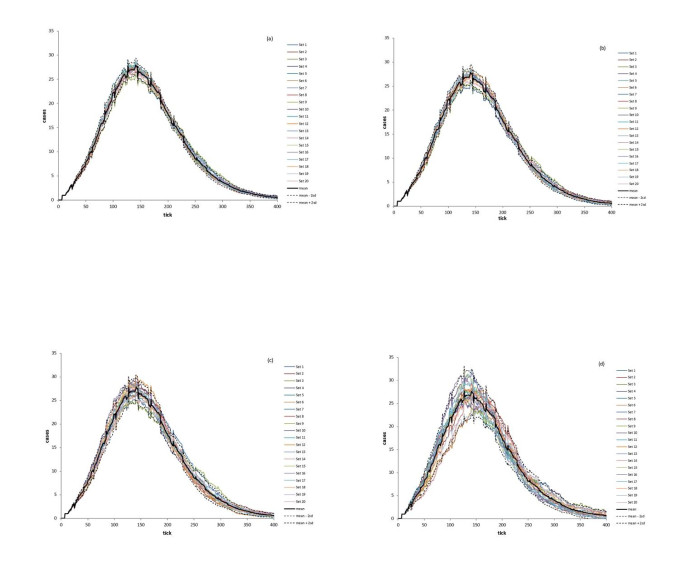
Once the structure of the SAmort model was completed, we proceeded to verify that the full model adequately represented the scenario for which it was designed. The first step of this process was to complete a replication study so that we could identify both the typical behavior of the model and the minimum number of runs necessary to ensure that the average results from a set of runs would be unlikely to be an unusual outcome. This knowledge is essential when addressing research-oriented and practical questions. For our replication study we completed 20 sets of 1000 runs each, generating a total of 20,000 runs of the model. We calculated the average number of cases of disease for each tick of the simulation across all 1000 runs in a set, and then calculated the grand mean per tick of all 20 sets of 1000 runs. We also calculated bounds of the mean number of cases per tick ± 2 standard deviations. All 20 mean epidemic curves plus the grand mean and bounds were then plotted to assess the normal behavior of the model.

The model is well behaved when using sets of 1000 runs—all curves parallel the grand mean, including, for the most part, the peaks and troughs of that grand mean, and all curves are within the bounds we set at all points of the simulations (Figure 4). Figures 5a–d show equivalent graphs using sets of 800,500,300, and 100 runs, respectively. These graphs indicate that although there is more observed spread in the sets of 800 and 500 runs, the curves still parallel the grand mean and are within ± 2 standard deviations of the grand mean. When sets are composed of only 300 runs (Figure 5c), some of the curves fall outside the bounds of the grand mean, but the pattern is still generally followed. However, the curves for sets of 100 runs clearly indicate that sets of this size produce more variation than desired (Figure 5d). As a result of this study, we determined that, for research-oriented questions, a minimum of 300 runs should be used if at all possible, that 500 runs would be better, but that running more than 500 simulations would produce diminishing returns that would not be well justified.

Figure 4.  Replication study. Each line represents the per tick mean of a set of 1000 runs. The thick black line is the grand mean of all 20 sets of 1000 runs, and the dotted lines are values ± 2 standard deviations from that grand mean.

DownLoad: Full-Size Img PowerPoint

Figure 5.  Replication study results using smaller numbers of runs per set. a) 800 run sets, b) 500 run sets, c) 300 run sets, d) 100 run sets.

DownLoad: Full-Size Img PowerPoint

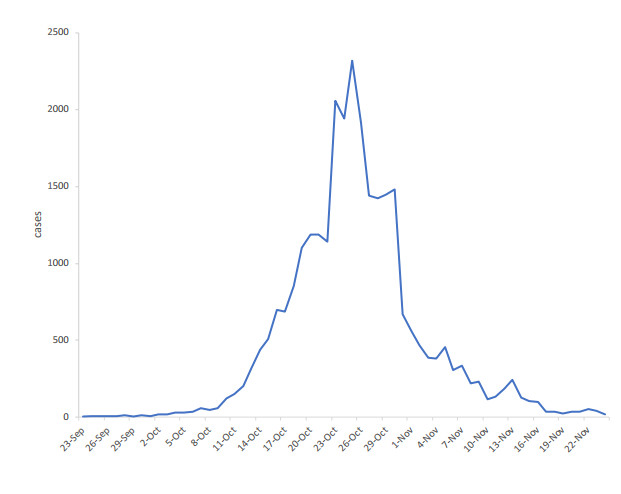
Results of the replication study also clearly illustrate that the model leads to epidemic curves that are typical for influenza epidemics. For example, standard epidemic curves, reflecting growth in the number of cases to one or more peaks followed by a decline as the epidemic runs its course, were observed in many simulations as well as in all the curves shown in Figures 4 and 5. Because influenza is highly contagious, actual influenza epidemics usually rise very quickly to a peak. Since the illness is not long-lasting, they also tend to drop fairly quickly and then die out as the number of contacts between susceptible and infectious individuals declines due to the increasing number of people who have recovered. This behavior can be clearly seen in Figure 6, which shows an actual influenza epidemic curve from the 1918 pandemic. Because our focus is more on understanding qualitative epidemic dynamics rather than using our model to predict the behavior of future epidemics, we have not quantitatively assessed how well the model approximates patterns like that seen in Figure 6; nonetheless, it is clear that our model generates realistic epidemic curves.

Figure 6.  Example of an epidemic curve from a real epidemic: Number of influenza notifications per day in San Francisco during the 1918 influenza pandemic. Data provided by G. Chowell. Original source of data: ^[33].

DownLoad: Full-Size Img PowerPoint

The next step of the model verification process was sensitivity analysis, and we have conducted innumerable studies of this type. Because these were designed to test the effects of different values for the parameters, with comparisons of a qualitative nature only, we limited our data to sets of 100 runs so that computation time would be reduced. This also allowed us to compare these results with those from earlier versions of the model, which used only 100 runs of the simulation.

We primarily used the "one factor at a time" strategy described above to determine the impact of different parameters on model outcomes, although we also analyzed the joint effect of two parameters to test whether interactions were important. Our parameters of interest were the duration of the latent and infectious periods in days, the transmission probability per contact, the mortality probability per tick, and the population size. Each parameter was varied singly across an extreme range of values, while all other parameters were held constant. Baseline values for parameters other than population size as well as minimum and maximum values were chosen based on assumptions about the biology of influenza; intermediate values were distributed throughout those ranges and spaced out so that analyses would generate reasonable curves to represent the effect of a parameter throughout the chosen range. When varying population size, we increased the population by a target of 50 people for each set of comparisons, but in order to retain our realistic distribution of household sizes and composition, we added full households rather than individuals to increase the population size. As a consequence, the actual population sizes varied slightly from the target sizes. Table 1 lists the baseline values for each parameter, as well as the values used when the parameter was varied. See Orbann et al. ^[21] and Sattenspiel et al. ^[22] for general discussions of many of these analyses.

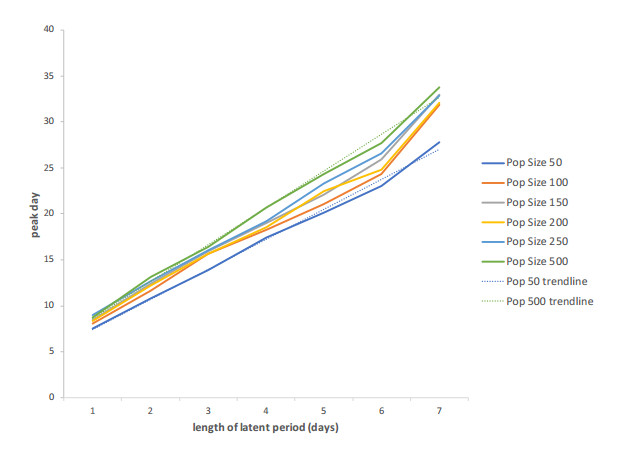
One unexpected finding from these analyses was that a latent period of 6 days resulted in values that departed from expected trends for a number of outcomes. This conclusion was suggested by the sharp upturn in all the graphs shown in Figure 7 and verified by trendlines. As the figure shows, a latent period of 6 days led to an earlier than expected peak day of the epidemic, and this effect occurred for all population sizes. Additionally, a latent period of 7 days resulted in a later than expected peak day of the epidemic (Figure 7). We hypothesized that these findings were related to the cyclic nature of weekly church attendance, as a latent period of 6 days in combination with default values of other parameters would result in the first case becoming infectious on Sundays, a situation that allowed them to transmit the pathogen at a time and place (the church) with the highest population density in the community. The increased density of susceptible agents with whom the infectious case came into contact could result in rapid early spread due to agents being infected in relatively large cohorts. Extending the latent period to 7 days would have meant that infected agents remained in the exposed class when they went to church and failed to transmit the disease at that time, which may have delayed epidemic spread to the small degree observed. The association of this delay with a latent period of only 7 days rather than other lengths may have been due to the fact that the initial cohort of secondary infections would have ended their 5-day infectious period before attending church for the first time after infection, a situation that would not be the case for other latent periods.

Figure 7.  Peak day of an epidemic when both length of the latent period and population size are varied. Dotted lines represent trendlines for the largest and smallest population sizes; similar lines occur for other population sizes.

DownLoad: Full-Size Img PowerPoint

4.   Using the model to address research questions

The main purpose of sensitivity analyses is to verify that the model is working as intended. However, similar analyses can be used to test hypotheses, consider research questions, and inform real-world decision-making and management strategies ^[13,14,16]. Although the main purpose of this paper is to highlight the model development process, a major goal of many modeling studies is to use models to extend our understanding of the real situation being modeled. Thus, we briefly illustrate how this can be done with our model by systematically testing the church day hypothesis through simultaneous variation of two inputs–the latent period and the day on which the epidemic begins. We simulated sets of 500 epidemics jointly varying latent period from 1–7 days and the epidemic starting day across the week, always beginning at 6:00 a.m., while all other parameters were held constant. More realistic baseline values of other parameters were drawn from the influenza literature and model calibration to reflect values for the 1918 influenza pandemic in Newfoundland communities. These values are an infectious period of 3 days, a per tick transmission probability of 0.042, and a per tick mortality probability of 0.00076 (see ^[22] for more details on how these values were derived).

The major practical goal of these analyses was to determine whether attendance in a crowded church early in an epidemic helped to drive outcomes. We hypothesized that if that were the case, results from parameter sets that had the end of the latent period coincidental with a church day would give different results from simulations that started on a day of the week that led to the latent period ending on a non-church day. For example, if a three-day latent period was assumed and the epidemic started on Thursday morning, the end of the latent period would coincide with Sunday church; in such a case, we expected that epidemics starting on Thursday and with a three-day latent period would spread much more quickly than epidemics with the same latent period that started on Wednesday or Friday.

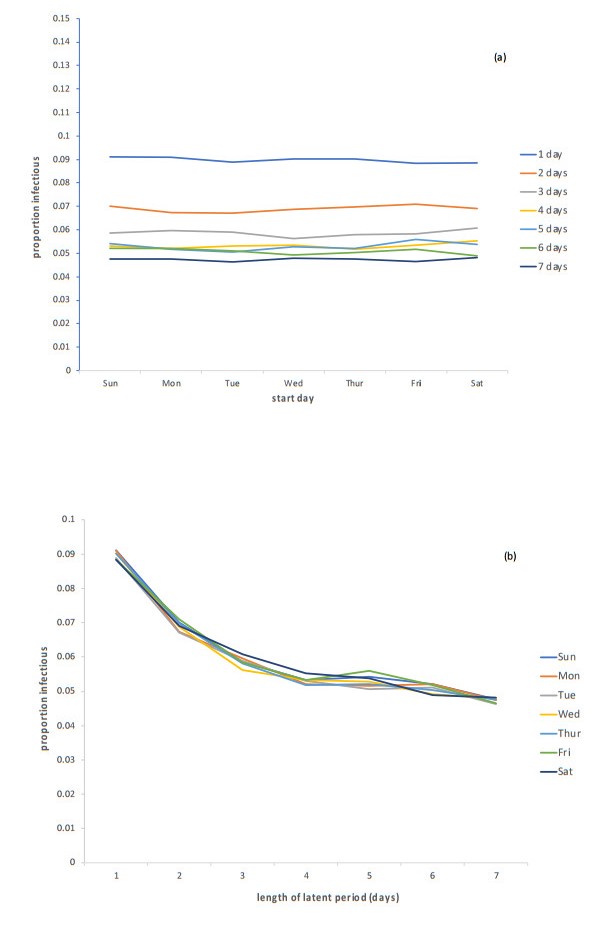
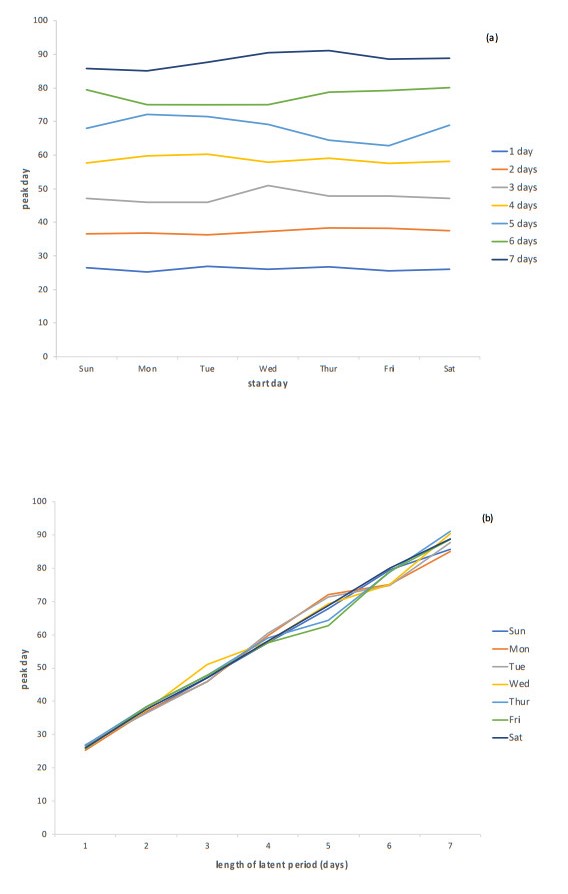
Results of these analyses indicate that the duration of the latent period drives the outcomes regardless of the starting day. This pattern is seen best when comparing outcomes related to the peak of the epidemic. The proportion of agents who are infectious at the peak remains relatively constant for a particular latent period across all starting days (Figure 8a), while all starting days follow a general pattern of declining proportions with longer latent periods (Figure 8b). Similarly, graphs of the peak day do not vary much for a specific latent period, regardless of starting day (Figure 9a), while values for all starting days increase in a linear fashion when graphed across latent periods (Figure 9b).

Figure 8.  Proportion of infectious agents at the epidemic peak: a) varying starting day, different latent periods, b) varying latent period, different starting days.

DownLoad: Full-Size Img PowerPoint

Figure 9.  Peak day of epidemic: a) varying starting day, different latent periods, b) varying latent period, different starting days.

DownLoad: Full-Size Img PowerPoint

Contrary to hypothesized expectations, no clear pattern in outcomes can be seen when investigating starting day/latent period combinations that result in early cases becoming infectious at the time of culturally important weekly activities such as church attendance (Table 2). In other words, there is no clear relationship between the ending of the latent period (i.e., onset of infectiousness) and the specific social event of church attendance. Some combinations do show possible differences. For example, Saturday/1-day (i.e., Saturday start, 1-day latent period) and Monday/6-days both produce final epidemic sizes different from expected patterns (Table 2). In the Saturday/1-day case, however, the final size is actually more than one standard deviation smaller than the average, suggesting a church day early in the epidemic did not facilitate rapid spread. Notably, most of the outcomes for the church-related parameter combinations are within one standard deviation of the corresponding grand mean for all epidemic outcomes, while most of the observed extreme values are produced by parameters outside of church-related combinations. While other potential patterns are not immediately forthcoming, these results (e.g. peak proportion and peak day for a latent period of 1 day in Table 2) more likely reflect the driving influence of the latent period duration on overall outcomes.

Table 2.  Epidemic outcomes comparing latent periods for specific starting days.

Start day	Grand mean across all latent periods (s.d.)	Latent period duration (days)1, 2
		1	2	3	4	5	6	7
Average final size (# ever infected)
Sunday	255.5 (5.0)				*		*
Monday	256.0 (5.7)	*					*
Tuesday	255.4 (5.9)	*	*				*
Wednesday	255.5 (5.6)			*		*		*
Thursday	255.2 (3.7)		*		*		*
Friday	258.3 (7.4)	*				*
Saturday	257.5 (4.3)	*
Average proportion of infectious agents at the peak
Sunday	0.06 (0.02)	**
Monday	0.06 (0.02)	**
Tuesday	0.06 (0.01)	**
Wednesday	0.06 (0.02)	**
Thursday	0.06 (0.02)	**
Friday	0.06 (0.01)	*
Saturday	0.06 (0.01)	*
Average peak day
Sunday	57.3 (22.0)	*					*	*
Monday	57.2 (21.9)	*						*
Tuesday	57.7 (22.1)	*						*
Wednesday	58.1 (22.2)	*						*
Thursday	58.0 (22.5)	*						*
Friday	57.1 (22.2)	*						*
Saturday	58.1 (22.8)	*						*
1.* = value is more than 1 standard deviation greater or less than the grand mean of the outcome for all latent periods for that particular starting day. ** = value is more than 2 standard deviations greater or less than the grand mean of the outcome for all latent periods for that particular starting day. 2.Shaded cells (rising diagonally from lower left corner) indicate the parameter combinations that would result in the first case becoming infectious on a Sunday (church day)

---

 | Show Table

DownLoad: CSV

5.   Discussion and conclusions

Construction of an ABM, particularly if it is complex and designed to realistically represent a process occurring in real populations, requires in-depth knowledge of the population on which the model is based so that the structures incorporated into the model truly reflect that population. Because this task is essential but perhaps unfamiliar to many modelers, including some who have designed their own ABMs, we have provided detailed descriptions of the types of data we have used in the development of our model. Designing the structure is not enough, however—the time-consuming tasks of verifying that the model works as intended and reflects the real-world situation are also critical. We focus in this paper on the approaches we have used for these tasks, but it is important to realize that a variety of approaches have been used in other models. We have briefly mentioned a few of these, but a full review of these topics is outside the scope of this paper. Nonetheless, every modeler who wishes to pursue the development of an ABM should carefully calibrate and verify the structures of their model before proceeding to address questions stimulated by practical needs. Without such careful testing of a model, there is no way to determine whether the results of the practical analyses represent normal model behavior or are unusual results due to the stochastic nature of the model.

Often during the testing process, results will be generated that stimulate interesting hypotheses related to the process being modeled and that can be pursued in future research. This was the case with our research. Sensitivity analyses of the SAmort model, previous research using the model, and observations of real-world epidemics have demonstrated that churches can be important locations for disease transmission because they bring together large groups in close settings. These observations led to our hypothesis that if the end of the latent period ended on Sunday, when the entire community congregated in church, epidemics would spread more readily throughout the population. The latent period length leading to this behavior would then depend on the particular starting day.

Although subsequent analyses did not support this hypothesis, the process of testing it has stimulated new ideas and hypotheses related to the consequences of the timing of daily or weekly activities, an aspect of infectious disease transmission patterns that has only rarely been addressed in existing literature. A few articles related to our hypothesis have recently appeared, however. Neal ^[34] built upon the equation-based household model he developed with Ball ^[5,6] and incorporated time-of-day effects by dividing a day into two parts (morning and night), with community-wide contacts assumed during the day and household-only contacts occurring at night. Numerical analyses indicated that the time during which an initial infection occurs can have a dramatic effect on the extinction probability of an epidemic. Towers and Chowell ^[35] compared the results of an equation-based model that incorporated separate weekend and weekday contact patterns to those from the same model using only the average contact matrix. They found that when there was no seasonality in the average contact rates, the models led to similar estimates of peak incidence time and final size, but that the weekday contact pattern model produced a marked weekday incidence pattern. Finally, Colman et al. ^[36] generated a similar hypothesis to ours—that diseases would be most pervasive when high levels of social activity coincided with the end of the latent behavior. Their model was an equation-based network model and they used standard network analysis techniques to assess model results. They also focused on the impact of sickness behaviors, which they assumed reduced the length of the effective infectious period. Their results supported their hypothesis of an interaction between levels of social activity and the length of the latent period.

Our hypothesis focused on the impact of church attendance, but church is not the only location where transmission happens, and there are other important places (e.g., schools) that also bring together large groups in close settings. It is also likely that the characteristics of the initial infected person impacted our results. For example, it may be that there is a relationship between the starting day of an epidemic and the length of the latent period, but the specific values for these parameters that cause an effect would be different for epidemics beginning with schoolchildren and those beginning with other people. In addition, incorporation of changes in behavior as a consequence of sickness may influence the patterns we have observed. The detail inherent in our model will allow us to explore these possibilities in future research.

Institutions like churches and schools are often central to the life of a community, especially when the community is small and tight-knit. Attendance at these institutions varies in predictable ways, as well as more irregularly, e.g. due to school breaks and religious holidays. During devastating pandemics, people may be more likely to attend church to seek spiritual comfort or protection or attend funerals, or they may cancel or avoid services out of fear of infection. Additionally, public health policymakers may focus on these institutions and associated behaviors for potential interventions. Therefore, it may be advisable to include them when designing simulation models. However, including these kinds of behavior requires in-depth knowledge of the communities being modeled as well as detailed data to use in determining appropriate model structures and estimates of parameters. Careful assessment of the results of sensitivity analyses may help to determine which types of data and model structures are essential and which can be approximated by making reasonable assumptions and using simpler forms.

This example illustrates how, once verification and calibration processes have been completed, a model can be used to address research questions of interest. Calibration, in the sense we have defined it, means ensuring that the structure of the model and estimates of essential parameters are suitably grounded in real understanding of the characteristics of the population being modeled. This understanding guarantees that we are able to test questions like those described here with confidence that the results will reflect true possibilities. We propose that this thorough exploration to ensure that model population characteristics are realistic should be a central concern in the development of any model, and especially of those intended to be used to address questions of importance in today's world.

Acknowledgements

Funding for this research was provided by the Government of Canada-Canada Studies Faculty Research Grant Program, the University of Missouri Research Board, and the University of Missouri Research Council. Additionally, we thank Amy Warren and Erin Miller for contributions to sensitivity analysis and other insights into this project and we thank the anonymous reviewers for their valuable critiques.

Conflict of interest

All authors declare no conflicts of interest in this paper.