The impacts of dispersal on the competition outcome of multi-patch competition models

In Memory of Geoffrey J. Butler and Herbert I. Freedman

1.   Introduction

Dispersal is one of the most important processes in spatially structured populations. It couples locally interacting populations from all connected patches and results in a metapopulation structure ^[1]. The movement of dispersing individuals between different habitat patches not only affects local dynamics, but also has global impacts on the persistence and resilience of populations, species coexistence, and ecosystem functions ^[2]. The role of the dispersal in the metapopulation dynamics has always been an interesting research topic and has attracted much attention. See, for example, ^[3,4] for experimental reports, ^[5,6] for work on single species models with dispersal.

When it comes to multi-species models with dispersal, tremendous work has focused on predator-prey systems. To name a few, see ^{[7,8,9,10,11,14,15,16,17,18]} and reference therein. Of which, Kuang and Takeuchi ^[11] found that the dispersal of prey can stabilize and destabilize the homogeneous coexistence equilibrium in a two-patch predator-prey system. Kang et al. ^[10] showed that in a two-patch predator-prey system with the dispersal of predator only, the dispersal may generate multiple interior equilibria inducing rich bistable phenomena and may also affect the existence of the interior equilibrium leading to the extinction of predator in one patch or both patches. Zhang et al. ^[18] incorporated a dispersal delay accounting for the travel time from one patch to the other into a two-patch predator-prey model and showed that the dispersal delay may stabilize an unstable coexistence equilibrium. Recently, Mai et al. considered predator-prey models with delayed dispersal over an arbitrary number of patches and showed that the dispersal delay can induce multiple stability switches ^[12,13].

Compared to predator-prey models, studies on competition models with dispersal are relatively scarce and have focused on dispersal between two patches only ^[19,20]. To the best of our knowledge, no work has yet incorporated the travel time into the dispersal process for competition models in patchy environments over an arbitrary number of patches. In this work, we shall consider a two-species competition model with one species dispersing between patches. More precisely, we consider two different connection configurations of $n$ patches (where $n$ is an arbitrary positive integer). Since the resulting model would be of high dimension ($2n$), we assume that the $n$ patches are identical and the dispersal rate is the same to make the analysis possible. Moreover, we incorporate the travel time into the dispersal process. Our objective is to investigate the impacts of dispersal on the dynamics of the multi-patch competition model under two connection configurations.

The rest of the paper is organized as follows. We summarize known results on a single-patch competition model in Section 2. Detailed stability analysis is presented in Section 3 and Section 4 for our multi-patch competition model under two different connection configurations. Numerical simulations are given in Section 5 to explore the impacts of dispersal on the competition outcome. A brief summary is given in Section 6.

2.   The single-patch model

Our multi-patch model is based on the single-patch model described below by a system of two ordinary differential equations

where $N_1(t)$ and $N_2(t)$ denote the population densities of two competing species at time $t$, respectively; The parameters $r_1$ and $r_2$ are their corresponding intrinsic growth rates; $K_1$ and $K_2$ are the carrying capacities of $N_1$ and $N_2$, respectively; The parameters $b_{12}$ and $b_{21}$ measure the competition strengths $N_2$ on $N_1$ and $N_1$ on $N_2$, respectively.

Setting $x = \frac{N_1}{K_1}, \; y = \frac{N_2}{K_2}, \; s = r_1t, \; \rho = \frac{r_2}{r_1}, \; a_{12} = b_{12}\frac{K_2}{K_1}, \; a_{21} = b_{21}\frac{K_1}{K_2},$ we obtain the dimensionless form as follows:

System (2.1) admits four possible equilibria: $(0, 0)$, $(1, 0)$, $(0, 1)$ and $(x^{*}, y^{*})$ with

The dynamics of (2.1) is summarized in the following result (See [21]).

Theorem 2.1. For system (2.1), we have the following conclusions:

$(i)$ The coexistence equilibrium $(x^{*}, y^{*})$ exists if and only if $a_{12} > 1, \; a_{21} > 1$ (strong competition case) or $a_{12} < 1, \; a_{21} < 1$ (weak competition case).

$(ii)$ The coexistence equilibrium $(x^{*}, y^{*})$ is stable if $a_{12} < 1$ and $a_{21} < 1$, and is unstable if $a_{12} > 1$ and $a_{21} > 1$.

$(iii)$ The boundary equilibrium $(0, 1)$ is stable if $a_{12} > 1$, and is unstable if $a_{12} < 1$.

$(iv)$ The boundary equilibrium $(1, 0)$ is stable if $a_{21} > 1$, and is unstable if $a_{21} < 1$.

3.   The fully connected patchy model

In this section, we assume that the $n$ (identical) habitat patches are fully connected in the sense that individuals from one patch can disperse to all other $n-1$ patches and the dispersal of one species is at the same rate with a fixed travel time. That is, we consider the following $n$-patch competition model (in dimensionless form):

where $n$ is the total number of patches. $x_i$ and $y_i$ denote the densities of species $x$ and $y$ in patch $i$, respectively, $i = 1, 2, \dots, n$. $d > 0$ is the rescaled dispersal rate. The dispersal delay $\tau\geq 0$ accounts for the rescaled travel time from one patch to another. $\tau = 0$ means the movement between patches is instantaneous, while $\tau > 0$ implies that the dispersal is not instantaneous.

For model (3.1), we call an equilibrium $(\bar{x}_1, \bar{y}_1, \bar{x}_2, \bar{y}_2, \cdots, \bar{x}_n, \bar{y}_n)$ an $x-$homogeneous equilibrium if $\bar{x}_1\equiv\bar{x}_2\equiv \cdots \equiv \bar{x}_n$, a $y-$homogeneous equilibrium if $\bar{y}_1\equiv\bar{y}_2\equiv \cdots \equiv \bar{y}_n$, and a homogeneous equilibrium if it is both an $x-$homogeneous equilibrium and a $y-$homogeneous equilibrium.

If $a_{12} > 1, \; a_{21} > 1$ or $a_{12} < 1, \; a_{21} < 1$, then (3.1) always admits a homogeneous coexistence equilibrium

We first give a result on the existence of the coexistence equilibria.

Theorem 3.1. Consider system (3.1). For the weak competition case (i.e., $a_{12} < 1$ and $a_{21} < 1$), system (3.1) admits a unique coexistence equilibrium $E_n^*$, which is homogeneous; while for the strong competition case (i.e., $a_{12} > 1$ and $a_{21} > 1$), besides the homogeneous coexistence equilibrium $E_n^*$, there may exist multiple coexistence equilibria provided that the dispersal rate $d$ is small.

Proof. Suppose that $E = (x_1, y_1, x_2, y_2, \cdots, x_n, y_n)$ is a coexistence equilibrium of system (3.1), then there must hold

for $i = 1, 2, \cdots, n$. Plugging the expression of $y_i$ into the first equation of (3.2) immediately yields

Summing (3.3) over $i$ yields

This shows that if $E$ is an $x-$homogeneous coexistence equilibrium, then $x_1 = x_2 = \cdots = x_n = x^*$ and hence $y_1 = y_2 = \cdots = y_n = y^*$. Therefore, $E = E_n^*$ is the unique homogeneous coexistence equilibrium provided that $a_{12} < 1, a_{21} < 1$ or $a_{12} > 1, a_{21} > 1$.

Next we seek for equilibria which are not $x-$homogeneous. It follows from (3.3) that

Consequently, for $\forall i \neq j$, either $x_i = x_j$ or $x_i + x_j = \frac{1 - a_{12} - nd}{1 - a_{12}a_{21}}$. Without loss of generality, we can assume that there exists an integer $1\leq m\leq n-1$ such that $x_1 = x_2 = \cdots = x_m = : \alpha$ and $x_{m+1} = x_{m+2} = \cdots = x_n = : \beta$ with $\alpha\neq \beta$. Then we have

and

It follows from (3.6) that

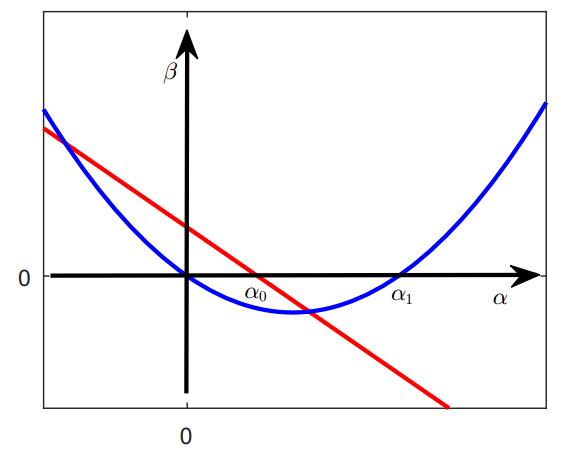
We first consider the weak competition case. Note that $a_{12} < 1$ and $a_{21} < 1$, then $1-a_{12}a_{21} > 0$. In the $\alpha-\beta$ plane, (3.7) defines a parabola that opens up and intersects the $\alpha-$axis at $\alpha = 0$ and $\alpha = \alpha_1: = \frac{(1-a_{12})-(n-m)d}{1-a_{12}a_{21}}$. Clearly

This implies that the line given by (3.5) and the parabola defined by (3.7) do not intersect in the first quadrant. A representative sketch of the line and the parabola for the case with $0 < \alpha_0$ is shown in Figure 1. Consequently, system (3.1) does not admit any other coexistence equilibria except for the homogeneous coexistence equilibrium $E_n^*$.

For the strong competition case, $a_{12} > 1$ and $a_{21} > 1$, then $1-a_{12}a_{21} < 0$ and the parabola defined in (3.7) opens down. In addition, $\alpha_0 > \alpha_1 > 0$. From (3.5) and (3.7), we obtain a quadratic equation

Since $a_{12}a_{21}-1 > 0$, $(a_{12}a_{21}-1)\alpha_1+(n-m)d > 0$ and $(n-m)d\alpha_0 > 0$, we see that (3.8) admits one or two positive roots if

Equivalently,

Therefore, if $d$ is small satisfying $d\leq d_m$ for some $m = 1, 2, \cdots, n-1$, then (3.8) admits one or two positive roots $\alpha = \alpha_m$ and if further $1-a_{21}\alpha_m > 0$, then system (3.1) admits multiple coexistence equilibria, which are not $x-$homogeneous. Furthermore, if $d$ is large enough, say, if $d > \max\{d_m: m = 1, 2, \cdots, n-1\}$, then (3.8) has no roots and hence system (3.1) admits exactly one coexistence equilibrium, which is the homogeneous coexistence equilibrium $E_n^*$.

In the sequel, we focus our analysis on the stability of the unique homogeneous coexistence equilibrium $E_n^*$. Linearizing system (3.1) at $E_n^*$, we see the associated characteristic equations are determined by $\det J = 0$, with $J$ given by

where

It follows from $\det J = \det(J_1 + (n-1) J_{\tau})\cdot \det (J_1 - J_{\tau})$ that the linear stability of $E_n^*$ is determined by the following two characteristic equations

and

where $A = \frac{a_{12}-1}{1-a_{12} a_{21}}$, $B = \frac{\rho (a_{21}-1)}{1-a_{12} a_{21}}$. Since $a_{12} > 1, \; a_{21} > 1$ or $a_{12} < 1, \; a_{21} < 1$, we always have $A < 0$ and $B < 0$.

When $\tau = 0$, the above two characteristic equations become

and

If $a_{12} < 1$ and $a_{21} < 1$, then all roots of the characteristic equations (3.12) and (3.13) have negative real parts and hence $E_n^*$ is locally asymptotically stable; while if $a_{12} > 1$ and $a_{21} > 1$, then the characteristic equation (3.13) has one positive root (since $(a_{12}-1)B < 0$) and consequently, $E_n^*$ is unstable.

Next we consider the case with $\tau > 0$. The homogeneous coexistence equilibrium $E_n^*$ of system (3.1) is stable if all characteristic roots of (3.10) and (3.11) have negative real parts. We regard $\tau$ as a bifurcation parameter, as $\tau$ increases, the number of roots with positive real parts changes only when there are roots crossing the imaginary axis ^[22,23,24]. Here we assume that $a_{12}-1\neq nd$. This ensures that zero is not a root of equation (3.11). Thus, we look for a pair of purely imaginary roots of characteristic equations (3.10) and (3.11).

We consider the characteristic equation (3.10) first. Substituting $\lambda = i\omega$ with $\omega > 0$ into (3.10) and separating the real and imaginary parts, we obtain

Set $\omega_{11}$ and $\omega_{12}$ as

and

Then $\omega = \omega_{1j}$ ($j = 1, 2$) is a feasible root of (3.14) provided that $\omega_{1j} > 0$ is well defined. A necessary condition is that $\Delta_1 : = \left(2B(a_{12}-1)+2(n-1)Ad-(A+B)^2\right)^2-4B^2(a_{12}-1)(a_{12}-1-2(n-1)d) > 0$. Note that if $\Delta_1 > 0$, then (3.14) may admit at most two positive roots, $\omega_{1j}$, $j = 1, 2$.

Further, we have the following lemma.

Lemma 3.2. Suppose at certain $\tau$, the characteristic equation (3.10) has a pair of purely imaginary roots $\pm i\omega_{1j}$, $(j\in \{1, 2\})$. Then the following transversality conditions

hold.

Proof. It follows from (3.10) that

Again, by (3.10) we note

Thus, for $j = 1, 2$, we have

By the expression of $\omega_{1j}$, we then obtain

The proof is complete.

Similarly, substituting $\lambda = i\omega$ into the characteristic equation (3.11), we obtain

If $\Delta_2 : = \left(2B(a_{12}-1)+2(n-1)Ad-(A+B)^2-n(n-2)d^2\right)^2 -4B^2(a_{12}-1-nd)(a_{12}-1-(n-2)d) > 0$, then (3.15) may admit at most two positive roots given by

and

Similar to Lemma 3.2, we can show that the following transversality conditions hold.

Lemma 3.3. Suppose at certain $\tau$, the characteristic equation (3.11) has a pair of purely imaginary roots $\pm i\omega_{2j}$, $(j = 1, 2)$. Then

Now we distinguish two cases to discuss the stability of system (3.1) at the homogeneous coexistence equilibrium $E_n^*$.

The weak competition case: $a_{12} < 1$ and $a_{21} < 1$.

We first consider the characteristic equation (3.10). Note that $B^2(a_{12}-1)(a_{12}-1-2(n-1)d) > 0.$ By the expression of $\omega_{11}$ and $\omega_{12}$, it is seen that (3.10) admits purely imaginary roots only if the following inequality is satisfied

Since $2(n-1)Ad < 0$, the left hand side of the inequality (3.16) is smaller than $2B(a_{12}-1)$, while the right hand side of the inequality (3.16) is larger than $2B(a_{12}-1)$ if $a_{12} < 1$. This implies that the inequality (3.16) can never hold. Consequently, (3.10) does not admit any purely imaginary roots if $a_{12} < 1$ and $a_{21} < 1$.

For the characteristic equation (3.11), we see that (3.11) admits purely imaginary roots only if the following inequality holds

However, using the same manner as for (3.10), we can show that the above inequality never holds. Thus, there are no purely imaginary roots for (3.11) if $a_{12} < 1$ and $a_{21} < 1$. That is, both the characteristic equations (3.10) and (3.11) do not admit purely imaginary roots. Note that the equilibrium $E_n^*$ is locally asymptotically stable when $\tau = 0$, we see that $E_n^*$ remains locally asymptotically stable for all values $\tau > 0$.

The strong competition case: $a_{12} > 1$ and $a_{21} > 1$.

We define $d_1$, $d_2$ and $d_3$ as follows:

In the following, we consider four subcases: (ⅰ) $d\in(0, d_1)$; (ⅱ) $d\in(d_1, d_2)$; (ⅲ) $d\in(d_2, d_3)$; (ⅳ) $d\in(d_3, \infty)$;

(ⅰ): $d\in(0, d_1)$.

In this case we have $B^2(a_{12}-1)(a_{12}-1-2(n-1)d) > 0$. Again, a necessary condition for (3.10) to admit purely imaginary roots is that the inequality (3.16) holds. Since $2B(a_{12}-1) < 0$ and $2(n-1)Ad < 0$, the left hand side of the inequality (3.16) is less than $0$. Consequently, the inequality (3.16) does not hold. On the other hand, for equation (3.11), if $d\in(0, d_1)$, then $a_{12}-1 > 2(n-1)d$, we have $B^2(a_{12}-1-nd)(a_{12}-1-(n-2)d) > 0$. Therefore, (3.11) admits purely imaginary roots only if the inequality (3.17) holds. However, the inequality (3.17) never holds since the left hand side is negative. Therefore, as $\tau$ increases, it is impossible for (3.10) or (3.11) to admit purely imaginary roots and hence the equilibrium $E_n^*$ remains unstable for all $\tau > 0$.

(ⅱ): $d\in(d_1, d_2)$.

In this case, we have $B^2(a_{12}-1)(a_{12}-1-2(n-1)d) < 0$ and $B^2(a_{12}-1-nd)(a_{12}-1-(n-2)d) > 0$. Thus, the characteristic equation (3.10) admits a pair of purely imaginary roots $\lambda = \pm i\omega_{11}$. Since the inequality (3.17) cannot be satisfied in this case, the characteristic equation (3.11) does not admit any purely imaginary roots. Note that $sign\left(\frac{d(Re\lambda)}{d\tau}\right)_{\lambda = i\omega_{11}} > 0$ (Lemma 3.2). This indicates that the equilibrium $E_n^*$ remains unstable for all $\tau\geq0$.

(ⅲ): $d\in(d_2, d_3)$.

In this case, we note that $B^2(a_{12}-1)(a_{12}-1-2(n-1)d) < 0$ and $B^2(a_{12}-1-nd)(a_{12}-1-(n-2)d) < 0$. The characteristic equation (3.10) admits a pair of purely imaginary roots $\lambda = \pm i\omega_{11}$, and the characteristic equation (3.11) admits a pair of purely imaginary roots $\lambda = \pm i\omega_{21}$, It follows from $sign\left(\frac{d(Re\lambda)}{d\tau}\right)_{\lambda = i\omega_{11}} > 0$ (Lemma 3.2) and $sign\left(\frac{d(Re\lambda)}{d\tau}\right)_{\lambda = i\omega_{21}} > 0$ (Lemma 3.3) that the equilibrium $E_n^*$ remains unstable for all $\tau\geq0$.

(ⅳ): $d\in(d_3, \infty)$.

In this case, we have $B^2(a_{12}-1)(a_{12}-1-2(n-1)d) < 0$ and $B^2(a_{12}-1-nd)(a_{12}-1-(n-2)d) > 0$. Similar to the case (ⅱ), we can show that equilibrium $E_n^*$ remains unstable for all $\tau\geq0$.

Summarizing the above analysis, we have the following theorem.

Theorem 3.4. Consider system (3.1). If $a_{12} < 1$ and $a_{21} < 1$, then the homogeneous coexistence equilibrium $E_n^*$ is locally asymptotically stable for all $\tau\geq 0$. If $a_{12} > 1$ and $a_{21} > 1$, then the homogeneous coexistence equilibrium $E_n^*$ is unstable for $\tau\geq0$.

Remark 3.5 Note that the stability and instability conditions of the homogeneous coexistence equilibrium of the system with $n$ patches are the same as those of the coexistence equilibrium of the single-patch system. This means that the delayed dispersal between patches does not affect the stability and instability of the homogeneous coexistence equilibrium.

We also have the following result on the stability of some boundary equilibria.

Theorem 3.6. Consider system (3.1).

(i) The boundary equilibrium $E_{10} = (1, 0, 1, 0, \cdots, 1, 0)$ is stable for $\tau\geq0$ if $a_{21} > 1$ and unstable for $\tau\geq0$ if $a_{21} < 1$.

(ii) The boundary equilibrium $E_{01} = (0, 1, 0, 1, \cdots, 0, 1)$ is stable for all $\tau\geq 0$ if $a_{12} > 1$ and unstable for $\tau\geq0$ if $a_{12} < 1$.

(iii) All other equilibria in the form of $(0, y_1, 0, y_2, \cdots, 0, y_n)$ are always unstable, where $y_i\in \{0, 1\}$ with $\sum_{i = 1}^ny_i < n$.

Proof. Linearizing system (3.1) at $E_{10}$ yields the associated characteristic equations:

Note that $a_{21} > 1$, when $\tau = 0$, there are three negative eigenvalues: $\lambda = -1, -1-nd, \rho(1-a_{21}) < 0$ and hence $E_{10}$ is stable. If $a_{21} < 1$ and $\tau = 0$, $E_{10}$ is unstable since one of its eigenvalues is $\lambda = \rho(1-a_{21}) > 0$. When $\tau > 0$, substituting $\lambda = i\omega$ ($\omega > 0$) into (3.18) and separating the real and imaginary parts, we have

Similarly, from (3.19), we obtain

Consequently, both (3.18) and (3.19) do not admit purely imaginary roots. This implies that $E_{10}$ remains stable for $\tau > 0$ if $a_{21} > 1$ and remains unstable for $\tau > 0$ if $a_{21} < 1$.

For the boundary equilibrium $E_{01}$, we have the associated characteristic equations:

When $\tau = 0$, it follows from (3.21)-(3.23) that the three eigenvalues are: $\lambda_1 = 1-a_{12}$, $\lambda_2 = 1-a_{12}-nd$ and $\lambda_3 = -\rho$. Thus the boundary equilibrium $E_{01}$ is stable if $a_{12} > 1$ and unstable if $a_{12} < 1$.

For $\tau > 0$, substituting $\lambda = i\omega$ ($\omega > 0$) into (3.21) and (3.22), respectively, yields, $\cos\omega\tau = 1+\frac{a_{12}-1}{(n-1)d} > 1$ and $\cos\omega\tau = -(n-1)-\frac{a_{12}-1}{d} < -1$ provided that $a_{12} > 1$. This is impossible. Thus $E_{01}$ remains stable for $\tau > 0$ if $a_{12} > 1$. Next we consider the case with $a_{12} < 1$. Suppose (3.21) admits a pair of purely imaginary roots $\lambda = \pm i\omega$. By (3.21), we have

Thus

A direct calculation yields

Note that the eigenvalue obtained from (3.21) is $\lambda_1 = 1-a_{12} > 0$ when $\tau = 0$ and $a_{12} < 1$, and as $\tau$ increases, due to (3.24), the characteristic roots cross the imaginary axis always from left to right. This implies, the number of eigenvalues with positive real parts is always increasing and thus there is no possibility for the boundary equilibrium $E_{01}$ to switch its stability and hence $E_{01}$ remains unstable for $\tau > 0$ if $a_{12} < 1$.

For all other equilibria in the form of $(0, y_1, 0, y_2, \cdots, 0, y_n)$ with $y_i\in \{0, 1\}$ and $\sum_{i = 1}^ny_i < n$. there always exists at least one positive characteristic root $\lambda = \rho > 0$, thus these equilibria are always unstable. Indeed, we can rearrange the variables in system (3.1) in the order of $(x_1, \cdots, x_n, x_1(t-\tau), \cdots, x_n(t-\tau), y_1(t-\tau), \cdots, y_n(t-\tau), y_1, \cdots, y_n)$ and linearize the resulting system. The associated characteristic equations are determined by $\det J_b = 0$, with $J_b$ given by

where

and

Note that there is at least one $y_i = 0$ for some $i\in \{1, 2, \cdots, n\}$. Thus there is at least one characteristic root $\lambda = \rho > 0$. This completes the proof.

Remark 3.7. Theorem 3.6 indicates that the dispersal does not affect the stability of the two boundary equilibria $E_{01}$ and $E_{10}$. If $a_{12} > 1$ and $a_{21} > 1$, then system (3.1) admits at least two stable boundary equilibria, $E_{10}$ and $E_{01}$. We should point out that, as demonstrated in Figure 3, besides $E_{10}$ and $E_{01}$, system (3.1) may also admit other stable boundary equilibria, which cannot be in the form of $(0, y_1, 0, y_2, \cdots, 0, y_n)$ with $y_i\in \{0, 1\}$ satisfying $\sum_{i = 1}^ny_i < n$. System (3.1) exhibits multi-stability and the competition outcome is initial condition dependent.

4.   The ring-structured patchy model

In this section, we assume that the $n$ identical patches are connected via dispersal of species $x$ in the configuration of a ring structure. That is, we consider the model described by

for $i = 1, 2, \cdots, n (n\geq 3)$. The definitions of $x_i$, $y_i$, $a_{12}$, $a_{21}$, $\rho$, $d$, $\tau$ are the same as in model (3.1). Here we used the conventional notation: $x_0 = x_n$, $x_{n+1} = x_1$, $y_{0} = y_n$ and $y_{n+1} = y_1$ to close the ring.

Similar to system (3.1), we can show that system (4.1) admits a unique homogeneous coexistence equilibrium $E_n^*$. Linearizing system (4.1) at $E_n^*$, we obtain the corresponding Jacobian matrix in the following form:

with

and $J_{\tau}$ is defined in Section 3. The determinant of $J_r$ is obtained by ^[25]

Due to the symmetric property of the function $\cos\frac{2k\pi}{n}$, it is seen that system (4.1) has $[\frac{n}{2}]+1$ characteristic equations:

where $k = 0, 1, 2, \cdots, [\frac{n}{2}]$, and $[\cdot]$ is the greatest integer function, $A < 0$ and $B < 0$ are defined the same as in Section 3.

When $\tau = 0$, for each $k = 0, 1, 2, \cdots, [\frac{n}{2}]$, equation (4.2) becomes

Note that if $a_{12} < 1$ and $a_{21} < 1$, then $A+B-2d(1-\cos\frac{2k\pi}{n}) < 0$ and $B[a_{12}-1-2d (1-\cos\frac{2k\pi}{n})] > 0$. Thus all roots of the characteristic equation (4.3) have negative real parts for all $k$ and the homogeneous coexistence equilibrium $E_n^*$ is stable. If $a_{12} > 1$ and $a_{21} > 1$, then $A+B-2d(1-\cos\frac{2k\pi}{n}) < 0$ and $B[a_{12}-1-2d (1-\cos\frac{2k\pi}{n})] < 0$ for $k = 0$. This implies that there is at least one root with positive real part. Thus the homogeneous coexistence equilibrium $E_n^*$ is unstable.

We assume that $a_{12}-1\neq 2d(1-\cos\frac{2k\pi}{n})$ for any $k = 0, 1, 2, \cdots, [\frac{n}{2}]$, which ensures that $\lambda = 0$ is not a root of equation (4.2). As in Section 3, substituting $\lambda = i\omega$ with $\omega > 0$ into (4.2) and separating the real and imaginary parts, for each $k$, we obtain

where

Similar to Section 3, we can have the following transversality conditions.

Lemma 4.1. Suppose at certain values of $\tau$, for each $k$, the characteristic equation (4.2) has a pair of purely imaginary roots $\pm i\omega^{(k)}_{\pm}$. Then

Next we analyze the stability of the homogeneous coexistence equilibrium $E_n^*$ under two cases: (1) $a_{12} < 1$ and $a_{21} < 1$ and (2) $a_{12} > 1$ and $a_{21} > 1$.

The weak competition case: $a_{12} < 1$ and $a_{21} < 1$.

By the expression of $\omega^{(k)}_{\pm}$ and note that $(a_{12}-1)^2-4d(a_{12}-1)+4d^2\sin^2\frac{2k\pi}{n} > 0$, we can show that, for each $k$, the characteristic equation (4.2) admits two pairs of purely imaginary roots if the following inequality is satisfied

It follows from $a_{12} < 1$ that $2|B|\sqrt{(a_{12}-1)^2-4d(a_{12}-1)+4d^2\sin^2\frac{2k\pi}{n}} > 2B(a_{12}-1)$. On the other hand, since $4Ad-(A+B)^2-4d^2\sin^2\frac{2k\pi}{n} < 0$, we know that $2B(a_{12}-1)+4Ad-(A+B)^2-4d^2\sin^2\frac{2k\pi}{n} < 2B(a_{12}-1)$. That is, the inequality (4.4) can never be satisfied. Consequently, no characteristic roots would cross the imaginary axis as $\tau$ increases. This means that all characteristic roots have negative real parts. Thus, the homogeneous coexistence equilibrium $E_n^*$ remains stable for all $\tau > 0$.

The strong competition case: $a_{12} > 1$ and $a_{21} > 1$.

We define three sets as

Note that if $k\in\mathcal{M}$, the characteristic equation (4.2) admits two pairs of purely imaginary roots if the inequality (4.4) holds. However, the inequality (4.4) can never hold since the left hand side of the inequality (4.4) is less than $0$. This indicates that the characteristic equation (4.2) does not admit any purely imaginary roots if $k\in\mathcal{M}$.

On the other hand, if $k\in\mathcal{N}$, the characteristic equation (4.2) admits a pair of purely imaginary root $\lambda = \pm i\omega^{(k)}_{+}$. Note that from Lemma 4.1, $sign\left(\frac{d(Re\lambda)}{d\tau}\right)_{\lambda = i\omega^{(k)}_{+}} > 0$. This indicates the characteristic roots cross the imaginary axis through $\pm i\omega^{(k)}_{+}$ at certain values of $\tau$ from left to right and the number of the characteristic roots with positive real parts is always increasing. Since $a_{12} > 1$, $a_{21} > 1$, the homogeneous coexistence equilibrium $E_n^*$ is unstable with $\tau = 0$. As $\tau$ increases, the are always characteristic roots with positive real parts. As a result, the homogeneous coexistence equilibrium $E_n^*$ remains unstable for all $\tau > 0$.

The above analysis immediately yields the following result.

Theorem 4.2. Consider system (4.1). If $a_{12} < 1$ and $a_{21} < 1$, then the homogeneous coexistence equilibrium $E_n^*$ is locally asymptotically stable for all $\tau\geq 0$. If $a_{12} > 1$ and $a_{21} > 1$, then the homogeneous coexistence equilibrium $E_n^*$ is unstable for $\tau\geq0$.

Remark 4.3 Theorem 4.2 indicates that dispersal of one species between patches in the configuration of $n$ ring-structured patches does not change the stability and instability of the homogeneous coexistence equilibrium.

Similar to the proof of Theorem 3.6, we can establish the following result concerning the stability of some boundary equilibria.

Theorem 4.4. Consider system (4.1). The boundary equilibrium $E_{10}$ is stable for $\tau\geq0$ if $a_{21} > 1$ and unstable for $\tau\geq 0$ if $a_{21} < 1$, and the boundary equilibrium $E_{01}$ is stable for all $\tau\geq 0$ if $a_{12} > 1$ and unstable for $\tau\geq 0$ if $a_{12} < 1$. All equilibria in the form of $(0, y_1, 0, y_2, \cdots, 0, y_n)$ are always unstable, where $y_i\in \{0, 1\}$ with $\sum_{i = 1}^ny_i < n$.

5.   Numerical simulations

In this section, we present some numerical simulations to explore the impact of dispersal on competition outcome. Since we have shown that for the weak competition case, the homogeneous coexistence equilibrium $E_n^*$ is the only coexistence equilibrium and is stable, we focus our numerical simulations on the strong competition case ($a_{12} > 1$ and $a_{21} > 1$).

Theorem 3.1 indicates that small dispersal rate $d$ can induce multiple coexistence equilibria in the strong competition case. To illustrate this phenomenon, we take $n = 4$, $a_{12} = 2 > 1$ and $a_{21} = 4 > 1$. Then it follows from Theorem 3.1 that there is only $1$ coexistence equilibrium if $d > \max\{d_m: m = 1, 2, 3\} = \frac{1}{2\sqrt{3}}$ and there may exist multiple coexistence equilibria if $d\in (0, \frac{1}{2\sqrt{3}}]$. Solving the system of equilibrium equations (3.2), we find that system (3.1) admits $5$ coexistence equilibria when $d = 1/4$, which include the unique homogeneous coexistence equilibrium $E_4^* = (1/7, 3/7, 1/7, 3/7, 1/7, 3/7, 1/7, 3/7)$ and $4$ other non-homogeneous coexistence equilibria: $(1/14, 5/7, 1/14, 5/7, 1/14, 5/7, 3/14, 1/7)$, $(1/14, 5/7, 1/14, 5/7, 3/14, 1/7, 1/14, 5/7)$, $(1/14, 5/7, 3/14, 1/7, 1/14, 5/7, 1/14, 5/7)$, $(3/14, 1/7, 1/14, 5/7, 1/14, 5/7, 1/14, 5/7)$. If $d = 1/5$, then there are $15$ coexistence equilibria. For the ring-structured model, we also observe the existence of multiple coexistence equilibria when $d$ is small. For instance, with $n = 4$, $a_{12} = 2$ and $a_{21} = 4$, system (4.1) admits $9$ coexistence equilibria when $d = 1/4$ and $15$ coexistence equilibria when $d = 1/5$.

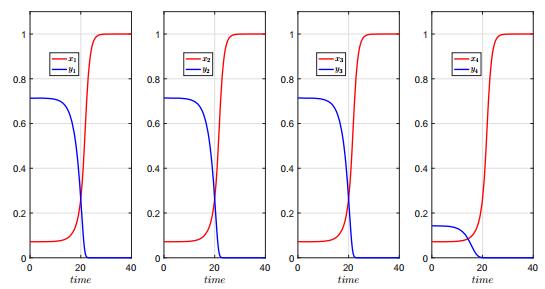
Numerical simulations suggest these coexistence equilibria are all unstable. However, the existence of multiple coexistence equilibria makes transient coexistence in all patches become possible, especially when the initial conditions are very close to some coexistence equilibrium. This transient coexistence of both $x$ and $y$ species in all patches is illustrated in Figure 2, where both species coexist for a short time interval before the $y$ species is driven to extinction in all $4$ patches.

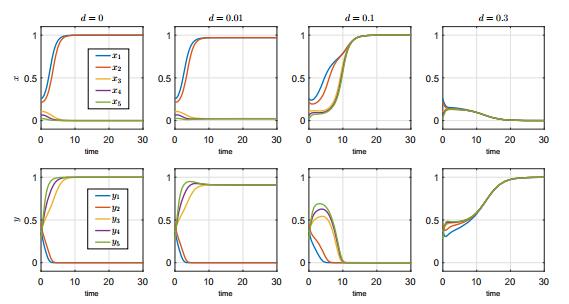
Essentially, if $a_{12} > 1$ and $a_{21} > 1$, the unique homogeneous equilibrium $E_n^*$ is unstable, both the homogeneous boundary equilibria $E_{10}$ and $E_{01}$ are stable, and there may exist other stable equilibria. Next we use numerical simulations to demonstrate that the dispersal rate $d$ does play an important role in determining the competition outcome in the fully connected patchy model. To this purpose, in system (3.1), we take $a_{12} = 2$, $a_{21} = 4$, $\rho = 2$, $\tau = 1$ and $n = 5$. We fix initial conditions as $(x_1(\theta), y_1(0), x_2(\theta), y_2(0), \cdots, x_5(\theta), y_5(0)) = (0.26, 0.40, 0.22, 0.46, 0.1, 0.36, 0.06, 0.32, 0.02, 0.28)$. In the case that the $5$ patches are isolated ($d = 0$), as shown in Figure 3, the solution tends to $(1, 0, 1, 0, 0, 1, 0, 1, 0, 1)$ as $s\to\infty$. This means the $x$ species wins the competition in patches $1$ and $2$. If $d$ takes the value $d = 0.01$, the solution tends to a non-homogeneous equilibrium $(0.9707, 0, 0.9707, 0, 0.0225, 0.91, 0.0225, 0.91, 0.0225, 0.91)$ as $s\to\infty$. That is, species $x$ and $y$ coexist in $3$ patches, species $x$ survives in all $5$ patches and species $y$ dies out only in patches $1$ and $2$. With $d = 0.1$ and $d = 0.3$, the solution tends to the homogeneous boundary equilibria $E_{10}$ (species $x$ wins competition and species $y$ dies out in all $5$ patches) and $E_{01}$(species $y$ drives species $x$ to extinction in all $5$ patches), respectively (See Figure 3).

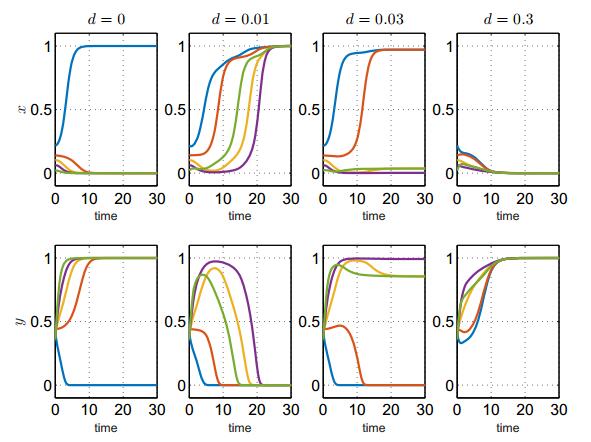
For the ring-structured patchy model (4.1), the dispersal rate $d$ also plays an important role in determining the competition outcome. For instance, in system (4.1), we take $a_{12} = 2$, $a_{21} = 4$, $\rho = 2$, $\tau = 1$ and $n = 5$. We fix initial conditions as $(x_1(\theta), y_1(0), x_2(\theta), y_2(0), \cdots, x_5(\theta), y_5(0)) = (0.36, 0.22, 0.42, 0.14, 0.44, 0.1, 0.40, 0.06, 0.38, 0.02)$. In the case that the $5$ patches are isolated ($d = 0$), as shown in Figure 4, the solution tends to $(1, 0, 0, 1, 0, 1, 0, 1, 0, 1)$ as $s\to\infty$, that is, the $x$ species wins competition only in patch $1$ and becomes extinct in all other four patches. If $d$ takes the value $d = 0.01$, the solution approaches the homogeneous boundary equilibrium $E_{10}$ as $s\to\infty$ and the $x$ species wins competition in all $5$ patches. While at $d = 0.03$ the solution tends to a non-homogeneous boundary equilibrium $(0.9711, 0, 0.9711, 0, 0.0362, 0.8552, 0.0021, 0.9917, 0.0362, 0.8552)$ and the $x$ species survives in all $5$ patches, while the $y$ species dies out in patches $1$ and $2$, and the coexistence of both species occurs in patches $3, 4$ and $5$. When $d = 0.3$, the solution approaches the homogeneous boundary equilibrium $E_{01}$ indicating the $x$ species dies out in all $5$ patches (See Figure 4).

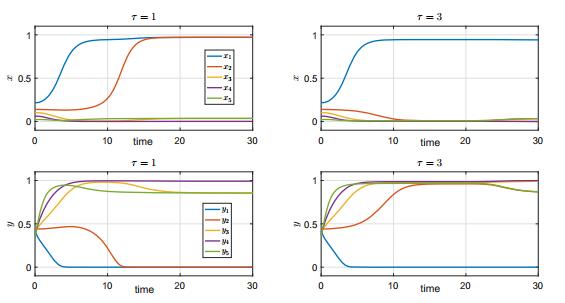
Simulations presented in Figure 5 show that the dispersal delay may also have an impact on determining the competition outcome. When $\tau = 1$, the solution of (4.1) approaches the boundary equilibrium ($0.9711$, $0$, $0.9711$, $0$, $0.0362$, $0.8552$, $0.0021$, $0.9917$, $0.0362$, $0.8552$). If $\tau$ is changed to $\tau = 3$, the solution approaches another boundary equilibrium $(0.9422, 0, 0.0346, 0.8616, 0.001, 0.9959, 0.001, 0.9959, 0.0346, 0.8616)$ when $\tau = 3$. This shows at $\tau = 1$, the $x$ species survives in all $5$ patches, but the $y$ species only survives at patches $3, 4$ and $5$, and if $\tau = 3$, the $x$ species and the $y$ species coexist in all patches except in patch $1$, where the $y$ species dies out and the $x$ species survives.

6.   Summary

For a model involving two competing species, we have shown that the dispersal of one species between patches under two configurations of an arbitrary number of patches (fully connected and ring-structured) does not affect the stability and instability of the homogeneous coexistence equilibrium. For the weak competition case, the competition outcome is simple: both species can coexist in all patches. However, if the competition is strong, namely, $a_{12} > 1$ and $a_{21} > 1$, then the competition outcome is complex: for small dispersal rate $d$, there could exist multiple coexistence equilibria, both the dispersal rate and the dispersal delay have impacts on determining the competition outcome and there could be multiple stable boundary equilibria. The existence of multiple coexistence equilibria leads to the observation of transient coexistence of both species, while the occurrence of multi-stability indicates that the coexistence of both species in some patches (though not in all patches) is possible.

Acknowledgments

The authors wish to thank the anonymous referees for their valuable comments and suggestions. Part of the work was carried out when AM and GS were visiting the University of New Brunswick (UNB), AM and GS wish to thank the hospitality they received from UNB. This work is partially supported by the National Natural Science Foundation of China (No. 11526183, No. 61573016), by China Scholarship Council (No. 201608140214), by the Natural Science Foundation of Shanxi Province (No. 201801D221035), by Yuncheng University (No. YQ-2017003, No. XK-2018033) and by NSERC of Canada.

Conflict of interest

The authors declare that they have no competing interests.