Discrete time darwinian dynamics and semelparity versus iteroparity

1.   Introduction

Life history strategies that individuals adopt play a central and important role in the dynamics of biological populations ^[1,2]. The timing of reproduction, the allocation of resources toward reproduction, survival, metabolism and so on will determine whether a population will grow or decay and whether it will successfully avoid extinction. The importance of resource allocation toward reproduction was recognized by Fisher in his now classic book on population genetics, in which he stated the importance of knowing "what circumstances in the life history and environment would render profitable the diversion of a greater or lesser share of the available resources toward reproduction" ^[3]. This question was focussed by Cole in his influential paper on life history modeling in terms of the two options: semelparity and iteroparity ^[4]. Semelparity means an individual has only one reproductive event before death while iteroparity is characterized by multiple reproductive events over the individual's life. For plants, this distinction is between annuals (or monocarpic plants) and perennials (polycarpic plants). As pointed out by Hughes ^[5], why organisms adopt one of these strategies or the other is a very old question that traces its roots to Aristotle and Linnaeus. In his paper Cole concluded that evolution should favor semelparity, a conclusion which, because iteroparity is widespread in the biological world (even more so than semelparity), became known as "Cole's Paradox". While this paradox was addressed by Charnov and Schaffer ^[6] by pointing out that Cole did not take juvenile and adult mortality adequately into account, researchers continue to explore explanations that account for the evolution of semelparity or iteroparity and to account for various mechanisms that favor one life history strategy over the other or the switching between one or the other. These include density dependence, stochasticity in demographic parameters, trade-offs and bet-hedging against environmental stochasticity, interactions with pathogens or mutualistic species, spatial structuring of habitats, and combinations of these. Furthermore, in his review of the large literature on this topic, Hughes states "that mathematical models purporting to explain the general evolution of semelparous life histories from iteroparous ones (or vice versa) should not assume that organisms can only display either an annual-semelparous life history or a perennial-iteroparous one" and argues in favor of a "continuum of modes of parity" ^[5]. In keeping with this point of view, our goal here is derive and analyze an evolutionary game theoretic model in which fertility and survival depend on a continuous trait that is subject to the Darwinian principles of evolution and to use the model to investigate the evolutionary stability or instability of semelparity and iteroparity.

Discrete time dynamic models, defined by maps or difference equations, have been widely used in model studies of life history strategies and in particular in the study of semelparity and iteroparity. Following the methodology of evolutionary game theory, or Darwinian dynamics ^[7], we will assume the model parameters in a general difference equation population model depend on a phenotypic trait $v$ subject to the axioms of Darwinian evolution. This modeling methodology assumes the trait $v$ is normally distributed throughout the population at all times with a constant variance and, consequently, the trait distribution is determined by the population mean trait $u$. The evolutionary game theoretic version of a population model is built from assumptions on how an individual's inherent fertility and survival rates and how the effects of population density on these vital rates depend on an individual's trait $v$ and the mean trait $u$ of the population. The population equation is then coupled with an equation for the mean trait, which together form a Darwinian dynamic model. The equation for the mean trait (which goes by numerous names: the canonical equation of evolution ^[8], Fisher's equation ^[3], Lande's equation ^[9] or the breeder's equation ^[10]) states that the change in the mean is proportional to the fitness gradient. For a discrete time model, fitness is the logarithm of the per capita population growth rate and the gradient is with respect to the trait $v$ (see (2.3)). For more on this modeling methodology see ^[7].

In Section 2 we develop a Darwinian model under the key assumption that there is a trade-off between fertility and survival (cf. (2.2) and (2.4)). That is to say, any change in the trait $v$ that increases survival is accompanied by a decrease in fertility (and vice versa). Since the fundamental issue is population survival versus extinction, in Section 3 we focus our model analysis on the existence and stability of extinction equilibria and on the bifurcation of positive equilibria when an extinction equilibrium destabilizes. This analysis culminates in Theorem 3.1 and the bifurcation Theorem 3.2.

In Section 4 we apply the analyses in Section 3 to a model in which there is assumed present both semelparous and iteroparous traits. The unit of time is such that an individual reproduces at most once during one time interval. We say a trait $v_{s}$ is semelparous if an individual with that trait has zero, or nearly zero, survival probability during one time interval (and therefore reproduces, with high probability, only once before death). Also in the model are traits $v_{i}$ that yield a high probability of survival and hence reproduction more than once. The trait $v$ has a continuous distribution throughout the population and hence, in this model, there are not two binary strategies of semelparity and iteroparity. Instead post-reproductive survival probability varies continuously from zero to positive values as a function of the trait $v$. A population whose mean trait $u$ equals a semelparous trait consists mostly of semelparous individuals (or with a high probability of being semelparous), but it would still be the case that some individuals might have a relatively high chance of survival and a second period of reproduction. Stearns ^[2] points out that this is indeed often the case in what are biologically classified as semelparous populations. For convenience we will refer to a population with mean trait $u_{s}$ near a semelparous trait $v_{s}$ as a semelparous population. Populations with mean traits sufficiently different from a semelparous trait (as determined by the modeler) will be called an iteroparous population. The analysis in Section 3 applied to the model provides conditions under which there exist stable semelparous equilibrium populations and/or stable iteroparous equilibrium populations.

According to the theory of evolutionary stable strategies (ESS)^*, stable equilibria a population or a Darwinian model are not, however, necessarily favored by evolution, that is to say are not immune from invasion by mutant strategies. The ESS Maximum Principle states that an equilibrium trait is an ESS if and only if it is the component of a stable equilibrium of the Darwinian equations and also lies on a global maximum of the adaptive landscape.

^*"Strategy" is equivalent here to "trait".

We say an equilibrium is an ESS equilibrium if its trait component is an ESS and discuss the bifurcation of ESS equilibria in the Remarks following Theorem 3.2. We apply the remarks to the model in Section 4 with the result that, near the bifurcation points, semelparous equilibria are ESS but iteroparous equilibria are not. On the other hand, equilibria outside the neighborhood of bifurcation points can be ESS iteroparous equilibria. For this to happen density effects play a determining role, since outside a neighborhood of a bifurcation point population densities are high. First we show (Section 4.1) that if density effects are not trait dependent, then the model has no ESS iteroparous equilibria at all. However, if density effects are trait dependent then we show, by means of simulations in Section 4.2, that there can exist ESS iteroparous equilibria. This occurs if the density dependence is not symmetrically distributed as a function of the trait $v$ around the mean (e.g., in a Gaussian-like manner), as is often assumed in Darwinian models ^[7]), but is instead hierarchical, i.e. the magnitude with which population density affects an individual's vital rates is a monotone function of its trait $v.$

We discuss our results and some of their the biological implications in Section 5.

2.   Model derivation

We begin with a population dynamic model in which a population of reproducing individuals is censused at discrete time intervals. The population at any given census time results from only two sources, namely, new individuals that were born, survived and matured since the last census and surviving individuals present at the last census. Let $b$ be the number of new reproducing individuals produced per individual (per unit time) and let $s$ denote the fraction of individuals that survive from one census to the next census. Denoting $x_{t}$ by the census count at time $t,$ we have

We are interested in the case when the fertility and survival rates are density dependent. Such density effects are due to intraspecific interactions amount individuals, such as cooperation or competition for food resources, mates, territory, cannibalism, etc. Let $b_{0}$ and $s_{0}$ denote the inherent, i.e. density-free, vital rates and let $\beta\left(x\right)$ and $\sigma\left(x\right)$ denote factors that describe how population density affects fertility and survival:

In order for $b_{0}$ and $s_{0}$ to have the interpretation of inherent or intrinsic vita rates, we require

Familiar examples of density factors are

for $c > 0$.

For the evolutionary model, we assume fertility and survival are dependent on a specific trait of an individual and that this trait is subject to change by the principles of Darwinian evolution. To introduce the dynamic evolution of both the population and the trait we follow the methodology of evolutionary game theory (or Darwinian dynamics) ^[7]. The trait, which we denote by $v$, is assumed normally distributed throughout the population with a constant variance but a mean $u$ that will vary in time. Since the inherent per capita vital rates $b_{0}$ and $s_{0}$ are the fertility and survival rates of an individual in a density free environment, we assume they depend only on an individual's trait $v$ and not that of other individuals, as represented by the mean $u$. A key assumption we make is that there is a trade-off between fertility and survival (e.g. see ^[1,2]) so that as functions of $v$ the inherent vital rates have opposite monotonicities at every value of $v$. Increased (respectively decreased) fertility comes at the expense of decreased (respectively increased) survival. We model this assumption by replacing $b_{0}$ and $s_{0}$ by

where the distribution of these vital rates as a function of $v$ throughout the population is modeled by $f\left(v\right)$. We assume

so that $b_{0}$ has the interpretation of the maximal possible fertility of an individual.

On the other hand, the intraspecific density effects experienced by an individual with trait $v$ depend on the traits of the other individuals in the population, as represented by the mean trait $u$. We capture this by replacing $b$ and $s$ by

in which the factors $a_{i}\left(v, u\right)$ modify the density effects experienced by an individual with trait $v$ in a population with mean trait $u$. We assume $a_{i}\left(u, u\right) = 1$ so that $\beta\left(x\right)$ and $\sigma\left(x\right)$ describe the density effects on an individual whose trait equals population mean, i.e. when $v = u$.

For example, if one of the expressions (2.1) is used for the fertility density factor $\beta\left(x\right)$ in a population model equation, then in the evolutionary version of the model the density factor would be

Often used models for the factors $a_{i}\left(v, u\right)$ are functions of the difference between the individual's trait $v$ and the population mean $u$, such as

(For example, see ^[7]). This assumes that the competition intensity felt by an individual occurs when the individual's trait $v$ equals the population mean trait $u$ (i.e. the individual has a trait equal to that of most other individuals in the population). Another possibility is

which describes a hierarchical (asymmetric) competition scenario. By hierarchical is meant, when $w > 0$, that an individual with trait greater than the population mean trait experiences less competitive pressure while one with a trait less than the mean experiences more competitive pressure. (The situation is reversed if $w < 0$.)

Following the modeling methodology in ^[7] we track the time trajectories of both the population and the mean trait by means of the equations

for $t = 0, 1, 2, ...$ where

is the density and trait dependent per capita population growth rate of the population. We assume that one and only one reproductive event occurs for an individual during the time unit.

The logarithm $\ln\left(r\left(x, v, u\right) \right)$ appearing in (2.3b) is called the fitness function. Equation (2.3b) states that the change in the mean trait is proportional to the fitness gradient (with respect to an individual's trait). The constant of proportionality $\delta^{2}$ is called the speed of evolution. Depending on what underlying biological principles are used to derive (2.3b), $\delta^{2}$ is either equal or proportional to the assumed constant variance of the trait within the population. Since the model assumes a normal distribution of $v$ throughout the population with a fixed variance, the distribution at any point in time is completely determined by its mean $u_{t}$ whose dynamic is governed by the Darwinian equations (2.3).

We summarize the mathematical assumptions we impose on the model equations (2.3) in the following statement in which $R$ is the set of real numbers, $R_{+}$ the set of positive real numbers, $\bar{R}_{+}$ is the set of non-negative real numbers, and $\Gamma$ is an open set in $R$ that contains $\bar{R}_{+}$. We denote partial derivatives by the notation

and derivatives for single variable functions by primes:

With regard to the inherent vital rates and the density terms in (2.3)-(2.4) we assume the following.

    H1. The inherent vital rates satisfy $0 < s_{0} < 1$ and $b_{0} > s_{0}.$ The density terms $\beta\left(z\right)$ and $\sigma\left(z\right)$ are twice continuously differentiable functions mapping $\Gamma$ into $\bar{R} _{+}$ that satisfy $\beta\left(0\right) = \sigma\left(0\right) = 1$. Furthermore, $\beta\left(z\right) z$ is bounded and $0\leq s_{0} \sigma\left(z\right) < 1$ for all $z\in\bar{R}_{+}$

Note that if $b_{0} < s_{0}$ then (2.3a) and (2.4) imply $x_{t+1} < s_{0}x_{t}$ for all $t$ and any population with $x_{0} > 0$ goes extinct, regardless of the trait dynamics.

With regard to the trait dependencies we make the following assumptions.

    H2. $f$ and $a_{i}$ are twice continuously differentiable functions on $R$ and $R\times R$ respectively that satisfy $0\leq f\left(v\right) \leq1$ and $a_{i}\left(v, u\right) \geq0$, $a_{i}\left(u, u\right) = 1$ respectively.

The Darwinian equations (2.3) model evolutionary changes in the distributions of a trait $v$ within an inter-breeding population. Another notion of evolutionary change concerns the invasibility of a population by a low density population of mutant individuals that do not interbreed with the original population. This notion has played a central role in theories of speciation. If a population with mean trait $u$ is immune to such an invasion, then the trait $u$ is called an evolutionarily stable strategy or trait (ESS). The ESS maximum principle ^[7] states that the trait component $u_{e}$ of a (locally asymptotically) stable equilibrium $\left(x_{e}, u_{e}\right)$ of the Darwinian equations (2.3) is an ESS if (and only if) the adaptive landscape $\ln r\left(x_{e}, v, u_{e}\right)$ has a global maximum at $v = u_{e}$.

In the next section we investigate the existence and stability properties of equilibria of equations (2.3). We are interested in two types of equilibria $\left(x, u\right)$, those with $x = 0$ which we call extinction equilibria, and those with $x > 0$, which we call positive equilibria.

3.   A bifurcation analysis of the Darwinian model (2.3)

The equilibrium equations associated with the Darwinian equations (2.3) are (assuming $\delta^{2}\neq0$, so that evolution occurs)

$\left(x, u\right) = \left(0, u\right)$ is an extinction equilibrium if and only if $u$ solves the equation

We refer to solutions $u$ of this equation as critical traits$.$ The equations for equilibria $\left(x, u\right)$ with $x\neq0$ are

By the linearization principle, we study the local asymptotic stability (LAS) of an equilibrium of the Darwinian equations (2.3) by investigating the eigenvalues of the Jacobian $J\left(x, u\right)$ evaluated at the equilibrium$.$ The Jacobian of (2.3) is

From the fact that $\partial_{v}r\left(x, v, u\right) = 0$ at an equilibrium, it follows that the differential terms in the second row reduce, when evaluated at an equilibrium, to

The Jacobian, when evaluated at an equilibrium, is then

At a nonzero equilibrium, $r\left(x, u, u\right) = 1$ in $J\left(x, u\right)$. Our point of view will be to study the existence and stability of equilibria as they depend on $b_{0}$, i.e. we will use $b_{0}$ as a bifurcation parameter.

3.1.   Extinction equilibria

From (2.4) the equation (3.2) for a critical trait $u = u_{c}$ reduces to

i.e. critical traits are critical points of $f\left(v\right)$. The upper right entry of the Jacobian $J\left(0, u_{c}\right)$ vanishes and therefore its eigenvalues are the diagonal terms. Using (2.4) we calculate these eigenvalues to be

Recall from H1 that $b_{0} > s_{0}$. If $f^{\prime\prime}\left(u_{c}\right) > 0$ then $\lambda_{2} > 1$ and the extinction equilibrium $\left(x, u\right) = \left(0, u_{c}\right)$ is unstable for all values of $b_{0} > s_{0}$.

Assume $f^{\prime\prime}\left(u_{c}\right) < 0.$ The eigenvalue $\lambda _{2}$ is a decreasing function of $b_{0} > s_{0}$ which at $b_{0} = s_{0}$ equals $1$ and satisfies

Thus, if

then $\left\vert \lambda_{2}\right\vert < 1$ for all $b_{0} > s_{0}$ and the stability by linearization of the extinction equilibrium is determined by $\lambda_{1}.$ Define

Note that $s_{0} < 1$ in H1 implies

The linearization principle yields the following theorem.

Theorem 3.1. Assume H1 and H2 hold for the Darwinian equations (2.3) with (2.4) and that $u_{c}$ is a generic critical trait (i.e. a critical trait such that $f^{\prime\prime}\left(u_{c}\right) \neq0$) for which $f\left(u_{c}\right) > 0$.

(a) If $f^{\prime\prime}\left(u_{c}\right) < 0$ and $\delta^{2}$ satisfies (3.7) (i.e. the speed of evolution is not too fast) then the extinction equilibrium $\left(x, u\right) = \left(0, u_{c}\right)$ is unstable for $b_{0} > b_{0}^{c}$ and (locally asymptotically) stable for $b_{0} < b_{0}^{c}$.

(b) If $f^{\prime\prime}\left(u_{c}\right) > 0$ or if the inequality (3.7) for $\delta^{2}$ is reversed, then the extinction equilibrium $\left(x, u\right) = \left(0, u_{c}\right)$ is unstable for all $b_{0} > s_{0}$

3.2.   Positive equilibria

The extinction equilibrium's loss of stability in Theorem 3.1(a) suggests a canonical transcritical bifurcation of equilibria. This is the subject of Theorem 3.2 below, which establishes this local bifurcation, describes the global extent of the bifurcating continuum of positive equilibria, and deals with the relationship between the stability of bifurcating positive equilibria near the bifurcation point and the direction of bifurcation.

If $\left(x, u\right)$ is an equilibrium of (2.3)-(2.4) with parameter $b_{0}$, then we refer to

as an equilibrium pair. An equilibrium pair with $x > 0$ is a positive equilibrium pair and with $x = 0$ is an extinction equilibrium pair. If $u_{c}$ is a critical trait, then $[b_{0}, \left(0, u_{c}\right) ]$ is an extinction equilibrium pair for all values of $b_{0}.$ Let $S$ denote the closure of the set of positive equilibrium pairs of (2.3)-(2.4).

If an extinction equilibrium pair $[b_{0}, \left(0, u_{c}\right) ]$ lies in $S$ for some value of $b_{0},$ then we say this extinction pair is a bifurcation point and that positive equilibrium pairs bifurcate from $[b_{0}, \left(0, u_{c}\right) ]$. We say the bifurcation at $[b_{0}, \left(0, u_{c}\right) ]$ is forward (respectively backward) if $b_{0} > b_{0}^{c}$ (respectively $b_{0} < b_{0}^{c}$) for the positive solution pairs in a neighborhood of $[b_{0}, \left(0, u_{c}\right) ]$. We say the bifurcation is stable (respectively unstable) if the bifurcating positive equilibria lying in a neighborhood of $[b_{0}, \left(0, u_{c}\right) ]$ are locally asymptotically stable (respectively unstable) equilibria of the Darwinian equations (2.3).

The proof of the theorem below, which relies on the implicit function theorem and the celebrated global bifurcation theorems of Rabinowitz ^[11], appears in the Appendix. Define

A continuum is a closed and connected set.

Theorem 3.2. Assume H1 and H2 hold for the Darwinian equations (2.3) with (2.4) and that $u_{c}$ is a generic critical trait (i.e. a critical trait such that $f^{\prime\prime}\left(u_{c}\right) \neq0$) for which $f\left(u_{c}\right) > 0$. Assume $\kappa\neq0$ and let $b_{0}^{c}$ be defined by (3.6).

(a) $S$ contains a continuum $S_{+}$ that contains (i.e. bifurcates from) the extinction equilibrium $\left[ b_{0}^{c}, \left(0, u_{c}\right) \right],$ in a neighborhood of which $S^{+}\backslash\left\{ \left[ b_{0}^{c}, \left(0, u_{c}\right) \right] \right\}$ consists of positive equilibria. Moreover, $S^{+}\backslash\left\{ \left[ b_{0}^{c}, \left(0, u_{c}\right) \right] \right\}$ either contains only positive equilibrium pairs and is unbounded in $\Omega$ (with $b_{0} > s_{0}$) or it contains another extinction equilibrium pair $\left[ b_{0}^{\ast}, \left(0, u_{\ast}\right) \right]$ with $b_{0}^{\ast} > s_{0}$ and $u_{\ast}\neq u_{c}$.

(b) If $\kappa > 0$ then the bifurcation at $\left[ b_{0}^{c}, \left(0, u_{c}\right) \right]$ is forward and if $\kappa < 0$ then it is backward.

(c) Suppose $f^{\prime\prime}\left(u_{c}\right) < 0$ and that $\delta^{2}$ satisfies (3.5). If $\kappa > 0$ then the bifurcation at $\left[ b_{0}^{c}, \left(0, u_{c}\right) \right]$ is stable and if $\kappa < 0$ then it is unstable.

(d) If $f^{\prime\prime}\left(u_{c}\right) > 0$ or if the inequality (3.5) for $\delta^{2}$ is reversed, then the bifurcation at $[b_{0}, \left(0, u_{c}\right) ]$ is unstable (regardless of the direction of bifurcation).

Remark 1. Part (a) of Theorem 3.2 says that the continuum of positive equilibrium pairs $\left[ b_{0}, \left(x, u\right) \right]$, $x > 0$, of the Darwinian equations (2.3) bifurcates from $\left[ b_{0}^{c}, \left(0, u_{c}\right) \right]$ and is either unbounded in $\Omega$ or connects to another extinction equilibrium with a critical trait different from $u_{c}$.

Remark 2. From Theorems 3.1 and 3.2 we see that a bifurcation from an extinction equilibrium for a generic critical trait $u_{c}$ results in stable positive equilibria only when $f\left(v\right)$ has a local maximum at $v = u_{c}$ and the bifurcation at $b_{0} = b_{0}^{c}$ (where the extinction equilibrium loses stability) is forward (i.e. $\kappa > 0$). An unstable bifurcation occurs when $f\left(v\right)$ has a local minimum at $v = u_{c}$ regardless of the direction of bifurcation.

Remark 3. The ESS Maximum Principle states that a trait $u_{e}$ associated with an equilibrium $\left(x_{e}, u_{e}\right)$ of the Darwinian equations (2.3) is an ESS (evolutionarily stable trait or strategy) if and only if the equilibrium is (locally asymptotically) stable and the adaptive landscape $\ln r\left(x_{e}, v, u_{e}\right)$ has a global maximum at $v = u_{e}$ ^[7]. A population (mutant species) with a different trait cannot successfully invade, at low density, a population with an ESS mean trait.

If, in the Darwinian model (2.3), the distribution $f\left(v\right)$ has a local maximum at a critical trait $v = u_{c}$ then so does (for $b_{0} > s_{0}$) the inherent population growth rate

and hence so does the inherent adaptive landscape $\ln r\left(0, v, u\right)$. The trait $u_{e}$ of any positive equilibrium $\left(x_{e}, u_{e}\right)$ is, by the equilibrium equations (3.3), a critical trait of the adaptive landscape $\ln r\left(x_{e}, v, u_{e}\right)$ at which fitness $\ln r\left(x_{e}, u_{e}, u_{e}\right) = 0$.

Remark 4. For the positive equilibria bifurcating from, and sufficiently near, the extinction equilibrium $\left(0, u_{c}\right)$ at a generic critical trait $u_{c}$ which is a local maximum of $f\left(v\right)$ (cf. Theorem 3.2(c)) the fitness landscape $\ln r\left(x_{e}, v, u_{e}\right)$ has, by continuity, a local maximum at $v = u_{e}$. If the fitness landscape does not have a global maximum at $v = u_{e}$, then by the ESS Maximum Principle $u_{e}$ is not an ESS. Sufficient conditions that imply the fitness landscape has a global maximum at $v = u_{e},$ and hence that $u_{e}$ is an ESS, are (by continuity) that $f\left(v\right)$ has a unique global maximum at $v = u_{c}$ and that $f\left(\pm\infty\right) = 0$.

If the trait component $u_{e}$ of a stable positive equilibrium $\left(x_{e}, u_{e}\right)$ of the Darwinian equations (2.3) is an ESS, then we call $\left(x_{e}, u_{e}\right)$ an ESS equilibrium.

4.   Semelparity versus iteroparity

In model (2.3) inherent survival $s_{0}\left(1-f\left(v\right) \right)$ can vary from $0$ to $s_{0}$. If survival $s_{0}\left(1-f\left(v\right) \right)$ equals $0$ at a trait $v = u_{s}$ (i.e. $f\left(u_{s}\right) = 1$) then an individual reproduces only once and dies, i.e. an individual with trait $v = u_{s}$ is semelparous. We refer to a population with mean trait $u_{s}$ or "significantly near" $u_{s}$ as a semelparous population and to an equilibrium $\left(x_{e}, u_{e}\right)$ with $u_{e}\approx u_{s}$ as a semelparous equilibrium. If, on the other hand, $u_{e}$ is not "significantly close" to $u_{s}$, so that the inherent survival $s_{0}\left(1-f\left(u_{e}\right) \right)$ is significantly far from $0$, then the equilibrium is an iteroparous equilibrium. What is meant by "significantly" and what the cut-off survival probability between these two life histories strategies is, of course, arbitrary and up to the modeler to decide.

A trait $v = u_{s}$ such that $f\left(u_{s}\right) = 1$ is a semelparous trait$.$ Note by H2 that the distribution $f\left(v\right)$ has a global maximum at such semelparous trait and therefore individuals with mean trait $u_{s}$ maximize their inherent fertility $b_{0}f\left(u\right)$ at the expense of reproducing only once. By Remark 4 the positive equilibria $\left(x_{e}, u_{e}\right)$ forward bifurcating from and near the extinction equilibrium $\left(0, u_{s}\right)$ at $b_{0} ^{s} = 1$ in Theorem 3.2(c) are ESS semelparous equilibria.

Similarly, forward bifurcating positive equilibria have ESS iteroparous traits if the critical trait $u_{c}$ is located at a global maximum of $f\left(v\right)$, but $f\left(u_{c}\right)$ is significantly less that $1$. Of more interest here, however, is the case when both semelparous and iteroparous traits are present in the distribution $f\left(v\right)$, in order to study which trait is favored by evolution (i.e. which is an ESS). Toward this end we assume the following.

    H3. There exist two (generic) critical traits $u_{s}$ and $u_{i}$ at which maxima of $f\left(v\right)$ occur. We assume $f\left(u_{s}\right) = 1$ and hence $u_{s}$ is a semelparous trait at which $f\left(v\right)$ attains a global maximum. We also assume $u_{i}$ is an iteroparous trait, i.e. $f\left(u_{i}\right) < 1$ and hence $f\left(v\right)$ does not attain a global maximum at $u_{i}.$

Under the criteria of Theorem 3.2(c), forward bifurcating positive equilibria from the extinction equilibria $\left(0, u_{s}\right)$ and $\left(0, u_{i}\right)$ are, respectively, ESS semelparous equilibria and non-ESS iteroparous equilibria. These bifurcations occur at the critical $b_{0}$ values $b_{0}^{s}$ and $b_{0}^{i}$ given by (3.6) respectively, namely

Under assumption H3 there is, of course, a local minimum of $f\left(v\right)$ at a trait $u_{m}$ between $u_{s}$ and $u_{i}$ but the bifurcating positive equilibria from the extinction equilibrium $\left(0, u_{m}\right)$ are unstable, according to Theorem 3.2(d).

Corollary 1. In addition to the assumptions of Theorem 3.2 assume H3 holds for the Darwinian equations (2.3) with (2.4). Then no ESS iteroparous equilibria arise from bifurcations atextinction equilibria, at least locally in a neighborhood of the bifurcation points.

In the following examples we illustrate the conclusions of Theorem 3.2 and the Corollary 1. In Example 4.1 we show that in the absence of trait dependent density terms $\beta$ and $\sigma$, the only ESS equilibria of the Darwinian model (2.3) are semelparous. Example 4.2 is an example that shows, on the other hand, that it is possible for ESS iteroparous equilibria to occur outside the neighborhood of the bifurcation points (i.e. for sufficiently high equilibrium density), if density effect terms are trait dependent.

4.1.   Trait independent density terms

Assume H3 and suppose $a_{i}\left(v, u\right) \equiv1$ in the Darwinian equations (2.3) so that the density terms are trait independent. The equilibrium equations for positive equilibria $\left(x_{e}, u_{e}\right)$ are

Suppose $f^{\prime}\left(u_{e}\right) \neq0$. Then from the second equation we see that $b_{0}\beta\left(x_{e}\right) = s_{0}\sigma\left(x_{e}\right)$. But if this equality is used in the first equation, we obtain $s_{0} \sigma\left(x_{e}\right) = 1$ in contradiction to H1. If follows that $f^{\prime}\left(u_{e}\right) = 0$. That is to say, the trait component $u_{e}$ in any positive equilibrium $\left(x_{e}, u_{e}\right)$ must be a critical point $u_{e} = u_{c}$ of $f\left(v\right)$. It follows that the trait components $u_{e}$ of the positive equilibria $\left(x_{e}, u_{e}\right)$ that bifurcate from an extinction equilibrium $\left(0, u_{c}\right)$, as guaranteed by Theorem 3.2, are all equal to $u_{c}$. Thus, the positive equilibria retain the characteristics of the critical trait from which they bifurcate. In particular, if $u_{c} = u_{s}$ is a semelparous trait, then all equilibria on the (global) bifurcating continuum are semelparous. Similarly, for the (global) continuum bifurcating from an extinction equilibrium at an iteroparous extinction equilibrium $(0, u_{i})$.

Note that the first equilibrium equation evaluated at an equilibrium $\left(x, u\right) = \left(x_{e}, u_{e}\right)$, together with H1, imply

At a positive equilibrium

is a re-scaled and shifted version of $f\left(v\right)$ and therefore it, and the adaptive landscape $\ln r\left(x_{e}, v, u_{e}\right)$, has the same local and global maxima as $f\left(v\right)$.

We conclude, in this case of trait independent density terms, that the semelparous equilibria $\left(x_{e}, u_{s}\right)$ are ESS equilibria (even outside the neighborhood of the bifurcation point $\left(0, u_{s}\right)$ at $b_{0}^{s} = 1$). Similarly, the iteroparous equilibria $\left(x_{e}, u_{i}\right)$ are not ESS equilibria (even outside the neighborhood of the bifurcation point $\left(0, u_{s}\right)$ at $b_{0}^{i}$). In summary, in the absence of trait dependent density effects in the Darwinian model (2.3), there are no ESS iteroparous equilibria. The only ESS equilibria are semelparous. This supports Cole's conclusion that evolution favors semelparity.

4.2.   Trait dependent density terms

We showed in Section 4.1 that there are no ESS iteroparous equilibria of the Darwinian model (2.3) when density effects are trait independent. Even if density effects are trait dependent, we showed above that bifurcating iteroparous equilibria, in a neighborhood of the bifurcation point, are not ESS equilibria (while bifurcation semelparous equilibria are). In this section we show by means of an example that ESS iteroparous equilibria are possible outside a neighborhood of the bifurcation point.

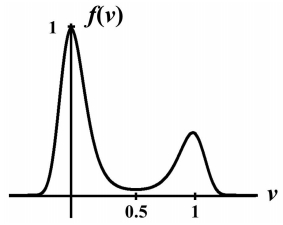
We assume the distribution $f\left(v\right)$ has exactly two maximum as shown in Figure 1. A global maximum occurs at the semelparous trait $u_{s} = 0$ and a local maximum occurs at a iteroparous trait $u_{i}$ near $1$. The specific mathematical expression used in the simulations is given in the caption of Figure 1.

To complete the Darwinian model (2.3) we need to choose expressions for the density terms $\beta$ and $\sigma$ and the trait dependent factors $a_{i}\left(v, u\right)$. For the density terms we choose the rational functions, often used in population modeling,

As is commonly done in Darwinian models, we assume the factors $a_{i}$ are functions of the difference $v-u.$ That is to say, the intensity of the intraspecific competitive interactions felt by an individual depends on how different the individual is from most other individuals (as measured by the mean trait).

In this example, we assume no trait dependence in the survival density term, i.e. $a_{2}\left(v, u\right) \equiv1$, and that the trait dependence in the fertility density term is a decreasing function of $v-u.$ This models a hierarchical trait dependence in intraspecific competition in that individuals with traits larger than the mean experience less competition. Specifically, we take

Under these assumptions, in the Darwinian model (2.3) we have

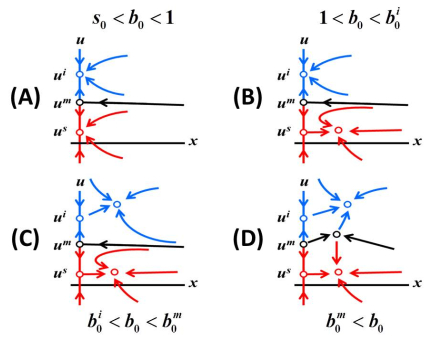
There are 3 critical traits $u_{s},$ $u_{m}$ and $u_{i}$ located at the critical points of $f\left(v\right)$. By Theorems 3.1 and 3.2, as $b_{0}$ increases bifurcations occur at three critical values $b_{0}^{s} < b_{0}^{i} < b_{0}^{m}$ given by (3.6). Since the density terms (4.1) are decreasing functions of $z$, the bifurcations are forward ($\kappa > 0$ at each bifurcation). By Remarks 2 and 4, the forward bifurcations at $b_{0}^{s}$ and $b_{0}^{i}$ are stable, since the semelparous trait $u_{s}$ and the iteroparous trait $u_{i}$ are located at local maxima of $f\left(v\right)$, and the bifurcation at $b_{0}^{m}$ is unstable, since $u_{m}$ is located at a local minimum. As pointed out above, locally near the bifurcations at $b_{0}^{s}$ and $b_{0}^{i}$ the bifurcating equilibria are ESS semelparous equilibria and non-ESS iteroparous equilibria respectively. This sequence of bifurcations is represented by the iconic phase plane portraits in Figure 2.

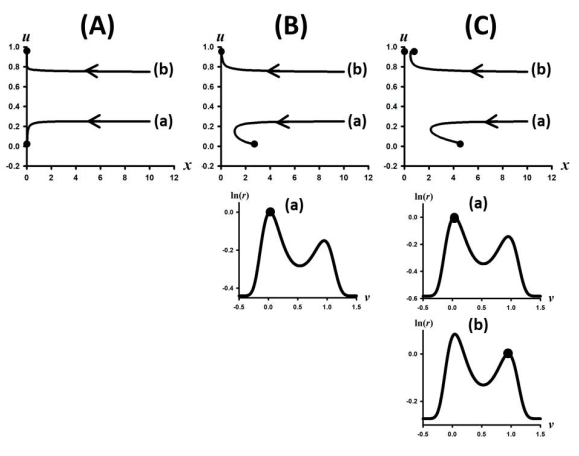
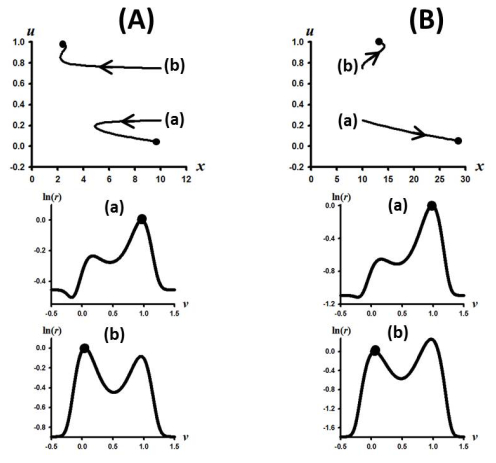
Sample orbits in Figures 3 illustrate the bifurcations and multiple attractors for the phase plane plots (B) and (C) in Figure 2. Parameter values are given in the figure captions. These sample orbits corroborate the occurrence of the sequential bifurcation of ESS semelparous equilibria followed by non-ESS iteroparous equilibria at the predicted bifurcation values of $b_{0}^{s}$ and $b_{0}^{i}$. They also illustrate that these bifurcations result in multiple attractors and hence initial condition dependent extinction and survival as well as initial condition dependent semelparous and iteroparous equilibria life history strategies. For selected larger values of $b_{0}$, Figure 4 shows orbits that approach ESS iteroparous equilibria (which are non-ESS equilibria at bifurcation). Interestingly it can occur that both semelparous and iteroparous equilibria are ESS equilibria (see Figure 4A) or that the iteroparous equilibrium becomes an ESS equilibrium and the semelparous becomes non-ESS equilibrium (see Figure 4B).

We note that when we used the symmetric distribution

instead of the hierarchical distribution (4.2), we found no simulation evidence of ESS iteroparous equilibria.

5.   Discussion and conclusion

The Darwinian equations (2.3) constitute a dynamic evolutionary model based on a scalar difference equation for the dynamics of a population in which a phenotypic trait, and hence the model coefficients, change over time due to Darwinian evolutionary principles. The model components accounting for density effects remain general. The key assumption with regard to the dependence of the inherent fertility and survival rates on the phenotypic trait is that they suffer a trade off, i.e. a change in an individual's trait that results in an increase (or a decrease) in fertility is accompanied by a decrease (or, respectively, an increase) in survival. Another key assumption is that the intensity of the density effects on an individual's fertility and survival is not only dependent on its phenotypic trait, but that of the remaining individuals in the population as represented by the population mean phenotypic trait.

Theorems 3.1 and 3.2 give conditions under which positive equilibria bifurcate from an extinction equilibrium and under which they are stable or unstable. Extinction equilibria $\left(x, u\right) = \left(0, u_{c}\right)$ occur at critical traits and in the model (2.3) a trait at which fertility is maximized, and hence survival drops to 0$,$ is a critical trait that describes a semelparous life history strategy. When the bifurcation is forward and when evolution does not occur too rapidly, the bifurcating positive equilibria are (locally asymptotically stable). By the ESS Maximum Principle, the bifurcating positive equilibria are ESS equilibria if (and only if) their trait component lies at a global maximum of the adaptive landscape.

A trait is a semelparous trait $u_{s}$ if the survival probability of an individual with that trait equals $0$ (and hence it has no second reproductive event). An individual with a trait $v$ near a semelparous trait $u_{s}$ has a low probability of survival and second reproduction, and this is true if the population mean $u$ is near $u_{s}$. We call a population a semelparous population if its mean trait is near a semelparous trait and an iteroparous population otherwise (how near is near enough is up to the modeler). Suppose both semelparous and iteroparous critical traits are present in the model, such as the one in Section 4, that the bifurcations are forward (which occurs if the density effects are negative), and that evolution is not too rapid. Then our analysis results in several broad conclusions concerning the evolution of semelparity or iteroparity and how it is influenced by the dependence of density effects on the evolving phenotypic trait:

1. If the density effects in a population model are not in any way dependent on the evolving phenotypic trait (but inherent fertility and/or survival are), then only semelparous equilibria are ESS equilibria (Section 4.1). This case supports Cole's contention that evolution should favor semelparity.

2. If density effects do depend on the evolving phenotypic trait, then bifurcating semelparous equilibria are ESS equilibria and bifurcating iteroparous equilibria are not ESS equilibria, at least in a neighborhood of the bifurcation points. This conclusion again supports Cole's contention, but only for equilibria in neighborhoods of bifurcation points.

3. Outside the neighborhood of a bifurcation point, it is possible for iteroparous equilibria to be ESS equilibria. We have not analytically proved this, but only illustrated it by means of simulations of an example model (Section 4.2). This example illustrates the possibility of the simultaneous existence of both an ESS semelparous equilibrium and an ESS iteroparous equilibrium. In this multiple attractor scenario, the evolution to iteroparity or semelparity is initial condition dependent. The example also illustrates the possibility that the ESS property of equilibria can reverse roles, with the iteroparous equilibria becoming ESS equilibria and semelparous equilibria becoming ESS equilibria outside the neighborhoods of the bifurcation points. There are two a key assumptions in this example that affect these results.

First, the trait effect on the fertility density factor is asymmetric (4.2), by which is meant that an individual with a trait larger than the population mean trait suffers a reduced effect of population density on its fertility. A hierarchy based on the trait with regard to intraspecific competition for resources would result in such an asymmetry. For example, if trees are competing for sunlight, then an individual tree will experience less competition if it is taller than most other trees, i.e. taller than the mean tree height. Similar competitive hierarchy could be based on any number physical attributes, such as body size or mobility, or behavioral traits such as agammaessiveness, etc. We also ran simulations using a symmetric density factor (4.4) but found no evidence of ESS iteroparous equilibria.

Second, in the example it is assumed that the iteroparous trait is larger than the semelparous trait. Thus, in this example, the benefits to an individual with the iteroparous trait, which result in it being an ESS, are twofold: not only does an iteroparous trait confer a higher inherent survival probability but also a reduced negative effect of density on fertility. This in turn raises the population growth rate $r$ at the iteroparous trait, which in the simulation example was enough to result in a global maximum at the iteroparous equilibrium.

4. Typically, with both semelparous and iteroparous traits are present, the Darwinian model (2.3) has multiple stable equilibria and, as a result, the asymptotic alternatives of extinction versus survival as well as the life history strategies of semelparity versus iteroparity are initial condition dependent.

In reaching the conclusions above, we focused on forward (stable) bifurcations at critical traits. Backward bifurcations can result from positive density effects at low density, i.e. component Allee effects, which can produce at negative $\kappa$ value. By Theorem 3.2 such bifurcations are always unstable, but it is common in population models (which typically have negative density effects at high densities) for backward bifurcations to produce strong Allee effects, i.e. multiple attractor scenarios for subcritical values of $b_{0}$ in which both the extinction equilibrium and a positive attractor exist (outside a neighborhood of the bifurcation point) ^[12]. What the nature of the equilibria are, semelparous or iteroparous, and what is their ESS status would be a interesting questions to investigate.

We also have restricted attention to scalar difference equations as population models and therefore ignored any population structure. General bifurcation results are available for both population and evolutionary models for structured populations (by means of matrix equations) ^[13], ^[14], ^[15], ^[16] and the study of semelparous and iteroparous evolution would be enhanced by a study of such models since they take into account more detailed life history patterns.

Acknowledgments

The author was supported by NSF grant DMS-1407564. The author is grateful to two anonymous reviewers whose careful reading and thoughtful suggestions improved the paper.

Conflict of interest

All authors declare no conflicts of interest in this paper.

Appendix

Proof of Theorem 3.2. (a) We introduce $y = u-u_{c}$ into the equilibrium equations (3.1) with (2.4), namely, into the two algebraic equations

and write the Taylor expansions (with remainder) of the left sides of the equations in $x$ and $y$ centered on $x = y = 0$ to obtain

where $\left\vert h_{i}\left(x, y\right) \right\vert = O\left(x^{2} +y^{2}\right)$ and we have introduced the notation

By moving all terms not involving the bifurcation parameter $b_{0}$ to the left sides of both equations and writing the result in matrix format, we obtain

Multiplying both sides of this equation by the inverse of the matrix on the left side, we get the nonlinear operator equation

where

to which we can apply the global bifurcation theorems in ^[11]. The result is the existence of a continuum in $S$ that contains (i.e. bifurcates from) an extinction equilibrium $[b_{0}, \left(0, u_{c}\right) ]$ where $b_{0}$ equals a characteristic value of $L,$ i.e. a reciprocal of the (simple) eigenvalues of $L$, which are (3.6) and $s_{0}$.

Consider first the case $b_{0} = b_{0}^{c}$. In a neighborhood of $[b_{0} ^{c}, \left(0, u_{c}\right) ]$, the bifurcating equilibria are approximated by an eigenvector of $L$ associated with eigenvalue $b_{0}^{c}$ (this is a well known fact of bifurcation theory, but also see the proof of (b) below) whose $x$ component is a multiple of

According to Theorem 1.25 in ^[11] the bifurcating continuum $S$ contains two subcontinua one of which $S_{+}$ consists, in a neighborhood of the bifurcation point, of positive equilibria (and the other of which consists of equilibria with $x < 0$, in which we are not interested). Moreover, according to this theorem, $S_{+}$ connects to

(ⅰ) either the boundary of $\Omega$

(ⅱ) or the extinction equilibrium $[s_{0}, \left(0, u_{c}\right) ],$ located at the other characteristic value $s_{0}$ of $L$.

It is possible that $S_{+}$ consists entirely of positive equilibrium pairs. If it does not, however, then there exists a sequence of positive equilibrium pairs $[b_{0}^{\left(i\right) }, \left(x^{\left(i\right) }, u^{\left(i\right) }\right) ]\in S_{+}$ such that

for some $b^{\ast}\geq s_{0}$ and $u^{\ast}\neq u_{c}$. Positive equilibria pairs satisfy the two algebraic equations (3.3), which implies as $i\rightarrow\infty$ that

If $b^{\ast} = s_{0},$ then the first equation implies the contradiction $s_{0} = 1.$ Therefore $f^{\prime}\left(u^{\ast}\right) = 0$ and $u^{\ast}$ is a critical trait. This rules out the alternative (ⅱ) and leaves us with the alternatives stated in part (a) of Theorem 3.2.

(b) We can use the implicit function theorem to solve the equilibrium equations (3.3) for $x$ and $u$ as functions of $b_{0}.$ By the definition (3.6) of $b_{0}^{c}$ these equations are satisfied by $x = 0$ and $u = u_{c}$ when $b_{0} = b_{0}^{c}.$ The implicit function theorem guarantees (twice continuously differentiable) solutions $x = \xi\left(b_{0}\right)$ and $u = \upsilon\left(b_{0}\right)$ of equations (3.3) that satisfy $\xi\left(b_{0} ^{c}\right) = 0$ and $\upsilon\left(b_{0}^{c}\right) = u_{c}$ provided the Jacobian of these equations is nonsingular at $x = 0$, $u = u_{c}$ and $b_{0} = b_{0}^{c}$. This Jacobian is the diagonal matrix

and hence is nonsingular under our assumptions that $\kappa\neq0$ and $f^{\prime\prime}\left(u_{c}\right) \neq0$. (The asterisk denotes an entry in the Jacobian that we do not need.)

An implicit differentiation of equation (3.3a)

with respect to $b_{0}$, followed by an evaluation at $b_{0} = b_{0}^{c}$, results in

and hence

Thus since $\xi\left(b_{0}^{c}\right) = 0$ it follows that if $\kappa > 0$ (respectively $\kappa < 0$) then $x = \xi\left(b_{0}\right) > 0$ for $b_{0}\gtrapprox b_{0}^{c}$ and the bifurcation is forward (respectively backward).

(c) To study the stability by linearization of the bifurcating positive equilibria, at least in a neighborhood of the bifurcation point $\left[ b_{0}^{c}, \left(0, u_{c}\right) \right]$, we consider the Jacobian (3.6) evaluated at a positive equilibrium (at which, by (3.4), $r\left(x, u, u\right) = 1$)

For the positive equilibria $x = \xi\left(b_{0}\right),$ $u = \upsilon\left(b_{0}\right)$ on the bifurcating continuum, this Jacobian becomes a function of $b_{0}$ which we denote by $J\left(b_{0}\right)$. In order to utilize the linearization principle, we need to investigate the two eigenvalues $\lambda_{1}\left(b_{0}\right)$ and $\lambda_{2}\left(b_{0}\right)$ for $b_{0}$ near $b_{0}^{c}$.

Because the appearance of $u$ in $r\left(x, v, u\right)$ given by (2.4) is always associated with a factor of $x$, any $u$ derivative of $r$ equals $0$ when evaluated at $x = 0$. Thus, $\partial_{uv}r\left(0, u_{c}, u_{c}\right) = 0$. A straightforward calculation shows

Thus,

and hence

Under the assumptions in (c), $\left\vert \lambda_{2}\left(b_{0}^{c}\right) \right\vert < 1$ and hence $\left\vert \lambda_{2}\left(b_{0}\right) \right\vert < 1$ for $b_{0}$ near $b_{0}^{c}.$ It follows that stability by linearization is determined by $\lambda_{1}\left(b_{0}\right)$. Specifically, the positive equilibrium will be stable (respectively unstable) for $b_{0}$ near $b_{0}^{c}$ if $\lambda_{1}^{\prime}\left(b_{0}^{c}\right) < 0$ (respectively $\lambda_{1}^{\prime}\left(b_{0}^{c}\right) > 0$). We need a formula for this derivative.

The left and right eigenvectors of $J\left(b_{0}\right)$ associated with eigenvalue $\lambda_{1}\left(b_{0}\right)$ are

An implicit differentiation of $J\left(b_{0}\right) \hat{w}_{R}\left(b_{0}\right) = \lambda_{1}\left(b_{0}\right) \hat{w}_{R}\left(b_{0}\right)$ with respect to $b_{0}$ followed by an evaluation at $b_{0} = b_{0}^{c}$ and an application of the Fredholm alternative yield the formula

Now

and

A calculation using (2.4) shows that $\partial_{x}r\left(0, u_{c}, u_{c}\right) = -\kappa$ so that we arrive at

In the case of a forward bifurcation when the bifurcating positive equilibria correspond to $b_{0}\gtrapprox b_{0}^{c},$ we conclude that $\lambda _{1}^{\prime}\left(b_{0}\right) \lessapprox1$ and the equilibria are stable by the linearization principle. However, in the case of a backward bifurcation when the bifurcating positive equilibria correspond to $b_{0}\lessapprox b_{0}^{c},$ we conclude that $\lambda_{1}^{\prime}\left(b_{0}\right) \gtrapprox1$ and the equilibria are unstable.

(d) In this case $\lambda_{2}\left(b_{0}\right)$ is either greater than $1,$ if $f^{\prime\prime}\left(u_{c}\right) > 0$, or less than $-1,$ if the inequality on $\delta^{2}$ in (3.7) is reversed.