Cell proliferation is controlled by many complex regulatory networks. Our purpose is to analyse, through mathematical modeling, the effects of growth factors on the dynamics of the division cycle in cell populations.
Our work is based on an age-structured PDE model of the cell division cycle within a population of cells in a common tissue. Cell proliferation is at its first stages exponential and is thus characterised by its growth exponent, the first eigenvalue of the linear system we consider here, a growth exponent that we will explicitly evaluate from biological data.Moreover, this study relies on recent and innovative imaging data (fluorescence microscopy) that make us able to experimentally determine the parameters of the model and to validate numerical results.This model has allowed us to study the degree of simultaneity of phase transitions within a proliferating cell population and to analyse the role of an increased growth factor concentration in this process.
This study thus aims at helping biologists to elicit the impact of growth factor concentration on cell cycle regulation, at making more precise the dynamics of key mechanisms controlling the division cycle in proliferating cell populations, and eventually at establishing theoretical bases for optimised combined anticancer treatments.
1.
Introduction
The training of artificial neural networks (ANNs) with rectified linear unit (ReLU) activation via gradient descent (GD) type optimization schemes is nowadays a common industrially relevant procedure which appears, for instance, in the context of natural language processing, face recognition, fraud detection, and game intelligence. Although there exist a large number of numerical simulations in which GD type optimization schemes are effectively used to train ANNs with ReLU activation, till this day in the scientific literature there is in general no mathematical convergence analysis which explains the success of GD type optimization schemes in the training of such ANNs.
GD type optimization schemes can be regarded as temporal discretization methods for the gradient flow (GF) differential equations associated to the considered optimization problem and, in view of this, it seems to be a natural direction of research to first aim to develop a mathematical convergence theory for time-continuous GF differential equations and, thereafter, to aim to extend such a time-continuous convergence theory to implementable time-discrete GD type optimization methods.
Although there is in general no theoretical analysis which explains the success of GD type optimization schemes in the training of ANNs in the literature, there are several auspicious analysis approaches as well as several promising partial error analyses regarding the training of ANNs via GD type optimization schemes and GFs, respectively, in the literature. For convex objective functions, the convergence of GF and GD processes to the global minimum in different settings has been proved, e.g., in [1,2,3,4,5]. For general non-convex objective functions, even under smoothness assumptions GF and GD processes can show wild oscillations and admit infinitely many limit points, cf., e.g., [6]. A standard condition which excludes this undesirable behavior is the Kurdyka-Łojasiewicz inequality and we point to [7,8,9,10,11,12,13,14,15,16] for convergence results for GF and GD processes under Łojasiewicz type assumptions. It is in fact one of the main contributions of this work to demonstrate that the objective functions occurring in the training of ANNs with ReLU activation satisfy an appropriate Kurdyka-Łojasiewicz inequality, provided that both the target function and the density of the probability distribution of the input data are piecewise polynomial. For further abstract convergence results for GF and GD processes in the non-convex setting we refer, e.g., to [17,18,19,20,21] and the references mentioned therein.
In the overparametrized regime, where the number of training parameters is much larger than the number of training data points, GF and GD processes can be shown to converge to global minima in the training of ANNs with high probability, cf., e.g., [22,23,24,25,26,27,28]. As the number of neurons increases to infinity, the corresponding GF processes converge (with appropriate rescaling) to a measure-valued process which is known in the scientific literature as Wasserstein GF. For results on the convergence behavior of Wasserstein GFs in the training of ANNs we point, e.g., to [29,30,31], [32, Section 5.1], and the references mentioned therein.
A different approach is to consider only very special target functions and we refer, in particular, to [33,34] for a convergence analysis for GF and GD processes in the case of constant target functions and to [35] for a convergence analysis for GF and GD processes in the training of ANNs with piecewise linear target functions. In the case of linear target functions, a complete characterization of the non-global local minima and the saddle points of the risk function has been obtained in [36].
In this article we establish two basic results for GF differential equations in the training of fully-connected feedforward ANNs with one hidden layer and ReLU activation. Specifically, in the first main result of this article, see Theorem 1.1 below, we establish in the training of such ANNs under the assumption that the probability distribution of the input data of the considered supervised learning problem is absolutely continuous with a bounded density function that every GF differential equation possesses for every initial value a solution which is also unique among a suitable class of solutions (see (1.6) in Theorem 1.1 for details). In the second main result of this article, see Theorem 1.2 below, we prove in the training of such ANNs under the assumption that the target function and the density function are piecewise polynomial (see (1.8) below for details) that every non-divergent GF trajectory converges with an appropriate speed of convergence (see (1.11) below) to a critical point.
In Theorems 1.1 and 1.2 we consider ANNs with $ d \in \mathbb{N} = \{ 1, 2, 3, \dots \} $ neurons on the input layer ($ d $-dimensional input), $ H \in \mathbb{N} $ neurons on the hidden layer ($ H $-dimensional hidden layer), and $ 1 $ neuron on the output layer ($ 1 $-dimensional output). There are thus $ H d $ scalar real weight parameters and $ H $ scalar real bias parameters to describe the affine linear transformation between $ d $-dimensional input layer and the $ H $-dimensional hidden layer and there are thus $ H $ scalar real weight parameters and 1 scalar real bias parameter to describe the affine linear transformation between the $ H $-dimensional hidden layer and the $ 1 $-dimensional output layer. Altogether there are thus
real numbers to describe the ANNs in Theorems 1.1 and 1.2. We also refer to Figure 1 for a graphical illustration of the architecture of an example ANN with $ d = 4 $ neurons on the input layer and $ H = 5 $ neurons on the hidden layer.
The real numbers $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $ in Theorems 1.1 and 1.2 are used to specify the set $ [\mathscr{a}, \mathscr{b}]^d $ in which the input data of the considered supervised learning problem takes values in and the function $ f \colon [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ in Theorem 1.1 specifies the target function of the considered supervised learning problem.
In Theorem 1.1 we assume that the target function is an element of the set $ C([\mathscr{a}, \mathscr{b}]^d, \mathbb{R}) $ of continuous functions from $ [\mathscr{a}, \mathscr{b}]^d $ to $ \mathbb{R} $ but beside this continuity hypothesis we do not impose further regularity assumptions on the target function.
The function $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}]^d \to [0, \infty) $ in Theorems 1.1 and 1.2 is an unnormalized density function of the probability distribution of the input data of the considered supervised learning problem and in Theorem 1.1 we impose that this unnormalized density function is bounded and measurable.
In Theorems 1.1 and 1.2 we consider ANNs with the ReLU activation function
The ReLU activation function fails to be differentiable and this lack of regularity also transfers to the risk function of the considered supervised learning problem; cf. (1.5) below. We thus need to employ appropriately generalized gradients of the risk function to specify the dynamics of the GFs. As in [34, Setting 2.1 and Proposition 2.3] (cf. also [33,37]), we accomplish this, first, by approximating the ReLU activation function through continuously differentiable functions which converge pointwise to the ReLU activation function and whose derivatives converge pointwise to the left derivative of the ReLU activation function and, thereafter, by specifying the generalized gradient function as the limit of the gradients of the approximated risk functions; see (1.3) and (1.5) in Theorem 1.1 and (1.9) and (1.10) in Theorem 1.2 for details.
We now present the precise statement of Theorem 1.1 and, thereafter, provide further comments regarding Theorem 1.2.
Theorem 1.1 (Existence and uniqueness of solutions of GFs in the training of ANNs). Let $ d, H, \mathfrak{d} \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, $ f \in C ([\mathscr{a}, \mathscr{b}]^d, \mathbb{R}) $ satisfy $ \mathfrak{d} = d H + 2 H + 1 $, let $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}]^d \to [0, \infty) $ be bounded and measurable, let $ \mathfrak{R}_r \in C (\mathbb{R}, \mathbb{R}) $, $ r \in \mathbb{N} \cup \left\{ {{ \infty }} \right\} $, satisfy for all $ x \in \mathbb{R} $ that $ (\cup_{r \in \mathbb{N}} \left\{ {{ \mathfrak{R}_r }} \right\}) \subseteq C^1(\mathbb{R}, \mathbb{R}) $, $ \mathfrak{R}_\infty (x) = \max \left\{ {{ x, 0 }} \right\} $, $ \sup_{r \in \mathbb{N}} \sup_{y \in [-|x|, |x|] } | (\mathfrak{R}_r)'(y)| < \infty $, and
for every $ \theta = (\theta_1, \ldots, \theta_ \mathfrak{d}) \in \mathbb{R}^ \mathfrak{d} $ let $ \mathbf{D} ^\theta \subseteq \mathbb{N} $ satisfy
for every $ r \in \mathbb{N} \cup \left\{ {{ \infty }} \right\} $ let $ \mathcal{L}_r \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R} $ satisfy for all $ \theta = (\theta_1, \ldots, \theta_ \mathfrak{d}) \in \mathbb{R}^{ \mathfrak{d}} $ that
let $ \theta \in \mathbb{R}^ \mathfrak{d} $, and let $ \mathcal{G} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R}^ \mathfrak{d} $ satisfy for all $ \vartheta \in \left\{ {{ v \in \mathbb{R}^ \mathfrak{d} \colon ((\nabla \mathcal{L}_r) (v)) _{r \in \mathbb{N}}\; \mathit{\text{is convergent}} }} \right\} $ that $ \mathcal{G} (\vartheta) = \lim_{r \to \infty} (\nabla \mathcal{L}_r) (\vartheta) $. Then
(i) it holds that $ \mathcal{G} $ is locally bounded and measurable and
(ii) there exists a unique $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ which satisfies for all $ t \in [0, \infty) $, $ s \in [t, \infty) $ that $ \mathbf{D}^{\Theta_t} \subseteq \mathbf{D}^{\Theta_s } $ and
Theorem 1.1 is a direct consequence of Theorem 3.3 below. In Theorem 1.2 we also assume that the target function $ f \colon [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ is continuous but additionally assume that, roughly speaking, both the target function $ f \colon [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ and the unnormalized density function $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}]^d \to [0, \infty) $ coincide with polynomial functions on suitable subsets of their domain of definition $ [\mathscr{a}, \mathscr{b}]^d $. In Theorem 1.2 the $ (n \times d) $-matrices $ \alpha^k_i \in \mathbb{R}^{ n \times d } $, $ i \in \left\{ {{ 1, 2, \ldots, n }} \right\} $, $ k \in \left\{ {{0, 1}} \right\} $, and the $ n $-dimensional vectors $ \beta^k_i \in \mathbb{R}^n $, $ i \in \left\{ {{ 1, 2, \ldots, n }} \right\} $, $ k \in \left\{ {{0, 1}} \right\} $, are used to describe these subsets and the functions $ P^k_i \colon \mathbb{R}^d \to \mathbb{R} $, $ i \in \left\{ {{ 1, 2, \ldots, n }} \right\} $, $ k \in \left\{ {{0, 1}} \right\} $, constitute the polynomials with which the target function and the unnormalized density function should partially coincide. More formally, in (1.8) in Theorem 1.2 we assume that for every $ x \in [\mathscr{a}, \mathscr{b}] ^d $ we have that
In (1.11) in Theorem 1.2 we prove that there exists a strictly positive real number $ \beta \in (0, \infty) $ such that for every GF trajectory $ \Theta \colon [0, \infty) \to \mathbb{R}^{ \mathfrak{d} } $ which does not diverge to infinity in the sense* that $ \liminf_{t \to \infty} ||\Theta_t || < \infty $ we have that $ \Theta_t \in \mathbb{R}^{ \mathfrak{d} } $, $ t \in [0, \infty) $, converges with order $ \beta $ to a critical point $ \vartheta \in \mathcal{G}^{ - 1 }(\left\{ {{ 0 }} \right\}) = \left\{ {{ \theta \in \mathbb{R}^{ \mathfrak{d} } \colon \mathcal{G} (\theta) = 0 }} \right\} $ and we have that the risk $ \mathcal{L} (\Theta_t) \in \mathbb{R} $, $ t \in [0, \infty) $, converges with order 1 to the risk $ \mathcal{L} (\vartheta) $ of the critical point $ \vartheta $. We now present the precise statement of Theorem 1.2.
*Note that the functions $ || \cdot || \colon (\cup_{n \in \mathbb{N}} \mathbb{R} ^n) \to \mathbb{R} $ and $ \left\langle {{ \cdot, \cdot }} \right\rangle \colon (\cup_{n \in \mathbb{N}} (\mathbb{R}^n \times \mathbb{R}^n)) \to \mathbb{R} $ satisfy for all $ n \in \mathbb{N} $, $ x = (x_1, \ldots, x_n) $, $ y = (y_1, \ldots, y_n) \in \mathbb{R}^n $ that $ || x || = [\sum _{i = 1}^n \left| x_i \right| ^2] ^{1/2} $ and $ \left\langle {{ x, y }} \right\rangle = \sum _{i = 1}^ \mathfrak{d} x_i y_i $.
Theorem 1.2 (Convergence rates for GFs trajectories in the training of ANNs). Let $ d, H, \mathfrak{d}, n \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, $ f \in C([\mathscr{a}, \mathscr{b}] ^d, \mathbb{R}) $ satisfy $ \mathfrak{d} = d H + 2 H + 1 $, for every $ i \in \left\{ {{1, 2, \ldots, n}} \right\} $, $ k \in \left\{ {{0, 1}} \right\} $ let $ \alpha_{i}^k \in \mathbb{R}^{n \times d} $, let $ \beta_{i }^k \in \mathbb{R}^n $, and let $ P_i^k \colon \mathbb{R}^d \to \mathbb{R} $ be a polynomial, let $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}] ^d \to [0, \infty) $ satisfy for all $ k \in \left\{ {{0, 1}} \right\} $, $ x \in [\mathscr{a}, \mathscr{b}] ^d $ that
let $ \mathfrak{R}_r \in C (\mathbb{R}, \mathbb{R}) $, $ r \in \mathbb{N} \cup \left\{ {{ \infty }} \right\} $, satisfy for all $ x \in \mathbb{R} $ that $ (\cup_{r \in \mathbb{N}} \left\{ {{ \mathfrak{R}_r }} \right\}) \subseteq C^1(\mathbb{R}, \mathbb{R}) $, $ \mathfrak{R}_\infty (x) = \max \left\{ {{ x, 0 }} \right\} $, $ \sup_{r \in \mathbb{N}} \sup_{y \in [-|x|, |x|] } | (\mathfrak{R}_r)'(y)| < \infty $, and
for every $ r \in \mathbb{N} \cup \left\{ {{ \infty }} \right\} $ let $ \mathcal{L}_r \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R} $ satisfy for all $ \theta = (\theta_1, \ldots, \theta_ \mathfrak{d}) \in \mathbb{R}^{ \mathfrak{d}} $ that
let $ \mathcal{G} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R}^ \mathfrak{d} $ satisfy for all $ \theta \in \left\{ {{ \vartheta \in \mathbb{R}^ \mathfrak{d} \colon ((\nabla \mathcal{L}_r) (\vartheta)) _{r \in \mathbb{N}}\; \mathit{\text{is convergent}} }} \right\} $ that $ \mathcal{G} (\theta) = \lim_{r \to \infty} (\nabla \mathcal{L}_r) (\theta) $, and let $ \Theta \in C ([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy $ \liminf_{t \to \infty } ||\Theta_t || < \infty $ and $ \forall \, t \in [0, \infty) \colon \Theta_t = \Theta_0 - \int_0^t \mathcal{G} (\Theta_s) \, \mathrm{d} s $. Then there exist $ \vartheta \in \mathcal{G}^{ - 1 } (\left\{ {{ 0 }} \right\}) $, $ \mathfrak{C}, \beta \in (0, \infty) $ which satisfy for all $ t \in [0, \infty) $ that
Theorem 1.2 above is an immediate consequence of Theorem 5.4 in Subsection 5.3 below. Theorem 1.2 is related to Theorem 1.1 in our previous article [37]. In particular, [37, Theorem 1.1] uses weaker assumptions than Theorem 1.2 above but Theorem 1.2 above establishes a stronger statement when compared to [37, Theorem 1.1]. Specifically, on the one hand in [37, Theorem 1.1] the target function is only assumed to be a continuous function and the unnormalized density is only assumed to be measurable and integrable while in Theorem 1.2 it is additionally assumed that both the target function and the unnormalized density are piecewise polynomial in the sense of (1.8) above. On the other hand [37, Theorem 1.1] only asserts that the risk of every bounded GF trajectory converges to the risk of critical point while Theorem 1.2 assures that every non-divergent GF trajectory converges with a strictly positive rate of convergence to a critical point (the rate of convergence is given through the strictly positive real number $ \beta \in (0, \infty) $ appearing in the exponent on the left inequality in (Eq 1.11) in Theorem 1.2) and also assures that the risk of the non-divergent GF trajectory converges with rate 1 to the risk of the critical point (the convergence rate $ 1 $ is ensured through the $ 1 $ appearing in the exponent on the right inequality in (Eq 1.11) in Theorem 1.2).
We also point out that Theorem 1.2 assumes that the GF trajectory is non-divergent in the sense that $ \liminf_{ t \to \infty } ||\Theta_t || < \infty $. In general, it remains an open problem to establish sufficient conditions which ensure that the GF trajectory has this non-divergence property. In this aspect we also refer to Gallon et al. [38] for counterexamples for which it has been proved that every GF trajectory with sufficiently small initial risk does in the training of ANNs diverge to $ \infty $ in the sense that $ \liminf_{ t \to \infty } ||\Theta_t || = \infty $.
The remainder of this article is organized in the following way. In Section 2 we establish several regularity properties for the risk function of the considered supervised learning problem and its generalized gradient function. In Subsection 3 we employ the findings from Section 2 to establish existence and uniqueness properties for solutions of GF differential equations. In particular, in Subsection 3 we present the proof of Theorem 1.1 above. In Subsection 4 we establish under the assumption that both the target function $ f \colon [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ and the unnormalized density function $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}]^d \to [0, \infty) $ are piecewise polynomial that the risk function is semialgebraic in the sense of Definition 4.3 in Subsection 4 (see Corollary 4.10 in Subsection 4 for details). In Subsection 5 we engage the results from Sections 2 and 4 to establish several convergence rate results for solutions of GF differential equations and, thereby, we also prove Theorem 1.2 above.
2.
Properties of the risk function and its generalized gradient function
In this section we establish several regularity properties for the risk function $ \mathcal{L} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R} $ and its generalized gradient function $ \mathcal{G} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R}^ \mathfrak{d} $. In particular, in Proposition 2.12 in Subsection 2.5 below we prove for every parameter vector $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ in the ANN parameter space $ \mathbb{R}^{ \mathfrak{d} } = \mathbb{R}^{ d H + 2 H + 1 } $ that the generalized gradient $ \mathcal{G} (\theta) $ is a limiting subdifferential of the risk function $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ at $ \theta $. In Definition 2.8 in Subsection 2.5 we recall the notion of subdifferentials (which are sometimes also referred to as Fréchet subdifferentials in the scientific literature) and in Definition 2.9 in Subsection 2.5 we recall the notion of limiting subdifferentials. In the scientific literature Definitions 2.8 and 2.9 can in a slightly different presentational form, e.g., be found in Rockafellar & Wets [39, Definition 8.3] and Bolte et al. [9, Definition 2.10], respectively.
Our proof of Proposition 2.12 uses the continuously differentiability result for the risk function in Proposition 2.3 in Subsection 2.2 and the local Lipschitz continuity result for the generalized gradient function in Corollary 2.7 in Subsection 2.4. Corollary 2.7 will also be employed in Subsection 3 below to establish existence and uniqueness results for solutions of GF differential equations. Proposition 2.3 follows directly from [37, Proposition 2.10, Lemmas 2.11 and 2.12]. Our proof of Corollary 2.7, in turn, employs the known representation result for the generalized gradient function in Proposition 2.2 in Subsection 2.2 below and the local Lipschitz continuity result for certain parameter integrals in Corollary 2.6 in Subsection 2.4. Statements related to Proposition 2.2 can, e.g., be found in [37, Proposition 2.2], [33, Proposition 2.3], and [34, Proposition 2.3].
Our proof of Corollary 2.6 uses the elementary abstract local Lipschitz continuity result for certain parameter integrals in Lemma 2.5 in Subsection 2.4 and the local Lipschitz continuity result for active neuron regions in Lemma 2.4 in Subsection 2.3 below. Lemma 2.4 is a generalization of [35, Lemma 7], Lemma 2.5 is a slight generalization of [35, Lemma 6], and Corollary 2.6 is a generalization of [37, Lemma 2.12] and [35, Corollary 9]. The proof of Lemma 2.5 is therefore omitted.
In Setting 2.1 in Subsection 2.1 below we present the mathematical setup to describe ANNs with ReLU activation, the risk function $ \mathcal{L} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R} $, and its generalized gradient function $ \mathcal{G} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R}^ \mathfrak{d} $. Moreover, in (2.6) in Setting 2.1 we define for a given parameter vector $ \theta \in \mathbb{R}^ \mathfrak{d} $ the set of hidden neurons which have all input parameters equal to zero. Such neurons are sometimes called degenerate (cf. Cheridito et al. [36]) and can cause problems with the differentiability of the risk function, which is why we exclude degenerate neurons in Proposition 2.3 and Corollary 2.7 below.
2.1. Mathematical description of artificial neural networks (ANNs)
In this subsection we present in Setting 2.1 below the mathematical setup that we employ to state most of the mathematical results of this work. We also refer to Figure 2 below for a table in which we briefly list the mathematical objects introduced in Setting 2.1.
Setting 2.1. Let $ d, H, \mathfrak{d} \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, $ f \in C ([\mathscr{a}, \mathscr{b}]^d, \mathbb{R}) $ satisfy $ \mathfrak{d} = d H + 2 H + 1 $, let $ \mathfrak{w} = ((\mathfrak{w}^{{ \theta }}_{ i, j })_{ (i, j) \in \left\{ {{ 1, \ldots, H }} \right\} \times \left\{ {{ 1, \ldots, d }} \right\} })_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H \times d } $, $ \mathfrak{b} = ((\mathfrak{b}^{{ \theta }}_1, \dots, \mathfrak{b}^{{ \theta }}_{ H }))_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H } $, $ \mathfrak{v} = ((\mathfrak{v}^{{\theta}}_1, \dots, \mathfrak{v}^{{\theta}}_{ H }))_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H } $, and $ \mathfrak{c} = (\mathfrak{c}^{{ \theta }})_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ satisfy for all $ \theta = (\theta_1, \ldots, \theta_{ \mathfrak{d}}) \in \mathbb{R}^{ \mathfrak{d}} $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} $, $ j \in \left\{ {{ 1, 2, \ldots, d }} \right\} $ that
let $ \mathfrak{R}_r \in C^1(\mathbb{R}, \mathbb{R}) $, $ r \in \mathbb{N} $, satisfy for all $ x \in \mathbb{R} $ that
and $ \sup_{r \in \mathbb{N}} \sup_{y \in [-|x|, |x|] } |(\mathfrak{R}_r)'(y)| < \infty $, let $ \lambda \colon \mathcal{B} (\mathbb{R}^d) \to [0, \infty] $ be the Lebesgue–Borel measure on $ \mathbb{R}^d $, let $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}] ^d \to [0, \infty) $ be bounded and measurable, let $ \mathscr{N} = (\mathscr{N} ^{ { \theta } })_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to C(\mathbb{R}^d, \mathbb{R}) $ and $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ satisfy for all $ \theta \in \mathbb{R}^{ \mathfrak{d} } $, $ x = (x_1, \dots, x_d) \in \mathbb{R}^d $ that
and $ \mathcal{L} (\theta) = \int_{[\mathscr{a}, \mathscr{b}] ^d} (f (y) - \mathscr{N} ^{ {\theta} } (y))^2 \mathfrak{p} (y) \, \lambda (\mathrm{d} y) $, for every $ r \in \mathbb{N} $ let $ \mathfrak{L}_r \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ satisfy for all $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ that
for every $ \varepsilon \in (0, \infty) $, $ \theta \in \mathbb{R}^ \mathfrak{d} $ let $ B_\varepsilon (\theta) \subseteq \mathbb{R}^ \mathfrak{d} $ satisfy $ B_\varepsilon (\theta) = \left\{ {{\vartheta \in \mathbb{R}^ \mathfrak{d} \colon ||\theta - \vartheta || < \varepsilon }} \right\} $, for every $ \theta \in \mathbb{R}^{ \mathfrak{d} } $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} $ let $ I_i^\theta \subseteq \mathbb{R}^d $ satisfy
for every $ \theta \in \mathbb{R}^ \mathfrak{d} $ let $ \mathbf{D} ^\theta \subseteq \mathbb{N} $ satisfy
and let $ \mathcal{G} = (\mathcal{G}_1, \dots, \mathcal{G}_ \mathfrak{d}) \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ satisfy for all $ \theta \in \left\{ {{ \vartheta \in \mathbb{R}^ \mathfrak{d} \colon ((\nabla \mathfrak{L}_r)(\vartheta))_{r \in \mathbb{N}}\; \mathit{\text{is convergent}} }} \right\} $ that $ \mathcal{G}(\theta) = \lim_{r \to \infty} (\nabla \mathfrak{L}_r) (\theta) $.
Next we add some explanations regarding the mathematical framework presented in Setting 2.1 above. In Setting 2.1
● the natural number $ d \in \mathbb{N} $ represents the number of neurons on the input layer of the considered ANNs,
● the natural number $ H \in \mathbb{N} $ represents the number of neurons on the hidden layer of the considered ANNs, and
● the natural number $ \mathfrak{d} \in \mathbb{N} $ measures the overall number of parameters of the considered ANNs
(cf. (1.1) and Figure 1 above). The real numbers $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $ in Setting 2.1 are employed to specify the $ d $-dimensional set $ [\mathscr{a}, \mathscr{b}]^d \subseteq \mathbb{R}^d $ in which the input data of the supervised learning problem considered in Setting 2.1 takes values in and which, thereby, also serves as the domain of definition of the target function of the considered supervised learning problem.
In Setting 2.1 the function $ f \colon [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ represents the target function of the considered supervised learning problem. In Setting 2.1 the target function $ f $ is assumed to be an element of the set $ C([\mathscr{a}, \mathscr{b}]^d, \mathbb{R}) $ of continuous functions from the $ d $-dimensional set $ [\mathscr{a}, \mathscr{b}]^d $ to the reals $ \mathbb{R} $ (first line in Setting 2.1).
The matrix valued function $ \mathfrak{w} = ((\mathfrak{w}^{{ \theta }}_{ i, j })_{ (i, j) \in \left\{ {{ 1, \ldots, H }} \right\} \times \left\{ {{ 1, \ldots, d }} \right\} })_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H \times d } $ in Setting 2.1 is used to represent the inner weight parameters of the ANNs considered in Setting 2.1. In particular, in Setting 2.1 we have for every $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ that the $ H \times d $-matrix $ \mathfrak{w}^{{ \theta }} = (\mathfrak{w}^{{ \theta }}_{ i, j })_{ (i, j) \in \left\{ {{ 1, \ldots, H }} \right\} \times \left\{ {{ 1, \ldots, d }} \right\} } \in \mathbb{R}^{ H \times d } $ represents the weight parameter matrix for the affine linear transformation from the $ d $-dimensional input layer to the $ H $-dimensional hidden layer of the ANN associated to the ANN parameter vector $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ (cf. (2.1), (2.3), and Figure 1).
The vector valued function $ \mathfrak{b} = ((\mathfrak{b}^{{ \theta }}_1, \dots, \mathfrak{b}^{{ \theta }}_{ H }))_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H } $ in Setting 2.1 is used to represent the inner bias parameters of the ANNs considered in Setting 2.1. In particular, in Setting 2.1 we have for every $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ that the $ d $-dimensional vector $ \mathfrak{b}^{{ \theta }} = (\mathfrak{b}^{{ \theta }}_1, \dots, \mathfrak{b}^{{ \theta }}_{ H }) \in \mathbb{R}^{ H } $ represents the bias parameter vector for the affine linear transformation from the $ d $-dimensional input layer to the $ H $-dimensional hidden layer of the ANN associated to the ANN parameter vector $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ (cf. (2.1), (2.3), and Figure 1).
The vector valued function $ \mathfrak{v} = ((\mathfrak{v}^{{\theta}}_1, \dots, \mathfrak{v}^{{\theta}}_{ H }))_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ H } $ in Setting 2.1 is used to describe the outer weight parameters of the ANNs considered in Setting 2.1. In particular, in Setting 2.1 we have for every $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ that the transpose of the $ H $-dimensional vector $ \mathfrak{v}^{{ \theta }} = (\mathfrak{v}^{{\theta}}_1, \dots, \mathfrak{v}^{{\theta}}_{ H }) \in \mathbb{R}^{ H } $ represents the weight parameter matrix for the affine linear transformation from the $ H $-dimensional hidden layer to the $ 1 $-dimensional output layer of the ANN associated to the ANN parameter vector $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ (cf. (2.1), (2.3), and Figure 1).
The real valued function $ \mathfrak{c} = (\mathfrak{c}^{{ \theta }})_{ \theta \in \mathbb{R}^{ \mathfrak{d} } } \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ in Setting 2.1 is used to represent the outer bias parameters of the ANNs considered in Setting 2.1. In particular, in Setting 2.1 we have for every $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ that the real number $ \mathfrak{c}^{{ \theta }} \in \mathbb{R} $ describes the bias parameter for the affine linear transformation from the $ H $-dimensional hidden layer to the $ 1 $-dimensional output layer of the ANN associated to the ANN parameter vector $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ (cf. (2.1), (2.3), and Figure 1).
In Setting 2.1 we consider ANNs with the ReLU activation function $ \mathbb{R} \ni x \mapsto \max\{ x, 0 \} \in \mathbb{R} $ (cf. (1.2)). The ReLU activation function fails to be differentiable and this lack of differentiability typically transfers from the activation function to the realization functions $ \mathscr{N} ^{ { \theta } } \colon \mathbb{R}^d \to \mathbb{R} $, $ \theta \in \mathbb{R}^{ \mathfrak{d} } $, of the considered ANNs and the risk function $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ of the considered supervised learning problem, both, introduced in (2.3) in Setting 2.1. In general, there thus do not exist standard derivatives and standard gradients of the risk function and, in view of this, we need to introduce suitably generalized gradients of the risk function to specify the GF dynamics. As in [34, Setting 2.1 and Proposition 2.3] (cf. also [33,37]), we accomplish this,
● first, by approximating the ReLU activation function through appropriate continuously differentiable functions which converge pointwise to the ReLU activation function and whose derivatives converge pointwise to the left derivative of the ReLU activation function,
● then, by using these continuously differentiable approximations of the ReLU activation function to specify approximated risk functions, and,
● finally, by specifying the generalized gradient function as the pointwise limit of the standard gradients of the approximated risk functions.
In Setting 2.1 the functions $ \mathfrak{R}_r \colon \mathbb{R} \to \mathbb{R} $, $ r \in \mathbb{N} $, serves as such appropriate continuously differentiable approximations of the ReLU activation function and the hypothesis in (2.2) ensures that these functions converge pointwise to the ReLU activation function and that the derivatives of these functions converge pointwise to the left derivative of the ReLU activation function (cf. also (1.3) in Theorem 1.1 and (1.9) in Theorem 1.2). These continuously differentiable approximations of the ReLU activation function are then used in (2.4) in Setting 2.1 (cf. also (1.5) in Theorem 1.1 and (1.10) in Theorem 1.2) to introduce continuously differentiable approximated risk functions $ \mathfrak{L}_r \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $, $ r \in \mathbb{N} $, which converge pointwise to the risk function $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ (cf., e.g., [37, Proposition 2.2]). Finally, the standard gradients of the approximated risk functions $ \mathfrak{L}_r \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $, $ r \in \mathbb{N} $, are then used to introduce the generalized gradient function $ \mathcal{G} = (\mathcal{G}_1, \dots, \mathcal{G}_ \mathfrak{d}) \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ in Setting 2.1. In this regard we also note that Proposition 2.2 in Subsection 2.2 below, in particular, ensures that the function $ \mathcal{G} = (\mathcal{G}_1, \dots, \mathcal{G}_ \mathfrak{d}) \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ in Setting 2.1 is indeed uniquely defined.
2.2. Differentiability properties of the risk function
Proposition 2.2. Assume Setting 2.1. Then it holds for all $ \theta \in \mathbb{R}^{ \mathfrak{d}} $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} $, $ j \in \left\{ {{ 1, 2, \ldots, d }} \right\} $ that
Proof of Proposition 2.2. Observe that, e.g., [37, Proposition 2.2] establishes 2.7. The proof of Proposition 2.2 is thus complete.
Proposition 2.3. Assume Setting 2.1 and let $ U \subseteq \mathbb{R}^ \mathfrak{d} $ satisfy $ U = \left\{ {{\theta \in \mathbb{R}^ \mathfrak{d} \colon \mathbf{D}^\theta = \varnothing }} \right\} $. Then
(i) it holds that $ U \subseteq \mathbb{R}^ \mathfrak{d} $ is open,
(ii) it holds that $ \mathcal{L} | _U \in C^1 (U, \mathbb{R}) $, and
(iii) it holds that $ \nabla (\mathcal{L} |_U) = \mathcal{G} |_U $.
Proof of Proposition 2.3. Note that [37, Proposition 2.10,Lemmas 2.11 and 2.12] establish items (i),
(ii), and (iii). The proof of Proposition 2.3 is thus complete.
2.3. Local Lipschitz continuity of active neuron regions
Lemma 2.4. Let $ d \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, for every $ v = (v_1, \ldots, v_{d+1}) \in \mathbb{R}^{d+1} $ let $ I^v \subseteq [\mathscr{a}, \mathscr{b}]^d $ satisfy $ I^v = \left\{ {{ x \in [\mathscr{a}, \mathscr{b}] ^d \colon v_{d+1} + \sum _{i = 1}^d v_i x_i > 0 }} \right\} $, for every $ n \in \mathbb{N} $ let $ \lambda_n \colon \mathcal{B} (\mathbb{R}^n) \to [0, \infty] $ be the Lebesgue–Borel measure on $ \mathbb{R}^n $, let $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}] ^d \to [0, \infty) $ be bounded and measurable, and let $ u \in \mathbb{R}^{d+1} \backslash \left\{ {{0}} \right\} $. Then there exist $ \varepsilon, \mathfrak{C} \in (0, \infty) $ such that for all $ v, w \in \mathbb{R}^{d+1} $ with $ \max \left\{ {{ ||u - v||, ||u - w || }} \right\} \le \varepsilon $ it holds that
Proof of Lemma 2.4. Observe that for all $ v, w \in \mathbb{R}^{d+1} $ we have that
Moreover, note that the fact that for all $ y \in \mathbb{R} $ it holds that $ y \geq - |y| $ ensures that for all $ v = (v_1, \ldots, v_{d+1}) \in \mathbb{R}^{d+1} $, $ i \in \left\{ {{1, 2, \ldots, d+1 }} \right\} $ with $ ||u-v|| < |u_i| $ it holds that
Next observe that for all $ v_1, v_2, w_1, w_2 \in \mathbb{R} $ with $ \min \left\{ {{|v_1|, |w_1|}} \right\} > 0 $ it holds that
Combining this and 2.10 demonstrates for all $ v = (v_1, \ldots, v_{d+1}) $, $ w = (w_1, \ldots, w_{d+1}) \in \mathbb{R}^{d+1} $, $ i \in \left\{ {{1, 2, \ldots, d}} \right\} $ with $ \max \left\{ {{||v-u||, ||w-u||}} \right\} < |u_1| $ that $ v_1 w_1 > 0 $ and
Hence, we obtain for all $ v = (v_1, \ldots, v_{d+1}) $, $ w = (w_1, \ldots, w_{d+1}) \in \mathbb{R}^{d+1} $, $ i \in \left\{ {{1, 2, \ldots, d}} \right\} $ with $ \max \left\{ {{||v-u||, ||w-u||}} \right\} \le \frac{|u_1|}{2} $ and $ |u_1| > 0 $ that $ v_1 w_1 > 0 $ and
In the following we distinguish between the case $ \max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i| = 0 $, the case $ (\max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i|, d) \in (0, \infty) \times [2, \infty) $, and the case $ (\max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i|, d) \in (0, \infty) \times \left\{ {{1}} \right\} $. We first prove 2.8 in the case
Note that (2.14) and the assumption that $ u \in \mathbb{R}^{d+1} \backslash \left\{ {{ 0 }} \right\} $ imply that $ | u_{d+1} | > 0 $. Moreover, observe that (2.14) shows that for all $ v = (v_1, \ldots, v_{d+1}) \in \mathbb{R}^{d+1} $, $ x = (x_1, \ldots, x_d) \in I^u \Delta I^v $ we have that
In addition, note that for all $ v = (v_1, \ldots, v_{d+1}) \in \mathbb{R}^{d+1} $, $ x = (x_1, \ldots, x_d) \in [\mathscr{a}, \mathscr{b}] ^d $ it holds that
This and (2.15) prove that for all $ v \in \mathbb{R}^{d+1} $ with $ || u - v || \le \frac{|u_{d+1}|}{2 + d \max \left\{ {{ | \mathscr{a}, \mathscr{b} | }} \right\}} $ we have that $ I^u \Delta I^v = \varnothing $, i.e., $ I^u = I^v $. Therefore, we get for all $ v, w \in \mathbb{R}^{d+1} $ with $ \max \left\{ {{ || u - v ||, ||u - w|| }} \right\} \le \frac{|u_{d+1}|}{2 + d \max \left\{ {{ | \mathscr{a}, \mathscr{b} | }} \right\}} $ that $ I^v = I^w = I^u $. Hence, we obtain for all $ v, w \in \mathbb{R}^{d+1} $ with $ \max \left\{ {{ || u - v ||, ||u - w|| }} \right\} \le \frac{|u_{d+1}|}{2 + d \max \left\{ {{ | \mathscr{a}, \mathscr{b} | }} \right\}} $ that $ \lambda_d(I^v \Delta I^w) = 0 $. This establishes (2.8) in the case $ \max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i| = 0 $. In the next step we prove 2.8 in the case
For this we assume without loss of generality that $ | u_1 | > 0 $. In the following let $ J_x^{v, w} \subseteq \mathbb{R} $, $ x \in [\mathscr{a}, \mathscr{b}]^{d-1} $, $ v, w \in \mathbb{R}^{d+1} $, satisfy for all $ x = (x_2, \ldots, x_d) \in [\mathscr{a}, \mathscr{b}] ^{d-1} $, $ v, w \in \mathbb{R}^{d+1} $ that $ J_x^{v, w} = \left\{ {{ y \in [\mathscr{a}, \mathscr{b}] \colon (y, x_2, \ldots, x_d) \in I^v \backslash I^w }} \right\} $. Next observe that Fubini's theorem and the fact that for all $ v \in \mathbb{R}^{d+1} $ it holds that $ I^v $ is measurable show that for all $ v, w \in \mathbb{R}^{d+1} $ we have that
Furthermore, note that for all $ x = (x_2, \ldots, x_d) \in [\mathscr{a}, \mathscr{b}] ^{d-1} $, $ v = (v_1, \ldots, v_{d+1}) $, $ w = (w_1, \ldots, w_{d+1}) \in \mathbb{R}^{d+1} $, $ \mathfrak{s} \in \left\{ {{ - 1, 1 }} \right\} $ with $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $ it holds that
Hence, we obtain for all $ x = (x_2, \ldots, x_d) \in [\mathscr{a}, \mathscr{b}] ^{d-1} $, $ v = (v_1, \ldots, v_{d+1}) $, $ w = (w_1, \ldots, w_{d+1}) \in \mathbb{R}^{d+1} $, $ \mathfrak{s} \in \left\{ {{ - 1, 1 }} \right\} $ with $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $ that
Furthermore, observe that (2.10) demonstrates for all $ v = (v_1, \ldots, v_{d+1}) \in \mathbb{R}^{d+1} $ with $ ||u - v|| < |u_1| $ that $ u_1 v_1 > 0 $. This implies that for all $ v = (v_1, \ldots, v_{d+1}) $, $ w = (w_1, \ldots, w_{d+1}) \in \mathbb{R}^{d+1} $ with $ \max \left\{ {{||u - v||, ||u - w|| }} \right\} < |u_1| $ there exists $ \mathfrak{s} \in \left\{ {{-1, 1 }} \right\} $ such that $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $. Combining this and (2.13) with (2.20) proves that there exists $ \mathfrak{C} \in \mathbb{R} $ such that for all $ x \in [\mathscr{a}, \mathscr{b}]^{d-1} $, $ v, w \in \mathbb{R}^{d+1} $ with $ \max \left\{ {{ || u - v ||, ||u - w || }} \right\} \le \frac{ | u_1 | }{2} $ we have that $ \lambda_1(J_x^{v, w}) + \lambda_1 (J_x^{w, v}) \leq \mathfrak{C} || v - w || $. This, (2.18), and (2.9) establish (2.8) in the case $ (\max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i|, d) \in (0, \infty) \times [2, \infty) $. Finally, we prove (2.8) in the case
Note that (2.21) demonstrates that $ |u_1| > 0 $. In addition, observe that for all $ v = (v_1, v_2) $, $ w = (w_1, w_2) \in \mathbb{R}^{2} $, $ \mathfrak{s} \in \left\{ {{ - 1, 1 }} \right\} $ with $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $ it holds that
Therefore, we get for all $ v = (v_1, v_2) $, $ w = (w_1, w_2) \in \mathbb{R}^{2} $, $ \mathfrak{s} \in \left\{ {{ - 1, 1 }} \right\} $ with $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $ that
Furthermore, note that (2.10) ensures for all $ v = (v_1, v_2) \in \mathbb{R}^2 $ with $ ||u - v || < |u_1| $ that $ u_1 v_1 > 0 $. This proves that for all $ v = (v_1, v_2) $, $ w = (w_1, w_2) \in \mathbb{R}^2 $ with $ \max \left\{ {{||u - v ||, ||u - w|| }} \right\} < |u_1| $ there exists $ \mathfrak{s} \in \left\{ {{-1, 1 }} \right\} $ such that $ \min \left\{ {{ \mathfrak{s} v_1, \mathfrak{s} w_1 }} \right\} > 0 $. Combining this with (2.23) demonstrates for all $ v = (v_1, v_2) $, $ w = (w_1, w_2) \in \mathbb{R}^2 $ with $ \max \left\{ {{||u - v ||, ||u - w || }} \right\} < |u_1| $ that $ \min \left\{ {{ |v_1|, |w_1|}} \right\} > 0 $ and
This, (2.13), and (2.9) establish (2.8) in the case $ (\max_{i \in \left\{ {{1, 2, \ldots, d }} \right\} } |u_i|, d) \in (0, \infty) \times \left\{ {{ 1 }} \right\} $. The proof of Lemma 2.4 is thus complete.
2.4. Local Lipschitz continuity properties for the generalized gradient function
Lemma 2.5. Let $ d, n \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, $ x \in \mathbb{R}^n $, $ \mathfrak{C}, \varepsilon \in (0, \infty) $, let $ \phi \colon \mathbb{R}^n \times [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ be locally bounded and measurable, assume for all $ r \in (0, \infty) $ that
let $ \mu \colon \mathcal{B}([\mathscr{a}, \mathscr{b}]^d) \to [0, \infty) $ be a finite measure, let $ I^y \in \mathcal{B} ([\mathscr{a}, \mathscr{b}]^d) $, $ y \in \mathbb{R}^n $, satisfy for all $ y, z \in \left\{ {{ v \in \mathbb{R}^n \colon ||x-v|| \le \varepsilon }} \right\} $ that $ \mu (I^y \Delta I^z) \leq \mathfrak{C} ||y - z || $, and let $ \Phi \colon \mathbb{R}^n \to \mathbb{R} $ satisfy for all $ y \in \mathbb{R}^n $ that
Then there exists $ \mathscr{C} \in \mathbb{R} $ such that for all $ y, z \in \left\{ {{ v \in \mathbb{R}^n \colon ||x - v|| \le \varepsilon }} \right\} $ it holds that $ |\Phi (y) - \Phi (z) | \leq \mathscr{C} ||y - z|| $.
Proof of Lemma 2.5. The proof is analogous to the proof of [35, Lemma 6].
Corollary 2.6. Assume Setting 2.1, let $ \phi \colon \mathbb{R}^ \mathfrak{d} \times [\mathscr{a}, \mathscr{b}]^d \to \mathbb{R} $ be locally bounded and measurable, and assume for all $ r \in (0, \infty) $ that
Then
(i) it holds that
is locally Lipschitz continuous and
(ii) it holds for all $ i \in \left\{ {{ 1, 2, \ldots, H}} \right\} $ that
is locally Lipschitz continuous.
Proof of Corollary 2.6. First observe that Lemma 2.5 (applied for every $ \theta \in \mathbb{R}^ \mathfrak{d} $ with $ n \curvearrowleft \mathfrak{d} $, $ x \curvearrowleft \theta $, $ \mu \curvearrowleft (\mathcal{B} ([\mathscr{a}, \mathscr{b}] ^d) \ni A \mapsto \int_A \mathfrak{p} (x) \, \lambda (\, \mathrm{d} x) \in [0, \infty)) $, $ (I^y)_{y \in \mathbb{R}^n} \curvearrowleft ([\mathscr{a}, \mathscr{b}]^d)_{y \in \mathbb{R}^ \mathfrak{d}} $ in the notation of Lemma 2.5) establishes item (i). In the following let $ i \in \left\{ {{1, 2, \ldots, H}} \right\} $, $ \theta \in \left\{ {{\vartheta \in \mathbb{R}^ \mathfrak{d} \colon i \notin \mathbf{D}^\vartheta }} \right\} $. Note that Lemma 2.4 shows that there exist $ \varepsilon, \mathfrak{C} \in (0, \infty) $ which satisfy for all $ \vartheta_1, \vartheta_2 \in \mathbb{R}^ \mathfrak{d} $ with $ \max \left\{ {{ ||\theta - \vartheta_1||, ||\theta - \vartheta_2|| }} \right\} \le \varepsilon $ that
Combining this with Lemma 2.5 (applied for every $ \theta \in \mathbb{R}^ \mathfrak{d} $ with $ n \curvearrowleft \mathfrak{d} $, $ x \curvearrowleft \theta $, $ \mu \curvearrowleft (\mathcal{B} ([\mathscr{a}, \mathscr{b}] ^d) \ni A \mapsto \int_A \mathfrak{p} (x) \, \lambda (\, \mathrm{d} x) \in [0, \infty)) $, $ (I^y)_{y \in \mathbb{R}^n} \curvearrowleft (I_i^y)_{ y \in \mathbb{R}^ \mathfrak{d}} $ in the notation of Lemma 2.5) demonstrates that there exists $ \mathscr{C} \in \mathbb{R} $ such that for all $ \vartheta_1, \vartheta_2 \in \mathbb{R}^ \mathfrak{d} $ with $ \max \left\{ {{ ||\theta - \vartheta_1||, ||\theta - \vartheta_2|| }} \right\} \le \varepsilon $ it holds that
This establishes item (ii). The proof of Corollary 2.6 is thus complete.
Corollary 2.7. Assume Setting 2.1. Then
(i) it holds for all $ k \in \mathbb{N} \cap (H d + H, \mathfrak{d}] $ that
is locally Lipschitz continuous,
(ii) it holds for all $ i \in \left\{ {{ 1, 2, \ldots, H}} \right\} $, $ j \in \left\{ {{ 1, 2, \ldots, d}} \right\} $ that
is locally Lipschitz continuous, and
(iii) it holds for all $ i \in \left\{ {{1, 2, \ldots, H}} \right\} $ that
is locally Lipschitz continuous.
Proof of Corollary 2.7. Observe that (2.7) and Corollary 2.6 establish items (i), (ii), and (iii). The proof of Corollary 2.7 is thus complete.
2.5. Subdifferentials
Definition 2.8 (Subdifferential). Let $ n \in \mathbb{N} $, $ f \in C(\mathbb{R}^n, \mathbb{R}) $, $ x \in \mathbb{R}^n $. Then we denote by $ \hat{\partial} f(x) \subseteq \mathbb{R}^n $ the set given by
Definition 2.9 (Limiting subdifferential). Let $ n \in \mathbb{N} $, $ f \in C(\mathbb{R}^n, \mathbb{R}) $, $ x \in \mathbb{R}^n $. Then we denote by $ \partial f(x) \subseteq \mathbb{R}^n $ the set given by
(cf. Definition 2.8).
Lemma 2.10. Let $ n \in \mathbb{N} $, $ f \in C(\mathbb{R}^n, \mathbb{R}) $, $ x \in \mathbb{R}^n $. Then
(cf. Definitions 2.8 and 2.9).
Proof of Lemma 2.10. Note that (2.36) establishes (2.37). The proof of Lemma 2.10 is thus complete.
Lemma 2.11. Let $ n \in \mathbb{N} $, $ f \in C (\mathbb{R}^n, \mathbb{R}) $, let $ U \subseteq \mathbb{R}^n $ be open, assume $ f | _U \in C^1 (U, \mathbb{R}) $, and let $ x \in U $. Then $ \hat{\partial} f(x) = \partial f(x) = \left\{ {{ (\nabla f) (x) }} \right\} $ (cf. Definitions 2.8 and 2.9).
Proof of Lemma 2.11. This is a direct consequence of, e.g., Rockafellar & Wets [39, Exercise 8.8]. The proof of Lemma 2.11 is thus complete.
Proposition 2.12. Assume Setting 2.1 and let $ \theta \in \mathbb{R}^ \mathfrak{d} $. Then $ \mathcal{G} (\theta) \in \partial \mathcal{L} (\theta) $ (cf. Definition 2.9).
Proof of Proposition 2.12. Throughout this proof let $ \vartheta = (\vartheta_n)_{n \in \mathbb{N}} \colon \mathbb{N} \to \mathbb{R}^ \mathfrak{d} $ satisfy for all $ n \in \mathbb{N} $, $ i \in \left\{ {{ 1, 2, \ldots, H}} \right\} $, $ j \in \left\{ {{ 1, 2, \ldots, d}} \right\} $ that $ \mathfrak{w}^{{\vartheta_n}}_{i, j} = \mathfrak{w}^{{\theta}}_{i, j} $, $ \mathfrak{b}^{{\vartheta_n}}_i = \mathfrak{b}^{{\theta}}_i - \frac{1}{n} \mathbf{1}_{\smash{{ \mathbf{D}^\theta }}} (i) $, $ \mathfrak{v}^{{\vartheta_n}} _ i = \mathfrak{v}^{{\theta}}_i $, and $ \mathfrak{c}^{{\vartheta_n}} = \mathfrak{c}^{{\theta}} $. We prove Proposition 2.12 through an application of Lemma 2.10. Observe that for all $ n \in \mathbb{N} $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} \backslash \mathbf{D}^\theta $ it holds that $ \mathfrak{b}^{{\vartheta_n}}_i = \mathfrak{b}^{{\theta}}_i $. This implies for all $ n \in \mathbb{N} $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} \backslash \mathbf{D}^\theta $ that
In addition, note that for all $ n \in \mathbb{N} $, $ i \in \mathbf{D}^\theta $ it holds that $ \mathfrak{b}^{{\vartheta_n}}_i = - \frac{1}{n} < 0 $. This shows for all $ n \in \mathbb{N} $, $ i \in \mathbf{D}^\theta $ that
Hence, we obtain for all $ n \in \mathbb{N} $ that $ \mathbf{D}^{\vartheta_n} = \varnothing $. Combining this with Proposition 2.3 and Lemma 2.11 demonstrates that for all $ n \in \mathbb{N} $ it holds that $ \hat{\partial} \mathcal{L} (\vartheta_n) = \left\{ {{ (\nabla \mathcal{L}) (\vartheta_n) }} \right\} = \left\{ {{ \mathcal{G} (\vartheta_n) }} \right\} $ (cf. Definition 2.8). Moreover, observe that $ \lim_{n \to \infty} \vartheta_n = \theta $. It thus remains to show that $ \mathcal{G} (\vartheta _n) $, $ n \in \mathbb{N} $, converges to $ \mathcal{G} (\theta) $. Note that Corollary 2.7 ensures that for all $ k \in \mathbb{N} \cap (H d + H, \mathfrak{d}] $ it holds that
Furthermore, observe that Corollary 2.7, (2.38) and (2.39) assure that for all $ i \in \left\{ {{ 1, 2, \ldots, H}} \right\} \backslash \mathbf{D}^\theta $, $ j \in \left\{ {{ 1, 2, \ldots, d }} \right\} $ it holds that
In addition, note that for all $ n \in \mathbb{N} $, $ i \in \mathbf{D}^\theta $ we have that $ I_i^{\vartheta_n } = I_i^\theta = \varnothing $. Hence, we obtain for all $ i \in \mathbf{D}^\theta $, $ j \in \left\{ {{ 1, 2, \ldots, d}} \right\} $ that
Combining this, (2.40) and (2.41) demonstrates that $ \lim_{n \to \infty} \mathcal{G} (\vartheta _ n) = \mathcal{G} (\theta) $. This and Lemma 2.10 assure that $ \mathcal{G} (\theta) \in \partial \mathcal{L} (\theta) $. The proof of Proposition 2.12 is thus complete.
3.
Existence and uniqueness properties for solutions of gradient flows (GFs)
In this section we employ the local Lipschitz continuity result for the generalized gradient function in Corollary 2.7 from Section 2 to establish existence and uniqueness results for solutions of GF differential equations. Specifically, in Proposition 3.1 in Subsection 3.1 below we prove the existence of solutions GF differential equations, in Lemma 3.2 in Subsection 3.2 below we establish the uniqueness of solutions of GF differential equations among a suitable class of GF solutions, and in Theorem 3.3 in Subsection 3.3 below we combine Proposition 3.1 and Lemma 3.2 to establish the unique existence of solutions of GF differential equations among a suitable class of GF solutions. Theorem 1.1 in the introduction is an immediate consequence of Theorem 3.3.
Roughly speaking, we show in Theorem 3.3 the unique existence of solutions of GF differential equations among the class of GF solutions which satisfy that the set of all degenerate neurons of the GF solution at time $ t \in [0, \infty) $ is non-decreasing in the time variable $ t \in [0, \infty) $. In other words, in Theorem 3.3 we prove the unique existence of GF solutions with the property that once a neuron has become degenerate it will remain degenerate for subsequent times.
Our strategy of the proof of Theorem 3.3 and Proposition 3.1, respectively, can, loosely speaking, be described as follows. Corollary 2.7 above implies that the components of the generalized gradient function $ \mathcal{G} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ corresponding to non-degenerate neurons are locally Lipschitz continuous so that the classical Picard-Lindelöf local existence and uniqueness theorem for ordinary differential equations can be brought into play for those components. On the other hand, if at some time $ t \in [0, \infty) $ the $ i $-th neuron is degenerate, then Proposition 2.2 above shows that the corresponding components of the generalized gradient function $ \mathcal{G} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ vanish. The GF differential equation is thus satisfied if the neuron remains degenerate at all subsequent times $ s \in [t, \infty) $. Using these arguments we prove in Proposition 3.1 the existence of GF solutions by induction on the number of non-degenerate neurons of the initial value.
3.1. Existence properties for solutions of GF differential equations
Proposition 3.1. Assume Setting 2.1 and let $ \theta \in \mathbb{R}^ \mathfrak{d} $. Then there exists $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ which satisfies for all $ t \in [0, \infty) $, $ s \in [t, \infty) $ that
Proof of Proposition 3.1. We prove the statement by induction on the quantity $ H - \# (\mathbf{D}^\theta) \in \mathbb{N} \cap [0, H] $. Assume first that $ H - \# (\mathbf{D}^\theta) = 0 $, i.e., $ \mathbf{D}^\theta = \left\{ {{1, 2, \ldots, H}} \right\} $. Observe that this implies that $ \mathfrak{w}^{{\theta}} = 0 $ and $ \mathfrak{b}^{{\theta}} = 0 $. In the following let $ \kappa \in \mathbb{R} $ satisfy
Note that the Picard–Lindelöf Theorem shows that there exists a unique $ c \in C([0, \infty), \mathbb{R}) $ which satisfies for all $ t \in [0, \infty) $ that
Next let $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy for all $ t \in [0, \infty) $, $ i \in \left\{ {{ 1, 2, \ldots, H }} \right\} $, $ j \in \left\{ {{1, 2, \ldots, d}} \right\} $ that
Observe that (2.7), (3.3), and (3.4) ensure for all $ t \in [0, \infty) $ that
Next note that (3.4) and (2.7) show for all $ t \in [0, \infty) $, $ i \in \mathbb{N} \cap [1, \mathfrak{d}) $ that $ \mathbf{D}^{\Theta_t} = \left\{ {{1, 2, \ldots, H}} \right\} $ and $ \mathcal{G}_i (\Theta_t) = 0 $. Combining this with (3.4) and (3.5) proves that $ \Theta $ satisfies 3.1. This establishes the claim in the case $ \# (\mathbf{D}^\theta) = H $.
For the induction step assume that $ \# (\mathbf{D}^\theta) < H $ and assume that for all $ \vartheta \in \mathbb{R}^ \mathfrak{d} $ with $ \# (\mathbf{D}^\vartheta) > \# (\mathbf{D}^\theta) $ there exists $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ which satisfies for all $ t \in [0, \infty) $, $ s \in [t, \infty) $ that $ \Theta_t = \vartheta - \int_0^t \mathcal{G} (\Theta_u) \, \mathrm{d} u $ and $ \mathbf{D}^{\Theta_t} \subseteq \mathbf{D}^{\Theta_s} $. In the following let $ U \subseteq \mathbb{R}^ \mathfrak{d} $ satisfy
and let $ \mathfrak{G} \colon U \to \mathbb{R}^ \mathfrak{d} $ satisfy for all $ \vartheta \in U $, $ i \in \left\{ {{ 1, 2, \ldots, \mathfrak{d} }} \right\} $ that
Observe that (3.6) assures that $ U \subseteq \mathbb{R}^ \mathfrak{d} $ is open. In addition, note that Corollary 2.7 implies that $ \mathfrak{G} $ is locally Lipschitz continuous. Combining this with the Picard–Lindelöf Theorem demonstrates that there exist a unique maximal $ \tau \in (0, \infty] $ and $ \Psi \in C([0, \tau), U) $ which satisfy for all $ t \in [0, \tau) $ that
Next observe that (3.7) ensures that for all $ t \in [0, \tau) $, $ i \in \mathbf{D}^\theta $, $ j \in \left\{ {{1, 2, \ldots, d}} \right\} $ we have that
This, (3.7), and (2.7) demonstrate for all $ t \in [0, \tau) $ that $ \mathcal{G} (\Psi_t) = \mathfrak{G} (\Psi_t) $. In addition, note that (3.6) and (3.9) imply for all $ t \in [0, \tau) $ that $ \mathbf{D}^{\Psi_t} = \mathbf{D}^\theta $. Hence, if $ \tau = \infty $ then $ \Psi $ satisfies (3.1). Next assume that $ \tau < \infty $. Observe that the Cauchy-Schwarz inequality and [37, Lemma 3.1] prove for all $ s, t \in [0, \tau) $ with $ s \leq t $ that
Hence, we obtain for all $ (t_n) _{n \in \mathbb{N}} \subseteq [0, \tau) $ with $ \liminf_{n \to \infty} t_n = \tau $ that $ (\Psi_{t_n}) $ is a Cauchy sequence. This implies that $ \vartheta : = \lim_{t \uparrow \tau} \Psi_t \in \mathbb{R}^ \mathfrak{d} $ exists. Furthermore, note that the fact that $ \tau $ is maximal proves that $ \vartheta \notin U $. Therefore, we have that $ \mathbf{D}^\vartheta \backslash \mathbf{D}^\theta \not = \varnothing $. Moreover, observe that (3.9) shows that for all $ i \in \mathbf{D}^\theta $, $ j \in \left\{ {{1, 2, \ldots, d}} \right\} $ it holds that $ \mathfrak{w}^{{\vartheta}}_{i, j} = \mathfrak{b}^{{\vartheta}}_i = 0 $ and, therefore, $ i \in \mathbf{D}^\vartheta $. This demonstrates that $ \# (\mathbf{D}^\vartheta) > \# (\mathbf{D}^\theta) $. Combining this with the induction hypothesis ensures that there exists $ \Phi \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ which satisfies for all $ t \in [0, \infty) $, $ s \in [t, \infty) $ that
In the following let $ \Theta \colon [0, \infty) \to \mathbb{R}^ \mathfrak{d} $ satisfy for all $ t \in [0, \infty) $ that
Note that the fact that $ \vartheta = \lim_{t \uparrow \tau} \Psi_t $ and the fact that $ \Phi_0 = \vartheta $ imply that $ \Theta $ is continuous. Furthermore, observe that the fact that $ \mathcal{G} $ is locally bounded and (3.8) ensure that
Hence, we obtain for all $ t \in [\tau, \infty) $ that
This shows that $ \Theta $ satisfies (3.1). The proof of Proposition 3.1 is thus complete.
3.2. Uniqueness properties for solutions of GF differential equations
Lemma 3.2. Assume Setting 2.1 and let $ \theta \in \mathbb{R}^ \mathfrak{d} $, $ \Theta^1, \Theta^2 \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy for all $ t \in [0, \infty) $, $ s \in [t, \infty) $, $ k \in \left\{ {{ 1, 2}} \right\} $ that
Then it holds for all $ t \in [0, \infty) $ that $ \Theta_t^1 = \Theta_t^2 $.
Proof of Lemma 3.2. Assume for the sake of contradiction that there exists $ t \in [0, \infty) $ such that $ \Theta_t^1 \not = \Theta_t^2 $. By translating the variable $ t $ if necessary, we may assume without loss of generality that $ \inf \left\{ {{t \in [0, \infty) \colon \Theta_t^1 \not = \Theta_t^2}} \right\} = 0 $. Next note that the fact that $ \Theta^1 $ and $ \Theta^2 $ are continuous implies that there exists $ \delta \in (0, \infty) $ which satisfies for all $ t \in [0, \delta] $, $ k \in \left\{ {{ 1, 2}} \right\} $ that $ \mathbf{D}^{\Theta_t^k} \subseteq \mathbf{D}^\theta $. Furthermore, observe that 3.15 ensures for all $ t \in [0, \infty) $, $ i \in \mathbf{D}^\theta $, $ k \in \left\{ {{ 1, 2}} \right\} $ that $ i \in \mathbf{D}^{\Theta_t^k} $. Hence, we obtain for all $ t \in [0, \infty) $, $ i \in \mathbf{D}^\theta $, $ j \in \left\{ {{1, 2, \ldots, d}} \right\} $, $ k \in \left\{ {{ 1, 2}} \right\} $ that
In addition, note that the fact that $ \Theta^1 $ and $ \Theta^2 $ are continuous implies that there exists a compact $ K \subseteq \left\{ {{\vartheta \in \mathbb{R}^ \mathfrak{d} \colon \mathbf{D}^\vartheta \subseteq \mathbf{D}^\theta }} \right\} $ which satisfies for all $ t \in [0, \delta] $, $ k \in \left\{ {{1, 2}} \right\} $ that $ \Theta_t^k \in K $. Moreover, observe that Corollary 2.7 proves that for all $ i \in \left\{ {{1, 2, \ldots, H}} \right\} \backslash \mathbf{D}^\theta $, $ j \in \left\{ {{1, 2, \ldots, d}} \right\} $ it holds that $ \mathcal{G}_{(i - 1) d + j }, \mathcal{G}_{ H d + i }, \mathcal{G}_{ H (d+1) + i }, \mathcal{G} _ \mathfrak{d} \colon K \to \mathbb{R} $ are Lipschitz continuous. This and (3.16) show that there exists $ L \in (0, \infty) $ such that for all $ t \in [0, \delta] $ we have that
In the following let $ M \colon [0, \infty) \to [0, \infty) $ satisfy for all $ t \in [0, \infty) $ that $ M_t = \sup_{s \in (0, t] } ||\Theta_s^1 - \Theta_s^2|| $. Note that the fact that $ \inf \left\{ {{t \in [0, \infty) \colon \Theta_t^1 \not = \Theta_t^2}} \right\} = 0 $ proves for all $ t \in (0, \infty) $ that $ M_t > 0 $. Moreover, observe that (3.17) ensures for all $ t \in (0, \delta) $ that
Combining this with the fact that $ M $ is non-decreasing shows for all $ t \in (0, \delta) $, $ s \in (0, t] $ that
This demonstrates for all $ t \in (0, \min \left\{ {{L^{-1}, \delta }} \right\}) $ that
which is a contradiction. The proof of Lemma 3.2 is thus complete.
3.3. Existence and uniqueness properties for solutions of GF differential equations
Theorem 3.3. Assume Setting 2.1 and let $ \theta \in \mathbb{R}^ \mathfrak{d} $. Then there exists a unique $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ which satisfies for all $ t \in [0, \infty) $, $ s \in [t, \infty) $ that
Proof of Theorem 3.3. Proposition 3.1 establishes the existence and Lemma 3.2 establishes the uniqueness. The proof of Theorem 3.3 is thus complete.
4.
Semialgebraic sets and functions
In this section we establish in Corollary 4.10 in Subsection 4.3 below that under the assumption that both the target function $ f \colon [\mathscr{a}, \mathscr{b}] ^d \to \mathbb{R} $ and the unnormalized density function $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}]^d \to [0, \infty) $ are piecewise polynomial in the sense of Definition 4.9 in Subsection 4.3 we have that the risk function $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ is a semialgebraic function in the sense of Definition 4.3 in Subsection 4.1. In Definition 4.9 we specify precisely what we mean by a piecewise polynomial function, in Definition 4.2 in Subsection 4.1 we recall the notion of a semialgebraic set, and in Definition 4.3 we recall the notion of a semialgebraic function. In the scientific literature Definitions 4.2 and 4.3 can in a slightly different presentational form, e.g., be found in Bierstone & Milman [40, Definitions 1.1 and 1.2] and Attouch et al. [8, Definition 2.1].
Note that the risk function $ \mathcal{L} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R} $ is given through a parametric integral in the sense that for all $ \theta \in \mathbb{R}^{ \mathfrak{d} } $ we have that
In general, parametric integrals of semialgebraic functions are no longer semialgebraic functions and the characterization of functions that can occur as such integrals is quite involved (cf. Kaiser [41]). This is the reason why we introduce in Definition 4.6 in Subsection 4.2 below a suitable subclass of the class of semialgebraic functions which is rich enough to contain the realization functions of ANNs with ReLU activation (cf. (4.30) in Subsection 4.2 below) and which can be shown to be closed under integration (cf. Proposition 4.8 in Subsection 4.2 below for the precise statement).
4.1. Semialgebraic sets and functions
Definition 4.1 (Set of polynomials). Let $ n \in \mathbb{N}_0 $. Then we denote by $ \mathscr{P}_n \subseteq C(\mathbb{R}^n, \mathbb{R}) $ the set† of all polynomials from $ \mathbb{R}^n $ to $ \mathbb{R} $.
†Note that $ \mathbb{R}^0 = \{ 0 \} $, $ C(\mathbb{R}^0, \mathbb{R}) = C(\{ 0 \}, \mathbb{R}) $, and $ \#(C(\mathbb{R}^0, \mathbb{R})) = \#(C(\{ 0 \}, \mathbb{R})) = \infty $. In particular, this shows for all $ n \in \mathbb{N}_0 $ that $ \operatorname{dim}(\mathbb{R}^n) = n $ and $ \#(C(\mathbb{R}^n, \mathbb{R})) = \infty $.
Definition 4.2 (Semialgebraic sets). Let $ n \in \mathbb{N} $ and let $ A \subseteq \mathbb{R}^n $ be a set. Then we say that $ A $ is a semialgebraic set if and only if there exist $ k \in \mathbb{N} $ and $ (P_{i, j, \ell })_{ (i, j, \ell) \in \left\{ {{1, 2, \ldots, k}} \right\} ^2 \times \left\{ {{0, 1}} \right\}} \subseteq \mathscr{P}_n $ such that
(cf. Definition 4.1).
Definition 4.3 (Semialgebraic functions). Let $ m, n \in \mathbb{N} $ and let $ f \colon \mathbb{R}^n \to \mathbb{R}^m $ be a function. Then we say that $ f $ is a semialgebraic function if and only if it holds that $ \left\{ {{ (x, f (x)) \colon x \in \mathbb{R}^n }} \right\} \subseteq \mathbb{R}^{m+n} $ is a semialgebraic set (cf. Definition 4.2).
Lemma 4.4. Let $ n \in \mathbb{N} $ and let $ f, g \colon \mathbb{R}^n \to \mathbb{R} $ be semialgebraic functions (cf. Definition 4.3). Then
(i) it holds that $ \mathbb{R}^n \ni x \mapsto f(x) + g(x) \in \mathbb{R} $ is semialgebraic and
(ii) it holds that $ \mathbb{R}^n \ni x \mapsto f(x) g(x) \in \mathbb{R} $ is semialgebraic.
Proof of Lemma 4.4. Note that, e.g., Coste [42, Corollary 2.9] (see, e.g., also Bierstone & Milman [40, Section 1]) establishes items (i) and (ii). The proof of Lemma 4.4 is thus complete.
4.2. On the semialgebraic property of certain parametric integrals
Definition 4.5 (Set of rational functions). Let $ n \in \mathbb{N} $. Then we denote by $ \mathscr{R}_n $ the set given by
(cf. Definition 4.1).
Definition 4.6. Let $ m \in \mathbb{N} $, $ n \in \mathbb{N}_0 $. Then we denote by $ \mathscr{A}_{m, n} $ the $ \mathbb{R} $-vector space given by
(cf. Definitions 4.1 and 4.5).
Lemma 4.7. Let $ m \in \mathbb{N} $, $ f \in \mathscr{A}_{m, 0 } $ (cf. Definition 4.6). Then $ f $ is semialgebraic (cf. Definition 4.3).
Proof of Lemma 4.7. Throughout this proof let $ r \in \mathbb{N} $, $ A_1, A_2, \ldots, A_r \in \left\{ {{ \left\{ {{0}} \right\}, [0, \infty), (0, \infty)}} \right\} $, $ R \in \mathscr{R}_m $, $ P = (P_i)_{ i \in \left\{ {{1, 2, \ldots, r }} \right\}} \subseteq \mathscr{P}_m $, and let $ g \colon \mathbb{R}^m \to \mathbb{R} $ satisfy for all $ \theta \in \mathbb{R}^m $ that
(cf. Definitions 4.1 and 4.5). Due to the fact that sums of semialgebraic functions are again semialgebraic (cf. Lemma 4.4), it suffices to show that $ g $ is semialgebraic. Furthermore, observe that for all $ y \in \mathbb{R} $ it holds that $ \mathbf{1}_{\smash{{(0, \infty)}}} (y) = 1 - \mathbf{1}_{\smash{{[0, \infty) }}} (- y) $ and $ \mathbf{1}_{\smash{{\left\{ {{0}} \right\}}}} (y) = \mathbf{1}_{\smash{{[0, \infty) }}} (y) \mathbf{1}_{\smash{{[0, \infty) }}} (- y) $. Hence, by linearity we may assume for all $ i \in \left\{ {{1, 2, \ldots, r }} \right\} $ that $ A_i = [0, \infty) $. Next let $ Q_1, Q_2 \in \mathscr{P}_m $ satisfy for all $ x \in \mathbb{R}^m $ that
Note that the graph of $ \mathbb{R}^m \ni \theta \mapsto R(\theta) \in \mathbb{R} $ is given by
Since both of these sets are described by polynomial equations and inequalities, it follows that $ \mathbb{R}^m \ni \theta \mapsto R(\theta) \in \mathbb{R} $ is semialgebraic. In addition, observe that for all $ i \in \left\{ {{1, 2, \ldots, r}} \right\} $ the graph of $ \mathbb{R}^m \ni \theta \mapsto \mathbf{1}_{\smash{{[0, \infty) }}} \left({{ P_i (\theta) }} \right) \in \mathbb{R} $ is given by
This demonstrates for all $ i \in \left\{ {{1, 2, \ldots, r}} \right\} $ that $ \mathbb{R}^m \ni \theta \mapsto \mathbf{1}_{\smash{{[0, \infty) }}} \left({{ P_i (\theta) }} \right) \in \mathbb{R} $ is semialgebraic. Combining this and (4.5) with Lemma 4.4 demonstrates that $ g $ is semialgebraic. The proof of Lemma 4.7 is thus complete.
Proposition 4.8. Let $ m, n \in \mathbb{N} $, $ \mathscr{a} \in \mathbb{R} $, $ \mathscr{b} \in (\mathscr{a}, \infty) $, $ f \in \mathscr{A}_{m, n} $ (cf. Definition 4.6). Then
Proof of Proposition 4.8. By linearity of the integral it suffices to consider a function $ f $ of the form
where $ r \in \mathbb{N} $, $ \left({{P_{i, j}}} \right)_{(i, j) \in \left\{ {{1, 2, \ldots, r}} \right\} \times \left\{ {{0, 1, \ldots, n }} \right\} } \subseteq \mathscr{P}_m $, $ A_1, A_2, \ldots, A_r \in \left\{ {{ \left\{ {{0}} \right\}, (0, \infty), [0, \infty) }} \right\} $, $ Q \in \mathscr{P}_n $, and $ R \in \mathscr{R}_m $ (cf. Definitions 4.1 and 4.5). Moreover, note that for all $ y \in \mathbb{R} $ it holds that $ \mathbf{1}_{\smash{{(0, \infty)}}} (y) = 1 - \mathbf{1}_{\smash{{[0, \infty) }}} (- y) $ and $ \mathbf{1}_{\smash{{\left\{ {{0}} \right\}}}} (y) = \mathbf{1}_{\smash{{[0, \infty) }}} (y) \mathbf{1}_{\smash{{[0, \infty) }}} (- y) $. Hence, by linearity we may assume that $ A_i = [0, \infty) $ for all $ i \in \left\{ {{1, 2, \ldots, r }} \right\} $. Furthermore, by linearity we may assume that $ Q $ is of the form
with $ i_1, i_2, \ldots, i_n \in \mathbb{N}_0 $. In the following let $ \mathfrak{s} \colon \mathbb{R} \to \mathbb{R} $ satisfy for all $ x \in \mathbb{R} $ that $ \mathfrak{s} (x) = \mathbf{1}_{\smash{{(0, \infty)}}} (x) - \mathbf{1}_{\smash{{(0, \infty) }}} (- x) $, for every $ \theta \in \mathbb{R}^m $, $ k \in \left\{ {{-1, 0, 1}} \right\} $ let $ \mathcal{S}_k^\theta \subseteq \left\{ {{1, 2, \ldots, r}} \right\} $ satisfy $ \mathcal{S}_k^\theta = \left\{ {{ i \in \left\{ {{1, 2, \ldots, r }} \right\} \colon \mathfrak{s} (P_{i, n} (\theta)) = k }} \right\} $, and for every $ i \in \left\{ {{1, 2, \ldots, r}} \right\} $ let $ Z_i \colon \mathbb{R}^m \times \mathbb{R}^n \to \mathbb{R} $ satisfy for all $ (\theta, x) \in \mathbb{R}^m \times \mathbb{R}^n $ that
Observe that (4.10), (4.11), and (4.12) imply for all $ \theta \in \mathbb{R}^m $, $ x = (x_1, \ldots, x_n) \in \mathbb{R}^n $ that
This shows that $ f(\theta, x) $ can only be nonzero if
Hence, if for given $ \theta \in \mathbb{R}^m $, $ (x_1, \ldots, x_{n-1}) \in \mathbb{R}^{n-1} $ there exists $ x_n \in [\mathscr{a}, \mathscr{b}] $ which satisfies these conditions then (4.13) and the fact that $ \int y ^{i_ n } \, \mathrm{d} y = \frac{1}{i_n + 1 } y^{i_n + 1 } $ imply that
Otherwise, we have that $ \int_ \mathscr{a}^ \mathscr{b} f (\theta, x_1, \ldots, x_n) \, \mathrm{d} x_n = 0 $. It remains to write these expressions in the different cases as a sum of functions of the required form in Definition 4.6 by introducing suitable indicator functions. Note that there are four possible cases where the integral is nonzero:
● It holds that $ \mathscr{a} < \max_{j \in \mathcal{S}_1^\theta} \frac{ Z_j (\theta, x) }{ P_{j, n} (\theta) } < \min_{j \in \mathcal{S}_{-1}^\theta} \frac{Z_j (\theta, x) }{ P_{j, n} (\theta) } < \mathscr{b} $. In this case, we have
● It holds that $ \mathscr{a} < \max_{j \in \mathcal{S}_1^\theta} \frac{ Z_j (\theta, x) }{ P_{j, n} (\theta) } < \mathscr{b} \le \min_{j \in \mathcal{S}_{-1}^\theta} \frac{Z_j (\theta, x) }{ P_{j, n} (\theta) } $. In this case, we have
● It holds that $ \max_{j \in \mathcal{S}_1^\theta} \frac{ Z_j (\theta, x) }{ P_{j, n} (\theta) } \le \mathscr{a} < \min_{j \in \mathcal{S}_{-1}^\theta} \frac{Z_j (\theta, x) }{ P_{j, n} (\theta) } < \mathscr{b} $. In this case, we have
● It holds that $ \max_{j \in \mathcal{S}_1^\theta} \frac{ Z_j (\theta, x) }{ P_{j, n} (\theta) } \le \mathscr{a} < \mathscr{b} \le \min_{j \in \mathcal{S}_{-1}^\theta} \frac{Z_j (\theta, x) }{ P_{j, n} (\theta) } $. In this case, we have
Since these four cases are disjoint, by summing over all possible choices $ A, B, C \subseteq \left\{ {{1, 2, \ldots, r}} \right\} $ of the sets $ \mathcal{S}^\theta_k $, $ k \in \left\{ {{-1, 0, 1}} \right\} $, and all choices of (non-empty) subsets $ \mathcal{I}, \mathcal{J} $ of $ \mathcal{S}^\theta_1 $, $ \mathcal{S}_{-1}^\theta $ where the maximal/minimal values are achieved, we can write
where $ (I), (II), (III), (IV) $ denote the functions of $ \theta \in \mathbb{R}^m $ and $ (x_1, \ldots, x_{n-1}) \in \mathbb{R}^{ n - 1 } $ given by
and
Note that the first products over all elements of $ A, B, C $ precisely describe the conditions that $ \mathcal{S}_1^\theta = A $, $ \mathcal{S}_{ - 1 }^\theta = B $, $ \mathcal{S}_0^\theta = C $, and $ \forall \, j \in \mathcal{S}_0^\theta \colon - Z_j (\theta, x) \ge 0 $. Furthermore, observe that, e.g., in $ (I) $ we we must have for all $ i \in \mathcal{I} $, $ j \in A \backslash \mathcal{I} $ that $ \frac{Z_j (\theta, x)}{ P_{j, n } (\theta) } < \frac{ Z_{\min \mathcal{I}} (\theta, x) }{P_{ \min \mathcal{I}, n} (\theta) } = \frac{Z_i (\theta, x)}{ P_{i, n } (\theta) } \in (\mathscr{a}, \mathscr{b}) $ in order to obtain a non-zero value. In other words, the maximal value of $ \frac{Z_i (\theta, x)}{ P_{i, n } (\theta) } $, $ i \in A $, is achieved exactly for $ i \in \mathcal{I} $, and similarly the minimal value of $ \frac{Z_j (\theta, x)}{ P_{j, n } (\theta) } $, $ j \in B $, is achieved exactly for $ j \in \mathcal{J} $ (and analogously in $ (II), (III) $). Moreover, note that we have for all $ i \in \mathcal{I} \subseteq A $ that
Here $ Z_i (\theta, x) $ is polynomial in $ \theta $ and linear in $ x_1, \ldots, x_{n-1} $, and thus of the form required by Definition 4.6. Similarly, the other indicator functions can be brought into the correct form, taking into account the different signs of $ P_{j, n} (\theta) $ for $ j \in A $ and $ j \in B $. Moreover, observe that the remaining terms can be written as linear combinations of rational functions in $ \theta $ and polynomials in $ x $. Hence, we obtain that the functions defined by $ (I), (II), (III), (IV) $ are elements of $ \mathscr{A}_{m, n-1} $. The proof of Proposition 4.8 is thus complete.
4.3. On the semialgebraic property of the risk function
Definition 4.9. Let $ d \in \mathbb{N} $, let $ A \subseteq \mathbb{R}^d $ be a set, and let $ f \colon A \to \mathbb{R} $ be a function. Then we say that $ f $ is piecewise polynomial if and only if there exist $ n \in \mathbb{N} $, $ \alpha_1, \alpha_2, \ldots, \alpha_n \in \mathbb{R}^{n \times d} $, $ \beta_{1}, \beta_2, \ldots, \beta_n \in \mathbb{R}^n $, $ P_1, P_2, \ldots, P_n \in \mathscr{P}_d $ such that for all $ x \in A $ it holds that
(cf. Definition 4.1).
Corollary 4.10. Assume Setting 2.1 and assume that $ f $ and $ \mathfrak{p} $ are piecewise polynomial (cf. Definition 4.9). Then $ \mathcal{L} $ is semialgebraic (cf. Definition 4.3).
Proof of Corollary 4.10. Throughout this proof let $ F \colon \mathbb{R}^d \to \mathbb{R} $ and $ \mathfrak{P} \colon \mathbb{R}^d \to \mathbb{R} $ satisfy for all $ x \in \mathbb{R}^d $ that
Note that (4.27) and the assumption that $ f $ and $ \mathfrak{p} $ are piecewise polynomial assure that
(cf. Definition 4.6). In addition, observe that the fact that for all $ \theta \in \mathbb{R}^ \mathfrak{d} $, $ x \in \mathbb{R}^d $ we have that
demonstrates that
Combining this with (4.28) and the fact that $ \mathscr{A}_{ \mathfrak{d}, d} $ is an algebra proves that
This, Proposition 4.8, and induction demonstrate that
Fubini's theorem hence implies that $ \mathcal{L} \in \mathscr{A}_{ \mathfrak{d}, 0 } $. Combining this and Lemma 4.7 shows that $ \mathcal{L} $ is semialgebraic. The proof of Corollary 4.10 is thus complete.
5.
Convergence rates for solutions of GF differential equations
In this section we employ the findings from Sections 2 and 4 to establish in Proposition 5.2 in Subsection 5.2 below, in Proposition 5.3 in Subsection 5.2, and in Theorem 5.4 in Subsection 5.3 below several convergence rate results for solutions of GF differential equations. Theorem 1.2 in the introduction is a direct consequence of Theorem 5.4. Our proof of Theorem 5.4 is based on an application of Proposition 5.3 and our proof of Proposition 5.3 uses Proposition 5.2. Our proof of Proposition 5.2, in turn, employs Proposition 5.1 in Subsection 5.1 below. In Proposition 5.1 we establish that under the assumption that the target function $ f \colon [\mathscr{a}, \mathscr{b}] ^d \to \mathbb{R} $ and the unnormalized density function $ \mathfrak{p} \colon [\mathscr{a}, \mathscr{b}] ^d \to [0, \infty) $ are piecewise polynomial (see Definition 4.9 in Subsection 4.3) we have that the risk function $ \mathcal{L} \colon \mathbb{R}^ \mathfrak{d} \to \mathbb{R} $ satisfies an appropriately generalized Kurdyka-Łojasiewicz inequality.
In the proof of Proposition 5.1 the classical Łojasiewicz inequality for semialgebraic or subanalytic functions (cf., e.g., Bierstone & Milman [40]) is not directly applicable since the generalized gradient function $ \mathcal{G} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ is not continuous. We will employ the more general results from Bolte et al. [9] which also apply to not necessarily continuously differentiable functions.
The arguments used in the proof of Proposition 5.2 are slight adaptions of well-known arguments in the literature; see, e.g., Kurdyka et al. [12, Section 1], Bolte et al. [9, Theorem 4.5], or Absil et al. [6, Theorem 2.2]. On the one hand, in Kurdyka et al. [12, Section 1] and Absil et al. [6, Theorem 2.2] it is assumed that the object function of the considered optimization problem is analytic and in Bolte et al. [9, Theorem 4.5] it is assumed that the objective function of the considered optimization problem is convex or lower $ C^2 $ and Proposition 5.2 does not require these assumptions. On the other hand, Bolte et al. [9, Theorem 4.5] consider more general differential dynamics and the considered gradients are allowed to be more general than the specific generalized gradient function $ \mathcal{G} \colon \mathbb{R}^{ \mathfrak{d} } \to \mathbb{R}^{ \mathfrak{d} } $ which is considered in Proposition 5.2.
5.1. Generalized Kurdyka-Łojasiewicz inequality for the risk function
Proposition 5.1 (Generalized Kurdyka-Łojasiewicz inequality). Assume Setting 2.1, assume that $ \mathfrak{p} $ and $ f $ are piecewise polynomial, and let $ \vartheta \in \mathbb{R}^ \mathfrak{d} $ (cf. Definition 4.9). Then there exist $ \varepsilon, \mathfrak{D} \in (0, \infty) $, $ \alpha \in (0, 1) $ such that for all $ \theta \in B_\varepsilon (\vartheta) $ it holds that
Proof of Proposition 5.1. Throughout this proof let $ \mathbf{M} \colon \mathbb{R}^ \mathfrak{d} \to [0, \infty] $ satisfy for all $ \theta \in \mathbb{R}^ \mathfrak{d} $ that
Note that Proposition 2.12 implies for all $ \theta \in \mathbb{R}^ \mathfrak{d} $ that
Furthermore, observe that Corollary 4.10, the fact that semialgebraic functions are subanalytic, and Bolte et al. [9, Theorem 3.1 and Remark 3.2] ensure that there exist $ \varepsilon, \mathfrak{D} \in (0, \infty) $, $ \mathfrak{a} \in [0, 1) $ which satisfy for all $ \theta \in B_\varepsilon (\vartheta) $ that
Combining this and (5.3) with the fact that $ \sup_{\theta \in B_\varepsilon (\vartheta) } | \mathcal{L} (\theta) - \mathcal{L} (\vartheta) | < \infty $ demonstrates that for all $ \theta \in B_\varepsilon (\vartheta) $, $ \alpha \in (\mathfrak{a}, 1) $ we have that
This completes the proof of Proposition 5.1.
5.2. Local convergence for solutions of GF differential equations
Proposition 5.2. Assume Setting 2.1 and let $ \vartheta \in \mathbb{R}^ \mathfrak{d} $, $ \varepsilon, \mathfrak{D} \in (0, \infty) $, $ \alpha \in (0, 1) $ satisfy for all $ \theta \in B_\varepsilon (\vartheta) $ that
Then there exists $ \delta \in (0, \varepsilon) $ such that for all $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ with $ \Theta_0 \in B_\delta (\vartheta) $, $ \forall \, t \in [0, \infty) \colon \Theta_t = \Theta_0 - \int_0^t \mathcal{G} (\Theta_s) \, \mathrm{d} s $, and $ \inf_{t \in \left\{ {{ s \in [0, \infty) \colon \Theta_s \in B_\varepsilon (\vartheta) }} \right\} } \mathcal{L} (\Theta_t) \geq \mathcal{L} (\vartheta) $ there exists $ \psi \in \mathcal{L}^{ - 1 }(\left\{ {{ \mathcal{L}(\vartheta) }} \right\}) $ such that for all $ t \in [0, \infty) $ it holds that
Proof of Proposition 5.2. Note that the fact that $ \mathcal{L} $ is continuous implies that there exists $ \delta \in (0, \varepsilon / 3) $ which satisfies for all $ \theta \in B_\delta (\vartheta) $ that
In the following let $ \Theta \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy $ \forall \, t \in [0, \infty) \colon \Theta_t = \Theta_0 - \int_0^t \mathcal{G} (\Theta_s) \, \mathrm{d} s $, $ \Theta_0 \in B_\delta (\vartheta) $, and
In the first step we show that for all $ t \in [0, \infty) $ it holds that
Observe that, e.g., [37, Lemma 3.1] ensures for all $ t \in [0, \infty) $ that
This implies that $ [0, \infty) \ni t \mapsto \mathcal{L} (\Theta_t) \in [0, \infty) $ is non-increasing. Next let $ L \colon [0, \infty) \to \mathbb{R} $ satisfy for all $ t \in [0, \infty) $ that
and let $ T \in [0, \infty] $ satisfy
We intend to show that $ T = \infty $. Note that (5.10) assures for all $ t \in [0, T) $ that $ L(t) \geq 0 $. Moreover, observe that (5.12) and (5.13) ensure that for almost all $ t \in [0, T) $ it holds that $ L $ is differentiable at $ t $ and satisfies $ L ' (t) = \frac{ \mathrm{d}}{ \mathrm{d} t} (\mathcal{L} (\Theta_t)) = - || \mathcal{G} (\Theta_t) || ^2 $. In the following let $ \tau \in [0, T] $ satisfy
Note that the fact that $ L $ is non-increasing implies that for all $ s \in [\tau, T) $ it holds that $ L(s) = 0 $. Combining this with (5.12) demonstrates for almost all $ s \in (\tau, T) $ that $ \mathcal{G} (\Theta_s) = 0 $. This proves for all $ s \in [\tau, T) $ that $ \Theta_s = \Theta_\tau $. Next observe that (5.6) ensures that for all $ t \in [0, \tau) $ it holds that
Combining this with the chain rule proves for almost all $ t \in [0, \tau) $ that
In addition, note that the fact that $ [0, \infty) \ni t \mapsto L(t) \in \mathbb{R} $ is absolutely continuous and the fact that for all $ r \in (0, \infty) $ it holds that $ (r, \infty) \ni y \mapsto y^{1 - \alpha } \in \mathbb{R} $ is Lipschitz continuous demonstrate for all $ t \in [0, \tau) $ that $ [0, t] \ni s \mapsto [L (s)]^{ 1 - \alpha } \in \mathbb{R} $ is absolutely continuous. Integrating (5.17) hence shows for all $ s, t \in [0, \tau) $ with $ t \le s $ that
This and the fact that for almost all $ s \in (\tau, T) $ it holds that $ \mathcal{G} (\Theta_s) = 0 $ ensure that for all $ s, t \in [0, T) $ with $ t \le s $ we have that
Combining this with (5.9) demonstrates for all $ t \in [0, T) $ that
This, the fact that $ \delta < \varepsilon / 3 $, and the triangle inequality assure for all $ t \in [0, T) $ that
Combining this with (5.14) proves that $ T = \infty $. This establishes (5.11).
Next observe that the fact that $ T = \infty $ and (5.20) prove that
In the following let $ \sigma \colon [0, \infty) \to [0, \infty) $ satisfy for all $ t \in [0, \infty) $ that
Note that (5.22) proves that $ \limsup_{t \to \infty} \sigma (t) = 0 $. In addition, observe that (5.22) assures that there exists $ \psi \in \mathbb{R}^ \mathfrak{d} $ such that
In the next step we combine the weak chain rule for the risk function in (5.12) with (5.11) and (5.6) to obtain that for almost all $ t \in [0, \infty) $ we have that
In addition, note that the fact that $ L $ is non-increasing and (5.9) ensure that for all $ t \in [0, \infty) $ it holds that $ L (t) \leq L (0) \leq 1 $. Therefore, we get for almost all $ t \in [0, \infty) $ that
Combining this with the fact that for all $ t \in [0, \tau) $ it holds that $ L (t) > 0 $ establishes for almost all $ t \in [0, \tau) $ that
The fact that for all $ t \in [0, \tau) $ it holds that $ [0, t] \ni s \mapsto L (s) \in (0, \infty) $ is absolutely continuous hence demonstrates for all $ t \in [0, \tau) $ that
Therefore, we infer for all $ t \in [0, \tau) $ that
This and the fact that for all $ t \in [\tau, \infty) $ it holds that $ L(t) = 0 $ prove that for all $ t \in [0, \infty) $ we have that
Furthermore, observe that (5.24) and the fact that $ \mathcal{L} $ is continuous imply that $ \limsup_{t \to \infty} | \mathcal{L} (\Theta_t) - \mathcal{L} (\psi) | = 0 $. Hence, we obtain that $ \mathcal{L} (\psi) = \mathcal{L} (\vartheta) $. This shows for all $ t \in [0, \infty) $ that
In the next step we establish a convergence rate for the quantity $ ||\Theta_t - \psi|| $, $ t \in [0, \infty) $. We accomplish this by employing an upper bound for the tail length of the curve $ \Theta_t \in \mathbb{R}^ \mathfrak{d} $, $ t \in [0, \infty) $. More formally, note that (5.19), (5.11), and (5.6) demonstrate for all $ t \in [0, \infty) $ that
Next observe that the fact that for all $ t \in [0, \infty) $ it holds that $ \sigma (t) = \int_0^\infty || \mathcal{G} (\Theta_s)|| \, \mathrm{d} s - \int_0^t || \mathcal{G} (\Theta_s) || \, \mathrm{d} s $ shows that for almost all $ t \in [0, \infty) $ we have that $ \sigma' (t) = - || \mathcal{G} (\Theta_t) || $. This and (5.32) yield for almost all $ t \in [0, \infty) $ that $ \sigma(t) \leq \mathfrak{D}^{1 / \alpha} \left({{1-\alpha}} \right)^{-1} \left[{{- \sigma ' (t) }} \right]^{\frac{1-\alpha}{\alpha}} $. Therefore, we obtain for almost all $ t \in [0, \infty) $ that
Combining this with the fact that $ \sigma $ is absolutely continuous implies for all $ t \in [0, \infty) $ that
In the following let $ \beta, \mathfrak{C} \in (0, \infty) $ satisfy $ \beta = \max \left\{ {{ 1, \frac{\alpha}{1-\alpha} }} \right\} $ and $ \mathfrak{C} = \left({{ (1-\alpha) \mathfrak{D} ^{ -1 / \alpha} }} \right)^{\frac{\alpha}{1-\alpha}} $. Note that (5.34) and the fact that for all $ t \in [0, \infty) $ it holds that $ \sigma (t) \leq \sigma (0) \leq 1 $ ensure that for all $ t \in [0, \infty) $ it holds that
This, the fact that $ \sigma $ is non-increasing, and the fact that for all $ t \in [0, \infty) $ it holds that $ 0 \leq \sigma(t) \leq 1 $ prove that for all $ t \in [0, \infty) $ we have that
Hence, we obtain for all $ t \in [0, \infty) $ that $ \sigma(t) \leq \left({{ 1 + \mathfrak{C} t }} \right)^{-\frac{1}{\beta}} $. Combining this with the fact that for all $ t \in [0, \infty) $ it holds that
shows that for all $ t \in [0, \infty) $ we have that $ ||\Theta_t - \psi || \le (1 + \mathfrak{C} t) ^{- 1 / \beta} $. This, (5.11), (5.22), and (5.31) establish (5.8). The proof of Proposition 5.2 is thus complete.
5.3. Global convergence for solutions of GF differential equations
Proposition 5.3. Assume Setting 2.1, assume that $ \mathfrak{p} $ and $ f $ are piecewise polynomial, and let $ \Theta \in C ([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy
(cf. Definition 4.9). Then there exist $ \vartheta \in \mathcal{G}^{ - 1 } (\left\{ {{ 0 }} \right\}) $, $ \mathfrak{C}, \tau, \beta \in (0, \infty) $ which satisfy for all $ t \in [\tau, \infty) $ that
Proof of Proposition 5.3. First observe that [37, Lemma 3.1] ensures that for all $ t \in [0, \infty) $ it holds that
This implies that $ [0, \infty) \ni t \mapsto \mathcal{L} (\Theta_t) \in [0, \infty) $ is non-increasing. Hence, we obtain that there exists $ \mathbf{m} \in [0, \infty) $ which satisfies that
Moreover, note that the assumption that $ \liminf_{t \to \infty } ||\Theta_t || < \infty $ ensures that there exist $ \vartheta \in \mathbb{R}^ \mathfrak{d} $ and $ \tau = (\tau_n)_{n \in \mathbb{N}} \colon \mathbb{N} \to [0, \infty) $ which satisfy $ \liminf_{n \to \infty} \tau_n = \infty $ and
Combining this with (5.41) and the fact that $ \mathcal{L} $ is continuous shows that
Next observe that Proposition 5.1 demonstrates that there exist $ \varepsilon, \mathfrak{D} \in (0, \infty) $, $ \alpha \in (0, 1) $ such that for all $ \theta \in B_\varepsilon (\vartheta) $ we have that
Combining this and (5.42) with Proposition 5.2 demonstrates that there exists $ \delta \in (0, \varepsilon) $ which satisfies for all $ \Phi \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ with $ \Phi_0 \in B_\delta (\vartheta) $, $ \forall \, t \in [0, \infty) \colon \Phi_t = \Phi_0 - \int_0^t \mathcal{G} (\Phi_s) \, \mathrm{d} s $, and $ \inf_{ t \in \left\{ {{ s \in [0, \infty) \colon \Phi_s \in B_{ \varepsilon }(\vartheta) }} \right\} } \mathcal{L}(\Phi_t) \ge \mathcal{L}(\vartheta) $ that it holds for all $ t \in [0, \infty) $ that
Moreover, note that (5.42) ensures that there exists $ n \in \mathbb{N} $ which satisfies $ \Theta_{\tau_n } \in B_\delta (\vartheta) $. Next let $ \Phi \in C([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy for all $ t \in [0, \infty) $ that
Observe that (5.43) and (5.47) assure that
Combining this with (5.46) proves for all $ t \in [\tau_n, \infty) $ that
and
Next note that [37, Corollary 2.15] shows that $ \mathbb{R}^ \mathfrak{d} \ni \theta \mapsto || \mathcal{G} (\theta) || \in [0, \infty) $ is lower semicontinuous. The fact that $ \liminf_{s \to \infty} || \mathcal{G} (\Theta_s) || = 0 $ and the fact that $ \limsup_{t \to \infty} ||\Theta_t - \vartheta || = 0 $ hence imply that $ \mathcal{G} (\vartheta) = 0 $. Combining this with (5.49) and (5.50) establishes (5.39). The proof of Proposition 5.3 is thus complete.
By choosing a sufficiently large $ \mathscr{C} \in (0, \infty) $ we can conclude a simplified version of Proposition 5.3. This is precisely the subject of the next result, Theorem 5.4 below. Theorem 1.2 in the introduction is a direct consequence of Theorem 5.4.
Theorem 5.4. Assume Setting 2.1, assume that $ \mathfrak{p} $ and $ f $ are piecewise polynomial, and let $ \Theta \in C ([0, \infty), \mathbb{R}^ \mathfrak{d}) $ satisfy $ \liminf_{t \to \infty } ||\Theta_t || < \infty $ and $ \forall \, t \in [0, \infty) \colon \Theta_t = \Theta_0 - \int_0^t \mathcal{G} (\Theta_s) \, \mathrm{d} s $ (cf. Definition 4.9). Then there exist $ \vartheta \in \mathcal{G}^{ - 1 } (\left\{ {{ 0 }} \right\}) $, $ \mathscr{C}, \beta \in (0, \infty) $ which satisfy for all $ t \in [0, \infty) $ that
Proof of Theorem 5.4. Observe that Proposition 5.3 assures that there exist $ \vartheta \in \mathcal{G}^{ - 1 } (\left\{ {{ 0 }} \right\}) $, $ \mathfrak{C}, \tau, \beta \in (0, \infty) $ which satisfy for all $ t \in [\tau, \infty) $ that
and
In the following let $ \mathscr{C} \in (0, \infty) $ satisfy
Note that (5.53), (5.54), and the fact that $ [0, \infty) \ni t \mapsto \mathcal{L} (\Theta_t) \in [0, \infty) $ is non-increasing show for all $ t \in [0, \tau] $ that
and
Moreover, observe that (5.52) and (5.54) imply for all $ t \in [\tau, \infty) $ that
In addition, note that (5.53) and (5.54) demonstrate for all $ t \in [\tau, \infty) $ that
This completes the proof of Theorem 5.4.
Acknowledgments
This project has been partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy EXC 2044-390685587, Mathematics Münster: Dynamics-Geometry-Structure.
Conflict of interest
The authors declare that there are no conflicts of interest.
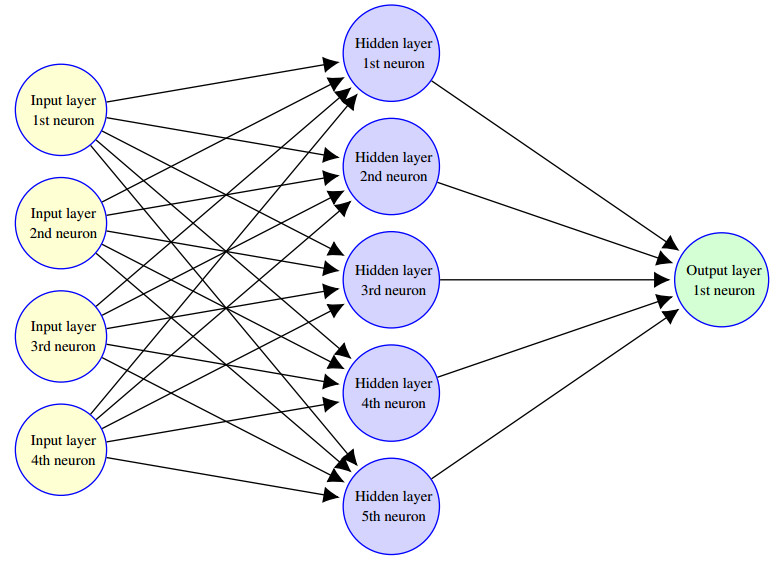









 DownLoad:
DownLoad: