This paper presented a numerical method based on the charge simulation method for calculating conformal mappings from the bounded multiply connected regions with a rectilinear slit onto the first category canonical slit domains. First, we proposed utilizing a pre-map function to expand a rectilinear slit in the bounded multiply connected regions. Second, to address pathologically constrained equation systems, we proposed a conjugate gradient squared (CGS) method combined with LU decomposition. Third, the conformal mappings were applied to simulate spiral point vortex bypass flow in regions with a rectilinear slit. Finally, numerical experiments validated the correctness of the mapping, the method's superiority, and its effectiveness in spiral point vortex bypass flow simulations.
Citation: Dongyi Li, Yibin Lu. A method of numerical conformal mapping of bounded regions with a rectilinear slit[J]. AIMS Mathematics, 2025, 10(4): 8422-8445. doi: 10.3934/math.2025388
| [1] | Nuraddeen S. Gafai, Ali H. M. Murid, Samir Naqos, Nur H. A. A. Wahid . Computing the zeros of the Szegö kernel for doubly connected regions using conformal mapping. AIMS Mathematics, 2023, 8(5): 12040-12061. doi: 10.3934/math.2023607 |
| [2] | Sharifah E. Alhazmi, M. A. Abdou, M. Basseem . The stresses components in position and time of weakened plate with two holes conformally mapped into a unit circle by a conformal mapping with complex constant coefficients. AIMS Mathematics, 2023, 8(5): 11095-11112. doi: 10.3934/math.2023562 |
| [3] | Xiaoguang Yuan, Quan Jiang, Zhidong Zhou, Fengpeng Yang . The method of fundamental solutions for analytic functions in complex analysis. AIMS Mathematics, 2022, 7(4): 6820-6851. doi: 10.3934/math.2022380 |
| [4] | Hu Ge-JiLe, Saima Rashid, Muhammad Aslam Noor, Arshiya Suhail, Yu-Ming Chu . Some unified bounds for exponentially $tgs$-convex functions governed by conformable fractional operators. AIMS Mathematics, 2020, 5(6): 6108-6123. doi: 10.3934/math.2020392 |
| [5] | Arthur Ecoffet, Geoffrey Woollard, Artem Kushner, Frédéric Poitevin, Khanh Dao Duc . Application of transport-based metric for continuous interpolation between cryo-EM density maps. AIMS Mathematics, 2022, 7(1): 986-999. doi: 10.3934/math.2022059 |
| [6] | Liliana Guran, Khushdil Ahmad, Khurram Shabbir, Monica-Felicia Bota . Computational comparative analysis of fixed point approximations of generalized $ \alpha $-nonexpansive mappings in hyperbolic spaces. AIMS Mathematics, 2023, 8(2): 2489-2507. doi: 10.3934/math.2023129 |
| [7] | Na Mi, Juhe Sun, Li Wang, Yu Liu . Alternating direction method for the fixed point problem of set-valued mappings with second-order cone double constraints. AIMS Mathematics, 2023, 8(3): 6389-6406. doi: 10.3934/math.2023323 |
| [8] | Noor Muhammad, Ali Asghar, Samina Irum, Ali Akgül, E. M. Khalil, Mustafa Inc . Approximation of fixed point of generalized non-expansive mapping via new faster iterative scheme in metric domain. AIMS Mathematics, 2023, 8(2): 2856-2870. doi: 10.3934/math.2023149 |
| [9] | Junaid Ahmad, Imen Ali Kallel, Ahmad Aloqaily, Nabil Mlaiki . On multi-valued generalized $ \alpha $-nonexpansive mappings and an application to two-point BVPs. AIMS Mathematics, 2025, 10(1): 403-419. doi: 10.3934/math.2025019 |
| [10] | Pengfei Zhu, Kai Liu . Numerical investigation of convergence in the $ L^{\infty} $ norm for modified SGFEM applied to elliptic interface problems. AIMS Mathematics, 2024, 9(11): 31252-31273. doi: 10.3934/math.20241507 |
This paper presented a numerical method based on the charge simulation method for calculating conformal mappings from the bounded multiply connected regions with a rectilinear slit onto the first category canonical slit domains. First, we proposed utilizing a pre-map function to expand a rectilinear slit in the bounded multiply connected regions. Second, to address pathologically constrained equation systems, we proposed a conjugate gradient squared (CGS) method combined with LU decomposition. Third, the conformal mappings were applied to simulate spiral point vortex bypass flow in regions with a rectilinear slit. Finally, numerical experiments validated the correctness of the mapping, the method's superiority, and its effectiveness in spiral point vortex bypass flow simulations.
Conformal mapping plays a crucial role in complex analysis and has widespread applications in fields such as fluid dynamics and image processing. For example, Shen et al. [1] applied conformal mapping to solve the problem of complete coverage path planning. Gu et al. [2] developed a computational method for mapping arbitrary topological surfaces onto canonical domains, which was subsequently used in image processing applications. Conformal mapping transforms complex planes into regular slit domains, and the methods employed to achieve such mappings are generally categorized into analytic and numerical approaches. Analytic methods, based on Riemann's theorem, establish the existence of mapping functions. However, for complex regions, numerical methods are more commonly used.
Koebe introduced 39 significant types of canonical slit domains, providing a foundation for future research [3]. In 1966, Symm [4] proposed the use of first-kind Fredholm integral equations to compute conformal mapping functions for singly and doubly connected regions. In 2006, Crowdy and Marshall [5] advanced the field by developing an analytic formula to map multiply connected circular domains to multiply connected slit domains. Amano et al. introduced a numerical method for conformal mapping based on the charge simulation method, this approach simplifies computations by avoiding complex integrations and provides highly accurate approximate mapping functions. Furthermore, the proposed method was employed to compute the conformal mapping functions from unbounded regions onto canonical domains, including the circular slits domains, the radial slits domains, and the parallel slits domains [6,7,8]. In addition, it was utilized to compute the conformal mappings from bounded regions onto a disk with concentric circular slits domain and an annulus with concentric circular slits domain [9]. Then, Nasser et al. further developed a generalized second-kind Fredholm integral equation approach for Neumann kernels [10], successfully computing conformal mapping functions from bounded regions to the first category canonical slit domains [11,12,13], from both bounded and unbounded regions to the second, third, and fourth category canonical slit domains [14], and from multiply connected regions to the fifth category canonical slit domains [15]. Furthermore, Trefethen has developed direct methods for solving Laplace's equation in multiply connected domains, employing the AAA algorithm (An algorithm for real and complex rational minimax approximation) [16,17] in conjunction with least squares to ensure the satisfaction of boundary conditions. This approach offers an alternative methodology for computing the spiral vortex solution [18].
In the theory of conformal mapping for both singly and multiply connected regions in complex planes, numerous canonical regions have been extensively examined. Among the classical regular slit domains, the first category slit domains stand out. These include the domains of a disk with concentric circular slits, an annulus with concentric circular slits, circular slits, radial slits, and parallel slits domains. Previous work by Amano has successfully achieved conformal mapping from bounded multiply connected regions to the domains of a disk and an annulus with concentric circular slits using the charge simulation method. Later, Nasser [11] computed approximate mapping functions from bounded multiply connected regions to circular slits, radial slits, and parallel slits domains.
The conformal mapping of bounded multiply connected regions in the $ D $-plane that contain a combination of a rectilinear slit, a curved slit, and semicircles remains an unresolved challenge. In conformal mapping using the charge simulation method, the region $ D $ must consist of closed Jordan curves to enable the placement of charge points within these curves. However, the distinct structure of the rectilinear slit imposes spatial constraints, complicating the placement of charge points within the required closed contours. While Amano et al. [19] proposed a method for conformal mapping in regions containing either a rectilinear, curved slit or semicircles in combination, a computational approach for the conformal mapping of multiply connected regions that specifically include a rectilinear slit has yet to be developed.
In the charge simulation method, when solving the system of constraint equations $ Ax = b $ established by boundary conditions, the matrix A often becomes ill-conditioned as the number of charge points increases. To address this matrix pathology, we introduce a novel CGS method, utilizing LU decomposition as a preprocessor to enhance the efficiency and stability of solving large sparse asymmetric constraint systems. By decomposing matrix A into a lower triangular matrix L and an upper triangular matrix U, the condition number of the new system is significantly reduced, simplifying the original system. CGS is an iterative method specifically designed for asymmetric or indeterminate sparse linear systems, making it particularly suitable for large-scale sparse systems [20,21,22,23]. As a variant of the dual conjugate gradient method, CGS mitigates algorithmic instability by squaring residuals, thereby accelerating convergence. Integrating the LU preprocessor with the CGS method not only provides a more accurate approximation function but also enhances system stability, effectively addressing the computational challenges of conformal mapping in complex slit domains.
The main contributions of this study are threefold: First, the conformal mapping of multiply connected regions with a rectilinear slit to first category canonical slit domains is achieved using the charge simulation method. Second, for the matrix pathology encountered in systems of constraint equations involving multiply connected regions with a rectilinear slit, we propose an iterative approach CGS method combined with LU decomposition. Third, the conformal mapping method is applied to simulate spiral point vortex bypass flow in regions with a rectilinear slit. Numerical experiments demonstrate the effectiveness of the proposed method. The conformal mapping is successfully implemented and applied to spiral point vortex bypass flow simulations, showcasing the algorithm's high accuracy and stability.
The paper is structured as follows: Section 2 introduces the pre-map function and charge simulation method. Section 3 presents the CGS method combined with the LU decomposition algorithm. Section 4 discusses the spiral point vortex bypass flow and the conformal mappings. Section 5 is devoted to the statement of conclusions.
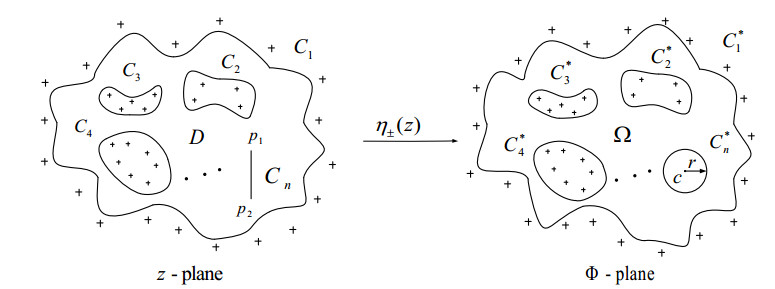
In this subsection, the fundamental theory of the pre-map function and its application to bounded multiply connected regions with a rectilinear slit will be discussed in detail [19]. The pre-map function is highly effective in slit expansion, as it ensures both the smooth transition of the region and the structural integrity of the domain, while also preserving and leveraging the advantages of the charge simulation method. The pre-map function diagram is presented below (as shown in Figure 1).
Let $ D $ be a bounded $ n $-connected region in the extended complex plane $ \mathbb{C}\cup\{\infty\} $ containing $ z = 0 $, where $ D $ is bounded by: $ C: = \partial D = \mathop{\cup}\limits_{k = 1}^nC_k $. Here, $ C_1, \; C_2, \dots, \; C_{n} $ are $ n $ closed Jordan curves. Assume that one of the closed curves $ C_n $ is replaced by a rectilinear slit, with the two endpoints of the rectilinear slit denoted by $ p_1 $ and $ p_2 $, thereby forming a bounded multiply connected region $ D $ containing the rectilinear slit (as shown on the Figure 1). Since the charge simulation method can only be applied in regions with closed boundary curves, to transform the rectilinear slit into a closed curve, we introduce a pre-map function defined as follows:
| $ \begin{align} \eta_\pm(z) = \begin{cases} z\pm \sqrt{z-p_{1}}\sqrt{z-p_{2}}, \; \; \; \; \; \; \; \; \; \; \; \; \; \; z\in C_{n}, \cr \; \; \; \; \; \cr z + \sqrt{z-p_{1}}\sqrt{z-p_{2}}, \; \; \; \; \; \; \; \; \; \; \; \; \; \; z\in D\backslash C_{n}. \end{cases} \end{align} $ | (2.1) |
The pre-map function $ \eta_+(z) $ and $ \eta_-(z) $ map the rectilinear slit $ C_n $ onto the left and right semicircles, thus expanding $ C_n $ into a circle. This circle, with center $ c = \frac{|p_1+p_2|}{2} $ and radius $ r = \frac{|p_1-p_2|}{2} $, is denoted as $ C_n^* $. The other closed curves in the $ D $ region, as well as the charge points, are mapped by the function: $ \eta(z) = z+\sqrt{z-p_1}\sqrt{z-p_2} $ onto $ C_1^*, \; C_2^*, \dots, \; C_{n-1}^* $ and $ \zeta_{1j}^*, \; \zeta_{2j}^*, \dots, \zeta_{(n-1)j}^*\; (j = 1, 2, \dots, N_l) $, where these pre-mapped closed boundary curves together form the bounded $ n $-connected $ \Omega $ region. After the rectilinear slit is unfolded, there is sufficient space inside to configure the charge points. We place the charge points $ \zeta_{nj}^* $ inside the closed curve $ C_n^* $.
In this subsection, we introduce the basic theory of the charge simulation method in detail.
In the $ \Phi $-plane, consider the region $ \Omega $ formed by the $ n $ boundary curves $ C_1^*, C_2^*, \dots, C_n^* $, which are mapped onto the first category canonical slit domains, including a disk circular slits domain $ W_{a} $, an annulus circular slits domain $ W_{b} $, the circular slits domain $ W_{c} $, the radial slits domain $ W_{d} $, and the parallel slits domain $ W_{e} $. The closed curves $ C_1^*, \; C_2^*, \dots, \; C_n^* $ are mapped to the corresponding domains $ S_1, \; S_2, \dots, \; S_n $, and the region $ \Omega $ is mapped to the $ W $ regions as shown in Figure 2.
To solve the approximate mapping functions for the five cases described above, we will employ the charge simulation method. This method converts the conformal mapping problem into the task of solving a pair of conjugate harmonic functions $ a(z) = g(z)+ih(z) $, which can be approximated by a linear combination of complex logarithmic functions
| $ \begin{equation} a(z)\approx A(z) = G(z)+\text{i}H(z) = Q_0+i\sum\limits_{l = 1}^n \text{e}^{i\theta_l}\sum\limits_{j = 1}^{N_l} Q_{lj}\ln\left(z-\zeta_{lj}\right) , \; z \in \Omega \cup \partial \Omega, \end{equation} $ | (2.2) |
where $ Q_{lj}\in \mathbb{R} $ are undetermined variables called charges and $ Q_0 $ is a constant. $ A(z) $ serves as an approximation to $ a(z) $, while $ G(z) $ and $ H(z) $ represent approximations to $ g(z) $ and $ h(z) $, respectively.
The charge points $ \zeta_{lj}^{*} $ on the curve $ N_l $ are located outside the mapping regions, i.e., outside $ C_1^* $, and inside $ C_l^* (l = , 2, \ldots, n) $. The function $ A(z) $ must satisfy the following three conditions [6,9]:
(1) The $ A(z) $ is single-valued in the region $ \Omega $ if, and only if,
| $ \begin{equation} \int_{C^{*}}dh(z) = 0. \end{equation} $ | (2.3) |
Thus, for $ H(z) $ we have
| $ \begin{equation} \begin{aligned} \int_{C_l^*}dH(z) = \int_{C_l^*}d\sum\limits_{l = 1}^n \sum\limits_{j = 1}^{N_l} Q_{lj}\arg\left(z-\zeta_{lj}\right) = 2\pi\sum\limits_{j = 1}^{N_l}Q_{lj} = 0, \cr l = 2, \; 3, \dots, \; n. \end{aligned} \end{equation} $ | (2.4) |
(2) Maintaining the scale invariance of the coordinate system of the approximating function on the problem domain $ \Omega $ [9,24], i.e.,
| $ \begin{equation} \sum\limits_{j = 1}^{N_1}Q_{1j} = -1. \end{equation} $ | (2.5) |
(3) According to Figure 2 and [25], satisfying the conditions for normalization, we have
| $ \begin{align*} &W_{a}, W_{b}:\; \; \; \; \; \; \; \; \; \; \; A(v) = Q_0+\sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left(v-\zeta_{lj}\right) = -\ln{(v-u)}, & \end{align*} $ | (2.6) |
| $ \begin{align*} &W_{c}, W_{d}, W_{e}:\; \; \; \; \; \; A(v) = Q_0+\sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left(v-\zeta_{lj}\right) = 0.& \end{align*} $ | (2.7) |
It follows that eliminating $ Q_0 $, then the approximate form is written as
| $ \begin{align*} &W_{a}, W_{b}:\; \; \; \; \; \; \; \; A(z) = A(z)-A(v) = \sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\frac{z-\zeta_{lj}}{v-\zeta_{lj}}-\ln{(v-u)}, & \end{align*} $ | (2.8) |
| $ \begin{align*} &W_{c}, W_{d}, W_{e}:\; \; \; \; \; \; \; \; \; \; \; \; \; A(z) = A(z)-A(v) = \sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\frac{z-\zeta_{lj}}{v-\zeta_{lj}}.& \end{align*} $ | (2.9) |
In this section, when solving the charges in the charge simulation method, factors such as an increase in the number of charge points can lead to a rise in the condition number of the coefficient matrix $ A $, which may result in the matrix becoming pathological [20,21,22,23,26]. We proposed that a CGS method combined with LU decomposition effectively addresses the issue of matrix pathology in the conformal mapping. First, consider a system of linear equations
| $ Ax = b, $ |
where $ A\in\mathbb{R}^{(N_1+N_2+\ldots+N_n+n)\times (N_1+N_2+\ldots+N_n+n)} $ is a large dense asymmetric matrix. We apply LU decomposition as a preprocessor for the coefficient matrix $ A $ as follows:
| $ A = LU, $ |
where $ L $ is a lower triangular matrix and $ U $ is an upper triangular matrix.
In Algorithm 1, the decomposition is a preprocessor for the original search direction $ p $, which makes the matrix system have a better condition number after preprocessing and, thus, improves the iterative convergence.
According to the previous analysis, the CGS method combined with LU decomposition for numerical conformal mapping based on the charge simulation method is summarized as follows.
(1) For each of the closed boundary curves $ C_l $, except for the rectilinear slit, we place charge points on them, denoted as $ \zeta_{lj} $. Additionally, we configure the constraint points $ z_{lj} $ on the curves $ C_1, \; C_2, \dots, \; C_{n-1} $, where $ l = 1, 2, \dots, n-1 $ and $ j = 1, \; 2, \dots, \; N_l $.
(2) By applying the pre-map function, the rectilinear slit $ C_n $ is mapped onto a closed boundary curve $ C_n^* $. Additionally, charge points $ \zeta_{nj}^* $($ j = 1, \; 2, \dots, \; N_n $) are placed inside the closed curve $ C_n^* $.
(3) Meanwhile, the pre-map function maps the boundary curves $ C_1, \; C_2, \dots, \; C_{n-1} $ onto $ C_1^*, \; C_2^*, \dots, \; C_{n-1}^* $. The mapped charge points are denoted as $ \zeta_{lj}^* $, while the constraint points are denoted as $ z_{lj}^* $ ($ l = 1, \; 2, \dots, \; n-1 $, $ j = 1, \; 2, \dots, \; N_l $).
(4) Based on the charge simulation method, we derive a set of constraint equations for mapping from the bounded multiply connected regions to the first category canonical slit domains. According to Algorithm 1, we input the coefficient matrix $ A $, the vector $ b $, the error tolerance, and the maximum number of iterations. The algorithm then outputs the vector $ x $, which contains the computed charges $ Q_{lj} $($ l = 1, \; 2, \dots, \; n $, $ j = 1, \; 2, \dots, \; N_l $).
(5) By solving for the resulting charges $ Q_{lj} $, we compute the function $ A(z) $. Subsequently, we subsitute $ A(z) $ into the approximate mapping function.
| Algorithm 1 CGS method combined with LU decomposition for the charges |
| Input: $ A, \; b, \; x_0, \; {\rm ItMax}, \; \varepsilon $. |
| Initialize: $ r_0 = b-Ax_0 $; $ r_0^{*} $ is an arbitrary vector satisfying $ (r_0^{*}, r_0) \neq 0 $. For example, $ r_0^{*} = r_0 $. |
| Define: $ q_0 = p_{0} = 0 $; $ \rho_{-1} = 1 $; n = 0; |
| while $ residual > tolerance$ do |
| begin |
| $ \rho_n = (r_0^{*}, r_{n}) $; $ \beta_{n} = (\rho_n/\rho_{n-1}) $; |
| $ u_{n} = r_{n}+\beta_{n} q_{n} $; |
| $ p_{n} = u_{n}+\beta_{n}(q_{n}+\beta_{n} p_{n-1}) $; |
| $ p_{n}^{*} = U^{-1}(L^{-1}p_{n}) $; |
| $ \nu_{n} = Ap_{n}^{*} $; |
| $ \sigma_{n} = (r_0^{*}, \nu_{n}) $; |
| $ \alpha_{n} = \rho_{n}/\sigma_{n} $; |
| $ q_{n} = U^{-1}(L^{-1}u_{n}) $; |
| $ x_{n+1} = x_{n}+\alpha*(p_{n}^{*}+q_{n}) $; |
| $ r_{n+1} = r_{n}-\alpha_{n}*A*(p_{n}^{*}+q_{n}) $; |
| $ n = n+1 $; |
| end |
| Output: $ x_{n+1} $. |
Remark. ItMax and $ \varepsilon $ are the specified maximum number of iterations allowed and the tolerance, respectively, while $ x_0 $ denotes the initial approximation, which is set to the zero vector in this context. For the numerical experiments conducted, $ ItMax = 500, \; \varepsilon = 1e-14 $ is utilized.
In this subsection, we explore the theoretical foundations of point vortex flow, which simplifies the analysis of fluid dynamics through the use of a complex potential function. The application of conformal mapping techniques allows the transformation of complex geometries associated with vortex flow problems into simpler canonical shapes, thereby facilitating the solution process [27,28].
Conformal mapping offers substantial benefits for modeling flows around objects by providing a mathematical framework for transforming complex geometries. The approximate mapping function $ w = f(z) $ conformally maps the region $ D $ into the region $ W $, ensuring that the flow lines and isentropes in the $ D $-plane are transformed to their counterparts in the $ W $-plane. Within this framework, the complex potentials of the flow in regions $ D $ and $ W $ are denoted as $ c(z) = \psi(x, y)+{\rm i}\sigma(x, y) $ and $ C(w) $, respectively. Here, $ \psi(x, y) $ represents the velocity potential, while $ \sigma(x, y) $ denotes the stream function. Thus, when $ C(w) $ is determined, the complex potential $ c(z) $ in region $ D $ can be expressed as
| $ C(w) = C(f) = c(z), z\in D. $ |
We simulate the bypassing of a spiral point vortex in the region $ D $ for the conformal mapping from a bounded multiply connected region with a rectilinear slit to the bounded multiply connected regular slits domain, using the spiral point vortex model
| $ \begin{equation} C(w) = \frac{\tau+\mu i}{2i\pi}\ln(w). \end{equation} $ | (4.1) |
In the numerical experiments, the parameters are specified as $ \tau = -\sqrt{3} $ and $ \mu = 1 $.
Considering the approximate conformal mapping $ F_{a}(z) $ from the bounded multiply connected regions to a disk with concentric circular slits [9,25], the boundary conditions are defined as follows:
| $ \begin{equation} \left|F_{a}(z)\right| = r_l, \; \; \; z\in C_{l}^*, \; \; \; l = 1, 2, \dots, n. \end{equation} $ | (4.2) |
The $ r_l $ ($ l = 1, 2, \dots, n $) in the equation represents the radius of the circles and circular slits. The normalization conditions are defined as:
| $ \begin{equation} F_{a}(u) = 0, \; \; \; F_{a}(v) = 1. \end{equation} $ | (4.3) |
Here, $ u $ is a fixed point within the region $ \Omega $ and $ v $ is a fixed point on the outer boundary $ C_1^* $. The approximate mapping function is determined by the normalization conditions
| $ \begin{equation} F_{a}(z) = (z-u)\text{e}^{A(z)}. \end{equation} $ | (4.4) |
By applying Eq (4.4) to the boundary condition (4.2), a system of constraint equations is obtained:
| $ \begin{equation} A(z)-\ln r_l = -\ln|z-u|. \end{equation} $ | (4.5) |
The approximation $ A(z) $ (2.8) is derived by substituting it into the Eq (4.5), and we obtain a system of constraint equations of dimension $ N_1+ N_2+\dots+N_{n}+n $, as follows:
| $ \begin{equation} \sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left|\frac{z_{mk}-\zeta_{lj}}{v-\zeta_{lj}}\right|-\ln{r_{l}} = -\ln\left|\frac{z_{mk}-u}{v-u}\right|, \end{equation} $ | (4.6) |
where the unknown parameters requiring determination are the $ Q_{lj} $ and the radius of the circles and circular slits $ r_{l} $.
The experimental environment is Windows 11, MATLAB R2020b. The error expression for this conformal mapping is as follows:
| $ \begin{equation} E_{al} = \max \left|\left|F_{a}(Z)\right|-r_{l}\right|, \; \; \; \; \; Z\in C_{l}^*, \; \; \; \; l = 1, \; 2, \dots, \; n, \end{equation} $ | (4.7) |
where $ Z $ is the test point, located at the midpoint between every two neighboring constraints on $ C_{l}^{*} $.
Considering the bounded region defined by the curves $ C_1:{x^2}/{25^2}+{y^2}/{20^2} = 1, \; k_{1} = 0, \; s_{1} = 0 $; $ C_2:x = 0, \; y\in [7.05, 15] $; $ C_3:{x^2}/{4^2}+y^2 = 1, \; k_{3} = 11.5+7.5i, \; s_{3} = \pi/6 $; $ C_4:{x^2}/{4^2}+y^2 = 1, \; k_{4} = 3.5+6.5i, \; s_{4} = \pi/3 $; $ C_5:{x^2}/{4^2}+y^2 = 1, \; k_{5} = -3.5+6.5i, \; s_{5} = 2\pi/3 $; $ C_6:{x^2}/{4^2}+y^2 = 1, \; k_{6} = -11.5+7.5i, \; s_{6} = 5\pi/6 $; $ C_7:{x^2}/{4^2}+y^2 = 1, \; k_{7} = -11.5-7.5i, \; s_{7} = 7\pi/6 $; $ C_8:{x^2}/{4^2}+y^2 = 1, \; k_{8} = -3.5-6.5i, \; s_{8} = 8\pi/6 $; $ C_9:{x^2}/{4^2}+y^2 = 1, \; k_{9} = -12i, \; s_{9} = 9\pi/6 $; $ C_{10}:{x^2}/{4^2}+y^2 = 1, \; k_{10} = 3.5-6.5i, \; s_{10} = 10\pi/6 $; $ C_{11}:{x^2}/{4^2}+y^2 = 1, \; k_{11} = 11.5-7.5i, \; s_{11} = 11\pi/6 $; $ C_{12}:{x^2}/{4^2}+y^2 = 1, \; k_{12} = 17, \; s_{12} = 0 $; $ C_{13}:{x^2}/{4^2}+y^2 = 1, \; k_{13} = -17, \; s_{13} = 0 $, where $ k_{l} $ and $ s_{l}\; (l = 1, 3, \dots, 13) $ denote the center coordinates and rotation angle of the ellipse, respectively, as shown in Figure 3(a).
In Figure 3(c), the bounded 13-connected region with a rectilinear slit is successfully transformed into a disk with 12-connected concentric circular slits, the fixed point is $ u = -10i $, and $ v $ is an arbitrary point located on $ C_{1}^* $. A disk with concentric circular slits consists of a unit disk $ S_1 $ (i.e., $ r_1 = 1 $) and 12 circular slits $ S_2, S_3, \dots, S_{13} $.
In the charge simulation method, the placement of the charge points relative to the boundary curve influences the accuracy of the approximate mapping function. The charge point configurations utilized in the numerical experiments were referenced from the computational methodology outlined by Amano et al. [6,7,8,9,19,29]. According Eq (4.7), Figures 3(e), (f), (g), (h), and (i) display the error curves for charge points locations shrunk by factors of 0.3, 0.25, 0.2, 0.15, and 0.1 from the boundary curve, respectively. By comparing Algorithm 1 with the the generalized minimal residual (GMRES) method, it can be observed that the proposed algorithm outperforms GMRES method in terms of accuracy and stability. In Figure 3(d), the conformal mapping method is applied to simulate sipral point vortex bypass flow in regions with a rectilinear slit. In particular, since the complex logarithmic function $ \ln(w) $ is a multivalued function, its multivaluedness arises from the argument of a complex number. To make it single-valued, branch cuts are commonly introduced along which the function's argument undergoes a jump.
Consider the approximate conformal mapping $F_b(z)$ from multiply connected regions to an annulus with concentric circular slits, preserving boundary and normalization conditions, as well as approximate mapping functions similar to those for disks with concentric circular slits [9,25]. The boundary conditions are
| $ \begin{equation} \left|F_{b}(z)\right| = r_l, \; \; \; z\in C_{l}^*, \; \; \; l = 1, 2, \dots, n. \end{equation} $ | (4.8) |
The normalization conditions are
| $ \begin{equation} F_{b}(u) = 0, \; \; \; F_{b}(v) = 1. \end{equation} $ | (4.9) |
It is important to note that $ u $ is a fixed point within the interior region enclosed by $ C_n^* $, while $ v $ is a fixed point on the boundary curve $ C_1^* $, which differentiates this configuration from that of a disk with concentric circular slits. The approximate mapping function is then given by
| $ \begin{equation} F_{b}(z) = (z-u)\text{e}^{A(z)}. \end{equation} $ | (4.10) |
Substituting the approximate mapping function (4.10) into the boundary condition (4.8) results in the following:
| $ \begin{equation} A(z)-\ln r_l = -\ln|z-u|. \end{equation} $ | (4.11) |
The approximation $ A(z) $ (2.8) is derived by substituting it into the Eq (4.11), and we obtain a system of constraint equations of dimension $ N_1+ N_2+\dots+N_{n}+n $, as follows:
| $ \begin{equation} \sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left|\frac{z_{mk}-\zeta_{lj}}{v-\zeta_{lj}}\right|-\ln{r_{l}} = -\ln\left|\frac{z_{mk}-u}{v-u}\right|, \end{equation} $ | (4.12) |
where the unknown parameters requiring determination are the $ Q_{lj} $ and the radius of the circles and circular slits $ r_{l} $.
The experimental environment is Windows 11, MATLAB R2020b. The corresponding error expression for this conformal mapping is given as follows:
| $ \begin{equation} E_{bl} = \max \left|\left|F_{b}(Z)\right|-r_{l}\right|, \; \; \; \; \; Z\in C_{l}^*, \; \; \; \; l = 1, \; 2, \dots, \; n, \end{equation} $ | (4.13) |
where $ Z $ is the test point, located at the midpoint between each pair of neighboring constraints on $ C_{l}^{*} $.
Considering the bounded region defined by the following curves $ C_1:{x^2}/{25^2}+{y^2}/{20^2} = 1, \; k_{1} = 0, \; s_{1} = 0 $; $ C_2:x = 0, \; y\in [7.05, 15] $; $ C_3:{x^2}/{4^2}+y^2 = 1, \; k_{3} = 8.5+5.5i, \; s_{3} = \pi/6 $; $ C_4:{x^2}/{4^2}+y^2 = 1, \; k_{4} = 5.5+8.5i, \; s_{4} = \pi/3 $; $ C_5:{x^2}/{4^2}+y^2 = 1, \; k_{5} = -5.5+8.5i, \; s_{5} = 2\pi/3 $; $ C_6:{x^2}/{4^2}+y^2 = 1, \; k_{6} = -8.5+5.5i, \; s_{6} = 5\pi/6 $; $ C_7:{x^2}/{4^2}+y^2 = 1, \; k_{7} = -8.5-5.5i, \; s_{7} = 7\pi/6 $; $ C_8:{x^2}/{4^2}+y^2 = 1, \; k_{8} = -5.5-8.5i, \; s_{8} = 8\pi/6 $; $ C_9:{x^2}/{4^2}+y^2 = 1, \; k_{9} = -11i, \; s_{9} = 9\pi/6 $; $ C_{10}:{x^2}/{4^2}+y^2 = 1, \; k_{10} = 5.5-8.5i, \; s_{10} = 10\pi/6 $; $ C_{11}:{x^2}/{4^2}+y^2 = 1, \; k_{11} = 8.5-5.5i, \; s_{11} = 11\pi/6 $; $ C_{12}:{x^2}/{4^2}+y^2 = 1, \; k_{12} = 11, \; s_{12} = 0 $; $ C_{13}:{x^2}/{4^2}+y^2 = 1, \; k_{13} = -11, \; s_{13} = 0 $, where $ k_{l} $ and $ s_{l}\; (l = 1, 3, \dots, 13) $ denote the center coordinates and rotation angle of the ellipse, respectively, as shown in Figure 4(a).
In Figure 4(c), the bounded 13-connected region with a rectilinear slit is effectively mapped to an annulus with 12-connected concentric circular slits, the fixed point is $ u = (p_1+p_2)/2 $, and $ v $ is an arbitrary point located on $ C_{1}^* $. An annulus with concentric circular slits consists of a unit circle $S_1$ ($r_1 = 1$), a concentric circle $S_{13}$ ($0 < r_{13} < 1$), and 11 circular slits $S_2, S_3, \ldots, S_{12}$. The region $\Omega$ is mapped onto the bounded domain enclosed by $S_1$ and outside $S_{13}$. Figure 4(d) illustrates the simulation of a spiral point vortex bypass flow in a 13-connected bounded region containing a rectilinear obstacle.
According to Eq (4.13), Figures 4(e), (f), (g), (h), and (i) present the error curves for charge point locations shrunk by factors of 0.3, 0.25, 0.2, 0.15, and 0.1 from the boundary curve. A comparison of Algorithm 1 with the GMRES method reveals that the proposed algorithm outperforms GMRES method in terms of accuracy and stability for this conformal mapping.
For the approximate conformal mapping $ F_c(z) $ of the circular slits domain, the boundary conditions can be formulated based on the geometric constraints as follows [11,25]:
| $ \begin{equation} \left|F_{c}(z)\right| = r_l, \; \; \; z\in C_{l}^*, \; \; \; l = 1, 2, \dots, n. \end{equation} $ | (4.14) |
Here, $ r_l, \; (l = 1, 2, \dots, n) $ are the undetermined constants representing the radii of the circular slits. The normalization conditions are defined as:
| $ \begin{equation} F_{c}(u) = 0, \; \; \; F_{c}(v) = \infty, \; \; \; Res_{z = v}F_{c}(z) = 1, \end{equation} $ | (4.15) |
where $ u $ and $ v $ are distinct fixed points within the region $ \Omega $ ($ u \neq v $).
Based on the normalization conditions, the approximate mapping function can be uniquely determined as follows:
| $ \begin{equation} F_{c}(z) = \frac{z-u}{(z-v)(v-u)}\text{e}^{A(z)}. \end{equation} $ | (4.16) |
Substituting the approximate mapping function (4.16) into the boundary condition (4.14) yields the following:
| $ \begin{equation} A(z)-\ln r_l = -\ln\left|\frac{z-u}{(z-v)(v-u)}\right|. \end{equation} $ | (4.17) |
Substituting Eq (2.9) into Eq (4.17) results in the system of constraint equations, as follows:
| $ \begin{equation} \sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left|\frac{z_{mk}-\zeta_{lj}}{v-\zeta_{lj}}\right|-\ln{r_{l}} = -\ln\left|\frac{z_{mk}-u}{(z_{mk}-v)(v-u)}\right|, \end{equation} $ | (4.18) |
where the unknown parameters requiring determination are the $ Q_{lj} $ and the radius of the circular slits $ r_{l} $.
The experimental environment is Windows 11, MATLAB R2020b, with the corresponding error expression for this conformal mapping provided as follows
| $ \begin{equation} E_{cl} = \max \left|\left|F_{c}(Z)\right|-r_{l}\right|, \; \; \; \; \; Z\in C_{l}^*, \; \; \; \; l = 1, \; 2, \dots, \; n, \end{equation} $ | (4.19) |
where $ Z $ is the test point, located at the midpoint between every two neighboring constraints on $ C_{l}^{*} $.
Considering the bounded region defined by the following curves $ C_1:{x^2}/{25^2}+{y^2}/{20^2} = 1, \; k_{1} = 0, \; s_{1} = 0 $; $ C_2:x = 0, \; y\in [7.05, 15] $; $ C_3:{x^2}/{4^2}+y^2 = 1, \; k_{3} = 11.5+7.5i, \; s_{3} = \pi/6 $; $ C_4:{x^2}/{4^2}+y^2 = 1, \; k_{4} = 3.5+6.5i, \; s_{4} = \pi/3 $; $ C_5:{x^2}/{4^2}+y^2 = 1, \; k_{5} = -3.5+6.5i, \; s_{5} = 2\pi/3 $; $ C_6:{x^2}/{4^2}+y^2 = 1, \; k_{6} = -11.5+7.5i, \; s_{6} = 5\pi/6 $; $ C_7:{x^2}/{4^2}+y^2 = 1, \; k_{7} = -11.5-7.5i, \; s_{7} = 7\pi/6 $; $ C_8:{x^2}/{4^2}+y^2 = 1, \; k_{8} = -3.5-6.5i, \; s_{8} = 8\pi/6 $; $ C_9:{x^2}/{4^2}+y^2 = 1, \; k_{9} = -12i, \; s_{9} = 9\pi/6 $; $ C_{10}:{x^2}/{4^2}+y^2 = 1, \; k_{10} = 3.5-6.5i, \; s_{10} = 10\pi/6 $; $ C_{11}:{x^2}/{4^2}+y^2 = 1, \; k_{11} = 11.5-7.5i, \; s_{11} = 11\pi/6 $; $ C_{12}:{x^2}/{4^2}+y^2 = 1, \; k_{12} = 17, \; s_{12} = 0 $; $ C_{13}:{x^2}/{4^2}+y^2 = 1, \; k_{13} = -17, \; s_{13} = 0 $, where $ k_{l} $ and $ s_{l}\; (l = 1, 3, \dots, 13) $ denote the center coordinates and rotation angle of the ellipse, respectively, as shown in Figure 5(a).
In Figure 5(c), the bounded 13-connected region with a rectilinear slit is effectively mapped to the circular slits domain, the fixed point is $ u = 15-10i $, and $ v = 10-10i $. The circular slits domain is an unbounded multiply connected domain comprising 13 circular slits with varying radii as boundary curves, along with the entire $ W $-plane.
As shown in Eq (4.19), Figures 5(d), (e), (f), (g), and (h) illustrate the error curves corresponding to charge point locations shrunk by factors of 0.3, 0.25, 0.2, 0.15, and 0.1 from the boundary curve, respectively. A comparison of Algorithm 1 with the GMRES method reveals that the proposed algorithm demonstrates superior accuracy and stability.
Considering the approximate conformal mapping $ F_{d}(z) $ from the bounded multiply connected regions to the radial slits domain [11,25], the boundary conditions are defined based on the geometric constraints as follows:
| $ \begin{equation} \arg(F_{d}(z)) = r_l, \; \; \; z\in C_{l}^*, \; \; \; l = 1, 2, \dots, n. \end{equation} $ | (4.20) |
The $ r_l $ in the equation represents the angle between each radial slit and the positive horizontal semi-axis. According to the normalization conditions,
| $ \begin{equation} F_{d}(u) = 0, \; \; \; F_{d}(v) = \infty, \; \; \; Res_{z = v}F_{d}(z) = 1, \end{equation} $ | (4.21) |
where $ u $ and $ v $ are distinct fixed points within the region $ \Omega $ ($ u \neq v $).The approximate mapping function is uniquely determined as follows:
| $ \begin{equation} F_{d}(z) = \frac{z-u}{(z-v)(v-u)}\text{e}^{iA(z)}. \end{equation} $ | (4.22) |
Bringing the approximate mapping function (4.22) to the boundary condition (4.20) yields the following:
| $ \begin{equation} \arg(iA(z))-r_l = -\arg\left|\frac{z-u}{(z-v)(v-u)}\right|. \end{equation} $ | (4.23) |
Substituting Eq (2.9) into Eq (4.23) yields the following system of constraint equation:
| $ \begin{equation} \arg\bigg(i\bigg(\sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left|\frac{z_{mk}-\zeta_{lj}}{v-\zeta_{lj}}\right|\bigg)\bigg)-r_l = -\arg\left|\frac{z_{mk}-u}{(z_{mk}-v)(v-u)}\right|. \end{equation} $ | (4.24) |
The parameters requiring estimation include $ Q_{lj} $ and the angle $ r_{l} $, the latter being defined relative to the horizontal positive semi-axis.
The experimental environment is Windows 11, MATLAB R2020b, with the associated error expression for this conformal mapping presented as follows:
| $ \begin{equation} E_{dl} = \max \left|\arg(F_{d}(Z))-r_{l} \right|, \; \; \; \; \; Z\in C_{l}^*, \; \; \; \; l = 1, \; 2, \dots, \; n, \end{equation} $ | (4.25) |
where $ Z $ is the test point, located at the midpoint between each pair of neighboring constraints on $ C_{l}^{*} $.
Considering the bounded region defined by the following curves $ C_1:{x^2}/{25^2}+{y^2}/{20^2} = 1, \; k_{1} = 0, \; s_{1} = 0 $; $ C_2:x = 0, \; y\in [7.05, 15] $; $ C_3:{x^2}/{4^2}+y^2 = 1, \; k_{3} = 11.5+7.5i, \; s_{3} = \pi/6 $; $ C_4:{x^2}/{4^2}+y^2 = 1, \; k_{4} = 3.5+6.5i, \; s_{4} = \pi/3 $; $ C_5:{x^2}/{4^2}+y^2 = 1, \; k_{5} = -3.5+6.5i, \; s_{5} = 2\pi/3 $; $ C_6:{x^2}/{4^2}+y^2 = 1, \; k_{6} = -11.5+7.5i, \; s_{6} = 5\pi/6 $; $ C_7:{x^2}/{4^2}+y^2 = 1, \; k_{7} = -11.5-7.5i, \; s_{7} = 7\pi/6 $; $ C_8:{x^2}/{4^2}+y^2 = 1, \; k_{8} = -3.5-6.5i, \; s_{8} = 8\pi/6 $; $ C_9:{x^2}/{4^2}+y^2 = 1, \; k_{9} = -12i, \; s_{9} = 9\pi/6 $; $ C_{10}:{x^2}/{4^2}+y^2 = 1, \; k_{10} = 3.5-6.5i, \; s_{10} = 10\pi/6 $; $ C_{11}:{x^2}/{4^2}+y^2 = 1, \; k_{11} = 11.5-7.5i, \; s_{11} = 11\pi/6 $; $ C_{12}:{x^2}/{4^2}+y^2 = 1, \; k_{12} = 17, \; s_{12} = 0 $; $ C_{13}:{x^2}/{4^2}+y^2 = 1, \; k_{13} = -17, \; s_{13} = 0 $, where $ k_{l} $ and $ s_{l}\; (l = 1, 3, \dots, 13) $ denote the center coordinates and rotation angle of the ellipse, respectively, as shown in Figure 6(a).
The bounded 13-connected region with a rectilinear slit is effectively mapped to the radial slits domain, the fixed point is $ u = 5-10i $, and $ v = 10-10i $ as shown in Figure 6(c). The radial slits domain is an unbounded multiply connected domain consisting of 13 radial slits radiating from the origin, along with the entire $ W $-plane.
According to Eq (4.25), Figures 6(d), (e), (f), (g), and (h) present the error curves for charge point locations shrunk by factors of 0.3, 0.25, 0.2, 0.15, and 0.1 from the boundary curve. A comparison of Algorithm 1 with the GMRES method reveals that the proposed algorithm outperforms GMRES method in terms of accuracy and stability for this conformal mapping.
Considering the approximate conformal mapping $ F_{e}(z) $ from the bounded multiply connected regions to the parallel slits domain, the boundary conditions defined according to the geometric constraints are as follows [11,25]:
| $ \begin{equation} Re(\text{e}^{i(\frac{\pi}{2}-\theta)}F_{e}(z)) = r_l, \; \; \; z\in C_{l}^*, \; \; \; l = 1, 2, \dots, n. \end{equation} $ | (4.26) |
According to the normalization conditions:
| $ \begin{equation} F_{e}(v) = \infty, \; \; \; \lim\limits_{z = v}(F_{e}(z)-\frac{1}{z-v}) = 0, \end{equation} $ | (4.27) |
where $ v $ is a fixed point within the region $ \Omega $, the approximate mapping function is uniquely determined as follows:
| $ \begin{equation} F_{e}(z) = \frac{1}{z-v}+\text{e}^{i(\theta-\frac{\pi}{2})}A(z). \end{equation} $ | (4.28) |
Substituting the approximate mapping function (4.28) into the boundary condition (4.26) yields the following:
| $ \begin{equation} Re(\text{e}^{i(\frac{\pi}{2}-\theta)}A(z))-r_l = -Re(\text{e}^{i(\frac{\pi}{2}-\theta)}\frac{1}{z-v}). \end{equation} $ | (4.29) |
The approximation $ A(z) $ (2.9) is derived by substituting it into the Eq (4.29), and we obtain a system of constraint equations of dimension $ N_1+ N_2+\dots+N_{n}+n $, as follows:
| $ \begin{equation} Re\bigg(\text{e}^{i\left(\frac{\pi}{2}-\theta\right)}\sum\limits_{l = 1}^n\sum\limits_{j = 1}^{N_l}Q_{lj}\ln\left|\frac{z_{mk}-\zeta_{lj}}{v-\zeta_{lj}}\right|\bigg)-r_{l} = -Re(\text{e}^{i(\frac{\pi}{2}-\theta)}\frac{1}{z_{mk}-v}). \end{equation} $ | (4.30) |
The experimental environment is Windows 11, MATLAB R2020b, with the associated error expression for this conformal mapping provided as follows:
| $ \begin{equation} E_{el} = \max\left| Re(\text{e}^{i(\frac{\pi}{2}-\theta)}F_{e}(Z))-r_{l}\right|, \; \; \; \; \; Z\in C_{l}^*, \; \; \; \; l = 1, \; 2, \dots, \; n, \end{equation} $ | (4.31) |
where $ Z $ is the test point, located at the midpoint between every two neighboring constraints on $ C_{l}^{*} $.
Considering the bounded region defined by the following curves $ C_1:{x^2}/{25^2}+{y^2}/{20^2} = 1, \; k_{1} = 0, \; s_{1} = 0 $; $ C_2:x = 0, \; y\in [7.05, 15] $; $ C_3:{x^2}/{4^2}+y^2 = 1, \; k_{3} = 8.5+5.5i, \; s_{3} = \pi/6 $; $ C_4:{x^2}/{4^2}+y^2 = 1, \; k_{4} = 5.5+8.5i, \; s_{4} = \pi/3 $; $ C_5:{x^2}/{4^2}+y^2 = 1, \; k_{5} = -5.5+8.5i, \; s_{5} = 2\pi/3 $; $ C_6:{x^2}/{4^2}+y^2 = 1, \; k_{6} = -8.5+5.5i, \; s_{6} = 5\pi/6 $; $ C_7:{x^2}/{4^2}+y^2 = 1, \; k_{7} = -8.5-5.5i, \; s_{7} = 7\pi/6 $; $ C_8:{x^2}/{4^2}+y^2 = 1, \; k_{8} = -5.5-8.5i, \; s_{8} = 8\pi/6 $; $ C_9:{x^2}/{4^2}+y^2 = 1, \; k_{9} = -11i, \; s_{9} = 9\pi/6 $; $ C_{10}:{x^2}/{4^2}+y^2 = 1, \; k_{10} = 5.5-8.5i, \; s_{10} = 10\pi/6 $; $ C_{11}:{x^2}/{4^2}+y^2 = 1, \; k_{11} = 8.5-5.5i, \; s_{11} = 11\pi/6 $; $ C_{12}:{x^2}/{4^2}+y^2 = 1, \; k_{12} = 11, \; s_{12} = 0 $; $ C_{13}:{x^2}/{4^2}+y^2 = 1, \; k_{13} = -11, \; s_{13} = 0 $, where $ k_{l} $ and $ s_{l}\; (l = 1, 3, \dots, 13) $ denote the center coordinates and rotation angle of the ellipse, respectively, as shown in Figure 7(a).
In Figure 7(c), the bounded 13-connected region containing a rectilinear slit is accurately transformed into the parallel slits domain, with the fixed point $ v = -10i $. The parallel slits domain is an unbounded multiply connected domain consisting of 13 parallel linear slits $ S_1, S_2, \dots, S_{13} $ and the entire $ W $ plane. Each linear slit makes an angle $ \theta = \pi/3 $ with the positive horizontal coordinate axis.
As shown in Eq (4.31), Figures 7(d), (e), (f), (g), and (h) display the error curves corresponding to the reduction of the charge point location error relative to the boundary curve by factors of 0.3, 0.25, 0.2, 0.15, and 0.1. A comparison of Algorithm 1 with the GMRES method demonstrates that the proposed algorithm offers superior accuracy and stability.
This paper first successfully achieves the conformal mapping of bounded multiply connected regions with a rectilinear slit onto the first category canonical slit domains using the charge simulation method. Second, CGS combined with LU decomposition proves to be highly effective and applicable for the conformal mapping of bounded multiply connected regions to the first category canonical slit domains in the context of the charge simulation method. Finally, a spiral point vortex is simulated in a bounded multiply connected region with a rectilinear slit for bypassing.
This paper focuses on conformal mappings from bounded multiply connected regions with a rectilinear slit to the first category canonical slit domains. However, the conformal mapping of multiply connected regions with a rectilinear slit to other canonical slit domains remains unexplored. Moreover, the CGS with the random projection method remains unexplored in terms of whether it can be applied to conformal mapping based on the charge simulation method. In a forthcoming work, this method is considered for computing conformal mapping of multiply connected domains. These two issues will be addressed in future research efforts.
Dongyi Li: Conceptualization, Formal analysis, Writing-original draft preparation; Yibin Lu: Conceptualization, Methodology, Validation, Reviewing and editing, Funding acquisition. All authors have read and approved the final version of the manuscript for publication.
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Authors are grateful to the reviewers and editors for their suggestions and comments to improvethe manuscript. Authors also thank the financial support from National Natural Science Foundation of China (NSFC) (Grant No. 12461079, 11461037).
The authors declare no conflicts of interest in this paper.
| [1] |
C. Shen, S. Mao, B. Xu, Z. Wang, X. Zhang, S. Yan, et al., Spiral complete coverage path planning based on conformal slit mapping in multi-connected domains, Int. J. Robot. Res., 43 (2024), 2183–2203. http://doi.org/10.1177/02783649241251385 doi: 10.1177/02783649241251385

|
| [2] |
X. D. Gu, W. Zeng, F. Luo, S.-T. Yau, Numerical computation of surface conformal mappings, Comput. Meth. Funct. Th., 11 (2012), 747–787. http://doi.org/10.1007/bf03321885 doi: 10.1007/bf03321885

|
| [3] |
P. Koebe, Abhandlungen zur theorie der konformen abbildung: Ⅳ. Abbildung mehrfach zusammenhängender schlichter bereiche auf schlitzbereiche, Acta Math., 41 (1916), 305–344. http://doi.org/10.1007/bf02422949 doi: 10.1007/bf02422949

|
| [4] |
G. T. Symm, An integral equation method in conformal mapping, Numer. Math., 9 (1966), 250–258. http://doi.org/10.1007/bf02162088 doi: 10.1007/bf02162088

|
| [5] |
D. Crowdy, J. Marshall, Conformal mappings between canonical multiply connected domains, Comput. Meth. Funct. Th., 6 (2006), 59–76. http://doi.org/10.1007/bf03321118 doi: 10.1007/bf03321118

|
| [6] |
K. Amano, A charge simulation method for numerical conformal mapping onto circular and radial slit domains, SIAM J. Sci. Comput., 19 (1998), 1169–1187. http://doi.org/10.1137/s1064827595294307 doi: 10.1137/s1064827595294307

|
| [7] |
K. Amano, D. Okano, Numerical conformal mappings onto the canonical slit domains, Theoretical and Applied Mechanics Japan, 60 (2012), 317–332. https://doi.org/10.11345/nctam.60.317 doi: 10.11345/nctam.60.317

|
| [8] |
K. Amano, D. Okano, A circular and radial slit mapping of unbounded multiply connected domains, JSIAM Lett., 2 (2010), 53–56. http://doi.org/10.14495/jsiaml.2.53 doi: 10.14495/jsiaml.2.53

|
| [9] |
D. Okano, H. Ogata, K. Amano, M. Sugihara, Numerical conformal mappings of bounded multiply connected domains by the charge simulation method, J. Comput. Appl. Math., 159 (2003), 109–117. http://doi.org/10.1016/s0377-0427(03)00572-7 doi: 10.1016/s0377-0427(03)00572-7

|
| [10] |
R. Wegmann, A. H. M. Murid, M. M. S. Nasser, The Riemann–Hilbert problem and the generalized Neumann kernel, J. Comput. Appl. Math., 182 (2005), 388–415. http://doi.org/10.1016/j.cam.2004.12.019 doi: 10.1016/j.cam.2004.12.019

|
| [11] |
M. M. S. Nasser, A boundary integral equation for conformal mapping of bounded multiply connected regions, Comput. Meth. Funct. Th., 9 (2009), 127–143. http://doi.org/10.1007/bf03321718 doi: 10.1007/bf03321718

|
| [12] |
A. W. K. Sangawi, A. H. M. Murid, M. M. S. Nasser, Linear integral equations for conformal mapping of bounded multiply connected regions onto a disk with circular slits, Appl. Math. Comput., 218 (2011), 2055–2068. http://doi.org/10.1016/j.amc.2011.07.018 doi: 10.1016/j.amc.2011.07.018

|
| [13] |
M. M. S. Nasser, Numerical conformal mapping via a boundary integral equation with the generalized Neumann kernel, SIAM J. Sci. Comput., 31 (2009), 1695–1715. http://doi.org/10.1137/070711438 doi: 10.1137/070711438

|
| [14] |
M. M. S. Nasser, Numerical conformal mapping of multiply connected regions onto the second, third and fourth categories of Koebe's canonical slit domains, J. Math. Anal. Appl., 382 (2011), 47–56. http://doi.org/10.1016/j.jmaa.2011.04.030 doi: 10.1016/j.jmaa.2011.04.030

|
| [15] |
M. M. S. Nasser, Numerical conformal mapping of multiply connected regions onto the fifth category of Koebe's canonical slit regions, J. Math. Anal. Appl., 398 (2013), 729–743. http://doi.org/10.1016/j.jmaa.2012.09.020 doi: 10.1016/j.jmaa.2012.09.020

|
| [16] |
Y. Nakatsukasa, O. Sète, L. N. Trefethen, The AAA algorithm for rational approximation, SIAM J. Sci. Comput., 40 (2018), A1494–A1522. https://doi.org/10.1137/16m1106122 doi: 10.1137/16m1106122

|
| [17] |
Y. Nakatsukasa, L. N. Trefethen, An algorithm for real and complex rational minimax approximation, SIAM J. Sci. Comput., 42 (2020), A3157–A3179. https://doi.org/10.1137/19m1281897 doi: 10.1137/19m1281897

|
| [18] |
L. N. Trefethen, Numerical conformal mapping with rational functions, Comput. Meth. Funct. Th., 20 (2020), 369–387. http://doi.org/10.1007/s40315-020-00325-w doi: 10.1007/s40315-020-00325-w

|
| [19] |
D. Okano, H. Ogata, K. Amano, A method of numerical conformal mapping of curved slit domains by the charge simulation method, J. Comput. Appl. Math., 152 (2003), 441–450. http://doi.org/10.1016/s0377-0427(02)00722-7 doi: 10.1016/s0377-0427(02)00722-7

|
| [20] |
H. A. Van der Vorst, Bi-CGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems, SIAM J. Sci. Stat. Comput., 13 (1992), 631–644. http://doi.org/10.1137/0913035 doi: 10.1137/0913035

|
| [21] |
P. Sonneveld, CGS, a fast Lanczos-type solver for nonsymmetric linear systems, SIAM J. Sci. Stat. Comput., 10 (1989), 36–52. http://doi.org/10.1137/0910004 doi: 10.1137/0910004

|
| [22] |
Z. Yang, Adaptive stochastic conjugate gradient for machine learning, Expert Syst. Appl., 206 (2022), 117719. https://doi.org/10.1016/j.eswa.2022.117719 doi: 10.1016/j.eswa.2022.117719

|
| [23] |
Z. Chen, W. Wang, X. Kong, L. Deng, Moving force identification based on the nonnegative flexible conjugate gradient least square method and experimental verification, J. Sound Vib., 572 (2024), 118177. https://doi.org/10.1016/j.jsv.2023.118177 doi: 10.1016/j.jsv.2023.118177

|
| [24] |
K. Murota, Comparison of conventional and "invariant" schemes of fundamental solutions method for annular domains, Japan J. Indust. Appl. Math., 12 (1995), 61–85. https://doi.org/10.1007/bf03167382 doi: 10.1007/bf03167382

|
| [25] | Z. Nehari, Conformal mapping, Dover Publications, 2012. |
| [26] |
J. Lin, V. Cevher, Kernel conjugate gradient methods with random projections, Appl. Comput. Harmon. Anal., 55 (2021), 223–269. https://doi.org/10.1016/j.acha.2021.05.004 doi: 10.1016/j.acha.2021.05.004

|
| [27] | G. K. Batchelor, An introduction to fluid dynamics, Cambridge university press, 2000. https://doi.org/10.1017/CBO9780511800955 |
| [28] | L. M. Milne-Thomson, Theoretical hydrodynamics, Dover Publications, 2011. |
| [29] |
K. Amano, A charge simulation method for the numerical conformal mapping of interior, exterior and doubly-connected domains, J. Comput. Appl. Math., 53 (1994), 353–370. https://doi.org/10.1016/0377-0427(94)90063-9 doi: 10.1016/0377-0427(94)90063-9

|