A novel computational fractional modeling approach for the global dynamics and optimal control strategies in mitigating Marburg infection

1.   Introduction

Marburg virus disease (MVD) is a viral infection caused by a member of the Filoviridae family ^[1]. It is extremely fatal, with a mortality rate of 90% among those affected. The virus's incubation period spans 3 to 9 days, with symptoms usually manifesting between 5 and 10 days post-infection. Initial symptoms include fever, joint and muscle pain and headache. As the illness progresses, symptoms can worsen and may include nausea, vomiting, bloody diarrhea, eye redness, chest pain, skin rash, sore throat, cough, stomach pain, and significant weight loss. The transmission of the virus may occurs through bodily fluids such as sweat, saliva, and blood. Although the virus originated in African bats, its first outbreak occurred in the German cities of Marburg and Frankfurt. It was linked to the exposure of German workers to monkey tissues within industrial settings. In these outbreaks, a total of 31 people became infected, and seven of them died. Subsequently, the disease emerged in several African countries at different times, including Uganda, Angola, the Congo, and Tanzania. Recently, in March 2023, officials from the Ministry of Health in Equatorial Guinea announced that 13 people had contracted MVD, resulting in nine deaths since its emergence in the country. Consequently, the early control of the spread of MVD before it escalates into an epidemic has become a critical issue. In the absence of effective treatment or a vaccine for MVD ^[1], developing optimal quarantine strategies in the affected countries that may help to limit its new outbreaks and further incidence.

The application of mathematical models is extremely useful in the exploration of various dynamical aspects of a disease outbreak. These models have proven to be valuable tools in the study of various dynamical aspects and control of different diseases. The primary reason for the efficacy of models based on fractional derivatives lies in the non-locality property that is inherent in fractional operators, also known as the memory effect. This feature is particularly important in exploration of biological systems where the state at a given moment is influenced by its configuration at preceding times. Moreover, differential operators with non-integer order plays a key role in the minimization of errors that arise from neglected parameters. Consequently, the application of fractional calculus-based models can be found in various fields of science, including biology ^{[2,3,4,5,6,7]}, medicine ^[8], physics ^[9], chemistry ^[10,11], engineering ^[12,13], and psychological research ^[14].

Optimized control theory is a significant and successful mathematical approach that can be employed to make decisions regarding the development of optimal intervention strategies for infectious diseases ^[15]. Various mathematical models have been developed to present an optimal control system for the eradication of a disease outbreak. The well-established Pontryagin's maximum principle is employable in the context of both ordinary and fractional differential equations ^[16]. Ayele et al. conducted an optimal control study in Ethiopia, examining a mathematical model of HIV/AIDS ^[17]. Alrabaiah et al. analyzed an optimal control model of the hepatitis B virus ^[18]. In ^[19], the authors applied an optimal control theory to a fractional model of coronavirus transmission in Algeria.

To investigate the dynamics of MVD transmission, various studies have been presented in ^[20,21]. In ^[20], the authors applied four preventive controls related to prevention, screening, continuous vaccination, and treatment to a SIERDVT model of MVD. They found that implementing the four controls simultaneously resulted in greater effectiveness in mitigating the spread of MVD. However, due to a lack of real data and the utilization of classical derivatives in formulation of the mathematical model in this research, the results may be less accurate than those obtained by using of fractional operators as demonstrated in ^[21]. However, it is worth noting that in ^[21], there is no preventive control for MVD, which makes this study less effective in terms of preventive measures.

Based on the discussion presented above, we designed this study to explore the dynamics of MVD transmission in both humans and animals. Subsequently, we will delve into the application of fractional optimal control strategies to mitigate its spread. In this study, we will introduce a novel fractional model of MDV transmission, employing the Caputo derivative. We divided both the human population and the animal population into five and three groups respectively named as the susceptible class $S(t)$, exposed class $E(t)$, quarantine class $Q(t)$, infectious individuals $I(t)$, recovered individuals $R(t)$, susceptible animals $S_b(t)$, the exposed animal host $E_b(t)$, and $I_b(t)$. To establish effective control strategies, we will first discuss the sensitivity of the reproduction number for MDV disease transmission in order to determine the most critical parameters that have the greatest impact on disease dynamics. Based on this analysis, we will then determine the appropriate controls to reduce the spread of MVD in the community.

The rest of this paper is arranged as follows. In Section 2, we will review the fundamental definitions of fractional calculus. Section 3 introduces the mathematical model for MVD. In Section 4, we will present a theoretical analysis of the fractional MVD model, including a discussion on the existence, positivity, and uniqueness of the fractional model's solution, as well as the local and global stability of the equilibria. Next, we will present numerical simulations to approximate solutions to our fractional system in Section 5. Following this, in Section 6, we formulate an optimal control problem that is subject to our fractional model characterize the optimal controls and derive the necessary optimal system employing Pontryagin's maximum principle. Concluding remarks are summarized in Section 7.

2.   Basics on fractional calculus

Some fundamental definitions and necessary results of fractional calculus are provided in this section.

Definition 2.1. ^[22] Riemann-Liouville fractional integration of the function $\mathsf{F}:\mathbb{R^+}\rightarrow \mathbb{R}$ with order $\gamma$ is defined as follows

Definition 2.2. ^[22] The non-integer case Caputo type operator of a function $\mathsf{F}:\mathbb{R^+}\rightarrow \mathbb{R}$ with $\gamma$ as the order is given by

where, $m = [\gamma] +1, \, \, m\in \mathbb{N}$, with $[\gamma]$ as the integer part of $\gamma$.

Let $\mathsf{F}, \mathsf{G}:\mathbb{R^+}\rightarrow \mathbb{R}$ be such that $^CD_{0, t}^{\gamma} \mathsf{F}(x)$ and $^CD_{0, t}^{\gamma} \mathsf{G}(x)$, exist and $q_1, \; \; q_2, \; \; q_3$ be three real constants; then, the following properties hold:

●

● If $\gamma$ is such that $0 < \gamma < 1$, then:

●

● $^CD_{0, t}^{\gamma} q_1 = 0$.

Theorem 2.1. ^[22] The Caputo fractional differential operator's Laplace transform $\gamma$ ($\gamma > 0$), is presented as follows

3.   Formulation of the fractional MVD model

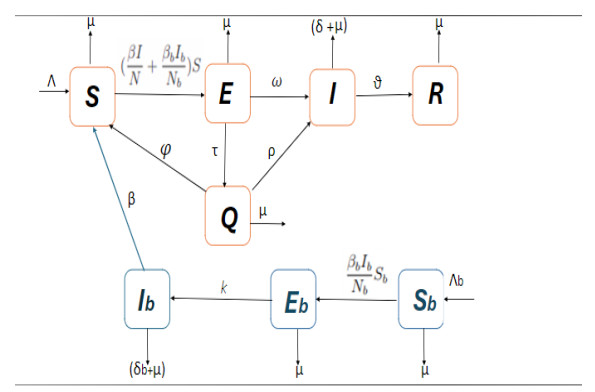
In this section we introduce a fractional model that describes the transmission of MVD among humans and Egyptian fruit bats (the animal host), employing a Caputo fractional derivative. The model is formulated by following the study outlined in ^[23], where the human population and the animal population are divided into five and three compartments, respectively. These compartments include the following: $S(t)$, denoting the total susceptible class among humans; $E(t),$ representing the exposed class among humans; $Q(t)$, the quarantine compartment among humans; $I(t),$ representing the density of the infectious class; and $R(t)$ indicating the number of recovered individuals among humans. For the animal population, we have the following: susceptible animals represented by $S_b(t)$, the exposed animal host represented by $E_b(t)$, and $I_b(t),$ which is the infectious animal host compartment. As illustrated in Figure 1, $\Lambda$ represents the recruitment rate for the human population. The probabilities of MVD transmission by humans and bats are denoted by $\beta$ and $\beta_b$ respectively. Exposed humans become infected at a rate of $\omega$ and are quarantined at a rate of $\tau$. At a rate of $\varphi$ exposed individuals return to the susceptible compartment. Conversely, quarantined humans become infected at a rate of $\rho$. The disease induced death rates in humans and bats are represented by $\delta$ and $\delta_b$ respectively. Finally, we indicate the rate of recovery from MVD by $\vartheta$ and the natural death rate by $\mu$ in all classes. To construct the fractional model of MVD, we use the Caputo fractional operator ${^C}D^{\gamma}$, where $\gamma$ represents the order. We introduce an auxiliary parameter $\sigma$ in the model. This procedure allows us to ensure that both sides of the resulting equation have the same dimension ^[24]. The MVD fractional model is then defined as follows:

The initial conditions are listed below:

4.   Theoretical analysis of the fractional MVD model

Let $C([0, T], \mathbb{R}^8)$ represent a Banach space consisting of continuous functions with the corresponding norm denoted by $||.||$.

4.1.   Existence and uniqueness of solution

Using fixed point theory, along with the Picard-Lindelof method, the existence and uniqueness of the aforementioned fractional model's solution will be discussed in this section. First, we can write the system (3.1)–(3.2) as the following initial value problem (IVP):

and

defines a vector of state variables. Moreover,

Further, express IVP (4.1) as an integral equation by applying the non-integer integral defined in (2.1) on both sides of (4.1).

Using the definition of $I_{0, t}^{\gamma}$, and (4.3) we obtain:

Alternatively,

where $X(t)$ and $F(y, X(y))$ have been defined in (4.2) and (4.3), respectively. Next, we state the operator as follows:

such that

Therefore, the integral equation (4.6) is equivalent to $X = G(X)$ and fixed points of $G,$ are the solutions of IVP (4.1). To get a fixed point of $G$ by using Picard iteration, we construct the following equations, which represent the Picard iterations according to (4.5) such that

To ensure the unique solution existence of IVP (4.1), we must prove that $G$ is a contraction operator.

First, we need to establish the following lemma:

Lemma 4.1. $F(t, X(t)),$ as presented in (4.3) fulfill the Lipschitz criteria that is,

such that

Proof. For $f_1(t, S(t))$ we have

such that

Using the same procedure, we derive the subsequent results for the remaining equations:

Let

Therefore, we get:

□

Theorem 4.1. Suppose that (4.9) holds; then, the system given by (3.1)–(3.2) has a unique solution if

Proof. We know that the solution of the system given by (3.1)–(3.2) is $X(t) = G (X(t))$, where $G$ denotes the corresponding Picard operator defined in (4.7). Moreover, we have:

If $\frac{ \Phi t^{\gamma}}{\Gamma(\gamma +1)} < 1$, then $G$ is a contraction mapping; thus, the system given by (3.1)–(3.2) possesses a unique solution. □

4.2.   Nonnegative solution

We define the next two sets:

Lemma 4.2. The solutions of the system given by (3.1)–(3.2) are all positive for $t\geq 0$ and belongs to $\mathcal{H} \bigcup \mathcal{R}$.

Proof. We proceed with the system's first equation given in (3.1)–(3.2) as follows:

Solving the above inequality, we get

Since $S_0 > 0$ and $0 \leq E_{\gamma}(-\sigma^{(1-\gamma)}(\mu +\beta + \beta_b) t^{\gamma}) \leq 1$, then $S(t) \geq 0, \, \, \, \, \forall t \geq 0$. It is the same for the other equations this, we have

By following the same arguments as above, we obtain that $E(t) \geq 0, Q(t) \geq 0, I(t) \geq 0, R(t) \geq 0, S_b(t) \geq 0, E_b(t)\; and\; \geq 0, I_b(t) \geq 0$. □

4.3.   Biologically feasible region of the solution

Lemma 4.3. The feasible domain for solutions of the fractional problem given by (3.1)–(3.2) is $K = K_h \bigcup K_b,$ and it exists such that

It is bounded, invariant set, where $N_h$ is the humans population ($N_h(t) = S(t)+E(t)+Q(t)+I(t)+R(t)$), and $N_b$ is the Egyptian fruit bats population ($N_b(t) = S_b(t)+I_b(t)+E_b(t)$).

Proof. By adding the first five equations of the system given by (3.1)–(3.2), we get

In the absence of MVD in a population ($I = 0$), we have

Solving the above inequality we obtain

such that $E_{\gamma}, E_{\gamma, \gamma}$ are the Mittag-Leffler functions, respectively defined as follows:

We get that $\lim _{t \rightarrow \infty} N_h(t) \leq \frac{\Lambda}{\mu}$. In the same way we get

Thus, $\lim _{t \rightarrow \infty} N_b(t) \leq \frac{\Lambda_b}{\mu}$. □

4.4.   Stability results of the MVD fractional model

First, we determine the system's equilibrium points by setting

4.4.1.   Disease-free equilibrium

The MVD model has two equilibrium points. The disease-free equilibrium (DFE) point can be obtained as follows:

4.4.2.   Endemic equilibrium

The endemic equilibrium (EE) expresses the situation in which the disease is prevalent among the members of the community in the MVD model, and it is given by ^[23]:

such that

where,

4.4.3.   The basic reproduction number

In view of ^[25], the basic reproduction number of the model of MVD i.e., $R_0 = \rho(F V^{-1})$ such that

and

After calculation, we obtain

4.5.   Local and global stability of DFE and EE

Conditions of the local and global stability of DFE and EEs can be proven by using monotone matrices and dynamical systems theories (see ^[26]). From ^[23], we recall the following stability results of the proposed model:

Theorem 4.2. The DFE $\mathcal{E}_0$ is asymptotically stable in the local case whenever $R_0 < 1$. Global asymptotic stability when, $R_0 \leq 1$.

Lemma 4.4. ^[27] If the real function $\mathcal{K}(t)$ is continuous as well as derivable, then for every $t \geq t_0$, we have

Lemma 4.5. ^[27] If the real positive function $\mathcal{K}(t)$ is continuous and derivable then for every $t \geq t_0$, we have

Proof. We use the following function to evaluate the Lyapunov stability of the MVD model in fractional case

This function exists such that

where

In view of Lemma 4.4,

Since $E, Q, I, E_b, I_b \in K$, then

and

Further, we get

At the equilibrium, we obtain

Moreover, we know that $S\leq D_1$; it follows that $\frac{S}{\beta_b}\leq \frac{D_1}{\beta_b}$. Then using the above expressions we get

Because $\frac{S}{N}\leq 1$ and $\frac{S_b}{N_b}\leq 1$; it follows that $\beta I (\frac{S}{N}-1)\leq 0$ and $\beta_b I_b (\frac{S_b}{N_b}-1) \leq 0$.

Then if $R_0 \leq 1$, we get that ${\sigma^{\gamma-1}} {^C}D^{\gamma}\mathcal{V}(t) \leq 0$. Thus, using Theorem 1 in ^[28], it is proven that the DFE of (3.1) is asymptotically globally stable if $R_0 \leq 1$. □

Theorem 4.3. The EE $\mathcal{E}_e$ is asymptotically globally stable in K if $R_0\geq 1$.

Proof. Initially, we normalize the total number of humans and animals to be equal to 1 (i.e., $N_h = N_b = 1$).

A Lyapunov function is considered as follows to prove the desired result

Using the result in Lemma 4.5, we obtain

At the EE, we can get

Introducing (4.14)–(4.20) into above, with some calculation we get

Since the arithmetic mean exceeds the geometric mean ^[27], then

In addition if $(\frac{I_b E^* S}{I_b^* I^* E S^*}-\frac{I}{I^* I_b^*}-\frac{E^* I S}{E I^* S^* I_b}-\frac{I_b S_b E_b^*}{I_b^*S_b^* E_b I^*})$, is negative, then ${\sigma^{\gamma-1}} {^C}D^{\gamma} \mathcal{L}(t) \leq 0$. Furthermore, we have that ${\sigma^{\gamma-1}} {\sigma^{\gamma-1}} {^C}D^{\gamma} \mathcal{L}(\mathcal{E}_e) = 0$ $\Leftrightarrow$ $(S(t), E(t), Q(t), I(t), R(t), S_b(t), E_b(t), I_b(t)) = \mathcal{E}_e$. Thus, the maximum invariant set for

is $\mathcal{E}_e$. It follows that the EE $\mathcal{E}_e$ is asymptotically globally stable if $R_0 > 1$. □

5.   Simulation of the MVD Caputo case model

The dynamics of the individuals in the susceptible, exposed, infected, recovered and quarantined groups over time are illustrated in Figure 2. Meanwhile, the dynamics of the bat population are illustrated in Figure 3. The numerical scheme presented in Appendix A has been employed to compute approximate solutions for the model (3.1). Parameter values and initial conditions estimated from literature has been adopted as provided in Table 1. The auxiliary parameter $\sigma$ was assumed to be $\sigma = 0.99$.

Figure 2 demonstrates the behavior of the susceptible, exposed, infected, quarantined, and recovered subclasses showing that they converge to the steady state for $\gamma = 1, \; 0.95, \; 0.90, \; 0.85$. Figure 3 depicts the stability of the bat population classes for four values of $\gamma$. When varying the values of the fractional order $\gamma$, it was observed that the rates of decay and growth in the solution curves are slower for smaller values compared to larger values. This observation highlights the significant influence of the memory index in fractional epidemiological models. Furthermore, upon comparing the behaviors of the curves between the classical case $(\gamma = 1)$ and fractional case, it becomes evident that in the fractional case, the model's solution exhibits stability over a shorter time period. This consistency with the theoretical findings discussed in the stability section underscores the accuracy and realism of the fractional operators.

6.   Fractional optimization of MVD model

The objective of this section is to identify effective control strategies for the MDV disease and it is aimed at minimizing the class of susceptible, exposed, and infected human individuals. The most critical parameters that have a significant influence on disease dynamics, particularly those affecting $R_0$ values need to be determined. To achieve this, we need to evaluate the sensitivity indices for $R_0$ of disease transmission.

6.1.   Sensitivity analysis of $R_0$

The sensitivity analysis can be utilized to calculate the respective shift in the model's variables, as caused by a specific parameter. Sensitivity analysis is used to measure how much $R_0$ changes relative to changes in the model's embedded parameters. It is defined by the following formula ^[18]:

The expressions of normalized sensitivity indices are as follows:

Next, using the estimated parameter values presented in ^[23], we depict the table and the graph of sensitivity results below, which show the values for $R_0$'s sensitivity indices as compared to the parameter system.

In Table 2 and Figure 4, the model's parameters with positive indices indicate an enhancement in the value of $R_0$, showing that MVD would increase in the population, while parameters with negative indices indicate that the infection would decrease in the population. On the basis of the sensitivity indices shown in Table 2, the most crucial parameters on the spread of MVD include the probability of MVD transmission by humans ($\beta$), which contributes to an increase in the spread of MVD in population. As for the parameters that participate in prevalence reduction, they are $\tau, \; \; \vartheta,$ and $\omega$. Moreover, it is evident that the sensitivity index of the quarantine rate $(\tau)$ is greater than the indices of $\vartheta$ and $\omega$. Therefore, for more effectively eliminate the virus, we need to adopt an optimal strategy to enhance the quarantine rate $(\tau)$ and reduce the virus transmission rate $(\beta)$.

6.2.   Formulation of fractional optimal control

In this section, we employ the aforementioned facts to establish the following two control schemes.

● $\Psi_1$: represents the control variable for prevention of MVD transmission between humans by regularly washing hands with soap or a hand sanitizer that contains alcohol, wearing protective clothing when coming into contact with sick people, and not touching the body of a deceased person. Moreover, avoid locations where Egyptian fruit bats congregate.

● $\Psi_2$: represents the control variable for an increase in the rate at which exposed humans get quarantined.

Further, to explore the impact of the above control measures we extended the MVD fractional model (3.1) by incorporating two Lebesgue measurable functions of time $t$ $(\Psi_1(t) \Psi_2(t)$. The formulation of the system given by (3.1) with control functions denoted by $\Psi_j(t) (j = 1, 2)$ is as follows:

with the initial conditions as defined in (3.2). The objective functional is given by:

where $q_i, i = \overline{1, 3}$ denotes positive balancing coefficients, $\rho_i, i = \overline{1, 2}$, denotes the effort used to curtail the transmission of the MVD $\overline{\Psi} = (\Psi_1, \Psi_2)$, and $T$ is the final time. The objective of the optimal control problem under study is to minimize the objective functional by finding a control $\overline{\Psi}$. In other words, the goal is to determine the optimal control pairs $(\overline{U}, \overline{\Psi^{*}})$ such that

$\mathfrak{A}$ is the set of controls, and is defined as follows:

This set is bounded closed by construction.

6.2.1.   Existence and optimality criteria

The system (3.1) is written in the classical form as follows:

where $U = (S(t), E(t), Q(t), I(t), R(t), S_b(t), E_b(t), I_b(t))$ denotes the state variables and $\overline{\Psi} (t) = (\Psi_1(t), \Psi_2(t))$ presents the control function.

Further,

The following conditions must be proved to guarantee the existence of the two optimal controls ^[19].

$(1)$ The control problem solutions' set is non-empty:

It is easy to see that there exists $\Psi_1 = 0$ and $\Psi_2 = 1$ which define the controls in $\mathfrak{A}$, and $\overline{U} = (S, E, Q, I, R, S_b, E_b, I_b)$ is a solution that aligns with controls $\Psi_1 = 0$ an d $\Psi_2 = 1$. So, this condition has been satisfied.

$(2)$ The set of admissible controls is closed, bounded, and convex. This condition is guaranteed by definition of $\mathfrak{A}$.

Remark 6.1. From Theorem 4.1 and Lemma 4.3, the system (6.1) has at least one solution which is bounded in $K$.

$(3)$ The function $K(t, u(t)) + L(t, u(t))\overline{\Psi}$ is bounded by a linear function in the state and control variables. The matrix $K$ can be written as follows:

Then

We know that $\Lambda \leq S$ and $\Lambda_b \leq S_b$; then, we get

Similarly, we obtain

From (6.8) and (6.9) it is obvious that $K(t, u(t)) + L(t, u(t))\overline{\Psi}$ is bound by a linear function in the state and control variables as given below

where

$(4)$ The convexity of $Z(t, \overline{U}, \overline{\Psi}) = q_1 S +q_2 E +q_3 Q+q_4 I+ \frac{\rho_1}{2} \Psi_1^{2} +\frac{\rho_2}{2} \Psi_2^{2}$.

Lemma 6.1. The functional $Z(t, \overline{U}, \overline{\Psi})$, is convex.

Proof. Let

be the Hessian matrix of the functional $Z(t, \overline{U}, \overline{\Psi})$. Clearly, it is positive definite in $\mathfrak{A}$, so $Z(t, \overline{U}, \overline{\Psi})$ and also it is strictly convex in $\mathfrak{A}$. □

Consequently, from conditions (1)–(4) and Remark (6.1), there exists $\overline{\Psi^{*}} = (\Psi_1^{*}, \Psi_2^{*})$ and a corresponding solution $\overline{U^*} = (S^*, E^*, Q^*, I^*, R^*, S_b^*, E_b^*, I_b^*)$ that minimize $J(\overline{\Psi})$ on $\mathfrak{A}$.

6.2.2.   Necessary condition for optimality

We rely on Pontryagin's theorem ^[33] to get the desired condition for the optimal control system. First, we transform the system (6.1) into a pointwise problem that minimizes a Hamiltonian function $\mathbb{H}$ with respect to $(\Psi_1, \Psi_2)$. The Hamiltonian function is as follows:

and it exists that $\Xi = (\lambda_S, \lambda_E, \lambda_Q, \lambda_I, \lambda_R, \lambda_{S_b}, \lambda_{E_b}, \lambda_{I_b})$ represents the adjoint variables s they are related to their respective state variables.

Theorem 6.1. Suppose that $\Psi_i^{*}\; (i = 1, 2)$ denotes the optimal controls and $S^*, E^*, Q^*, I^*, R^*, S_{b}^*, E_b^*, I_b^*$ represent the solution of the state variables of the system (6.1) which minimize the objective functional $J(\overline{\Psi})$ across $\mathfrak{A}$; then, there exists the adjoint variables $\lambda_S, \lambda_E, \lambda_Q, \lambda_I, \lambda_R, \lambda_{S_b}, \lambda_{E_b}, \lambda_{I_b},$ satisfying

with the corresponding transversality conditions $\lambda_k (T) = 0$ and

Proof. The pontryagin's maximum principal gives the following results:

First, we have

Next, utilizing the condition $\frac{\partial}{\partial \Psi_i} \mathbb{H}(t, \Psi_i^{*}, \lambda_i) = 0, \; \; i = \overline{1, 2}$ we obtain

Then, we get

Finally, we can take

6.3.   Simulation of the optimal control problem

This section presents the numerical simulation of the MVD fractional model with and without controls. We have used the Newton numerical scheme for (A) to perform the simulation. The values of parameters are listed in Table 1. Moreover the weight and the balancing coefficients were considered as follows: $\rho_1 = \rho_2 = 0.00001$, and $q_i = 1 \, \, \, i = \overline{1, 3}$ respectively. We executed the simulation for two values of $\gamma$ i.e., the classical case $\gamma = 1.00$ and the fractional case $\gamma = 0.80$. Numerical results for $\gamma = 0.80$ and $\gamma = 1.00$ are illustrated in Figures 5 and 6 respectively. In the presence of optimal control, a notable and evident decrease in the number of exposed individuals is observed, resulting in corresponding decreases in the infected and quarantined populations. It is observed that the decay and growth rates are faster for the classical order $(\gamma = 1.00)$ than the fractional order $(\gamma = 8.00)$. Thus, the suggested control measures can be effectively used for the mitigation of MVD outbreaks.

7.   Conclusions

We introduced a novel computational fractional modeling approach to analyze the global dynamics and optimal control strategies for MVD infection mitigation. In this context, we developed a fractional order model of MVD transmission by using the Caputo fractional operator and performed some theoretical and numerical analysis. The existence, uniqueness and positivity of the solution with a detailed discussion on the local and global stability have been provided comprehensively. The theoretical findings revealed that the DFE is asymptotically locally stable if $R_0 < 1$, and it is asymptotically globally stable if $R_0 \leq 1$. To examine the model numerically, we established numerical schemes by using two-step Newton polynomial approximation. The numerical simulation of the fractional model for MVD confirmed the impact of the fractional operator. We observed that the decay and growth rates in the solution curves are slower for smaller values of the $\gamma$ than for the larger values. Furthermore, we observed that in the fractional case, stability is maintained in the solution curves for the model. In the pursuit of mitigating NVD, we initially evaluated the sensitivity indices, revealing that certain parameters significantly influence MVD transmission, notably the effective contact rate $\beta$ and the rate at which exposed individuals are quarantined $\tau$. Building upon these insights, we developed a fractional optimal control model by introducing two time-dependent control measures, $\Psi_1$ and $\Psi_2$, corresponding to prevention and quarantine respectively. Utilizing the Pontryagin maximum principle, we derived a solution to the optimal control problem. Finally, we numerically simulated the MVD transmission model with and without control by considering both fractional and classical orders. The numerical findings validated the efficacy of the proposed optimal control strategies. The results of this study will be helpful in prevention the spread of MVD.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this study.

Acknowledgments

Researchers Supporting Project number (RSPD2024R576), King Saud University, Riyadh, Saudi Arabia. Further, Muhammad Bilal Riaz is thankful to the Ministry of Education, Youth and Sports of the Czech Republic for their support through the e-INFRA CZ (ID:90254).

Authors contribution statement

Meroua Medjoudja, Muhammad Bilal Riaz and Mohammed El hadi Mezabia, conceptualized the main problem, wrote the original manuscript, and derived theoretical and simulation results. Ahmed Boudaoui and Saif Ullah, reviewed all of the mathematical results and wrote the manuscript. Fuad A. Awwad performed the statistical analysis, validated all of the results and performed the quantitative analysis. Muhammad Bilal Riaz also participated in the funding acquisition and supervision.

Conflict of interest

The authors declare no conflict of interest.

Appendix A.   Scheme for the fractional MVD model

Here, we present detail procedure of Newton polynomial two-step approach that was used to formulate numerical schemes for the proposed fractional model that describes the dynamics of MVD.

We transform the above fractional problem to be as follows

At the point $t_{n+1}$, we proceed as follows:

This can be written in the form of the following system

Applying of two-steps Newton polynomial approximation, we have

After performing some manipulations, we derive the numerical scheme for the model describing the epidemic MVD as follows:

Appendix B.   The optimality system

The optimality system consists of the state system (6.1) with its initial conditions, together with the adjoint system (6.12) with the respective transversality conditions. This can be expressed as follows: