On perturbation of aesthetic curves

1.   Introduction

The aesthetic aspect is very important in industrial production design. The notion of an aesthetic curve plays an essential role in this process. Farin defined the notion of aesthetic curve by considering that its curvature is monotone with respect to the parameter of the curve ^[7,8]. A family of curves with this property are log-aesthetic curves and their generalizations. Harada and Yoshimoto studied the planer curves having a monotone curvature by using the Logarithmic Distribution of Curvature (LDC) ^[9,10]. Another approach of aesthetic curves was proposed in ^[13] by Kanaya by using Logarithmic Curvature Histograms (LCH) instead LDC. For further information on LCH see also ^[14,15]. Gobithaasan et al. proposed to use the Logarithmic Curvature Graph's (LCG) Gradient for the definition of aesthetic curves in ^[12]. The authors of ^[12] obtained also a classification of aesthetic curves taking into consideration the sign of LCH (see also ^[11,16]). In the definition of an aesthetic form the Golden Ratio (GR) is also frequently used. In ^[5,6] the authors propose some new aesthetic standards based on GR and its generalization.

The aesthetic perception varies from one individual to another even if there are unanimously accepted criteria. For a physiological point of view concerning visual processing we refer the reader to ^[1,2]. For this reason, in ^[4] the authors proposed the notion of approximate aesthetic curves. A curve for which the curvature satisfies approximately the equation of an aesthetic curve is called an approximate aesthetic curve. In ^[4], it is studied the behavior of the solutions of the equation of an aesthetic curve under various perturbations. If small perturbations of an equation produce small perturbations of its solutions then we say that the equation is stable in Ulam sense.

The problem of Ulam stability was introduced in 1940 in the field of functional equations by S.M. Ulam. Nowadays, results on Ulam stability for different types of equations and operators have been obtained. For a comprehensive approach to Ulam stability we refer the reader to the book ^[3] and the references therein. In this paper, we study the behavior of the equation of a neutral curve by perturbations to equations for convergent and divergent curves and we obtain some results on its Ulam stability.

The stability of an equation or a dynamic system is very important in practical problems because small deviations from the mathematical model caused, for example, by measurement errors or small changes occurring when adapting the model to a practical situation will not have a strong effect on the solution. For this reason, the model realized in practice corresponds to the one provided by the mathematical equations that describe it. Stability theory offers priceless information about the answer of a system of an equation to small perturbations. From an aesthetic point of view, the problem of stability is even more complex because the perception of aesthetics is one of the most interesting topics for philosophers, scientists, and psychologists; see for instance ^[1,2]. Except for the mathematical behavior, there is also interesting to see how aesthetics is represented in objects and how a specific curve or shape of an object could convey the feelings we had during perception. Despite the vast number of studies on this topic in philosophy and science, there are no clear boundaries to decide on the aesthetics of a curve or shape, we do not know all the conditions under which aesthetic perception holds. Having this background in mind, we consider it important to talk about approximate aesthetic curves and to study, as well the stability of equations of aesthetic curves with respect to small perturbations.

The outline of the paper is as follows. In the introduction, we have presented a short historical background of the problem of aesthetic curves. In section 2 we provide the ingredients and the general setup for the study, we give some definitions and the preliminary notions and results necessary to make this paper self-sufficient. The third section is devoted to our main results, namely, we obtain some stability results (in Ulam sense) for the case of the equation of neutral curves perturbed to the equation of convergent curves as well as for the equation of neutral curves of finite length perturbed to the equation of divergent curves. In Theorem 4 we prove that the equation of neutral curves of infinite length is unstable with respect to perturbation to divergent curves. The last section contains some conclusions and remarks.

2.   Aesthetic curves

Consider a curve $(C)$ given by its natural parametric equation

where $S$ is the total length of the curve and $r$ is a point of coordinates $x, y$ on $(C).$ If the curve $(C)$ has infinite length then $s\in[0, \infty).$

The Logarithmic Curvature Graph (LCG) Gradient of the curve $(C)$ is given by the relation

where $K$ is the curvature of $(C).$ We suppose $K$ is a non-constant function. The notion of aesthetic curve is defined as follows (see ^[12]).

Definition 1. A curve is said to be an aesthetic curve if its LCG gradient is either constant or the gradient is represented by a straight line with a nonzero slope.

Taking into account the sign of the LCG gradient we obtain the following classification:

Definition 2. An aesthetic curve is called:

1) Convergent- if the LCG gradient is positive;

2) Divergent- if the LCG gradient is negative;

3) Neutral- if the LCG gradient is zero.

A characterization of convergent, divergent, and neutral curves is obtained in ^[4], based on the monotonicity of $K$.

Theorem 1. Let $(C)$ be a curve given by the equation (2.1). Then:

1. $(C)$ is convergent if and, only if $|K|$ is strictly decreasing;

2. $(C)$ is divergent if and only if $|K|$ is strictly increasing;

3. $(C)$ is neutral if and only if there exist $C_1, C_2\in\mathbb{R}$ such that

Remark 1. Remark that the class of convergent curves (divergent curves) and the class of neutral curves are not disjoint classes. Consequently, the neutral curves with curvature given by $K(s) = C_2e^{C_1s}$ with $C_2 < 0$ $(C_2 > 0)$ are as well convergent (divergent) curves.

For a curve of given curvature, its representation can be obtained from the following relations (see ^[4])

where $\theta(s),$ $0\leq s\leq S,$ is the measure in radians of the angle from the positive axis $x$ to the unit tangent vector to the curve.

On the other hand, if the LCG gradient of the curve is known then its curvature can be explicitly obtained, see Theorem 4, ^[4]. For the reader's convenience, we present this result in the following.

Theorem 2. Let $(C)$ be a curve of gradient $\lambda$ with $K'(0)\neq0$. Then its curvature $K$ is given by the relation:

where $C_1,$ $C_2$ are real constants. Moreover $C_1 = \frac{K(0)}{K'(0)},$ $C_2 = K(0).$

3.   Perturbation of neutral curves

In ^[4] is defined the notion of approximate aesthetic curves. This definition is introduced taking into account that the aesthetic value of a curve increases when the LCG gradient approximates to a straight line (as stated in ^[12]). A curve with LCG gradient close to a straight line is called perturbation of an aesthetic curve. For the case of neutral curves (which are aesthetic curves since their gradient is constant) this perturbation is defined as follows (see ^[4]).

Definition 3. Let $\varepsilon > 0.$ We say that a curve

is an $\varepsilon-$ neutral curve if its LCG gradient $\lambda$ satisfies the relation

for all $s \in [0, S].$

A curve satisfying $(3.1)$ for some positive $\varepsilon$ is called approximate neutral curve.

Using the notion introduced in Definition 3 we study the stability (in Ulam's sense) of the equation of the neutral curves. A curve with the gradient satisfying $(3.1)$ for some positive $\varepsilon$ is called a perturbation of a neutral curve.

Definition 4. The equation

is called Ulam stable if for every $\varepsilon > 0$ there exists $\delta(\varepsilon) > 0$ such that for every curve $(C)$ of curvature $K$ satisfying the relation

there exist a neutral curve $(\widetilde{C})$ of curvature $\widetilde{K}(s)$ such that

If $\delta(\varepsilon) = L\varepsilon$ for some positive constant $L,$ then $L$ is called an Ulam constant of the equation (3.2). If the infimum of all Ulam constants of an equation is also a Ulam constant, then we call it the best Ulam constant. Intuitively the stability of the equation of neutral curves, means that for every solution $K$ of this equation there exists a neutral curve with the curvature $\widetilde{K}$ close to $K$.

In what follows we study the stability of the equation (3.2) by a perturbation of it to an equation for convergent and divergent curves, respectively. Therefore the relation (3.3) is replaced either by

for the case of convergent curves, or by

for the case of divergent curves.

Let $m, M$ be given positive numbers. We denote, in what follows by $\mathcal{C}_M$ the class of functions defined by

and by $\mathcal{C}_{m, M}$ the class of functions given by

The first result concerns the stability of the equation of neutral curves of infinite length by perturbation to an equation for convergent curves.

Theorem 3. Let $\varepsilon > 0.$ Then for every convergent curve $(C)$ of curvature $K\in\mathcal{C}_M$ satisfying the relation

there exists a neutral curve $(\widetilde{C})$ of curvature $\widetilde{K}$ such that

with $\delta(\varepsilon) = \max{f_{\varepsilon}},$ where $f_{\varepsilon}:[0, \infty)\to\mathbb{R}$ is defined by

Proof. Suppose that $(C)$ is a curve of curvature $K\in\mathcal{C}_M$ satisfying the relation (3.8) and let

Then $K$ is given by

where $C_1 = \frac{K(0)}{K'(0)}$ and $C_2 = K(0),$ according to Theorem 2

The relation $0\leq \lambda(s)\leq \varepsilon,$ $s > 0$ leads to

Remark that since $(C)$ is a convergent curve then $C_1 < 0,$ in view of Theorem 1, so it follows

Integrating on $[0, s]$ we get

and

Let $(\widetilde{C})$ be a neutral curve of curvature $\widetilde{K}(s) = \widetilde{C}_2 e^{\widetilde{C}_1s},$ $s\geq 0,$ with $\widetilde{C}_1 = \frac{1}{C_1}$ and $\widetilde{C}_2 = C_2.$ Then, according to (3.11), we get

or

where $t = -\frac{s}{C_1}.$

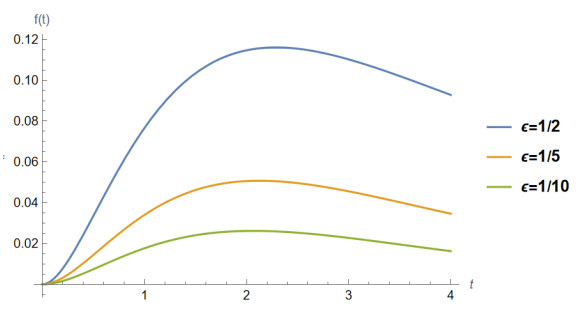
Next, we prove that $f_{\varepsilon}$ admits a maximum on $[0, \infty);$ (see Figure 1 for the graphical representation of $f_{\varepsilon}$ and its corresponding maximum values).

Since

the equation $f_{\varepsilon}'(t) = 0$ is equivalent to

Let $h(t) = t-\frac{\varepsilon +1}{\varepsilon}\ln(1+\varepsilon t).$ Then

Taking account of the monotonicity of $h$ and of the fact that $h(0) = 0,$ $h(1) < 0$ and $\lim\limits_{t\to\infty}h(t) = +\infty$ we conclude that the equation $h(t) = 0$ has a unique solution $t_0\in(1, \infty).$

Since $f_{\varepsilon}'(t) > 0,$ for $t\in(0, t_0)$ and $f_{\varepsilon}'(t) < 0$ for $t\in(t_0, \infty)$ and $\lim\limits_{t\to\infty}f(t) = 0,$ we conclude that $h$ admits a maximum at $t_0.$

Hence

where $\delta(\varepsilon) = f_{\varepsilon}(t_0)$ is the maximum of $f_{\varepsilon}.$

Then, according to $(3.12)$ and $(3.13)$ we get

The theorem is proved.

□

For a better understanding of our main stability results, in Figure 2, an example of an equation of a neutral curve of infinite length perturbed by an equation of a convergent curve is given.

The next result concerns the stability of the equation of neutral curves of infinite length by perturbation to an equation for divergent curves. In this case, we prove that the equation is not stable.

Theorem 4. Let $\varepsilon > 0.$ Then there exists a divergent curve $(C)$ of curvature $K$ satisfying the relation

such that for every neutral curve $(\widetilde{C})$ of curvature $\widetilde{K}$ we have

Proof. Let $(C)$ be a curve with curvature $K$ which satisfies the relation

and $K(0) = K'(0) = 1.$ Then according to Theorem 2

Let now $(C)$ be any neutral curve. Then

where $\widetilde{C_1} = \frac{\widetilde{K}(0)}{\widetilde{K'}(0)}$ and $\widetilde{C_2} = \widetilde{K}(0).$

If $\widetilde{C}_2\neq0,$ then

If $\widetilde{C}_2 = 0,$ then

Therefore

and the theorem is proved. □

In the next two figures, an example of an equation of a neutral curve of infinite length perturbed by an equation of a divergent curve is given. In Figure 3 the graphical representation of the curvatures of the neutral and of the perturbed curve is given, while in Figure 4 the corresponding curves are plotted.

However, the equation of neutral curves of finite length is Ulam stable with respect to perturbation to an equation for divergent curves. In this direction, we have the following result.

Theorem 5. Let $\varepsilon > 0$ and let $(C)$ be a curve of curvature $K\in\mathcal{C}_{m, M}$ satisfying the relation

Then there exists a neutral curve $(\widetilde{C})$ of curvature $\widetilde{K}$ such that

where $f_{\varepsilon}(t) = e^{t}-(1+\varepsilon t)^{\frac{1}{\varepsilon}},$ $\forall t\in[0, \infty).$

Proof. Suppose that $(3.14)$ is satisfied on $[0, S]$ and let $\lambda(s) = \frac{K^{\prime\prime}(s)K(s)}{(K^{\prime}(s))^2}-1.$ Then

where

Then, analogously to the proof of Theorem 3, we get

and integrating the previous relation on $[0, s]$ it follows

or equivalently to

Let $(\widetilde{C})$ be a neutral curve with the curvature

with $\widetilde{C_2} = C_1$ and $\widetilde{C_1} = \frac{1}{C_1}.$ Then

Let $f(t) = e^t-(1+\varepsilon t)^{\frac{1}{\varepsilon}},$ $t\in[0, \infty).$ We prove that $f(t) > 0$ for all $t\in[o, \infty).$ Indeed, the well known inequality

leads to $e^{t\varepsilon}\geq t\varepsilon+1,$ $t\geq 0,$ which is equivalent to

We prove that $f$ is increasing on $[0, \infty).$ Indeed, we have

and, taking account of

it follows $f'_{\varepsilon}(t)\geq 0,$ $\forall t\geq 0.$ Since $k\in \mathcal{C}_{m, M}$ it follows that

so

Then, according to the monotonicity of $f$ we get

The theorem is proved.

□

It is clear that the value of $\varepsilon$ in the previous theorems determines the degree of perturbation of the equation of aesthetic curves. A sharp estimation between the approximate and the exact solution of the equation is given by the best Ulam constant of it.

4.   Discussions and conclusions

One of the main requirements in the design of industrial products is their aesthetic form. The notion of aesthetics plays an essential role in art and science as well. Therefore, over time, scientists and artists tried to define various aesthetic standards and used them to generate aesthetic forms. One of the oldest criteria for the generation of aesthetic forms is the Golden Ratio. It was used by architects, engineers, and artists from antiquity to the present day to define the proportion between aesthetic objects. Following this idea Birkhoff introduced in ^[17] a measure of aesthetic forms taking into account the order and the complexity of an object. Extensions of the Golden Ratio and some applications are presented in the papers ^[5,6]. But for the generation of an aesthetic form, the notion of aesthetic curve plays an essential role. Due to the fact that the perception of beauty is subjective, depending on each individual, it makes sense to talk about approximately aesthetic forms. To the best of our knowledge the notion of the approximately aesthetic curve, i.e., a curve that satisfies approximately the equation of an aesthetic curve, was first considered in ^[4]. In this paper, we prove that small perturbations of the equation of aesthetic curves produce small perturbations of its solutions, i.e., the equation of aesthetic curves is Ulam stable under appropriate conditions. Extrapolating we can conclude that the notion of the aesthetic curve is Ulam stable for some classes of curves.

Acknowledgments

This research was partially supported by the project 38 PFE IN THE FRAME OF THE PROGRAMME PDI-PFE-CDI 2021.

Conflict of interest

The authors declare no conflict of interest.