Multi-criteria decision-making based on Pythagorean cubic fuzzy Einstein aggregation operators for investment management

1.   Introduction

Multi-criteria decision-making (MCDM) is a process of choosing the best course of action among several alternatives that are evaluated based on multiple criteria. MCDM is widely used in real life to solve complex problems that involve multiple objectives or goals and where there is no clear or objective single criterion for decision-making. In MCDM, different criteria are identified, and weights are assigned to them based on their relative importances. Then, the alternatives are evaluated against each criterion, and scores are assigned based on their performances. Finally, the scores are combined to determine the overall ranking of the alternatives, and the best course of action is selected. MCDM is widely used in various fields, such as finance, engineering, healthcare, environmental management and business management. For example, in finance, MCDM can be used to select the best investment portfolio that balances risk and return. In healthcare, MCDM can be used to select the best treatment option for a patient based on factors such as efficacy, side effects and cost. Li and Sun ^[1] proposed an intelligent investment strategy for stocks using historical data by developing a support vector machine (SVM) parameter optimization algorithm. In their 2021 study ^[2], they also applied a radial basis function (RBF) neural network optimal segmentation algorithm to credit rating, demonstrating improved accuracy in predicting credit ratings and its potential usefulness in credit risk assessment in financial institutions.

Aggregation operators are mathematical functions that combine multiple criteria or objectives into a single value that represents the overall performance of an alternative. Aggregation operators are widely used in decision-making to simplify complex problems that involve multiple criteria and objectives. For example, Garg and Rani ^[3] introduced aggregation operators that incorporate weighted averaging to combine various intricate intuitionistic fuzzy sets through t-norm operations. By employing Aczel Alsina operations, Senapati et al. ^[4] developed a variety of new aggregation operators that handle interval-valued intuitionistic fuzzy sets. Liu and Wang ^[5] introduced a series of aggregation operators that combine decision information expressed through linguistic intuitionistic fuzzy numbers. Akram et al. ^[6] proposed Hamacher weighted averaging and geometric aggregation operators for aggregating complex intuitionistic fuzzy information. Picture fuzzy aggregation operators were introduced by Riaz ^[7] and offer several benefits in handling practical situations. Verma and Merigó ^[8] created arithmetic and geometric aggregation operators to combine information from 2-dimensional linguistic intuitionistic fuzzy variables. Garg ^[9] introduced several weighted averaging and geometric operators, which were then employed to address decision-making problems. Abdullah et al. ^[10] suggested the use of Pythagorean cubic fuzzy Hamacher aggregation operators in solving the green supplier selection problem. Interval-valued Pythagorean fuzzy aggregation operators were developed by Peng and Yang ^[11] to combine interval-valued Pythagorean fuzzy information. Zulqarnain et al. ^[12] developed operational laws for Pythagorean fuzzy hypersoft numbers which consider their interaction. This led to the introduction of a variety of aggregation operators that depend on the established interaction operational laws. Amin et al. ^[13] introduced a set of generalized cubic Pythagorean fuzzy aggregation operators. These operators are designed to aggregate fuzzy information that is expressed in the form of Pythagorean fuzzy numbers and offer a flexible framework that can handle a wide range of applications. Nevertheless, in addition to these methods, several other authors have introduced alternative approaches to tackle decision-making problems, including ranking functions and aggregation operators ^{[14,15,16,17,18,19,20,21,22,23,24,25]}. These techniques provide further options for decision-makers seeking to optimize their decision-making processes.

Einstein operations, which include Einstein addition and multiplication, have a wide range of applications in various fields such as physics, computer science and image processing. For example, Einstein addition is used to calculate the relativistic velocities of objects moving at high speeds. It allows for the addition of velocities that approach the speed of light, which cannot be accomplished using ordinary addition. In decision-making, Einstein operations can be used to aggregate fuzzy information to obtain a more accurate representation of the underlying data. This can help to improve the decision-making process and increase the quality of the decisions made. Einstein operations and related aggregation operators have been utilized by numerous researchers across various fields to handle fuzzy information in diverse environments. These methods have been proposed and implemented in multiple applications, ranging from finance and economics to image processing and decision-making. For example, Wang and Liu ^[26] proposed operational laws on intuitionistic fuzzy sets which consist of several fundamental operations, including Einstein sum, Einstein product and Einstein exponentiation. Furthermore, they developed a set of geometric aggregation operators based on these operations to enhance the ability to deal with uncertainty and imprecision in decision-making. Riaz et al. ^[27] have introduced a class of aggregation operators, called q-rung orthopair fuzzy Einstein prioritized aggregation operators, to handle decision-making problems that involve q-rung orthopair fuzzy information. Complex q-rung picture fuzzy Einstein averaging operators were suggested by Akram et al. ^[28] as a means of addressing MCDM problems. Riaz et al. presented some prioritized operators in a q-rung orthopair fuzzy environment. To obtain additional information concerning Einstein aggregation operators and their application in MCDM, we can consult ^{[29,30,31,32,33,34,35,36,37]}. Table 1 provides explanations for the abbreviations used in this article.

Although the above extensions only consider membership and non-membership degrees, in real-world scenarios, it can be challenging to express the degree of membership accurately using a fuzzy set. In such situations, it may be easier to represent vagueness and uncertainty in the real world by using both interval and exact values instead of unique interval/exact values. Consequently, a hybrid form of an interval value, such as the Pythagorean cubic fuzzy set (PCFS), can be very useful in representing uncertainties caused by hesitant judgments in complex decision-making problems. Khan et al. ^[15,38] introduced the concept of the PCFS, which is described in two parts simultaneously: One represents the membership degrees using an interval-valued Pythagorean fuzzy number (IVPFN), while the other represents the membership degrees using a fuzzy number (FN). Thus, a PCFS is a hybrid set that combines an IVPFN and an FN. The advantage of PCFS is that it can contain much more data to express both the IVPFN and FN simultaneously. Table 2 contains the list of notations utilized in this article.

Motivations

Scholars have proposed many aggregation operators in the past for solving real-world decision-making problems. However, traditional fuzzy sets assign only a single value of membership, whereas Pythagorean cubic fuzzy sets use cubic polynomials and offer more flexibility in handling uncertainty. This helps decision-makers to assess decision-making criteria more comprehensively and accurately, leading to better outcomes. Although PCFSs provide a more robust framework for uncertain information in MCDM problems, unfortunately, there has not yet been any study conducted on the aggregation operators for PCFSs using Einstein operations. The present study expands the current aggregation operators by utilizing Einstein norm operations and proposing a series of aggregation operators. For this, we defined some new operations based on Einstein norm and conorm for Pythagorean cubic fuzzy numbers (PCFNs). By using operational laws in aggregation operators, it is possible to simplify and manipulate expressions, which in turn can help to improve the efficiency of computations and optimize the performance of systems. In addition, it is necessary to create a scoring and accuracy function that can effectively compare two PCFNs. By developing these functions, it will be possible to make more informed decisions and draw more accurate conclusions based on the comparison of PCFNs. Finally, a new method for solving MCDM problems has been introduced in this paper, based on the use of the proposed operators. The proposed work is outlined, and its objectives are presented in a summary fashion. These objectives are itemized and listed below to provide a clear and concise overview of the study's goals.

(1) To construct new score and accuracy functions that can effectively evaluate the performance of PCFNs by taking into account their unique characteristics.

(2) To define a framework for data processing and analysis by developing new operational laws that employ the Einstein t-norm and t-conorm for Pythagorean cubic fuzzy numbers. These operational laws will enable a more accurate representation of available information and improve decision-making quality.

(3) To propose new aggregation operators based on the proposed operational laws to aggregate different preferences of decision-makers in the PCFS environment.

(4) To propose an algorithm that utilizes the aforementioned operators to address the challenges of multi-criteria decision-making (MCDM) problems. This technique offers a practical and effective means of handling decision-making scenarios where multiple criteria or factors need to be considered.

(5) The study demonstrates the practical application of the proposed approach by implementing an established MCDM model and conducting a case study focused on identifying the optimal investment market.

To attain this objective, the remainder of the paper is outlined in the following manner: Section 2 clarifies the fundamental terminologies of PCFS and Einstein operations. Within Section 3, we present basic operational laws and their corresponding weighted aggregation operators for a collection of PCFSs. Also, the properties of the proposed operators are analyzed in detail. In Section 4, we expound on an MCDM technique that depends on the proposed operators for ranking different alternatives, wherein assessments linked to the criteria are presented in the form of PCFNs. Section 5 provides an example to demonstrate the approach and verify its feasibility and effectiveness. Finally, Section 6 summarizes the study.

2.   Preliminaries

The crucial background information employed in this study is presented in this section.

2.1.   Pythagorean cubic fuzzy sets

Definition 1. ^[15,38] Let $H$ be a non-empty finite set. A PCFS $D$ of an element $h\in H$ is defined as

where ${\mathcal{C}}_{D}\left(h\right) = \left\langle{{Z}_{D}\left(h\right); {\mu }_{D}\left(h\right)}\right\rangle$, the membership grade, while ${\mathcal{D}}_{D}\left(h\right) = \left\langle{{\tilde{Z}}_{D}\left(h\right); {\nu }_{D}\left(h\right)}\right\rangle$ represents the non-membership grade. Furthermore, ${Z}_{D}\left(h\right)$ and ${\tilde{Z}}_{D}\left(h\right)$ are interval-valued fuzzy sets, while ${\xi }_{D}\left(h\right)$ and ${\zeta }_{D}\left(h\right)$ represent fuzzy sets. Let ${Z}_{D}\left(h\right) = [{\xi }_{D}^{L}\left(h\right), {\xi }_{D}^{U}(h\left)\right]$ and ${\tilde{Z}}_{D}\left(h\right) = [{\zeta }_{D}^{L}\left(h\right), {\zeta }_{D}^{U}(h\left)\right]$. Then, ${\mathcal{C}}_{D}\left(h\right) = \left(\left\langle{[{\xi }_{D}^{L}\left(h\right), {\xi }_{D}^{U}(h); {\xi }_{D}(h)}\right\rangle\right)$ describes the degree of membership, while ${\mathcal{D}}_{D}\left(h\right) = \left(\left\langle{[{\zeta }_{D}^{L}\left(h\right), {{\zeta }_{D}^{U}}_{\widehat{p}}(h\left)\right]; {\zeta }_{D}\left(h\right)}\right\rangle\right)$ represents the non-membership degree of an element $h\in H$, such that ${0\preccurlyeq \left({\xi }_{D}^{U}\left(h\right)\right)}^{2}+\left({\zeta }_{D}^{U}\left(h\right)\right)\preccurlyeq 1$ and ${0\preccurlyeq \left({\xi }_{D}\left(h\right)\right)}^{2}+{\left({\zeta }_{D}\left(h\right)\right)}^{2}\preccurlyeq 1$. For simplicity, we call $\left(\left\langle{Z\left(h\right); \xi \left(t\right)}\right\rangle, \left\langle{\tilde{Z}\left(h\right); \zeta \left(t\right)}\right\rangle\right)$ a CPF number (PCFN), denoted by $\beta = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\tilde{Z}, \zeta }\right\rangle\right).$

Definition 2. ^[15,38] Let $\alpha = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\tilde{Z}, \zeta }\right\rangle\right)$, ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\tilde{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\tilde{Z}}_{2};{\zeta }_{2}\right)$ be three PCFNs, and $\eta$ is any positive real number, where ${Z}_{1} = [{\xi }_{1}^{L}, {\xi }_{1}^{U}]$, ${\tilde{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = [{\xi }_{2}^{L}, {\xi }_{2}^{U}]$, ${\tilde{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$, $Z = [{\xi }^{L}, {\xi }^{U}]$, and $\tilde{Z} = [{\zeta }^{L}, {\zeta }^{U}]$. Then, the operational laws are defined as

(1) ${\alpha }_{1}\oplus{\alpha }_{2} = \left(\begin{array}{c}\left\langle{\begin{array}{c}\left[\begin{array}{c}\sqrt{{\left({\xi }_{1}^{L}\right)}^{2}+{\left({\xi }_{2}^{L}\right)}^{2}-{\left({\xi }_{1}^{L}\right)}^{2}{\left({\xi }_{2}^{L}\right)}^{2}}, \\ \sqrt{{\left({\xi }_{1}^{U}\right)}^{2}+{\left({\xi }_{1}^{U}\right)}^{2}-{\left({\xi }_{1}^{U}\right)}^{2}{\left({\xi }_{1}^{U}\right)}^{2}}\end{array}\right]; \\ \sqrt{{\xi }_{1}^{2}+{\xi }_{2}^{2}-{\xi }_{1}^{2}{\xi }_{2}^{2}}\end{array}}\right\rangle, \\ \left\langle{\left[{\zeta }_{1}^{L}{\zeta }_{2}^{L}, {\zeta }_{1}^{U}{\zeta }_{2}^{U}\right]; {\zeta }_{1}{\zeta }_{2}}\right\rangle\end{array}\right),$

(2) ${\alpha }_{1}\otimes {\alpha }_{2} = \left(\begin{array}{c}\left\langle{\left[{\xi }_{1}^{L}{\xi }_{2}^{L}, {\xi }_{1}^{U}{\xi }_{2}^{U}\right]; {\xi }_{1}{\xi }_{2}}\right\rangle, \\ \left\langle{\begin{array}{c}\left[\begin{array}{c}\sqrt{{\left({\zeta }_{1}^{L}\right)}^{2}+{\left({\zeta }_{2}^{L}\right)}^{2}-{\left({\zeta }_{1}^{L}\right)}^{2}{\left({\zeta }_{2}^{L}\right)}^{2}}, \\ \sqrt{{\left({\zeta }_{1}^{U}\right)}^{2}+{\left({\zeta }_{1}^{U}\right)}^{2}-{\left({\zeta }_{1}^{U}\right)}^{2}{\left({\zeta }_{1}^{U}\right)}^{2}}\end{array}\right]; \\ \sqrt{{\zeta }_{1}^{2}+{\zeta }_{2}^{2}-{\zeta }_{1}^{2}{\zeta }_{2}^{2}}\end{array}}\right\rangle\end{array}\right),$

(3) $\eta \alpha = \left(\begin{array}{c}\left\langle{\begin{array}{c}\left[\begin{array}{c}\sqrt{{1-\left(1-{\left({\xi }^{L}\right)}^{2}\right)}^{\eta }}, \\ \sqrt{1-{\left(1-{\left({\xi }^{U}\right)}^{2}\right)}^{\eta }}\end{array}\right]; \\ \sqrt{1-{\left(1-{\xi }^{2}\right)}^{\eta }}\end{array}}\right\rangle, \\ \left\langle{\left[{\left({\zeta }^{-}\right)}^{\eta }, {\left({\zeta }^{+}\right)}^{\eta }\right]; {\zeta }^{\eta }}\right\rangle\end{array}\right),$

(4) ${\alpha }^{\eta } = \left(\begin{array}{c}\left\langle{\left[{\left({\xi }^{L}\right)}^{\eta }, {\left({\xi }^{U}\right)}^{\eta }\right]; {\xi }^{\eta }}\right\rangle, \\ \left\langle{\begin{array}{c}\left[\begin{array}{c}\sqrt{{1-\left(1-{\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }}, \\ \sqrt{1-{\left(1-{\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }}\end{array}\right]; \\ \sqrt{1-{\left(1-{\zeta }^{2}\right)}^{\eta }}\end{array}}\right\rangle\end{array}\right).$

Definition 3. ^[15,38] Let $\alpha = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\tilde{Z}; \zeta }\right\rangle\right)$ be a PCFN, where $Z = [{\xi }^{L}, {\xi }^{U}]$, and $\tilde{Z} = [{\zeta }^{L}, {\zeta }^{U}]$. Then, the score function $Sc\left(\rho \right)$ is defined as

while the accuracy function is defined as

where $-1\preccurlyeq Sc\left(\alpha \right)\preccurlyeq 1$ and $0\preccurlyeq Ac\left(\alpha \right)\preccurlyeq 1$. Let ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\tilde{Z}}_{1}{, \zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2}, {\xi }_{2}}\right\rangle, \left\langle{{\tilde{Z}}_{2}, {\zeta }_{2}}\right\rangle\right)$ be two PCFNs. If $Sc\left({\alpha }_{1}\right)\prec Sc\left({\alpha }_{2}\right)$ or $Ac\left({\alpha }_{1}\right)\prec Ac\left({\alpha }_{2}\right)$, then ${\alpha }_{1} \; \prec {\alpha }_{2}$. If $Sc\left({\alpha }_{1}\right)\succ Sc\left({\alpha }_{2}\right)$ or $Ac\left({\alpha }_{1}\right)\succ Ac\left({\alpha }_{2}\right)$, then ${\alpha }_{1}\succ {\alpha }_{2}$. If $Sc\left({\alpha }_{1}\right) = Sc\left({\alpha }_{2}\right)$ and $Ac\left({\alpha }_{1}\right) = Ac\left({\alpha }_{2}\right)$, then ${\alpha }_{1} = {\alpha }_{2}$.

Definition 4. ^[15,38] Let $\alpha$, ${\alpha }_{1}$ and ${\alpha }_{2}$ be any three PCFNs, and $\varphi$, ${\varphi }_{1}$ and ${\varphi }_{2}$ are positive real numbers. Then, the following properties hold.

(1) ${\alpha }_{1}\oplus{\alpha }_{2} = {\alpha }_{2}{⨁\alpha }_{1}$,

(2) ${\alpha }_{1}⨂{\alpha }_{2} = {\alpha }_{2}⨂{\alpha }_{1}$,

(3) $\eta \left({\alpha }_{1}⨁{\alpha }_{2}\right) = {\eta \alpha }_{1}⨁{\eta \alpha }_{2}$,

(4) $\left({\eta }_{1}{+\eta }_{2}\right)\alpha = {\eta }_{1}\alpha {⨁\eta }_{2}\alpha$,

(5) ${\left({\alpha }_{1}⨂{\alpha }_{2}\right)}^{\eta } = {\alpha }_{1}^{\eta }⨂{\alpha }_{2}^{\eta }$,

(6) ${\alpha }^{\left({\eta }_{1}+{\eta }_{2}\right)} = {\alpha }^{{\eta }_{1}}{⨂\alpha }^{{\eta }_{2}}$.

2.2.   Einstein operations

Definition 5. ^[39] Einstein product ${T}_{E}$ and Einstein sum ${S}_{E}$ are defined as follows:

(1) ${T}_{E}(a, b) = \frac{a.b}{1+(1-a)(1-b)}$, for all $a, b\in {\left[\mathrm{0, 1}\right]}^{2}$,

(2) ${S}_{E}(a, b) = \frac{a+b}{1+ab}$, for all $a, b\in {\left[\mathrm{0, 1}\right]}^{2}$.

3.   Einstein operations for Pythagorean cubic fuzzy sets

This section is dedicated to establishing a set of operational laws for PCFSs using two key elements, namely, ${T}_{E}$ and ${S}_{E}$. The operational laws outlined in this section represent a significant contribution to the study of PCFSs and their real-world applications.

Definition 6. Let ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right)$ be two PCFNs, where ${Z}_{1} = [{\alpha }_{1}, {\xi }_{1}^{U}]$, ${\stackrel{~}{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = [{\xi }_{2}^{L}, {\xi }_{2}^{U}]$, and ${\stackrel{~}{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$. Then, some of the Einstein operations over ${\alpha }_{1}$ and ${\alpha }_{2}$ are defined as follows:

(1) ${\alpha }_{1}{\oplus}_{E}{\alpha }_{2} = \left(\begin{array}{c}\left\langle{\left[\sqrt{\frac{{\left({\xi }_{1}^{L}\right)}^{2}+{\left({\xi }_{2}^{L}\right)}^{2}}{1+{\left({\xi }_{1}^{L}\right)}^{2}{\times }_{E}{\left({\xi }_{2}^{L}\right)}^{2}}}, \sqrt{\frac{{\left({\xi }_{1}^{U}\right)}^{2}+{\left({\xi }_{2}^{U}\right)}^{2}}{1+{\left({\xi }_{1}^{U}\right)}^{2}{\times }_{E}{\left({\xi }_{2}^{U}\right)}^{2}}}\right]; \sqrt{\frac{{\left({\xi }_{1}\right)}^{2}+{\left({\xi }_{2}\right)}^{2}}{1+{\left({\xi }_{1}\right)}^{2}{\times }_{E}{\left({\xi }_{2}\right)}^{2}}}}\right\rangle, \\ \left\langle{\left[\begin{array}{c}\frac{{\zeta }_{1}^{L}{\times }_{E}{\zeta }_{2}^{L}}{\sqrt{1+\left(1-{\left({\zeta }_{1}^{L}\right)}^{2}\right){\times }_{E}\left(1-{\left({\zeta }_{2}^{L}\right)}^{2}\right)}}, \\ \frac{{\zeta }_{1}^{U}{\times }_{E}{\zeta }_{2}^{U}}{\sqrt{1+\left(1-{\left({\zeta }_{1}^{U}\right)}^{2}\right){\times }_{E}\left(1-{\left({\zeta }_{2}^{U}\right)}^{2}\right)}}\end{array}\right]; \frac{{\zeta }_{1}{\times }_{E}{\zeta }_{2}}{\sqrt{1+\left(1-{\left({\zeta }_{1}\right)}^{2}\right){\times }_{E}\left(1-{\left({\zeta }_{2}\right)}^{2}\right)}}}\right\rangle\end{array}\right)$,

(2) ${\alpha }_{1}{\otimes }_{E}{\alpha }_{2} = \left(\begin{array}{c}\left\langle{\left[\begin{array}{c}\frac{{\xi }_{1}^{L}{\times }_{E}{\xi }_{2}^{L}}{\sqrt{1+\left(1-{\left({\xi }_{1}^{L}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}^{L}\right)}^{2}\right)}}, \\ \frac{{\xi }_{1}^{U}{\times }_{E}{\xi }_{2}^{U}}{\sqrt{1+\left(1-{\left({\xi }_{1}^{U}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}^{U}\right)}^{2}\right)}}\end{array}\right]; \frac{{\xi }_{1}{\times }_{E}{\xi }_{2}}{\sqrt{1+\left(1-{\left({\xi }_{1}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}\right)}^{2}\right)}}}\right\rangle\\ \left\langle{\left[\sqrt{\frac{{\left({\zeta }_{1}^{L}\right)}^{2}+{\left({\zeta }_{2}^{L}\right)}^{2}}{1+{\left({\zeta }_{1}^{L}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}^{L}\right)}^{2}}}, \sqrt{\frac{{\left({\zeta }_{1}^{U}\right)}^{2}+{\left({\zeta }_{2}^{U}\right)}^{2}}{1+{\left({\zeta }_{1}^{U}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}^{U}\right)}^{2}}}\right]; \sqrt{\frac{{\left({\zeta }_{1}\right)}^{2}+{\left({\zeta }_{2}\right)}^{2}}{1+{\left({\zeta }_{1}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}\right)}^{2}}}}\right\rangle\end{array}\right)$.

Example 1. Let ${\alpha }_{1} = \left(\left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.6}\right\rangle, \left[\mathrm{0.3, 0.4}\right]; 0.2\right)$ and ${\alpha }_{2} = \left(\left\langle{\left[\mathrm{0.2, 0.3}\right]; 0.5}\right\rangle, \left[\mathrm{0.6, 0.7}\right]; 0.4\right)$ are two PCFNs. Then, the operations ${\alpha }_{1}{\oplus}_{E}{\alpha }_{2}$ and ${\alpha }_{1}{\otimes }_{E}{\alpha }_{2}$ can be calculated as follows:

Definition 7. Let $\alpha = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\stackrel{~}{Z}, \zeta }\right\rangle\right)$ be a PCFN, where $Z = [{\xi }^{L}, {\xi }^{U}]$ and $\stackrel{~}{Z} = [{\zeta }^{L}, {\zeta }^{U}]$. For any positive real number $\eta$,

(1) $\eta {.}_{E}\alpha = \left(\begin{array}{c}\left\langle{\left[\begin{array}{c}\sqrt{\frac{\left(1+{\left({\left({\xi }^{L}\right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left({\xi }^{L}\right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left({\xi }^{L}\right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left({\xi }^{L}\right)}^{2}\right)}^{\eta }\right)}}, \\ \sqrt{\frac{\left(1+{\left({\left({\xi }^{U}\right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left({\xi }^{U}\right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left({\xi }^{U}\right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left({\xi }^{U}\right)}^{2}\right)}^{\eta }\right)}}\end{array}\right]; \sqrt{\frac{\left(1+{\left({\left(\xi \right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left(\xi \right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left(\xi \right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left(\xi \right)}^{2}\right)}^{\eta }\right)}}}\right\rangle, \\ \left\langle{\left[\begin{array}{c}\frac{\sqrt{2}{\left({\zeta }^{L}\right)}^{\eta }}{\sqrt{{\left(2-{\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }+{\left({\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }}}, \\ \frac{\sqrt{2}{\left({\zeta }^{U}\right)}^{\eta }}{\sqrt{{\left(2-{\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }+{\left({\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }}}\end{array}\right]; \frac{\sqrt{2}{\left(\zeta \right)}^{\eta }}{\sqrt{{\left(2-{\left(\zeta \right)}^{2}\right)}^{\eta }+{\left({\left(\zeta \right)}^{2}\right)}^{\eta }}}}\right\rangle\end{array}\right)$,

(2) ${\alpha }^{{E}^{\eta }} = \left(\begin{array}{c}\left\langle{\left[\begin{array}{c}\frac{\sqrt{2}{\left({\xi }^{L}\right)}^{\eta }}{\sqrt{{\left(2-{\left({\xi }^{L}\right)}^{2}\right)}^{\eta }+{\left({\left({\xi }^{L}\right)}^{2}\right)}^{\eta }}}, \\ \frac{\sqrt{2}{\left({\xi }^{U}\right)}^{\eta }}{\sqrt{{\left(2-{\left({\xi }^{U}\right)}^{2}\right)}^{\eta }+{\left({\left({\xi }^{U}\right)}^{2}\right)}^{\eta }}}\end{array}\right]; \frac{\sqrt{2}{\left(\xi \right)}^{\eta }}{\sqrt{{\left(2-{\left(\xi \right)}^{2}\right)}^{\eta }+{\left({\left(\xi \right)}^{2}\right)}^{\eta }}}}\right\rangle, \\ \left\langle{\left[\begin{array}{c}\sqrt{\frac{\left(1+{\left({\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left({\zeta }^{L}\right)}^{2}\right)}^{\eta }\right)}}, \\ \sqrt{\frac{\left(1+{\left({\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left({\zeta }^{U}\right)}^{2}\right)}^{\eta }\right)}}\end{array}\right]; \sqrt{\frac{\left(1+{\left({\left(\zeta \right)}^{2}\right)}^{\eta }\right)-\left(1-{\left({\left(\zeta \right)}^{2}\right)}^{\eta }\right)}{\left(1+{\left({\left(\zeta \right)}^{2}\right)}^{\eta }\right)+\left(1-{\left({\left(\zeta \right)}^{2}\right)}^{\eta }\right)}}}\right\rangle\end{array}\right)$.

Example 2. Let $\alpha = \left(\left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.6}\right\rangle, \left[\mathrm{0.3, 0.4}\right]; 0.2\right)$ and $\eta = 0.5$. Then, the operations $\eta {.}_{E}\alpha$ and ${\alpha }^{{E}^{\eta }}$ can be calculated as

Definition 8. Let ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right)$ be two PCFNs, where ${Z}_{1} = [{\xi }_{1}^{L}, {\xi }_{1}^{U}]$, ${\stackrel{~}{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = \left[{\xi }_{2}^{L}, {\xi }_{2}^{U}\right],$ and ${\stackrel{~}{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$. Then, the Einstein union and Einstein intersection of ${\alpha }_{1}$ and ${\alpha }_{2}$ are defined as follows:

(1) ${\alpha }_{1}{\cup }_{E}{\alpha }_{2} = \left(\left\langle{\left[\begin{array}{c}\mathrm{max}\left({\xi }_{1}^{L}, {\xi }_{2}^{L}\right), \\ \mathrm{max}\left({\xi }_{1}^{U}, {\xi }_{2}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{a}\mathrm{x}({\xi }_{1}, {\xi }_{2})}\right\rangle, \left\langle{\left[\begin{array}{c}\mathrm{min}\left({\zeta }_{1}^{L}, {\zeta }_{2}^{L}\right), \\ \mathrm{min}\left({\zeta }_{1}^{U}, {\zeta }_{2}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{i}\mathrm{n}({\zeta }_{1}, {\zeta }_{2})}\right\rangle\right)$,

(2) ${\alpha }_{1}{\cap }_{E}{\alpha }_{2} = \left(\left\langle{\left[\begin{array}{c}\mathrm{min}\left({\xi }_{1}^{L}, {\xi }_{2}^{L}\right), \\ \mathrm{min}\left({\xi }_{1}^{U}, {\xi }_{2}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{i}\mathrm{n}({\xi }_{1}, {\xi }_{2})}\right\rangle, \left\langle{\left[\begin{array}{c}\mathrm{max}\left({\zeta }_{1}^{L}, {\zeta }_{2}^{L}\right), \\ \mathrm{max}\left({\zeta }_{1}^{U}, {\zeta }_{2}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{a}\mathrm{x}({\zeta }_{1}, {\zeta }_{2})}\right\rangle\right)$.

Example 3. Let ${\alpha }_{1} = \left(\left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.6}\right\rangle, \left[\mathrm{0.3, 0.4}\right]; 0.2\right)$ and ${\alpha }_{2} = \left(\left\langle{\left[\mathrm{0.2, 0.3}\right]; 0.5}\right\rangle, \left[\mathrm{0.6, 0.7}\right]; 0.4\right)$. Then, the operations ${\alpha }_{1}{\oplus}_{E}{\alpha }_{2}$ and ${\alpha }_{1}{\otimes }_{E}{\alpha }_{2}$ can be calculated as

Theorem 1. Let ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right)$ be any two PCFNs, where ${Z}_{1} = [{\xi }_{1}^{L}, {\xi }_{1}^{U}]$, ${\stackrel{~}{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = [{\xi }_{2}^{L}, {\xi }_{2}^{U}]$, and ${\stackrel{~}{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$. Then, their accumulated value is also a PCFNs, by using Definition 6.

Proof. For two PCFNs ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right),$ we have, $0\preccurlyeq {\xi }_{1}^{L}\preccurlyeq {\xi }_{1}^{U}\preccurlyeq 1$, $0\preccurlyeq {\zeta }_{1}^{L}\preccurlyeq {\zeta }_{1}^{U}\preccurlyeq 1$, $0\preccurlyeq {\xi }_{2}^{L}\preccurlyeq {\xi }_{2}^{U}\preccurlyeq 1$, $0\preccurlyeq {\zeta }_{2}^{L}\preccurlyeq {\zeta }_{2}^{U}\preccurlyeq 1$, $0\preccurlyeq {\xi }_{1}, {\zeta }_{1}\preccurlyeq 1$, and $0\preccurlyeq {\xi }_{1}, {\zeta }_{1}\preccurlyeq 1$ such that ${\left({\xi }_{1}^{U}\right)}^{2}+{\left({\zeta }_{1}^{U}\right)}^{2}\preccurlyeq 1$, ${\left({\xi }_{2}^{U}\right)}^{2}+{\left({\zeta }_{2}^{U}\right)}^{2}\preccurlyeq 1$, $0\preccurlyeq {\xi }_{1}^{2}+{\zeta }_{1}^{2}\preccurlyeq 1$, and $0\preccurlyeq {\xi }_{2}^{2}+{\zeta }_{2}^{2}\preccurlyeq 1$. Therefore,

$\frac{{\xi }_{1}^{L}{\times }_{E}{\xi }_{2}^{L}}{\sqrt{1+\left(1-{\left({\xi }_{1}^{L}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}^{L}\right)}^{2}\right)}}\preccurlyeq \frac{{\xi }_{1}^{U}{\times }_{E}{\xi }_{2}^{U}}{\sqrt{1+\left(1-{\left({\xi }_{1}^{U}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}^{U}\right)}^{2}\right)}}\preccurlyeq 1$, and

$\sqrt{\frac{{\left({\zeta }_{1}^{L}\right)}^{2}+{\left({\zeta }_{2}^{L}\right)}^{2}}{1+{\left({\zeta }_{1}^{L}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}^{L}\right)}^{2}}}\preccurlyeq \sqrt{\frac{{\left({\zeta }_{1}^{U}\right)}^{2}+{\left({\zeta }_{2}^{U}\right)}^{2}}{1+{\left({\zeta }_{1}^{U}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}^{U}\right)}^{2}}}\preccurlyeq 1$, which implies that

$\frac{{\xi }_{1}^{U}{\times }_{E}{\xi }_{2}^{U}}{\sqrt{1+\left(1-{\left({\xi }_{1}^{U}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}^{U}\right)}^{2}\right)}}+\sqrt{\frac{{\left({\zeta }_{1}^{U}\right)}^{2}+{\left({\zeta }_{2}^{U}\right)}^{2}}{1+{\left({\zeta }_{1}^{U}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}^{U}\right)}^{2}}}\preccurlyeq 1.$

Similarly, we can prove that $\frac{{\xi }_{1}{\times }_{E}{\xi }_{2}}{\sqrt{1+\left(1-{\left({\xi }_{1}\right)}^{2}\right){\times }_{E}\left(1-{\left({\xi }_{2}\right)}^{2}\right)}}+\sqrt{\frac{{\left({\zeta }_{1}\right)}^{2}+{\left({\zeta }_{2}\right)}^{2}}{1+{\left({\zeta }_{1}\right)}^{2}{\times }_{E}{\left({\zeta }_{2}\right)}^{2}}}\preccurlyeq 1$.

Thus, ${\alpha }_{1}{\otimes }_{E}{\alpha }_{2}$ is a PCFN. Part (1) can be demonstrated using the same method.

Theorem 2. Let $\alpha = \left(\left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.6}\right\rangle, \left[\mathrm{0.3, 0.4}\right]; 0.2\right)$ and $\eta = 0.5$. Then, the results of the operational laws $\eta {.}_{E}\alpha$ and ${\alpha }^{{E}^{\eta }}$ are also PCFNs.

Proof. The proof bears resemblance to Theorem 1.

Theorem 3. Let $\alpha = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\stackrel{~}{Z}, \zeta }\right\rangle\right)$, ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right)$ be three PCFNs, and $\eta$, ${\eta }_{2}$ and ${\eta }_{3}$ are any positive real numbers, where ${Z}_{1} = [{\xi }_{1}^{L}, {\xi }_{1}^{U}]$, ${\stackrel{~}{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = [{\xi }_{2}^{L}, {\xi }_{2}^{U}]$, ${\stackrel{~}{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$, $Z = [{\xi }^{L}, {\xi }^{U}]$, and $\stackrel{~}{Z} = [{\zeta }^{L}, {\zeta }^{U}]$. Then, we have

(1) ${\alpha }_{1}{\oplus}_{E}{\alpha }_{2} = {\alpha }_{2}{\oplus}_{E}{\alpha }_{1}$,

(2) ${\alpha }_{1}{\otimes }_{E}{\alpha }_{2} = {\alpha }_{2}{\otimes }_{E}{\alpha }_{1}$,

(3) ${\left({\alpha }_{1}{\otimes }_{E}{\alpha }_{2}\right)}^{\eta } = {\left({\alpha }_{1}\right)}^{\eta }{\otimes }_{E}{\left({\alpha }_{2}\right)}^{\eta }$,

(4) $\eta {.}_{E}\left({\alpha }_{1}{\oplus}_{E}{\alpha }_{2}\right) = \eta {.}_{E}{\alpha }_{1}\oplus\eta {.}_{E}{\alpha }_{2}$,

(5) ${\alpha }^{{\eta }_{1}}\otimes {\alpha }^{{\eta }_{2}} = {\alpha }^{{\eta }_{1}+{\eta }_{2}}$,

(6) ${\eta }_{1}{.}_{E}\alpha \oplus{\eta }_{2}{.}_{E}\alpha = \left({\eta }_{1}+{\eta }_{1}\right){.}_{E}\alpha$.

Proof. (1) By Definition 6, we have

(2) Again by Definition 6, we have

The proof of the remaining part is relatively straightforward.

Definition 9. Let $\alpha = \left(\left\langle{Z; \xi }\right\rangle, \left\langle{\stackrel{~}{Z}, \zeta }\right\rangle\right)$ be a PCFN, where $Z = [{\xi }^{L}, {\xi }^{U}]$ and $\stackrel{~}{Z} = [{\zeta }^{L}, {\zeta }^{U}]$. The complement of $\alpha$ is denoted by ${\alpha }^{C}$ and defined as ${\alpha }^{C} = \left(\left\langle{\stackrel{~}{Z}, \zeta }\right\rangle, \left\langle{Z; \xi }\right\rangle\right)$.

Theorem 4. Let ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right)$ and ${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, {\stackrel{~}{Z}}_{2};{\zeta }_{2}\right)$ be two PCFNs, where ${Z}_{1} = [{\xi }_{1}^{L}, {\xi }_{1}^{U}]$, ${\stackrel{~}{Z}}_{1} = [{\zeta }_{1}^{L}, {\zeta }_{1}^{U}]$, ${Z}_{2} = [{\xi }_{2}^{L}, {\xi }_{2}^{U}]$, and ${\stackrel{~}{Z}}_{2} = [{\zeta }_{2}^{L}, {\zeta }_{2}^{U}]$. Then, we have

(1) ${\alpha }_{1}^{C}{\cap }_{E}{\alpha }_{2}^{C} = {\left({\alpha }_{1}{\cup }_{E}{\alpha }_{2}\right)}^{C}$,

(2) ${\alpha }_{1}^{C}{\cup }_{E}{\alpha }_{2}^{C} = {\left({\alpha }_{1}{\cap }_{E}{\alpha }_{2}\right)}^{C}$,

(3) ${\alpha }_{1}^{C}{\otimes }_{E}{\alpha }_{2}^{C} = {\left({\alpha }_{1}{\oplus}_{E}{\alpha }_{2}\right)}^{C}$,

(4) ${\alpha }_{1}^{C}{\oplus}_{E}{\alpha }_{2}^{C} = {\left({\alpha }_{1}{\otimes }_{E}{\alpha }_{2}\right)}^{C}$.

Proof. Since ${\alpha }_{1} = \left(\left\langle{{Z}_{1};{\xi }_{1}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle\right) = \left(\left\langle{\left[{\xi }_{1}^{L}, {\xi }_{1}^{U}\right]; {\xi }_{1}}\right\rangle, \left\langle{\left[{\zeta }_{1}^{L}, {\zeta }_{1}^{U}\right]; {\zeta }_{1}}\right\rangle\right)$, and

${\alpha }_{2} = \left(\left\langle{{Z}_{2};{\xi }_{2}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{2}, {\zeta }_{2}}\right\rangle\right) = \left(\left\langle{\left[{\xi }_{2}^{L}, {\xi }_{2}^{U}\right]; {\xi }_{2}}\right\rangle, \left\langle{\left[{\zeta }_{2}^{L}, {\zeta }_{2}^{U}\right]; {\zeta }_{2}}\right\rangle\right)$, by Definition 9, we have

${\alpha }_{1}^{C} = \left(\left\langle{{\stackrel{~}{Z}}_{1}, {\zeta }_{1}}\right\rangle, \left\langle{{Z}_{1};{\xi }_{1}}\right\rangle\right) = \left(\left\langle{\left[{\zeta }_{1}^{L}, {\zeta }_{1}^{U}\right]; {\zeta }_{1}}\right\rangle, \left\langle{\left[{\xi }_{1}^{L}, {\xi }_{1}^{U}\right]; {\xi }_{1}}\right\rangle\right)$, and

${\alpha }_{2}^{C} = \left(\left\langle{{\stackrel{~}{Z}}_{2}, {\zeta }_{2}}\right\rangle, \left\langle{{Z}_{2};{\xi }_{2}}\right\rangle\right) = \left(\left\langle{\left[{\zeta }_{2}^{L}, {\zeta }_{2}^{U}\right]; {\zeta }_{2}}\right\rangle, \left\langle{\left[{\xi }_{2}^{L}, {\xi }_{2}^{U}\right]; {\xi }_{2}}\right\rangle\right).$

By Definition 8, we have

On the other hand,

Thus, ${\alpha }_{1}^{C}{\cap }_{E}{\alpha }_{2}^{C} = {\left({\alpha }_{1}{\cup }_{E}{\alpha }_{2}\right)}^{C}$.

As the proof of the remaining portion is relatively simple, it has been excluded from this discussion.

4.   Pythagorean cubic fuzzy Einstein weighted averaging AOs

This section focuses on exploring the Pythagorean cubic fuzzy averaging AOs using Einstein operations.

4.1.   PCFEWA operator

Definition 10. Let ${\alpha }_{i} = \left(\left\langle{{Z}_{i}; {\xi }_{i}}\right\rangle, \left\langle{{\stackrel{~}{Z}}_{i}, {\zeta }_{i}}\right\rangle\right)$ be a collection of PCFNs, and ${\mu }_{i}$ is the weight of ${\alpha }_{i} \; (i = \mathrm{1, 2}, \dots, n)$ such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$and $\sum _{i = 1}^{n}{\mu }_{i} = 1$. Then, a PCFEWA operator of dimension $n$ is a mapping $PCFEWA:{\mathrm{\Delta }}^{n}\to \mathrm{\Delta }$, and

Theorem 5. Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right)$ be a collection of PCFNs, and ${\mu }_{i}$ is the weight of ${\alpha }_{i} \; (i = \mathrm{1, 2}, \dots, n)$ such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$ and $\sum _{i = 1}^{n}{\mu }_{i} = 1$. Then, the aggregated value by using Eq (4) is PCFN, and

Proof. To demonstrate the validity of Eq (5), we will utilize the principle of mathematical induction for the variable $n$. This approach involves establishing a base case and then demonstrating that if the equation holds for any arbitrary value of $n$, it must also hold for the next value of $n$ in succession. By using this iterative process, we can establish the equation's validity for all possible values of $n$.

When $n = 2$, $PCFEWA({\alpha }_{1}, {\alpha }_{2}) = {\mu }_{1}{.}_{E}{\alpha }_{1}{\oplus}_{E}{\mu }_{2}{.}_{E}{\alpha }_{2}$. According to Theorem 1, ${\mu }_{1}{.}_{E}{\alpha }_{1}$ and ${\mu }_{2}{.}_{E}{\alpha }_{2}$ are PCFNs. Also, by Theorem 3, we can see that ${\mu }_{1}{.}_{E}{\alpha }_{1}{\oplus}_{E}{\mu }_{2}{.}_{E}{\alpha }_{2}$ is a PCFN.

Thus, the result is true for $n = 2$.

Suppose that the assertion is valid when $n$ is equal to some particular value, denoted as $k$. In this case, we can state that Eq (5) holds, which means that the result holds for the given value of $k$. That is,

Our present goal is to demonstrate the truth of Eq (5) when $n$ is equal to $\mathrm{k}+1$. By Eq (4), we get

To summarize, the proof shows that Eq (2) is valid for $n = k+1$, and we can conclude that Eq (5) holds for all values of $n$. Therefore, we have successfully proven the validity of Eq (5) across all possible values of $n$.

Property 1. (Idempotency) If ${\alpha }_{i} = \alpha$ where $\alpha = \left(\left\langle{\left[{\xi }^{L}, {\xi }^{U}\right]; \xi }\right\rangle, \left\langle{\left[{\zeta }^{L}, {\zeta }^{U}\right], \zeta }\right\rangle\right)$, and ${\mu }_{i}$ is the associated weight of ${\alpha }_{i}$ such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$ and $\sum _{i = 1}^{n}{\mu }_{i} = 1$, then $\mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right) = \alpha$.

Proof. As ${\alpha }_{i} = \left(\left\langle{\left[{\xi }^{L}, {\xi }^{U}\right]; \xi }\right\rangle, \left\langle{\left[{\zeta }^{L}, {\zeta }^{U}\right], \zeta }\right\rangle\right)$ for all $i$,

since $\sum _{i = 1}^{n}{\mu }_{i} = 1$. Therefore, $\mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right) = \left(\left\langle{\left[{\xi }^{L}, {\xi }^{U}\right]; \xi }\right\rangle, \left\langle{\left[{\zeta }^{L}, {\zeta }^{U}\right], \zeta }\right\rangle\right) = \alpha$.

Property 2. (Monotonicity) Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right)$ and

${\dot{\alpha }}_{i} = \left(\left\langle{\left[{\dot{\xi }}_{i}^{L}, {\dot{\xi }}_{i}^{U}\right]; {\dot{\xi }}_{i}}\right\rangle, \left\langle{\left[\left[{\dot{\zeta }}_{i}^{L}, {\dot{\zeta }}_{i}^{U}\right]\right], {\dot{\zeta }}_{i}}\right\rangle\right)$ be PCFNs. If ${\alpha }_{i}\preccurlyeq {\dot{\alpha }}_{i}$, then

Proof. As the proof is straightforward, we will omit it here.

Property 3. (Boundedness) Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right) \; (i = \mathrm{1, 2}, \dots, n)$ be a collection of PCFNs. If

${\alpha }^{+} = \left(\left\langle{\left[\begin{array}{c}\mathrm{max}\left({\xi }_{i}^{L}\right), \\ \mathrm{max}\left({\xi }_{i}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{a}\mathrm{x}\left({\xi }_{i}\right)}\right\rangle, \left\langle{\left[\begin{array}{c}\mathrm{min}\left({\zeta }_{i}^{L}\right), \\ \mathrm{min}\left({\zeta }_{i}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{i}\mathrm{n}\left({\zeta }_{i}\right)}\right\rangle\right),$

${\alpha }^{-} = \left(\left\langle{\left[\begin{array}{c}\mathrm{min}\left({\xi }_{i}^{L}\right), \\ \mathrm{min}\left({\xi }_{i}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{i}\mathrm{n}\left({\xi }_{i}\right)}\right\rangle, \left\langle{\left[\begin{array}{c}\mathrm{max}\left({\zeta }_{i}^{L}\right), \\ \mathrm{max}\left({\zeta }_{i}^{U}\right)\end{array}\right]; \mathrm{m}\mathrm{a}\mathrm{x}\left({\zeta }_{i}\right)}\right\rangle\right),$

then ${\alpha }^{-}\preccurlyeq \mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right)\preccurlyeq {\alpha }^{+}$.

Proof. As the proof is straightforward, we will omit it here.

Property 4. (Homogeneity) Let $\varphi$ be a positive real number. Then, we have

Proof. It is simple to demonstrate.

Corollary 1. The relationship between the PCFEWA and PCFWA operators can be expressed as follows:

Example 4. Let ${\alpha }_{1} = \left(\left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.6}\right\rangle, \left\langle{\left[\mathrm{0.3, 0.4}\right]; 0.2}\right\rangle\right)$, ${\alpha }_{2} = \left(\left\langle{\left[\mathrm{0.2, 0.3}\right]; 0.5}\right\rangle, \left\langle{\left[\mathrm{0.6, 0.7}\right]; 0.4}\right\rangle\right)$ and ${\alpha }_{3} = \left(\left\langle{\left[\mathrm{0.2, 0.4}\right]; 0.3}\right\rangle, \left\langle{\left[\mathrm{0.5, 0.6}\right]; 0.4}\right\rangle\right)$ be three PCFNs. The weight vector is $\mu = (\mathrm{0.25.0}.\mathrm{35, 0.4})$. Then,

Now, by using the PCFWA operator ^[36] to aggregate these three PCFNs,

By Eq (2), we get

Clearly, we can see that $\mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right)\succcurlyeq \mathrm{P}\mathrm{C}\mathrm{F}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right)$.

4.2.   PCFEWA operator

Definition 11. A PCFEOWA is a mapping defined as ${\mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}:\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }\Delta }^{n}\to \Delta$ on a collection of PCFNs ${\beta }_{i}$, $(i = \mathrm{1, 2}, \dots n)$ as follows:

where $\rho$ is a permutation of $(1, 2, \dots, n)$, such that ${\alpha }_{\rho (i-1)}\succcurlyeq {\alpha }_{\rho \left(i\right)}$ for $i = \mathrm{1, 2}, \dots, n$, and $\mu = {({\mu }_{1}, {\mu }_{2}\dots, {\mu }_{n})}^{T}$ is its weight vector, such that $\mu \succ 0$ and ${\sum }_{i = 1}^{n}{\mu }_{i} = 1$. Moreover, the ${i}^{th}$ largest PCFN among ${\alpha }_{i}\mathrm{\text{'}}\mathrm{s}$ is ${\alpha }_{\rho \left(i\right)}$.

Theorem 6. Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right)$ be a collection of PCFNs, and ${\mu }_{i}$ is the weight of ${\alpha }_{i} \; (i = \mathrm{1, 2}, \dots, n)$ such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$and $\sum _{i = 1}^{n}{\mu }_{i} = 1$. Then, the aggregated value by using Eq (4) is PCFN, and

Property 5. (Idempotency) If ${\alpha }_{i} = \alpha$ where $\alpha = \left(\left\langle{\left[{\xi }^{L}, {\xi }^{U}\right]; \xi }\right\rangle, \left\langle{\left[{\zeta }^{L}, {\zeta }^{U}\right], \zeta }\right\rangle\right)$, and ${\mu }_{i}$ is the associated weight of ${\alpha }_{i}$ such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$ and $\sum _{i = 1}^{n}{\mu }_{i} = 1$, then $\mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right) = \alpha$.

Property 6. (Monotonicity) Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right)$ and

${\dot{\alpha }}_{i} = \left(\left\langle{\left[{\dot{\xi }}_{i}^{L}, {\dot{\xi }}_{i}^{U}\right]; {\dot{\xi }}_{i}}\right\rangle, \left\langle{\left[\left[{\dot{\zeta }}_{i}^{L}, {\dot{\zeta }}_{i}^{U}\right]\right], {\dot{\zeta }}_{i}}\right\rangle\right)$ be PCFNs. If ${\alpha }_{i}\preccurlyeq {\dot{\alpha }}_{i}$, then

Property 7. (Boundedness) Let ${\alpha }_{i} = \left(\left\langle{\left[{\xi }_{i}^{L}, {\xi }_{i}^{U}\right]; {\xi }_{i}}\right\rangle, \left\langle{\left[\left[{\zeta }_{i}^{L}, {\zeta }_{i}^{U}\right]\right], {\zeta }_{i}}\right\rangle\right) \; (i = \mathrm{1, 2}, \dots, n)$ be a collection of PCFNs. If

then ${\alpha }^{-}\preccurlyeq \mathrm{P}\mathrm{C}\mathrm{F}\mathrm{E}\mathrm{O}\mathrm{W}\mathrm{A}\left({\alpha }_{1}, {\alpha }_{2}, \dots, {\alpha }_{n}\right)\preccurlyeq {\alpha }^{+}$.

Property 8. (Homogeneity) Let $\varphi$ be a positive real number. Then, we have

Corollary 2. The relationship between the PCFEOWA and PCFOWA operators can be expressed as follows:

5.   MCDM approach based on proposed operators

This section will employ the proposed Einstein aggregation operator to address MCDM problems in the context of PCFSs. To facilitate this, we will introduce several assumptions and notations to define the MCDM problems and evaluate them using PCFSs.

Let $\vartheta = \left\{{\vartheta }_{1}, {\vartheta }_{2}, \dots, {\vartheta }_{m}\right\}$ be the set of $m$ alternatives, which have been analyzed under the set of $n$ different criteria $\psi = \left\{{\psi }_{1}, {\psi }_{2}, \dots, {\psi }_{n}\right\}$. Suppose that an expert assesses the alternatives, providing their opinions on each alternative ${\vartheta }_{i}$ (where $i$ ranges from $1$ to $m$) within the context of a Pythagorean cubic fuzzy environment. The expert's evaluations are based on their preferences and priorities with respect to the different criteria in the set $\psi$, and these values can be considered as Pythagorean cubic fuzzy numbers (PCFNs) $G = {\left({g}_{ij}\right)}_{mn}$ where ${g}_{ij} = \left(\left\langle{\left[{\xi }_{ij}^{L}, {\xi }_{ij}^{U}\right]; {\xi }_{ij}}\right\rangle, \left\langle{\left[{\zeta }_{ij}^{L}, {\zeta }_{ij}^{U}\right], {\zeta }_{ij}}\right\rangle\right)$ refers to the priority values assigned to alternative ${\vartheta }_{i}$ by the decision maker such that $\left[{\xi }_{ij}^{L}, {\xi }_{ij}^{U}\right]$, $\left[{\zeta }_{ij}^{L}, {\zeta }_{ij}^{U}\right]\subseteq \left[\mathrm{0, 1}\right]$, $0\preccurlyeq {\xi }_{ij}$, ${\zeta }_{ij}\preccurlyeq 1$, ${\left({\xi }_{ij}^{U}\right)}^{2}+{\left({\zeta }_{ij}^{U}\right)}^{2}\preccurlyeq 1$ and ${\left({\xi }_{ij}\right)}^{2}+{\left({\zeta }_{ij}\right)}^{2}\preccurlyeq 1$. Let $\mu = {\left({\mu }_{1}, {\mu }_{2}, \dots, {\mu }_{n}\right)}^{T}$ be the weight vector of criteria such that $0\preccurlyeq {\mu }_{i}\preccurlyeq 1$ and $\sum _{j = 1}^{n}{\mu }_{j} = 1$ ($i = \mathrm{1, 2}, \dots, m; j = \mathrm{1, 2}, \dots, n$).

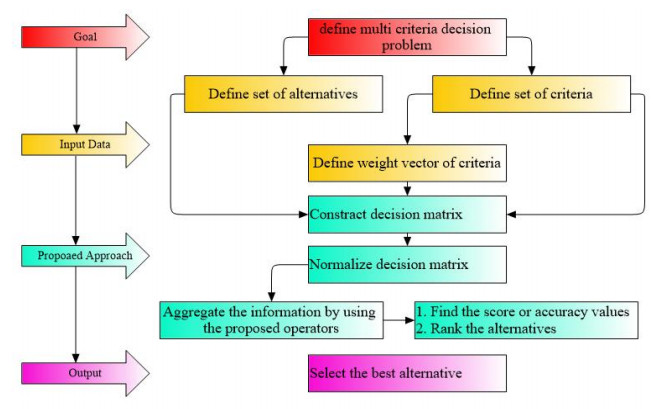
The proposed method is shown in Figure 1 for identifying the best alternative(s).

Step 1. To comprehensively evaluate various alternatives, it is necessary to collect relevant information and rate them based on specific criteria. The rating values are expressed as a decision matrix $G$:

where ${g}_{ij} = \left(\left\langle{\left[{\xi }_{ij}^{L}, {\xi }_{ij}^{U}\right]; {\xi }_{ij}}\right\rangle, \left\langle{\left[{\zeta }_{ij}^{L}, {\zeta }_{ij}^{U}\right], {\zeta }_{ij}}\right\rangle\right)$ such that $\left[{\xi }_{ij}^{L}, {\xi }_{ij}^{U}\right]$, $\left[{\zeta }_{ij}^{L}, {\zeta }_{ij}^{U}\right]\subseteq \left[\mathrm{0, 1}\right]$, $0\preccurlyeq {\xi }_{ij}$, ${\zeta }_{ij}\preccurlyeq 1$, ${\left({\xi }_{ij}^{U}\right)}^{2}+{\left({\zeta }_{ij}^{U}\right)}^{2}\preccurlyeq 1$ and ${\left({\xi }_{ij}\right)}^{2}+{\left({\zeta }_{ij}\right)}^{2}\preccurlyeq 1$.

Step 2. When making a decision, criteria are used to assess and compare alternative options. Two types of criteria exist: Benefit criteria and cost criteria. Benefit criteria evaluate the positive aspects of the alternatives being considered, measuring their advantages or benefits to determine the best solution to a particular problem. Cost criteria, on the other hand, assess the negative aspects or expenses associated with each alternative, measuring their disadvantages or costs, and are important for determining the overall feasibility of a solution. We will use the negation operator below for normalization.

To normalize the criteria, we will apply the following operator: If the criterion being assessed is a benefit criterion, no further action is necessary. However, if the criterion is a cost criterion, it will be converted into a benefit criterion, and the results will be condensed and organized into the decision matrix $R = {\left({r}_{ij}\right)}_{mn}$.

Step 3. One way to aggregate the various preference values ${r}_{ij}$ of the alternatives ${\vartheta }_{i}$ into a single collective value ${r}_{i}$ is by utilizing either the PCFEWA or PCFEOWA operator.

Step 4. To calculate the score of the combined PCFN value ${r}_{i}$, you can use Eq (2). Arrange the alternatives ${\vartheta }_{i}$ in order of their score value $Sc\left({r}_{i}\right)$, starting with the highest value and ending with the lowest.

5.1.   Illustrative example

To demonstrate the application of MCDM in engineering investment decision-making, we have chosen an illustrative example that highlights various investment alternatives. This example serves as a demonstration of how MCDM can be utilized to make informed decisions in complex engineering investment scenarios.

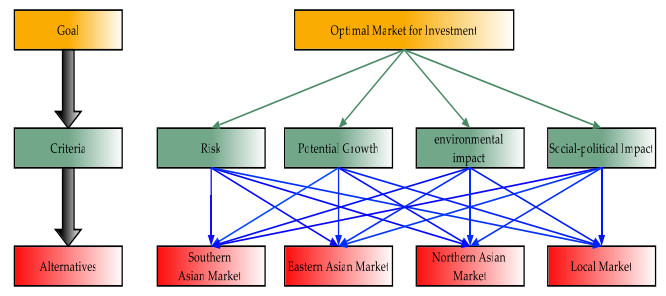
Let us examine the realm of investing, where an individual is interested in putting some amount of money into an investment. In current times, numerous companies are enticing customers by lowering prices and offering additional perks, making it challenging for investors to determine the optimal market for investment. To mitigate market risks and improve decision-making clarity, a committee was established to invest funds in four key markets: Southern Asian (${\vartheta }_{1}$), Eastern Asian (${\vartheta }_{2}$), Northern Asian (${\vartheta }_{3}$) and Local (${\vartheta }_{4}$). The committee enlisted the expertise of an analyst who evaluated each market based on four primary factors: risk (${\psi }_{1}$), growth potential (${\psi }_{2}$), environmental impact (${\psi }_{3}$) and social-political impact (${\psi }_{4}$). The weight vector, denoted as $\mu = {\left(\mathrm{0.35, 0.3, 0.15, 0.2}\right)}^{T}$, is associated with the four primary analyses ${\psi }_{i}$. Using the established method, we proceed to determine the optimal alternative as follows.

Step 1. The information about each alternative's preferences is condensed into a set of PCFNs. These PCFNs serve as a way to summarize the nuanced and complex preferences of the decision-makers. Additionally, the collection of ratings given for each alternative is recorded in a decision matrix, which is presented in Table 3. The decision matrix provides a clear and concise overview of the various ratings and their corresponding alternatives. The structure of the proposed model is systematically outlined in Figure 2.

Step 2. Since ${\psi }_{1}$ and ${\psi }_{4}$ pertain to costs, while ${\psi }_{2}$ and ${\psi }_{3}$ are related to benefits, the criteria can be categorized accordingly. Therefore, to create a normalized Pythagorean cubic fuzzy decision matrix $R$, Eq (10) is utilized. This process takes into account the various types of criteria and ensures that the resulting decision matrix accurately reflects the relative importances of both costs and benefits. The resulting decision matrix can be seen in Table 4.

Step 3. To combine the individual preference values ${r}_{ij}$ associated with each alternative Ai into a unified value ${r}_{i}$, two operators can be employed: PCFEWA or PCFEOWA. These operators offer a means of aggregation that can effectively take into account the diverse and often complex preferences of decision-makers.

(1) By PCFEWA operator

By utilizing the PCFEWA operator and taking into consideration the provided evidence, the various performance values can be effectively aggregated. This process allows for the calculation of comprehensive overall performance values for each alternative, which are summarized in Table 5.

(2) By PCFOWA operator

By taking into account the provided evidence and using the PCFEOWA operator, it is possible to aggregate the different performance values effectively. Before utilizing the PCFEOWA operator to aggregate different alternatives, we ranked their original positions based on their score. The results are summerized in Table 6.

Step 4. Equation (2) can be utilized to compute the score of the combined PCFN value ${r}_{i}$. After obtaining the scores, arrange the alternatives ${\vartheta }_{i}$ in descending order of their score value, beginning with the highest value and concluding with the lowest. The outcomes are then summarized in Table 7.

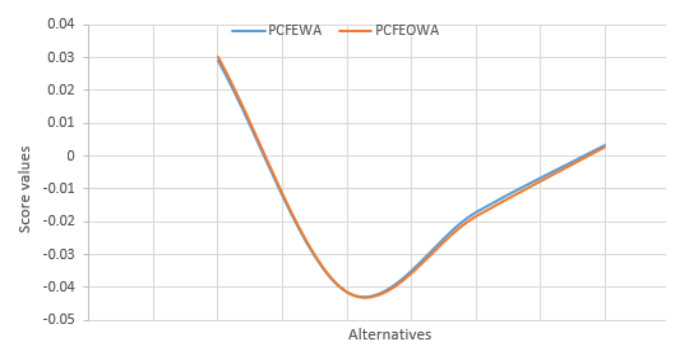
Table 7 reveals that the alternative ${\vartheta }_{1}$ has the highest score value among all the alternatives. Therefore, it can be concluded that ${\vartheta }_{1}$ is the most suitable option for the investment based on the given criteria and the evaluation method used. It is noteworthy that the score values of the other alternatives are comparatively lower than ${\vartheta }_{1}$, indicating that they may not be as favorable as ${\vartheta }_{1}$ for the investment. Consequently, the decision-makers should consider investing in ${\vartheta }_{1}$, as it has demonstrated superior performance and has the potential to yield the desired outcomes. Figure 3 displays a graphical representation of the proposed aggregation operators. Upon examination of the figure, it becomes evident that the outcomes of both operators are quite similar. This similarity between the results supports the notion that the proposed method is stable, as it can consistently generate similar results using different aggregation operators.

5.2.   Comparative study

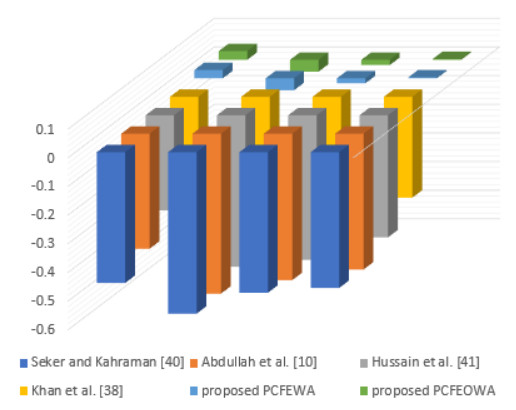
To determine the effectiveness of our proposed method in identifying the best alternatives, we conducted a comparative analysis with several previous approaches described by various authors. The objective was to assess the performance of our method compared to these existing methods. The results of this comparison are presented in Table 8, where each method is evaluated based on its ability to identify the best alternatives according to the given criteria. This analysis provides valuable insights into the strengths and weaknesses of each method and allows us to determine the efficacy of our proposed approach in identifying the most suitable alternatives for the investment.

Based on the comparison, we can conclude that the best alternative identified by our proposed approach is consistent with the results obtained from the existing methods. However, the aggregated PCFN values generated by our approach are more conservative than those produced by the other methods. As observed from the table, the relative score values of the alternatives follow a similar trend (either increasing or decreasing) across all the methods. This indicates that our proposed approach is equally effective in addressing decision-making problems in a PCFS environment as the existing methods. Overall, the comparative analysis provides evidence of the efficacy of our proposed approach in identifying the most suitable alternatives for the investment.

Based on the information presented in Figure 4, it can be observed that the outcomes achieved through the proposed approach are comparable to those of other approaches. However, it is worth noting that the proposed approach exhibits a higher level of stability and provides significantly more detailed information when compared to the other approaches. These findings suggest that the proposed approach may have distinct advantages over the other methods in terms of reliability and the depth of information it can provide.

From the above discussion, we have observed that the proposed approach produces the best alternative, which validates its stability in comparison to the state-of-the-art methods. In contrast to the existing decision-making methods that use either IVPFSs or FSs, the proposed approach considers both IVPFSs and FSs simultaneously, resulting in a more comprehensive evaluation of the alternatives. This is important as existing approaches may lose crucial information on either IVPFNs or FNs, which could potentially impact the decision results. Additionally, the proposed approach uses a different computational procedure than the existing approaches, but it yields more realistic results due to the consideration of the consistent priority degree between argument pairs in the decision process.

Overall, the proposed model offers a significant improvement over existing approaches by relaxing many of their constraints and limitations. In doing so, it provides a more flexible and adaptable environment that can effectively address complex decision-making problems. By enabling decision-makers to consider a broader range of factors and criteria, the proposed model empowers them to make more informed and nuanced decisions that reflect the real-world complexities of their specific situations. Furthermore, the proposed model incorporates advanced algorithms and techniques that enhance its robustness and scalability, allowing it to handle large and diverse data sets with ease. By leveraging these innovative features, the proposed model provides decision-makers with a powerful and reliable tool that can help them achieve their goals more efficiently and effectively.

5.3.   Advantages of proposed operators

(1) The Pythagorean cubic fuzzy aggregation operators that have been proposed exhibit a higher degree of flexibility in comparison to the currently existing Einstein aggregation operators for both Pythagorean fuzzy sets and interval-valued Pythagorean fuzzy sets. These new aggregation operators can incorporate more complex and nuanced relationships between input variables, allowing for more accurate and precise results. Moreover, the Pythagorean cubic fuzzy aggregation operators have a wider range of applications, making them a more versatile and adaptable tool for decision-making processes in a variety of fields.

(2) The Pythagorean cubic fuzzy set (PCFS) is a generalized form that can handle incomplete, indeterminate and inconsistent information commonly found in real-world problems. As a result, current studies using PCFS are more suitable for solving day-to-day problems than existing ones.

5.4.   Limitations

Limitations are inherent in all research, and this study is no exception. As with any research, these limitations will serve as a guide for future studies in this area.

(1) The study proposes new weighted averaging and ordered weighted averaging operators that use Einstein operations within a PCF environment. It is important to note that further advancements can be made by defining weighted geometric and ordered weighted geometric operators that utilize Einstein operations in the PCF environment in the future.

(2) In the current study, the demonstration is conducted using four criteria and four alternatives. However, in future research, data can be collected from multiple experts across various locations to validate the results of this study.

6.   Conclusions

The Pythagorean cubic fuzzy set is a significant and innovative framework where the degrees of membership and non-membership of an element are represented by cubic sets. By leveraging the benefits offered by these sets, the existing Einstein operations are extended to the Pythagorean cubic fuzzy environment. This extension of the Einstein operations allows for a more accurate and nuanced representation of uncertain or imprecise information, which is often encountered in decision-making processes. Drawing on these operational laws, a collection of aggregation operators, namely, Pythagorean cubic fuzzy Einstein weighted averaging and Pythagorean cubic fuzzy Einstein ordered weighted averaging operators, has been proposed to facilitate the aggregation of Pythagorean cubic fuzzy information. These operators offer enhanced flexibility and accuracy in dealing with uncertain or vague information and can be applied in various decision-making contexts. Furthermore, an MCDM algorithm is provided to deal with PCF information. To illustrate the proposed approach, a relevant example of investment decision-making in an optimal market has been provided. Lastly, the proposed results are compared with other existing approaches to confirm the stability and reliability of the proposed method.

In the future, the applicability of the findings in this paper could be extended to various uncertain and fuzzy environments such as interval 2-tuple linguistic multi-attribute decision-making ^[42], risk analysis ^[43] and others ^[44]. Also, Pythagorean cubic fuzzy numbers can only be utilized when the condition ${\left({\xi }^{U}\right)}^{2}+{\left({\zeta }^{U}\right)}^{2}\preccurlyeq 1$ is met. However, in certain real-world situations, this condition may not be satisfied, thereby posing a challenge to decision-makers. For instance, when a decision-maker rates an alternative as (0.8, 0.7), it cannot be accommodated by the proposed algorithm. Consequently, it may be necessary to conduct additional research to investigate these limitations.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the Small Groups Project under grant number (R.G.P.1/109/44).

Conflict of interest

The authors declare no conflict of interest.