Star edge coloring of $K_{2, t}$-free planar graphs

1.   Introduction

The graphs discussed in this paper are simple. When possibly multiple edges occurs, we call it a multigraph. The edge set, vertex set, minimum degree and maximum degree of $G$ are denoted by $E(G), V(G), \delta(G)$, and $\Delta(G)$, respectively. We sometimes use $E, V, \delta$, and $\Delta$ for short if $G$ is understood in the context. In a multigraph $G$, an edge coloring satisfying any two adjacent edges assigned distinct colors is called a proper edge coloring. The chromatic index $\chi'(G)$ denotes the minimum integer $s$ such that $G$ admits a proper edge coloring using $s$ colors. In 1964, Vizing ^[1] obtained a celebrated theorem stating that $\Delta+1 \ge \chi'(G)\ge \Delta$ for every simple graph $G$.

In 1983, Fouquet and Jolivet ^[2] first introduced and studied the notion of strong edge coloring. Here strong edge coloring means proper edge coloring such that any two edges with a distance at most $2$ have different colors. Similarly, we use $\chi'_{s}(H)$, called the strong chromatic index, to denote the minimum integer $c$ such that $H$ has a strong edge $c$-coloring. Introduced by Liu and Deng ^[3] in 2008, a star edge coloring of a graph $H$ is a proper edge coloring such that the edges of all cycles and paths of length $4$ are colored by at least three distinct colors, i.e., there is neither a bicolored path nor cycle with length $4$. The star chromatic index $\chi_{st}'(H)$ is the minimum integer $s$ such that $H$ admits a star edge coloring using color set $\{1, 2, \ldots, s\}$. According to the above definition, it is natural to obtain $\chi'(G)\le \chi'_{st}(G)\le \chi'_{s}(G).$

From the computational complexity point of view, Lei, Shi, and Song ^[4] showed that determining whether $\chi'_{st}(G)\le 3$ or not for a given graph is NP-complete. Given the difficulty of computing $\chi_{st}'(G)$, it is natural to consider its valid upper bounds. Liu and Deng ^[3] first proved a general result that, when $\Delta \geq 7$,

For sufficiently large $\Delta$, Dvořák et al. ^[5] further showed that

In addition, the star edge coloring problem remains hard for many graph classes. It is difficult even for complete graph $K_t$, where in ^[5] it is proved that

On the other hand, much better results are known for sparse graphs. In ^[5] it is obtained that every subcubic graph $H$ satisfies $\chi'_{st}(H)\le 7$. For trees, Deng et al. ^[6] and Bezegová et al. ^[7] showed a sharp bound below, independently.

Theorem 1.1 (^[7], ^[6]). For any tree $T$ with maximum degree $\Delta$, we have

and the bound is sharp.

Planar graphs are graphs that can be drawn on a plane without any edge crossing. If a graph has a plane embedding such that all vertices of the graph belong to the unbounded face of the drawing, we call it an outerplanar graph. For the star edge coloring of outerplanar graphs, Bezegová et al. ^[7] showed the results blow.

Theorem 1.2. ^[7] Suppose $G$ is an outerplanar graph.

(i) If $\Delta\ge 4$, then $\chi{'}_{st}(G)\le \lfloor 1.5\Delta \rfloor+12$;

(ii) If $\Delta\le 3$, then $\chi{'}_{st}(G)\le 5$.

Wang et al. ^[8] improved the above bounds of outerplanar graphs and studied more general graphs without $4$-cycles by introducing some novel edge-partition techniques. Their results are as below.

Theorem 1.3. ^[8] (i) For a planar graph $G$, $\chi{'}_{st}(G)\le 2.75\Delta+18$.

(ii) For a planar graph $G$ having no $4$-cycles, $\chi{'}_{st}(G)\le \lfloor 1.5\Delta \rfloor+18.$

(iii) For any outerplanar graph $H$, $\chi{'}_{st}(H)\le \lfloor 1.5\Delta \rfloor+5.$

If a planar graph $G$ has no $4$-cycles or $G$ is outerplanar, then $G$ is certainly $K_{2, 3}$-free, i.e., $G$ contains no complete bipartite graph $K_{2, 3}$ as a subgraph. By extending Theorem 1.3, we study the star edge coloring problem of more general planar graphs without $K_{2, t}$ for every $t\ge 2$ and prove the following main result.

Theorem 1.4. Let $t\ge 2$ be an integer. Then every $K_{2, t}$-free planar graph satisfies

Note that, as constructed in ^[9], there exists a family of planar graphs with maximum degree $\Delta$ containing $K_{2, \Delta}$ as a subgraph such that their star chromatic indices are at least $\frac{13}{8}\Delta -\frac{3}{4}$. So the upper bound in Theorem 1.4 is essentially sharp up to the constant term.

The rest of this paper is divided into several steps for discussion. We first describe the properties of $K_{2, t}$-free graphs in Lemma 2.1. Then, using those properties and some edge-partition methods, we show that $K_{2, t}$-free planar graphs can be edge decomposed into several parts and colored with different strategies to obtain the desired star edge coloring, thus proving our main result Theorem 1.4. Finally, we end this paper with a few concluding remarks.

2.   Star edge coloring of $K_{2, t}$-free planar graphs

For vertex $x\in V(G)$ in graph $G$, let $d_{G}(x)$(or $d(x)$ for short) be the degree of vertex $x$. If $d(x) = k$ ($d(x)\ge k$, or $d(x)\le k$, respectively), then $x$ is called a $k$-vertex($k^{+}$-vertex, or $k^{-}$-vertex, respectively). Let $N_G(x)$ denote the set of neighbors of $x$. A neighbor of vertex $x$ in $N_G(x)$ with degree $k$ (at most $k$, or at least $k$, respectively) is called a $k$-neighbor($k^{-}$-neighbor, or $k^{+}$-neighbor, respectively).

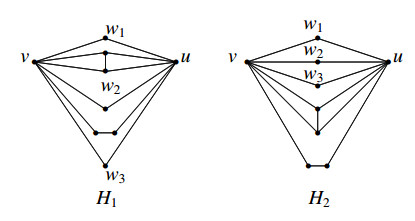
For a planar graph $G$ with a fixed plane embedded, let $F(G)$ be its face set. For $f\in F(G)$, $d_{G}(f)$ is used to denote the number of edges contained in face $f$. If $d_G(f)\ge 4$, then $f$ is called a $4^{+}$-face. A planar embedding of a planar graph $G$ is said an elegant drawing if it satisfies the following condition: for each pair of vertices $v, u\in V(G)$ with $\{w_1, w_2, \cdots, w_t\}$ being their common $2$-neighbors, in such an embedding the $2$-vertices $w_1, w_2, \cdots, w_t$ are all located successively in clockwise (or anticlockwise) order. That is, we require that each $4$-cycle $vw_{i}uw_{i+1}$ for $i\in \{1, 2, \cdots, t-1\}$ is not separating in such an embedding for any pair of vertices. For instance, in Figure 1 graph $H_2$ is an elegant drawing, while graph $H_1$ is not.

The key to our proof is the following lemma concerning the structure of planar graphs, which we prove below by discharging method.

Lemma 2.1. Given an integer $t\ge 2$, let $G$ be a simple planar graph with $\delta(G)\ge 2$. Then either there exists an edge $xy\in E(G)$ with $\max\{d(x), d(y)\}\le 5t+5$ or there exist $t$ $2$-vertices with two common neighbors.

Proof. By contradiction, suppose that such counterexamples to Lemma 2.1 exist. Let ${\mathcal P}$ denote the set of graphs $G$ satisfying the following two conditions:

(i) $G$ is a counterexample to Lemma 2.1,

(ii) for every $2$-vertex $u$ with $N_G(u) = \{u_1, u_2\}$, $u_1$ and $u_2$ are adjacent in $G$, i.e., $u_1u_2\in E(G)$.

We first claim that set ${\mathcal P}$ is nonempty.

Claim 1. We have ${\mathcal P}\neq \emptyset$.

Proof Let $G$ be an arbitrary counterexample. That is, we have $\max\{d(x), d(y)\}\ge 5t+6$ for every edge $xy\in E(G)$ and there do not exist $t$ $2$-vertices with two common neighbors in graph $G$.

If condition (ⅱ) is not satisfied, let $u$ be a $2$-vertex with two neighbors $a, b$ which are non-adjacent. Since $G$ is a counterexample, considering the edges $ua, ub$, we must have $d(a)\ge 5t+6$ and $d(b)\ge 5t+6$. Now we obtain a new graph from $G$ by connecting $b$ and $a$. Since the degrees of $b$ and $a$ are at least $5t+7$ now, the obtained graph is still a counterexample. So by a finite number of edge addition operations, the condition $(ii)$ can be satisfied. Note that the resulting graph is still a simple graph. Hence ${\mathcal P}\neq \emptyset$.

The rest of the proof will involve multigraphs, in which multiple edges may exist. Note that a simple graph itself is also a multigraph. Let ${\mathcal Q}$ be the collection of multigraphs $H$ satisfying the following three conditions:

($\alpha$-i) there do not exist $t$ $2$-vertices with two common neighbors in $H$, and for each edge $yx\in E(H)$ we have $\max\{d_H(y), d_H(x)\}\ge 5t+6$,

($\alpha$-ii) for every $2$-vertex $u$ with $N_H(u) = \{u_1, u_2\}$, $u_1$ and $u_2$ are adjacent in $H$;

($\beta$) the multigraph $G' = H-V_2(H)$ is a planar triangulation, where $G'$ is obtained from $H$ by eliminating all $2$-vertices of $H$, denoted by $V_2(H)$.

We now prove that the set ${\mathcal Q}$ is nonempty.

Claim 2. We have ${\mathcal Q}\neq \emptyset$.

Proof By Claim 1, ${\mathcal P}\neq \emptyset$, and so there exists a graph or multigraph $H\in {\mathcal P}$ satisfying conditions ($\alpha$-i) and ($\alpha$-ⅱ). Choose a multigraph $H$ satisfying conditions ($\alpha$-i) and ($\alpha$-ⅱ) such that the total length of all the $4^+$-faces in $G' = H-V_2(H)$ is minimized. We shall show below that $G' = H-V_2(H)$ is a triangulation.

By contradiction, fix arbitrary $4^{+}$-face $f$ in $G'$, and denote the vertices in the boundary of $f$ by $v_1, v_2, v_3, v_4, \ldots, v_p$ in a clockwise order. If $\max\{d_H(v_1), d_H(v_3)\}\ge 5t+6$, we add a new edge $v_1v_3$ in $H$ to obtain a new multigraph $H_1$. If $\max\{d_H(v_1), d_H(v_3)\}\le 5t+5$, then we must have $d_H(v_2)\ge 5t+6$ as $v_1v_2\in E(H)$ and by ($\alpha$-i). So we add a new edge $v_2v_4$ in $H$ to obtain a new multigraph $H_2$. Let $J = H_1$ or $H_2$. Then as

the multigraph $J$ still satisfies conditions ($\alpha$-i) and ($\alpha$-ⅱ). But by the construction of adding a new edge in a $4^+$-face, the total length of all the $4^+$-faces in $J$ is strictly smaller than that of $H$. This is a contradiction to the minimality of $H$. Thus there exists a multigraph $H\in {\mathcal Q}$ satisfying conditions ($\alpha$-i), ($\alpha$-ⅱ), and ($\beta$), proving this lemma. Note that $H$ may be a multigraph.

Now by Claim 2 we choose a multigraph $G\in {\mathcal Q}$. Denote $G' = G-V_2(G)$ as a planar triangulation by Claim 2. Then we provide some restrictions on the degrees in $G'$ and $G$.

Claim 3. We have $td_{G'}(v)\ge d_G(v)\ge d_{G'}(v)$ for any vertex $v$.

Proof Let $v\in V(G')$ be a vertex in $G'$. Denote $N_{G'}(v) = \{u_1, u_2, \cdots, u_{d_{G'}(v)}\}$. Note that $G' = G-V_2(G)$ is constructed from $G$ by eliminating all $2$-vertices. By condition ($\alpha$-i), for any edge $vu_i\in E(G')$, where $1\le i\le d_{G'}(v)$, there exists at most $t-1$ $2$-vertices in $G$ with $v, u_i$ as common neighbors. In other words, the edge $vu_i$ corresponds to at most $t-1$ $2$-vertices in an elegant drawing of $G$. Hence we obtain the desired inequality

Claim 4. We have $\delta(G')\ge 3$.

Proof Assume $\delta(G')\le 2$ and a minimum degree vertex of $G'$ is denoted by $v$. By the construction of $G'$ and by $\delta(G)\ge 2$, we have $d_G(v)\ge 3$, which implies that $v$ is adjacent to no less than one $2$-vertex $u$ in $G$. By Claim 3, $d_G(v)\le 2t$ and we obtain an edge $uv\in E(G)$ satisfying $\max\{d_G(u), d_G(v)\}\le 5t+5$, which is a contradiction to condition ($\alpha$-i) and Claim 2.

Claim 5. Each of the following holds.

(a) For each $u\in V(G')$ with $d_{G'}(u)\le 5$, $d_{G}(u) = d_{G'}(u).$

(b) Each $5^{-}$-vertex in $G'$ is neither adjacent to any $5^{-}$-vertex in $G'$ nor any $5^{-}$-vertex in $G$.

(c) Each $5^{-}$-vertex in $G'$ can not be adjacent to any $6$-vertex in $G'$.

Proof If (a) is not true, then $d_{G}(v) > d_{G'}(v).$ Hence the vertex $v$ is adjacent to at least one $2$-vertex $w$ in $G$. By Claim 3, it holds $d_G(v)\le td_{G'}(v)\le 5t$. Now we get an edge $vw\in E(G)$ with $\max \{d_G(v), d_G(w)\}\le 5t+5$, which is a contradiction to condition ($\alpha$-i) and Claim 2.

To prove (b), suppose that a $5^{-}$-vertex is adjacent to a $5^{-}$-vertex in $G'$ or $G$. This implies that a $(5t)^{-}$-vertex is adjacent to a $(5t)^{-}$-vertex in $G$ by Claim 4, which is a contradiction to condition ($\alpha$-i).

To prove (c), suppose that a $5^{-}$-vertex $v$ is adjacent to a $6$-vertex $u$. By Claim 5 (a), we obtain $d_G(v) = d_{G'}(v)$ which implies that the edge $uv$ does not correspond to any $2$-vertex of $G$ in an elegant drawing by condition ($\alpha$-i). For each other edge incident to $u$, by condition ($\alpha$-i) it corresponds to at most $t-1$ $2$-vertices of $G$ in an elegant drawing. Hence the vertex $u$ has degree $d_G(u)\le 6+5(t-1) < 5t+5$. Now $vu\in E(G)$ satisfies $\max \{d_G(v), d_G(u)\}\le 5t+5$, which is a contradiction to condition ($\alpha$-i) and Claim 2.

Claim 6. For any $u\in V(G')$, if $u$ is adjacent to at most five $6^{+}$-vertices in $G'$, then any neighbor $v$ of vertex $u$ has $d_{G'}(v)\ge 6.$

Proof By contradiction, suppose that a neighbor $v$ of vertex $u$ has $d_{G'}(v)\le 5$. By Claim 5(a), we have $d_G(v) = d_{G'}(v)\le 5$. By Claim 5 (b) again, each $5^{-}$-neighbor of $u$ have no $2$-vertex of $G$ as their common neighbor in $G$. For each $6^{+}$-neighbor of $u$, it has at most $t-1$ common $2$-neighbors with $u$ in $G$. Thus we have

Notice that $G'$ is a planar triangulation. By Claim 5 (b), considering the embedding of $6^{+}$-vertices neighbors around vertex $u$ in an elegant drawing, there is at most one $5^{-}$-neighbor of $u$ between two consecutive $6^{+}$-neighbors. Hence $d_{G'}(u)\le 10$ as $u$ is adjacent to at most five $6^{+}$-neighbors in $G'$. Therefore, we have $d_G(u)\le d_{G'}(u)+5(t-1)\le 5t+5$, and thus $vu\in E(G)$ satisfies $\max \{d_G(v), d_G(u)\}\le 5t+5$, contrary to condition ($\alpha$-i) and Claim 2.

Finally, we are able to complete the proof by a discharging method on $G'$. Assign initial charges by setting $m(x) = d_{G'}(x)-6$ for each vertex $x\in V(G')$ and $m(f) = 2(d_{G'}(f)-3)$ for each face $f\in F(G')$. Since $G'$ is a planar triangulation, we have $m(f) = 0$ for every face $f\in F(G')$. By rewriting Euler formula, it follows that

We shall use the following discharging rule.

Discharging Rule: Every $5^{-}$-vertex $v$ takes charges $\frac{6-d_{G'}(v)}{d_{G'}(v)}$ from each $7^{+}$-neighbor in $G'$.

We will derive the final contradiction from the next claim.

Claim 7. Each vertex in $G'$ has a non-negative charge after discharging.

Proof By Claim 5(c), every neighbor of each $5^{-}$-vertex in $G'$ has a degree of at least $7$. Hence the final charge of each $5^{-}$-vertex is at least zero by the discharging rule.

Assume that $u\in V(G')$ has degree $d_{G'}(u) = k\in \{7, 8, 9, 10\}$. We claim that $u$ is adjacent to at most $k-6$ $5^-$-vertex in $G'$. Otherwise, $u$ is adjacent to at most five $6^{+}$-vertices. Let $a$ be any $5^-$-neighbor of $u$. Then we have $d_G(a) = d_{G'}(a)\le 5$ by Claim 5(a). Since $\max\{d_G(u), d_G(a)\} > 5t+5$, we have $d_G(u) > 5t+5 > d_{G'}(u)$. But as $u$ has at most five $6^{+}$-neighbors, and for each $6^{+}$-neighbor at most $t-1$ $2$-vertices are added from $G'$ to $G$, and thus $d_G(u)\le 5(t-1) +k\le 5t+5$, a contradiction. This verifies our claim that $u$ is adjacent to at most $k-6$ $5^-$-vertex in $G'$. By the discharging rule, the vertex $u$ loses at most $d_{G'}(u)-6$ charges and remains non-negative.

Assume instead that $u\in V(G')$ has degree $d_{G'}(u)\ge 11$. If $u$ is adjacent to at least six $6^{+}$-vertices, then $u$ is adjacent to at most $d_{G'}(u)-6$ $5^-$-vertices in $G'$, and hence the final charge is non-negative by our discharging rule. If $u$ is adjacent to at most five $6^{+}$-vertices, then it follows from Claim 6 that the final charge of $u$ is $d_{G'}(u)-6 > 0$. Therefore, we have proved that each vertex in $G'$ has a non-negative charge after discharging.

As $G'$ is a planar triangulation, the final charge of each face in $G'$ is zero. By Claim 7, each vertex has a non-negative final charge. Hence total final charge is non-negative, which is a contradiction to Equation (2.1). This contradiction proves Lemma 2.1.

Lemma 2.1 leads to the following edge-partition result on $K_{2, t}$-free planar graphs.

Lemma 2.2. Let $G$ be a $K_{2, t}$-free planar graph, where $t\ge 2$ is an integer. Then we can edge-partition $G$ into a forest $T$ and a subgraph $H\subseteq G$ with $\Delta(H)\le 5t+5.$

Proof. Let $G$ be a minimal counterexample with $|E(G)|+|V(G)|$ as small as possible. If $\delta(G) = 1$, then we denote a $1$-vertex by $u$ and its unique neighbor by $v$. By the minimal counterexample property, we can edge-partition the graph $G' = G-\{uv\}$ into a forest $T'$ and a subgraph $H'\subseteq G'$ with $\Delta(H')\le 5t+5.$ Denote $T = T'+{uv}$ and $H = H'$. By $d_G(u) = 1$, $T$ has no cycle, and thus it is a forest with $\Delta(T)\le \Delta(G)$, and we have further $\Delta(H)\le 5t+5$, which is a contradiction. Hence we obtain $\delta(G)\ge 2$. It follows from Lemma 2.1 that we have an edge $xy\in E(G)$ with $\max\{d_G(x), d_G(y)\}\le 5t+5$. Let $G^* = G-\{xy\}$. So $E(G^*)$ can be decomposed into a forest $T^*$ and a subgraph $H^*\subseteq G^*$ with $\Delta(H^*)\le 5t+5$. Let $H = H^*+\{xy\}$. Since $\Delta(H)\le \max\{\Delta(H^*), d_G(x), d_G(y)\}$, $T = T^*$ and $H = H^*+\{xy\}$ are the desired partition of $G$, which is a contradiction.

We need one more result on edge coloring as part of the prerequisites.

Theorem 2.3 (^[10], ^[11]). Let $H$ be a planar graph with maximum degree $\Delta$. If $k = \max\{\Delta, 7\}$, then $H$ is $k$-edge-colorable.

Now it is ready to demonstrate the main result of Theorem 1.4 restated below.

Theorem 2.4. Let $G$ be a $K_{2, t}$-free planar graph, where $t\ge 2$ is an integer. We have

Proof. By Lemma 2.2, we can edge-partition $G$ into a forest $T$ with $\Delta(T)\le \Delta(G)$ and a planar subgraph $H\subseteq G$ with $\Delta(H)\le 5t+5$. By Theorem 1.1, $\chi'_{st}(T) = k\le \lfloor1.5\Delta\rfloor$, thus we have a star $k$-edge-coloring $\phi:E(T)\mapsto \{f_1, f_2, \ldots, f_k\}$ for $T$. By Theorem 2.3 and $\Delta(H)\le 5t+5$, $H$ is $(5t+5)$-edge-colorable, and consequently $H$ has an edge-partition $E_1, E_2, \ldots, E_{5t+5}$, where $E_i$ denotes the collection of edges of color-$i$ for each $1\le i\le 5t+5$. For fixed $i\in \{1, \ldots, 5t+5\}$, consider the graph $G_i$ constructed from $G$ by contracting edge set $E_i$. By the planarity of $G_i$, it follows from the Four Color Theorem that $G_i$ is $4$-vertex colorable with colors saying $\{a_i, b_i, c_i, d_i\}$. Note that every edge $e$ in $E_i$ of $G$ corresponds a contracted vertex in $G_i$, and we use its color to color the edge $e$. After performing this coloring process for all $i\in \{1, \ldots, 5t+5\}$, we obtain a $4(5t+5)$-edge-coloring $\psi: E(H)\mapsto \cup_{i = 1}^{5t+5}\{a_i, b_i, c_i, d_i\}$. Furthermore, each pair of edges $e_1, e_2\in E(H)$ with distance at most $2$ receive different colors in the coloring $\psi$ by its construction.

Then we show below that $\phi\cup\psi$ is a star edge coloring of $G$ using $k+4(5t+5)\le \lfloor1.5\Delta\rfloor +4(5t+5)$ colors. Clearly, $\phi\cup\psi$ is a proper edge coloring of $G$, i.e., any adjacent edges get distinct colors. Let $P = x_1x_2x_3x_4x_5$ denote a path or cycle with $4$ edges. Note that each edge in $E(T)$ receives a color in $\{f_1, f_2, \ldots, f_k\}$, and each edge in $E(H)$ receives a color in $\cup_{i = 1}^{5t+5}\{a_i, b_i, c_i, d_i\}$. If $x_1x_2$ and $x_3x_4$ receive the same color, then by the construction of coloring $\phi\cup\psi$, we must have both $x_1x_2\in E(T)$ and $x_3x_4\in E(T)$, as any two edges with distance two in $E(H)$ receive distinct colors. If $x_2x_3$ and $x_4x_5$ receive the same color, then we also have $x_2x_3, x_4x_5\in E(T)$ for the same reason. But since $\phi$ is a star edge coloring of $T$, $\phi(x_2x_1) = \phi(x_4x_3)$ and $\phi(x_3x_2) = \phi(x_5x_4)$ can not occur simultaneously. Therefore, $\phi\cup\psi$ is a star edge coloring of $G$ by definition.

3.   Conclusions

This paper has shown that every $K_{2, t}$-free planar graph admits a star $(\lfloor1.5\Delta\rfloor+20t+20)$-edge coloring, which is sharp up to the constant term. This can be evident by the planar graph constructed in ^[9], whose star chromatic index is at least $\frac{13}{8}\Delta -\frac{3}{4}$ and contains $K_{2, \Delta}$ as a subgraph. On the other hand, it would be interesting to push further on the constant term to determine the optimal upper bound. In ^[7], a similar problem is proposed for outerplanar graphs by the authors, who conjectured that every outplanar graph is star $(\lfloor1.5\Delta\rfloor +1)$-edge colorable. Another related research direction is to consider the list version of star edge coloring. The edge-partition techniques in this paper (and in the literature) could not be generalized to list star edge coloring. There are some other techniques, such as that of ^[9], which may be helpful in handling list star edge coloring. It should be of interest to search for a similar list version of Theorem 1.4, or its subclass of graphs like outerplanar graphs and $C_4$-free planar graphs.

Acknowledgments

The authors would like to thank all the reviewers for their very helpful comments and constructive suggestions. This research is partially supported by the National Natural Science Foundation of China (No. 11901434).

Conflict of interest

The authors declare there is no conflict of interest.