The optimization of fractional-order (FO) chaotic systems is challenging when simulating a considerable number of cases for long times, where the primary problem is verifying if the given parameter values will generate chaotic behavior. In this manner, we introduce a methodology for detecting chaotic behavior in FO systems through the analysis of Poincaré maps. The optimization process is performed applying differential evolution (DE) and accelerated particle swarm optimization (APSO) algorithms for maximizing the Kaplan-Yorke dimension (DKY) of two case studies: a 3D and a 4D FO chaotic systems with hidden attractors. These FO chaotic systems are solved applying the Grünwald-Letnikov method, and the Numba just-in-time (jit) compiler is used to improve the optimization process's time execution in Python programming language. The optimization results show that the proposed method efficiently optimizes FO chaotic systems with hidden attractors while saving execution time.
Citation: Daniel Clemente-López, Esteban Tlelo-Cuautle, Luis-Gerardo de la Fraga, José de Jesús Rangel-Magdaleno, Jesus Manuel Munoz-Pacheco. Poincaré maps for detecting chaos in fractional-order systems with hidden attractors for its Kaplan-Yorke dimension optimization[J]. AIMS Mathematics, 2022, 7(4): 5871-5894. doi: 10.3934/math.2022326
| [1] | Alqahtani Bushra Abdulshakoor M, Weibin Liu . Li-Yorke chaotic property of cookie-cutter systems. AIMS Mathematics, 2022, 7(7): 13192-13207. doi: 10.3934/math.2022727 |
| [2] | Hany A. Hosham, Thoraya N. Alharthi . Bifurcation and chaos in simple discontinuous systems separated by a hypersurface. AIMS Mathematics, 2024, 9(7): 17025-17038. doi: 10.3934/math.2024826 |
| [3] | Nehad Ali Shah, Iftikhar Ahmed, Kanayo K. Asogwa, Azhar Ali Zafar, Wajaree Weera, Ali Akgül . Numerical study of a nonlinear fractional chaotic Chua's circuit. AIMS Mathematics, 2023, 8(1): 1636-1655. doi: 10.3934/math.2023083 |
| [4] | Ying Sun, Yuelin Gao . An improved composite particle swarm optimization algorithm for solving constrained optimization problems and its engineering applications. AIMS Mathematics, 2024, 9(4): 7917-7944. doi: 10.3934/math.2024385 |
| [5] | Najeeb Alam Khan, Samreen Ahmad . Framework for treating non-Linear multi-term fractional differential equations with reasonable spectrum of two-point boundary conditions. AIMS Mathematics, 2019, 4(4): 1181-1202. doi: 10.3934/math.2019.4.1181 |
| [6] | Asharani J. Rangappa, Chandrali Baishya, Reny George, Sina Etemad, Zaher Mundher Yaseen . On the existence, stability and chaos analysis of a novel 4D atmospheric dynamical system in the context of the Caputo fractional derivatives. AIMS Mathematics, 2024, 9(10): 28560-28588. doi: 10.3934/math.20241386 |
| [7] | A. E. Matouk . Chaos and hidden chaos in a 4D dynamical system using the fractal-fractional operators. AIMS Mathematics, 2025, 10(3): 6233-6257. doi: 10.3934/math.2025284 |
| [8] | Jun Moon . The Pontryagin type maximum principle for Caputo fractional optimal control problems with terminal and running state constraints. AIMS Mathematics, 2025, 10(1): 884-920. doi: 10.3934/math.2025042 |
| [9] | Martin Do Pham . Fractal approximation of chaos game representations using recurrent iterated function systems. AIMS Mathematics, 2019, 5(6): 1824-1840. doi: 10.3934/math.2019.6.1824 |
| [10] | Iqbal M. Batiha, Reyad El-Khazali, Osama Y. Ababneh, Adel Ouannas, Radwan M. Batyha, Shaher Momani . Optimal design of $ PI^\rho D^\mu $-controller for artificial ventilation systems for COVID-19 patients. AIMS Mathematics, 2023, 8(1): 657-675. doi: 10.3934/math.2023031 |
The optimization of fractional-order (FO) chaotic systems is challenging when simulating a considerable number of cases for long times, where the primary problem is verifying if the given parameter values will generate chaotic behavior. In this manner, we introduce a methodology for detecting chaotic behavior in FO systems through the analysis of Poincaré maps. The optimization process is performed applying differential evolution (DE) and accelerated particle swarm optimization (APSO) algorithms for maximizing the Kaplan-Yorke dimension (DKY) of two case studies: a 3D and a 4D FO chaotic systems with hidden attractors. These FO chaotic systems are solved applying the Grünwald-Letnikov method, and the Numba just-in-time (jit) compiler is used to improve the optimization process's time execution in Python programming language. The optimization results show that the proposed method efficiently optimizes FO chaotic systems with hidden attractors while saving execution time.
Chaos theory is the branch of mathematics that deals with complex behavior emerging in dynamical systems [1]. Chaotic systems possess special features such as extreme sensitivity to initial conditions, random-like unpredictable behavior and ergodicity. Improving these characteristics enhance applications in almost every field of science and engineering, such as: Biology [2], astrophysics [3], mechanics [4], economics [5], secure communications [6], cryptography [7], robotics [8], control [9] and so on. With the study of fractional calculus, it has been found that Fractional-Order (FO) derivatives serve as an extra-degree freedom for enhancing chaos-based applications, this thanks to the FO derivatives that have inheritance or memory properties that preserve complex phenomena with more accuracy [10,11]. For instance, in cryptography and secure communications, FO chaotic systems can generate larger keyspace than their integer counterpart [12,13].
According to the literature, attractors of dynamical systems can be divided into two categories depending on the localization of their equilibrium points in the corresponding basin of attraction [14]. On the one hand, chaotic systems with self-excited attractors are those whose basin of attraction intersects with an unstable equilibrium. On the other hand, chaotic systems with hidden attractors have a basin of attraction that does not intersect with any open neighborhoods of equilibria. Since the first hidden attractor was found in the classical Chua's circuit [15], much more attention has been shifted towards this new type of attractors. Firstly, the dynamics of hidden attractors are highly complex to analyze since they can lead to unexpected behavior. For instance, complex phenomena such as "Multistability" [16], which refers to when two or more different attractors coexist under the same parameters are likely to appear in dynamical systems with hidden attractors. The multistability phenomena depend on the initial conditions to switch between one attractor to a totally different one, and this property can be used as an additional source of randomness for potential applications. For instance, but not limited to, they might enhance the performance on cryptography [17], and secure communications [18].
There exist few studies related to FO chaotic systems with hidden attractors, but FO derivatives can generate several families of hidden chaotic attractors in their commensurate and incommensurate models where multistability phenomena can also be observed [19,20]. Therefore, the research effort oriented to FO chaotic systems with hidden attractors is an area of opportunity to enhance chaos-based applications. One of the critical factors that guarantees the success of those applications, is the complexity degree of the chaotic attractor that can be quantified by its Kaplan-Yorke dimension (DKY). In this manner, the application of metaheuristics, such as: Differential Evolution (DE) and Accelerated Particle Swarm Optimization (APSO) algorithms, has gained interest in recent years for solving optimization problems of FO chaotic systems [21]. In [22] the optimization through metaheuristics of the DKY is achieved on four FO chaotic systems with self-excited attractors, a similar approach is presented in [23]. To the best of the authors' knowledge, there are no works that explore the optimization of FO chaotic systems with hidden attractors.
Motivated by the above discussion, this paper aims to introduce the optimization of FO chaotic systems with hidden attractors. One of the challenges in the optimization process, is that hidden attractors have small basin of attraction [24,25,26], and thus, tiny variations in the parameters, and fractional-order derivatives or initial conditions can easily shift the chaotic behavior to a periodic dynamics. Hence, careful considerations needs to be taken to ensure that the optimization process is performing correctly. The literature reports several methods for detecting Chaos in dynamical systems, such as phase portraits, bifurcation diagrams, equilibrium points analysis through Shilnikov theorem, Lyapunov exponents (LEs), Poincaré maps, among others. It is well-known that LEs provide quantitative information over the stretching and folding of the chaotic attractors. However, accurate computation of Lyapunov exponents requires the analysis of large time series by specialized library packages such as TISEAN [27], which can be high computational expensive, but LEs are necessary for calculating the DKY of a chaotic attractor. For such problem, one can introduce constraints that ensures the chaotic motion for its LEs computation through TISEAN. In this manner, Poincaré maps provide a qualitative understating of the dynamical characteristics of a n-dimensional system into a (n−1) representation [28]. This is done by the intersection analysis of a hyper-plane transverse to the flow of the dynamical system, then the Poincaré map corresponding to a chaotic system should display enough distribution over a 2-D plane. In this regard, the contribution of this work is to detect chaotic motion in FO chaotic systems with hidden attractors through the distribution quantification of Poincaré maps. Moreover, to save execution time, the optimization algorithms are implemented by using the Numba just-in-time (jit) compiler in the Python programming language.
The rest of the paper is organized as follows: Section 2 summarizes the background of this work. DE and APSO algorithms are described in Section 3. Section 4 shows the numerical analysis of the FO chaotic systems. Section 5 details the optimization process whereas the discussion of the optimization results is presented in Section 6. Finally, the authors' conclusions are given in Section 7.
Although one can cite various definitions of FO derivatives such as as the Grünwald-Letnikov [29], Riemman Liouville [30] and Caputo definitions [31], these mathematical interpretations do not allow a direct understanding of the derivative solution. Therefore, the solution of FO differential equations are often obtained through numerical approximations accordingly the used fractional derivative definition [32,33,34,35]. For instance, the Adams Bashforth Moulton (ABM) method is a predictor-corrector scheme highly recognized as a valuable fractional calculus tool due to the good approximation that it produces [36]. Drawbacks of this scheme are related to the complexity for representing the memory properties of FO derivatives, that requires from long time computation. The Grünwald Letnikov (GL) method is another numerical scheme very suitable for solving FO systems. It can be considered as a generalization of the Euler method for solving ordinary differential equations [37]. The GL method is of low computational cost and has approximately the same order of accuracy and good match of numerical solutions as ABM [38]. Therefore, this work uses the Grünwald-Letnikov method for solving the FO differential equations that comprises the FO chaotic systems that are the case study. The mathematical description is given below.
According to the explicit numerical approximation of the Grünwald-Letnikov derivative [39], the FO derivative 0<q<1 for a discrete function f(tk), can be described by (2.1), h is the integration step-size, and Cqj are binomial coefficients which are recursively calculated by (2.2).
| Dqtkf(tk)≈h−qk∑j=0Cqjf(tk−j), | (2.1) |
| Cq0=1,Cqj=(1−1+qj)Cqj−1,j=1,2,...,k. | (2.2) |
The solution of a FO system in the form Dqtkx(tk)=f(x(tk)), can be obtained by (2.3), which ideally requires infinite memory length for numerical simulation since the summation term depends on the discretized time tk.
| x(tk)=f(x(tk−1))hq−k∑j=1Cqjx(tk−j). | (2.3) |
One of the features of chaos behavior is the existence of a dense set of periodic orbits, which implies that any periodic trajectory of the orbit visits an arbitrarily small neighborhood of a non-periodic one [40]. In this manner, and since Poincaré maps preserve many of the orbits of dynamical systems, it is a viable tool for detecting chaos in both integer and FO systems [41,42]. Below is described the elaboration of a Poincaré map.
Lets consider a FO system of the form given in (2.4), where 0<q<1, x(t)=[x1(t),x2(t),...,xn(t)]T∈Rn and f(x(t))=[f1(x(t)),f2(x(t)),...,fn(x(t))]T.
| Dqtx(t)=f(x(t)), | (2.4) |
The Poincaré map of the system given in (2.4) is obtained as follows:
(1) Without loss of generality, let Σ∈Rn−1 be the Poincaré section of system (2.4) such that Σ∩x(t)=[x1(t),x2(t),...,xn−1(t)]T.
(2) Next, the Poincaré section is settled on a given xn=σ.
(3) Finally, all states [x1(t),x2(t),...,xn−1(t)]T are captured each time the dynamical flow intersects the Poincaré section.
The captured points by the above procedure portrait the Poincaré map of system (2.4), then, the behavior of the system is obtained by analyzing the distribution of the distinct points of the Poincaré map. If the Poincaré map consists neither of a small number of points or filling a continuous line but instead a large and irregular distribution, then it is a strong indicator of chaos [43].
The Kaplan Yorke dimension DKY describes the fractal dimension of an attractor by means of its Lyapunov exponents as follows [44]:
| DKY=j+1|λj+1|j∑k=1λk, | (2.5) |
herein, the Lyapunov exponents are sorted from highest to lowest λ1≥λ2≥⋯≥λj+1 and j∈N is the largest integer for which λ1+λ2+⋯+λj≥0. The DKY gives a meaningful measure to quantify the complexity of a chaotic attractor [45,46]. Therefore, it is the interest of this optimization work to determine a set of parameters and fractional orders that leads to a higher DKY.
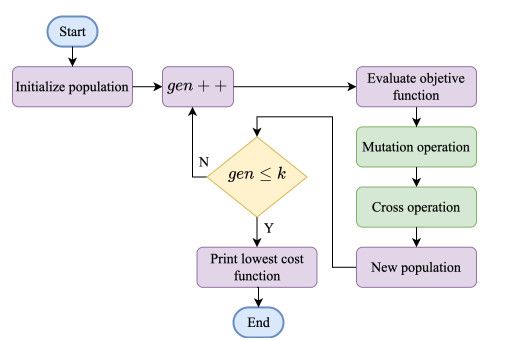
The Differential Evolution (DE) algorithm belongs to the family of algorithms based on biological evolution, which uses genetic cross and mutation operators to generate new candidate solutions [47]. The structure of DE is illustrated in the chart flow of Figure 1, whose description is as follows:
(1) In the first step, the initial population is generated within the range of interest.
| Xi∈Rn,i=1,2,...,p, | (3.1) |
(2) Next, the objective function is evaluated for each individual in the population
| ∀Xi,dof(Xi)∈R. | (3.2) |
(3) In the next step, the mutation operation is carried out:
● (3.1) First, three randomly individuals X1, X2 and X3 are selected.
● (3.2) Then, the following operation is performed:
| wi=X1+μ(X2−X3) | (3.3) |
where μ∈R is a scaling parameter.
(4) In the next step, individuals are crossed according to the condition
| Fi(j)={wi(j), rand≤Cr,Xi(j),other. | (3.4) |
Specifically, if the random number (rand) is less than or equal to the cross parameter Cr, then the term Fi(j) takes the value wi(j), otherwise it will be Xi(j). Next, the first generation of individuals generates new individuals through mutation and cross operations. Subsequently, the objective function is evaluated in the new individual.
(5) Steps 2–5 are repeated for a number of k generations.
(6) In the last step, the lowest cost function is printed.
In the Accelerated Particle Swarm Optimization (APSO) algorithm, the tentative solutions are called particles. This algorithm consists of disturbing the behavior of the particles in such a way that they can move within a search space and finding the solution to the optimization problem [48]. The algorithm is inspired by the flight of birds to find food in an unknown field with the lowest possible energy expenditure, which can be translated into finding the minimum value of a function. The structure of the APSO is illustrate in the chart flow of Figure 2, and its description is given as follows:
(1) In the first step, the initial population is generated, meaning the particles position within a range of interest.
| Xi∈Rn,i=1,2,...,p. | (3.5) |
(2) Next, the objective function is evaluated for each particle
| ∀Xi,dof(Xi)∈R. | (3.6) |
(3) In the next step, the position of the particles is disturbed:
● (3.1) First, the best particles are selected
| g∗=min(f(Xi)). | (3.7) |
● (3.2) Then, the position is updated
| Xi(k+1)=(1−β)+βg∗+αϵn. | (3.8) |
Specifically, the new population is generated from the change in position of the particles. The value for ϵn is randomly initialized within the range [0,1] whereas α and β are estimated experimentally.
(4) Steps 2–5 are repeated for a number of k generations.
(5) In the last step, the lowest cost function is printed.
This section shows the numerical simulations and Poincaré maps of the FO chaotic systems that are case study. For instance, the authors in [19] introduced the 3D FO chaotic system given in (4.1), where 0<qi<1, (i=1,2,3) and a∈R. According to expression (4.2), it can be seen that by setting the parameter a>1/4, the 3D FO chaotic system does not posses an equilibrium point (Ep=(ˉx,ˉy,ˉz)), and thus, any existing basin of attraction is considered as hidden.
| Dq1tx=yz+x(y−a),Dq2ty=1−|x|,Dq3tz=−xy−z, | (4.1) |
| Ep1=(1,(1+√1−4a)/2,−(1+√1−4a)/2),Ep2=(−1,(1−√1−4a)/2,(1−√1−4a)/2),Ep3=(1,(1−√1−4a)/2,−(1−√1−4a)/2),Ep4=(−1,(1+√1−4a)/2,(1−√1−4a)/2). | (4.2) |
By taking into account (2.3), the solution of the 3D FO chaotic system by means of the Grünwald-Letnikov method is given in (4.3), whereas Figure 3 shows the simulation results. Figure 4 shows the LEs spectra by varying the fractional derivative.
| x(tk)=(y(tk−1)z(tk−1)+x(tk−1)(y(tk−1)−a))hq1−k∑j=1Cq1jx(tk−j),y(tk)=(1−|x(tk−1)|)hq2−k∑j=1Cq2jy(tk−j),z(tk)=(−x(tk−1)y(tk−1)−z(tk−1))hq3−k∑j=1Cq3jz(tk−j). | (4.3) |

To demonstrate the usefulness of Poincaré maps in detecting chaotic behavior, a Poincaré section Σ∈R2 on y=2 is defined as depicted in Figure 5 (a), then, by following the steps of Section 2.2, the Poincaré map of Figure 5 (b) is obtained. It can be seen that the displayed points resembles the xz phase portrait of Figure 3 (b), the markers illustrates if the flow intersects the Poincaré section on y>2 (blue, in-direction) and if it intersects on y<2 (red, out-direction).
It is worthy to mention that the number of points portrayed in the Poincaré map is in relation to the amount of used data. However, the number of points itself says nothing about the dynamical behavior. For instance, lets us consider the dynamical behavior of the system (4.1) illustrated in Figure 6, then, a Poincaré section Σ∈R2 on y=2 is defined as depicted in Figure 7 (a). The obtained Poincaré map in Figure 7 (b) displays only two points, indicating the flow intersects twice in different in-out directions of the Poincaré section, and thus, resembling a periodic behavior. Nevertheless, this is only apparent, due to the fact of the non-existence of exactly periodic solutions in FO systems [49,50], thereby, the importance of the distribution quantization of the Poincaré map. The next step is the distribution quantization of the Poincaré map. Herein, a simple procedure is proposed as follows:

(1) Verify that the solution of a system (4.1) remains bounded but does not converge to a fixed point.
(2) Next, the first 10 % samples of the time series are deleted to avoid the initial transient.
(3) Then, the Poincaré map is portrayed with the obtained points when the flow intersects on y<2 (out-direction).
(4) In the next step, only the points that satisfies the condition (4.4) are considered, where (uj,vj) and (uk,vk) denotes the coordinates of the Pj and Pk points respectively, p is the total number of points intersecting the Poincaré section and ϵ=0.1, this ensures to preserve only the points distributed over the plane and remove those located closer than (ϵ,ϵ),
| |Pj(uj,vj)−Pk(uk,vk)|≥(ϵ,ϵ),k=j+1,⋯,p,∀j=1,2,⋯p−1. | (4.4) |
(5) Finally, the number of points remaining in the Poincaré map is co-related with the dynamical behavior.
For instance, Figures 8 and 9 illustrates the hidden attractors and its corresponding Poincaré maps when system (4.1) behaves quasi-periodic. After applying 1–5 from above procedure, the obtained results in Table 1 shows that the remaining points are 10 and 3 respectively. On the other hand, when system (4.1) behaves chaotic such as in Figure 5, the remaining points in the Poincaré map must portrait ≈100 points.
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=0.35 | q1=0.97, q2=0.97, q3=0.97 |
107 | λ1=0.0011, λ2=−0.0006, λ3=−0.0036 |
2.1504 | chaotic |
| a=0.3 | q1=0.993, q2=1, q3=0.75 |
96 | λ1=0.0010, λ2=−0.0009, λ3=−0.0047 |
2.0208 | chaotic |
| a=0.325 | q1=1, q2=0.99, q3=0.85 |
104 | λ1=0.0018, λ2=−0.0006, λ3=−0.0057 |
2.2071 | chaotic |
| a=0.337 | q1=0.966, q2=0.968, q3=0.926 |
105 | λ1=0.0013, λ2=−0.0008, λ3=−0.0036 |
2.1452 | chaotic |
| a=0.6 | q1=0.992, q2=0.938, q3=0.968 |
94 | λ1=0.0022, λ2=−0.0009, λ3=−0.0051 |
2.2452 | chaotic |
| a=0.437 | q1=0.993, q2=0.956, q3=0.874 |
105 | λ1=0.0010, λ2=−0.0009, λ3=−0.0043 |
2.003 | chaotic |
| a=0.322 | q1=0.982, q2=0.955, q3=0.985 |
96 | λ1=0.0017, λ2=−0.0009, λ3=−0.0052 |
2.1593 | chaotic |
| a=0.29 | q1=0.986, q2=0.967, q3=0.981 |
17 | λ1=0.0008, λ2=−0.0017, λ3=−0.0018 |
1.5219 | quasi-periodic |
| a=0.436 | q1=0.998, q2=0.989, q3=0.986 |
10 | λ1=0.0007, λ2=−0.0012, λ3=−0.0028 |
1.8214 | quasi-periodic |
| a=0.277 | q1=0.988, q2=0.948, q3=0.881 |
3 | λ1=0.0009, λ2=−0.0038, λ3=−0.0183 |
1.8415 | quasi-periodic |
| a=0.382 | q1=0.994, q2=0.922, q3=97 |
2 | λ1=−0.0003, λ2=−0.0011, λ3=−0.0015 |
1.06 | quasi-periodic |
| a=0.387 | q1=0.976, q2=0.968, q3=0.804 |
2 | λ1=0.0001, λ2=−0.0011, λ3=−0.0016 |
1.375 | quasi-periodic |
The second case study is a 4D FO chaotic system introduced in [51] as a 4D integer chaotic system with coexisting hidden attractors. Later on, in [52] the FO version given in (4.5) was proposed, where 0<qi<1, (i=1,2,3) and a∈R. According to expression (4.6), it can be seen that for a≠0, the 4D FO chaotic system does not present an equilibrium point (Ep=(ˉx,ˉy,ˉz,ˉw)), and thus, any existing basin of attraction is considered as hidden.
| Dq1tx=y−x,Dq2ty=−xz+w,Dq3tz=xy−a,Dq4tz=−by, | (4.5) |
| y−x=0,−xz+w=0,xy−a=0,−by=0. | (4.6) |
By taking into account (2.3), the solution of the 4D FO chaotic system by means of the Grünwald-Letnikov method is given in (4.7), whereas Figure 10 shows the simulation results. Figure 11 shows the LEs spectra by varying the fractional derivative.
| x(tk)=(y(tk−1)−x(tk−1))hq1−k∑j=1Cq1jx(tk−j),y(tk)=(−x(tk−j)z(tk−j)+w(tk−j))hq2−k∑j=1Cq2jy(tk−j),z(tk)=(x(tk−1)y(tk−1)−a))hq3−k∑j=1Cq3jz(tk−j),z(tk)=(−by(tk−1))hq3−k∑j=1Cq4jw(tk−j). | (4.7) |

In the same manner, a Poincaré map is elaborated for analyzing the behavior of the 4D FO chaotic system. Herein, the Poincaré section Σ∈R2 is settled on z=0 as depicted in Figure 12 (a), then, by following the steps of Section 2.2, the Poincaré map of Figure 12 (b) is obtained.
The distribution quantization of the Poincaré map of the 4D FO chaotic system is quite similar to the quantization of the Poincaré map of the 3D FO chaotic system. Herein, only the obtained points when the flow intersects on z>0 (in-direction) are considered with a separation of ϵ=0.1. This procedure is repeated for different parameters and fractional order for the system (4.5). The obtained results with a number of data of 1.20×105 are shown in Table 2. It can be seen that for chaotic behavior to exist in the system (4.1), its corresponding Poincaré map must portrait ≈40−60 points.
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=3.5, b=0.1 |
q1=0.98, q2=0.98, q3=0.98, q4=0.98 |
43 | λ1=0.0011, λ2=0, λ3=−0.0001, λ4=−0.0024 |
3.4257 | chaotic |
| a=3.5, b=0.1 |
q1=1.0, q2=0.997, q3=1.0, q4=0.45 |
50 | λ1=0.0030, λ2=0, λ3=−0.0017, λ4=−0.0040 |
3.3368 | chaotic |
| a=2.9, b=0.1 |
q1=0.45, q2=0.95, q3=1.0, q4=0.985 |
40 | λ1=0.0008, λ2=0, λ3=−0.0003, λ4=−0.0030 |
3.1666 | chaotic |
| a=3.162, b=0.182 |
q1=0.980, q2=0.942, q3=0.978, q4=0.975 |
42 | λ1=0.0008, λ2=0.0001, λ3=0, λ4=−0.0018 |
3.5029 | hyper-chaotic |
| a=3.128, b=0.285 |
q1=0.946, q2=0.964, q3=0.957, q4=0.923 |
41 | λ1=0.0003, λ2=0.0001, λ3=0, λ4=−0.0006 |
3.5103 | hyper-chaotic |
| a=3.131, b=0.285 |
q1=0.945, q2=0.963, q3=0.956, q4=0.922 |
41 | λ1=0.0004, λ2=0.0002, λ3=0, λ4=−0.0011 |
3.5282 | hyper-chaotic |
| a=3.088, b=0.12 |
q1=0.925, q2=0.948, q3=0.933, q4=0.932 |
38 | λ1=0.0016, λ2=0, λ3=−0.0004, λ4=−0.0031 |
3.387 | chaotic |
| a=3.601, b=0.3 |
q1=0.999, q2=0.999, q3=0.999, q4=0.962 |
48 | λ1=0.0005, λ2=0, λ3=−0.0001, λ4=−0.0022 |
3.2014 | chaotic |
| a=9.4, b=0.01 |
q1=0.936, q2=0.935, q3=0.958, q4=0.946 |
60 | λ1=0.0009, λ2=0, λ3=−0.0001, λ4=−0.0013 |
3.5972 | chaotic |
| a=8.4, b=0.1 |
q1=0.990, q2=0.980, q3=0.980, q4=0.981 |
8 | λ1=0, λ2=−0.0002, λ3=−0.0014, λ4=−0.0039 |
2.5897 | quasi-periodic |
| a=7.8, b=0.1 |
q1=0.990, q2=0.980, q3=0.970, q4=0.981 |
10 | λ1=0, λ2=−0.0002, λ3=−0.0011, λ4=−0.0041 |
2.6829 | quasi-periodic |
| a=7.3, b=0.08 |
q1=0.989, q2=0.998, q3=0.967, q4=0.981 |
11 | λ1=−0.0001, λ2=−0.0002, λ3=−0.0007, λ4=−0.0042 |
2.7619 | quasi-periodic |
This section details the maximization process of the DKY for the 3D and 4D FO chaotic systems. Given the nature of the DE and APSO, the optimization problem is given as follows:
| Maximize(f(X))=Minimize(−f(X)),f(X)∈R, | (5.1) |
where X∈Rn are the parameters and fractional order derivative values of the FO chaotic system of interest and f(X) returns the DKY.
The optimization process is performed applying DE and APSO who are programmed in Python, because it is a multi-paradigm programming language highly versatile for creating all kind of applications and, therefore, it has become one of the most used in recent years. However, Python based applications pays a penalty in the form of speed execution, thereby complex projects can benefit from the use of the Numba JIT compiler [53], which allows to translate Python functions to optimized machine code and thus obtaining better speed performance [54]. Moreover, the implementation of the Numba JIT compiler only requires from slight modifications in the original Python code and, therefore, maintaining the flexibility of the language. Table 3 shows a comparison of the speed performance between a normal Python code and one Python code using the Numba JIT compiler. In both executions, the argument is to solve the proposed FO chaotic system and elaborate its corresponding Poincaré maps for the chaotic behavior validation. It can be seen, that the optimized Python code performs ≈375 times faster than the non-optimized. Thereby the interest of using this compiler in the optimization process.
| FO chaotic system | Python code | Code using the Numba Jit compiler | Number of generated data |
| 3D | 1.025×103s | 2.61s | 146,666 |
| 4D | 2.085×103s | 5.55s | 133,332 |
Algorithms 1 and 2 show the pseudocodes for the implementation of DE and APSO, respectively. It can be seen that the implementation is quite similar in both algorithms. The Numba JIT compiler is used in most of the Python code with the exception of the Lyapunov exponents (LEs) computation DKY computation, in this step, the computation of the Lyapunov exponents λi, (i=1,2,...,n) is made with the TISEAN package by removing the first 10% samples of the time series.
| Algorithm 1 Maximizing DKY applying DE |
| Require: μ, Cr, p, gen. Ensure: best Dj, j=0,2,...,gen Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) store D0← best DKYi for j=1:gen do for k=1:p do generate Xk using (3.3) and (3.4) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) store Dj← best DKYk |
| Algorithm 2 Maximizing DKY applying APSO |
| Require: α, β, p, gen. Ensure: Best Dj, for j=0,2,…,gen. Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) Store D0← best DKYi for j=1:gen do for k=1:p do Generate Xk using (3.8) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) Store Dj← best DKYk |
The DE and APSO were executed for a 100 population and for 50–100 generations. Table 4 shows the ranges of interest and the configuration of the metaheuristics for the optimization of the 3D and 4D FO chaotic systems, respectively. The values of the parameters and fractional-order derivatives in the search space, were encoded within three decimal places. For convenience, the initial population is set with parameters and fractional-order derivatives that lead to chaotic behavior and, therefore, the elaboration of Poincaré maps is not necessary for this step. In Tables 5 and 6 are shown the optimization results of the 3D and 4D FO chaotic systems by DE and APSO, respectively. It can be seen that in all cases, the obtained results lead to higher DKY than those shown in Tables 1 and 2, thus validating the optimization process. The best results for the 3D FO chaotic system are those obtained APSO by using 50 generations whereas the best results for the 4D FO chaotic system are obtained with DE by using 100 generations.
| FO chaotic system | Parameters | FO derivative | DE parameters | APSO parameters |
| 3D | a∈[0.251,0.5] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.1, β=0.1 |
| 4D | a∈[0.251,0.45], b∈[−0.1,0.3] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.3, β=0.1 |
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.351 | q1=0.976, q2=0.956, q3=0.906 |
101 | λ1=0.0023, λ2=−0.0004, λ3=−0.0034 |
2.5282 | chaotic |
| 100 | a=0.322 | q1=0.986, q2=0.927, q3=0.971 |
92 | λ1=0.0029, λ2=−0.0005, λ3=−0.0032 |
2.6120 | chaotic | |
| 4D | 50 | a=3.291, b=0.099 |
q1=0.936, q2=0.965, q3=0.936, q4=0.887 |
42 | λ1=0.0020, λ2=0, λ3=−0.0003, λ4=−0.0023 |
3.6803 | chaotic |
| 100 | a=2.688, b=0.152 |
q1=0.951, q2=0.970, q3=0.910, q4=0.970 |
41 | λ1=0.0144, λ2=0.0027, λ3=0, λ4=−0.0201 |
3.8543 | hyperchaotic |
| APSO optimization results | |||||||
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.378 | q1=0.999, q2=0.969, q3=0.902 |
101 | λ1=0.0026, λ2=−0.0005, λ3=−0.0032 |
2.66 | chaotic |
| 109 | a=0.38 | q1=0.998, q2=0.970, q3=0.902 |
113 | λ1=0.0034, λ2=−0.0006, λ3=−0.0045 |
2.5978 | chaotic | |
| 4D | 50 | a=3.193, b=0.299 |
q1=0.965, q2=0.980, q3=0.985, q4=0.967 |
40 | λ1=0.0007, λ2=0.0003, λ3=−0.0001, λ4=−0.0011 |
3.7633 | hyperchaotic |
| 100 | a=3.106, b=0.19 |
q1=0.878, q2=0.957, q3=0.945, q4=0.970 |
41 | λ1=0.0008, λ2=0.0002, λ3=0, λ4=−0.0015 |
3.6358 | hyperchaotic | |
In this paper, the optimization of the DKY of a 3D and a 4D FO chaotic systems was performed by applying two metaheuristics, DE and APSO. The main contribution of this work is the use of Poincaré maps for validating the chaotic behavior in FO chaotic systems with hidden attractors. Herein a simple numerical procedure was proposed for the analysis of points distribution in Poincaré maps. It has been shown that with this simple procedure, it is possible to differentiate a chaotic attractor from a periodic or quasi-periodic attractor. Moreover, the use of the Numba JIT compiler in the Python programming language has been an essential tool to save execution time, while preserving the versatility in the implementation of the metaheuristics. This last part is essential and it has been demonstrated that it facilitates the optimization process of FO chaotic systems with hidden attractors. Finally, it is worthy to mention that Poincaré maps can be used in both FO and integer chaotic systems regardless of the attractor nature (hidden or self-excited). The proposed approach can be applied in FO chaotic systems with self-excited attractor as done in integer chaotic systems with hidden and self-excited attractors.
Daniel Clemente-López acknowledges CONACYT for PhD scholarship with CVU no. 859036.
The authors declare no conflicts of interests.
| [1] | Y. Bolotin, A. Tur, V. Yanovsky, Chaos: Concepts, control and constructive use, Springer, 2009. |
| [2] |
B. Dubey, Sajan, A. Kumar, Stability switching and chaos in a multiple delayed prey-predator model with fear effect and anti-predator behavior, Math. Comput. Simulat., 188 (2021), 164–192. https://doi.org/10.1016/j.matcom.2021.03.037 doi: 10.1016/j.matcom.2021.03.037

|
| [3] | J. K. Zink, K. Batygin, F. C. Adams, The great inequality and the dynamical disintegration of the outer solar system, Astron. J., 160 (2020), 232. |
| [4] | M. Sajid, Recent developments on chaos in mechanical systems, Int. J. Theor. Appl. Res. Mech. Eng., 2 (2013), 121–124. |
| [5] | B. A. Idowu, S. Vaidyanathan, A. Sambas, O. I. Olusola, O. S. Onma, A new chaotic finance system: Its analysis, control, synchronization and circuit design, In: Nonlinear dynamical systems with self-excited and hidden attractors, Springer, 2018,271–295. https://doi.org/10.1007/978-3-319-71243-7_12 |
| [6] |
B Wang, S. M. Zhong, X. C. Dong, On the novel chaotic secure communication scheme design, Commun. Nonlinear Sci. Numer. Simul., 39 (2016), 108–117. https://doi.org/10.1016/j.cnsns.2016.02.035 doi: 10.1016/j.cnsns.2016.02.035

|
| [7] |
D. Arroyo, F. Hernandez, A. B. Orúe, Cryptanalysis of a classical chaos-based cryptosystem with some quantum cryptography features, Int. J. Bifurcat. Chaos, 27 (2017), 1750004. https://doi.org/10.1142/S0218127417500043 doi: 10.1142/S0218127417500043

|
| [8] |
X. Zang, S. Iqbal, Y. Zhu, X. Liu, J. Zhao, Applications of chaotic dynamics in robotics, Int. J. Adv. Robotic Syst., 13 (2016), 60. https://doi.org/10.5772/62796 doi: 10.5772/62796

|
| [9] |
K. Tian, C. Grebogi, H. P. Ren, Chaos generation with impulse control: Application to non-chaotic systems and circuit design, IEEE T. Circuits Syst. I, 68 (2021), 3012–3022. https://doi.org/10.1109/TCSI.2021.3075550 doi: 10.1109/TCSI.2021.3075550

|
| [10] |
V. E. Tarasov, Generalized memory: Fractional calculus approach, Fractal Fract., 2 (2018), 23. https://doi.org/10.3390/fractalfract2040023 doi: 10.3390/fractalfract2040023

|
| [11] |
K. M. Owolabi, A. Atangana, J. F. Gómez-Aguilar, Fractional adams-bashforth scheme with the liouville-caputo derivative and application to chaotic systems, Discrete Cont. Dyn. Syst.-S, 14 (2021), 2455–2469. https://doi.org/10.3934/dcdss.2021060 doi: 10.3934/dcdss.2021060

|
| [12] |
M. Ahmad, U. Shamsi, I. R. Khan, An enhanced image encryption algorithm using fractional chaotic systems, Procedia Comput. Sci., 57 (2015), 852–859. https://doi.org/10.1016/j.procs.2015.07.494 doi: 10.1016/j.procs.2015.07.494

|
| [13] |
M. Bettayeb, U. M. Al-Saggaf, S. Djennoune, Single channel secure communication scheme based on synchronization of fractional-order chaotic Chua's systems, T. I. Meas. Control, 40 (2018), 3651–3664. https://doi.org/10.1177/0142331217729425 doi: 10.1177/0142331217729425

|
| [14] |
H. Natiq, M. R. M. Said, M. R. K. Ariffin, S. He, L. Rondoni, S. Banerjee, Self-excited and hidden attractors in a novel chaotic system with complicated multistability, Eur. Phys. J. Plus, 133 (2018), 1–12. https://doi.org/10.1140/epjp/i2018-12360-y doi: 10.1140/epjp/i2018-12360-y

|
| [15] |
G. A. Leonov, N. V. Kuznetsov, Hidden attractors in dynamical systems. From hidden oscillations in hilbert-kolmogorov, aizerman, and kalman problems to hidden chaotic attractor in chua circuits, Int. J. Bifurcat. Chaos, 23 (2013), 1330002. https://doi.org/10.1142/S0218127413300024 doi: 10.1142/S0218127413300024

|
| [16] |
P. R. Sharma, M. D. Shrimali, A. Prasad, N. V. Kuznetsov, G. A. Leonov, Control of multistability in hidden attractors, Eur. Phys. J. Spec. Top., 224 (2015), 1485–1491. https://doi.org/10.1140/epjst/e2015-02474-y doi: 10.1140/epjst/e2015-02474-y

|
| [17] |
A. K. Farhan, R. S. Ali, H. Natiq, N. M. G. Al-Saidi, A new s-box generation algorithm based on multistability behavior of a plasma perturbation model, IEEE Access, 7 (2019), 124914–124924. https://doi.org/10.1109/ACCESS.2019.2938513 doi: 10.1109/ACCESS.2019.2938513

|
| [18] |
F. Yu, Z. Zhang, L. Liu, H. Shen, Y. Huang, C. Shi, et al., Secure communication scheme based on a new 5D multistable four-wing memristive hyperchaotic system with disturbance inputs, Complexity, 2020 (2020), 5859273. https://doi.org/10.1155/2020/5859273 doi: 10.1155/2020/5859273

|
| [19] |
J. M. Munoz-Pacheco, E. Zambrano-Serrano, C. Volos, S. Jafari, J. Kengne, K. Rajagopal, A new fractional-order chaotic system with different families of hidden and self-excited attractors, Entropy, 20 (2018), 564. https://doi.org/10.3390/e20080564 doi: 10.3390/e20080564

|
| [20] |
N. Debbouche, S. Momani, A. Ouannas, M. T. Shatnawi, G. Grassi, Z. Dibi, et al., Generating multidirectional variable hidden attractors via newly commensurate and incommensurate non-equilibrium fractional-order chaotic systems, Entropy, 23 (2021), 261. https://doi.org/10.3390/e23030261 doi: 10.3390/e23030261

|
| [21] |
D. A. Yousri, A. M. AbdelAty, L. A. Said, A. S. Elwakil, B. Maundy, A. G. Radwan, Parameter identification of fractional-order chaotic systems using different meta-heuristic optimization algorithms, Nonlinear Dynam., 95 (2019), 2491–2542. https://doi.org/10.1007/s11071-018-4703-2 doi: 10.1007/s11071-018-4703-2

|
| [22] |
A. Silva-Juárez, E. Tlelo-Cuautle, L. G. de la Fraga, R. Li, Optimization of the kaplan-yorke dimension in fractional-order chaotic oscillators by metaheuristics, Appl. Math. Comput., 394 (2021), 125831. https://doi.org/10.1016/j.amc.2020.125831 doi: 10.1016/j.amc.2020.125831

|
| [23] |
J. C. Nunez-Perez, V. A. Adeyemi, Y. Sandoval-Ibarra, F. J. Perez-Pinal, E. Tlelo-Cuautle, Maximizing the chaotic behavior of fractional order chen system by evolutionary algorithms, Mathematics, 9 (2021), 1194. https://doi.org/10.3390/math9111194 doi: 10.3390/math9111194

|
| [24] |
S. Jafari, J. C. Sprott, F. Nazarimehr, Recent new examples of hidden attractors, Eur. Phys. J. Spec. Top., 224 (2015), 1469–1476. https://doi.org/10.1140/epjst/e2015-02472-1 doi: 10.1140/epjst/e2015-02472-1

|
| [25] |
W. S. Sayed, A. G. Radwan, Self-reproducing hidden attractors in fractional-order chaotic systems using affine transformations, IEEE Open J. Circuits Syst., 1 (2020), 243–254. https://doi.org/10.1109/OJCAS.2020.3030756 doi: 10.1109/OJCAS.2020.3030756

|
| [26] |
M. F. Danca, P. Bourke, N. Kuznetsov, Graphical structure of attraction basins of hidden chaotic attractors: The rabinovich-fabrikant system, Int. J. Bifurcat. Chaos, 29 (2019), 1930001. https://doi.org/10.1142/S0218127419300015 doi: 10.1142/S0218127419300015

|
| [27] | C. W. Kulp, B. J. Niskala, Characterization of time series data, 2017. |
| [28] |
S. Zamen, E. Dehghan-Niri, Observation and diagnosis of chaos in nonlinear acoustic waves using phase-space domain, J. Sound Vib., 463 (2019), 114959. https://doi.org/10.1016/j.jsv.2019.114959 doi: 10.1016/j.jsv.2019.114959

|
| [29] |
M. S. Abdelouahab, N. E. Hamri, The grünwald-letnikov fractional-order derivative with fixed memory length, Mediterr. J. Math., 13 (2016), 557–572. https://doi.org/10.1007/s00009-015-0525-3 doi: 10.1007/s00009-015-0525-3

|
| [30] | A. Carpinteri, F. Mainardi, Fractals and fractional calculus in continuum mechanics, Vol. 378, Springer, 2014. |
| [31] |
K. M. Owolabi, B. Karaagac, Chaotic and spatiotemporal oscillations in fractional reaction-diffusion system, Chaos Solitons Fract., 141 (2020), 110302. https://doi.org/10.1016/j.chaos.2020.110302 doi: 10.1016/j.chaos.2020.110302

|
| [32] |
L. F. Ávalos-Ruiz, J. F. Gomez-Aguilar, A. Atangana, K. M. Owolabi, On the dynamics of fractional maps with power-law, exponential decay and Mittag-Leffler memory, Chaos, Solitons Fract., 127 (2019), 364–388. https://doi.org/10.1016/j.chaos.2019.07.010 doi: 10.1016/j.chaos.2019.07.010

|
| [33] |
K. M. Owolabi, J. F. Gómez-Aguilar, G. Fernández-Anaya, J. E. Lavín-Delgado, E. Hernández-Castillo, Modelling of chaotic processes with caputo fractional order derivative, Entropy, 22 (2020), 1027. https://doi.org/10.3390/e22091027 doi: 10.3390/e22091027

|
| [34] |
K. M. Owolabi, Computational techniques for highly oscillatory and chaotic wave problems with fractional-order operator, Eur. Phys. J. Plus, 135 (2020), 1–23. https://doi.org/10.1140/epjp/s13360-020-00873-z doi: 10.1140/epjp/s13360-020-00873-z

|
| [35] |
K. M. Owolabi, Robust synchronization of chaotic fractional-order systems with shifted chebyshev spectral collocation method, J. Appl. Anal., 27, 2021. https://doi.org/10.1515/jaa-2021-2053 doi: 10.1515/jaa-2021-2053

|
| [36] |
C. Li, C. Tao, On the fractional adams method, Comput. Math. Appl., 58 (2009), 1573–1588. https://doi.org/10.1016/j.camwa.2009.07.050 doi: 10.1016/j.camwa.2009.07.050

|
| [37] |
R. Scherer, S. L. Kalla, Y. Tang, J. Huang, The Grünwald-Letnikov method for fractional differential equations, Comput. Math. Appl., 62 (2011), 902–917. https://doi.org/10.1016/j.camwa.2011.03.054 doi: 10.1016/j.camwa.2011.03.054

|
| [38] | I. Petráš, Fractional-order nonlinear systems: Modeling, analysis and simulation, Springer Science & Business Media, 2011. |
| [39] |
S. Pooseh, R. Almeida, D. F. M. Torres, Discrete direct methods in the fractional calculus of variations, Comput. Math. Appl., 66 (2013), 668–676. https://doi.org/10.1016/j.camwa.2013.01.045 doi: 10.1016/j.camwa.2013.01.045

|
| [40] | P. A. Cook, Nonlinear dynamical systems, 2 Eds., Prentice Hall International (UK) Ltd., GBR, 1994. |
| [41] |
M. H. Arshad, M. Kassas, A. E. Hussein, M. A. Abido, A simple technique for studying chaos using jerk equation with discrete time sine map, Appl. Sci., 11 (2021), 437. https://doi.org/10.3390/app11010437 doi: 10.3390/app11010437

|
| [42] |
L. Chen, W. Pan, J. A. T. Machado, A. M. Lopes, R. Wu, Y. He, Design of fractional-order hyper-chaotic multi-scroll systems based on hysteresis series, Eur. Phys. J. Spec. Top., 226 (2017), 3775–3789. https://doi.org/10.1140/epjst/e2018-00012-8 doi: 10.1140/epjst/e2018-00012-8

|
| [43] |
M. Z. De la Hoz, L. Acho, Y. Vidal, A modified chua chaotic oscillator and its application to secure communications, Appl. Math. Comput., 247 (2014), 712–722. https://doi.org/10.1016/j.amc.2014.09.031 doi: 10.1016/j.amc.2014.09.031

|
| [44] |
J. Theiler, Estimating fractal dimension, JOSA A, 7 (1990), 1055–1073. https://doi.org/10.1364/JOSAA.7.001055 doi: 10.1364/JOSAA.7.001055

|
| [45] |
S. Haykin, S. Puthusserypady, Chaotic dynamics of sea clutter, Chaos: Interdisc. J. Nonlinear Sci., 7 (1997), 777–802. https://doi.org/10.1063/1.166275 doi: 10.1063/1.166275

|
| [46] |
K. E. Chlouverakis, Color maps of the kaplan–yorke dimension in optically driven lasers: Maximizing the dimension and almost-hamiltonian chaos, Int. J. Bifurcat. Chaos, 15 (2005), 3011–3021. https://doi.org/10.1142/S0218127405013848 doi: 10.1142/S0218127405013848

|
| [47] |
C. R. Suribabu, Differential evolution algorithm for optimal design of water distribution networks, J. Hydroinform., 12 (2010), 66–82. https://doi.org/10.2166/hydro.2010.014 doi: 10.2166/hydro.2010.014

|
| [48] | G. G. Wang, A. H. Gandomi, X. S. Yang, A. H. Alavi, A novel improved accelerated particle swarm optimization algorithm for global numerical optimization, Eng. Comput., 31 (2014). |
| [49] |
M. S. Tavazoei, M. Haeri, A proof for non existence of periodic solutions in time invariant fractional order systems, Automatica, 45 (2009), 1886–1890. https://doi.org/10.1016/j.automatica.2009.04.001 doi: 10.1016/j.automatica.2009.04.001

|
| [50] |
E. Kaslik, S. Sivasundaram, Non-existence of periodic solutions in fractional-order dynamical systems and a remarkable difference between integer and fractional-order derivatives of periodic functions, Nonlinear Anal.: Real World Appl., 13 (2012), 1489–1497. https://doi.org/10.1016/j.nonrwa.2011.11.013 doi: 10.1016/j.nonrwa.2011.11.013

|
| [51] |
C. Li, J. C. Sprott, Coexisting hidden attractors in a 4-d simplified lorenz system, Int. J. Bifurcat. Chaos, 24 (2014), 1450034. https://doi.org/10.1142/S0218127414500345 doi: 10.1142/S0218127414500345

|
| [52] |
M. Wang, X. Liao, Y. Deng, Z. Li, Y. Su, Y. Zeng, Dynamics, synchronization and circuit implementation of a simple fractional-order chaotic system with hidden attractors, Chaos, Solitons Fract., 130 (2020), 109406. https://doi.org/10.1016/j.chaos.2019.109406 doi: 10.1016/j.chaos.2019.109406

|
| [53] | Numba: A high performance python compiler, 2021. Available from: http://numba.pydata.org/. |
| [54] | N. Watkinson, P. Tai, A. Nicolau, A. Veidenbaum, Numbasummarizer: A python library for simplified vectorization reports, In: 2020 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), IEEE, 2020, 1–7. https://doi.org/10.1109/IPDPSW50202.2020.00058 |
| 1. | Kulpash Iskakova, Mohammad Mahtab Alam, Shabir Ahmad, Sayed Saifullah, Ali Akgül, Gülnur Yılmaz, Dynamical study of a novel 4D hyperchaotic system: An integer and fractional order analysis, 2023, 208, 03784754, 219, 10.1016/j.matcom.2023.01.024 | |
| 2. | Jiahui Wang, Chengwei Dong, Hantao Li, A New Variable-Boostable 3D Chaotic System with Hidden and Coexisting Attractors: Dynamical Analysis, Periodic Orbit Coding, Circuit Simulation, and Synchronization, 2022, 6, 2504-3110, 740, 10.3390/fractalfract6120740 | |
| 3. | Muhammad Marwan, Vagner Dos Santos, Muhammad Zainul Abidin, Anda Xiong, Coexisting Attractor in a Gyrostat Chaotic System via Basin of Attraction and Synchronization of Two Nonidentical Mechanical Systems, 2022, 10, 2227-7390, 1914, 10.3390/math10111914 | |
| 4. | Aceng Sambas, Ardashir Mohammadzadeh, Sundarapandian Vaidyanathan, Ahmad Faisal Mohamad Ayob, Amiral Aziz, Mohamad Afendee Mohamed, Ibrahim Mohammed Sulaiman, Mohamad Arif Awang Nawi, Investigation of chaotic behavior and adaptive type-2 fuzzy controller approach for Permanent Magnet Synchronous Generator (PMSG) wind turbine system, 2022, 8, 2473-6988, 5670, 10.3934/math.2023285 | |
| 5. | Shaohui Yan, Hanbing Zhang, Defeng Jiang, Jiawei Jiang, Yu Cui, Yuyan Zhang, Finite-time synchronization of fractional-order chaotic system based on hidden attractors, 2023, 98, 0031-8949, 105226, 10.1088/1402-4896/acf308 | |
| 6. | Seong Oun Hwang, Hafiz Muhammad Waseem, Noor Munir, Billiard Quantum Chaos: A Pioneering Image Encryption Scheme in the Post-Quantum Era, 2024, 12, 2169-3536, 85150, 10.1109/ACCESS.2024.3415083 | |
| 7. | Hamid Taghavifar, Ardashir Mohammadzadeh, Chunwei Zhang, A non-singleton type-3 neuro-fuzzy fixed-time synchronizing method, 2024, 189, 09600779, 115671, 10.1016/j.chaos.2024.115671 | |
| 8. | Jing Zhou, Yaan Li, Mingzhou Wang, Research on the Threshold Determination Method of the Duffing Chaotic System Based on Improved Permutation Entropy and Poincaré Mapping, 2023, 25, 1099-4300, 1654, 10.3390/e25121654 | |
| 9. | Daniel Clemente-López, Jesus M. Munoz-Pacheco, José de Jesus Rangel-Magdaleno, Experimental validation of IoT image encryption scheme based on a 5-D fractional hyperchaotic system and Numba JIT compiler, 2024, 25, 25426605, 101116, 10.1016/j.iot.2024.101116 | |
| 10. | Atefeh Ahmadi, Sriram Parthasarathy, Nikhil Pal, Karthikeyan Rajagopal, Sajad Jafari, Esteban Tlelo-Cuautle, Extreme Multistability and Extreme Events in a Novel Chaotic Circuit with Hidden Attractors, 2023, 33, 0218-1274, 10.1142/S0218127423300161 | |
| 11. | Ankit Tiwari, Binoy Krishna Roy, Signatures of Routes to Chaos, 2025, 35, 0218-1274, 10.1142/S021812742530006X |
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=0.35 | q1=0.97, q2=0.97, q3=0.97 |
107 | λ1=0.0011, λ2=−0.0006, λ3=−0.0036 |
2.1504 | chaotic |
| a=0.3 | q1=0.993, q2=1, q3=0.75 |
96 | λ1=0.0010, λ2=−0.0009, λ3=−0.0047 |
2.0208 | chaotic |
| a=0.325 | q1=1, q2=0.99, q3=0.85 |
104 | λ1=0.0018, λ2=−0.0006, λ3=−0.0057 |
2.2071 | chaotic |
| a=0.337 | q1=0.966, q2=0.968, q3=0.926 |
105 | λ1=0.0013, λ2=−0.0008, λ3=−0.0036 |
2.1452 | chaotic |
| a=0.6 | q1=0.992, q2=0.938, q3=0.968 |
94 | λ1=0.0022, λ2=−0.0009, λ3=−0.0051 |
2.2452 | chaotic |
| a=0.437 | q1=0.993, q2=0.956, q3=0.874 |
105 | λ1=0.0010, λ2=−0.0009, λ3=−0.0043 |
2.003 | chaotic |
| a=0.322 | q1=0.982, q2=0.955, q3=0.985 |
96 | λ1=0.0017, λ2=−0.0009, λ3=−0.0052 |
2.1593 | chaotic |
| a=0.29 | q1=0.986, q2=0.967, q3=0.981 |
17 | λ1=0.0008, λ2=−0.0017, λ3=−0.0018 |
1.5219 | quasi-periodic |
| a=0.436 | q1=0.998, q2=0.989, q3=0.986 |
10 | λ1=0.0007, λ2=−0.0012, λ3=−0.0028 |
1.8214 | quasi-periodic |
| a=0.277 | q1=0.988, q2=0.948, q3=0.881 |
3 | λ1=0.0009, λ2=−0.0038, λ3=−0.0183 |
1.8415 | quasi-periodic |
| a=0.382 | q1=0.994, q2=0.922, q3=97 |
2 | λ1=−0.0003, λ2=−0.0011, λ3=−0.0015 |
1.06 | quasi-periodic |
| a=0.387 | q1=0.976, q2=0.968, q3=0.804 |
2 | λ1=0.0001, λ2=−0.0011, λ3=−0.0016 |
1.375 | quasi-periodic |
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=3.5, b=0.1 |
q1=0.98, q2=0.98, q3=0.98, q4=0.98 |
43 | λ1=0.0011, λ2=0, λ3=−0.0001, λ4=−0.0024 |
3.4257 | chaotic |
| a=3.5, b=0.1 |
q1=1.0, q2=0.997, q3=1.0, q4=0.45 |
50 | λ1=0.0030, λ2=0, λ3=−0.0017, λ4=−0.0040 |
3.3368 | chaotic |
| a=2.9, b=0.1 |
q1=0.45, q2=0.95, q3=1.0, q4=0.985 |
40 | λ1=0.0008, λ2=0, λ3=−0.0003, λ4=−0.0030 |
3.1666 | chaotic |
| a=3.162, b=0.182 |
q1=0.980, q2=0.942, q3=0.978, q4=0.975 |
42 | λ1=0.0008, λ2=0.0001, λ3=0, λ4=−0.0018 |
3.5029 | hyper-chaotic |
| a=3.128, b=0.285 |
q1=0.946, q2=0.964, q3=0.957, q4=0.923 |
41 | λ1=0.0003, λ2=0.0001, λ3=0, λ4=−0.0006 |
3.5103 | hyper-chaotic |
| a=3.131, b=0.285 |
q1=0.945, q2=0.963, q3=0.956, q4=0.922 |
41 | λ1=0.0004, λ2=0.0002, λ3=0, λ4=−0.0011 |
3.5282 | hyper-chaotic |
| a=3.088, b=0.12 |
q1=0.925, q2=0.948, q3=0.933, q4=0.932 |
38 | λ1=0.0016, λ2=0, λ3=−0.0004, λ4=−0.0031 |
3.387 | chaotic |
| a=3.601, b=0.3 |
q1=0.999, q2=0.999, q3=0.999, q4=0.962 |
48 | λ1=0.0005, λ2=0, λ3=−0.0001, λ4=−0.0022 |
3.2014 | chaotic |
| a=9.4, b=0.01 |
q1=0.936, q2=0.935, q3=0.958, q4=0.946 |
60 | λ1=0.0009, λ2=0, λ3=−0.0001, λ4=−0.0013 |
3.5972 | chaotic |
| a=8.4, b=0.1 |
q1=0.990, q2=0.980, q3=0.980, q4=0.981 |
8 | λ1=0, λ2=−0.0002, λ3=−0.0014, λ4=−0.0039 |
2.5897 | quasi-periodic |
| a=7.8, b=0.1 |
q1=0.990, q2=0.980, q3=0.970, q4=0.981 |
10 | λ1=0, λ2=−0.0002, λ3=−0.0011, λ4=−0.0041 |
2.6829 | quasi-periodic |
| a=7.3, b=0.08 |
q1=0.989, q2=0.998, q3=0.967, q4=0.981 |
11 | λ1=−0.0001, λ2=−0.0002, λ3=−0.0007, λ4=−0.0042 |
2.7619 | quasi-periodic |
| FO chaotic system | Python code | Code using the Numba Jit compiler | Number of generated data |
| 3D | 1.025×103s | 2.61s | 146,666 |
| 4D | 2.085×103s | 5.55s | 133,332 |
| Algorithm 1 Maximizing DKY applying DE |
| Require: μ, Cr, p, gen. Ensure: best Dj, j=0,2,...,gen Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) store D0← best DKYi for j=1:gen do for k=1:p do generate Xk using (3.3) and (3.4) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) store Dj← best DKYk |
| Algorithm 2 Maximizing DKY applying APSO |
| Require: α, β, p, gen. Ensure: Best Dj, for j=0,2,…,gen. Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) Store D0← best DKYi for j=1:gen do for k=1:p do Generate Xk using (3.8) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) Store Dj← best DKYk |
| FO chaotic system | Parameters | FO derivative | DE parameters | APSO parameters |
| 3D | a∈[0.251,0.5] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.1, β=0.1 |
| 4D | a∈[0.251,0.45], b∈[−0.1,0.3] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.3, β=0.1 |
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.351 | q1=0.976, q2=0.956, q3=0.906 |
101 | λ1=0.0023, λ2=−0.0004, λ3=−0.0034 |
2.5282 | chaotic |
| 100 | a=0.322 | q1=0.986, q2=0.927, q3=0.971 |
92 | λ1=0.0029, λ2=−0.0005, λ3=−0.0032 |
2.6120 | chaotic | |
| 4D | 50 | a=3.291, b=0.099 |
q1=0.936, q2=0.965, q3=0.936, q4=0.887 |
42 | λ1=0.0020, λ2=0, λ3=−0.0003, λ4=−0.0023 |
3.6803 | chaotic |
| 100 | a=2.688, b=0.152 |
q1=0.951, q2=0.970, q3=0.910, q4=0.970 |
41 | λ1=0.0144, λ2=0.0027, λ3=0, λ4=−0.0201 |
3.8543 | hyperchaotic |
| APSO optimization results | |||||||
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.378 | q1=0.999, q2=0.969, q3=0.902 |
101 | λ1=0.0026, λ2=−0.0005, λ3=−0.0032 |
2.66 | chaotic |
| 109 | a=0.38 | q1=0.998, q2=0.970, q3=0.902 |
113 | λ1=0.0034, λ2=−0.0006, λ3=−0.0045 |
2.5978 | chaotic | |
| 4D | 50 | a=3.193, b=0.299 |
q1=0.965, q2=0.980, q3=0.985, q4=0.967 |
40 | λ1=0.0007, λ2=0.0003, λ3=−0.0001, λ4=−0.0011 |
3.7633 | hyperchaotic |
| 100 | a=3.106, b=0.19 |
q1=0.878, q2=0.957, q3=0.945, q4=0.970 |
41 | λ1=0.0008, λ2=0.0002, λ3=0, λ4=−0.0015 |
3.6358 | hyperchaotic | |
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=0.35 | q1=0.97, q2=0.97, q3=0.97 |
107 | λ1=0.0011, λ2=−0.0006, λ3=−0.0036 |
2.1504 | chaotic |
| a=0.3 | q1=0.993, q2=1, q3=0.75 |
96 | λ1=0.0010, λ2=−0.0009, λ3=−0.0047 |
2.0208 | chaotic |
| a=0.325 | q1=1, q2=0.99, q3=0.85 |
104 | λ1=0.0018, λ2=−0.0006, λ3=−0.0057 |
2.2071 | chaotic |
| a=0.337 | q1=0.966, q2=0.968, q3=0.926 |
105 | λ1=0.0013, λ2=−0.0008, λ3=−0.0036 |
2.1452 | chaotic |
| a=0.6 | q1=0.992, q2=0.938, q3=0.968 |
94 | λ1=0.0022, λ2=−0.0009, λ3=−0.0051 |
2.2452 | chaotic |
| a=0.437 | q1=0.993, q2=0.956, q3=0.874 |
105 | λ1=0.0010, λ2=−0.0009, λ3=−0.0043 |
2.003 | chaotic |
| a=0.322 | q1=0.982, q2=0.955, q3=0.985 |
96 | λ1=0.0017, λ2=−0.0009, λ3=−0.0052 |
2.1593 | chaotic |
| a=0.29 | q1=0.986, q2=0.967, q3=0.981 |
17 | λ1=0.0008, λ2=−0.0017, λ3=−0.0018 |
1.5219 | quasi-periodic |
| a=0.436 | q1=0.998, q2=0.989, q3=0.986 |
10 | λ1=0.0007, λ2=−0.0012, λ3=−0.0028 |
1.8214 | quasi-periodic |
| a=0.277 | q1=0.988, q2=0.948, q3=0.881 |
3 | λ1=0.0009, λ2=−0.0038, λ3=−0.0183 |
1.8415 | quasi-periodic |
| a=0.382 | q1=0.994, q2=0.922, q3=97 |
2 | λ1=−0.0003, λ2=−0.0011, λ3=−0.0015 |
1.06 | quasi-periodic |
| a=0.387 | q1=0.976, q2=0.968, q3=0.804 |
2 | λ1=0.0001, λ2=−0.0011, λ3=−0.0016 |
1.375 | quasi-periodic |
| Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| a=3.5, b=0.1 |
q1=0.98, q2=0.98, q3=0.98, q4=0.98 |
43 | λ1=0.0011, λ2=0, λ3=−0.0001, λ4=−0.0024 |
3.4257 | chaotic |
| a=3.5, b=0.1 |
q1=1.0, q2=0.997, q3=1.0, q4=0.45 |
50 | λ1=0.0030, λ2=0, λ3=−0.0017, λ4=−0.0040 |
3.3368 | chaotic |
| a=2.9, b=0.1 |
q1=0.45, q2=0.95, q3=1.0, q4=0.985 |
40 | λ1=0.0008, λ2=0, λ3=−0.0003, λ4=−0.0030 |
3.1666 | chaotic |
| a=3.162, b=0.182 |
q1=0.980, q2=0.942, q3=0.978, q4=0.975 |
42 | λ1=0.0008, λ2=0.0001, λ3=0, λ4=−0.0018 |
3.5029 | hyper-chaotic |
| a=3.128, b=0.285 |
q1=0.946, q2=0.964, q3=0.957, q4=0.923 |
41 | λ1=0.0003, λ2=0.0001, λ3=0, λ4=−0.0006 |
3.5103 | hyper-chaotic |
| a=3.131, b=0.285 |
q1=0.945, q2=0.963, q3=0.956, q4=0.922 |
41 | λ1=0.0004, λ2=0.0002, λ3=0, λ4=−0.0011 |
3.5282 | hyper-chaotic |
| a=3.088, b=0.12 |
q1=0.925, q2=0.948, q3=0.933, q4=0.932 |
38 | λ1=0.0016, λ2=0, λ3=−0.0004, λ4=−0.0031 |
3.387 | chaotic |
| a=3.601, b=0.3 |
q1=0.999, q2=0.999, q3=0.999, q4=0.962 |
48 | λ1=0.0005, λ2=0, λ3=−0.0001, λ4=−0.0022 |
3.2014 | chaotic |
| a=9.4, b=0.01 |
q1=0.936, q2=0.935, q3=0.958, q4=0.946 |
60 | λ1=0.0009, λ2=0, λ3=−0.0001, λ4=−0.0013 |
3.5972 | chaotic |
| a=8.4, b=0.1 |
q1=0.990, q2=0.980, q3=0.980, q4=0.981 |
8 | λ1=0, λ2=−0.0002, λ3=−0.0014, λ4=−0.0039 |
2.5897 | quasi-periodic |
| a=7.8, b=0.1 |
q1=0.990, q2=0.980, q3=0.970, q4=0.981 |
10 | λ1=0, λ2=−0.0002, λ3=−0.0011, λ4=−0.0041 |
2.6829 | quasi-periodic |
| a=7.3, b=0.08 |
q1=0.989, q2=0.998, q3=0.967, q4=0.981 |
11 | λ1=−0.0001, λ2=−0.0002, λ3=−0.0007, λ4=−0.0042 |
2.7619 | quasi-periodic |
| FO chaotic system | Python code | Code using the Numba Jit compiler | Number of generated data |
| 3D | 1.025×103s | 2.61s | 146,666 |
| 4D | 2.085×103s | 5.55s | 133,332 |
| Algorithm 1 Maximizing DKY applying DE |
| Require: μ, Cr, p, gen. Ensure: best Dj, j=0,2,...,gen Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) store D0← best DKYi for j=1:gen do for k=1:p do generate Xk using (3.3) and (3.4) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) store Dj← best DKYk |
| Algorithm 2 Maximizing DKY applying APSO |
| Require: α, β, p, gen. Ensure: Best Dj, for j=0,2,…,gen. Initialize population Xi∈Rn,i=1,2,...,p for i=1:p do Compute numerical solution for each Xi using (2.3) Calculate DKYi using (2.5) Store D0← best DKYi for j=1:gen do for k=1:p do Generate Xk using (3.8) Compute numerical solution for each new Xi using (2.3) Detect chaotic behavior using Poincaré map Compute LEs using Tisean Calculate DKYk using (2.5) Store Dj← best DKYk |
| FO chaotic system | Parameters | FO derivative | DE parameters | APSO parameters |
| 3D | a∈[0.251,0.5] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.1, β=0.1 |
| 4D | a∈[0.251,0.45], b∈[−0.1,0.3] | qi∈[0.3,0.999] | μ=0.5, Cr=0.6 | α=0.3, β=0.1 |
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.351 | q1=0.976, q2=0.956, q3=0.906 |
101 | λ1=0.0023, λ2=−0.0004, λ3=−0.0034 |
2.5282 | chaotic |
| 100 | a=0.322 | q1=0.986, q2=0.927, q3=0.971 |
92 | λ1=0.0029, λ2=−0.0005, λ3=−0.0032 |
2.6120 | chaotic | |
| 4D | 50 | a=3.291, b=0.099 |
q1=0.936, q2=0.965, q3=0.936, q4=0.887 |
42 | λ1=0.0020, λ2=0, λ3=−0.0003, λ4=−0.0023 |
3.6803 | chaotic |
| 100 | a=2.688, b=0.152 |
q1=0.951, q2=0.970, q3=0.910, q4=0.970 |
41 | λ1=0.0144, λ2=0.0027, λ3=0, λ4=−0.0201 |
3.8543 | hyperchaotic |
| APSO optimization results | |||||||
| FO chaotic system | Generations | Parameters | Fractional order derivative | Number of points | LEs | DKY | Dynamical behavior |
| 3D | 50 | a=0.378 | q1=0.999, q2=0.969, q3=0.902 |
101 | λ1=0.0026, λ2=−0.0005, λ3=−0.0032 |
2.66 | chaotic |
| 109 | a=0.38 | q1=0.998, q2=0.970, q3=0.902 |
113 | λ1=0.0034, λ2=−0.0006, λ3=−0.0045 |
2.5978 | chaotic | |
| 4D | 50 | a=3.193, b=0.299 |
q1=0.965, q2=0.980, q3=0.985, q4=0.967 |
40 | λ1=0.0007, λ2=0.0003, λ3=−0.0001, λ4=−0.0011 |
3.7633 | hyperchaotic |
| 100 | a=3.106, b=0.19 |
q1=0.878, q2=0.957, q3=0.945, q4=0.970 |
41 | λ1=0.0008, λ2=0.0002, λ3=0, λ4=−0.0015 |
3.6358 | hyperchaotic | |