Adaptive event-triggered state estimation for complex networks with nonlinearities against hybrid attacks

1.   Introduction

In recent decades, the development of information technology has brought great portability to people's production and life ^[1]. CNs can be used to portray smart grids, intelligent transportation, social networks and neural systems, etc., and have been given significant research significance and wide application context by academia and industry ^[2]. It is well known that nodes and connection relationships are two key factors that constitute CNs ^[3]. For example, in a power system network, power plants are connected to each other by transmission lines, where power plants can be abstractly considered as nodes, and similarly, transmission lines between power plants can be considered as connection relations ^[4]. For a multi-robot system, each mobile robot is considered as a node in the network, and the mutual sensing and intercommunication between robots are seen as the connection relationship. When the number of controlled objects is large, the cooperation and formation maintenance for the multi-robot system can be studied with the help of the theory of CNs. Similarly, the above ideas are also applicable to the study of multi-UAS. It can be seen that the connection relations, nodes, and the interactions between connection relations and nodes constitute CNs ^[5]. From the perspective of control discipline, some works such as state estimation, synchronization and control, and topology identification of CNs are still widely studied ^[6,7,8]. In addition, many practical problems are inevitable in information transmission, such as channel redundancy, cyber-attacks, time delay, packet loss, and noise ^[9,10]. The authors in ^[7] studied the partial-nodes-based state estimation problem on estimating the entire network state using partial outputs of the available nodes. In this paper, the impact of cyber-attacks and channel redundancy on the state estimation for CNs is discussed.

In practical engineering, the network bandwidth available to a system is usually limited ^[11,12]. Due to the limitation of network resources, channel redundancy, data congestion, network-induced delay, and packet loss inevitably occur when the components within the system perform network access and information transmission ^[13,14]. To mitigate the impact of these problems on system performance, various data transmission mechanisms have been proposed, such as event-triggered schemes (ETSs), communication protocol scheduling, and codec strategies. Currently, ETS is a common data transmission scheduling strategy in networked systems ^[15,16]. The core idea of the scheme is to determine in real time whether the current system state satisfies the triggering conditions to control the task execution on demand and meet the system performance ^[17]. On this basis, data transmission strategies such as distributed ETS, AETS, self-triggered scheme, and dynamic ETS have been proposed one after another ^{[18,19,20,21]}. By introducing the AETS, a fuzzy dynamic output feedback controller is designed for the nonlinear system with actuator failure and packet loss ^[20]. In ^[21], the authors propose a co-design method for filter and distributed AETS for nonlinear interconnected systems.

ETSs bring great convenience to networked systems, but open networks are vulnerable to malicious attackers, which poses a potential security risk to networked systems ^[22,23]. In networked systems, network attacks appear in various ways and affect or even destroy system performance, such as DoS attacks and deception attacks ^[24]. DoS attacks: attackers can block the transmission of information in the communication network between sensors and controllers (estimators), resulting in no available data ^[25]. Deception attack: attackers can tamper with the available data received by the controller (estimator) from the sensor, thus corrupting the integrity of the data ^[26]. In recent years, the security of networked systems has attracted widespread attention from the community, for example, on May 11, 2021, Belgium's public sector Internet service provider Belnet was subjected to a massive distributed DoS attack, which took all internal systems of the Belgian government and public-facing websites offline and forced many government websites and services in Belgium offline; on August 1, 2021, Italy The local vaccination appointment system was forced to shut down due to the cyber-attacks. In ^[10], the authors investigated the state estimation problem for a class of uncertain complex networks with partial node failures resistant to deception attacks. A co-design approach for dynamic ETS and observer-based PID controller against deception attacks has been presented in ^[27]. In ^[28], the authors studied the problem of state estimation for cyberphysical systems constrained by communication resources, DoS attacks, and sensor saturation. The authors in ^[29] presented event-triggered control countermeasures for the multiple cyber-attacks that can occur in cyberphysical systems. Since large-scale CNs have a large number of nodes with intricate connections, their states are usually unmeasurable and only partial information about the network nodes can be obtained through the output of the communication channel ^[30]. Due to the limitation of network bandwidth and the threat of cyber-attacks, only part of the node information is generally measurable ^[31]. In order to solve the node state agnosticism, the design of state estimator for CNs is necessary. In this paper, we use two sets of Bernoulli distribution variables and arbitrary functions related to the system state to characterize randomly occurring DoS attacks and deception attacks.

Inspired by the above mentioned work, it can be seen that although event-triggered state estimation for CNs has been extensively studied, relevant research on CNs with multiple attack scenarios is very limited. Second, we also discuss how to efficiently conserve network resources under the condition of limited communication channel capacity. The above two points are the two motivations that motivate the completion of this paper.

Based on the above discussion, we focus on the design of event-triggered state estimators for CNs with malicious attacks. In addition, an AETS is introduced to avoid sensors from sending unnecessary packets to the remote estimator for the purpose of saving network bandwidth. Then, based on the derived sufficient conditions for system stability, a feasible approach for co-design is proposed. Finally, a numerical example verifies the effectiveness of the proposed method. The main contributions of this paper are as follows.

● In order to reflect the real network environment, multiple scenarios of possible malicious attacks in the transmission channel are considered. By introducing Bernoulli distribution variables and an arbitrary function based on the system state, a mathematical model of the deception attacks is developed. Then the action sequence of the DoS attacks is portrayed by introducing another set of Bernoulli variables. The so-called hybrid network attack is modeled.

● We incorporate the plant to be studied, the state estimator, the network resource scheduling policy, and the aforementioned attack model into a unified architecture and describe them through an augmented system.

● We derive sufficient conditions to ensure the asymptotic stability of the above system (Theorem I). Then we give a co-design method for computing the estimation gain of the estimator and the weight matrix of the AETS (Theorem II).

Notations: $\mathbb{R}^{n\times{m}}$ means $n\times{m}$ real matrix; $\mathbb{R}^{n}$ denotes n-dimensional Euclidean space; $A > 0(A\ge0)$ implies positive definite (positive semi-definite) symmetric matrix; $\mathbb{E}\begin{Bmatrix} A \end{Bmatrix}$ represents mathematical expectation of random variable $A$; $col_N\{X_i\}$ and $diag_N\{Y_i\}$ stand for the block-column matrix $col\{X_1, X_2, \dots, X_N\}$ and the block-diagonal matrix $col\{Y_1, Y_2, \dots, Y_N\}$, respectively; $\otimes$ denotes Kronecker product.

2.   Preliminaries

Consider the following class of CNs:

where $x_i(t)$, $y_i(t)$, and $z_i(t)$ denote, respectively, the state vector, the measurement output, and the output of the i-th node. $w_i(t)\in\mathcal{L}_2[0, \infty)$ denotes the disturbance noise. $\phi$ is the initial conditions. $g(\cdot)$ is the the nonlinear vector-valued function. $\Gamma = diag\{\gamma_1, \gamma_2, \dots, \gamma_n\}$ is an inner-coupling matrix. $A = (a_{ij})_{N\times N}$ is thecoupled configuration matrix with $a_{ij} > 0(i\ne j)$ but not all zero. As usual, the diagonal element is described by $a_{ii} = -\sum_{j = 1, j\ne i}^{N}a_{ij}$. $C_i, D_i, E_i$, and $M_i$ are the known matrices.

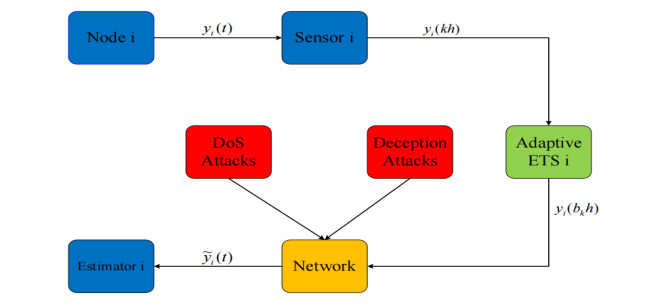
In a networked system, the instant information in the communication network is usually transmitted in an equal-period transmission scheme, which can cause unnecessary waste of limited network bandwidth. The event-based transmission strategy allows the communication channel not to be occupied all the time, thus reducing the network burden and achieving the goal of saving network resources. However, an open network environment also exposes the system to potential security risks, and for this reason, the impact of cyber attacks on the system is further discussed. The main work of this paper is to discuss a co-design approach of state estimators and AETS for a class of complex networks suffering from hybrid cyber attacks. Then, we incorporate the above-mentioned complex network model with AETS, hybrid cyber attack model and state estimator into a unified framework as shown in Figure 1. In the rest of this section, AETS, hybrid cyber attack modeling, and system modeling are discussed respectively. The details are as follows:

2.1.   Adaptive event-triggered scheme

With the booming development of network technology, the ETS has been very effective in scheduling network resources. Under the ETS, the successful transmission of sampled data needs to satisfy a triggering condition:

Based on the traditional ETS, a new ETS with variable threshold is proposed to save more network resources. Under the AETS, the threshold in the triggering condition can be described as:

where $0 < \varrho(0)\le 1$, $\varpi > 0$, and $e_{ki}(t) = y_i(b_kh)-y_i(b_kh+lh)$.

Define that $\tau_k = t_k-b_kh$ and $\ell_k = b_{k+1}-b_k-1$, where $\tau_k$ is network-induced delay, and $\tau_k\in[\tau_m, \tau_M]$. According to $t_k < t_{k+1}$, the interval $[t_k, t_{k+1})$ can be divided as $\bigcup_{l = 0}^{\ell_k}\Im_l$, where

By setting $d(t) = t-(b_kh+lh)$, we have

From (2.1)–(2.6), the actual measurement output under AETM can be expressed as:

where $0 < \tau_m\le d(t)\le h+\tau_M = d_M$.

Remark 1. In the ith sensor-to-estimator channel, the ith trigger determines whether the current sampled data of the ith sensor corresponding to the node needs to be sent, i.e., whether the current sampled data in sensor i satisfies the ith adaptive event-triggered condition (2.2). The above scheme is introduced to ensure that the information transmission efficiency can be effectively improved under the limitation of network bandwidth.

2.2.   Hybrid cyber attack modeling

The AETS greatly facilitate the transfer of data between components in a networked system. However, the actual network network environment is complex and volatile, and there may be potential security threats. From the defender's standpoint, the attack type and attack moment cannot be determined. For this reason, both deception attacks and DoS attacks are considered, both of which are the most common attack behaviors in network. Also, two sets of Bernoulli distributed variables are introduced to characterize the moment of occurrence of the two attack behaviors. Denote that $\mathscr{F} = f(y_i(t-\eta(t)))$. The hybrid attack model can be expressed as follows:

where, $\alpha_i(t)$ and $\beta_i(t)$ are BDVs, and satisfy the following statistical properties:

Remark 2. Equation (2.8) is a hybrid-driven cyber-attack behavior, i.e., the deception attacks and the DoS attacks both switch with each other at different frequencies in the communication channel. The BDVs $\alpha(t)$ and $\beta(t)$ describe the occurrence sequence of deception attacks and DoS attacks, respectively. For example, if $\beta(t) = 1$, the communication network is under DoS attacks, which means that all transmission data is blocked. If $\alpha(t) = 1$, the communication network suffers from under deception attack, which means that the real transmission data is replaced by the deception attack signal.

Remark 3. For the hybrid attack model, a nonlinear function with time delay $\eta(t)$ on the interval $(0, \eta_M]$ is introduced to express the deception attack signal $\mathscr{F}$, and satisfies the following assumption:

where $F$ is a known matrix.

2.3.   System modeling

Under AETM and hybrid attacks, the estimator on the node i is given as follows:

where $\hat{x}\in\mathbb{R}^n$ is the estimated state on the node i, $\hat{z}_i(t)\in\mathbb{R}^m$ is the estimate of $z_i(t)$, and $L_i$ is the estimator gain to be designed.

Define

and

For simplicity, we denote that

Then, by combining (2.1)–(2.11) and utilizing Kronecker product, we have

Denote $\tilde{x}(t) = \begin{bmatrix} x(t)\\e(t) \end{bmatrix}$, and the augmented system can be obtained from (2.1) and (2.11) as follows:

where

system (2.13) can be written as:

where

Assumption 1. ^[24] For positive diagonal maxtrix $U = diag\{\mu_{1}, \mu_{2}, \cdots, \mu_{n}\}$, the following inequality holds:

where

Lemma 1. ^[24] For any matrices $\mathfrak{R}_{1|2} > 0$, positive scalars $d_M|\eta_M$, and $d(t)|\eta(t)\in[0, d_M|\eta_M]$, if there exist matrices $\mathfrak{N}_{1|2}\in\mathbb{R}^{n\times n}$ such that $\begin{bmatrix}\mathfrak{R}_{1|2} & \ast\\\mathfrak{N}_{1|2} & \mathfrak{R}_{1|2}\end{bmatrix} > 0$, the following inequality holds:

where $\Xi = \begin{bmatrix} \tilde{x}(t)\\\tilde{x}(t-d(t)|\eta(t))\\\tilde{x}(t-d_M|\eta_M) \end{bmatrix}$.

Lemma 2. ^[11] For any positive-definite matrices $\mathcal{R}, \mathcal{Z}$ and scalar $\epsilon$, the following inequality holds.

3.   Main results

This section is concerned with the design problem for adaptive event-triggered state estimators such that the augmented dynamics (2.14) of the CNs (2.1) is asymptotically stable.

Theorem 1. For given constants $d_M, \eta_M, \bar{\alpha}, \bar{\beta}, \varpi$, estimator gain $L$, and weighting matrix $\Omega$, the augmented dynamics (2.14) is asymptotically stable if there exist matrices $\mathfrak{P} > 0, \mathfrak{Q}_i > 0, \mathfrak{R}_i > 0$, and $\mathfrak{N}_i$, such that the following inequalities are satisfied for $i = 1, 2$:

where

Proof. Contruct an Lyapunov functional candidate:

where

The derivative and mathematical expectation of (3.4) can be calculated as:

where $\Xi = d_M^2\mathfrak{R}_1+\eta_M^2\mathfrak{R}_2$.

Then, the following inequality can be obtained from Remark 3:

Combining (3.5) and (3.6), using Lemma 1 to estimate one cross term in (3.5), taking the adaptive triggering condition (2.2) and (2.3) to bound the term $\frac{1}{\varrho(t)}e_k^T(t)\Omega e_k(t)$ in (3.5), and adding (2.15) in Assumption 1 to the right-hand side of (3.5), one obtains

where $\xi(t) = \{\tilde{x}(t), \tilde{x}(t-d(t)), \tilde{x}(t-d_M), \tilde{x}(t-\eta(t)), \tilde{x}(t-\eta_M), e_k(t), \mathscr{F}, g(\tilde{x}(t)), w(t)\}$.

Utilizing Schur complement, we can obtain that (3.7) is equivalent to (3.1)–(3.3). When $w(t) = 0$, it can be seen that the system (2.14) is asymptotically stable from the LMIs (3.1)–(3.3). This completes the proof.

So far, the stability analysis problem of augmented systems for state estimation about complex network has been solved. Based on Theorem 1, we can easily obtain the estimator gains. Details are as follows.

Theorem 2. For given constants $d_M, \eta_M, \bar{\alpha}, \bar{\beta}, \varpi$, the estimator (2.11) for the system (2.14) can be designed if there exist matrices $\mathfrak{P} = diag\{\mathfrak{P}_1, \mathfrak{P}_2\} > 0, \mathfrak{Q}_i > 0, \mathfrak{R}_i > 0$, and $\mathfrak{N}_i$, such that the following inequalities are satisfied for $i = 1, 2$:

(3.2) and (3.3), where

In addition, the estimator gains can be obtained by $L_i = P_{2i}^{-1}X_i (i = 1, 2, \dots, N)$.

Proof. By applying Lemma 2, replacing $-\mathfrak{P}\mathfrak{R}_1\mathfrak{P}$ in (3.1) by $\varepsilon\mathfrak{R}_1-2\varepsilon\mathfrak{P}$, a new $\widehat{\mathfrak{R}}^*$ is obtained as:

Noticing that $X = P_2L$, (3.8) can be obtained. This completes the proof.

4.   Examples and simulations

In this section, we provide numerical simulations to demonstrate the validity of the theoretical approach. We take a complex network with three nodes as an example.

Example 1. The system parameters are given as follows:

The deception attack signal is chosen as

Moreover, other parameters are selected by

By utilizing the MATLAB LMI Toolbox, the feasible solutions can be obtained based on the constraints (3.8), (3.2) and (3.3) in Theorem 2.

Further, the estimator gains can be designed as:

Given the initial state $x_1(0) = \begin{bmatrix} 1 & -1 \end{bmatrix}^T$, $x_2(0) = \begin{bmatrix} 1 & 0 \end{bmatrix}^T$, $x_3(0) = \begin{bmatrix} 0 & -1 \end{bmatrix}^T$, $\hat{x}_i(0) = \begin{bmatrix} 0 & 0 \end{bmatrix}^T$, and $\varrho_i(0) = 0.25 (i = 1, 2, 3)$, numerical simulations further verify the validity of our theoretical approach. Figures 2–4 show the state responses for node i. Figures 2–7 plot the output estimation error for node i. Figures 8 and 9 depict the occurring instants of deception attacks and DoS attacks, respectively. Figures 10–12 present the release instants and intervals under AETS for node i. In addition, the release instants and intervals of ETS are plotted in Figures 13–15, respectively. The average period, maximum release interval, and transmission rate by Theorem 2 and reported in ^[24] are listed in Table 1, which the transmission rate indicates $\frac{{the{\rm{ }}\; \; transmitted\; {\rm{ }}data}}{{the{\rm{ }}\; sampled{\rm{ }}\; data}} \times 100\%$. Obviously, the AETS can obtain a larger release interval than the traditional ETS, and have a lower data delivery rate.

5.   Conclusions

The issue of event-triggered state estimation has been studied for CNs under hybrid cyber-attacks in this paper. AETS has been introduced to alleviate the network congestion problem. With the help of two sets of BDVs and an arbitrary function related to the system state, a mathematical model of the hybrid cyber-attacks has been established to portray randomly occurring DoS attacks and deception attacks. Then, CNs, AETS, hybrid cyber-attacks, and state estimators have been incorporated into a unified architecture. As a result, an augmented system has been presented. Furthermore, based on Lyapunov stability theory and LMIs, sufficient conditions to ensure the asymptotic stability of the augmented system have been derived, and the corresponding state estimator has been designed. Finally, the effectiveness of the theoretical method has been demonstrated by numerical examples and simulations. In the future, security state estimation problems for a class of CNs suffered by underlying attacks will be studied.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.