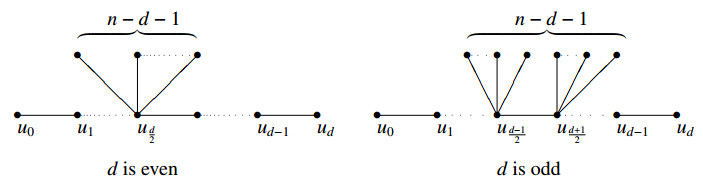On the eccentric connectivity coindex in graphs

1.   Introduction

Throughout this paper, all graphs considered are finite, simple, undirected and connected. For a graph $G = (V, E)$ with vertex set $V = V(G)$ and edge set $E = E(G)$. The degree of a vertex $v \in V(G)$, denoted by $d_G (v)$, is the number of edges incident with $v$. For vertices $u, v \in V(G)$, the distance $d(u, v)$ is defined as the length of a shortest path between $u$ and $v$ in $G$. The eccentricity $\varepsilon_{G}(v)$ or $\varepsilon (v)$ of a vertex $v$ is the maximum distance from $v$ to any other vertex in a graph $G$. The diameter of a connectd graph is the maximum eccentricity of any vertex in the graph. A pendent vertex is a vertex of degree 1. Let $P_n$, $S_n$ and $C_n$ denote the path, the star and the cycle on $n$ vertices, respectively. By $G-v$ or $G\backslash v$ we denote the graph obtained from $G$ by deleting a vertex $v\in V(G)$. By $G-uv$ we denote the graph obtained from $G$ by deleting an edge $uv \in E(G)$ (This notation is naturally extended if more than one edge are deleted). Similarly, $G+uv$ is obtained from $G$ by adding an edge $uv \notin E(G)$. A path in a connected graph is said to be a diametrical path, if this path is of length equal to the diameter. A connected graph is said to be a tree if it contains no cycles. Connected graphs in which the number of edges equals the number of vertices are called unicyclic graphs. A cactus is a connected graph in which any two simple cycles have at most one vertex in common. The set of cacti with $n$ vertices and $k$ cycles is denoted by $\mathcal{C} (n, k)$. If $G \in \mathcal{C} (n, k)$, then $|E(G)| = n+k-1$. Other notation and terminology not defined here will conform to those in ^[4]. In organic chemistry, a molecular graph represents the topology of a molecule. A topoloical index is a function defined on a molecular graph regardless of the labeling of its vertices. Till now, a number of topological indices are introduced and widely used in QSAR/QSPR studies. One of them is the eccenric connectivity index (ECI) of graph $G$, denoted by $\xi^{c}(G)$, was introduced by Gupta et al. ^[12], which is defined as

The eccentric connectivity index has been shown to give a high degree of predictability properties and may provide leads for the development of safe and potent anti-HIV compounds ^[5,13]. Furthermore, the eccentric connectivity index also has a lot of applications in neural science and entropy, see ^[14,18]. For the mathematical properties of this index see ^[1,9,11,17] and the references cited therein.

The eccentric connectivity index of a connected graph $G$ can be rewritten as

As is know that the eccentric connectivity index has been used extensively in physical and biological properties. They are defined as sums of contributions dependent on the eccentricity of adjacent vertices over all edges of a graph. By considering analogous contributions from pairs of non-adjacent vertices capturing and quantifying a possible influence of remote pairs of vertices to the molecule's properties, and motivated from ^[2,3], Hua and Miao ^[8] considered the total eccentricity sum of non-adjacent vertex pairs which is defined for a connected graph $G$ as

and call this eccentricity-based graph invariant the eccentric connectivity coindex $\overline{\xi}^{c}(G)$. By $(1)$, eccentric connectivity coindex can be rewritten as

The cactus graph has many applications in real life and much works has been done to study the extremal graph according to different index. For more results on the cactus one may be referred to ^{[6,7,10,15,16]}. In this paper, we continue the above direction of research by considering the extremal problems on the eccentric connectivity coindex.

This paper is complied as follows. In Section $2$, we present the sharp lower bounds on $\overline{\xi}^{c}$ for general connecteds graphs. In Section $3$, we characterize the extremal graphs with the minimum $\overline{\xi}^{c}$ among cacti of given order and cycles. In Section $4$, we characterize the minimal and maximal $\overline{\xi}^{c}$ of trees with given order and diameter. In Section $5$, we study the minimal $\overline{\xi}^{c}$ among unicyclic graphs on $n$ vertices with diameter and characterize the extremal graphs.

2.   Eccentric connectivity coindex of connected graphs

Hua (2019) characterize all extremal graphs with the maximum and minimum eccentric connectivity coindex among all connected graphs of given order and establish various lower bounds for this index in terms of several other graph parameters. In this section, we continue the investigation along the lines of ^[8] and present the sharp lower bounds on $\overline{\xi}^{c}$ for general connected graphs with minimum degree.

Theorem 2.1. Let $G$ ($\neq K_n$) be a connected graph of order $n$ with minimum degree $\delta$. Then

with equality if and only if $G \cong K_n^{\delta}$ ($\delta < n-1$). Where $K_n^{\delta}$ is a connected graph of order $n$ obtained by joining a vertex to the $\delta$ vertices in $K_{n-1}$.

Proof. Let $v_n$ be one vertex of degree $\delta$. Denote by $N_G (v_n) = \{v_1, v_2, \cdots, v_{\delta}\}$, also let $S = \{v_{\delta+1}, \cdots, v_{n-1}\}$. Since $G\neq K_n$, we have $\delta \leq n-2$ and $|s|\geq 1$. Thus $V(G) = N_G (v_n) \cup {S_n} \cup S$. For $v_i \in N_G (v_n)$, we have $\varepsilon_G (v_i) \geq 1$ and $d_G (v_i) \leq n-1$. For $v_i \in S$, we have $d_G (v_i)\leq n-2$ and $\varepsilon_G (v_i) \geq 2$. Moreover, $\varepsilon_G (v_n) \geq 2$ and $d_G (v_n) = \delta$. By the definition of $\overline{\xi}^{c} (G)$, we have

Suppose the equality holds in above equation, then all the inequalities in the above must be equalities. Thus, we have $d_G (v_i) = n-2$, $\varepsilon_G (v_i) = 2$ for each $v_i \in S$, $d_G (v_i) = n-1$, $\varepsilon_G (v_i) = 2$ for each $v_i \in N_G (v_n)$ and $d_G (v_n) = \delta$, $\varepsilon_G (v_n) = 2$. Hence, we find that vertex $v_n$ is adjacent to the vertices of degree $n-1$ and each vertex in $S$ is degree $n-2$. So $G\cong K_n^{\delta}$ ($\delta < n-1$). This completes the proof.

3.   Eccentric connectivity coindex of cacti

In this section, we turn our attention to eccentric connectivity coindex for cacti and in particular on extremal cacti regarding $\overline{\xi}^{c}$.

We start with a useful lemma.

Lemma 3.1 (^[8]). Let $G$ be a connected graph of order $n$, size $m$ and diameter $d$. Then

with equality if and only if $d\leq 2$.

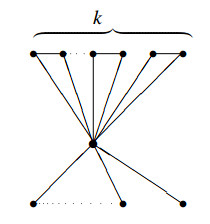
Let $\mathcal{C}_{n} ^{k}$ be the cactus by adding $k$ indepent edges among pendent vertices of $S_n$ (see Figure 1).

Theorem 3.2. Let $G$ be a cactus on $n\geq 5$ vertices with $k$ cycles. Then

The equality holds if and only if $T \cong \mathcal{C}_{n} ^{k}$.

Proof. Suppose that $N$ is the set of vertices of degree $n-1$. $n_0$ is the number of elements in $N$. Assume that $n_0 \geq 2$, let $u$, $v$ be two vertices in $G$ such that $d_G (u) = d_G (v) = n-1$. Then $\varepsilon_{G}(u) = \varepsilon_{G}(v) = 1$. It follows that $G$ is not a cactus. Since there exists cycles sharing common edges in $G$, then $n_0 = 0$ or $n_0 = 1$. If $n_{0} = 1$, then there is a unique vertex $v$ in $G$ such that $d_{G} (v) = n-1$, thus $\varepsilon_{G}(v) = 1$, hence each vertex in $G\backslash v$ is adjacent to $v$. Therefore the cacutus $G$ is obtained by introducing $k$ indepedent edges among pendent vertices of $S_{n}$, then $G \cong \mathcal{C}_{n} ^{k}$ and $\overline{\xi}^{c} (G) = 2n^2-6n-4k+4.$

Now, we assume that $n_0 = 0$. Let $d$ be the diameter of $G$. Then $d\geq 3$. Otherwise, if $d\leq 2$, let $u$ be the vertex of maximal degree in $G$. Then any other vertex of $G\backslash u$ must be adjacent to $u$, otherwise $d\geq 3$, then $n_0\geq 1$, a contradiction. By Lemma 3.1,

Note that, there are exactly $n+k-1$ edges in cacutus on $n$ vertices and $k$ cycles. This completes the proof.

4.   Eccentric connectivity coindex of trees with given diameter

In this section, we shall determine the tree of diameter $d$ with the minimum and maximum $\overline{\xi}^{c}$ respectively.

The volcano graph $V_{n, d}$ is the graph obtained from a path $P_{d+1}$ and a set $S$ of $n-d-1$ vertices by joining vertex in $S$ to the central vertex of $P_{d+1}$. Obviously, if $d$ is even, there is only one center of $P_{d+1}$. If $d$ is odd, there are two central vertices of $P_{d+1}$ (See Figure 2). The caterpillar tree with respect to $P_{d+1} = u_0u_1\cdots u_d$, denoted by $CP(S_1, \cdots, S_{d-1})$, is the tree obtained from $P_d$ by attaching $S_i$ new vertices to $u_i$, for $1\leq i\leq d-1$.

Let

Theorem 4.1. Let $T$ be a tree on $n$ ($n\geq 5$) vertices with diameter $d\geq 2$. Then

The equality holds if and only if $T \cong V_{n, d}$.

Proof. Let $T_0$ be a graph chosen among all trees of order $n$ with diameter $d$ such that $T_0$ has the smallest $\overline{\xi}^{c}$. First, we have the following claim.

Claim 1. Among all trees $T$ with order $n$ and diameter $d$, $min(\overline{\xi}^{c} (T))$ is achived on caterpillars.

Proof of Claim 1. Let $T$ be any tree that is not a caterpillar with order $n$ and diameter $d$. Let $P$ be the diametral path of $T$, connecting $u_0$ to $u_d$. Then the eccentricity of each vertex $w$ of $T$ is equal to $max\{d(w, u_0), d(w, u_d)\}$. Let $z \notin \{u_0, u_d\}$ be a vertex of $P$ and let $T_z$ be a maximal subtree of $T$ which contains $z$ but no other vertex of $P$. We may assume that $z$ can be selected such that $\varepsilon_{T_z} (z) = k\geq 2$, for otherwise $T$ is a caterpillar. Let $u$ be vertex of $T_z$ with $d(u, z) = k-1$ and let $v$ be the neighbor of $u$ with $d(v, z) = k-2$. Let $S = N(u)\backslash {v}$ and let $s = |S|$. Note that $s\geq 1$. Let $T^{'}$ be the tree from $T$ by replacing the edges between $u$ and the vertices of $S$ with the edges between $v$ and the vertices of $S$. Then we have

Note that $\varepsilon_{T} (u) = \varepsilon_{T} (v) +1$, $\varepsilon_{T} (w)\geq \varepsilon_{T'} (w)+1$ for $w\in S$ and since $d\geq 2$, we get that $d_T (w) < n-2$. Hence

Therefore,

If $T'$ is not a caterpillar, we can repeat the construction as many times as required to arrive at a caterpillar. Since at each step the value of $\overline{\xi}^{c} (T)$ is decreased. Thus the claim is proven.

Since $T_0$ is the extremal tree with diametral path $P = u_0u_1, \cdots, u_d$. By claim 1, we conclude that all vertices of $V(T)\backslash V(P)$ must be pendent vertices attached at some vertices of $P$, we denote this tree $T_1$. We now consider the case when $d$ is even, if there exists some vertex $u_i$ ($i\neq \frac{d}{2}$) of $P$ with pendent vertices (say $w_1, \, w_2\, \cdots, w_t \; t\geq 1$) attached. Let

By the definition of $\overline{\xi}^{c}$, we have

As $d_{T_1} (w_k) = d_{T_2} (w_k) = 1$, ($k = 1, 2, \cdots, t$) and $\varepsilon_{T_1} (w_k) > \varepsilon_{T_2} (w_k)$, $\varepsilon_{T_1} (u_i) = \varepsilon_{T_2} (u_i) > \varepsilon_{T_1} (u_{\frac{d}{2}}) = \varepsilon_{T_2} (u_{\frac{d}{2}}) , \; \varepsilon_{T_1} (w_k)-\varepsilon_{T_2} (w_k) = \varepsilon_{T_1} (u_i)- \varepsilon_{T_2} (u_{\frac{d}{2}}).$

Then, we have

Therefore,

Continue this procedure, forming new trees, untill all the pendent vertices in $T_1$ are adjacent to $u_{\frac{d}{2}}$. If $d$ is odd, similarly, the extremal graph must be the graph obtained from a path $P_{d+1}$ by some pendent vertices attched on the center of $P_{d+1}$. That is to say, $T_0 \cong V_{n, d}$. This completes the proof.

For even $d$,

Let $f(x) = \frac{n(n-2)(x+2)}{2}-\frac{(n-2)(x^2+3x+2)}{2}+\frac{x(x-2)(3n-7)}{4}+2x(n-2)$, ($x\geq 2$). It remains to determine which value of $x$ minimizes $f(x)$. For this, we use the first and second derivative test. Noting that

$f''(x)$ is positive for $x\geq 2$, then $f'(x)$ is an increasing function for $x\geq 2$. So

Therefore, $f(x)$ is an increasing function for $x\geq 2$.

Then

For odd $d$, we obtain the same result. Therefore, we obtain the following chain inequality

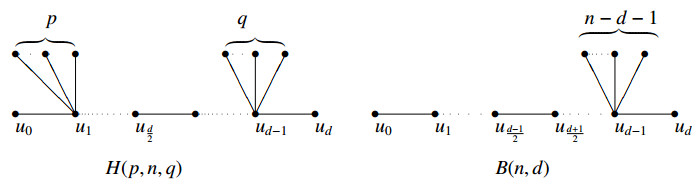
We denote by $H(p, n, q)$ one double starlike tree which is obtained by attaching the centers of two stars $K_{1, p}$ and $K_{1, q}$ to the ends of path $P_{d-2}$, respectively, where $p+q = n-d-1$. The broom graph $B_{n, d}$ consists of a path $P_{d-1}$, together with $n-d$ pendent vertices all adjacent to the same pendent vertex of $P_{d-1}$, obviously, $B_{n, d} = H(0, n, n-d-1)$, see Figure 3.

For any tree $T\in H(p, n, q)$, we have $\overline{\xi}^{c} (T) = \overline{\xi}^{c} (B_{n, d}) = f_2 (n, d)$. Let

Theorem 4.2. If $T$ is a tree of order $n$ and diameter $d$, then

The equality holds if and only if $T\cong H(p, n, q)$.

Proof. Let $P = u_0u_1, \cdots, u_d$ be a diametral path in $T$. Asssume that $T$ is not the graph $H(p, n, q)$, then there exists a pendent vertex $v$ of $T , \; v\neq u_0$ such that $v$ is adjacent to a vertex $u$, where $u\neq u_{d-1}$ and $u\neq u_1$ (It is possible that $u$ lies on $P$). Denote by $\{v_1, v_2, \cdots, v_k\}$ be the set of pendent vertices which are adjacent to $u$ and $v_i \neq u_0$ for $i = 1, 2, \cdots, k$. Let

Note that $T'$ has the same order and diameter as $T$. We will show that $T'$ has a larger eccentric connectivity coindex than $T$.

As $d_{T'} (v_i) = d_{T} (v_i) = 1$, ($i = 1, 2, \cdots, k$) and $\varepsilon_{T'} (v_i) > \varepsilon_{T} (v_i)$, $\varepsilon_{T'} (u) = \varepsilon_{T} (u) < \varepsilon_{T'} (u_{d-1}) = \varepsilon_{T} (u_{d-1}) , \; \varepsilon_{T'} (v_i)-\varepsilon_{T} (v_i) = \varepsilon_{T'} (u_{d-1})- \varepsilon_{T} (u).$ Then, we have

Then

Continue this procedure, forming new trees untill all vertices outside $P$ having degree one are adjacent to $x_{d-1}$. Thus a tree $H(p, n, q)$ of order $n$ and diameter $d$ is obtained, one has

This completes the proof.

Similar to previous discussion, we have $\overline{\xi}^{c} (B_{n, d}) < \overline{\xi}^{c} (B_{n, d+1})$ for any $d\geq 2$. Therefore, it follows that

Summarizing theorems 4.1, 4.2 and these inequlities $(3)$, $(4)$, we have the following result.

Theorem 4.3. Let $T$ be a tree on $n$ vertices. Then

Where $f_2 (n, n-1)$ as mentioned in theorem 4.2. The left quality holds if and only if $T\cong S_n$ and the right equality holds if and only if $T\cong P_n$.

5.   Eccentric connectivity coindex of unicyclic graphs with given diameter

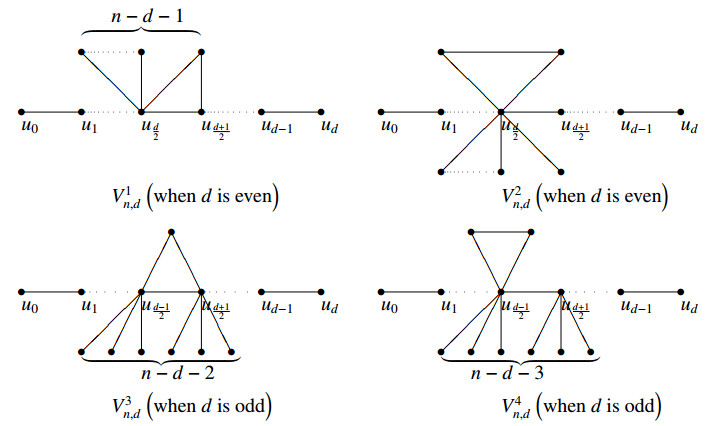
In this section, we consider the minimum $\overline{\xi}^{c}$ of unicyclic graphs with given diameter. Let $\mathcal{G}_{n}^d$ be the unicyclic graph with order $n$ and diameter $d$. First, for even $d$, let $V_{n, d}^{1}$ be the graph obtained from $P_{d+1} = u_0u_1.\cdots, u_d$ by attaching $n-d-1$ pendent edges to $u_{\frac{d}{2}}$ and adding an edge between $u_{\frac{d}{2}+1}$ and one of the attached pendent vertices of $u_{\frac{d}{2}}$. Let $V_{n, d}^{2}$ be the graph obtained from $P_{d+1} = u_0u_1.\cdots, u_d$ by attaching $n-d-1$ pendent edges to $u_{\frac{d}{2}}$ and adding an edge between two attached pendent vertices of $u_{\frac{d}{2}}$, (see Figure 4).

For odd $d$, let $V_{n, d}^{3}$ be the unicyclic graphs in which there are $s, \, \, t$ ($s+t = n-d-2$) pendent vertices adjacent to $u_{\frac{d-1}{2}}$ and $u_{\frac{d+1}{2}}$ of diametrel path respectively. Let $V_{n, d}^{4}$ be the unicyclic graphs in which there are $p, \, \, q$ ($p+q = n-d-3$) pendent vertices adjacent to $u_{\frac{d-1}{2}}$ and $u_{\frac{d+1}{2}}$ of diametrel path respectively, (see Figure 4).

By direct calculation, for even $d$,

For odd $d$, any $G\in V_{n, d}^{3}$, we have

If $G_1\in V_{n, d}^{3}$ and $G_2\in V_{n, d}^{4}$. By direct calculation we find that, $\overline{\xi}^{c} (G_1) < \overline{\xi}^{c} (G_2)$. Let

Theorem 5.1. Let $G$ be a unicyclic graph on $n\, \, (\geq 7)$ vertices with diameter $d\geq 2$. Then

The equality holds if and only if $G\cong V_{n, d}^{1}$ or $G\cong V_{n, d}^{2}$ for even $d$ and $G\cong V_{n, d}^{3}$ for odd $d$.

Proof. Choose $G_0$ in $\mathcal{G}_{n}^d$ such that $\overline{\xi}^{c} (G_0)$ is as small as possible. Let $P_{d+1} = u_0u_1, \cdots, u_d$ be a diametral path and $C_k$ be the unique cycle in $G_0$. Similar as the proof of theorem 4.1 all vertices in $V(G_0)\backslash \{V(P)\mathop{\cup} V(C_k)\}$ must be pendent vertices and adjacent to some vertices of $V(P)\mathop{\cup} V(C_k)$, we denote it by $G^*$. First, we consider when the diameter $d$ is even, we proceed by considering the following possible cases.

Case 1. $|V(C_k)\cap V(P_{d+1})| = 1$.

In this case, let $V(C_k)\cap V(P_{d+1}) = {u_i}$. In the following, we show three facts.

Fact 1. All vertices in $V(G^*)\backslash \{V(P)\mathop{\cup} V(C_k)\}$ must be adjacent to $u_{\frac{d}{2}}$ of $P$.

Proof of Fact 1. If there exists a vertex $u_s$ (with $s\neq \frac{d}{2}$) of $P$ with pendent vertices, say $w_1, w_2, \cdots, w_k$ attached in $G^{*}$. Let

By a similar approach in the proof of theorem 4.1, we get $\overline{\xi}^{c} (G^*) > \overline{\xi}^{c} (G_1)$, a contradiction to our choice of $G^{*}$. Similarly, we conclude that there is no pendent vertices attached the vertex of cycle $C_k$ in $G^*$ other than $u_i$. That is to say, each of the vertices other $u_i$ on cycle $C_k$ in $G^*$ is of degree $2$. This completes the proof of fact 1.

Fact 2. The length of the cycle $C_k$ is equal to $3$, i.e., $k = 3$ in $G^*$.

Proof of Fact 2. If the length of the cycle $k\neq 3$.

Let $C_k = u_iv_1v_2, \cdots, v_{k-1}u_i$ and $N_{G^*} (u_i)\cap V(C_k) = \{v_1, v_{k-1}\}$. Let

Clearly, $G_2$ is in $\mathcal{G}_{n}^d$ and $C_3$ is the unique cycle in $G_2$. It is routine to check that

Note that $\varepsilon_{G^*} (u_i) = \varepsilon_{G_2} (u_i) , \; \varepsilon_{G^*} (v_1) = \varepsilon_{G_2} (v_1)$, $\varepsilon_{G^*} (v_{k-1}) = \varepsilon_{G_2} (v_{k-1})$ and $\varepsilon_{G^*} (v_j)\geq \varepsilon_{G_2} (v_j) > \varepsilon_{G^*} (u_i)$ for $j = 2, \cdots, k-2$ and $\varepsilon_{G^*} (v_2) = \varepsilon_{G^*} (u_i)+2$, $\varepsilon_{G_2} (v_2) = \varepsilon_{G_2} (u_i)+1$.

Therefore,

Then $\overline{\xi}^{c} (G^*) > \overline{\xi}^{c} (G_2)$, a contradiction. This completes the proof of fact 2.

Fact 3. $u_i$ is the center of the diametral path $P$ in $G^*$.

Proof of Fact 3. Based on fact $2$, we know that $P_{d+1} = u_0u_1, \cdots, u_d$ and $C_k = u_iv_1v_{k-1}$. If $u_i\neq u_{\frac{d}{2}}$, we assume without loss of generality that $d_{G^*} (u_0, u_i) < \frac{d}{2}$, that is to say, $d_{G^*} (u_0, u_i) < d_{G^*} (u_{i+1}, u_d)$. Move the triangle and all the pendent edges from $u_i$ to $u_{\frac{d}{2}}$ in $G^*$ and denote the result graph by $G_3$. It is routine to check that $G_3$ in $\mathcal{G}_{n}^d$. Since

We have

Then $\overline{\xi}^{c} (G^*) > \overline{\xi}^{c} (G_3)$, a contradiction again. This completes the proof of fact 3.

Case 2. $P$ and $C_k$ are vertex and edge disjoint.

Let $Q = u_iz_1z_2, \cdots, z_{s-1}z_s$ be a path connecting path $P$ and $C_k$. By the similar approach in the proof of theorem 4.1, we can contract the whole path $Q$ (i.e., $u_i$ and $z_s$ coincide and then attaching suitable number of pendent vertices at $u_i$) to get a new graph $G_4$ with $P$ and $C_k$ having exactly one vertex in common. So the following procedure similar as case $1$.

By the discussion as above, we obtain that for all $G$ in $\mathcal{G}_{n}^d$. If the unique cycle and the diameter in $G$ have no edges in common, then the extremal graph is $V_{n, d}^{2}$ when $d$ is even. When $d$ is even, the diameter path has only one center, while when $d$ is odd, the diameter path has two centers. In either case, the pendent vertices in the minimum graph except the endpoints of the diameter path are all adjacent to the center of the diameter path, the proof process is exactly the same. Here we omit the proof when $d$ is odd. Hence, the extremal graph is $V_{n, d}^{4}$ when $d$ is odd. As is depicted in Figure 4.

Case 3. $|V(C_k)\cap V(P_{d+1})|\geq 2$.

If there exist common edges between $P_{d+1}$ and $C_k$, then we get that all vertices in $V(G_0)\backslash \{V(P)\mathop{\cup} V(C_k)\}$ must be adjacent to $u_{\frac{d}{2}}$ of $P$ similar as case $1$. We denote it by $G^*$. Let $P_{d+1} = u_0u_1, \cdots, u_d$ and $C_k = u_iu_{i+1}, \cdots, u_jy_1y_2, \cdots, y_mu_i$. In this case, we first show that the unique cycle $C_k$ contained in $G^*$ is just $C_3$, that is to say, $k = 3$, otherwise, we assume that $k\geq 4$. First we consider the diameter $d$ is even. Let

By the definition of $\overline{\xi}^{c}$ and bearing in mind that it is possible $u_{j-1} = u_i$. As $\varepsilon_{G^*} (y_i)\geq \varepsilon_{G_5} (y_i)$, $i = 1, \cdots, m$ and $\varepsilon_{G_5} (y_1) = \varepsilon_{G_5} (y_2) = \varepsilon_{G_5} (y_3) = \cdots = \varepsilon_{G_5} (y_m)$. $\varepsilon_{G_5} (u_i) = \varepsilon_{G^*} (u_i)$ and $\varepsilon_{G_5} (u_{j+1}) = \varepsilon_{G^*} (u_{j+1})$, $\varepsilon_{G_5} (y_i)\geq \varepsilon_{G_5} (u_\frac{d}{2})+1$, $\varepsilon_{G^*} (y_i)\geq \varepsilon_{G^*} (u_\frac{d}{2})+2$, $\varepsilon_{G_5} (u_\frac{d}{2}) = \varepsilon_{G^*} (u_\frac{d}{2})$, $\varepsilon_{G_5} (u_{\frac{d}{2}+1}) = \varepsilon_{G^*} (u_{\frac{d}{2}+1})$,

Moreover, $d_{G^*} (y_i) = 2$, $d_{G_5} (y_i) = 1$, $i = 2, \cdots, m \; d_{G^*} (y_1) = 2$, $d_{G_5} (y_1) = 2$ and $d_{G_5} (u_\frac{d}{2}) = d_{G^*} (u_\frac{d}{2})+m$, $d_{G_5} (u_{\frac{d}{2}+1}) = d_{G^*} (u_\frac{d}{2}+1)+1$

It follows that

Therefore,

which contradicts the chioce of $G^*$.

Hence, the structure of $G^*$ can be described as follows: its unique cycle $C_3$ and its diametral path $P_{d+1} = u_0u_1, \cdots, u_d$ have only one edge $u_\frac{d}{2}u_{\frac{d}{2}+1}$ in common and there are some pendent edges attached to $u_\frac{d}{2}$ in $G^*$.

Summarizing the discussion as in case $3$, we obtain that for all $G$ in $\mathcal{G}_{n}^d$, if the unique cycle and the diameter in $G$ have edge in common. When $d$ is even, then the graph say $V_{n, d}^1$ with the minimum $\overline{\xi}^{c}$ and when $d$ is odd, we can similarly get that the extremal graph belongs to $V_{n, d}^3$.

Summarizing cases 1–3, when $d$ is odd, for any $G_1\in V_{n, d}^3$ and $G_2\in V_{n, d}^4$, we can easily obtain that $\overline{\xi}^{c} (G_1) < \overline{\xi}^{c} (G_2)$. Therefore, $V_{n, d}^3$ achieved the minimum $\overline{\xi}^{c}$ for $d$ is odd.

When $d$ is even, $\overline{\xi}^{c} (V_{n, d}^1) = \overline{\xi}^{c} (V_{n, d}^2)$, $V_{n, d}^1$ and $V_{n, d}^2$ obtain the minimum value of Eccentric connectivity coindex at the same time (See Figure 4).

This completes the proof.

6.   Conclusions

In this paper, we first present the sharp lower bounds on $\overline{\xi}^{c}$ for general connecteds graphs and present a structure of the extremal graphs for eccentric connectivity coindex over cacti graphs with $n$ vertices and $k$ cycles, then characterize the extremal trees with given order and diameter on the eccentric connectivity coindex. Moreover, we optimize the extremal structure of unicyclic graphs with given order and diameter. Along this line, some other interesting extremal problems on the eccentric connectivity coindex are valuable to be considered.

Acknowledgements

H. Z. Wang is the corresponding author and was partially supported by the National Nature Science Foundation of China (No.11971011) and Natural Science Foundation of Jiangsu Province of China (No. BK20191047). The authors would like to thank the anonymous referees for their careful reading and helpful suggestions that improve the presentation of the paper.

Conflict of interest

All authors in the paper have no conflict of interest.