1.
Introduction
Fractional calculus is one of the most widely used mathematical analysis which deals with different ways to represent the real and complex number powers of the differentiation or integration operator and creating a calculus for the same operators in the generalized form. This calculus has numerous applications in the fields of science and engineering viz viscoelasticity, engineering mechanics, control systems, biological population models, etc. In specific, this branch of mathematics involves the methods and notion to solve the differential equations concern with a fractional derivative of unknown function which is also called fractional differential equations (FDEs). Moreover, this fractional calculus has been widely employed for modeling the engineering and physical processes which are possibly represented in terms of FDEs. This type of fractional derivative model is utilized in order to provide accurate modeling of those systems which needs to be accurate modeling of damping and also has the capability of modeling the complex engineering problems [10,11,12,14,15,16,17,23]. In recent years, a variety of numerical and analytical modeling approaches with their applications to new problems have been addressed in the research field of mechanics, electrodynamics of complex medium, and aerodynamics, etc. The application of Erdélyi-Kober fractional integrals is discussed in detail with the examples in [7,11,12,25,27,31]. Unlike integer derivatives, fractional derivatives access the system's global evolution rather than just its local characteristics; as a result, when dealing with certain phenomena, they provide more accurate models of real-world behaviour than standard derivatives. In real life, differential equations of fractional order are used to calculate the movement or flow of electricity, the motion of an object back and forth like a pendulum, and to explain thermodynamic concepts, etc. Additionally, in medical terms, they are used to visualize the progression of diseases. They represent real-world behaviour more accurately than standard derivatives. The coupled system consists of a couple of differential equations with pair of dependent variables and a single independent variable. The coupled system of FDEs becomes a more popular research field due to its vast applications in real-time problems namely anomalous diffusion, ecological models, chaotic systems, and disease models [1,2,8,20,24,26]. Boundary value problems (BVPs) applied to a coupled system with non-linear differential equations attracting researchers because of its applications in plasma physics and heat conduction; see [3,4,5,6,18,19,21,22,28,29,32], and the references cited therein. The nonlinear coupled system of Riemann-Liouville FDEs
for 0<t<T and 1<q,p≤2, was investigated in [30], where RLDq, RLDp denote the Riemann-Liouville fractional derivatives (RLFDs) of order q, p, f, g:[0,T]×R×R→R are given continuous functions, and αi, βi∈R, i=1,2,⋯,n are positive real constants. Fixed-point theorems were also employed to prove the main results. The Caputo type FDEs nonlinear coupled system
for 0<t<1, n−1<α1≤n, m−1<α2≤m, and n,m≥2, were examined in [34], where λi>0 is a parameter, Dαi0+ is the standard Caputo derivative; μi>0 is a constant, ∫10a(s)v(s)dA1(s), ∫10b(s)u(s)dA2(s) denote the Riemann-Stieltjes integrals. Leray-Schauder's alternative and the contraction mapping principle proved the existence and uniqueness of solutions.
In this study, a coupled system with non-linear FDEs is considered and which is represented as in (1.3).
Equation (1.3) is subjected to the Erdélyi-Kober, Riemann-Liouville integral boundary conditions are given in Eq (1.4).
where cDj represents the Caputo derivatives of order j,{j=ς,ϱ,ϱ1,ς1}, Jp and Jq are the Riemann-Liouville integrals of order p,q>0 and Iϵi,θiσi(i=1,2) is the Erdélyi-Kober integrals of order σi>0,θi>0,ϵi∈R(i=1,2),f,g:H×R×R→R are continuous functions and μi,τi(i=1,2) are real constants. The structure of this proposed work is as follows: Section 2 deals with some facts and definitions related to this study. Section 3 gives a solution for the system described in Eq (2) and (3). The examples of the proposed problem are drawn to validate the applications in Section 4. Finally, the discussion is presented.
2.
Preliminaries
This section recollects the definitions and some basics facts related to the proposed study are presented [9,12,23,33].
Definition 2.1. The Riemann-Liouville integral of order ϱ>0 for a function f(τ) is defined as
provided that the right hand side is point wise defined on [0,∞).
Definition 2.2. The Caputo derivative of order ϱ>0 of a function f:[0,∞)→R is defined as
where n=[ϱ]+1 and [ϱ] denotes the integral part of the real number.
Definition 2.3. The Erdélyi-Kober fractional integral of order ς1>0 with η>0 and ϱ1∈R of a continuous function f:(0,∞)→R is defined by
provided the right hand side is point wise defined on R+.
Remark 2.4. For η=1, the above operator is reduced to the Kober operator
that was introduced for the first time by Kober in [13]. For ϱ1=0, the kober operator is reduced to the Riemann-Liouville integral with a power weight:
Lemma 2.5. Given the functions ν,ρ∈C(H,R), the solution of the problem
is equivalent to the fractional integral equations
and
Here the non zero constants Λ1 and Λ2 are
where
and
Proof. The general solution for the Eq (2.1) can be expressed as
where c0,c1,d0,d1 are arbitrary constants.
Substituting the (1.4) in Eqs (2.9) and (2.10), the following equations will be obtained.
where a1,a2,a3,a4,b1,b2,b3,b4 are given by (2.5)–(2.8). Substituting the values of c0,c1,d0,d1 in (2.9) and (2.10) respectively, we get the solution for (2.1).
3.
Main results
Let us introduce the space U={u:u∈C(H,R) and cDς1u∈C(H,R)} with the norm defined by
Then (U,‖.‖U) is a Banach space and also let us introduce the space V={v:v∈C(H,R) and cDϱ1v∈C(H,R)} with the norm defined by
Then (V,‖.‖V) is a Banach space.
Clearly, the product space (U×V,‖.‖U×V) is a Banach space with the norm defined by
In view of Lemma 2.5, we define an operator F:U×V→U×V by
where
and
Let us present the following assumptions that are used afterward here:
(H1) Assume that f,g:H×R×R→R are continuous functions and there exists constants K1,K2>0, such that
for each τ∈H and all ui,vi∈R,i=1,2.
(H2) χ1=Δ1+Δ2Γ(2−ς1), χ2=Δ′1+Δ′2Γ(2−ϱ1), where χ=max{χ1,χ2}.
(H3) Assume that f,g:H×R×R→R are continuous functions and there exists real constants li,λi≥0(i=1,2) and l0,λ0>0 such that for all ui∈R(i=1,2). We have
For making a simplified expression, the following terms are introduced throughout this study:
Δ1=K1G1, P1=G1M1, Δ2=K1G2, P2=G2M1, Δ′1=K2G′1, P′1=G′1M2, Δ′2=K2G′2, P′2=G′2M2,
Theorem 3.1. Suppose that (H3) condition holds. Furthermore, it is assumed that max{B,C}<1. Then, on H, the BVP (1.3) and (1.4) have at least one solution.
Proof. The F:U×V→U×V operator is shown to be completely continuous. It follows that the F operator is continuous by the continuity of the f and g functions.
Let Θ⊂U×V be bounded. Then there exists positive constants N1 and N2 such that f(τ,v(τ),cDϱ1v(τ))≤N1 and g(τ,u(τ),cDς1u(τ))≤N2 for all (u,v)∈Θ.
Step 1: To show that F is uniformly bounded.
For each τ∈H, we have
and
which implies that
Thus, we have
Similarly, we get
and
which implies that
As a result, the following expression is obtained,
Therefore, the above equation follows the inequalities in which operator F is uniformly bounded.
Step 2: To show that F is equicontinuous. Let τ1,τ2∈H with τ1<τ2. Then we have
and
Also, we obtain
and
This operator with Eqs (3.8)–(3.11) tends to zero when τ2→τ1. Subsequently, the F operator is equicontinuous and completely continuous according to Arzelˊa-Ascoli Theorem.
Step 3: To prove that the set ϖ={(u,v)∈U×V:(u,v)=μF(u,v),0<μ≤1} is bounded.
Let (u,v)∈ϖ. Then (u,v)=μF(u,v). For any τ∈[0,1], we have
Then
and
which implies that
Hence we have
We can have in a similar way,
and
which implies that
Hence we have
Thus, we find that
which implies that
The above equation proves that the set ϖ is bounded. Therefore, the F operator consists of at least a single fixed point according to the (see [33] Theorem 1.9). As a result, the boundary value problem is represented in Eqs (1.3) and (1.4) also, consist of at least a single solution on H.
Theorem 3.2. Suppose that (H1), (H2) and χ<12 hold, then the BVP (1.3) and (1.4) has a unique solution on H.
Proof. Let us fix M1=supτ∈[0,1]|f(τ,0,0)|<∞ and M2=supτ∈[0,1]|g(τ,0,0)|<∞ and we define
Consider the set Bˆρ={(u,v)∈U×V:‖(u,v)‖U×V≤ˆρ}.
Now, to prove that FBˆρ⊂Bˆρ. For (u,v)∈Bˆρ, we have
and
which implies that
Hence,
In this same way, we have
and
which implies that
In consequence, we get
Hence, we get
Hence, FBˆρ⊂Bˆρ.
Next to prove that F is a contraction mapping on Bˆρ.
For ui,vi∈Bˆρ,i=1,2 and for each τ∈H, we have
and
Thus, we obtain
Therefore,
In a similar way, we can find
and
which implies that
In consequence, we get
Consequently, we obtain
Thus, the F operator is referred to as a contraction operator (see [33] Theorem 1.4) and produced a unique fixed point that generates a unique solution for the BVP of (1.3) and (1.4) on H.
4.
Examples
Example 4.1. Consider the following coupled system of non-integer order differential equations subject to the Riemann-Liouville, Erdélyi-Kober integral conditions:
Here, ς=7/6,ϱ=5/4,ϱ1=1/3,ς1=1/5,μ1=1,μ2=4,τ1=4,τ2=1,p=4/3,q=6/5, σ1=3/2,ϵ1=1/6,θ1=5/4,σ2=7/6,ϵ2=6/4,θ2=1/8,ω=1/3,ζ=1/2,ξ=1/5,η=1/7, and also
Clearly,
Thus, l0=1/6,l1=49/300,l2=35/180,λ0=1/4,λ1=39/240,λ2=25/380. Using the given data, we find that a1=0.8059,a2=0.0277,a3=−1.9549,a4=0.6521,Λ1=0.4713 and b1=−0.5802,b2=0.3591,b3=0.0876,b4=0.8751,Λ2=−0.4763 and also G1=2.3068,G2=2.4740,G′1=2.2666,G′2=2.1105. Furthermore, we can find
Thus, max{B,C}=0.9650<1.
All of the hypotheses of the theorem 3.1 are satisfied. Therefore, there is a solution for the problem (4.1) on H.
Example 4.2. Consider the following coupled system of non-integer order differential equations subject to the Riemann- Liouville, Erdélyi-Kober integral conditions:
Here, ς=5/3,ϱ=6/5,ϱ1=4/5,ς1=3/5,μ1=2,μ2=1,τ1=1,τ2=2,p=3/2,q=1/2, σ1=5/2,ϵ1=1/3,θ1=4/3,σ2=5/4,ϵ2=7/6,θ2=6/4,ω=1/4,ζ=1/5,ξ=1/6,η=1/8 and also K1=1/10,K2=1/5. Clearly,
Using the given data, we find that a1=0.8119,a2=0.0188,a3=0.4065,a4=0.9283, Λ1=0.7608,b1=0.4954,b2=0.0673,b3=0.4605,b4=0.9563,λ2=0.5047 and also G1=1.3483G2=1.7870,G′1=1.9601,G′2=2.0589,Δ1=0.0539,Δ2=0.0715,Δ′1=0.0560, Δ′2=0.0588. We can find
Thus, χ=max{χ1,χ2}=0.1345<1.
All of the hypotheses of the theorem 3.2 are satisfied. Therefore, there is a unique solution for the problem (4.2) on H.
5.
Discussion
This paper implemented the Riemann-Liouville, Erdélyi-Kober integral conditions with Leray-Schauder and Banach fixed point theorems based solution for a Caputo type coupled differential equations of non-integer order. The results are obtained through fixing the parameters of interest for the proposed problem (1.3) and (1.4), such as (p,q,μ1,μ2,τ1,τ2) which makes the distinctive classes of the problem. For example, by applying the value for p,q=1 with a boundary condition in the proposed solution, the following equation will be obtained for the problem (1.3) and (1.4):
the result will be in the form of (1.3)–(1.4):
when applying the μ1=μ2=0.
Acknowledgments
We thank the reviewers for their constructive remarks on our work.
Conflict of interest
All authors declare no conflicts of interest in this paper.









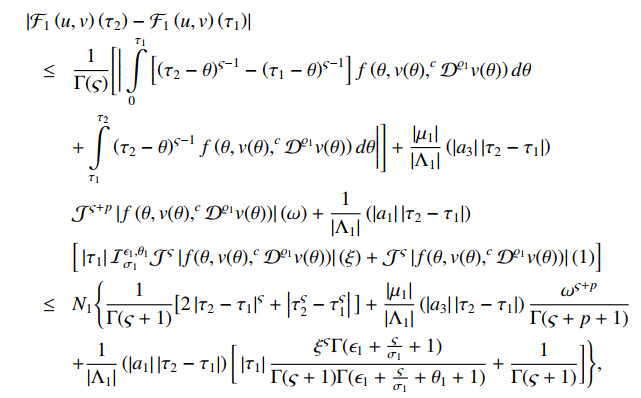




 DownLoad:
DownLoad: