Bounded random fluctuations on the input flow in chemostat models with wall growth and non-monotonic kinetics

1.   Introduction

Chemostat refers to a laboratory device, invented at the same time in the 1950s by Monod (see ^[1]) and Novick and Szilard (see ^[2]), very used in practice for growing microorganisms in a cultured environment. The chemostat has been regarded as an idealization of nature to study microbial ecosystems at steady state, which is an important and interesting problem for researchers from many areas due to its large number of applications, for instance, it can be used to study genetically altered microorganisms (see e.g. ^[3,4]), waste-water treatment process (see e.g. ^[5,6]), models of mammalian large intestine (see e.g. ^[7,8]) and plays an important role in theoretical ecology (see e.g. ^{[9,10,11,12,13,14,15,16,17,18,19,20]}).

It is worth mentioning that the chemostat has been subject to a large number of scientific publications, not only in applied sciences but also in Mathematics. It is due to the fact that it is very interesting also as a mathematical object, in fact, it constitutes a very active branch of applied mathematics which, in addition, proposes a recent formal framework called the theory of the chemostat centered around a well-identified community of mathematicians.

The reputation of the chemostat is mainly due to the fact that it is a very simple device that allows to develop many different works and reproduces the real experiments in a very loyal way. Those are some of the reasons that encouraged us to consider this model as part of our research.

Concerning the biological aspects, the chemostat device consists of three tanks, the feed bottle, the culture vessel and the collection vessel, that are interconnected by means of pumps. The substrate stored in the feed bottle is pumped to the culture vessel, where the interactions between the substrate and the species take place. In addition, another flow is pumped from the culture vessel to the collection vessel in order to keep the volume of the culture vessel constant.

The classical mathematical model used to describe the dynamics into the culture vessel in the chemostat device consists of a system of two ordinary differential equations (see e.g. ^[21,22]) given by

where $s = s(t)$ and $x = x(t)$ denote the concentration of substrate (or nutrient) and species (or microorganisms), respectively, $s_{in}$ is the input concentration of substrate, $D$ is the removal rate, also called input flow, and $\mu$ is a function describing the consumption kinetics of the consumer species.

Among the different assumptions made when dealing with the deterministic model (1.1)–(1.2), one is to assume that the input flow $D$ is fast enough such that species are removed to the collection vessel before having the opportunity of sticking to the wall of the culture vessel. However, this phenomenon, introduced by Pilyugin and Waltman (see ^[23]) and known as wall growth, is quite usual and it can be easily observed in practice. In fact, these observations motivate us to go further from the classical deterministic chemostat model (1.1)–(1.2) and consider the corresponding chemostat model with wall growth given by the following differential system (see ^[22])

where $s = s(t)$ denotes again the concentration of the nutrient and we divide in this case the total concentration of species $x = x(t)$ as follows: on the one hand, $x_1 = x_1(t)$ refers to the concentration of the species in the liquid media (the also called planktonic biomass) and $x_2 = x_2(t)$ is the concentration of the species sticked on the wall of the culture vessel (the attached biomass).

In addition, the rate $b\in(0, 1)$ describes the fraction of dead biomass which is recycled and $\nu > 0$ is the collective death rate coefficient of the microbial biomass representing factors such as diseases, aging, etc. Apart from that, $r_1 > 0$ and $r_2 > 0$ represent the rates at which the species stick on to and shear off from the walls of the culture vessel, respectively. Finally $\mu$ is, as in the classical chemostat, the consumption function of the consumer species and $y > 0$ denotes the yield coefficient of transformation of substrate into biomass.

As explained before, we consider Haldane kinetics in this paper, a non-monotonic function introduced by Haldane (see ^[24]) and defined by

where $\bar{\mu}_0$ corresponds to the growth rate coefficient of the species, $k_s$ denotes the so-called Monod constant and $k_i$ is the inhibition constant modeling the inhibition of species to take substrate when it is at high concentration. We would also like to highlight that, in industrial setup, large input concentrations $s_{in}$ can be observed and it is also very well-known that microorganisms may suffer growth inhibition under high concentrations of substrate. This is precisely what the non-monotonic consumption function (1.6) models (see ^[25]).

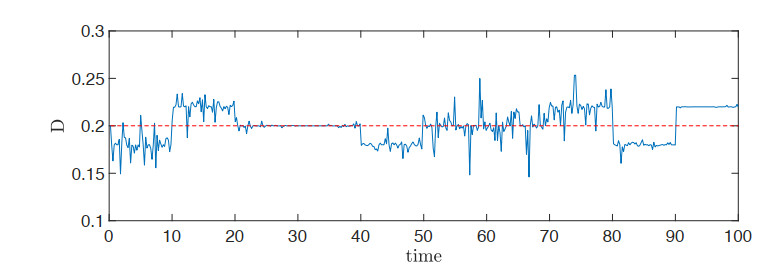
There are many papers in the literature dedicated to investigate different versions of the deterministic classical chemostat model, either (1.1)–(1.2) or (1.3)–(1.5), even though a few of them take into account the wall growth, see e.g. ^{[14,21,22,26,27,28,29]}. Nevertheless, most of them need to assume restrictions that are quite strong from the biological point of view. For instance, a very representative example of this is the case of the input flow $D$, that is typically considered to be constant in spite of the fact that it is often subject to suffer bounded random fluctuations in real devices (see Figure 1 were we display the evolution of the input flow in a real experiment).

Motivated by the previous facts, our aim in this work consists in modeling and investigating the dynamics of the deterministic classical chemostat with wall growth (1.3)–(1.5) and Haldane consumption kinetics where the input flow is subject to random disturbances. To this end, since the perturbed input flow should be bounded (as observed in real devices) we propose to model the random fluctuations on the input flow by means of the Ornstein-Uhlenbeck process, which has proved to be a useful tool when modeling bounded noises (see ^{[30,31,32,33,34]} for more details about modeling bounded noises).

To this end, we replace the input flow $D$ in the deterministic system (1.3)–(1.5) by $D+\Phi(z^*(\theta_t\omega))$, where $z^*(\theta_t\omega)$ denotes the Ornstein-Uhlenbeck process (which will be introduced in the next section) and $\Phi:{\mathbb{R}}\rightarrow[-d, d]$, where $d > 0$, is a function given by

Hence, the resulting random chemostat is given by the following random differential system

where $\mu_0: = \bar{\mu}_0/y$ and $\mu_0\geq\bar{\mu}_0$.

We recall that modeling bounded perturbations is a very interesting topic for most of researchers in applied sciences when trying to find a way to model real noises, since they are random but bounded. Apart from that, as it will be observed in this paper, such bounded perturbations will allow us to ensure the persistence of the species, one of the most important goals pursued by practitioners. In fact, persistence is the object of study in many papers (see ^{[30,31,32,33,34,35,36]}).

The rest of the paper is organized in the following way: in Section 2 we present some brief preliminaries about the classical deterministic chemostat with Haldane kinetics, the Ornstein-Uhlenbeck process, whose properties will be continually used in the paper, and the way in which bounded perturbations are modeled in this work; in Section 3 we investigate the existence and uniqueness of global positive solutions of the random chemostat (1.8)–(1.10), the existence of deterministic absorbing and attracting sets and we provide conditions under which both extinction of species and persistence can be ensured; in Section 4 we display several numerical simulations to support the theoretical work; finally, in Section 5 we present some final comments.

2.   Preliminaries

In this section we recall briefly some classical results concerning the deterministic chemostat model (1.1)–(1.2) with non-monotonic growth and present the Ornstein-Uhlenbeck (OU) process, providing some results about relevant properties that will be used further and will help us to set up the way to model bounded random perturbations.

2.1.   The deterministic chemostat model with non-monotonic growth

The next proposition presents the classical results about the classical chemostat model (1.1)-(1.2) with non-monotonic consumption function $\mu$. We refer every interested reader to ^[21,37] for proofs and more details.

Proposition 2.1. Assume that there exists $\hat s \in (0, s_{in})$ such that the function $\mu$ is increasing on $(0, \hat s)$ and decreasing on $(\hat s, s_{in})$. Define the break-even concentrations $\lambda^-(D)$, $\lambda^+(D)$ as follows

1. If $D > \mu(\hat s)$, the system (1.1)-(1.2) possesses a unique equilibrium $E^0: = (0, s_{in})$, which is globally asymptotically stable on ${\mathbb{R}}_+^2$.

2. If $D < \mu(s_{in})$, the system (1.1)-(1.2) admits an unique positive equilibrium $E^-: = (s_{in}-\lambda^-(D), \lambda^-(D))$ which is globally asymptotically stable on ${\mathbb{R}}_+^\star\times{\mathbb{R}}_+$.

3. If $D \in [\mu(s_{in}), \mu(\hat s)]$, the system (1.1)-(1.2) presents a bi-stability between $E^-$ and $E^0$. From any initial condition in ${\mathbb{R}}_+^\star\times{\mathbb{R}}_+$ excepted on a set of null measure, the solution converges asymptotically to $E^-$ or $E^0$.

Remark 1. In practice, only the second case is desirable because it guarantees that in any situation the wash-out of the biomass is avoided.

Remark 2. For the Haldane expression (1.6), one has explicit expressions of the functions $\lambda^{\pm}$

Let us note that, even though the concept of break-even concentrations has been revisited in the context of stochastic models of the chemostat ^[38,39], we will not need it here. We keep the classical deterministic definition.

In the rest of the paper, we shall consider that we are in conditions of Proposition 2.1, that is $\mu$ non-monotonic on the interval $[0, s_{in}]$ (otherwise the analysis is similar to monotonic growth function and cannot present bi-stability). Throughout the paper we shall consider the following hypothesis

Assumption 1. There exists $s_m\in(0, s_{in})$ such that the function $\mu$ is increasing on $(0, s_m)$ and decreasing on $(s_m, s_{in})$.

2.2.   The Ornstein-Uhlenbeck process

The OU process is a stationary mean-reverting Gaussian stochastic process defined as the following random variable

where $\omega$ denotes a standard Wiener process in a probability space, namely $(\Omega, \mathcal{F}, \mathbb{P})$, $\beta > 0$ is the mean reverting constant describing how our system reacts under perturbations, $\gamma > 0$ is the volatility constant representing the variation of the noise and $\theta_t$ denotes the usual Wiener shift flow given by

We notice that the OU process (2.1) can be obtained as the stationary solution of the Langevin equation

From now on, we consider $\beta$ and $\gamma$ fixed.

Once presented the OU process, we state in the following proposition some essential properties which will be crucial to study this paper.

Proposition 2.2 (See ^[40]). There exists a $\theta _t$-invariant subset $\widetilde{\Omega }\in \mathcal{F}$ of $\Omega$ of full ${\mathbb{P}}-$measure such that for $\omega \in \widetilde{\Omega }$ and $\beta, \gamma > 0$, we have

1. the random variable $|z^*(\omega)|$ is tempered with respect to $\{\theta_t\}_{t\in{\mathbb{R}}}$, i.e., for a.e. $\omega\in\widetilde{\Omega}$,

2. the mapping

is a stationary solution of (2.2) with continuous trajectories;

3. for any $\omega \in \tilde \Omega$ one has

From now on, we will denote $\widetilde{\Omega}$ by $\Omega$.

2.3.   Modeling bounded random perturbations

Once introduced the OU process, our aim in this section is to present a way to model mathematically bounded random perturbations that fit the real disturbances observed in labs.

To this end, assume we are given an interval $[D^l, D^r]$ (this interval is typically provided by practitioners from observation), $0 < D^l < D < D^r < \infty$ and let us define $d = D^r-D = D-D^l > 0$. Consider now the function $\Phi:{\mathbb{R}}\rightarrow[-d, d]$ defined by

as in (1.7). Thus,

whence the random perturbations in system (1.8)–(1.10) remain bounded (as the real ones) in the desired interval.

In addition, the random perturbations in system (1.8)–(1.10) have the following ergodic property.

Proposition 2.3. Let $\Phi(z) = {\frac{2d}{\pi}}\arctan(z)$ be defined as in (1.7). Then

Proof. From the definition of $\Phi$ it yields that

whence $\Phi(z^*(\cdot))\in L^1(\Omega, \mathcal{F}, \mathbb{P})$. Therefore, since $\mathbb{P}$ is invariant by $\theta$ (see ^[26,41]), from the Birkhoff ergodic theorem we obtain

Then, it remains to prove that $\mathbb{E}[\Phi(z^*(\omega))] = 0$. In fact,

where $f_{\text{OU}}$ denotes the density function of the random variable $z^*(\cdot)$, which is an even function since it is gaussian, and $\Phi$ is an odd function.

Remark 3. From the proof of Proposition 2.3 we notice that we could consider any odd measurable function $\Phi$ such that

Remark 4. We would like to point out that the resulting random system (1.8)–(1.10) generates a random dynamical system and then we could use the theory of random dynamical systems and pullback attractors (see ^[26]). Nevertheless, we will study the solutions of the random system (1.8)–(1.10) for fixed events $\omega\in\Omega$ since, thanks to this, every result in this work can be proved in forward sense, which is more natural from the biological point of view than the pullback one.

We refer readers to ^{[30,31,33,34]} for more details about modeling bounded perturbations with the OU process not only in chemostat models but also when dealing with other models in population dynamics. Moreover, readers can compare the results in those works with the ones in ^[42,43] where the usual Wiener process was used to model stochastic perturbations in different versions of the chemostat model.

3.   Random chemostat with wall growth and Haldane consumption kinetics

In this section we investigate the random chemostat model with wall growth (1.8)–(1.10) presented in the introductory section. We first prove that there exists a unique global positive solution of system (1.8)–(1.10). After that, by studying the asymptotic behavior of system (1.8)–(1.10), we prove the existence of absorbing and attracting sets (forwards in time) that do not depend on the noise. Then, in order to have more detailed information about the random dynamics inside the attracting set, we go further and investigate the long-time behavior of the state variables involved in the model. Thanks to this fact, we provide conditions under which species go to extinction and also conditions to ensure the persistence of species.

3.1.   Existence and uniqueness of global positive solution

In this section we prove that system (1.8)-(1.10) has a unique global positive solution that remains positive for every positive initial condition.

From now on $\mathcal{X} = \left\{(s, x_1, x_2)\in{\mathbb{R}}^3\, :\, s\geq 0, x_1\geq 0, x_2\geq 0\right\}$ denotes the positive cone in the three dimensional space.

Theorem 3.1. For every initial condition $u_0: = (s_0, x_{10}, x_{20})\in\mathcal{X}$, random system (1.8)-(1.10) possesses a unique global solution

which remains in $\mathcal{X}$ for every $t > 0$.

Proof. Let us write our random system (1.8)-(1.10) as

where^* $u = \left(s, x_1, x_2\right)^t$,

^*We note that $^t$ denotes the transposed of the vector.

and $F(u, \omega) = \left(s_{in}(D+\Phi(z^*(\theta_t\omega)))-(\mu(s)/y)(x_1+x_2), \mu(s)x_1, \mu(s)x_2\right)^t.$

On the one hand, from Proposition 2.2 (ii) one has that $t\mapsto z(t, \omega): = z^*(\theta_t\omega)$ is continuous. Apart from that, it is easy to check that $F(\cdot, \omega)\in\mathcal{C}^1(\mathcal{X})$ (recall that $\mu$ is given by (1.6)) whence we deduce that $F$ is locally Lipschitz with respect to the state variables $(s, x_1, x_2)$. Hence, the right side of (3.1) is continuous respect to the time and locally Lipschitz respect to $u$ and, from classical arguments from the theory of ODEs, it yields that the random system (1.8)–(1.10) possesses a unique local solution.

Let us now define the new state variable $y = s+x_1+x_2$ as the sum of the substrate and both species concentrations. By differentiation, one has that $y$ satisfies the following random differential inequality

where $m = \min\{D^l, \nu\}$ and we used (2.3) and the fact that $b < 1$.

Then, by solving (3.2), we obtain

for all $t > 0$, any $\omega\in\Omega$ and every initial condition $y_0 = s_0+x_{10}+x_{20} > 0$.

Thus, $y = s+x_1+x_2$ is bounded from above (and from below by zero, as we will prove next). As a consequence, one can define the unique local solution of the random system (1.8)-(1.10) on the whole interval $t\in(0, +\infty)$ and then it is in fact a global one.

It remains to prove that every state variable remains in $\mathcal{X}$ for any initial condition $u_0 = (s_0, x_{10}, x_{20})\in\mathcal{X}$. To this end, let us consider in the rest of the proof $\widetilde{s}\geq 0$, $\widetilde{x}_1\geq 0$ and $\widetilde{x}_2\geq 0$.

Assume that we reach the plane $x_2 = 0$ at some point $(\widetilde{s}, \widetilde{x}_1, 0)$. Since our initial condition is in the positive cone $\mathcal{X}$ then the rest of the state variables remain positive. By computing the derivative of $x_2$ at $(\widetilde{s}, \widetilde{x}_1, 0)$ we obtain

whence we deduce that the solution will not cross the plane $x_2 = 0$ and then $x_2$ will always remain non-negative.

By similar arguments one also has

when assuming that the solution reaches some point in the plane $x_1 = 0$ and

when reaching $s = 0$.

Summing up, $s$, $x_1$ and $x_2$ remain non-negative and then the unique global solution of the random system (1.8)–(1.10) is in $\mathcal{X}$ for every time.

3.2.   Existence of absorbing and attracting sets

In this section, we study the long-time behavior of the state variables involved in system (1.8)–(1.10) to prove the existence of absorbing and attracting sets (forwards in time).

Theorem 3.2. For any $\varepsilon > 0$, the random system (1.8)–(1.10) possesses an absorbing set (forwards in time) given by

where $m = \min\{D^l, \nu\}$. As a consequence,

is an attracting set for the solutions of the random system (1.8)–(1.10) forwards in time^†. In addition, both the absorbing and attracting sets are deterministic, i.e., they do not depend on the realization of the noise.

^†which means

where $E$ denotes a bounded set in $\mathcal{X}$.

Proof. Let us recall that $y = s+x_1+x_2$ satisfies (3.3) for all $t\geq 0$. Thus, for any $\varepsilon > 0$ and every $\omega\in\Omega$, there exists some time $T^y_\varepsilon(\omega) > 0$ such that

for any $t\geq T^y_\varepsilon(\omega)$ and everty initial condition $y_0: = s_0+x_{10}+x_{20} > 0$.

Hence, it follows that

is a forward absorbing set for the solutions of the random system (1.8)–(1.10) which, in addition, does not depend on the realization of the noise and then

is a forward deterministic attracting set for the solutions of the random system (1.8)–(1.10).

3.3.   Random dynamics inside the attracting set

Once the existence of an attracting set is proved, our goal now is to obtain more detailed information about its random dynamics. To this end, we introduce two new state variables

where $x$ denotes the total concentration of species and $p$ the proportion of the first species.

From now on, as in (3.10), we will write $x$ and $p$, instead of $x(t; 0, \omega, x_0)$ and $p(t; 0, \omega, p_0)$, for the sake of clarity.

By differentiation, we obtain the following random system satisfied by the substrate $s$ and the new variables $x$ and $p$ which will be the object of study in the next sections

Our goal now is to investigate the long-time dynamics of the random system (3.11)-(3.13).

We note first that the equation describing the dynamics of the proportion (3.13) is uncoupled of the rest of the system. Then, we will study this equation individually.

Theorem 3.3. For any $\varepsilon > 0$, the deterministic set

is an absorbing set for the solutions of the random equation (3.13), and then

is a deterministic attracting set for the solutions of the random equation (3.13), where

and

Proof. From the equation of the proportion (3.13) we have

thanks to (2.3).

Define now the mapping $H:p\in[0, 1]\rightarrow H(p)\in{\mathbb{R}}$, where $H(p) = D^lp^2-(D^r+r_1+r_2)p+r_2$. Then $H$ defines a convex parabolic function where, since $D^l > 0$, one can use the Bolzano's Theorem and find a unique^‡ $p^l\in(0, 1)$ such that

^‡The uniqueness is easy to prove and it is left to the reader.

In addition, the value of $p^l$ can be computed by solving $H(s) = 0$ and we obtain

Then, for all $\bar{p} < p^l$, we have

Thus, from (3.19), for any $\varepsilon > 0$ and every $\omega\in\Omega$, there exists $T^p_\varepsilon(\omega) > 0$ such that

for every $t > T^p_\varepsilon(\omega)$ and $p_0\in(0, 1)$.

On the other hand, from (3.13), one also has

thanks to (2.3).

Define in this second case the mapping $M:p\in[0, 1]\rightarrow M(p)\in{\mathbb{R}}$, where $M(p) = D^lp^2-(D^l+r_1+r_2)p+r_2$. Then $M$ defines a convex parabolic function where, since $D^l > 0$, one can use the Bolzano's Theorem and find, as in the previous case, a unique $p^r\in(0, 1)$ such that

In addition, the value of $p^r$ can be computed by solving $M(s) = 0$ and we obtain

Then, for all $\bar{p} > p^r$, we have

Hence, from (3.23), for any $\varepsilon > 0$ and every $\omega\in\Omega$, there exists $\bar{T}^p_\varepsilon(\omega) > 0$ such that

for every $t > \bar{T}^p_\varepsilon(\omega)$ and $p_0\in(0, 1)$.

Thus,

is a deterministic absorbing set for the solutions of the random equation (3.13), whence

is a deterministic attracting set for the solutions of the random equation (3.13).

Once studied the equation of the proportion (3.13), we focus on investigating the system (3.11)–(3.12).

From now on, we will denote $\mathcal{Y}: = \{(s, x)\in{\mathbb{R}}^2\, :\, s\geq0, x\geq0\}$.

Theorem 3.4. For any $\varepsilon > 0$, the random system (3.11)–(3.12) has a deterministic absorbing set (forwards in time) given by

where

Then

is a deterministic attracting set (forwards in time) for the solutions of the random system (3.11)–(3.12).

Proof. To study the dynamics of system (3.11)–(3.12) we first define a new state variable $z = \bar{\mu}_0s+\mu_0x$ involving $s$ and $x$.

By differentiation, it yields that $z$ satisfies the random ODE

Then, from (3.28), thanks to (3.20), one obtains

whence, by solving (3.29), one has

for all $t\geq 0$, any $\omega\in\Omega$ and every initial condition $z_0\in\mathcal{Y}$.

Similarly, from (3.28), it follows

and then

for all $t\geq 0$, any $\omega\in\Omega$ and every initial condition $z_0\in\mathcal{Y}$.

Hence, since the right side of (3.30) and (3.32) tend to $z^r$ and $z^l$ (defined as in (3.26)), respectively, when $t$ goes to infinity, for any $\varepsilon > 0$ and every $\omega\in\Omega$, there exists $T^x_\varepsilon(\omega) > 0$ such that

for all $t\geq T^x_\varepsilon(\omega)$ and every initial condition $(s_0, x_0)\in\mathcal{Y}$, which means that

is a deterministic absorbing set (forwards in time) for the solutions of the random system (3.11)–(3.12) and then

is a deterministic attracting set (forwards in time) for the solutions of system (3.11)–(3.12).

The last theorem in this section concerns some bounds from above for the concentration of both species $x_1$ and $x_2$ and conditions under which extinction cannot be avoided.

Theorem 3.5. The following statements hold

1. Assume

holds true, with $s_m = \sqrt{k_sk_i} = \arg\max \mu(s)$. Then, for every $\varepsilon > 0$,

is a deterministic absorbing set for the solutions of the equation of the first species, and then

is a deterministic attracting set for the solutions of the equation of the first species, where

2. As long as

is fulfilled, then, for any $\varepsilon > 0$,

is a deterministic absorbing set for the solutions of the equation of the second species, and then

is a deterministic attracting set for the solutions of the equation of the second species, where

3. Provided that

then, for any $\omega\in\Omega$ and initial condition $x_{0} = x_{10}+x_{20} > 0$,

which means the extinction of both species.

Proof. We start proving the first statement. To this end, from the equation describing the dynamics of the first species (1.9), it yields

where we used (2.3), (3.33) and the fact that $\mu(s)\leq\mu(s_m)$ for every $s\geq 0$.

By solving (3.40), we obtain

for every $t > 0$, $\omega\in\Omega$ and any initial value $x_{10} > 0$.

Then, since the limit when $t$ goes to infinity of the right side of (3.41) is $x_1^r$, defined as in (3.36), it is easy to finish this part of the proof.

To prove the second statement, from the equation describing the dynamics of the second species (1.10) we have

where we used (3.33) and the fact that $\mu(s)\leq\mu(s_m)$ for every $s\geq 0$.

Similarly to the previous case, by solving (3.42), we obtain

for every $t > 0$, $\omega\in\Omega$ and any initial condition $x_{20} > 0$.

Then, since the limit when $t$ goes to infinity of the right side of (3.43) is $x_2^r$, defined as in (3.37), it is easy to finish this part of the proof.

Finally, to prove the third statement, from the equation describing the dynamics of the total concentration of species (3.12) one has

where we used the fact that $\mu(s)\leq\mu(s_m)$ for every $s > 0$ and $p^l < 1$.

Now, by solving (3.44) we obtain

for every $t > 0$, $\omega\in\Omega$ and any initial condition $x_0 = x_{10}+x_{20} > 0$.

Hence, it is easy to check that

for any $\omega\in\Omega$ and every initial condition $x_0 > 0$, as long as (3.38) is satisfied.

3.4.   Persistence of species

In this section we provide conditions on the parameters involved in system (1.8)–(1.10) to ensure the persistence of species. To this end, we firstly prove that the total concentration of species persists and then we use this fact and some properties proved about the dynamics of the proportion to prove coexistence of each group of species, the planktonic biomass and the attached biomass.

Theorem 3.6. Assume

where every constant was already defined. Then, the attracting set (3.8) is reduced to

where

with

Proof. We start proving the lower bound for the concentration of the species. To this end, from (3.11), we have

where we used (2.3) and (3.33).

Let us consider $\varepsilon < \bar{\mu}_0\bar{s}$, where $\bar{s} > 0$ such that

Hence, from (3.49) one has

and, from (3.51), we obtain

Then, our goal now is to prove the existence of some $\bar{s} > 0$ such that (3.50) holds. To do this, by doing some calculations, it is easy to verify that (3.50) is equivalent to

where $a_2$, $a_1$ and $a_0$ are defined as in the statement of Theorem 3.6.

Define now the map $F: s\in[0, +\infty)\mapsto F(s)\in{\mathbb{R}}$ where $F(s) = a_2s^2+a_1s+a_0$. Since $a_2 < 0$, then $F$ defines a concave parabolic function. In addition, $a_0 > 0$ then it follows that there exists $s^* > 0$ such that $F(s)\geq 0$ for every $s\in[0, s^*]$ and $F(s) < 0$ when $s\in(s^*, +\infty)$. Hence, (3.50) fulfills by considering $\bar{s} = s^* > 0$, where the value $s^*$ can be easily calculated by solving $F(s^*) = 0$.

As a consequence, we find that

where $a_0$, $a_1$ and $a_2$ are defined as in the statement of Theorem 3.6.

The second part of the proof consists of proving the existence of a lower bound for the total concentration of species. Thanks to this fact, we will be able to ensure that, at least, some of both species will persist. To this end, from (3.12) one has

where we used (2.3) and (3.46).

Let us consider $\varepsilon < \delta\bar{x}$, where $\bar{x} > 0$ such that

Then, the right hand side of (3.55) can be bounded from below by

Then, we have

whence $\bar{x} > 0$ provides a lower bound for the total concentration of species.

Hence, our goal now is to prove that there exists $\bar{x} > 0$ such that (3.56) is fulfilled. To this end, by making some calculations, from (3.56) one obtains

where

Define now the map $G: x\in[0, +\infty)\mapsto G(x)\in{\mathbb{R}}$ where $G(x) = b_2(\delta)x^2+b_1(\delta)x+b_0$. Since $b_2(\delta) < 0$ for every $\delta > 0$, then $G$ defines a concave parabolic function for every $\delta > 0$. In addition, $b_0 > 0$ as long as (3.46) is satisfied. Then, for every $\delta > 0$, there exists $x^*_\delta > 0$ such that $G(x)\geq 0$ for every $x\in[0, x^*_\delta]$ and $G(x) < 0$ when $(x^*_\delta, +\infty)$. Hence, the value $x^*_\delta$ can be easily calculated by solving $G(x) = 0$ whence

where $b_2(\delta)$, $b_1(\delta)$ and $b_0$ were defined above.

Hence, (3.50) fulfills when considering

Remark 5. Recall that the chemostat model (1.8)-(1.10) studied in this work does not only incorporate wall growth but also nutrient recycling (coefficient $b$). Then, one could wonder how this feature is favorable or not to species persistence, i.e., the difference with case $b = 0$. To answer this question, since $z^r$ (defined as in (3.26)) is the only parameter in (3.46) (condition to ensure persistence of species) that involves $b$, and the value of $z^r$ decreases if $b = 0$, we conclude that $b = 0$ would help condition (3.46) to be true, i.e., $b = 0$ would favor the persistence of the species.

Finally, we prove that not only the total concentration of species remains positive as long as (3.46) holds true but also both the planktonic biomass and the attached biomass persist. To this end, we use Theorem 3.6 and the dynamics of the proportion.

Theorem 3.7. Assume that (3.46) holds true. Then, for every initial condition $x_{10} > 0$ and $x_{20} > 0$, $\omega\in\Omega$ and $t > 0$ large enough, the following lower bounds hold true

where

i.e., both the planktonic biomass and the attached biomass persist.

Proof. From the definition of the proportion (3.10), we have

for any initial condition $x_{10} > 0$, $p_0\in(0, 1)$ and $x_0 = x_{10}+x_{20} > 0$.

Then, from Theorem 3.3 and assuming (3.46), one can apply Theorem 3.6 and obtain

for every $t$ large enough, any $\omega\in\Omega$ and every initial condition $x_{10} > 0$, where $p^l$ and $\bar{x}$ are defined in (3.16) and (3.48).

Similarly, from the definition of the proportion (3.10) one has

for every $t$ large enough, any $\omega\in\Omega$ and every initial condition $x_{20} > 0$, $p_0\in(0, 1)$ and $x_0 = x_{10}+x_{20} > 0$.

Then, from Theorem 3.3 and assuming (3.46), we can use Theorem 3.6 and one has

for every $t$, any $\omega\in\Omega$ and every initial condition $x_{20} > 0$, where $p^r$ and $\bar{x}$ are defined in (3.22) and (3.48).

4.   Numerical simulations

In this section we depict several numerical simulations to support the theoretical study presented in the previous section and help every reader to understand better the dynamics of the random chemostat model with wall growth (1.8)–(1.10).

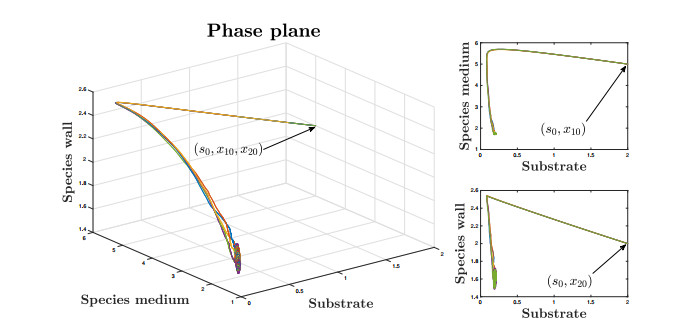
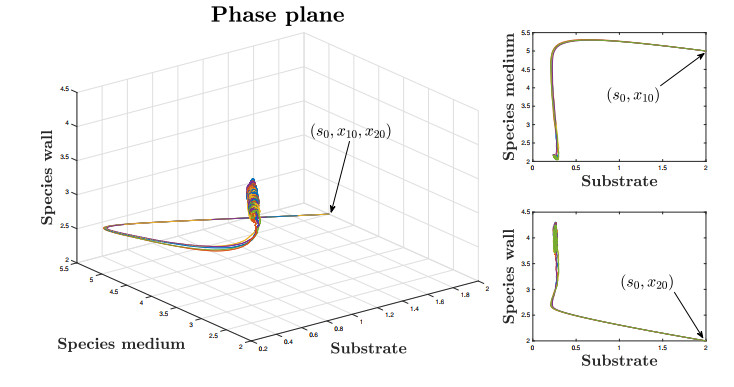
Every figure in this section shows three different panels: the biggest one displays the three dimensional phase plane of system (1.8)–(1.10); the one placed on the right at the top shows the dynamics of the species in the liquid media versus the substrate; finally, the panel on the right at the bottom displays the dynamics of the species sticked on the wall of the culture vessel versus the substrate. In such a way, it will be easy to observe in the little panels when the species go to extinction or persist. Apart from that, in every panel a label next to an arrow is depicted to point the initial condition.

In every figure we plot five realizations of the solution of the random chemostat (1.8)–(1.10) with $s_0 = 2$, $x_{10} = 5$ and $x_{20} = 2$ as initial condition. In addition, we set $\beta = 1$ and $\gamma = 1$ to simulate the realizations of the OU process. The rest of parameters will be specified further in every case.

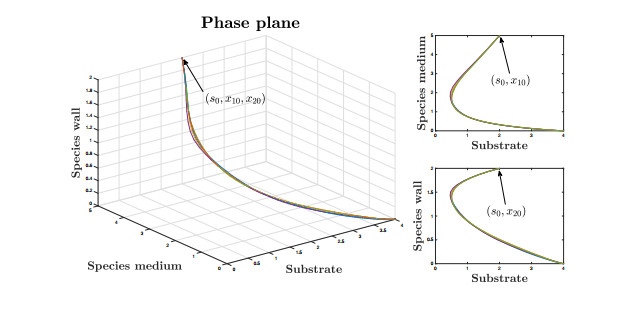
In Figure 2 we consider $s_{in} = 4$, $k_s = 1.7$, $\mu_0 = 8$, $k_i = 7$, $\bar{\mu}_0 = 7.5$, $b = 0.1$, $\nu = 0.4$, $r_1 = 0.4$, $r_2 = 0.8$. Concerning the removal rate, we set $D = 0.7$, $D^r = 0.8$, $D^l = 0.7$ and $d = 0.1$. One can check that condition (3.46) is fulfilled ($128.3377 > 114.5576$) and then persistence of both groups of species is ensured, as observed in the figure.

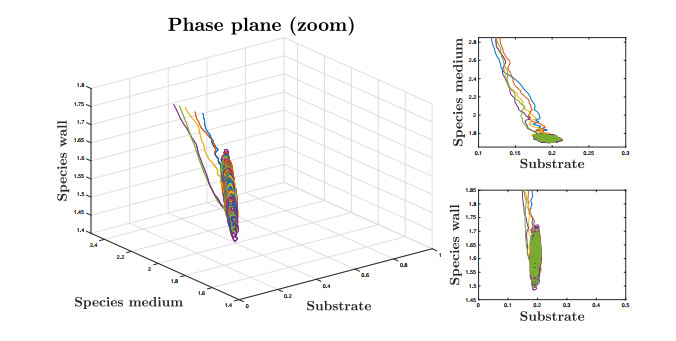
Figure 3 displays a zoom of the different panels of Figure 2 to let the reader observe the long-time random dynamics of system (1.8)–(1.10) more clearly, in fact, we can notice how the solutions of the system reach some place in which the attracting set $\mathcal{A}$ given by (3.47) is.

In this case we can observe how the substrate concentration $s$ decreases at the beginning while the concentration of both species $x_1$ and $x_2$ increases until both species reach their maximum values. Then, both species start decreasing and, as a consequence, the concentration of substrate increases slightly up to reaching the attracting set.

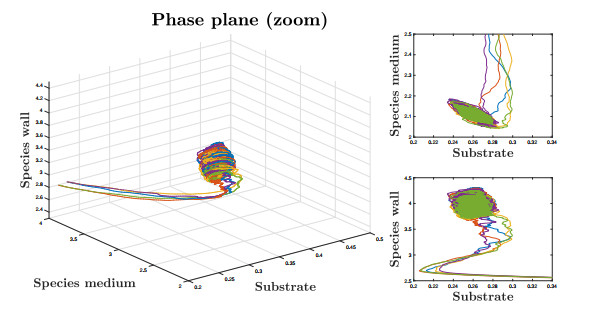
In order to have a better panoramic of the dynamics of the system near the attracting set, Figure 7 shows a zoom of every panel of Figure 4.

The main difference between the behavior of our system in this last case, respect to the first one, is due to the change in the removal rate $D$, which is one of the most important parameters when modeling chemostats, due to its influence on the dynamics of the device. To be more precise, recall that species sticked on to the wall of the culture vessel cannot be removed by the flow passing through the pumps, differently to the species in the medium that can be easily removed from their tank (specially when increasing the removal rate as in this case). This is the reason why we observe how fast the first species decreases whereas the second species behaves in a total different way.

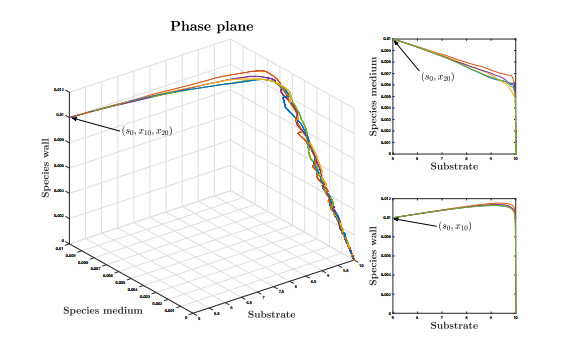
Now, in Figure 6 we present the case of extinction of both species studied in Theorem 3.5. To this end, we do not change the value of the input flow respect to the value in the last figure but we consider $s_{in} = 4$, $k_s = 0.4$, $\mu_0 = 4$, $k_i = 0.5$, $\bar{\mu}_0 = 1.4$, $b = 0.1$, $\nu = 1.4$, $r_1 = 0.4$, $r_2 = 0.8$. It is easy to notice that we decreased considerably the the Monod constant $k_s$, the inhibition $k_i$ and the consumption of both species whereas we increased the death rate $\nu$. Then it is not a surprise that condition (3.38) in Theorem (3.5) is fulfilled ($3.1 > 2.7548$) and condition (3.46) in Theorem 3.5 is not true ($1.6261\ngtr 41.9151$), whence we have extinction of both species, as one can observe.

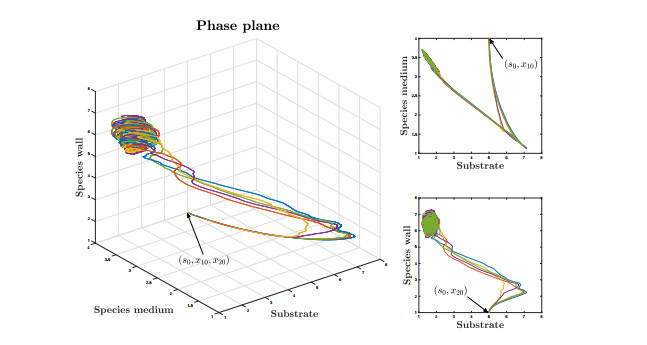
Finally, we show that bi-stability also happens when considering wall growth, as we do in this work. To this end, we set $s_{in} = 10$, $k_s = 1.8$, $\mu_0 = 3.4$, $k_i = 7.7$, $\bar{\mu}_0 = 2.3$, $b = 0.1$, $\nu = 0.4$, $r_1 = 0.4$, $r_2 = 0.8$. Concerning the removal rate, in this case we take $D = 1.7$, $D^r = 1.3$, $D^l = 2.1$ and $d = 0.4$. It is easy to check that $\mu(s_{in})\leq D\leq\mu(s_m)$ ($1.3717 < 1.7 < 1.7285$), the same condition under which bi-stability is observed in the deterministic framework (see Proposition 2.1 (3)). The initial condition will be specified later.

In Figure 7 we can notice how both the planktonic biomass and the attached biomass go to extinction when considering their initial concentrations $x_{10}$ and $x_{10}$ closed to the wash-out.

On the other hand, in Figure 8 we consider the initial condition far enough from the wash-out. Thus, we observe persistence of both the planktonic biomass and the attached biomass.

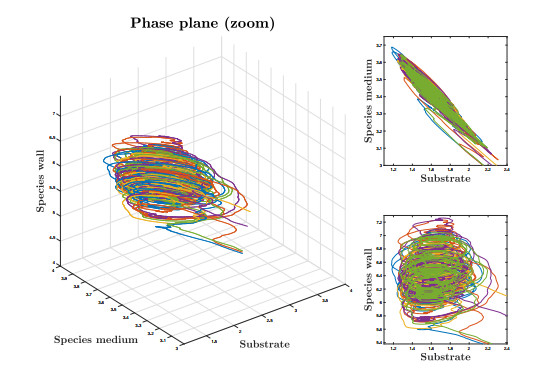
Eventually, Figure 9 presents a zoom of the previous case in order to help the reader to see how the dynamics inside the attracting set of our model is.

5.   Conclusions

In this final section of our paper we would like to summarize the results obtained in Section 3 and observed in the numerical simulations displayed in Section 4.

We have considered the chemostat model (1.8)–(1.10) with wall growth and Haldane consumption kinetics, under bounded perturbations on the removal rate, motivated by observations in real devices in industrial setup and biotechnology. To this end, we make use of a function and the Ornstein-Uhlenbeck process to ensure the random fluctuations be bounded in some interval (that is typically observed in practice).

Thanks to standard techniques from the classical theory of ordinary differential equations and, of course, due to the properties satisfied by the bounded noise $\Phi(z^*(\theta_t\omega))$, we proved in Theorem 3.1 that the random chemostat (1.8)–(1.10) possesses a unique global solution which, in addition, remains positive as long as we consider positive initial conditions.

Then, we proved in Theorem 3.2 the existence of an absorbing set for the solutions of system (1.8)–(1.10). This allowed us to ensure the existence of an attracting set (forwards in time) for the solutions of system (1.8)–(1.10). In addition, we proved that both absorbing and attracting set enjoys a very nice property: They are deterministic, i.e., they do not depend on the realization of the noise.

After that, we went further and we investigated the internal structure of the deterministic attracting set obtained in Theorem 3.2 in order to have more detailed information about the long-time dynamics of our system. To this end, we proved two theorems that can be interesting for both mathematicians and biologists: On the one hand, Theorem 3.5 provides conditions under which extinction of both species cannot be avoided as well as some conditions leading in upper bounds for both species; on the other hand, Theorem 3.6 and 3.7 states a condition under which not only the persistence of the total concentration of species but also the persistence of both the planktonic biomass and the attached biomass is ensured. This last point is undoubtedly the most meaningful since it is the main goal pursued by practitioners.

We would also like to highlight again the importance of considering the non-monotonic growth rate (1.6), since it allows us to study mathematical models that really fit better the devices displayed in real life, as underlined in the introduction. Concerning the non-monotonic growth of species, it is worth to mention some aspects observed in this work compared to the classical deterministic model (1.1)–(1.2) with Haldane consumption function.

More precisely, the dynamics of the deterministic chemostat (1.1)–(1.2) with non-monotonic consumption function may exhibit a bi-stability for certain values of the removal rate $D$ (see ^[21]), as explained in Section 2.1. In such a case, the concentration of the biomass converges asymptotically either to the wash-out equilibrium (which is not desirable since it means the extinction of the species) or to a positive steady state. This type of instability is observed in practice and entails an issue in industrial applications since it requires a good monitoring of the system to prevent it from going to the wash-out equilibrium (see ^{[44,45,46,47]}). Then, practitioners normally decide on avoiding this behavior by sizing the process such that the system has an unique globally stable equilibrium (see ^[48,49]) which mathematically means to have the following condition

In addition, we supported every theoretical result with several numerical simulations depicting the random dynamics of the system when considering different values of the parameters involved in the model. Moreover, this also allowed us to illustrate the bi-stability for some values of the parameters involved in the model and the huge importance that the removal rate $D$ has on the dynamics of the chemostat giving another justification of our interest in introducing the random perturbations on it.

Finally, we would like to highlight that the Ornstein-Uhlenbeck process has proved again to be a very powerful tool when modeling real bounded fluctuations, not only when studying chemostats but also when dealing with any model involving bounded perturbations, as the ones in real life.

Acknowledgments

This work has been partially supported by Proyecto de Excelencia P12-FQM-1492 from Junta de Andalucía, Project PGC2018-096540-B-I00 from Ministerio de Ciencia, Innovación y Universidades (Spanish government), Project I+D+i FEDER US-1254251 from Consejería de Economía y Conocimiento (Junta de Andalucía) and Project P18-FR-4509 from Consejería de Economía y Conocimiento (Junta de Andalucía).

We thank the referees for their helpful comments which allowed us to add some details that made this work more elegant and interesting, not only for mathematicians, but also for people from other areas who are interested in this research.

Conflict of interest

The authors declare there is no conflict of interests.