Nonlinear dynamics of dewetting thin films

1.   Introduction

Fluid dynamics is a long-standing source of challenging problems for mathematical analysis; one of these is describing the spreading of thin layers of viscous fluids on solid surfaces. Sometimes called "coating flows" ^[163,185], these problems occur ubiquitously in nature (dew on leaves of plants ^[29,57,136] and tear films on the eye ^[31]) and in applications like painting of surfaces and lubrication of machine parts. Parallel to the long history of use of lubrication models in basic physics and engineering applications, the past few decades have seen the growth of mathematical interest in the nonlinear partial differential equations (PDE) that describe these systems. These problems can exhibit very rich forms of behaviors including finite-time singularities, self-similar solutions, free boundary problems, pattern-forming instabilities and long-time coarsening. This paper gives a brief overview of one class of these problems that includes these behaviors.

While second-order linear advection-diffusion models for transport in bulk flows of fluids have been well studied, there is a strong need to better understand the more complicated behaviors occurring in free-surface flows where surface tension and materials properties play important roles. Advances in engineering processes (for biological testing and other applications in microfluidics) allowing for more precise control of small quantities of fluids have sparked the need to explore these subtle influences. Avoiding loss of volume and contamination of tiny samples of fluids is another key concern in these processes. Fluid samples are more easily and reliably moved if their tendency to adhere to the solid substrate is reduced – achieving this has motivated a lot of work on the development of hydrophobic (water-repelling) materials making use of chemical properties of the materials or physical texturing of the surface (commonly used in synthetic fabrics and materials like teflon). Fluids placed on such repellent surfaces will undergo dewetting, which is manifested as a sequence of instabilities that progressively reduce the overall contact of the fluid with the solid ^{[13,57,101,106,143,172,186,187,188,189]}.

Mathematical modeling of dewetting behavior has produced a rich body of research showing that most of the essential features of the dynamics can be obtained from analysis and numerical simulations of partial differential equations of the general form

where $h(x, y, t)$ gives the evolving local height (thickness) of the fluid film and the disjoining pressure function $\Pi(h)$ characterizes the wetting properties of the solid surface relative to the fluid's tendency to spread under the influence of surface tension and other forces.

Following a brief sketch of the formulation of (1.1), we review the mathematical development of the various stages of the dewetting process spanning multiple length- and time-scales:

$1.$ Short-time: initial linear instability and finite-time rupture

$2.$ Intermediate: propagation of dewetting rims and instabilities of fluid ridges

$3.$ Long-time: formation of quasi-steady droplets and multi-scale models of coarsening dynamics

and closing comments will address further directions for mathematical analysis.

2.   Formulation of the model equation

The mathematical formulation of classical lubrication models for thin film flows relies on two key assumptions – that the viscosity of the fluid is large, and that the fluid film is slender and slowly varying. These allow for the governing equations of fluid dynamics to be reduced down to a more tractable problem – a single nonlinear PDE as an evolution equation for the local height of the fluid layer.

The flow of incompressible Newtonian fluids is governed by the Navier-Stokes equations,

where $\vec{\mathrm{\bf{{u}}}}$ is the fluid's velocity, $p$ the pressure field and the Reynolds number $\mathrm{Re}$ is a dimensionless parameter that describes the relative importance of inertial effects vs. viscous dissipation. For the slow motion of very viscous fluids, the "creeping flow" limit of $\mathrm{Re}\to 0$ reduces the equations to the Stokes equations ^[1,128,158],

While these governing equations are linear and time-invariant, the overall problem is nonlinear and time-dependent due to the boundary conditions that are imposed at the free surface of the fluid mass. In general, numerical methods are needed for these free boundary problems for Stokes flows ^[170,173].

However, if the fluid occupies a long thin layer, namely a region with $0\le (x, y)\le L$ and $0\le [z = h(x, y, t)] < H$ then considering the aspect ratio, $\delta = H/L$, as a small parameter, a long-wave limit can be applied to obtain an asymptotic reduction for $\delta\to 0$, see Figure 2. The velocity can then be separated into components parallel and perpendicular to the solid boundary, $\vec{\mathrm{\bf{{u}}}} = \vec{\mathrm{\bf{{u}}}}_{\parallel} + u_{\perp} {\hat{\bf{n}}}$ and here ${\hat{\bf{n}}} = {\hat{{\bf{k}}}}$. For $\delta\to 0$, the leading order velocity is $\vec{\mathrm{\bf{{u}}}}\sim \vec{\mathrm{\bf{{u}}}}_{\parallel}$ and the quasistatic pressure is uniform across the thickness of the film, $p\sim p(x, y, t)$. Applying boundary conditions on $u_\perp$ at the impermeable solid surface and free surface of the layer yields an equation for the conservation of the fluid mass of the form

where $m(h)$ is a mobility coefficient and the mass flux is ${\bf J} = -m(h) \nabla p$. The form of the mobility depends on the boundary conditions for $\vec{\mathrm{\bf{{u}}}}_\parallel$; the classic no-slip boundary condition ^[122] (zero tangential velocity at a fixed solid boundary) gives $m(h) = h^3$ yielding the classic Reynolds lubrication equation ^{[4,42,147,161]},

Some forms for the mobility can be derived from models with slip effects at the solid surface, i.e. $m(h) = \beta h^2 +h^3$ corresponds to the Navier slip boundary condition ^[93]. For flows with stronger slip effects, or larger velocities, inertial effects can become important and different classes of models can be constructed involving coupled equations for $h$ and the mass flux ^{[111,145,175]}. In single-equation lubrication models, all physical effects considered are expressed by contributions to pressure functional, $p[h]$. In the simplest case, gravity-driven spreading is described by a hydrostatic pressure, $p = h$, yielding the classic porous medium equation ^[9,210],

In problems involving global coupling of the film flow (with electric fields or thermodynamic effects) the pressure can be a nonlocal operator ^[67,205].

If surface tension is the only effect considered, the pressure is proportional to the Gaussian curvature of the free surface $z = h(x, y, t)$. In the long wave limit, the leading order form is $p\sim -\nabla^2 h$; using this with $m(h) = h^n$ for $n\ge 0$ yields the thin film equation ^{[17,19,30,79,80,81,113,114,147]}

This equation has been the focus of many rigorous analytical studies starting from the key paper of Bernis and Friedman in 1990 ^[16]. Physically meaningful solutions representing fluid film thicknesses must be non-negative, $h\ge 0$, but in contrast to (2.3), (2.4) does not have a maximum principle and consequently solutions starting from positive initial data may not remain positive for all times. Careful analysis showed that positivity is maintained for solutions if $n$ is large enough ($n\ge 3.5$) ^[16,20]. Analysis of singularities in problems for (2.4) has been a source of continuing interest ^[23,24,41]. Further studies have addressed questions about the regularity, existence, uniqueness and speed of propagation of compactly supported weak solutions representing fluid droplets ^[15,23,24]. Existence of non-negative solutions was shown for $n\ge 1$ ^[16] and results on some properties have been obtained on ranges of $n$ (and might be restricted to one dimension) ^[26,35,48]. Additionally, physical arguments for spreading drops in the viscous, no-slip case, $n = 3$ in (2.4), showed that motion of the edge of support (also called the "contact line" or interface) would require unphysical singular forces ^[103].

Consequently, many approaches have been proposed for addressing these issues using PDE analysis ^{[16,22,23,38,80,81,89]}, physical considerations ^[113,191] and numerical methods for computing solutions ^[95,225]. In ^[16] a positivity-preserving regularization of (2.4) was introduced by modifying the mobility function $m(h)$; this was also extended to numerical methods in ^[225]. Other papers have focused on removing the stress singularity at moving contact lines by incorporating slip in the mobility ^[145,191].

A different physically-motivated approach regularizes solutions by modifying the pressure in (2.2) ^[29,56]. Since (2.4) describes flows driven by surface tension effects only, it cannot distinguish differences due to material properties of the substrate, like water's tendency to spread on glass (a hydrophilic solid) vs. water's break-up into droplets on a hydrophobic surface like a teflon-coated frying pan. Such fluid-solid interactions can be characterized by calculating an effective potential for the averaged influence of molecular forces between the fluid and the solid ^{[102,105,192]}. For the simplest models, based on van der Waals interactions, this yields a potential depending only on the local fluid film thickness, $U(h)$. The derivative of $U$ with respect to changes in film height gives a contribution to the pressure called the disjoining pressure, $\Pi(h) = dU/dh$. Consequently, writing the total pressure as

we recover equation (1.1),

as a basic thin film model incorporating the influences of both surface tension and substrate wetting properties. The dynamics in this model, and (2.1) more generally, can be described in terms of a monotone decreasing energy functional,

The resulting gradient flow description from (2.7) has been used extensively in many analytical studies ^[39,125] and formulation of extended models ^[199,200]. Another important basic property of (2.6) is that the mass, $M = \iint h\, dA$, is conserved, which follows from the equation being in divergence form.

Typical forms of the disjoining pressure decay like $\Pi(h) = O(h^{-3})\to 0$ as $h\to\infty$ ^[102]. This is consistent with the expectation that molecular effects should have negligible influences on the dynamics of thick films. The coefficient scaling the disjoining pressure is proportional to the Hamaker constant, which describes the strength of van der Waals molecular forces ^[192]. Disjoining pressures $\Pi(h)\sim A/h^3$ with $A > 0$ describe disjoining forces for the hydrophobic interactions while $A < 0$ represents conjoining forces in the hydrophilic case. These two cases correspond to whether the second order operator in (2.6), $\nabla\cdot(h^3 \nabla [\Pi(h)])$, is destabilizing or diffusive respectively.

3.   Early-stage dynamics

For fluids starting as nearly uniform layers describing the early-time dynamics of fluid coating layers on hydrophobic surfaces can be accomplished from the most basic representation of the van der Waals disjoining pressure, $\Pi(h) = 1/(3h^3)$ ^[179,211]. In one spatial dimension this yields the evolution equation

as studied in ^[217] and many later papers ^[112,224]. We will go on to describe the richer behaviors that occur in two dimensions in later sections.

On a finite domain with length $L$, with Neumann no-flux boundary conditions, uniform layers of constant thickness, $h = \bar{h}$, are equilibrium solutions for any $\bar{h} > 0$. Linear stability analysis with respect to infinitesimal perturbations,

yields

and shows that the second order term has a destabilizing influence. Further, there is a critical thickness, $\bar{h}_c = \sqrt{{L/ \pi}}$, below which the uniform film is unstable ^[220],

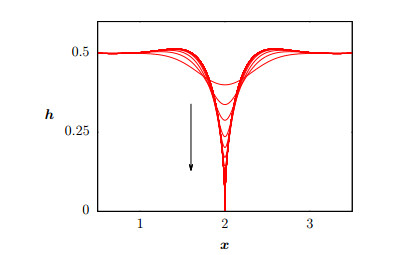
More comprehensive studies of the steady states of a class of fourth-order parabolic PDEs including (3.1) were done in ^{[110,124,123,125,126]} and further analysis of the dynamics in ^[23,24,49]. Applying bifurcation theory at the critical thickness $\bar{h}_c$ shows it to be a subcritical pitchfork bifurcation point ^[220] with another branch of equilibria having non-trivial spatial structure existing for average thickness $\bar{h}\ge \bar{h}_c$. These spatially periodic solutions can be shown to be unstable and they act as a separatrix between two stable regimes of dynamics, either: (ⅰ) relaxation to the uniform thick film, or (ⅱ) film rupture, where the minimum thickness vanishes in finite-time at some point $x_c$ (see Figure 3),

which yields a singularity of the disjoining pressure term.

3.1.   Finite-time rupture singularities

Dimensional analysis of (3.1) shows that it is scale-invariant with respect to solutions of the form

where $\tau = t_c-t\to 0$ is the time to the rupture (sometimes called a pinch-off ^[40] or touchdown ^[28,90] singularity). A consequence of this is that the problem can have a first-kind similarity solution ^[11,12] of the form

such similarity solutions reaching singular behaviors at finite critical times are also called backward self-similar solutions ^[82]. Solution (3.6) can also be called a focusing solution since its spatial scale shrinks as the singularity is approached.

Zhang and Lister ^[224] showed that the rupture singularity of (3.1) is approached through a first-kind self-similar solution of the form (3.6). The similarity profile $H(\eta)$ satisfies a boundary value problem for the nonlinear ordinary differential equation (ODE),

The far-field boundary condition follows from the localized nature of the singularity; namely, as the critical time is approached, while the singularity is approached at $x_c$, the evolution of the solution at finite distances away from $x_c$ continues smoothly, $h_t = O(1)$ for $|x-x_c| = O(1)$ as $t\to t_c$ ^[219,220].

Solving (3.7) numerically, it was found that an infinite sequence of distinct solutions, $H = H_j(\eta)$ with $j = 1, 2, 3, \cdots$, exist with different values for the far-field constant $C = C_j$, $C_1 > C_2 > C_3 > \cdots$ with $C_j\to 0$ as $j\to\infty$ ^{[219,220,224]}. Analytical support for these results was obtained by rescaling the problem as $H(\eta) = {\epsilon}^{2/5} \phi(z)$ with $\eta = {\epsilon}^{-1/5}z$ and ${\epsilon} = C^2\to 0$ to yield the singular perturbation problem,

Exponential asymptotics was used to consider Stokes phenomenon for the solutions analytically continued in the complex plane and determine a selection mechanism for the discrete ${\epsilon}_j = C_j^2$ values ^[37]. Further studies of self-similar rupture in related models have been recently considered in ^[50,51].

From all of the solutions of (3.7), linear stability analysis showed that only the first ($j = 1$) is stable to one-dimensional perturbations ^[220]. This is consistent with it being the only behavior leading to rupture observed in numerical simulations of (3.1). In the context of the full two-dimensional problem,

one-dimensional solutions, $h = h(x, t)$, represent uniform rupture along lines. Analysis of the stable one-dimensional solution showed it to be linearly unstable to transverse two-dimensional perturbations ^[220]. Further work showed that only the $j = 1$ axisymmetric self-similar solution, $h = \tau^{1/5} H_1(r/\tau^{2/5})$, is linearly stable, corresponding to locally axisymmetric rupture at isolated points ^[219,220]. This behavior is consistent with experimental observations in early-stage dynamics of dewetting films ^[131,189].

The occurrence of singularities in models of fluid dynamics has been studied in many contexts as signs of dramatic transitions such as changes in topology ^[64,65,66]. Some aspects of the dynamics at the singularity may be unphysical (e.g. infinite forces, sub-atomic lengthscales) indicating that assumptions used to justify the governing equations have broken down and should be replaced by a more comprehensive model. Still, the simpler models make very valuable contributions by capturing the qualitative dynamics leading up to the singularity in a simple form (often as a self-similar solution).

A fundamental limitation of (3.1) is that its solutions cannot be continued to times after rupture occurs due to the singularity of the disjoining pressure term for $h\to 0$ ^[39]. To move forward in describing the rest of the dynamics of dewetting, we will see that it can be sufficient to keep (2.6) but to consider a revised form for the disjoining pressure.

3.2.   The revised dewetting thin film model

Finite-time rupture can be prevented by retaining higher-order terms in the expansion of the disjoining pressure. The balance of leading order disjoining forces with secondary conjoining forces (or "Born repulsion" ^[160]) can set a scale for molecular thin films (also called precursor or wetting layers) that are strongly adsorbed to the substrate, we will write this as $h = O({\epsilon})\ll 1$. A simple example of such a disjoining pressure is ^[85,87,88] (see Figure 4)

This and similar forms have been used in many physics and engineering studies of thin films ^{[159,160,161,183,184]}. In ^[21] it was shown that for a family of $\Pi(h)$ functions ^[96] including (3.10), solutions of (2.6) starting from positive initial data remain smooth and positive for all times. The resulting positive lower bound, $h\ge O({\epsilon})$, eliminates the possibility of rupture singularities and removes the trouble with moving contact lines for any ${\epsilon} > 0$. Consequently, (2.6) with $\Pi$ given by (3.10) is a physically motivated regularization of (3.1) that allows us to study all stages of dewetting.

Noting that (3.10) is a non-monotone function, (2.6) can be compared with Cahn-Hilliard models for the dynamics of binary phase separation in materials science ^{[68,104,123,139,156,181,182]}

where $u(x, t)$ is a conserved order parameter and $f$ is the derivative of a potential energy, $f(u) = F'(u)$. Mitlin ^[141] was one of the first researchers to draw attention to the connections between these models (with $h$ being analogous to $u$ and $\Pi(h)$ corresponding to $f(u)$), which have been used extensively in later studies ^{[69,104,123,169,204]}. For one example, generalizing the linear stability results (3.2, 3.3) for general mobilities and disjoining pressures yields

This form shows that thin homogeneous films with $\bar{h} < {h_{\mathrm{peak}}}$ (where $\Pi'({h_{\mathrm{peak}}}) = 0$) will be stable while there will be an unstable range for films with negative $\Pi'(\bar{h})$. For Cahn-Hilliard models, the growth of instabilities from small-amplitude perturbations to unstable uniform states is called spinodal decomposition ^[91]; the analogous situation for unstable thin films has been called spinodal dewetting ^{[27,167,169,190,208]}

However, there are also some notable differences. For the Cahn-Hilliard equation, the potential energy $F(u)$ is a double-well function that determines two finite values for the stable homogeneous states from a common-tangent construction ^[157]. Between those two states is a finite unstable range of $u$ where $f'(u)$ is negative. Phase separation for (3.11) consists of the solution approaching one of the two stable homogeneous states everywhere except for narrow transition regions between those states. In contrast, for (3.10), the potential energy

has only a single minimum and has $\Pi'(\bar{h}) < 0$ for all $\bar{h}$ in ${h_{\mathrm{peak}}} < \bar{h} < \infty$ where ${h_{\mathrm{peak}}} = 4{\epsilon}/3$ (see Figure 4). We will see that a consequence of this degenerate single-well form is that for (2.6), phase separation consists of the solution everywhere approaching either a nearly uniform precursor layer, $h = O({\epsilon})$, or one of a continuous family of near-equilibrium fluid droplet solutions. This behavior will be described in more detail in the later section on the long-time dynamics of dewetting.

4.   Intermediate-time dynamics

The intermediate dynamics in dewetting extend the short-time local dynamics to give rise to patterned solutions depending on larger scales up to the size of the problem domain. We begin by giving a more complete description of the dynamics for the regularized model (2.6, 3.10) under conditions where the un-regularized model (3.9) would yield finite-time rupture. To build intuition we will examine behavior in the one-dimensional problem,

before describing the richer geometric structures occurring in the two-dimensional problem.

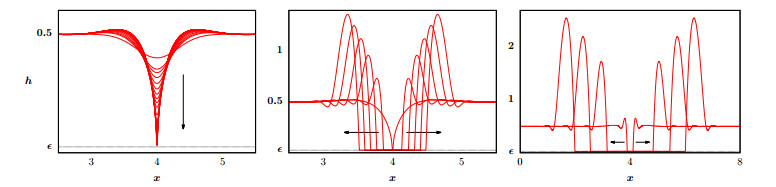
Starting from a perturbed nearly-uniform unstable layer with mean thickness $\bar{h} = O(1)$ the leading order evolution of (4.1) will follow the rupture dynamics described in section 3.1 during the times when $h\gg {\epsilon}$ everywhere since the disjoining pressure will be dominated by the destabilizing leading order term, $\Pi\sim {\epsilon}^2/h^3$, see Figure 5a. Because of the lower bound for solutions of (4.1), the singularity will not be achieved and the "near-rupture" self-similar dynamics will proceed only until reaching $h_{\min} = O({\epsilon})$ ^[21]. After that, the minimum thickness remains bounded and the region where $h = O({\epsilon})$ expands to form a "hole" or "dry spot" ^{[2,27,78,140,148,149,161,190,209]}. These terms are very widely used and are appropriately suggestive of the structure of the solution but should not be taken to mean that the solution is literally changing topology or its region of support. The apparent "hole" is based on the distinct separation in scales between the nearly-uniform $O({\epsilon})$ precursor relative to the $h = O(1)$ film and the well-defined boundary between phases given by the effective contact line (made possible by the near-degeneracy of the mobility $m(h)$ for $h\ll 1$), see Figure 5. As assured by the results from ^[21], the entire substrate surface remains wetted with fluid ($h > 0$) and the solution is smooth everywhere for all $t\ge 0$ as the process of phase separation progresses to form the precursor and droplets.

The fluid displaced from the dry spots collects into growing "rims" or "ridges" that propagate into the surrounding film layer as the hole grows ^[189], see Figure 5b. The structure and dynamics of these dewetting rims approach an asymptotically self-similar form for long times when their growing heights become much larger than the $h = O(1)$ surrounding film ^[71,144], see Figure 5c. The analysis involves several intermediate timescales and the motion of the rims is sensitive to slip effects ^[71,72]. Whether the advancing face of the rims has monotone or oscillatory decay as it matches to the uniform surrounding film has been shown to relate to slip in the mobility function $m(h)$ and compares well against experimental studies of growing dry spots in the dewetting of polymer films ^{[71,73,144,145]}.

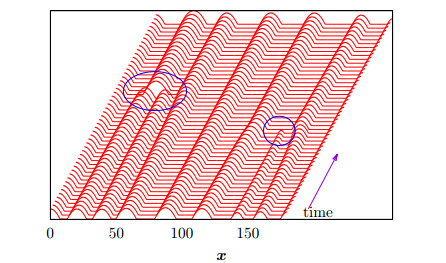
The dry spots and the rims continue to grow as long as there is a surrounding film to expand into. In problems on larger domains where several holes have developed from rupture dynamics at different locations, the rims of adjacent holes will eventually run into each other, see Figure 6a. In one dimension, the colliding rims will merge to form a quasi-steady droplet, which will be the fundamental starting point for the long-time dynamics to be described in Section 5, see Figure 6b.

In the context of the rupture of two-dimensional films at isolated points, the profiles shown in Figure 5 can be understood to qualitatively correspond to one-dimensional cross-sections through an axisymmetric solution. Whether growing circular dry spots are stable to non-axisymmetric perturbations is a very important question for understanding the further stages of dewetting. Linear stability analysis of the dewetting rims to transverse perturbations (potentially leading to fingering or other pattern forming phenomena) is a challenging problem because the uniform rim is a time-dependent base state with growing lengthscales and hence traditional approaches for linear stability analysis can only provide short-time estimates ^[115] and examinations of transient growth is needed ^[62,116]. Recent numerical studies have demonstrated that careful choices for the form of the mobility $m(h)$ to properly represent slip effects on different materials will change the stability of moving rims, causing them to shed secondary droplets, in good agreement with experimentally observed behaviors ^[166].

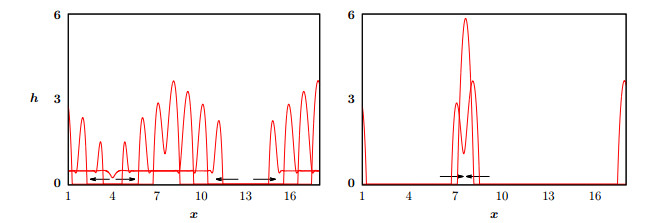
In two dimensions, colliding dewetting rims will form a nearly-stationary polygonal network of fluid ridges. Locally the ridges are nearly cylindrical with cross-sections being quasi-steady solutions of the one-dimensional problem (4.1), $h(x, y)\sim h(x)$. On a larger scale, the network structure can resemble a Voronoi diagram having cells centered at the well-separated original rupture points. Subsequently, each of the ridge segments can undergo a Rayleigh-type "pearling" instability and break-up into linear arrays of drops ^[59,60]. Consequently, there would be lines of drops along the former positions of the ridges and large regions with no drops in the polygonal dry spots. This form of dynamics, based on stable growth of dry spots and break-up into droplets only after a network has formed, has been observed in experimental studies under appropriate conditions ^{[106,130,166]}. However there are also other scenarios for the intermediate dynamics that yield significantly different arrangements of droplets and have been approached using different modes of analysis. When the propagating dewetting rims are unstable, they can yield a more spatially uniform distribution of drops that were shed before the ridge network gets formed. At the other extreme, in ^[13] it was observed in experiments and numerical models that instabilities could generate a cascade of satellite dry spots forming in fractal-like patterns.

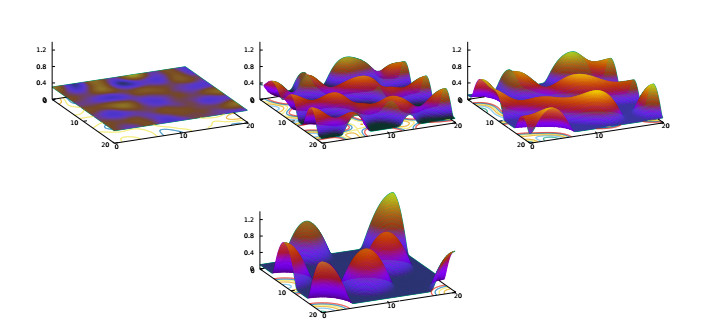
The scenarios outlined above involve localized perturbations initiating rupture at isolated locations followed by propagating instabilities determining the larger spatial patterns; these are generally called nucleation-dominated dewetting ^[100,112]. A numerical simulation of this type of dynamics in a small domain is shown in Figure 7. The influence of the original rupture position can be seen to persist for significant lengths of time, see Figure 7bc.

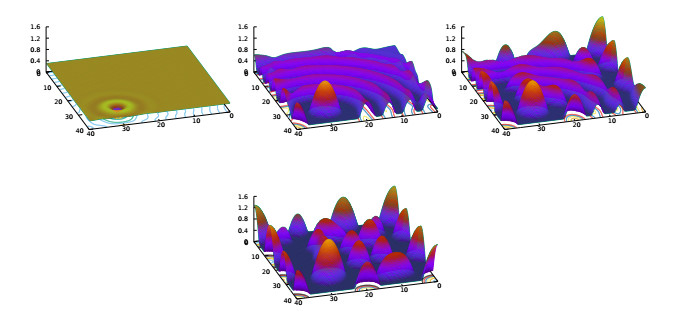
In contrast, a different form of dynamics occurs for perturbation amplitudes growing uniformly across the entire domain. Figure 1 shows an example of such evolution, starting from small-amplitude random perturbations to a spatially uniform film. The early stages of the pattern-forming evolution of these solutions closely follow the predictions of linear stability analysis (3.12). In particular, in homogeneous dewetting rupture is reached at roughly the same time in the whole domain rather than spreading from isolated nucleations points. This mode of dynamics is called spatially homogeneous instability or spinodal dewetting.

Thiele and collaborators ^[169,204] and others ^{[27,142,149,188]} have carefully considered nucleation vs. spinodal dewetting, making use of connections to stability analysis for Cahn-Hilliard models. The dramatically different dynamics shown in Figures 1 and 7 are directly tied to their initial conditions as both simulations were done on the same domain and with the same parameters in (2.6). While for short times they exhibit significantly different transients, for longer times they both might be thought to reach comparable states composed of droplets and precursor layers when phase separation is achieved (see final plots in each Figure). However, a close examination of these solutions show that they retain important differences – spinodal dewetting solutions have droplets that are closer to being uniform in size and spatial spacing, in contrast, nucleation creates drops with wider distributions of droplet sizes and spacings. These resulting arrays of near-equilibrium droplets form the initial conditions for the next stage of dynamics.

5.   Long-time dynamics

In the aftermath of the dramatic changes in film structure and spatial transport of fluid mass produced by the intermediate dynamics, the fluid layer has been phase-separated into isolated fluid droplets and the nearly-uniform precursor, $h = O({\epsilon})$, between them. The subsequent dynamics will occur over long timescales since locally, each of the remaining droplets is close to being a steady state. However, globally the system is far from equilibrium ^[43] since any arrangement of non-identical droplets will lead to local mass fluxes. Moreover, since even spatial periodic arrangements of identical droplets are unstable equilibria ^[123], evolution from generic initial conditions must proceed further until a final stable equilibrium (a single droplet) is achieved. This gives rise to coarsening dynamics. We will present an overview of this regime of dynamics in terms of the one-dimensional model (4.1) following ^[87,88] before describing the extension to two dimensions ^[86].

Equilibrium solutions, $h = H(x)$, of (4.1) occur when the pressure is a uniform constant. In one-dimension, this yields a second-order ordinary differential equation for $H(x)$ parametrized by $\bar{p}$,

For each value of $\bar{p}$ in $0 < \bar{p} < \Pi({h_{\mathrm{peak}}})$, this equation has a homoclinic solution that approaches a far-field constant precursor height $H\to h_*\equiv {\epsilon} +O({\epsilon}^2 \bar{p})$ as $|x|\to\infty$. A simplified representation of the structure of this solution can be obtained by using matched asymptotics in the limit of ${\epsilon}\to 0$ ^[21,87]. The droplet has a finite core region with $|h|\gg {\epsilon}$ where the pressure sets the constant curvature of the surface,

where the droplet width can be shown to be inversely related to pressure and scaled by the potential to satisfy matching conditions to the surrounding thin film, $\bar{w}(\bar{p}) \sim \sqrt{2|U({\epsilon})|}/\bar{p}$. Consequently, the mass of the droplet is inversely proportional to the square of the pressure,

These droplet solutions can now be employed to reduce the evolution of the PDE to finite-dimensional dynamical system for the degrees of freedom associated with the drops.

Noting the existence of the continuous family of drops for any $\bar{M} > 0$ and the translational invariance of (4.1), every steady drop can be characterized by specifying its position $X$ and its pressure $P$. Quasi-steady evolution of an individual droplet can be examined by allowing these parameters to be slowly evolving functions of time on some timescale, $\tau = \sigma t$ with $\sigma\ll 1$, with comparable small perturbations to the solution,

The slow evolution can be expected to be driven by comparably small mass fluxes imposed on the droplet through the surrounding thin film, say due to the presence of other nearby drops ^[87]

At leading order in $\sigma$, the quasi-steady droplet solution satisfies (4.1) identically; at $O(\sigma)$ we obtain

where $\mathcal{L}$ is the spatial operator for (4.1) linearized about $H(x-X; P)$ ^[87],

This is a non-self-adjoint singular operator with a two-dimensional nullspace corresponding to the two degrees of freedom in the leading order solution. To ensure the existence of solutions for $h_1$, the Fredholm alternative must be applied to project (5.6) onto each of the adjoint nullfunctions. The resulting solvability conditions yield two evolution equations for the droplet's position and pressure in terms of the boundary fluxes,

where the coefficient functions are given in terms of integrals of $H(x)$ and can be reduced to functions of the droplet's pressure alone ^[87,88]. Note that the artificial small parameter $\sigma$ scales out of (5.8) exactly and the dependence on the assumed domain size has a negligible influence.

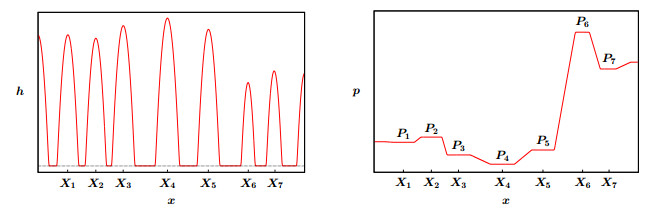
It may seem tempting to use (5.3) to re-write (5.8) in terms of the more-intuitive mass of the droplet core. However while the droplet mass is only well-defined in the droplet cores, the pressure field is defined everywhere by (2.5) and is essential for closing the model by providing a relation between the pressures and the flux for interacting adjacent droplets. Figure 8 shows the height profile and pressure field at a given time from a numerical solution of (4.1) consisting of a typical array of droplets produced by dewetting. The drops vary in sizes but all have the characteristic parabolic core profile given by (5.2). Within the region of support of each drop ($X_n-\bar{w}(P_n) < x < X_n+\bar{w}(P_n)$) the pressure is nearly constant, $p(x)\approx P_n$, consistent with (5.1). The pressure is continuous everywhere and its value in the molecular thin film between the droplets matches the values $P_n$ at the drops. Under the assumptions that the molecular film is quasi-steady and nearly flat, Eq (4.1) can be reduced to an elliptic problem on the region between drops,

which can be re-written as Laplace's equation applied to a new potential function,

This potential then has a linear profile between drops, $V = Ax+B$, that is determined by Dirichlet boundary conditions to match the pressures/heights at the edges of the neighboring droplets. Then the flux through the thin film is a constant, $J = -h^3 \partial_x p = - \partial_x V$, and can be expressed in terms of the properties of the adjacent drops as

This relation for the flux combined with (5.8) yields a closed model for the evolution of the positions and pressures for a set of $N$ interacting droplets, $n = 1, 2, \cdots, N$,

The heuristic argument from ^[87,88] reviewed above has been also been examined using rigorous analysis based on a center manifold reduction ^[117,118].

Numerical simulations ^[87,88] show that the reduced ODE model (5.11ab) accurately predicts the evolution of the droplets in the PDE (4.1) while the solutions of the ODEs remain bounded and slowly varying. However the ODEs can generate finite-time singularities. These behaviors are not a spurious effect of simplifications used in the derivation but directly correspond to crucial behaviors in the PDE when the assumption of quasi-steady evolution are briefly violated.

Figure 9 shows a numerical simulation of (4.1) starting from the initial state composed of seven droplets shown in Figure 8. Over long ranges of time, the drops are seen to evolve smoothly, but the figure also highlights two types of events that would produce singular behavior in (5.11):

(a) Collapse: disappearance of an individual droplet due to its mass vanishing, $M_n\to 0$, corresponding to a finite-time singularity in its pressure, $P_n\to\infty$.

(b) Collision: merging of two adjacent drops when their regions of support overlap.

In both of these cases, the flux (5.11a) becomes singular; for collision because the denominator vanishes with the numerator remaining finite, and for collapse with the numerator diverging since $V(P\to \infty)\to \infty$ while the denominator remains finite. Further, in both cases, after the time of the singular event ($t_c$), the solution will contain one drop less, i.e. $N\to N-1$; these are coarsening events for this problem.

The implications of coarsening for the ODE system (5.11) are that the dynamical system must be understood to be defined piecewise in time. Namely, ODEs (5.11b) can be integrated in time from appropriate initial conditions until a singularity occurs at $t\to t_c^-$. At that time, when PDE (4.1) would be briefly exhibiting rapid far-from equilibrium dynamics, the ODEs must be replaced by a different relation to map from the quasi-steady state of the droplets before $t_c$ to a new post-coarsening quasi-steady state for $t > t_c^+$ from which the ODEs can be resumed. Sometimes called a coarsening rule, this would reduce the order of the ODE system, $N\to N-1$, and re-assigning drop-adjacency after removing the collapsed droplet or merging the masses of the collided droplets at a new effect droplet position. Models combining smooth evolution generated by differential equations with maps that are applied at discrete times to represent singular events are generally called hybrid dynamical systems and have been used in modeling problems like mechanical systems with impacts ^[58]. In the context of coarsening in a Cahn-Hilliard problem, this type of model has been called a coarsening dynamical system ^[214], and similar models have been used in other physical systems having interacting localized structures ^[97].

The extension of these dynamics to the full problem for a set of droplets on a two-dimensional surface builds in a natural way from the model described above. The individual droplet states will now be solutions of the semilinear elliptic PDE,

The stable solutions will be axisymmetric droplets analogous to (5.2),

where $\bar{w}$ now gives the effective radius of the droplet. Consequently the quasi-steady form of droplets becomes

Linearizing about this solution gives three solvability equations determining the motion in the plane and the evolution of the droplet pressure. These equations are now given in terms of line integrals of the flux around the perimeter of the droplet core ^[84,86,168]. Finally, extending (5.10), the flux is given in terms of the gradient of a potential, ${\bf J} = -\nabla V$, which satisfies Laplace's equation, $\nabla^2 V = 0$, in the precursor region (the region exterior to droplet cores), subject to Dirichlet boundary conditions $V = V(h_*(P_n))$ at the droplet perimeters.

5.1.   Multi-scale modeling of dewetting

Having reviewed the possible behaviors in individual coarsening events, we turn to problems of interest for systems on large physical scales which may contain very large numbers of drops, $N\gg 1$. For such large problems, accurate direct numerical simulations of the PDE are not feasible. Computations of the reduced ODE model may still be possible, but may be excessive since the particular details of how or when individual droplets coarsen out is no longer the focus. At a macro-scopic scale, what is needed is a further level of faithful reformulation of the underlying system that can efficiently capture global properties without the need for resolving the solution to full detail. This practical strategy is common to approaches for many types of complex physical systems studied using multiscale modeling ^[63]. For the study of dewetting films, this means that questions of interest address how the number of remaining droplets in the system evolves, $N(t)$, what is the lengthscale between drops, $L(t)$, and further questions on the distribution of droplet sizes that can be understood from considering the set of droplets as an evolving population model.

To briefly illustrate how a statistical scaling law for the number of droplets can be obtained, we give a sketch of the heuristic argument from ^[87]. Assume we start with a large number of droplets on a fixed domain. The average spacing between drops will scale like $L = O(1/N)$, and since the total mass in the system is conserved for all times, the average mass similarly scales as $M = O(1/N)$. From (5.3), the typical droplet pressure will be $P = O(1/\sqrt{M}) = O(\sqrt{N})$. If we consider only collapse events and treat all other drops to be fixed while an individual droplet collapses, its pressure can be shown to obey

For a droplet starting with $P = O(\sqrt{N})$, this yields an estimate on the time to collapse as $T_c = O(P^{-3}L) = O(N^{-3/2}N^{-1}) = O(N^{-5/2})$. This establishes a timescale that can be used for subsequent collapses, assuming them to be independent and uncorrelated events,

Numerical simulations of (5.11ab) show very good agreement with this scaling law. Rigorous results on upper bounds for average coarsening rates for Cahn-Hilliard equations, in terms of growth of characteristic lengthscales between localized structures, were obtained by Kohn and Otto ^[119]. Their analysis depends on conservation of mass in the system and estimates of the rate of dissipation of the energy. Noting that the energy (2.7) can be related to the number of drops by

their approach was extended to provide rigorous validation for the estimate (5.16) ^[162].

An alternative to using global estimates from the PDE is to do further analysis of the lower-dimensional ODE model. In ^[47], upper bounds on coarsening rates for a model of particle growth through interaction with a dynamic mean-field was studied. That work motivated the approach in ^[92] to consider a simplified version of the ODE system (5.11b) restricted to collapse events only and now expressed in terms of droplet masses,

where the $L_n$'s are the separation between adjacent drops and (5.3) has been used to re-write the ODE for $P_n(t)$. This system of coupled ODEs for interacting droplets can be approximated by replacing the separations with the mean separation, $L_* = L_{\mathrm{total}}/N$, and by replacing the nearest-neighbor coupling by an effective mean-field pressure,

where the form of $M_*$ ensures conservation of mass in this discrete system. Further analyses of this system are given in ^[45,46]. System (5.18) can be called a discrete mean-field model because while its coupling between droplets is now done in a nonlocal manner through the mean-field $M_*$, the evolution of the system still involves integrating the system of $N$ ODEs. Further, like (5.17) and (5.11b), finite-time singularities occur at each of the coarsening events and hence $N$ and $L_*$ are piecewise-defined in time between successive singularities.

A continuous mean-field model can be obtained by considering the evolution of the population of droplets as described by a distribution function $\phi = \phi(m, t)$, for the number density of drops of a given mass. In terms of this continuous distribution function, the number of droplets is given by

and the mean-field pressure is the expected value of the pressure with respect to $\phi$,

Then a conservation law for the droplet size distribution can be written as

where the mass-transition rate follows from the discrete model (5.18). Equation (5.21) is a non-local conservation law since the transition rate depends on integrals of $\phi$. Following the pioneering works of Lifshitz, Slyozov, and Wagner in the 1960s ^[129,212] such models are called LSW equations ^[135]. LSW models have been the focus of extensive analysis on stability and long-time behavior of solutions ^{[150,151,152,153,154,155]}. Numerical simulations of the ODE and discrete mean field model suggest that for long times, the size droplet distribution appears to approach a self-similar form; scaling analysis of (5.21) determines this to be of the form,

which directly yields $N(t) = O(t^{-2/5})$ from (5.19).

6.   Open questions and directions for further work

The various stages of dewetting provide very rich problems for further study. Analysis of the dynamics in the intermediate stages may be the area of greatest need of further study as simulations and experiments have shown that many different types of patterns can develop ^[166]. Better understanding of the geometric aspects of instabilities in this regime may provide crucial information for describing the long-time behavior. Approaches used in studies of fluid foams ^[33,193,194] may be relevant for films forming ridge networks. While the long-time asymptotics of coarsening may follow the predictions of LSW models, it should be noted that the very long time scales involved (weeks or months in some situations) may make those limiting cases irrelevant to more typical real-world problems over seconds to minutes. Consequently, bounds on transient dynamics occurring on moderate timescales may be the results that can have greatest relevance for applications.

While dewetting is generally undesirable in many applications where uniform coatings are needed (as in painting and printing), there are important cases where dewetting can be very helpful, if it can be controlled.

One such application is the cooling of high-power electrical devices. One approach to maintain stable operating conditions in such systems, is to use heat transfer to drive phase change (evaporation/condensation) of fluids in contact with the devices ^[127,177]. Engineering studies have suggested that heat transfer from solid surfaces in contact with fluids is more efficient when the fluid is in the form of sets of small drops ("dropwise condensation") rather than a single uniform film ("filmwise condensation") ^[127,176]. Consequently this is a context where dewetting is very desirable. Recent experimental studies have designed strongly hydrophobic surfaces to enhance droplet formation and coarsening dynamics ^{[8,70,138,180]}. One study showed that having a temperature gradient across the solid surface can dramatically change the form of the drop size distribution from that expected from LSW models for uniform temperature ^[134]. Other studies considered the coarsening dynamics of droplets that exchange mass through a porous substrate layer ^[8,207]. Controlling the dynamics of droplet coarsening in such systems is crucial as both extremes (remaining thin precursor only or "flooded" thick film) are sub-optimal for heat transfer.

While there is a lot of research on evaporation of individual fluid droplets ^[36], the problem of how evaporation and condensation change the dynamics of dewetting in equations like (1.1) has received less attention ^{[7,34,146,159,203,215]}. Such models can be written as

where $Q[h]$ is a non-conservative mass flux due to phase changes. Various forms for this flux have been used in different studies ^[198], but perhaps most notable is a form derived from thermodynamic conditions ^[3,6] which fits in a class of forms making (6.1) a gradient flow ^{[197,198,199,200]}. Some results have been obtained for early stage dynamics ^[108], however the fact that fluid mass is not conserved in these models suggests that the LSW and Kohn-Otto approaches for describing the long-time coarsening dynamics will not work without novel modifications. Noting that even very weak evaporation and condensation can be expected to have cumulative influences on long-time dewetting dynamics, they could dramatically change behaviors from the mass-conserving case. In ^[107,109] it was shown that $Q$ violating gradient-flow form can yield more complicated mathematical properties for (6.1) including time-periodic solutions and different forms of finite-time rupture singularities.

Microfluidics ^[195,216] is another important application using surface wetting properties to manipulate small samples of fluids. Some studies have used substrates with carved channels to direct the motion of fluid droplets ^[99], however using flat substrates with spatially varying wetting properties can have some advantages ^[52,54]. Equation (1.1) can be used to describe dynamics on a heterogeneous or "chemically patterned" substrates by including spatial dependence in the disjoining pressure, $\Pi = \Pi(h, x)$ ^{[10,32,53,98,120,133,202]}. Designs with hydrophilic stripes surrounded by hydrophobic regions have proved effective in confining and directing thin film flows in experiments ^[54]. But there are many open physical questions and need for further mathematical analysis to fully describe the dynamics and stability of such systems ^[5,196]. More studies of the long-time behaviors of thin films since there is potential for different interesting behaviors to arise from the competition between coarsening (causing droplets to grow) and pinning at heterogeneous interfaces (which limits growth) ^[32].

We conclude by briefly noting other important directions for further related research:

● For very thin films at the scale where the disjoining pressure and molecular interactions become significant, the influences of surface roughness and thermal fluctuations may likewise be important. Several papers have examined how to derive models which include stochastic forcing and how this can affect the dynamics ^{[55,61,74,94,137,171]}.

● There has been a lot of interest in seeing how the gradient flow framework (2.7) can be extended to model and analyze more complicated physical systems with dewetting coupled to other dynamics, for example surfactants ^[200,201], complex fluids ^[198,199] or multi-layer flows ^[75,169,213].

● Other interesting generalizations of (1.1) in a variational framework have been obtained by including a height-dependent coefficient in the interfacial energy term in (2.7) ^[164,165].

● Dewetting in flows on curved surfaces ^{[136,174,178,185]} is of great interest for many physical applications and would also address questions on how large-scale spatial heterogeneities could be incorporated into mean-field models of coarsening. There are also many results for multi-dimensional problems that need different analytical approaches than in one spatial dimension and should be studied further ^[21,26,48].

● Further study is needed to see how improved models of the disjoining pressure that include curvature dependence ^[44,223] modify the regularized rupture dynamics leading to dry spot formation. For non-wetting droplets on superhydrophobic substrates ^[138], lubrication theory can not be directly employed and dewetting dynamics may need to be derived for general Stokes flows. Other problems for merging droplets with significant inertial effects require full Navier-Stokes flows ^[132].

● Many of the ideas used to study finite-time rupture can also be applied to singularity formation (blow-up or pinch-off) in other higher-order PDE problems ^{[18,24,25,221]} and materials science problems like solid thin films ^[76,77].

● Developing better understandings of the interesting dynamics in the range of problems described above provides many challenges for both analysis and in creating efficient numerical methods that can simulate long-time dynamics of large scale systems ^{[14,83,121,222,]} and resolving finite-time singularities ^[69,206,218].

Acknowledgments

The author wishes to express his appreciation to his collaborators and other colleagues in the thin films research community whose work has educated, challenged, and motivated him.

Conflict of interest

The author declares no conflicts of interest in this paper.