Citation: Wei Sun, Yan Wang, Shiyong Li. An optimal resource allocation scheme for virtual machine placement of deploying enterprise applications into the cloud[J]. AIMS Mathematics, 2020, 5(4): 3966-3989. doi: 10.3934/math.2020256
| [1] | Cunlin Li, Wenyu Zhang, Hooi Min Yee, Baojun Yang . Optimal decision of a disaster relief network equilibrium model. AIMS Mathematics, 2024, 9(2): 2657-2671. doi: 10.3934/math.2024131 |
| [2] | Nawras H. Sabbry, Alla Levina . Nonce generation techniques in Schnorr multi-signatures: Exploring EdDSA-inspired approaches. AIMS Mathematics, 2024, 9(8): 20304-20325. doi: 10.3934/math.2024988 |
| [3] | Justin Tzou, Brian Wetton . Optimal covering points and curves. AIMS Mathematics, 2019, 4(6): 1796-1804. doi: 10.3934/math.2019.6.1796 |
| [4] | Ibrahim Attiya, Mohammed A. A. Al-qaness, Mohamed Abd Elaziz, Ahmad O. Aseeri . Boosting task scheduling in IoT environments using an improved golden jackal optimization and artificial hummingbird algorithm. AIMS Mathematics, 2024, 9(1): 847-867. doi: 10.3934/math.2024043 |
| [5] | Zhimin Liu . Data-driven two-stage sparse distributionally robust risk optimization model for location allocation problems under uncertain environment. AIMS Mathematics, 2023, 8(2): 2910-2939. doi: 10.3934/math.2023152 |
| [6] | Kobkoon Janngam, Suthep Suantai, Rattanakorn Wattanataweekul . A novel fixed-point based two-step inertial algorithm for convex minimization in deep learning data classification. AIMS Mathematics, 2025, 10(3): 6209-6232. doi: 10.3934/math.2025283 |
| [7] | Kai Wang, Xiheng Wang, Xiaoping Wang . Curvature estimation for point cloud 2-manifolds based on the heat kernel. AIMS Mathematics, 2024, 9(11): 32491-32513. doi: 10.3934/math.20241557 |
| [8] | Li Shen, Jian Liu, Guo-Wei Wei . Evolutionary Khovanov homology. AIMS Mathematics, 2024, 9(9): 26139-26165. doi: 10.3934/math.20241277 |
| [9] | Yunjae Nam, Dongsun Lee . Efficient one asset replacement scheme for an optimized portfolio. AIMS Mathematics, 2022, 7(9): 15881-15903. doi: 10.3934/math.2022869 |
| [10] | Seonghyun Choi, Woojoo Lee . Developing a Grover's quantum algorithm emulator on standalone FPGAs: optimization and implementation. AIMS Mathematics, 2024, 9(11): 30939-30971. doi: 10.3934/math.20241493 |
Cloud computing is the integration of computer technologies such as distributed computing, network storage, utility computing, virtualization computing, load balancing, and modern network technologies. The cloud computing platform presents a variety of services by centralizing the pool of computing resources connected to the network, such as IaaS (Infrastructure as a Service), PaaS (Platform as a Service), and SaaS (Software as a Service). Regarding the definition of cloud computing, the literature [1] defines the hardware and software of the data center as "cloud", and defines the service as "utility computing", and the sum of software services and utility computing becomes cloud computing. According to the National Institute of Standards and Technology (NIST) definition [2], cloud computing is a method to access computing resources (including networks, servers, storage, applications, services, etc.) in a convenient, pay-as-you-go manner over a network. It takes advantage of the decentralized resources to support the flexibility of resource sharing and access. Cloud computing enables users to take advantage of the computing resources of the cloud data center as a service, rather than to deploy those resources costly by themselves, and does not require the end users to calculate their exact values of the required resources, which can be calculated and granted by the cloud service providers according to the need of users [3]. Due to the attractive features of cloud computing, more and more enterprises migrate and deploy their applications into the cloud so as to reduce their own IT investments, and some interesting resource allocation schemes are also presented and implemented from the social welfare point of view [4,5].
Data Center (DC) is used to host servers in the cloud and connects these servers through dedicated links and switches. A large number of distributed processing applications (such as cloud applications, search engines, social applications) are typically run in large data centers [6]. Data centers have become an important choice for data-intensive applications. Companies can reduce their own hardware deployment and maintenance costs, and achieve great revenue. Due to the different resource requirements of applications, many physical machines (PMs) in the data center are in low utilization at most of the time. A large number of running PMs are not being fully used, but at the same time they are occurring large management and maintenance costs, resulting in serious waste of resources. Virtualization is one of the most feasible ways to enhance data center utilization. Virtualization technologies can allocate resources of a single physical machine to multiple virtual machines (VMs) to improve scalability and resource utilization [7]. Virtualization technologies not only enable performance isolation between applications sharing the same computing node, but also enable dynamic or offline migration technology to migrate virtual machines from one node to another. In the actual environment, users are almost unaware of the impact of VM migration. On the other hand, real-time virtual machine reallocation can achieve dynamic load consolidation, so that virtual machines can be merged onto a smaller number of physical machines, thereby turning idle nodes into energy-saving mode. Virtualizing a physical machine can improve resource utilization, however, concentrating workloads on a subset of the physical machines can cause hot spots, and even degrade the actual performance of each application. Thus, how to achieve efficient VM placement has become a critical problem in the cloud [8]. Reasonable resource allocation for virtual machines can also reduce traffic transmission and management and maintenance costs.
Due to the importance of the placement of virtual machines on physical machines in the cloud computing environment, the efficient resource allocation for virtual machine has received a lot of research attention. Each virtual machine placement scenario has one or more targets or goals that are to achieve by designing placement algorithms. For example, some virtual machine placement schemes attempt to reduce network traffic and power consumption in the data center. In addition, the ideal VM placement scheme should reduce unnecessary migration of future VMs [9] and improve the utilization and availability of DC resources. The current research mainly focuses on optimal allocation of virtual machine resources in the cloud environment, so as to reduce energy consumption [10,11], or achieve the goal of maximizing utility [4,12]. At the same time, some researchers have concentrated their research on green cloud computing [13,14,15], minimizing the problem of data transmission time [16,17], improving the scalability of the system [18], and achieving the fairness of network resource allocation [19,20].
In this paper we consider enterprise applications deployment into the cloud for reducing its own IT investment, propose an optimization model for virtual machine resource allocation in the cloud environment, and present an optimal resource allocation algorithm. We try to place the virtual machines into the most suitable physical machines and realize the optimal resource allocation for these virtual machines under the constraints of physical machine resources, so as to achieve the goal of maximizing applications utility. We analyze the performance of the proposed resource allocation scheme by applying Lyapunov stability theory and find that all the trajectories along the scheme eventually converge to the optimum of the resource allocation problem. The simulation results show that the scheme can converge to the optimal resource allocation within a limited number of iteration times.
The remainder of this paper is organized as follows: Section 2 introduces the relevant research on virtual machine resource allocation; Section 3 presents the virtual machine resource allocation model and gives the corresponding analysis; Section 4 proposes the resource allocation algorithm and investigates its performance and implementation steps; Section 5 further discusses the utility functions for achieving fair resource allocation and presents the extended resource allocation scheme; Section 6 gives the simulation results of the proposed virtual machine resource allocation algorithm as well as the optimal solutions obtained by LINGO software; Section 7 finally summarizes this paper.
In recent years, cloud computing technologies have received a lot of research attention from academic and industrial researcher, and have been found to be useful and further implemented in many scenarios, such as ubiquitous industrial networks [21,22], power Internet of Things [23,24], social vehicular networks [25,26], 5G networks [27,28], space-terrestrial integrated networks [29,30], et al. In many cloud computing systems servers are typically underutilized, resulting in a large amount of resources being idle. Therefore, placing more VMs to fewer PMs is an effective way to reduce power consumption and improve resource utilization. The basic principle of VM placement is to allocate as many VMs as possible on the physical machines while meeting the various constraints specified in the system requirements. VM placement is the process of mapping VMs to the most appropriate location and number of PMs based on the actual needs of users. The existing virtual machine placement algorithms can be divided into two categories according to the targets: one is based on energy consumption, these methods mainly consider server-side constraints; the other is based on application service quality and users' needs, the purpose is to maximize the satisfaction of users. Several virtual machine placement algorithms are presented recently, including constraint programming [31,32], simulated annealing, boxing algorithm, stochastic programming [33], mixed integer linear programming [34,35], genetic algorithm [36,37,38], ant colony algorithm [39,40], et al., some of which involve virtual machine dynamic migration, while other algorithms only consider static placement.
The goal of the boxing approach is to minimize the number of PMs in operation, treating the VM as an object and the PM as a container, and the goal is to package those objects into as few containers as possible. Although traditional online boxing heuristics (such as Best Fit, BF) have been used to reduce the number of PMs used, there are problems with low utility. Wang et al. [41] established an energy consumption model in a cloud computing environment. Based on the analysis of energy consumption in the model, the online packing algorithm was improved, and the energy efficiency of a cloud computing environment composed of virtual machines was proposed. The new energy-aware approach not only improves resource utilization, but also makes the data center more energy efficient. Kaaouache et al. [42] considered a one-dimensional packing problem and proposed a new method based on correcting infeasible chromosomes to prevent package overflow. The application of the proposed chromosome to genetic algorithms helps to reduce execution time and minimize energy consumption in cloud data centers. This optimization is done by VM placement, resulting in the use of a minimum number of physical machines and another server that can be turned to sleep or shut down.
For the case where multiple targets are considered, Xu et al. [43] defined the VM placement problem as a multi-objective optimization problem, and proposed an improved genetic algorithm based on fuzzy multi-objective evaluation to minimize the total resource loss, energy consumption and heat dissipation costs. Dörterler et al. [44] formulated the VM placement problem as a multi-objective ant colony optimization algorithm to minimize SLA collisions, total resource loss, and power consumption. Jayasinghe et al. [45] proposed a structural constraint-aware virtual machine placement scheme that supports the constraints of requirements, communication, and availability, and effectively improves the performance and availability of services hosted on the IaaS cloud. Based on the analysis of data center topology characteristics and traffic patterns, Fang et al. [46] proposed a new virtual data center network power consumption reduction method to shut down as many unnecessary network nodes as possible, thereby saving power.
In addition, some scholars investigate VM placement and resource allocation by applying queuing theory and game theory. Guo et al. [47] used the queuing theory to establish a comprehensive optimization model for cloud computing, which is to optimize the average waiting time, average queue length and number of customers of the cloud system. Xiao et al. [48] proposed a new algorithm based on evolutionary game theory. By dynamically adjusting the resource allocation of virtual machines, energy consumption can be effectively reduced. Song et al. [49] studied the energy-saving and scalability issues of modern data centers based on convex optimization theory, and proposed a new virtual machine placement scheme. The scheme takes into account the inherent dependencies and traffic between virtual machines, reduces the cost of communication between virtual machines and increases the efficiency and scalability of the data center.
In the cloud computing architecture, virtualization technologies are used to realize the flexibility and scalability of resources in the cloud data center. Virtualization technologies can map a virtual machine to one or more physical machines to meet the user's flexible demand for resources [49]. At the same time, multiple virtual machines can also parallelly reside on the same physical machine and each virtual machine occupies only part of physical resources, so as to make rational use of the resources of physical machines.
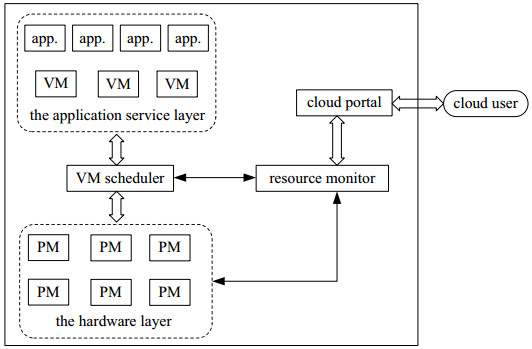
As shown in Figure 1, the VM scheduler is considered as a manager, which continuously monitors the physical resource mapping status provided by the hardware layer to the application service layer, thereby enabling efficient deployment of virtual machines for cloud applications. Generally, in order to improve the utilization of resources, the architecture sets the maximum and minimum thresholds. When the resource utilization of a physical machine is less than the minimum threshold, the physical machine will be shut down to save power consumption and move its virtual machines to other physical machines; when the resource utilization of a physical machine is greater than the maximum threshold, the architecture will no longer place a new virtual machine to the physical machine to ensure that the quality of service does not drop. The task of the resource monitor is to solve the problem of matching the requirements of the application service with the virtual machine resources, obtain the optimal resource allocation for virtual machines, and communicate VM scheduler to place the virtual machine on a suitable physical machine or perform dynamic virtual machine migration. Then, how to allocate the resources of these physical machines is a key issue to improve server utilization and reduce costs. This paper proposes an optimization model for virtual machine resource allocation and introduce a resource allocation scheme to achieve the optimum.
An enterprise user intends to reduce its own system infrastructure investment and maintenance cost, and wants to deploy its applications into the cloud. Indeed, each application is composed of a number of distributed components, generally including three functional tiers: A front-end tier, a business-logic tier, and a back-end tier [50]. A front-end tier mainly handles user requests such as web requests and consists of a number of components. A business-logic tier mainly performs specialized application logic. And a back-end tier generally stores some important operation data of an application, and comprises of various databases servers. In some scenarios the components of the back-end tier may not be deployed into the cloud and operate in enterprise local data center for data security consideration.
Consider there is a set P of physical machines in the cloud data center. Virtual machines will be effectively placed in the physical machines through the resource scheduler. Introduce the set S of applications that an enterprise user intends to deploy into the cloud and the set R of application components. Each application s∈S is composed of a set R(s) of components. Here we assume each component resides in one virtual machine. Multiple virtual machines can simultaneously reside on the same physical machine so as to improve the resource utilization. Let P(r) be the set of physical machines that provide resource for the corresponding virtual machine of component r. Introduce the set S(p) of applications whose components reside on the physical machine p and obtain resource allocation for the virtual machines from physical machine p.
Define xCPUsrp, xramsrp and xstosrp be the CPU, memory and storage resources offered by physical machine p to component r of application s, respectively. And denote yCPUs, yrams and ystos as the total CPU, memory and storage resources obtained by application s, respectively, that is, the summation of all its components for each type of resource. Introduce Us(⋅) be the deployment utility of application s which is a continuously differentiable and bounded function with respect to its variables. Let CCPUp, Cramp and Cstop be the maximum capacity of CPU, memory and storage of resource provider p, respectively.
When an enterprise deploys its applications into the cloud, the goal of resource allocation for virtual machine placement in the cloud is indeed to maximize the agammaegated deployment utility of all applications, so as to achieve effective utilization of the resources of physical machines. Then, we establish the following resource allocation optimization model for virtual machine placement in the cloud.
| Q:max∑s∈SUs(yCPUs×yrams×ystos)subject to∑r∈R(s)∑p∈P(r)xCPUsrp=yCPUs,s∈S∑r∈R(s)∑p∈P(r)xramsrp=yrams,s∈S∑r∈R(s)∑p∈P(r)xstosrp=ystos,s∈S∑s∈S(p)∑r∈R(s)xCPUsrp≤CCPUp,p∈P∑s∈S(p)∑r∈R(s)xramsrp≤Cramp,p∈P∑s∈S(p)∑r∈R(s)xstosrp≤Cstop,p∈PoverxCPUsrp≥0,xramsrp≥0,xstosrp≥0,s∈S,r∈R,p∈P. | (3.1) |
We investigate the resource allocation for virtual machines placement when enterprise applications are deployed into the cloud. Typically, tightly packing virtual machines onto a small number of working physical machines and turning off other idle machines is an effective way to maximize physical machine utilization and reduce energy consumption. However, concentrating workloads on a subset of the physical machines can cause hot spots, and even degrade the actual performance of each application resided and deployed in the cloud. An effective resource allocation strategy should achieve the tradeoffs between energy efficiency and fairness. Thus we adopt the fairness utility proposed for resource allocation in traditional IP Networks [51] and further in per-to-peer networks [52], which has the following logarithmic form.
| Us(yCPUs×yrams×ystos)=wslog(yCPUs×yrams×ystos), | (3.2) |
where ws is the payment that the enterprise user is willing to pay to its resource provider for its application s when the application s is deployed into the cloud.
We find that the application deployment utility function Us(⋅) is the summation of deployment utilities from CPU, memory and storage resources, i.e., Us(yCPUs)+Us(yrams)+Us(ystos). Then the resource allocation model (3.2) for virtual machines placement when applications are deployed into the cloud can be decomposed into three independent sub-problems for CPU, memory and storage resource allocation, respectively. For simplicity, in the following analysis, we do not further differentiate among the specic types of resource, and generalize these three sub-problems into the following one form
| QG:max∑s∈SUs(ys)subject to∑r∈R(s)∑p∈P(r)xsrp=ys,s∈S∑s∈S(p)∑r∈R(s)xsrp≤Cp,p∈Poverxsrp≥0,s∈S,r∈R,p∈P. | (3.3) |
For the generalization-form resource allocation model (3.3), the objective function is a strict concave function with respect to variable ys but not a strict concave function with respect to variable xsrp. At the same time, the constraints are linear, so the constraint set for this optimization problem is convex. Therefore, the following results can be obtained based on the convex optimization theory.
Theorem 1 When the enterprise user deploys its application into the cloud, the resource allocation model (3.3) for virtual machines placement is a convex optimization problem. The optimal resource allocation x∗=(x∗srp,r∈R,s∈S,p∈P) offered to each virtual machine that the component of an application resides on exists but is not unique. The optimal resource allocation y∗=(y∗s,s∈S) for each application exists and is unique.
In order to get the optimal solution of the resource allocation model, we firstly give the Lagrangian of this nonlinear optimization problem
| L(x,y;λ,μ)=∑s∈SUs(ys)+∑s∈Sλs(∑r∈R(s)∑p∈P(r)xsrp−ys)+∑p∈Pμp(Cp−∑s∈S(p)∑r∈R(s)xsrp), | (3.4) |
where λ=(λs,s∈S) is the price vector with element λs≥0, which can be considered as the price per unit cloud resource paid by the enterprise user for its application s; μ=(μp,p∈P) is the price vector with element μp≥0, which can be considered as the price per unit cloud resource charged by physical machine p.
We can also rewrite (3.4) with the following form
| L(x,y;λ,μ)=∑s∈S(Us(ys)−λsys)+∑s∈S∑r∈R(s)∑p∈P(r)xsrp(λs−μp)+∑p∈PμpCp | (3.5) |
It can be noted that the first expression in (3.5) is separable in variable ys, and the second expression is separable in variables xsrp. Thus the objective function of the dual problem can be written as:
| D(λ,μ)=maxx,yL(x,y;λ,μ)=∑s∈SSs(λs)+∑s∈S∑r∈R(s)∑p∈P(r)Psp(λs,μp)+∑p∈PμpCp, | (3.6) |
where
| Ss(λs)=maxysUs(ys)−λsys, | (3.7) |
| Psp(λs,μp)=maxxsrpxsrp(λs−μp). | (3.8) |
In equation (3.7), the enterprise user tries to maximize its own deployment utility for its applications, which depends on the total obtained resource ys of application s. λs is the price per unit resource that the enterprise user pays for application s, then λsys is the total payment that the user provides to the resource providers for its application deployment into the cloud. In equation (3.8), component r of application s obtains the resource allocation xsrp from physical machine p, then xsrpλs is the cost of the enterprise user paying for the physical machine p in the cloud deployment for the application s. Since μp is the price per unit resource charged by the physical machine p, then xsrpμp is the cost of physical machine p when offered resource xsrp to component r of application s, so equation (3.8) means that each physical machine is to maximize its own revenue.
Hence, the dual problem is
| D:minD(λ,μ)overλs≥0,μp≥0,s∈S,p∈P. | (3.9) |
The original resource allocation problem (3.1) or its generalization form (3.3) is to maximize the agammaegation of deployment utility of applications when deployed into the cloud under the constraints of physical machines capacity, and the dual problem (3.9) is to minimize the overall price of the cloud computing data center.
In order to obtain the optimal resource allocation for virtual machine placement when the applications are deployed into the cloud, let (x∗,y∗,λ∗,μ∗) be the optimal solution to the generalization-form problem (3.3) and the dual problem (3.9). Let ∂L(x,y;λ,μ)/∂ys=0, we can obtain
| y∗s=wsλs. | (3.10) |
Substituting (3.10) into (3.4), we obtain
| ˜L(x;λ,μ)=∑s∈S(wslog(wsλs)−ws+λs∑r∈R(s)∑p∈P(r)xsrp)+∑p∈Pμp(Cp−∑s∈S(p)∑r∈R(s)xsrp), | (3.11) |
Let ∂˜L(x;λ,μ)/∂λs=0, then we obtain
| λ∗s=ws∑r∈R(s)∑p∈P(r)xsrp. | (3.12) |
Substituting (3.12) into (3.11), we obtain
| ˆL(x;μ)=∑s∈S(wslog(∑r∈R(s)∑p∈P(r)xsrp))+∑p∈Pμp(Cp−∑s∈S(p)∑r∈R(s)xsrp), | (3.13) |
Assume that the virtual machine corresponding to the component r of application s obtains a certain amount of resource allocation from physical machine p, that is xsrp>0, then let ∂ˆL(x;μ)/∂xsrp=0, we can obtain the optimal resource allocation
| y∗s=∑r∈R(s)∑p∈P(r)xsrp=wsμp,p∈P(r),r∈R(s). | (3.14) |
Then we can obtain the following result.
Theorem 2 For the resource allocation optimization model (3.1) or its generalization form (3.4) for virtual machines placement, if there are two components of an application residing on two different physical machines and obtaining non-zero resource allocations from these machines, then the prices charged by these physical machines are both equal to the price paid by the enterprise user for this application. That is, if x∗sr1p1>0,p1∈P(r1) and x∗sr2p2>0,p2∈P(r2), then μ∗p1=μ∗p2=λ∗s.
Actually, from (3.14) we can find
| μ∗p1=μ∗p2=ws∑r∈R(s)∑p∈P(r)xsrp=λ∗s. | (3.15) |
Therefore, a bipartite graph consisting of physical machines P and applications S can be constructed. Each edge represents the relationship between a physical machine and an application, indicating that the physical machine provides resources for the virtual machine of the application to complete the cloud deployment. If the graph is fully connected, then μ∗p1=μ∗p2=μ∗, otherwise, it can be divided into multiple connected subetaaphs for analysis. In the following discussion, we assume μ∗p1=μ∗p2=μ∗. Then let ∂ˆL(x;μ)/∂μ=0, we can obtain
| μ∗=∑s∈Sws∑p∈PCp. | (3.16) |
Substituting (3.16) into (3.14),
| y∗s=ws∑p∈PCp∑s∈Sws. | (3.17) |
It can be found from (3.17) that when an enterprise application s is deployed into a cloud, the optimal resource allocation y∗s obtained by the virtual machines in which the components of this application are located depends on the total capacity of its physical machines, and the total payment of all applications that are hosted by the physical machines weighted by the payment ws for application s. At the same time, it can be seen that the total resource allocation y∗s for each application s is unique, which has been discussed in Theorem 1.
In order to enable enterprise users to deploy applications into the cloud, the virtual machines in which the components of each application are located should be provisioned with optimal resource allocation. Then this paper proposes the following resource allocation algorithm. Each physical machine p updates its resource allocation xsrp(t) for component r of application s according to the following rule
| ddtxsrp(t)=κxsrp(t)(λs(t)−ξp(t))+xsrp(t)−ε, | (4.1) |
| ξp(t)=∑j∈S(p)∑i∈R(j)xjip(t)λj(t)Cp. | (4.2) |
The price per unit resource that an enterprise user should pay to physical machine p when deploying application s into the cloud is
| λs(t)=wsmax{η,ys(t)}, | (4.3) |
| ys(t)=∑r∈R(s)∑p∈P(r)xsrp(t), | (4.4) |
where κ>0 is the step size of the algorithm, ε>0,η>0 are small constants to ensure the allocated resources xsrp(t) not lower than ε and the price λs(t) not higher than ws/η. Here a=(b)+c means a=b if c>0 and a=max{0,b} if c=0. In the above algorithm, ξp(t) can be regarded as the expected price when the physical machine p provides resources for virtual machines to host components of applications, and at the optimal resource allocation, the expected price ξ∗p of the physical machine p will be equal to the actual paid price λ∗s of the enterprise user for its applications.
Now we study the proposed resource allocation scheme (4.1)–(4.4) and analyze its equilibrium. By substituting (4.2) into (4.1) and setting (4.1) to zero, we can obtain the equilibrium (x∗,λ∗), that is,
| λ∗s=∑j∈S(p)∑i∈R(j)x∗jipλ∗jCp, | (4.5) |
Meanwhile, from (4.3) (4.4), at the equilibrium
| λ∗s=wsy∗s=ws∑r∈R(s)∑p∈P(r)x∗srp. | (4.6) |
Then
| ∑p∈PCp=∑p∈P∑j∈S(p)∑i∈R(j)x∗jipλ∗jλ∗s=1λ∗s∑p∈P∑j∈S(p)∑i∈R(j)x∗jipλ∗j=(a)y∗sws∑j∈Sλ∗j∑i∈R(j)∑p∈P(i)x∗jip=(b)y∗sws∑j∈Swj, |
where (a) and (b) follow from (4.6). Thus the total resource allocation for application s is
| y∗s=ws∑p∈PCp∑j∈Swj, | (4.7) |
and from (4.6) the price paid by the enterprise user for application s is
| λ∗s=∑j∈Swj∑p∈PCp. | (4.8) |
It is very important to emphasize that the optimal price paid by the enterprise user has no relationship with each application, but only depends on the ratio of the total payment of the enterprise user to the total capacity of physical machines. It is also equal to the optimal price charged by each physical machine. In the following stability analysis, we use λ∗s=λ∗ and μ∗p=μ∗ for simplicity.
Obviously, the equilibrium (4.7), (4.8) is equal to the optimum (3.16), (3.17) of the generalization-form resource allocation problem (3.3). At the same time, we can also find at the equilibrium point the following equality holds
| ∑s∈S(p)∑r∈R(s)x∗srp=Cp | (4.9) |
Then, the summation of the allocated resources by each physical machine to the virtual machines of applications is exactly the resource capacity of the physical machine, which also indicates that the resources provided by the physical machine are fully utilized at the equilibrium of the dynamic system described by the algorithm.
From the analysis above, we know that the equilibrium point of the dynamic systems (4.1)-(4.4) described by the algorithm is consistent with the optimal resource allocation of the resource allocation problem (3.3). Based on the asymptotic stability of the continuous dynamic system of Lyapunov stability theory, we can obtain the following result.
Theorem 3 The equilibrium point (4.7), (4.8) of the dynamic systems (4.1)–(4.4) described by the proposed algorithm is asymptotically stable. Therefore, all the trajectories along (4.1)–(4.4) eventually converge to the optimum of the resource allocation problem (3.3).
Proof
Define the following Lyapunov function
| V(t)=V1(t)+V2(t)=∑s∈S∫y∗sys(t)(wsυ−λ∗)dυ+∑p∈Pλ∗(Cp−ψp(t)), |
where ψp(t)=∑s∈S(p)∑r∈R(s)xsrp(t),p∈P, and λ∗=λ∗s,∀s∈S.
Since ys(t)≥0, y∗s≥0, the first part of the Lyapunov function is
| ∫y∗sys(t)(wsυ−λ∗)dυ=ws(logy∗s−logys(t))−λ∗(y∗s−ys(t))=ws(ys(t)y∗s−1−logys(t)y∗s)≥0. |
Obviously, V1(t)=0 if and only if ys(t)=y∗s (i.e., λs(t)=λ∗s=λ∗). Meanwhile, the second part of the Lyapunov function is V2(t)≥0 since ψp(t)=∑s∈S(p)∑r∈R(s)xsrp(t)≤Cp, and V2(t)=0 if and only if ψp(t)=∑s∈S(p)∑r∈R(s)x∗srp=Cp. Thus, the Lyapunov function V(t) is a positive definite function, and it is zero only at the equilibrium point (x∗,λ∗) (i.e., λs(t)=λ∗s=λ∗, ψp(t)=∑s∈S(p)∑r∈R(s)x∗srp=Cp).
The derivative of V(t) along the trajectories of the dynamic system (4.1)–(4.4) is
| dV(t)dt=∑s∈S∂V(t)∂ys(t)dys(t)dt+∑p∈P∂V(t)∂ψp(t)dψp(t)dt=−∑s∈S(wsys(t)−λ∗)∑r∈R(s)∑p∈P(r)dxsrp(t)dt−∑p∈Pλ∗∑s∈S(p)∑r∈R(s)dxsrp(t)dt=−∑s∈S(λs(t)−λ∗)∑r∈R(s)∑p∈P(r)dxsrp(t)dt−∑p∈Pλ∗∑s∈S(p)∑r∈R(s)dxsrp(t)dt=−∑s∈S∑r∈R(s)∑p∈P(r)κλs(t)xsrp(t)(λs(t)−∑j∈S(p)∑i∈R(j)xjip(t)λj(t)Cp)=−∑s∈S∑r∈R(s)∑p∈P(r)κλ2s(t)xsrp(t)+∑s∈S∑r∈R(s)∑p∈P(r)κxsrp(t)λs(t)Cp∑j∈S(p)∑i∈R(j)xjip(t)λj(t)=−∑s∈S∑r∈R(s)∑p∈P(r)κλ2s(t)xsrp(t)(1−xsrp(t)Cp)+∑s∈S∑r∈R(s)∑p∈P(r)κxsrp(t)λs(t)Cp∑j∈S(p)∖{s}∑i∈R(j)xjip(t)λj(t). |
Add ∑s∈S∑r∈R(s)∑p∈P(r)κλ2s(t)xsrp(t)1Cp∑j∈S(p)∖{s}∑i∈R(j)xjip(t) to the first part of the derivative above, and subtract the same term from the second part, then
| dV(t)dt=−∑s∈S∑r∈R(s)∑p∈P(r)κλ2s(t)xsrp(t)(1−∑j∈S(p)∑i∈R(j)xjip(t)Cp)+∑s∈S∑r∈R(s)∑p∈P(r)∑j∈S(p)∖{s}∑i∈R(j)κCp(xsrp(t)λs(t)xjip(t)λj(t)−λ2s(t)xsrp(t)xjip(t)). |
Hence
| dV(t)dt=−∑s∈S∑r∈R(s)∑p∈P(r)κλ2s(t)xsrp(t)(1−∑j∈S(p)∑i∈R(j)xjip(t)Cp)+∑s∈S∑r∈R(s)∑p∈P(r)∑j∈S(p)∖{s}∑i∈R(j)κxsrp(t)xjip(t)2Cp(λs(t)−λj(t))2. |
Thus, dV(t)/dt≤0 since ∑j∈S(p)∑i∈R(j)xjip(t)≤Cp,p∈P, and dV(t)/dt=0 if and only if λs(t)=λj(t)=λ∗, ∑j∈S(p)∑i∈R(j)x∗jip=Cp (i.e., the equilibrium point (x∗,λ∗)). Therefore, from the Lyapunov stability theory [53] the equilibrium point (4.7), (4.8) of the dynamic system (4.1)–(4.4) is asymptotically stable. All the trajectories along (4.1)–(4.4) eventually converge to the optimum of the resource allocation problem (3.3). The result is obtained.
In the practical implementation, the resource allocation scheme is updated according to the discrete form of the proposed algorithm. That is, at time t=1,2..., each physical machine p updates its resource allocation for component r of application s according to the following expression.
| xsrp[t+1]=((1−θ)xsrp[t]+θ˜xsrp[t]+θκxsrp[t](λs[t]−ξp[t]))+xsrp[t]−ε, | (4.10) |
| ˜xsrp[t+1]=(1−θ)˜xsrp[t]+θxsrp[t], | (4.11) |
| ξp[t]=∑j∈S(p)∑i∈R(j)xjip[t]λj[t]Cp. | (4.12) |
Here, we introduce an augmented variable ˜xsrp[t], which is considered to be the optimal allocation estimation for resource allocation xsrp[t]. Therefore, a low-pass filtering scheme is added to the original algorithm, where θ is the low-pass filtering parameter. By applying low-pass filtering approach, the augmented variable is assisted to remove possible oscillation due to the fact that the model is not strictly concave and optimal resource allocation is not necessarily unique, but not to change optimal resource allocation.
The price paid by the enterprise user for each application follows the rule
| λs[t]=wsmax{η,ys[t]}, | (4.13) |
| ys[t]=∑r∈R(s)∑p∈P(r)xsrp[t]. | (4.14) |
The practical implementation of the proposed resource allocation algorithm is summarized as follows:
Step 1: Initialize variables and parameters. Select step size parameter κ and small constants ε,η. At time t, initialize the resource allocation xsrp[t] for component r of application r by physical machine p.
Step 2: Calculate the price that the enterprise user should pay to the physical machine p. At time t, application s obtains the total resource allocation ys[t] for all its components from its available physical machines, and calculates the price λs[t] that should be paid for using the resource ys[t].
Step 3: Calculate the expected price of each physical machine. At time t, physical machine p calculates its expected price ξp[t].
Step 4: Update the resource allocation. At time t+1, physical machine p updates its resource allocation xsrp[t+1] for component r of application s.
Step 5: Set the stop criteria. When the algorithm reaches equilibrium, the iterative process can be stopped to obtain the optimal resource allocation.
In each iteration, the enterprise user separately calculates the price it should pay for each application when obtaining resources from its physical machines and communicates the price to the resource scheduler. Each physical machine updates its resource allocation based on the price paid by the enterprise for each application and reports the optimal resource allocation to the resource scheduler. The iterative process described above is repeated many times until the equilibrium is finally reached.
In this section we consider other forms of utility functions and discuss the proposed resource allocation scheme. We follow the well known α-fairness utility functions used for resource allocation in IP wired and wireless networks [54], which are summarized as the following form
| Us(ys)={wslogys, if α=1,wsy1−αs1−α, if α>0andα≠1, | (5.1) |
where α is the well known fairness parameter. If we choose different value of parameter α, we can achieve different objective of fair resource allocation. For example, we have achieved proportional fairness of resource allocation among applications when choosing α=1. We can also achieve harmonic mean fairness if we choose α=2. And, if α→∞, max-min fairness for resource allocation of the physical machines can be achieved when the enterprise user deploys its applications into the cloud.
As for the generalization-form resource allocation model (3.3) with the above utility functions, the objective is also concave but not strictly concave with respect to variables xsrp, thus the optimal resource allocation can also be obtained by following the aforementioned analysis approach. In details, the optimal resource allocation y∗s for each application i is
| y∗s=w1/αs∑p∈PCp∑s∈Sw1/αs, | (5.2) |
and the optimal price μ∗p charged by each physical machine p is also equal to the optimal price λ∗s paid by the enterprise user for its physical machines, that is,
| λ∗s=μ∗p=(∑s∈Sw1/αs∑p∈PCp)α. | (5.3) |
Then the optimal resource allocation depends not only on the total payment for applications and the total resource capacity of all physical machines, but also on the the fairness parameter α, i.e., other fairness goals of resource allocation can also be achieved if we choose different fairness parameters accordingly.
As for the extended form of utility function (5.1), we modify the original resource allocation scheme and propose an improved resource allocation algorithm. When an enterprise user deploys its applications into the cloud, each physical machine p updates its resource allocation for component r of application s with the following rule
| ddtxsrp(t)=κxsrp(t)(λ1αs(t)−ξp(t))+xsrp(t)−ε, | (5.4) |
| ξp(t)=∑j∈S(p)∑i∈R(j)xjip(t)λ1αj(t)Cp. | (5.5) |
And the price that the enterprise user pays to the physical machines is
| λs(t)=wsmax{η,ysα(t)}, | (5.6) |
| ys(t)=∑r∈R(s)∑p∈P(r)xsrp(t). | (5.7) |
Substituting (5.5) into (5.4) and setting (5.4) to zero, we can obtain the equilibrium of the dynamic system described by the improved algorithm, which is also equal to optimum (5.2), (5.3) of the generalization-form resource allocation model with the extended form of utility function (5.1). Furthermore, by applying the asymptotic stability approach for the continuous dynamic system, we also deduce that the equilibrium (5.1), (5.3) of the dynamic systems (5.4)–(5.7) described by the proposed algorithm is also asymptotically stable. All the trajectories along (5.4)–(5.7) eventually converge to the optimum of the resource allocation problem (3.3) with utility functions (5.1).
In this section we will analyze the performance of the proposed resource allocation scheme for virtual machines placement. We first consider a simple scenario and discuss the performance of resource allocation scheme, then we will further investigate the performance in some large scale scenarios.
Consider an enterprise user deploying its four applications into a cloud data center, where application 1 and application 3 are both composed of only one component, and application 2 and application 4 both consist of two components. Each component of an application is packaged separately into a virtual machine. There are two physical machines in the cloud data center to complete the deployment of virtual machines.
We all know that CPU is an critical resource of each physical machine. Therefore, we consider the performance of the resource allocation scheme by taking the CPU resource of the physical machines as an example. Assume that the CPU resource capacity of the physical machines is C=(C1,C2)=(1600,3200)MIPS, where MIPS (million instructions per second) is an indicator of CPU operation speed. The payment of this enterprise user for its four applications to deploy into the cloud is w=(w1,w2,w3,w4)=(1000,1500,2000,2500). The step size of the resource allocation scheme is κ=0.2, the filtering parameter is θ=0.2, and the positive constants are η=ε=0.01.
Here we consider the proportional fairness (i.e., α=1) of resource allocation among applications, and depict the performance of the proposed resource allocation scheme in Figure 2. It is not hard to find that the resource allocation scheme can converge to the equilibrium within a certain number of iterations, which is also verified through theoretical analysis in Theorem 3. The optimal prices that the enterprise user has to pay for the physical machines when placing virtual machines and obtaining resource are also illustrated in this figure. We can find they are all equal to the optimal price that each physical machine charges, which has been discussed in Theorem 2. Indeed, the optimal price obtained from this scheme is also equal to the value which is derived from the equation (3.16) (i.e., μ∗=∑s∈Sws/∑p∈PCp=7000/4800=1.4583).
Meanwhile, we give the equilibrium value obtained by the resource allocation scheme in Table 1. We also list the optimal solution solved by nonlinear programming software LINGO in the table. We can observe that the proposed scheme is efficient to achieve the optimal resource allocation for virtual machines placement into the cloud data center.
| variable | x∗111 | y∗1 | x∗211 | x∗222 | y∗2 |
| algorithm | 685.64 | 685.64 | 335.30 | 693.27 | 1028.57 |
| LINGO | 685.71 | 685.71 | 239.96 | 788.61 | 1028.57 |
| variable | x∗312 | y∗3 | x∗411 | x∗422 | y∗4 |
| algorithm | 1371.51 | 1371.51 | 579.09 | 1135.20 | 1714.29 |
| LINGO | 1371.43 | 1371.43 | 674.32 | 1039.96 | 1714.29 |
We know there are also some efficient VM placement methods for cloud data centers by applying genetic algorithms. For example, in [37] the authors present an energy-efficient VM placement method for cloud data centers by using a hybrid genetic algorithm. We also investigate the resource allocation for VM placement in the cloud center using Particle Swarm Optimization (PSO), a genetic algorithm which was first proposed by Kennedy and Eberhart [55]. In the PSO-based resource allocation scheme, the fitness function can be formed by the objective of the resource allocation model and its constraints, which is similar to that in [56]. The PSO strategy parameters are chosen as c1=c2=2 and ω=1 so as to guarantee the convergence [57].
In order to compare the performance, we first discuss the performance of the proposed resource allocation algorithm, obtain the simulation results with different step sizes, and depict them in the Figure 3(a). It is not difficult to find that as the step size of the proposed scheme increases, the convergence speed increases significantly. Indeed, the convergence performance of the proposed scheme mainly depends on the step size not the number of applications or physical machines. Similarly, we also select different particle swarm sizes and analyze the performance of the PSO-based resource allocation scheme, as shown in Figure 3(b). We can find that the PSO-based scheme converges faster at the beginning, but converges slower near the optimal value. At the same time, as the swarm size increases from 10 to 40, although the convergence speed of the scheme increases, it still cannot effectively converge to the global optimal value within a certain number of iterations.
Following the scenario above, we assume the four applications are all composed of two components. The first one component of these four applications is separately packaged into a virtual machine residing on physical machine 1, the second component of applications 1 and 2 is packaged into the corresponding virtual machine residing on physical machine 2, and the second component of applications 3 and 4 is packaged into the virtual machine residing on physical machine 3. The three physical machines have a capacity C=(C1,C2,C3)=(2400,1600,1600)MIPS of CPU resource to complete the deployment of virtual machines. The resource allocation scheme has the same algorithm parameters as the aforementioned simple scenario. the simulation results are illustrated in Figure 4. We can observe that the optimal resource allocation can be also achieved within a certain number of iterations.
We also analyze the performance of the proposed scheme with different step sizes, and depict the simulation results in Figure 5(a). We find that the convergence speed of the proposed scheme increases significantly as the step size increases. Meanwhile, we also study the performance of PSO-based resource allocation scheme with different swarm sizes and depict the simulation results in Figure 5(b). Similar to Figure 3, the PSO-based scheme converges faster at the beginning, but converges slower when it approaches the optimal value as it is compared with our scheme.
Now we consider the performance of the proposed resource allocation scheme for virtual machines placement of applications in the cloud data center in large scale scenarios, e.g., large numbers of applications as well as physical machines. Here, we assume each application is composed of two components. Each component is packaged into a separate virtual machine which is then placed into the physical machines in the cloud data center. We also take the CPU resource of the physical machines as an example to investigate the performance of the scheme. Each physical machine has a capacity 1600MIPS of its CPU resource. The applications are classified into four categories. The resource allocation scheme has the same parameters as the aforementioned simple scenario. We depict the evolution of agammaegated utility of applications in Figure 6. We observe that the size of applications or physical machines in the cloud data center has no obvious affect on the convergence of the proposed resource allocation scheme. The optimal objective (i.e., the agammaegated utility) increases with the number of applications or physical machines but, in all scenarios, the optimal value is obtained within almost the same number of iterations (e.g., 100 iterations).
With rapid development of the Internet and computer technology, the convenience and cost advantages brought by cloud computing have been adopted by more and more enterprises. At the same time, the resource allocation for virtual machine has become an important key to improve the efficiency and utilization of physical machines. Then, in this paper we establish a resource allocation for virtual machines placement in the cloud data center, deduce the expression of optimal resource allocation for each application, and propose a heuristic algorithm to achieve the optimal resource allocation within a certain number of iterations. We discuss the performance of the proposed resource allocation scheme through theoretical approach and further confirm it with simulation results.
The authors would like to thank the support from the National Natural Science Foundation of China (Nos.71971188, 71671159), the Humanity and Social Science Foundation of Ministry of Education of China (No.16YJC630106), the China Postdoctoral Science Foundation (No.2018T110205), the Natural Science Foundation of Hebei Province (Nos.G2018203302, G2020203005), and the project Funded by Hebei Education Department (No.BJ2017029).
The authors declare no conflict of interest.
| [1] | N. Alsaeed, M. Saleh, Towards cloud computing services for higher educational institutions: Concepts & literature review, IEEE International Conference on Cloud Computing (ICCC), 2015, 1-7, Riyadh, Saudi Arabia. |
| [2] | P. M. Mell, T. Grance, The NIST definition of cloud computing, National Institute of Standards & Technology, 2011. |
| [3] | M. Reza, Framework on large public sector implementation of cloud computing, IEEE International Conference on Cloud Computing and Social Networking (ICCCSN), 2012, 1-4, Bandung, Indonesia. |
| [4] | S. Li, Y. Zhang, W. Sun, Optimal resource allocation model and algorithm for elastic enterprise applications migration to the cloud, Mathematics, 7 (2019), 1-20. |
| [5] | S. Li, W. Sun, Utility maximisation for resource allocation of migrating enterprise applications into the cloud, Enterp. Inf. Syst., 2020. |
| [6] | P. D. Bharathi, P. Prakash, M. V. K. Kiran, Energy efficient strategy for task allocation and VM placement in cloud environment, IEEE Innovations in Power and Advanced Computing Technologies (i-PACT), 2017, 1-6, Vellore, India. |
| [7] | B. Zhang, Z. Qian, W. Huang, et al. Minimizing communication traffic in data centers with poweraware VM placement, IEEE Sixth International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, 2012, Palermo, Italy. |
| [8] | F. B. Hassen, Z. Brahmi, H. Toumi, VM placement algorithm based on recruitment process within ant colonies, IEEE International Conference on Digital Economy (ICDEc), 2016, Carthage, Tunisia. |
| [9] | M. Sindelar, P. K. Sitaraman, P. Shenoy, Sharing-aware algorithms for virtual machine colocation, ACM Symposium on Parallelism in Algorithms and Architectures, June 04-06, 2011, 367-378, San Jose, California, USA. |
| [10] |
A. Beloglazov, J. Abawajy, R. Buyya, Energy-aware resource allocation heuristics for efficient management of data centers for Cloud computing, Futur. Gener. Comp. Syst., 28 (2012), 755-768. doi: 10.1016/j.future.2011.04.017

|
| [11] |
S. B. Shaw, A. K. Singh, Use of proactive and reactive hotspot detection technique to reduce the number of virtual machine migration and energy consumption in cloud data center, Comput. Electr. Eng., 47 (2015), 241-254. doi: 10.1016/j.compeleceng.2015.07.020

|
| [12] |
N. K. Sharma, G. R. M. Reddy, Multi-objective energy efficient virtual machines allocation at the cloud data center, IEEE Trans. Serv. Comput., 12 (2019), 158-171. doi: 10.1109/TSC.2016.2596289

|
| [13] |
Z. Xiao, W. Song, Q. Chen, Dynamic resource allocation using virtual machines for cloud computing environment, IEEE Trans. Parallel Distrib. Syst., 24 (2013), 1107-1117. doi: 10.1109/TPDS.2012.283

|
| [14] |
A. Khosravi, L. L. H. Andrew, R. Buyya, Dynamic VM placement method for minimizing energy and carbon cost in geographically distributed cloud data centers, IEEE Trans. Sustainable Comput., 2 (2017), 183-196. doi: 10.1109/TSUSC.2017.2709980

|
| [15] |
S. K. Mishra, D. Puthal, B. Sahoo, et al. An adaptive task allocation technique for green cloud computing, J. Supercomput., 74 (2018), 370-385. doi: 10.1007/s11227-017-2133-4

|
| [16] | E. Mohammadi, M. Karimi, S. R. Heikalabad. A novel virtual machine placement in cloud computing, Aust. J. Basic Appl. Sci., 5 (2011), 1549-1555. |
| [17] |
S. Rahman, A. Gupta, M. Tornatore, et al. Dynamic workload migration over backbone network to minimize data center electricity cost, IEEE Trans. Green Commun. Netw., 2 (2018), 570-579. doi: 10.1109/TGCN.2017.2780133

|
| [18] | X. Meng, V. Pappas, L. Zhang, Improving the scalability of data center networks with traffic-aware virtual machine placement, Proceedings IEEE INFOCOM, 2010, 1-9, San Diego, CA, USA. |
| [19] |
W. Wang, B. Liang, B. Li, Multi-resource fair allocation in heterogeneous cloud computing systems, IEEE Trans. Parallel Distrib. Syst., 26 (2015), 2822-2835. doi: 10.1109/TPDS.2014.2362139

|
| [20] |
G. Wei, A. V. Vasilakos, Y. Zheng, et al. A game-theoretic method of fair resource allocation for cloud computing services, J. Supercomput., 54 (2010), 252-269. doi: 10.1007/s11227-009-0318-1

|
| [21] | K. Wang, W. Quan, N. Cheng, et al. Betweenness centrality based software defined routing: Observation from practical Internet datasets, ACM Trans. Internet. Technol., 19 (2019), 1-19. |
| [22] |
F. Song, Z. Ai, Y. Zhou, et al. Smart collaborative automation for receive buffer control in multipath industrial networks, IEEE Trans. Ind. Inform., 16 (2020), 1385-1394. doi: 10.1109/TII.2019.2950109

|
| [23] |
Z. Ai, Y. Zhou, F. Song, A smart collaborative routing protocol for reliable data diffusion in IoT scenarios, Sensors, 18 (2018), 1-21. doi: 10.1109/JSEN.2018.2870228

|
| [24] | F. Song, M. Zhu, Y. Zhou, et al. Smart collaborative tracking for ubiquitous power IoT in edgecloud interplay domain, IEEE Int. Things J., 2020. |
| [25] |
K. Wang, H. Yin, W. Quan, et al. Enabling collaborative edge computing for software defined vehicular networks, IEEE Netw., 32 (2018), 112-117. doi: 10.1109/MNET.2018.1700364

|
| [26] |
F. Lin, X. Lv, I. You, et al. A novel utility based resource management scheme in vehicular social edge computing, IEEE Access, 6 (2018), 66673-66684. doi: 10.1109/ACCESS.2018.2878879

|
| [27] |
G. H. S. Carvalho, I. Woungang, A. Anpalagan, et al. Intercloud and hetNet for mobile cloud computing in 5G systems: Design issues, challenges, and optimization, IEEE Netw., 31 (2017), 80-89. doi: 10.1109/MNET.2017.1600162

|
| [28] |
Z. Ai, Y. Liu, F. Song, et al. A smart collaborative charging algorithm for mobile power distribution in 5G networks, IEEE Access, 6 (2018), 28668-28679. doi: 10.1109/ACCESS.2018.2818790

|
| [29] |
F. Song, Y. Zhou, L. Chang, et al. Modeling space-terrestrial integrated networks with smart collaborative theory, IEEE Netw., 33 (2019), 51-57. doi: 10.1109/MNET.2018.1800187

|
| [30] |
F. Song, Y. Zhou, Y. Wang, et al. Smart collaborative distribution for privacy enhancement in moving target defense, Inf. Sci., 479 (2019), 593-606. doi: 10.1016/j.ins.2018.06.002

|
| [31] | C. Helene, G. L. Louet, J. M. Menaud, Virtual machine placement for hybrid cloud using constraint programming, IEEE 23rd International Conference on Parallel and Distributed Systems (ICPADS), 2017, 326-333. |
| [32] |
M. S. P. Mohamed, S. R. Swarnammal, An efficient framework to handle integrated VM workloads in heterogeneous cloud infrastructure, Soft Comput., 21 (2017), 3367-3376. doi: 10.1007/s00500-015-2014-9

|
| [33] |
S. Chaisiri, B. S. Lee, D. Niyato, Optimization of resource provisioning cost in cloud computing, IEEE Trans. Serv. Comput., 5 (2012), 164-177. doi: 10.1109/TSC.2011.7

|
| [34] |
X. Zheng, Y. Xia, Exploring mixed integer programming reformulations for virtual machine placement with disk anti-colocation constraints, Perform. Eval., 135 (2019), 1-18. doi: 10.1016/j.peva.2019.102035

|
| [35] |
B. Xu, Z. Peng, F. Xiao, et al. Dynamic deployment of virtual machines in cloud computing using multi-objective optimization, Soft Comput., 19 (2015), 2265-2273. doi: 10.1007/s00500-014-1406-6

|
| [36] |
D. Zhao, J. Zhou, K. Li, An energy-aware algorithm for virtual machine placement in cloud computing, IEEE Access, 7 (2019), 55659-55668. doi: 10.1109/ACCESS.2019.2913175

|
| [37] |
M. A. Kaaouache, S. Bouamama, An energy-efficient VM placement method for cloud data centers using a hybrid genetic algorithm, J. Syst. Inf. Technol., 20 (2018), 430-445. doi: 10.1108/JSIT-10-2017-0089

|
| [38] |
F. Stefanello, V. Aggarwal, L. S. Buriol, et al. Hybrid algorithms for placement of virtual machines across geo-separated data centers, J. Comb. Optim., 38 (2019), 748-793. doi: 10.1007/s10878-019-00411-3

|
| [39] |
X. Liu, Z. Zhan, J. D. Deng, et al. An energy efficient ant colony system for virtual machine placement in cloud computing, IEEE Trans. Evol. Comput., 22 (2018), 113-128. doi: 10.1109/TEVC.2016.2623803

|
| [40] |
F. Alharbi, Y. Tian, M. Tang, et al. An ant colony system for energy-efficient dynamic virtual machine placement in data centers, Expert Syst. Appl., 120 (2019), 228-238. doi: 10.1016/j.eswa.2018.11.029

|
| [41] | X. Wang, Z. Liu, An energy-aware VMs placement algorithm in cloud computing environment, IEEE Second International Conference on Intelligent System Design and Engineering Application, 2012, 627-630, Sanya, Hainan, China. |
| [42] |
M. A. Kaaouache, S. Bouamama, Solving bin packing problem with a hybrid genetic algorithm for VM placement in cloud, Procedia Comput. Sci., 60 (2015), 1061-1069. doi: 10.1016/j.procs.2015.08.151

|
| [43] | J. Xu, J. A. B. Fortes, Multi-objective virtual machine placement in virtualized data center environments, IEEE/ACM International Conference on Green Computing and Communications & International Conference on Cyber, Physical and Social Computing, 2010, 179-188, Hangzhou, China. |
| [44] | S. Dörterler, M. Dörterler, S. Ozdemir, Multi-objective virtual machine placement optimization for cloud computing, IEEE International Symposium on Networks, Computers and Communications (ISNCC), 2017, Marrakech, Morocco. |
| [45] | D. Jayasinghe, C. Pu, T. Eilam, et al. Improving performance and availability of services hosted on IaaS clouds with structural constraint-aware virtual machine placement, IEEE International Conference on Services Computing, 2011, 72-79, Washington, DC, USA. |
| [46] |
W. Fang, X. Liang, S. Li, et al. VMPlanner: Optimizing virtual machine placement and traffic flow routing to reduce network power costs in cloud data centers, Comput. Netw., 57 (2013), 179-196. doi: 10.1016/j.comnet.2012.09.008

|
| [47] | L. Guo, T. Yan, S. Zhao, et al. Dynamic performance optimization for cloud computing using M/M/m queueing system, J. Appl. Math., 2014 (2014), 1-8. |
| [48] |
Z. Xiao, J. Jiang, Y. Zhu, et al. A solution of dynamic VMs placement problem for energy consumption optimization based on evolutionary game theory, J. Syst. Softw., 101 (2015), 260-272. doi: 10.1016/j.jss.2014.12.030

|
| [49] |
F. Song, D. Huang, H. Zhou, et al. An optimization-based scheme for efficient virtual machine placement, Int. J. Parallel Program., 42 (2014), 853-872. doi: 10.1007/s10766-013-0274-5

|
| [50] |
D. Huang, L. Yi, F. Song, et al. A secure cost-effective migration of enterprise applications to the cloud, Int. J. Commun. Syst., 27 (2014), 3996-4013. doi: 10.1002/dac.2594

|
| [51] |
M. Chiang, S. H. Low, A. R. Calderbank, et al. Layering as optimization decomposition: a mathematical theory of network architectures, Proc. IEEE, 95 (2007), 255-312. doi: 10.1109/JPROC.2006.887322

|
| [52] | S. Li, W. Sun, Q. L. Li, Utility maximization for bandwidth allocation in peer-to-peer file-sharing networks, J. Ind. Manag. Optim., 16 (2020), 1099-1117. |
| [53] | W. E. Boyce, R. C. DiPrima, Elementary Differential Equations and Boundary Value Problems, Hoboken: John Wiley & Sons, 2005. |
| [54] |
Q. V. Pham, W. J. Hwang, Network utility maximization based congestion control over wireless networks: A survey and potential directives, IEEE Commun. Surv. Tut., 19 (2017), 1173-1200. doi: 10.1109/COMST.2016.2619485

|
| [55] | J. Kennedy, R. C. Eberhart, Particle swarm optimization, Proceeding of the 1995 IEEE International Conference on Neural Networks (ICNN), 1995, 1942-1948. |
| [56] |
S. Li, W. Sun, J. Liu, A mechanism of bandwidth allocation for peer-to-peer file-sharing networks via particle swarm optimization, J. Intell. Fuzzy Syst., 35 (2018), 2269-2280. doi: 10.3233/JIFS-172276

|
| [57] |
M. Clerc, J. Kennedy, The particle swarm-explosion, stability, and convergence in a multidimensional complex space, IEEE Trans. Evol. Comput., 6 (2002), 58-73. doi: 10.1109/4235.985692

|
| 1. | Darshan Maheshbhai Shah, M Vinayaka Murthy, Anand Kumar, 2020, A new approximation algorithm for virtual machine placement with resource constraints in multi cloud environment, 978-1-7281-9183-6, 1, 10.1109/ICAECC50550.2020.9339473 | |
| 2. | Shiyong Li, Wenzhe Li, Wei Sun, Jia Liu, Nonconvex resource allocation for inelastic enterprise applications deployment into the cloud via particle swarm optimization, 2023, 44, 10641246, 3807, 10.3233/JIFS-201239 | |
| 3. | Pundru Chandra Shaker Reddy, Yadala Sucharitha, An Energy-saving Data Transmission Approach based on Migrating Virtual Machine Technology to Cloud Computing, 2024, 17, 23520965, 573, 10.2174/2352096516666230713163440 | |
| 4. | Chayan Bhatt, Sunita Singhal, 2023, Chapter 21, 978-981-99-3249-8, 275, 10.1007/978-981-99-3250-4_21 |
| variable | x∗111 | y∗1 | x∗211 | x∗222 | y∗2 |
| algorithm | 685.64 | 685.64 | 335.30 | 693.27 | 1028.57 |
| LINGO | 685.71 | 685.71 | 239.96 | 788.61 | 1028.57 |
| variable | x∗312 | y∗3 | x∗411 | x∗422 | y∗4 |
| algorithm | 1371.51 | 1371.51 | 579.09 | 1135.20 | 1714.29 |
| LINGO | 1371.43 | 1371.43 | 674.32 | 1039.96 | 1714.29 |