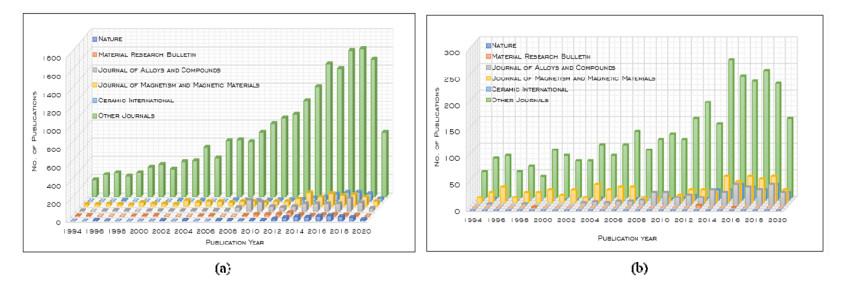
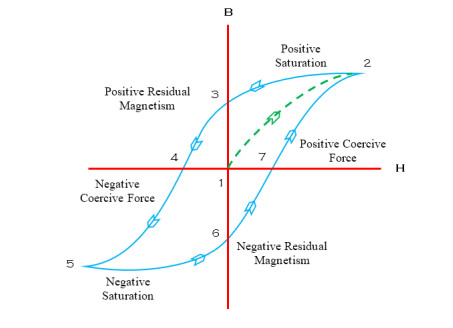
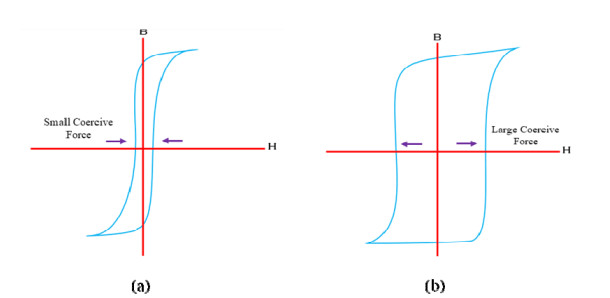
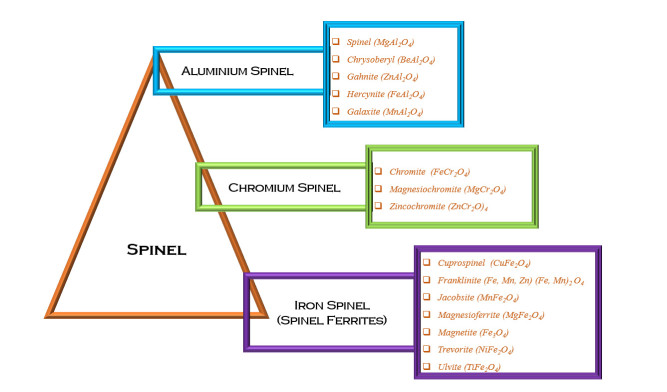
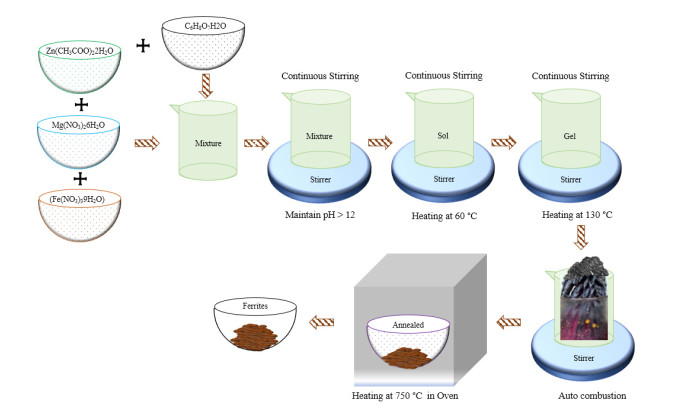
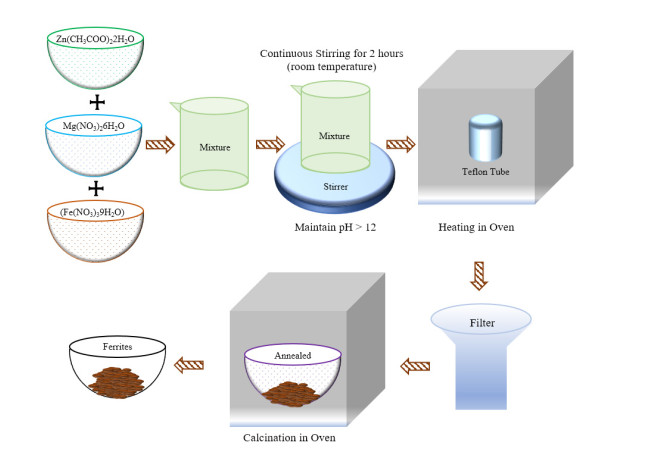
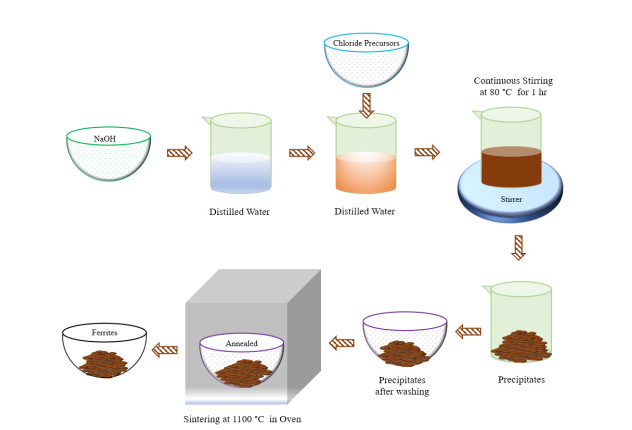
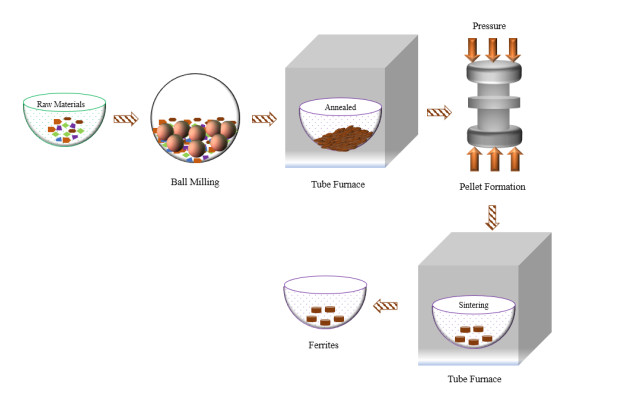
The research on ferrites is fast moving owing to their exponentially growing usage in magnetic shielding, magnetic biosensors, magnetic recording devices, information storage, mobile communication, electronic devices, gyromagnetic device, medical devices, transformers, pollution control, catalysis, and pigments. This review comprises the present state of the art on hexagonal ferrites (HFs) and spinel ferrites (SFs). The article covers the background, properties, classification schemes, synthesis and characterization of ferrites. It focuses on a comparative understanding of four synthesis routes, magnetic properties and characterization of the ferrites. The article emphases X-ray diffraction, scanning electron microscopy, transmission electron microscopy, vibrating sample magnetometer, spectroscopy, thermal analysis and vector network analyser results. The present work is meant for the faster understanding of this research area.
1.
Introduction
There has been significant progress in conducting research in the photovoltaic (PV) field over the last decade [1,2,3,4]. PV energy is generated by the conversion of sunlight and temperature. The particular interest in PV energy has driven researchers to enhance and optimize the efficiency of energy conversion within PV systems [5,6,7,8]. The autonomous functioning of a PV system in optimal conditions requires the optimization of several physical parameters related to the PV generator used [9,10,11]. Therefore, introducing an electronic converter between the PV generator and the load is essential. A step-up converter is suitable to achieve the goal of the studied work [12,13,14]. Indeed, as defined by the duty cycle, the factor characterizing the step-up device should be controlled by a specific technique of the PV power maximization [15,16].
In the literature, the numerous documented power maximization techniques are classified into three categories namely: Classical iterative methods, revolutionary methods based on artificial intelligence and hybrid methods [17,18,19,20]. The first class is mainly based on processing instantaneous values of power, currents and voltages, such as Perturb & Observe (P & O) and Incremental Conductance (INC). The second class includes techniques based on artificial intelligence, such as Artificial Neural Networks (ANN) and Fuzzy Logic (FL). On the other hand, the third class includes the techniques defined by the combination of two or more maximum power point tracker (MPPT) methods, namely the following: The hybrid two-stage adaptive method, the novel Lyapunov-based rapid and ripple-free method, and the adjustable variable step based MRAC method. In [21], the P & O method was observed with an oscillatory convergence around the maximum power point (MPP), thus causing instability and a margin of error in the found power value. These oscillations are explained by the difference between two instantaneous power values. Loukriz et al. [22] presented the INC method, known by its damped oscillation due to the small convergence step generated by the ratio of the instantaneous variation of current to the instantaneous variation of voltage. On the other hand, Goel et al. [23] displayed the ability of the ANN tool to rapidly and intelligently predict the value of the duty cycle to control the used converter. Moreover, [24] describes the converter control strategy as a set of linguistic rules that allow the value to reach the desired MPP quickly with a better performance. The hybrid, two-stage, adaptive MPPT method proposed by [25] is formed by two stages: The first stage presents a control block to find the reference voltage for each MPP; and the second stage is an adaptive model reference controller block that determines concise values of the duty cycle to hold on stable the found MPP. This strategy shows high performances under varying irradiances and temperatures. Manna et al. [26] suggested a Lyapunov-based robust model reference adaptive controller to quickly find the MPP for rapid variations in irradiance, temperature and output load. Singh et al. [27] experimented with an efficient technique for different weather scenarios defined by an adjustable P & O variable step.
In a detailed study, we separately applied P & O and ANN as an MPPT method to control a boost converter and closely observed their efficiencies and performances. We found that P & O is accurate, unstable, and sensitive to initial values while ANN is less accurate, stable, and did not require initial values. We combined these two techniques with the aim to start the convergence by ANN trained by the Levenberg-Marquardt (LM) method to approach the optimum of the duty cycle and then hand it over to P & O to continue the convergence. Therefore, the obtained method is sensitive to the irradiance changes considerably affecting the precision. These results can be explained by the high sensitivity of P & O toward the changing climatic conditions [28].
While trying to take advantage of the intelligent prediction quality of ANN and its low sensitivity towards initial values, we thought of improving its training process to enhance its low precision. In principle, the LM is the most used method to ensure the learning of ANNs. In the literature, the convergence of gradient descent methods, such as LM and Gauss-Newton (GN) tends towards a local minimum knowing that the shape of the error function to be optimized can have either a single global minimum or several local minimums [29]. This can explain the low precision observed when searching for MPP by an ANN trained by LM. On the other hand, in [30], we proposed an LM combined with simulated annealing (SA) for the parameter identification of the single diode model of the solar cell and we obtained the most accurate results compared to those reported in the literature. The interest behind the use of SA is interpreted by the existence of several local minima in the shape of the error function according to the damping factor, thus characterizing the equation of the LM method. In the present paper, for the first time, we proposed to combine the conventional GN method with the heuristic technique SA (GNSA) to guarantee global convergence during the optimization process treated in the training of ANN. Indeed, GNSA is proposed to ensure the training of the ANN network by adjusting the characteristic weights and bias wij, wjm, bij and bjm to predict the correct value of the duty cycle corresponding to a defined value of temperature and irradiance.
The three techniques (i.e., P & O, ANN and ANN-P & O) were studied to establish a comparative study and highlight the effectiveness of the proposed ANN trained by the GNSA (ANN-GNSA) approach. After an in-depth study under variable irradiance and temperature, it is observed that the proposed ANN-GNSA method demonstrates a significant efficiency, a good accuracy during the search for the MPP and a high robustness towards the meteorological condition's variation.
The main contributions of this work are presented as follows:
√ For the first time, this paper proposed the novel ANN-GNSA approach to precisely track the right MPP into a PV system based on a step-up converter with a high speed of convergence under variable irradiance and temperature values.
√ The idea behind the proposition of the improved GNSA to train the ANN network is explained by its descent directions quality guided by the globally convergent SA method to adjust correctly the weights and the bias of the hidden and the output layer of ANN tool at each iteration.
√ A fair comparison is carried out between the outcomes of the proposed method and those obtained by the P & O, ANN and ANN-P & O approaches to demonstrate the high performances of ANN-GNSA in terms of its outstanding accuracy and the speed of convergence toward the desired MPP.
• First, the ANN-GNSA is studied at fixed meteorological conditions (G = 1000 W/m2 and T = 25℃), where it reaches the right MPP = 18.59 W during a convergence time of 0.04832 s.
• The proposed method controls the step-up converter under variable irradiances G = [200 W/m2, 300 W/m2, 700 W/m2, 1000 W/m2, 800 W/m2, 400 W/m2], with an efficiency of 99.54% and under variable temperatures T = [15℃, 35℃, 45℃, 5℃] with an efficiency of 99.98%. The tracking of MPP in the both cases is ensured with a high speed compared to P & O, ANN and ANN-P & O.
2.
Materials and methods: Solar power system
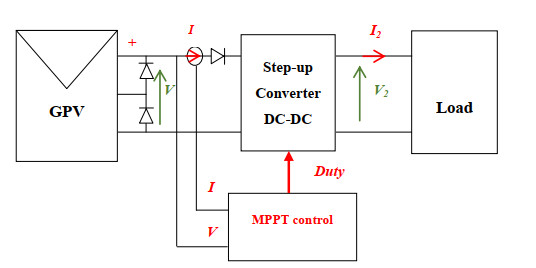
The functioning within a direct connection between a PV generator (GPV) and a load is carried out according to a non-optimal power. Certainly, the power transmitted by a GPV to the output might not align with the maximum power [31].
For this purpose, it is essential to utilize an impedance adaptation stage in direct-direct mode (DC-DC) in order to optimize the power at the output of the GPV. In this context, a step-up (Boost) chopper-type static electronic converter presents the most appropriate device for this work. A suitable MPPT settling the duty cycle of the boost device to its optimal values presents the appropriate solution to maximize the power and enable the optimal operation of the PV system.
2.1. Photovoltaic module modeling
A PV module is a collection of solar cells generating continuous electrical energy. The mode of connection of the cells, either in series or in parallel, is carried out according to the energy requirement of the PV voltage or the PV current [32].
The equivalent circuit of a PV module based on a single diode is simply the same circuit of the PV cell but scaled by Ns. The latter presents the count of solar cells linked in series. The multiplication by Ns is applied for series resistance (Rs), parallel resistance (Rsh) and the diode's ideality factor (n) [33].
Iph is the photocurrent, Is denotes the diode's saturation current, IPV indicates the PV current and VPV presents the PV voltage.
The mathematical equation deduced from the electrical characterization of the PV module, formulating Rs, Rsh, Iph, Is and n parameters as a function of IPV and VPV is presented by Eq 1 [34].
where Vth is the thermal voltage calculated using (A. T)/q, A presents the Boltzmann constant equal to 1.3806503 × 10-23 J/°K, q denotes the charge of the electron equal to 1.60217646 × 10-19 C and T is the temperature of the cell measured in Kelvin.
The expression of the five intrinsic parameters of the PV module in terms of climatic factors is crucial to establish a faithful representative model. Eqs (2) and (3) allow the modelling of a GPV, and show the relation with the irradiance (G) and the temperature (T) [35,36]:
where ΔT denotes the variation between the given T and Tn which is the nominal value of T, Voc, n is the nominal value of the open circuit voltage, Gn presents the nominal value of the irradiation, IPV, n indicates the nominal value of the photovoltaic current, Ki is the coefficient of the current and Isc, n presents the short circuit current of the solar cell.
2.2. Electronic boost converter
In this study, a boost type static electronic converter was used to increase the energy coming from the module intended to supply the output load. Figure 3 illustrates an electrical circuit of the boost converter based on an inductance L, an input capacitance Cint, an output capacitance Cout, a diode D, and a Mosfet K controlled by the duty cycle at its trigger [37].
VPV is the generated voltage by the PV module, Vs is the voltage at the output load and ipv is the input current.
The duty cycle D is calculated as follows:
where VD is the diode voltage, Vs is the output voltage at the load, Vsw is the Mosfet voltage and VPV is the voltage at the output of the PV module.
The inductance L is found by Eq 5 using ripple current inductors ΔiL [38]:
where fs is the switching frequency of the step-up device.
The value of the input capacitance can be found by the following equation [38]:
3.
MPPT control
3.1. Principal of MPPT technique
To guide the module towards its operating MPP, the power optimization process requires a specific mechanism called the "maximum power point tracker" (MPPT) settling an adaptation stage [39,40,41].
To achieve this, the implementation of a specific MPPT method is crucial. The most prevalent power maximization methods reported in the literature include the following:
• The conventional perturbation & observation (P & O) method,
• The classical artificial neural network (ANN) method,
• The ANN in conjunction with the P & O method.
These methods have been studied to underscore the performance of the novel ANN-GNSA methods.
3.2. Perturbation & Observation method
As its name indicates, the P & O method applies perturbations at the VPV voltage and observes the sign of the instantaneous power variation in order to decide the convergence direction [21].
The perturbation is ensured by applying either positive or negative adjustments, depending on the convergence orientation towards the MPP point. This process first begins by incrementing the voltage by adding a positive step. This increment addition operation is adopted if the adjusted value of the generated power is always positive. Once this variation turns negative, the voltage is either decreased or increased by either a negative step or by a positive step, respectively, depending on the position of the functioning point, placed either on the left or on the right of the MPP, respectively.
3.3. Artificial Neural Network
Due to its black box characteristic, this tool allows us to model problems without any prior knowledge of the physical or theoretical functioning of a system. The ANN helps to establish a significant liaison between its inputs and outputs. This connection is ensured by updating the characteristic parameters, named "weights" (wij and wjm) and "bias" (bij, bjm), thus marking its internal structure formed by layers of neurons [23].
The neural network operates as a MPPT command to automatically generate the exact duty cycle according to the temperature (T) and the irradiance (G) values given at the input. The effectiveness of an ANN highly depends on the success of the learning process as well as on the optimal number of hidden neurons, which was fixed at six neurons in this study. The learning process is generally ensured by the LM method whose training principle is based on the backpropagation technique. Typically, the inputs of the ANN network are T and G, and the output is simply represented by the duty cycle D, which is intended to control the activation of the chopper Mosfet. The proposed ANN network aimed to find the PPM point, which is illustrated as follows:
where i refers to the index of the output layer, j pertains to the index of the hidden layer, m denotes the index of the input layer, wij signifies the weight linking the hidden neurons to the output, wjm represents the weight linking the input neurons to the hidden ones, bij indicates the bias of the output neurons and bjm denotes the bias of the hidden neurons.
The generation of the exact value of the duty cycle strongly depends on the learning accuracy of the network and the optimal number of the hidden neurons. The training process mainly requires an experimental database presenting the examples (T, G), as well as the corresponding values of the duty cycle D. The database D = f (G, T) used in this paper includes 600 examples sweeping a large margin of T and G, thus allowing the network to be able to predict the exact value of D regardless of the value of T and G.
The training process is divided into two stages: the learning stage and the testing stage. During the learning stage, almost 500 examples are provided to the network during the convergence of the classical LM algorithm. During this phase, the network intelligently learns how to predict the value of the D factor according to T and G, which are given as inputs. The prediction capacity and efficiency of the network are demonstrated during the test phase using 100 examples of data D = f (G, T), which are completely different from the examples already processed during the learning stage.
The studied objective function "mean of sum squared errors (MSSE)" is defined as follows [42]:
where N is the number of examples, Ns is the number of output neurons, r denotes the index of the used target data, I indicates the index of the used output, Dpredicted presents the output value computed by the network and Dtarget is the target value of the output.
3.4. ANN in conjunction with P & O
The principle of this approach consists of starting the execution of the algorithm with the ANN model. The predicted value of D, which is close to the optimal one, is taken by the P & O method as an initial value to continue its convergence and judiciously seek the exact value of D corresponding to the MPP [43].
After correctly training the ANN network with approximately 600 examples of D = f (T, G) during the two phases (i.e., learning and testing in the optimization process and identification of the correct values of the weights and the bias), the ANN tool provides the well-determined wij, wjm, bij and bjm, which are able to predict the correct value of the duty D for any value of T and G.
The ANN executed first in the ANN-P & O algorithm is merely presented as a feedforward equation Eq 8 based on the well-identified wij, wjm, bij and bjm, thus resulting from the training process [44].
I denotes the index of the output neurons, j presents the index of the hidden neurons, m is the index of the input neurons, yi indicates the output of the network, xm is the inputs of the network [T, G], Fs is the activation function of the output neurons, Fc is the activation function of the hidden neurons and Nc is the number of hidden neurons.
3.5. Proposed method: ANN trained by GNSA
3.5.1. Gauss-Newton method associated with the heuristic Simulated Annealing (GNSA)
The GN method is a conventional iterative technique aimed to ensure a parameter identification using descent directions dn. In this paper, GN is used to train the ANN network through the adjustment of the weights and the biases wij, wjm, bij and bjm at each iteration n during the optimization process of the MSSE error function, according to the following expressions cited in [45]:
where dn is the descent direction at an iteration n, J is a matrix formed by four Jacobeans or the first four derivatives functions of Eq 8, J' presents the transpose of the Jacobean, α indicates either the step size factor or the length of descent direction, ϵ denotes the generated error between the computed Eq 8 and the experimental Dtarget, θ is the vector of the fours weights and biases to be adjusted [wij, wjm, bij, bjm] and n is the number of iterations.
The convergence of the GNSA algorithm requires declares the initial value of θ and the expression of either the four first derivatives or the Jacobeans "J" of Eq 8 at the start of its code. The latter presents D(θ). Each Jacobean among the four ones is obtained by deriving D(θ) according to a parameter from the four (wij, wjm, bij, bjm) parameters, such as: J = [δD/δwijδD/δwjmδD/δbijδD/δbjm]. During its execution, at an iteration n, GNSA determines the optimal value of αn by the SA technique and multiplies this value to the calculated value of the descent direction dn (Eq 10). The resulting value is added to the previously found value of θn to generate the adjusted value θn+1 to be processed during the next iteration. Just after, the iteration of n increments and this principle of GNSA functioning loops until finding the good value of θ, corresponding to the minimum error of MSSE.
The SA approach was chosen after a further study of the behavior of MSSE according to large marge of α values at each iteration n of GNSA convergence during the training of the ANN. From this, the MSSE is observed with many local minima. To reach the global minimum, the SA is executed at each run of GN to find the most precise α value that leads to a good identification of the weights and the biases wij, wjm, bij and bjm. This combination between the GN and SA techniques defined by GNSA is used in this research as a new neural network training approach presented by the enhanced ANN-GNSA method.
3.5.2. The flowchart of ANN-GNSA
The training process of the ANN by the novel optimization GNSA technique is illustrated in the following flowchart and then explained in detail step by step.
Step 1: - Give the experimental samples of the inputs (T, G) and the output D,
- iteration n = 1,
- Simultaneously start the two stages of learning and the test,
Step 2: - Learn the ANN model by the improved GNSA method using the characteristic equations Eq. 9 and Eq. 10 to adjust the four parameters θ = [wij, wjm, bij, bjm],
-The learning phase is carried out using its own experimental data of D and (T, G), fixed at 500 examples,
Step 3: - Compute the MSSElearning criterion at an iteration n based on 100 examples of test.
Step 4: - Give the adjusted weights θn at an iteration n,
Step 5: - Compute the feedforward equation Eq 8 based on the learning examples and by using the adjusted weights θn at a fixed iteration n,
- Compute the feedforward equation Eq 8 based on the 100 examples of the test data and by using the adjusted weights θn obtained at the same iteration n,
Step 6: - Compute the H(n) = MSSEtest criterion,
Step 7: - If H(n) < H(n - 1)
• Reset a counter variable "c = 0",
• Increment the iteration n = n + 1,
• Loop to step 2.
- Otherwise, increment the counter variable c = c + 1
Step 8: - If c different to 6
• Loop to step 2,
- Otherwise, if c equal to 6
• Stop the training process,
Step 9: Give the optimal and the well-adjusted value of the θ parameter.
4.
Results and discussions
To emphasize the efficiency of the new method, three techniques (P & O, ANN and ANN-P & O) have been examined in a detailed study to compare their results with those obtained by the new ANN-GNSA method.
4.1. Simulated modeling of the photovoltaic system under Simulink
The used PV module is Solarex MSX-20L. It is comprised of 36 cells attached in series and characterized by the parameter's values shown in Table 1. On the other hand, the overall parameters values characterizing the structure of the step-up converter is shown in Table 2.
The control of a PV system is given by the "MPPT" subsystem which contains the code of the algorithm being processed (P & O, ANN, ANN-P & O or ANN-GNSA). The load connected to the output is a 30 Ω resistor.
Equations (1), (2) and (3) have been implemented as blocks in the "Solarex module" subsystem to emulate the PV module, as shown in Figure 11.
The graphical presentation of the boost converter is shown in the model illustrated in Figure 4. The corresponding model is presented by the hereby illustration.
4.2. Training process of the ANN-GNSA by D= f (G, T) data set
A fixed value of the pair (G, T) corresponds to a given value of the response IPV(VPV). In this study, several responses measured experimentally for 600 different values of the pair (G, T) of the Solarex module were taken into consideration. Figures 13 and 14 show some experimental curves of IPV(VPV) for the variables G and T.
In order to extract all 600 values of D to be called out during the training of ANN at its output, we proposed to execute a P & O algorithm to generate the corresponding value of D for a precise curve of PPV (VPV). PPV is obtained by multiplying the VPV and the IPV. The P & O algorithm used is performed 600 times for 600 different PPV (VPV) curves obtained for 600 different values of T and G. The examples considered during the training process are formed by (G, T) and D.
Five hundred examples of D = f (G, T) are used during the learning of ANN-GNSA and 100 examples D = f (G, T) are employed during the test of its effectiveness.
The number of hidden neurons have been judiciously studied by observing MSSEtest for different number of hidden neurons, where 15 is the optimal number at which the obtained MSSEtest is the lowest one, as shown in Figure 15.
The learning process of ANN-GNSA is based on the minimization of the objective function MSSElearning. Figure 16 shows a decreasing curve until the iteration 270. The learning stop is decided at iteration 223 instead of 270 to avoid over-learning caused by the memorization of the network of the set of examples D = f (G, T), which leads to an erroneous prediction of the values of D at the output.
A good decision of the learning stop is made based on the convergence of ANN-GNSA during the test phase. Indeed, when the MSSEtest curve successively increases six times during a decrease of MSSElearning, the learning of the ANN should stop (Figure 17).
The values of D found by ANN-GNSA are shown in Figure 18. An illustration of the target values and the predicted values of D in the same figure shows the compatibility amongst the two, which proves the effectiveness of ANN-GNSA.
4.3. Study of the generated PV power controlled by the proposed ANN-GNSA technique
4.3.1. For climatic conditions: G = 1000 W/m2 and T = 25℃
To shed light on the exact maximum power value reached by each MPPT method (P & O, ANN, ANN-P & O or ANN-GNSA), the PPV have been presented according to time in Figure 19. The real target maximum power PPV corresponding to G = 1000 W/m2 and T = 25℃ is set at 18.59 W. As it is clearly seen, the ANN-GNSA method runs into an MPP equal to 18.59 W during 0.04382 s as compared to 18.55 W at 0.06667 s for the ANN-P & O, 18.28 W at 0.08008 s for the ANN and a range of power [18.31 W – 18.57 W] during [0.05808 s – 0.09156 s] for the P & O. Therefore, the proposed MPPT technique is the fastest and the most precise to track the right MPP value.
The generated value of the control factor D of the step-up converter varies depending on the used MPPT method. Indeed, Figure 20 shows that the values of D given by the P & O are changeable, thus leading to oscillations at the PPV curve (Figure 19). D is fixed at 0.3103 for the ANN and at 0.28 for the ANN-GNSA, where the second one is best explained by the achieved power PPV = 18.59 W, which is considered the desired value. On the other hand, the ANN-P & O starts from the value of D = 0.3103 generated by the ANN and converges to a value of D = 0.2863 close to that provided by the ANN-GNSA. From these observations, we deduce that the value of D = 0.28 is the most optimal value for G = 1000 W/m2 and T = 25℃.
In Figure 21, the evolutions of PPV(VPV) obtained by the four studied MPPT methods were also taken into consideration. In the latter a vertical offset of 0.5 W is established between the four curves to shed light on the tracking accuracy provided by the improved ANN-GNSA method.
4.3.2. For variable values of G and T = 25℃
The P & O, ANN and ANN-P & O methods can't correctly achieve the right MPPs, as is the case of G = 300 W/m2 and G = 400 W/m2. On other hand, the ANN method is less efficient at tracking the desired MPPs; it remains stuck in its neighborhood, especially in the case of G = 200 W/m2, G = 300 W/m2, G = 1000 W/m2 and G = 400 W/m2. However, the ANN-P & O and the proposed ANN-GNSA are more efficient in reaching the correct MPP values.
To evaluate the performance of the P & O, ANN, ANN-P & O and ANN-GNSA techniques to reach to optimal value of MPP, we are based on the convergence time to be concluded from Figure 22 and on the tracking efficiency η to be calculated from the obtained maximum PPV (MPP) of each MPPT method through the following expression [46]:
where PPVmean is the mean PV power delivered by the photovoltaic module, and PPVmax is either the maximum PV power or the MPP.
Table 3 shows the optimal power MPP to achieve at each irradiance, as well as the maximum power generated by each method among the four methods. The quality of the tracking of MPP by each technique is illustrated by the calculated efficiency values and by the reached convergence time (tc).
The P & O, ANN and ANN-P & O approaches take the longest time to reach the MPPs with a significant gap compared to their target values. The proposed ANN-GNSA is faster and tracks the MPP with high efficiency. The convergence time margins for the P & O are [0.1095 s-0.1152 s], [0.5772 s-0.5831 s], [1.045 s-1.047 s], [1.541 s-1.549 s], [2.025 s-2.039 s] and [2.598 s-2.604 s]. For the ANN method, the convergence times are 0.0239 s, 0.5659 s, 1.038 s, 1.547 s, 2.032 s and 2.606 s and for the ANN-P & O method, the convergence times are 0.1766 s, 0.6028 s, 1.105 s, 1.66 s, 2.082 s and 2.624 s. The speed of tracking the MPP by the proposed ANN-GNSA method is considered faster than the other three techniques for G set at (1000 W/m2, 800 W/m2 and 400 W/m2), as it is shown by the convergence times: 1.517 s, 2.005 s, 2.594 s. For a G defined at (200 W/m2, 300 W/m2 and 700 W/m2), the ANN is observed faster than the ANN-GNSA, though less precise in the reached MPP values. The MPP search efficiencies are as follows: 96.93% for the P & O, 92.34% for the ANN, 97.28% for the ANN-P & O and 99.54% for the proposed approach. From these all outcomes, the ANN-GNSA demonstrates its outstanding and its superiority to track the optimal MPP with a high efficiency during less convergence time.
4.3.3. For variable values of T and G = 1000 W/m2
From Figure 24 and Table 4, the ANN-GNSA outperforms the other comparative methods in terms of the convergence times and the efficiency. Indeed, the proposed method has an efficiency of 99.98% as compared to 99.87% for the P & O, 95.98% for the ANN and 99.16% for the ANN-P & O. Moreover, the ANN-GNSA demonstrates its high speed in tracking the MPP for different temperature values: For T = 15℃ the tc = 0.2096 s, for T = 35℃ the tc = 0.8198 s, for T = 45℃ the tc 1.549 s and for T = 5℃ the tc = 2.301 s.
5.
Conclusions
A novel and enhanced method, named the ANN trained by GNSA, is proposed in this paper to control a step-up converter within a PV system under varying irradiances and temperatures. The ANN-GNSA is evolved to ensure the fast and accurate tracking of the MPP, under variable irradiance and temperature values, without oscillations. Some MPPT methods such as the P & O, ANN and ANN-P & O are used to shed light on the performances of the proposed controller. For a fixed G = 1000 W/m2 and T = 25℃, the ANN-GNSA has the smallest tracking time (0.04382 s) compared to other MPPT methods [0.05808 s – 0.09156 s] for the P & O, 0.08008 s for the ANN and 0.06667 s for the ANN-P & O. Under a variable irradiance, the obtained efficiency is 99.54% compared to 96.93% for the P & O, 92.34% for the ANN and 97.28% for the ANN-P & O; on other side, the variable temperature is equal to 99.98% as compared to 99.87% for the P & O, 95.98% for the ANN and 99.19% for the ANN-P & O. By varying the irradiance in the margin [200 W/m2, 300 W/m2, 700 W/m2, 1000 W/m2, 800 W/m2, 400 W/m2], the proposed MPPT controller converges faster toward the MPP with convergence times of 0.1 s, 0.5887 s, 1.04 s, 1.517 s, 2.005 s and 2.594 s, respectively. A similar behavior is observed by varying the temperature in the margin [15℃, 35℃, 45℃, 5℃]; the convergence times are 0.2096 s, 0.8198 s, 1.549 s and 2.301 s, respectively. From these outcomes, the enhanced ANN-GNSA is considered a promising MPPT technique due to its outstanding performance under variable irradiances and temperatures.
In a future study, we will lead a comparative study of the behavior and the tracking time of the ANN-GNSA implemented on FPGA, Arduino and on a microcontroller.
Use of AI tools declaration
The author declares that Artificial Intelligence (AI) tools are not used in the creation of this article.
Conflict of interest
The author declares that there is no conflict of interest in this paper.









 DownLoad:
DownLoad: