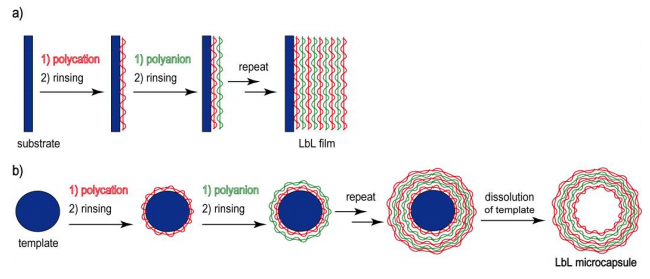
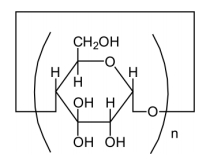
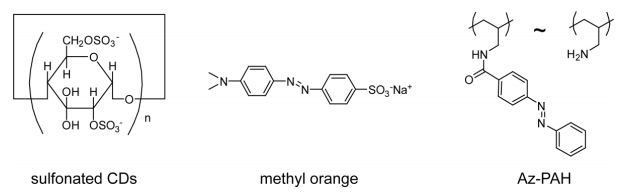
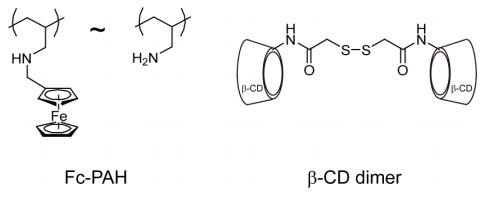
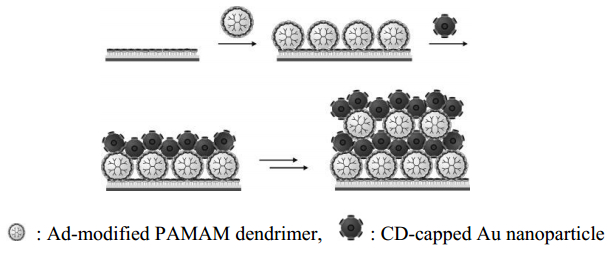
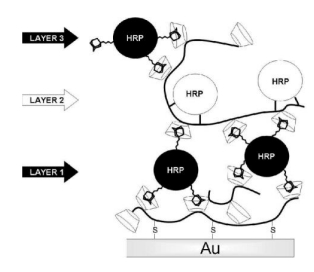
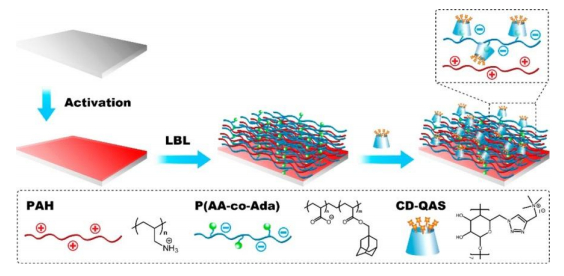
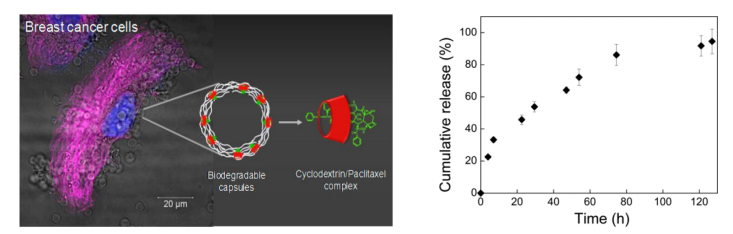
This article reviews the synthesis and applications of cyclodextrin (CD)-containing layer-by-layer (LbL) films and microcapsules. CD-containing LbL films and microcapsules have been synthesized through the electrostatic interactions between charged CDs and polyelectrolytes or the formation of host–guest complexes. In the former strategy, sulfonated and carboxylated CDs are often combined with oppositely charged polyelectrolytes. In contrast, in the latter strategy, CD-bearing polymers and guest-modified polymers are used as components of LbL assembly. Typical guest molecules include adamantane, ferrocene, and azobenzene derivatives. Electrochemical biosensors have been constructed by coating the surface of electrodes with CD-containing LbL films. In addition, CD-containing LbL assemblies are used as scaffolds for constructing drug delivery systems, in which hydrophobic, poorly soluble drugs are loaded on the film through host–guest complexation.
1.
Introduction
Symmetries linked to Lie groups appear naturally in many control systems problems [1,2,3,4,5,6,7,8,9,10,11,12,13]. Numerical integrators evolving on Lie groups are commonly employed to improve its accuracy, as well as to avoid singularities by working with coordinate-free expressions in the Lie algebra associated to the Lie group, on which the system evolves. Typical tasks include trajectory tracking and estimation algorithms for the pose of mechanical systems.
Optimization problems on Lie groups [14] have applications in control engineering. Indeed, there are many examples of robotic systems that possess invariant quantities steaming from existing symmetries. Invariant quantities can be used as leverage to reduce the complexity of the equations, by projecting them into lower dimensional spaces. Techniques taking advantage of symmetries have been studied in [15,16,17,18,19,20], among many others, mainly for applications in robotic and aerospace engineering and, in particular, for spacecraft attitude control and underwater vehicles [21]. Most of the applications provided in the literature focus on the single-agent situation and only a few works explore symmetry reduction in a multi-agent scenario (see for instance [22,23,24,25]). In this work, we employ symmetry reduction to study optimal control problems with broken symmetry for multi-agent systems on Lie groups, while agents avoid collisions and obstacles in the configuration space.
In [26], the authors studied symmetry reduction in optimal control problems with broken symmetry for single-agent systems. In this work, we advance on the results of [26] by considering a multi-agent scenario. Hence, a generalization of the previous variational principle and reduction by symmetries performance are needed. The results in this paper are the Lagrangian/variational counterpart of those in [22]; we also develop a discrete-time version of the results. At the continuous-time side, we obtain the Euler–Poincaré equations from a constrained variational principle while after discretizing the variational principle in time, we obtain the discrete-time Lie–Poisson equations.
The approach in this work to obtain the reduced optimality conditions is a generalization of the one followed in [26], and is as follows. First, we consider a collection of free agents evolving on a Lie group G and an artificial potential V0, used to prevent collisions with a fixed obstacle, which is not symmetry invariant. At the same time, we consider a representation of G on a dual vector space W∗ and a graph G to describe interactions between neighboring agents. Though the artificial potential is not symmetry invariant, the interaction between neighbouring agents is, which is the standard situation when the interaction is done through a potential dependent on relative positions. Coupling the artificial potential a parameter depending on vectors in W∗, we obtain a symmetry invariant potential function under the action of G. Loosely speaking, the agents are coupled with vectors in W∗ that are acted by the representation. The associated action considered at this stage restores the full Lie group symmetry in the cost function from our optimal control problem and allows us to apply the semi-direct product reduction theory [3,27,28,29,30,31,32], to obtain the corresponding Euler-Poincaré system on the semi-direct product Lie algebra g⋉W∗ at each node. This gives rise to a new system that finds no analogs in classical reduced-order models in optimal control of mechanical systems.
The paper is organized as follows, in Section 2, we introduce some preliminaries about geometric mechanics on Lie groups and Lie group actions. In Section 3.1, we present the problem together with a motivating example. In Section 4, we study the Euler–Poincaré reduction of optimal control problems for left-invariant multi-agent control systems on Lie groups with partial symmetry breaking cost functions. Furthermore, we consider the discrete-time framework and obtain the discrete-time Lie–Poisson equations in Section 5. In Section 6, an example is considered to illustrate the theory. Finally, some concluding remarks are given in Section 7.
2.
Lie group actions and representations
Consider a manifold Q to be the configuration space of a mechanical system and let it be differentiable of dimension d which can be described locally by coordinates q=(q1,…,qd). Denote by TQ the tangent bundle of Q, with local coordinates described by positions and velocities for the system, vq=(q1,…,qd,˙q1,…,˙qd)∈TQ with dim(TQ)=2d. Let T∗Q be its cotangent bundle, locally described by the positions and the momenta for the system, i.e., (q,p)∈T∗Q with dim(T∗Q)=2d. The tangent space at q∈Q has a vector space structure, and it is denoted as TqQ. The cotangent space at q∈Q is just the dual space of TqQ and is denoted as T∗qQ. The dynamics of a mechanical system is described by the equations of motion determined by a Lagrangian function L:TQ→R given by L(q,˙q)=K(q,˙q)−V(q), where K:TQ→R denotes the kinetic energy and V:Q→R the potential energy of the system. The equations of motion are given by the Euler-Lagrange equations ddt(∂L∂˙qi)=∂L∂qi,i=1,…,d, which determine a system of second-order differential equations. In case, the configuration space of the system is a Lie group, Euler-Lagrange equations can be reduced to a system of first-order ordinary differential equations.
Definition 2.1. Let G be a Lie group and Q a smooth manifold. A left-action of G on Q is a smooth map Φ:G×Q→Q, such that Φ(ˉe,g)=g and Φ(h,Φ(g,q))=Φ(hg,q) for all g,h∈G and q∈Q, where ˉe is the identity of the group G and the map Φg:Q→Q given by Φg(q)=Φ(g,q) is a diffeomorphism for all g∈G.
Definition 2.2. A function f:Q→R is called left invariant under Φg if f∘Φg=f for any g∈G.
For a finite dimensional Lie group G, its Lie algebra g is defined as the tangent space to G at the identity, g:=TˉeG. Let Lg:G→G be the left translation of the element g∈G given by Lg(h)=gh, where h∈G. Lg is a diffeomorphism on G and a left-action of G on G [33]. Its tangent map (i.e, the linearization or tangent lift) is denoted by ThLg:ThG→TghG. In a similar way, the cotangent map (cotangent lift), is denoted by (ThLg)∗, and is defined as the dual map of the tangent lift denoted by T∗hLg:T∗ghG→T∗hG, and determined by the relation ⟨(ThLg)∗(αgh),yh⟩=⟨αgh,(ThLg)yh⟩, yh∈ThG, αgh∈T∗ghG. As it is known, the tangent and cotangent lift of a Lie group action are Lie group actions as well. Here, ⟨⋅,⋅⟩:W∗×W→R with W a finite-dimensional vector space denotes the usual natural pairing between vectors and co-vectors, and defined by ⟨y,x⟩:=y⋅x for y∈W∗ and x∈W. For a matrix Lie algebra ⟨y,x⟩=yTx (see [33], Section 2.3). Using the natural pairing between vectors and co-vectors, for g,h∈G, y∈g∗ and x∈g, we write ⟨T∗gLg−1(y),TˉeLg(x)⟩=⟨y,x⟩.
Denote by ad∗:g×g∗→g∗, (ξ,μ)↦ad∗ξμ the co-adjoint operator, defined by ⟨ad∗ξμ,η⟩=⟨μ,adξη⟩ for all η∈g, where the ad:g×g→g denotes the adjoint operator on g given by the Lie-bracket, i.e., adξη=[ξ,η], ξ,η∈g. We also define the adjoint action of G on g, denoted by Adg:g→g and, in the case the Lie algebra is a matrix Lie group, it is given by Adgχ:=gχg−1, where χ∈g, and the co-adjoint action of G on g∗, denoted by Ad∗g:g∗→g∗, and given by ⟨Ad∗gα,ξ⟩=⟨α,Adgξ⟩ with α∈g∗.
For q∈Q, the isotropy (or stabilizer or symmetry) group of Φ at q is given by Gq:={g∈G|Φg(q)=q}⊂G. Since the map Φ(⋅,q)=Φq:G→Q is a continuous, Gq=(Φq)−1(q) is a closed subgroup, and thus, a Lie subgroup of G (see [34] Sec. 9.3 for instance).
Example 1. Consider the special Euclidean group SE(2) of rotations and translations on the plane. Elements on SE(2) can be expressed by transformations of R2 of the form z↦Rz+r, with r∈R2 and R∈SO(2). This transformation can be represented by g=(R,r), for R=(cosθ−sinθsinθcosθ) and r=[x,y]T. The composition law is (R,r)⋅(S,s)=(RS,Rs+r) with identity element (I,0) and inverse (R,r)−1=(R−1,−R−1r). Under this composition rule, SE(2) has the structure of the semidirect product Lie group SO(2)⋉R2. Here, as usual in the literature, we denote by ⋉ the semidirect product of Lie groups.
The Lie algebra se(2) of SE(2) is determined by se(2)={(Ab00)|A∈so(2)≃R,b∈R2}. In the following, for simplicity, we write A=−aJ, a∈R, where J=(01−10). Therefore, we denote ξ=(a,b)∈se(2). The adjoint action of SE(2) on se(2) is given by Ad(R,r)(a,b)=(a,aJr+Rb) (see [35], pp. 153 for instance), so, Ad(R,r)−1(a,b)=(a,RT(b−aJr)).
Next, we provide the infinitesimal description of a Lie group action, that will be an important concept in the remainder of the paper.
Definition 2.3. Given a Lie group action Φ:G×Q→Q, for ξ∈g, the map Φexp(tξ):Q→Q is a flow on Q, where exp is the exponential map of G. The corresponding vector field on Q, given by ξQ(q):=ddt∣t=0Φexp(tξ)(q) is called the infinitesimal generator of the action corresponding to ξ.
Definition 2.4. Let us denote the set of vector fields on a Lie group G by X(G). A left invariant vector field is an element X of X(G) such that ThLg(X(h))=X(Lg(h))=X(gh) ∀g,h∈G.
Especially, for h=ˉe, we have that a vector field X is left-invariant if X(g)=TˉeLgξ for ξ=X(ˉe)∈g. As a consequence, left invariant vector fields are identified with its corresponding element of g. Thus, for every g∈G and ξ∈g, we define the left-invariant vector field as ξ(g):=TˉeLg(ξ).
Example 2. Consider the Euclidean Lie group Rn with the sum as group operation. For all g∈Rn, the left translation Lg is the usual translation on Rn, that is, Lg(h)=g+h, h∈Rn. So that, the tangent map to Lg is the identity map on Rn, that is, T0Lg=idT0Rn, where we are using that ThRn≃Rn for all h∈Rn, since Rn is a vector space. Therefore, left-invariant vector fields are constant vector fields, that is, X=v1∂∂x1+…+vn∂∂xn for v=(v1,…,vn)∈T0Rn and x=(x1,…,xn)∈Rn.
Consider a Lie group G, a vector space W and the representation of G on W, given by ρ:G×W→W, (g,v)↦ρg(v), which is a left action, and it is defined by the relation ρg1(ρg2(v))=ρg1g2(v), g1,g2∈G. Its dual is given by ρ∗:G×W∗→W∗, (g,α)↦ρ∗g−1(α), satisfying ⟨ρ∗g−1(α),v⟩=⟨α,ρg−1(v)⟩, and it is also a left action of G now on W∗.
The infinitesimal generator of the left action of G on W is ρ′:g×W→W, (ξ,v)↦ρ′(ξ,v)=ddt|t=0ρexp(tξ)(v). For every v∈W, consider the linear transformation ρ′v:g→W, ξ↦ρ′v(ξ)=ρ′(ξ,v) and its dual ρ′∗v:W∗→g∗, α↦ρ′∗v(α). The last transformation defines the momentum map JW:W×W∗→g∗, (v,α)↦JW(v,α):=ρ′∗v(α), such that for every ξ∈g, ⟨JW(v,α),ξ⟩=⟨ρ′∗v(α),ξ⟩=⟨α,ρ′v(ξ)⟩=⟨α,ρ′(ξ,v)⟩.
For ξ∈g, consider the map ρ′ξ:W→W, v↦ρ′ξ(v)=ρ′(ξ,v) and its dual ρ′∗ξ:W∗→W∗, α↦ρ′∗ξ(α), such that ⟨ρ′∗ξ(α),v⟩=⟨α,ρ′ξ(v)⟩. Then, this satisfies ⟨JW(v,α),ξ⟩=⟨α,ρ′(ξ,v)⟩=⟨α,ρ′ξ(v)⟩=⟨ρ′∗ξ(α),v⟩. See [33] and [34] for more details on the momentum map.
Example 3. Let W=g and ρ the adjoint representation of G on W, i.e., ρg=Adg, for any g∈G. So, for α∈W∗=g∗, ρ∗ is the coadjoint representation of G on W∗, i.e., ρ∗g=Ad∗g. We also have that the infinitesimal generator for the adjoint representation is ρ′ξ=adξ for any ξ∈W (see [33], Def. 6.4, pp. 225), and it follows that ⟨JW(x,α),ξ⟩=⟨α,adξx⟩=⟨α,−adxξ⟩=⟨−ad∗xα,ξ⟩, for x∈W=g, which gives JW(x,α)=−ad∗xα.
Similarly, if now W=g∗ and the coadjoint representation of G on W is ρ, i.e., ρg=Ad∗g−1, for any g∈G, then ρ′ξ=−ad∗ξ for any ξ∈g. So, if x,ξ∈g and α∈g∗, it follows that ⟨JW(α,x),ξ⟩=⟨−ad∗ξα,x⟩=⟨α,adxξ⟩=⟨ad∗xα,ξ⟩, which gives JW(α,x)=ad∗xα.
3.
Problem formulation
3.1. Left-invariant multi-agent control systems
Denote, by N, a set consisting of s≥2 free agents, and by E⊂N×N the set describing the interaction between them. The neighboring relationships are illustrated by an undirected graph G=(N,E), where N is the set of vertices and E the set of edges for G. We further assume G is static and connected. For every agent i∈N the set Ni={j∈N:(i,j)∈E} denotes the neighbors of that agent. The agent i∈N evolves on an n-dimensional Lie group G, and its configuration is denoted by gi∈G. We denote by Gs and by TeGs=:gs the cartesian products of s copies of G and g, respectively, where e=(¯e,¯e,…,¯e) is the identity of Gs, and ¯e the identity element of G.
For each agent i∈N, there is an associated left-invariant control system described by the kinematic equations
where gi(t)∈C1([0,T],G),T∈R fixed, ui∈g is the control input and gi0∈G is considered as the initial state condition. Letting dimg=n, we can have as many basis for the Lie algebra as the number of agents. Thus, for each i∈N, we have g=span{e1,e2,…,en} and the control inputs may be described by coordinates ui=[u1i,u2i,…,umi]T, where ui(t)∈C1([0,T],g), with m≤n. Hence, the control input for each agent is given by ui(t)=ei0+m∑k=1uki(t)ek, where ei0∈g. Thus, the left-invariant control systems (3.1) for each agent i∈N can be written as
Note that the class of control systems described by (3.2) belongs to the family of underactuated control systems.
3.2. Motivating example
Following with Example 1, consider the agents i∈N and j∈Ni represented as gk=(Rk,rk), k∈{i,j}. Note that g−1igj=(RTiRj,−RTi(ri−rj)), then, Adg−1igj(1,0)=(1,JRTi(rj−ri)). The inner product on se(2) is given by ⟨ξ1,ξ2⟩=tr(ξT1ξ2) for ξ1,ξ2∈se(2) and, hence, the norm is given by ||ξ||=√tr(ξTξ), for any ξ∈se(2). For ξ=(a,b)∈se(2) we can write the norm of ξ as ||(a,b)||=√2a2+bTb. Therefore, ||Adg−1igj(1,0)||2=2+|JRTi(rj−ri)|2=2+|rj−ri|2, where we have used that R,J∈SO(2) for the last equality. Hence, it follows that |ri−rj|=√||Adg−1igj(1,0)||2−2.
The previous computation shows that, if the interaction between agents is determined by a function depending on the distances between them, that is, Vij:G×G→R, is such that Vij(gi,gj)=V(|ri−rj|) for some V:R≥0→R; then, Vij is SE(2)-invariant, that is Vij(hgi,hgj)=Vij(gi,gj). An alternative reasoning of this invariance property has been shown in [36].
Next, suppose that we wish to write the distance from an arbitrary point r∈R2 to a fixed point x0∈R2 in terms of the adjoint action. Consider ξ0=(1,Jx0)∈se(2). Then, for any (R,r)∈SE(2), we have Ad(R,r)−1(1,Jx0)=(1,RTJ(x0−r)), and, therefore, ||Ad(R,r)−1(1,Jx0)||2=2+|x0−r|2. Next, assume we have an obstacle avoidance function V0i:SE(2)→R for each agent i∈N which can be written as V0i(Ri,ri)=V(|ri|) with V:R≥0→R. Note that under this assumption, V may be chosen arbitrarily. Then, V0i is not SE(2)-invariant, but it is SO(2) invariant, i.e., V0i(R0Ri,ri)=V0i(Ri,ri) for any R0∈SO(2). Note also that SO(2) is the isotropy group for the coadjoint action, that is, SO(2)≃{g∈SE(2)∣Adg(ξ0)=ξ0}, therefore, the obstacle avoidance potential functions V0i are invariant under the left action of the isotropy group.
In this situation, one can redefine the potential function V0i to make it SE(2)-invariant as follows. Consider x0=0, so, ξ0=(R0,x0)=(−J,0)∈se(2), and ‖Ad(Ri,ri)−1ξ0‖=2+|ri|2. Hence, V0i(Ri,ri)=V(|ri|)=V(√||Ad(Ri,ri)−1ξ0||2−2). This gives a motivation to define an extended obstacle avoidance function Vexti,0:G⋉W∗→R with G⋉W∗=SE(2)⋉se(2) as Vexti,0(gi,ξ):=V(√||Adg−1iξ||2−2).
Note that the extended obstacle avoidance function possesses an SE(2)-symmetry (i.e., Vexti,0 is invariant under a left action of SE(2)) since Vexti,0∘˜Φ(h,(g,ξ))=Vexti,0(Lhg,Adhξ)=Vexti,0(g,ξ), for any h∈SE(2), with left action ˜Φ given by
3.3. Problem setting
The problem under study consists on finding reduced necessary conditions for optimality in an optimal control problem for (3.1) (or equivalently (3.2)). These solution curves should minimize a cost function and prevent collisions among agents, while they should also avoid static obstacles in the workspace.
Problem (collision and obstacle avoidance): Find reduced optimality conditions on g(t)=(g1(t),…,gs(t))∈Gs and the controls u(t)=(u1(t),…,us(t))∈gs avoiding collision among the agents and obstacles (which will be defined shortly) in the workspace, and such that (g(t),u(t))∈Gs×gs minimize the following cost function,
subject to the kinematics ˙gi(t)=T¯eiLgi(t)(ui(t)), boundary conditions g(0)=(g1(0),…,gn(0))=(g01,…,g0s) and g(T)=(g1(T),…,gs(T))=(gT1,…,gTs) with T∈R+ the final time, and under the following assumptions:
(i) There is a left representation ρ of G on a vector space V.
(ii) Ci:G×g→R are G-invariant functions for each i∈N (under a left action of G on G×g, which is given below) and are also differentiable almost everywhere.
(iii) Vij:G×G→R (collision avoidance potential functions) satisfying Vij=Vji are G-invariant functions under Φ, defined by
i.e., Vij∘Φg=Vij, for any g∈G, that is, Vij(Lg(gi),Lg(gj))=Vij(gi,gj), for any (gi,gj)∈E, j∈Ni and they are also differentiable almost everywhere.
(iv) V0i:G→R (obstacle avoidance potential functions) are not G-invariant functions and they are also differentiables almost everywhere, for i∈N.
(v) The obstacle avoidance functions V0i depend on a parameter α0∈W∗. Hence, we can define the extended potential function as Vexti,0:G×W∗→R, with Vexti,0(⋅,α0)=V0i, by making the parameter evolve - due to the group action - with initial value α0.
(vi) The extended obstacle avoidance functions are G-invariant under ˜Φ, defined by
where ρ∗g−1∈W∗ is the adjoint of ρg−1∈W, i.e., Vexti,0∘˜Φg=Vexti,0, for any g∈G, or Vexti,0(Lg(h),ρ∗g−1(α))=Vexti,0(g,α) where α∈W∗.
(vii) The obstacle avoidance potential functions are invariant under the left action of the isotropy group
Note that G×g is a trivial vector bundle over G and, in order to respect assumption (ⅱ), we define the left action of G on G×g as follows,
We further assume that each Ci:G×g→R is G-invariant under (3.8), i.e., Ci∘Ψg=Ci, for any g∈G. In addition, each agent i∈N occupies a disk of radius ¯r on G. This radius is consider to be small enough in order that all agents can be packed on G and, hence the potential functions are well defined and feasible for d(gi(t),gj(t))>2¯r for all t, where d(⋅,⋅):G×G→R denotes a distance function on G.
4.
Euler-Poincaré reduction for optimal control with broken symmetries
We next study reduced optimality conditions for extrema for the OCP. We address the problem as a constrained variational problem and obtain the Euler-Poincaré equations that extremal must satisfy in Theorem 4.1 and Proposition 4.2.
The optimal control problem (3.4) can be resolved as a constrained variational problem by utilizing the Lagrangian multipliers λgi=T∗giLg−1i(λi)∈T∗giG, where λi∈C1([0,T],g∗) into the cost functional.
Let {e1,…,em,em+1,…,en} be a basis of g∗ dual of the basis {ei} of g. Then λi=n∑k=m+1λikek, where λik are the components of the vector λi in the given basis of the Lie algebra g. Thus, we define the Lagrangian L:Gs×gs×(T∗giG)s→R by
where Vi:Gs→R,
By assumption (v), the obstacle avoidance potential functions V0i:G→R depend on a parameter α0∈W∗, so we can extend {them} to Vexti,0:G×W∗→R by making the parameter evolve under the Lie group action with α(0)=α0, and, therefore, we can consider the extended Lagrangian function on Gs×gs×(T∗giG)s×W∗,
where Lext(g,u,λ,α0)=L(g,u,λ).
By assumptions (ⅰ) to (ⅳ), and by taking advantage of the G-invariance of Ci, Vexti,0 and Vij (and so Vi), we can define the reduced extended Lagrangian ℓ:Gs−1×gs×(g∗)s×W∗→R by
defining g1 to be the identity ˉe1 on G. This is equivalent to consider the Lagrangian ˜Lext(h,u,λ,α)=Lext(ˉe1,h,u,λ,α) with h∈Gs−1. Then ℓ(g,u,λ,α) is obtained by considering a left action in each term of the sum. In fact, if Liext is each term in the sum from 1 to s in the definition of Lext, then
under the assumption that g1=ˉe1 and αi=ρ∗gi(α). Note here the slight abuse of notation regarding the positions g. In the definition of the reduced Lagrangian g∈Gs−1, while in that of the Lagrangian Lext, g∈Gs.
Theorem 4.1. For s≥2, an extremal for the OCP (3.4) satisfies the following Euler-Poincaré equations
where \mathit{\boldsymbol{J}}_W:T^{*}W\simeq W\times W^{*}\to \mathfrak{g}^{*} is the momentum map that corresponds to the left action of G on W , and it is defined through the left representation \rho of G on W , and where \Theta^{i}_{1} = 0 if i = 1 , otherwise \Theta^{i}_{1} = 1 .
Proof. Consider the variational equation
which holds for variations of g , that vanish at the endpoints, and u . Also, consider the constrained variational equation
that holds for variations of u_{i} and \alpha_{i} with \delta u_{i} = \dot{\eta}_{i}+ \text{ad}_{u_{i}}\eta_{i} and \delta \alpha_{i} = \rho'^*_{\eta_{i}}(\alpha_{i}) , where \eta_{i} is a path of \mathfrak{g}^s that vanishes at the endpoints, i.e. \eta_{i}(0) = \eta_{i} (T) = 0.
The two variational equations are equivalent since the cost functions C_i and the extended potential functions V_{i, 0}^{\text{ext}} are G -invariant, i.e. C_i\circ\Psi_g, \; \; V_{i, 0}^{\text{ext}}\circ\tilde{\Phi} = V_{i, 0}^{\text{ext}} and \langle\lambda_{g_i}, T_{\bar{e}_i}L_{g_i}u_i\rangle = \langle T^{*}_{g_i}L_{g_i^{-1}}\lambda_{g_i}, u_i\rangle = \langle\lambda_i, u_i\rangle . The variations \delta g_i of g_i induce and are induced by variations \delta u_i = \dot{\eta}_i+ \text{ad}_{u_i}\eta_i with \eta_i(0) = \eta_i(T) = 0 , where \eta_i = T_{g_i}L_{g_i}^{-1}(\delta g_i) and \delta u_i = T_{g_i}L_{g_i^{-1}}(\dot{g}_i) . Variations of \alpha_i are given by \delta\alpha_i = \rho'^*_{\eta_i}(\alpha_i) . Thus, we have
Using the variations of u_i , which are given by \delta u_i = \dot{\eta}_i+ \text{ad}_{u_i}\eta_i , applying integration by parts and by the definition of the co-adjoint action the first two terms, yield:
From the variations \delta\alpha_i = \rho'^*_{\eta_i}(\alpha_i) , the third term gives
Taking into account that T(L_{g_i}\circ L_{g_i^{-1}}) = TL_{g_i}\circ TL_{g_i^{-1}} is equivalent to the identity map on TG_i and \eta_i = T_{g_i}L_{g_i^{-1}}(\delta g_i) , the fourth term can be written as
Therefore, after performing a change of variables between indexes i and k in the fourth term, the above variational equation (4.4) yields
for i = 1 . Otherwise,
Finally, by taking the time derivative of \alpha_i = \rho_{g_i}(\alpha_0) , we have \dot{\alpha}_i = \rho_{u_i}^{\prime*}(\alpha_i) , together with \alpha(0) = \rho^{*}_{g_{0}^{i}}(\alpha_{0}^{i}).
Note that the above Euler-Poincaré equations (4.2) cannot, in fact, describe the motion properly because there are more unknowns than equations. In particular, observe that equations (4.2) together with (3.1) (or equivalently (3.2)), give rise to only two equations for the three unknown variables u_i , \lambda_i and g_i . However, we provide an additional structure to the Lie algebra, \mathfrak{g} , that allows one to decouple equations (4.2) into two equations. The next Proposition describes this process.
Proposition 4.2. If the structure of the Lie algebra permits a decomposition \mathfrak{g} = \mathfrak{r}\oplus\mathfrak{s} where \mathfrak{r} = {\rm{span}}\{e_1, \dots, e_m\} and \mathfrak{s} = {\rm{span}}\{e_{m+1}, \dots, e_n\} such that
then the Euler-Poincaré equations of motion (4.2) are given by the following equations:
where u_{i}\in \mathfrak{r} and the restrictions \big|_{\mathfrak{r}} and \big|_{\mathfrak{s}} give the projection onto \mathfrak{r}^* and \mathfrak{s}^* , respectively, with respect to the associated splitting of the dual space \mathfrak{g}^* = \mathfrak{r}^* \oplus \mathfrak{s}^* .
Remark 4. Note that this is the case for semisimple Lie algebras, they admit a Cartan decomposition, i.e., if \mathfrak{g} is semisimple, then \mathfrak{g} = \mathfrak{r}\oplus\mathfrak{s} such that [\mathfrak{r}, \mathfrak{r}]\subseteq\mathfrak{s}, \quad [\mathfrak{s}, \mathfrak{r}]\subseteq\mathfrak{r}, \quad [\mathfrak{s}, \mathfrak{s}]\subseteq\mathfrak{s}, \nonumber where the set \mathfrak{r} = \{x\in\mathfrak{g}\mid\theta(x) = -x\} is the -1 eigenspace of the Cartan involution \theta , whereas the set \mathfrak{s} = \{x\in\mathfrak{g}\mid\theta(x) = x\} is the +1 eigenspace of the Cartan involution \theta . Additionally, the Killing form is proven to be positive definite on \mathfrak{r} and negative definite on \mathfrak{s} (see, e.g., [15]). Thus, suitable candidates that satisfy the assumption of Proposition 4.2 are connected semisimple Lie groups. On the other hand, a Cartan decomposition determines a Cartan involution \theta (see, e.g., [37]). In particular, the proposed decomposition for the Lie algebra is not restrictive in the sense that the usual manifolds/work-spaces used in applications as SO(n) and SE(n) allow such a decomposition.
Proof. Given \mathfrak{g} = \mathfrak{r}\oplus\mathfrak{s} we get \mathfrak{g}^* = \mathfrak{r}^*\oplus\mathfrak{s}^* , where \mathfrak{r}^* = {\rm{span}}\{e^1, \dots, e^m\} and \mathfrak{s}^* = {\rm{span}}\{e^{m+1}, \dots, e^s\} . Thus, from (4.6) we have that \text{ad}^*_{\mathfrak{s}}\mathfrak{s}^*\subseteq\mathfrak{s}^*, \; \text{ad}^*_{\mathfrak{s}}\mathfrak{r}^*\subseteq\mathfrak{r}^*, \; \text{ad}^*_{\mathfrak{r}}\mathfrak{s}^*\subseteq\mathfrak{r}^*, \; \text{ad}^*_{\mathfrak{r}}\mathfrak{r}^*\subseteq\mathfrak{s}^* and given that u_{i}\in \mathfrak{r} , \frac{\partial C_i}{\partial u_i}\in\mathfrak{r}^* and \lambda_i\in\mathfrak{s}^* by definition we conclude that \text{ad}^*_{u_i}\frac{\partial C_i}{\partial u_i}\in\mathfrak{s}^* and \text{ad}^*_{u_i}\lambda_i\in\mathfrak{r}^*. Also, {\bf{J}}_W\Big(\frac{\partial V_{i, 0}^{\text{ext}}}{\partial\alpha_i}, \alpha_i\Big) \in \mathfrak{g}^* and \sum_{k = 1}^{s}T^*_{\overline{e}_i}L_{g_i}\bigg(\frac{\partial V_{k}}{\partial g_i}\bigg)\in \mathfrak{g}^* hence, they have a decomposition into \mathfrak{r}^* and \mathfrak{s}^* . Thus, the equations (4.2) split into the following equations
Remark 5. For the initial value problem guaranteeing a solution for the previous system of equations, we look for a solution to the equations with the initial condition u_i(0) = T_{g(0)}L_{g^{-1}(0)}(\dot{g}_i(0)) and the kinematic equation \dot{g}_i(t) = T_{\overline{e}}L_{g_i(t)}(u_i(t)) with g(0) = (g_1(0), \dots, g_s(0)) .
Remark 6. Assuming the reduced Lagrangian is hyperregular, we use the Legendre transformation and we can define the reduced Hamiltonian h: G^{s-1}\times (\mathfrak{g}^*)^s\times (\mathfrak{g}^*)^s\times W^*\to \mathbb{R} given by
where \mu = \frac{\partial \ell}{\partial u} = \left(\frac{\partial C}{\partial u}+\lambda\right)\in(\mathfrak{g}^*)^s . Under this assumption, the Euler-Poincare equations (4.2), (4.3) can be written as the Lie-Poisson equations (see, e.g., [22])
5.
Discrete-time reduced necessary conditions
In this section, we study the discrete-time reduction by symmetries for necessary conditions in the collision and obstacle avoidance optimal control problem. The goal is to construct a variational integrator based on the discretization of the augmented cost functional. Such integrator inherits discrete-time symmetries from its continuous counterpart and generates a well-defined (local) flow for reduced necessary conditions characterizing (local) extremal in the optimal control problem.
5.1. Trajectory discretization
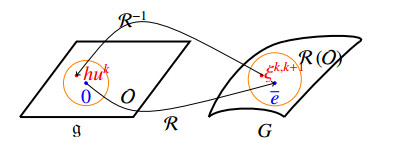
Given the set \mathcal{T} = \{t_k\in\mathbb{R}^{+}, \, t_{k} = kh\mid k = 0, \ldots, N\} , Nh = T , with T fixed (recall that T\in\mathbb{R}^{+} is the end point of the cost functional - see for instance equation (3.4)), a discrete trajectory for the agent i is determined by a set of N+1 points equally spaced in time, g^{0:N}_i = \{g^0_i, \ldots, g^{N}_i\} , where g^k_i\simeq g_i(kh)\in G , and h = T/N is the time step. The path between two adjacent points g_i^k and g_i^{k+1} must be given by a curve lying on the Lie group G . To construct such a curve we make use of a retraction map \mathcal{R}:\mathfrak{g}\to G .
Definition 5.1. A retraction map \mathcal{R}:\mathfrak{g}\to G is an analytic local diffeomorphism assigning a neighborhood \mathcal{O}\subset\mathfrak{g} of 0\in {\mathfrak g} to a neighborhood of the identity \overline{e}\in G .
The retraction map (see Figure 1) is used to express small discrete changes in the group configuration through unique Lie algebra elements given by u^k = \mathcal{R}^{-1}((g^{k})^{-1}g^{k+1})/h , where u^k\in\mathfrak{g} (see [38,39] for further details). That is, if u^{k} were regarded as an average velocity between g^{k} and g^{k+1} , then \mathcal{R} is an approximation to the integral flow of the dynamics. The difference \xi^{k, k+1}: = (g^{k})^{-1}\, g^{k+1}\in G , which is an element of a nonlinear space, can now be represented by a vector space element u^{k} . For the derivation of the discrete equations of motion, the right trivialized tangent retraction map will be used. It is the function d\mathcal{R}:\mathfrak{g}\times\mathfrak{g}\rightarrow \mathfrak{g} given by
where \eta\in\mathfrak{g} and R:G\to G the right translation on G and T\mathcal{R}(\xi)\cdot\eta is the directional derivative of \mathcal{R} at \xi in the direction of \eta (see [38,39] for the derivation of such a map). Here we use the following notation, d\mathcal{R}_\xi: = d\mathcal{R}(\xi):\mathfrak{g}\rightarrow \mathfrak{g}. The function d\mathcal{R} is linear, but only on one argument.
Remark 7. The natural choice of a retraction map is the exponential map at the identity \overline{e} of the group G, \mbox{exp}_{\overline{e}}:\mathfrak{g}\rightarrow G . Bear in mind that, for a finite-dimensional Lie group, \mbox{exp}_{\overline{e}} is locally a diffeomorphism and gives rise to a natural chart [40]. Then, there exists a neighborhood U of \overline{e}\in G such that \mbox{exp}_{\overline{e}}^{-1}:U\rightarrow \mbox{exp}_{\overline{e}}^{-1}(U) is a local \mathcal{C}^{\infty}- diffeomorphism. For an element g\in G a chart is given by \Psi_{g} = \mbox{exp}_{\overline{e}}^{-1}\circ L_{g^{-1}}.
Generally, it is not an easy task to work with the exponential map since the differential of the exponential map involves power series expansions with iterated Lie-brackets. Consequently, it will be more convenient to use a different retraction map. More concretely, the Cayley map, which is usually used in numerical integration with matrix Lie-groups configurations (see [38,39] for further details), will provide to us a proper framework in the application shown in the next Section.
5.2. Discretization of the Lagrangian function
Next, we consider a discrete cost function to construct variational integrators in the same way as in discrete mechanics [41]. In other words, consider the continuous-time Lagrangian {\bf{L}}:G^s\times\mathfrak{g}^s\to\mathbb{R} defined by the cost functional (3.4), that is,
and for a given h > 0 , we define the discrete Lagrangian L_d:G^s\times \mathfrak{g}^s\to\mathbb{R} as an approximation of the cost functional (3.4) along each discrete segment between g^{k} and g^{k+1} = g^{k}\mathcal{R}(hu^{k}) , that is,
where \kappa and \zeta are functions of (g^k, u^{k})\in G^s\times \mathfrak{g}^s which approximate the configuration g(t) and the control input u(t) , respectively, in that interval. In the following, for simplicity, \kappa will be the projection onto G^{s} and \zeta will be the projection onto \mathfrak{g}^{s} . Thus, we consider
We remark that different choices of \kappa and \zeta could result in higher-order numerical methods, such as, using the middle point rule with \kappa(g^k, u^{k}) = g^{k}\mathcal{R}(\frac{h}{2}u^{k}) .
5.3. Discrete-time optimal control problem and reduction of discrete-time necessary conditions for optimality
Next, we are going to define the optimal control problem for discrete-time systems and derive a variational integrator for L_{d}\colon G^s\times \mathfrak{g}^s\to \mathbb{R} , in a similar fashion as the variational equation presented in Theorem 4.1.
Problem: Consider the discrete-time optimal control problem for collision and obstacle avoidance of left-invariant multi agent control systems, which is given by finding the discrete configurations \{g^k\}_{k = 0}^{N} = \{(g_1^k, \ldots, g_s^k)\}_{k = 0}^{N} and discrete control inputs \{u^k\}_{k = 0}^{N} = \{(u_1^k, \ldots, u_s^k)\}_{k = 0}^{N} minimizing the discrete cost functional
subject to g_i^{k+1} = g_i^k\mathcal{R}(hu_i^k) (i.e., a first order approximation of equation (3.1)) with given boundary conditions g^0 and g^N , where h > 0 denotes the time step, \mathcal{R}:\mathfrak{g}\to G is a retraction map, u_i(0) and u_i(T) are given, and each cost function C_{i}:G\times\mathfrak{g}\to\mathbb{R} , potential functions V_{i}^{0} and V_{i} satisfy properties (ⅰ) - (ⅶ).
The discrete-time optimal control problem (5.3) can be considered as a discrete constrained variational problem by introducing the Lagrange multipliers \mu_{i}^k\in \mathfrak{g} into the cost functional. Consider the augmented discrete Lagrangian \mathcal{L}_{d}:G^s\times G^s\times \mathfrak{g}^s\times (\mathfrak{g}^{*})^s\to\mathbb{R} given by
where \xi^{k, k+1}_i = (g_i^k)^{-1}g_i^{k+1}\in G , for each i\in\mathcal{N} . Note that the last term in the augmented Lagrangian represents a first-order discretization of the kinematic constraint paired with a Lagrange multiplier in analogy with the variational equation presented in Section 4.
Now, extending the potential V_{i}^{0} , we obtain an extended Lagrangian \mathcal{L}_{ext, d}:G^s\times G^s\times\mathfrak{g}^s\times(\mathfrak{g}^{*})^s\times (W^{*})^{s}\to\mathbb{R} given by
which is invariant under the left action of G on G^s\times G^s\times \mathfrak{g}^s \times (\mathfrak{g}^{*})^s \times (W^{*})^s given by \tilde{\Phi}_{g}(h_{1}, h_{2}, u, \mu, \alpha) = (gh_{1}, gh_{2}, u, \mu, \rho_{g^{-1}}^{*}(\alpha)) by assumption (ⅵ). In particular, under assumptions (ⅳ)-(ⅵ), the extended discrete Lagrangian \mathcal{L}_{ext, d}(\cdot, \cdot, \cdot, \cdot, \alpha_0) = :\mathcal{L}_{ext, d, \alpha_0} is G_{\alpha_0} -invariant under \tilde{\Phi}_g .
The following result (Theorem 5.2) derives a variational integration for reduced optimality conditions for the discrete-time optimal control (5.3) in analogy with the results presented in Section 4. To derive the numerical algorithm, first we need the following result describing variations for elements on the Lie algebra and its relation with variations on the Lie group by using the retraction map, in addition to a property used in the proof of Theorem 5.2. Though it is a well-known result in the literature, we include it here to make the paper self-contained.
Lemma 5.1 (adapted from [38,39]). The following properties hold
(i)
where \eta^{k} = T_{g^k}L_{(g^k)^{-1}}(\delta g^k)\in\mathfrak{g} and \xi^{k, k+1} = (g^k)^{-1}g^{k+1} .
(ii)
where \mu^k\in(\mathfrak{g}^{*}) and d\mathcal{R}^{-1} is the inverse right trivialized tangent of the retraction map \mathcal{R} defined in (5.1).
Theorem 5.2. Under assumptions (i)-(vii), an extremal for the discrete-time optimal control problem (5.3) satisfies the following equations
for k = 1, \ldots, N-1 ; where \Theta^{i}_{1} = 0 if i = 1 , otherwise \Theta^{i}_{1} = 1 .
Proof. Since the cost functions and the potential functions satisfy assumptions (ⅰ) - (ⅶ), as in the continuous-time case, it is possible to induce the reduced augmented discrete Lagrangian \ell_{ext, d}:G^{s-1}\times G^s \times\mathfrak{g}^s\times(\mathfrak{g}^{*})^s\times (W^{*})^s\to\mathbb{R} as
where \bar\alpha^{k}_i = \rho_{g^{k}_i}^{*}(\alpha_i^0) for a fixed \alpha_i^0\in W^{*} satisfying \alpha_i^0 = \rho^*_{g_i^0}(\alpha_i^0) and, with a slight abuse of notation, C_{i}(u_{i}^k) = C_{i}(\overline{e}, u_{i}^k) and V_{i}^{0, ext}(\alpha^{k}_i) = V_{i}^{0, ext}(\overline{e}, \alpha^{k}_i) . Notice that, also here, g_{1}^{k} is set to be the identity element, so that we have g^{k}\in G^{s-1} .
As in the proof for Theorem 4.1, the technical part is to show that an extremal of the reduced variational equation
satisfies equations (5.6)-(5.8) for all variations of \mathcal{R}^{-1}(\xi^{k, k+1}) (induced by variations of g^k vanishing at the endpoints), u^k and \bar{\alpha}^k of the form \rho_{\eta^{k}}^{'*}(\bar\alpha^{k}) , where \eta^k\in\mathfrak{g}^s vanishes at the endpoints. Then, similarly as in the proof for Theorem 4.1, it follows that an extremal for the optimal control problem (5.3) satisfies the variational equation
for all variations of g^k (vanishing at the endpoints), \mathcal{R}^{-1}(\xi^{k, k+1}) (induced by variations of g^k ) and u^k .
Note that
where we used Lemma 5.1 to obtain the last term. Since variations \delta u_{i}^{k} are arbitrary, we obtain \mu_{i}^{k} = \frac{\partial C_{i}}{\partial u_{i}^{k}} . As for the second term, we have that
As we have show along the proof for Theorem 4.1, we have that
and the indexes might be interchanged. The last term to obtain equation (5.7) may be dealt with, using integration by parts in discrete-time, which is just rearranging the indexes, together with the second statement in Lemma 5.1 and the fact that \eta_{i}^{0} = \eta_{i}^{N} = 0 . Therefore,
and the equations (5.6)-(5.8) follow.
Remark 8. Equations (5.6)-(5.8) are as a discrete approximation of the Lie-Poisson equations for the Hamiltonian version of the optimal control problem considered in [22]. The equation {\mu_i^k = \left(\frac{\partial C_i}{\partial u^k_i}\right)} represents the discrete time version of the reduced Legendre transformation and the equation g^{k+1}_i = g^k_i\mathcal{R}(hu^k_i) is the analogous of the reconstruction equation in the discrete time counterpart. These three equations are used to compute u_i^{k}, \mu_i^{k} and g^{k+1}_i given u_i^{k-1} , \mu_i^{k-1} , g^{k-1}_i and g^{k}_i from k = 1 to k = N-1 .
To compute the discrete-time reduced necessary condition for the optimal control problem (5.3) we must enforce boundary conditions given by the continuous-time quantities. More precisely, we must set
relating the momenta at the initial and final times, and use to transform boundary values between the continuous and discrete representation. They follow from the principle that any variation with free boundary points of the action (5.10) along a solution of equations (5.6)-(5.9) equals the change in momentum \langle \frac{\partial C_i}{\partial u_i}(u_i(T)), g_{i}^N \delta g_{i}^{N} \rangle - \langle \frac{\partial C_i}{\partial u_i}(u_i(0)), g_{i}^0 \delta g_{i}^{0} \rangle (see [39] for a discussion in the single agent case). Therefore, we must enforce
where the variation is taken along a family of solutions of the discrete equations (5.6)-(5.9) whose boundary values are not fixed. By taking the variations of the discrete action, we eventually get a vanishing term corresponding to the fact that this family of sequences satisfies the discrete equations together with boundary terms multiplying \eta_{i}^{0} and \eta_{i}^{N} , and simplifying, to the above equations.
Remark 9. If we choose the midpoint rule to discretize the potential V_{i} , then we would obtain the following boundary conditions
The boundary condition g_s(T) for agent s is enforced by the relation
Recalling that \mathcal{R}(0) = \overline{e} , this last expression just means that g^N_s = g_s(T) . Moreover, by computing recursively the equation g^{k+1}_s = g^{k}_s\mathcal{R}(hu_s^k) for k = 1, \ldots, N-1 , using that g_s^{0} = g_s(0) and \mathcal{R}(0) = \overline{e} , it is possible to translate the final configuration g_s^N in terms of u^k_s , such that there is no need to optimize over any of the configurations g^k_s . In that sense, (5.7) for i = s , l = 0 together with
form a set of (nN) -equations (since \dim\mathfrak{g} = n ) where nN unknowns are for u^{0:N-1}_s , denoting the entire sequence of controls \{u_{s}^{0}, \dots, u_{s}^{N-1}\} for each agent s .
The numerical algorithm to compute the reduced optimality conditions is summarized in Algorithm 1.
Note also that the exact form of equations (5.6)-(5.8) depends on the choice of \mathcal{R} . This choice will also effect the computational efficiency of the optimization framework in the case, the above equalities are imposed as constraints. For instance, in Section 6, we will employ the Cayley transform on the Lie group SE(2) as a choice of \mathcal{R} to write in a compact form the numerical integrator [38], [17], but another natural choice would be to employ the exponential map, as we explained in Section 5.1.
6.
Case study
In this case study, we apply the proposed reduction by symmetry strategy to an optimal control for autonomous surface vehicles (ASVs). The configuration space whose elements determine the motion of each ASV is SE(2)\cong SO(2)\times \mathbb{R}^2 . An element g_i\in SE(2) is given by g_i = \begin{pmatrix} \cos\theta_i & -\sin\theta_i&x_i\\ \sin\theta_i & \cos\theta_i&y_i\\ 0 & 0 & 1 \end{pmatrix} , where (x_i, y_i)\in \mathbb{R}^2 represents the center of mass of a planar rigid body describing the ASV and \theta_i represents the angular orientation of the ASV. The control inputs, for each ASV, are given by u_i = (u_i^1, u_i^2) , where u_i^1 denotes the speed of the center of mass for the ASV and u_i^2 denotes the angular velocity of the ASV.
The kinematic equations for the multi-agent system are:
Using the notation of Example 1, the Lie algebra \mathfrak{se}(2) is identified with \mathbb{R}^2 through the isomorphism \begin{pmatrix} -a\mathbb{J}&b\\ 0 & 0 \end{pmatrix}\mapsto (a, b). The elements of the basis of the Lie algebra \mathfrak{se}(2) are {e_1 = \begin{pmatrix} 0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}, e_2 = \begin{pmatrix} 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}, e_3 = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0 \end{pmatrix}} ,
which satisfy [e_1, e_2] = e_3, \; [e_2, e_3] = 0, \; [e_3, e_1] = e_2 . Thus, the kinematic equations (6.1) take the form \dot{g_i} = g_iu_i = g_i(u_i^1e_1+u_i^2e_2) and give rise to a left-invariant control system on SE(2)^s\times \mathfrak{se}(2)^s . The inner product on \mathfrak{se}(2) is given by \langle\langle\xi_1, \xi_2\rangle\rangle: = tr(\xi_1^T\xi_2) for \xi_1, \xi_2\in \mathfrak{se}(2) and hence, the norm is given by ||\xi|| = \sqrt{tr(\xi^T\xi)}, for any \xi\in \mathfrak{se}(2) . The dual Lie algebra \mathfrak{se}(2)^* of SE(2) is defined through the dual pairing, \langle\alpha, \xi\rangle = tr(\alpha \xi) , where \alpha\in \mathfrak{se}(2)^* and \xi\in \mathfrak{se}(2) , hence, the elements of the basis of \mathfrak{se}(2)^* are {e^1 = \begin{pmatrix} 0 & \frac{1}{2} & 0\\ -\frac{1}{2} & 0 & 0\\ 0 & 0 & 0 \end{pmatrix}, e^2 = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 1 & 0 & 0 \end{pmatrix}, e^3 = \begin{pmatrix} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 1 & 0 \end{pmatrix}} .
Consider the cost function C_i(g_i, u_i) = \frac{1}{2}\langle u_i, u_i\rangle and the artificial potential function V_{ij}:SE(2)\times SE(2)\to \mathbb{R} given by {V_{ij}(g_i, g_j) = \frac{\sigma_{ij}}{2((x_i-x_j)^2+(y_i-y_j)^2-4\overline{r}^2)}} , where \sigma_{ij}\in \mathbb{R}_{\geq 0} and \overline{r} is the radius of the disk each agent occupies as defined at the end of Section Ⅲ. Consider a spherical obstacle with unit radius and without loss of generality let it be centered at the origin. Hence, consider the obstacle avoidance potential function V_i^0:SE(2)\to \mathbb{R} , {V_i^0(g_i) = \frac{\sigma_{i0}}{2(x^2+y^2-(\overline{r}+1)^2)}} , where \sigma_{i0}\in\mathbb{R}_{ > 0} .
Note that the obstacle avoidance potential functions are not SE(2) -invariant but SO(2) -invariant, so they break the symmetry. Using the norm of \mathfrak{se}(2) and for \overline{r} = 1 , V_{ij} and V_i^0 are equivalently given by {V_{ij}(g_i, g_j) = \frac{\sigma_{ij}}{2(|| \text{Ad}_{g_i^{-1}g_j}e_1||^2-6)}} and {V_i^0(g_i) = \frac{\sigma_{i0}}{2(|| \text{Ad}_{g^{-1}_i}e_1||^2-6)}} .
Let W = \mathfrak{se}(2)^* , so we define the extended potential functions V_{i, 0}^{\text{ext}}:SE(2)\times \mathfrak{se}(2)\to \mathbb{R} by V_{i, 0}^{\text{ext}}(g_i, \alpha) = \frac{\sigma_{i0}}{2(|| \text{Ad}_{g^{-1}_i}\alpha||^2-6)} , which are SE(2) -invariant under the action of \tilde{\Phi} given by (3.6), i.e. V_{i, 0}^{\text{ext}}\circ\tilde{\Phi} = V_{i, 0}^{\text{ext}}, for any g\in SE(2) . Since, W = \mathfrak{se}(2)^* we have {{\bf{J}}_W\Big(\frac{\partial V_{i, 0}^{\text{ext}}}{\partial\alpha_i}, \alpha_i\Big) = \text{ad}^*_{\alpha_i}\Big(\frac{\partial V_{i, 0}^{\text{ext}}}{\partial\alpha_i}\Big)} , and equations (4.2) and (4.3) yield
together with \dot{\alpha}_i = - \text{ad}_{u_i}\alpha_i and \alpha_i = \text{Ad}_{g_i^{-1}}\alpha_0 .
Note also that u_i = u_i^1e_1+u_i^2e_2 , \alpha_i = \alpha_i^1e_1+\alpha_i^2e_2+\alpha_i^3e_3 and \lambda_i = \lambda_3^ie^3 thus,
where x_{ij} = x_i-x_j, \; y_{ij} = y_i-y_j and { \text{Ad}_{g_i^{-1}}\alpha_0 = \begin{pmatrix} 0 & -1&x_i\sin\theta_i-y_i\cos\theta_i\\ 1 & 0&x_i\cos\theta_i+y_i\sin\theta_i\\ 0 & 0 & 0 \end{pmatrix}} .
Therefore, by applying Proposition 4.2 for \mathfrak{r} = \text{span} \{e_1, e_2\} and \mathfrak{s} = \text{span} \{e_3\} , Euler-Lagrange equations for the OCP (3.4) are
with
\begin{array}{ll} \dot{\alpha}_i^1 = 0, & \alpha_i^1(0) = 1, \\ \dot{\alpha}_i^2 = u_i^1\alpha_i^3, & \alpha_i^2(0) = x_i^0\sin\theta_i^0-y_i^0\cos\theta_i^0, \\ \dot{\alpha}_i^3 = -u_i^1\alpha_i^2+u_i^2\alpha_i^1, & \alpha_i^3(0) = x_i^0\cos\theta_i^0+y_i^0\sin\theta_i^0. \end{array}
For the discrete-time setting, one would choose
where {g^{k}_i = \begin{bmatrix}
\cos\theta^{k}_i & -\sin\theta^{k}_i & \phantom{-}x^{k}_i\\
\sin\theta^{k}_i & \phantom{-}\cos\theta^{k}_i & \phantom{-}y^{k}_i\\ 0 & \phantom{-}0 & \phantom{-}1 \end{bmatrix}\in SE(2)\nonumber} and {u^{k}_i = \sum\limits_{j = 1}^{3}u^{k}_{ij}e_{j}\in\mathfrak{se}(2)} . Also, in the discrete-time setting, the extended potential function V_{d, \text{ext}}: SE(2)\times \mathfrak{se}(2)\to\mathbb{R} can be constructed in exactly the same way as in the above example, and is given by
where {\alpha_{i}^{k} = \sum\limits_{j = 1}^{3} \alpha_{ij}^{k}e^{j}} . We do not give all the details again and leave it up to reader to verify that the assumptions (ⅰ) - (ⅶ) from (3.3) are satisfied. The discrete-time equations are
where
For numerical purposes, we first choose a suitable retraction map, like the Cayley map or the exponential map, and then compute the quantities (d\mathcal{R}_{hu^{k}_i}^{-1})^{*}\mu^{k}_i and (d\mathcal{R}_{-hu^{k-1}_i}^{-1})^{*}\mu^{k-1}_i . As an example, if we choose the Cayley map \text{cay}: \mathfrak{se}(2)\to\mathrm{SE}(2) as the retraction map, (see [38] and [17] for instance) then we have
where
and {\mu_{i}^{k} = \sum\limits_{j = 1}^{3} \mu_{ij}^{k}e^{j}} . Note that for {v = \sum\limits_{i = 1}^{3}v^{i}e_{i}\in\mathfrak{g}} , the matrix representation for d\text{cay}_{v}^{-1} is given by
7.
Conclusions
We studied the reduction by symmetry for optimality conditions of extremal in an OCP for collision and obstacle avoidance of left-invariant multi-agent control system on Lie groups, by exploiting the physical symmetries of the agents and obstacles. Reduced optimality conditions are obtained using techniques from variational calculus and Lagrangian mechanics on Lie groups, in the continuous-time and discrete-time settings. We applied the results to an OCP for multiple unmanned surface vehicles. The method proposed in this work allows the construction of position and velocity estimators, by discretizing the variational equation given in Theorem 4.1 - instead of discretizing the equations of motion - and by deriving variational integrators - see Theorem 5.2. The reduction of sufficient conditions for optimality will be also studied by using the notion of conjugate points, as in [42], in future work, as well as the reduction by symmetry of the variational obstacle avoidance problems [43] on semidirect products of Lie groups endowed with a bi-invariant metric on a Riemannian manifold.
Acknowledgments
L. Colombo is very grateful to A. Bloch, R. Gupta and T. Ohsawa for many useful comments and stimulating discussions during the last years on the topic of this paper, which is inspired by our common previous work.
The authors acknowledge financial support from the Spanish Ministry of Science and Innovation, under grants PID2019-106715GB-C21, MTM2016-76702-P.
Conflict of interest
We the authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: