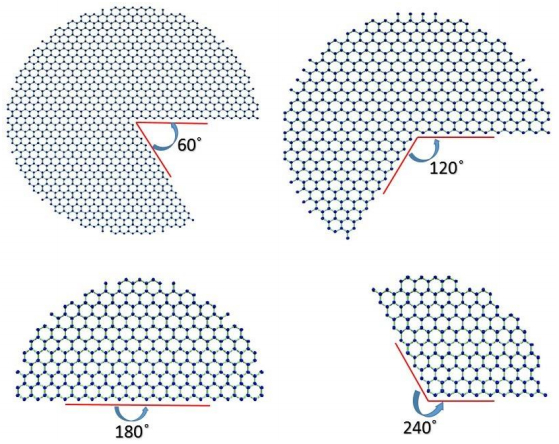
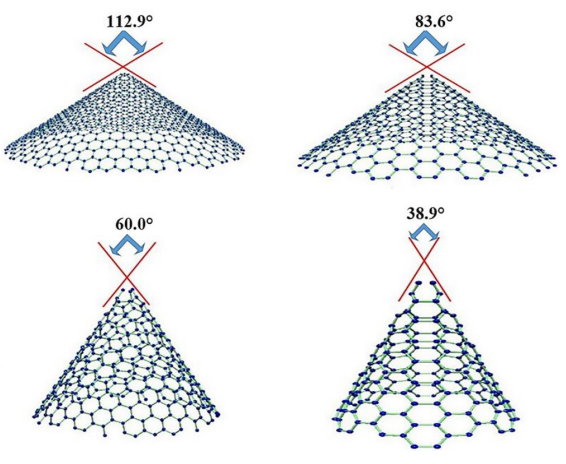
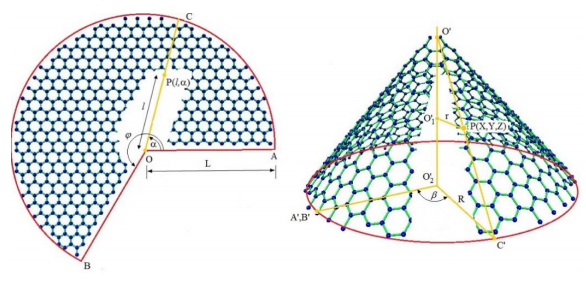
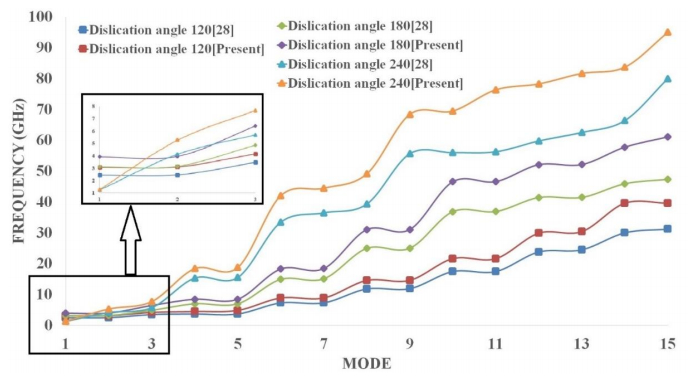
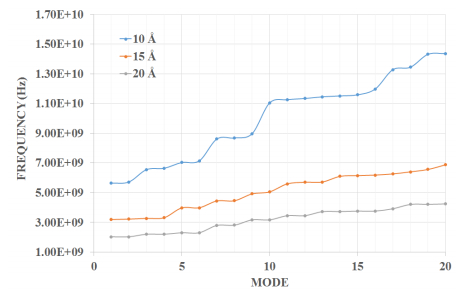
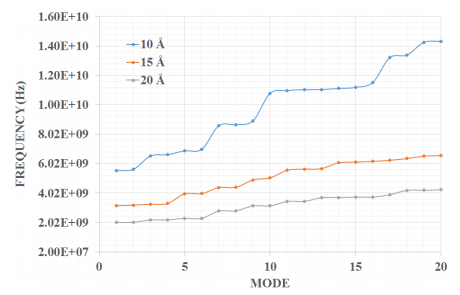
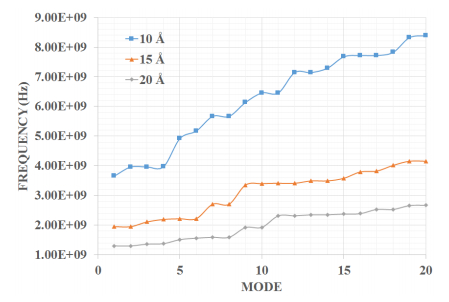
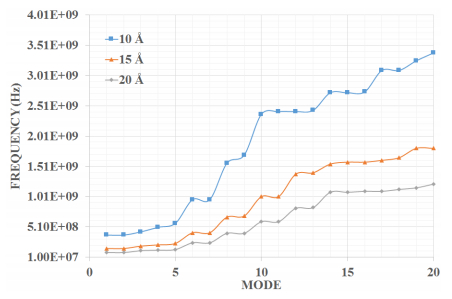
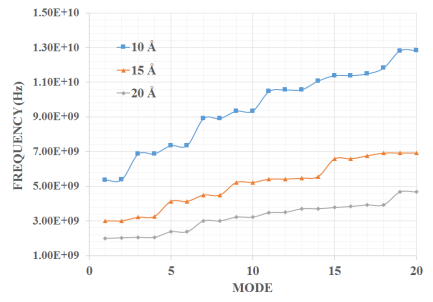
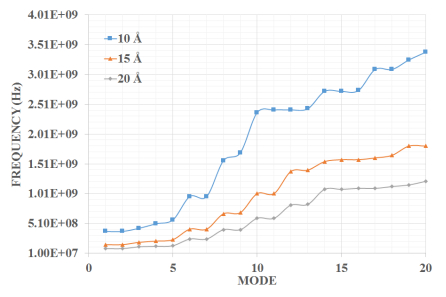
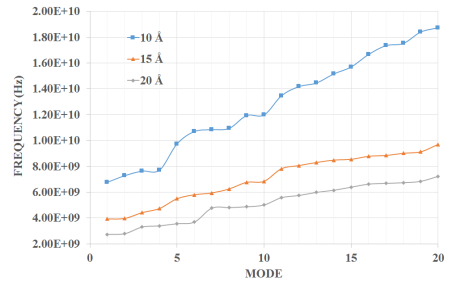
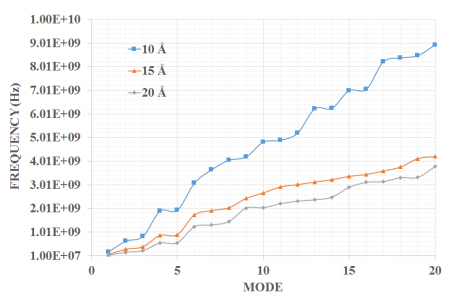
An approach to modelling and simulation of single-walled carbon nanocones for sensing applications

1.   Introduction

1.1.   Ostrowski type inequalities

In 1938, A. M. Ostrowski introduced the subsequent appealing integral-based inequality to relate the value of a function $\Psi$ with its integral from $\alpha$ to $\beta$:

Consider $\Psi:[\alpha, \beta] \to \mathcal{R}$ is continuous on $[\alpha, \beta]$ and differentiable in $(\alpha, \beta)$, such that ${\Psi^{'}}:(\alpha, \beta) \to \mathcal{R}$ is bounded in $(\alpha, \beta)$, i.e. ${\left\| {{\Psi^{'}}} \right\|_\infty }: = \mathop {\sup }\limits_{\hat{a} \in (\alpha, \beta)} \left| {{\Psi^{'}}}(\hat{a}) \right| < \infty$. Subsequently for any $\hat{a} \in [\alpha, \beta]$, we have:

If the fraction $\frac{1}{4}$ cannot be substituted by any smaller value then it leads to sharpness of the above inequality.

Afterward, several researchers have brought in few findings through the extensions and generalizations of Inequality (1.1). Such inequalities can be employed to guesstimate the inaccuracy of approximation in integration while investigating the steadiness and consistency of statistical calculation ^[1].

Stefan Hilger ^[2] developed the calculus of measure chains in 1988. His Ph.D. supervisor Bernd Aulbach described core contributions of this theory of Unification, Extension and Discretization. The concept of time scales is a novelty in applied sciences as well as in mathematics as it enlightens a number of indefinite points about differential equations and solutions of some fractional order differential equations, which have been proved to be inadequate for their solution. Additionally, it has enlarged its contribution to the literature with its applications in areas such as engineering, biostatistics, mathematical biology, functional spaces, optimization theory and dynamic inequalities. The theory of time scales has attracted a great attention of researchers for resolving many problems in analysis. Some dynamical inequalities on time scales can be found in ^[3,4,5], where researchers established convex function-based inequalities, new Hardy-type inequalities and inequalities for product of different kinds of convex functions respectively using various analytical and theoretical approach on time scales. Furthermore Hu & Wang ^[6] discussed dynamic inequalities on time scales with applications in permanence of predator-prey system and Saker ^[7] employed some dynamic inequalities of Opial-type on time scales to prove numerous results related to the spacing between successive zeros of a solution of a second order dynamic equation with a damping term. Bohner and Matthews ([8,Theorem 3.5]) characterized the following relation on $\Gamma$ as a generalization of the Ostrowski Inequality (1.1) :

Let $\alpha, \beta, \hat{u}, \hat{v} \in \Gamma, \alpha < \beta$, and $\Psi:{[\alpha, \beta]\cap\Gamma} = {[\alpha, \beta]_\Gamma} \to \mathcal{R}$ is differentiable. Then we have the inequality:

where $M = \mathop {\sup }\limits_{\alpha < \hat{v} < \beta} \left| {{\Psi^\Delta }(\hat{v})} \right| < \infty$ and ${[\alpha, \beta]_\Gamma}$ is a closed interval under $\Gamma$. If its R.H.S of Inequality (1.1) cannot be substituted by any smaller value then it leads to sharpness of the above inequality.

Liu & Ngô ([9,Lemma 3.2]) proved the following identity: Let $\alpha, \beta, \hat{u}, \hat{v} \in \Gamma, \alpha < \beta$ and $\Psi:{[\alpha, \beta]_\Gamma} \to \mathcal{R}$ is differentiable. Then the following relation for all $\eta \in [0, 1]$ holds.

where,

By making use of (1.2), they have expanded the Inequality (1.1) by considering parameter $\eta$ and developed the following Ostrowski type inequality involving parameter $\eta$ ([9,Theorem 3.1]):

Let $\alpha, \beta, \hat{u}, \hat{v} \in \Gamma, \alpha < \beta$, and that $\Psi:{[\alpha, \beta]_\Gamma} \to \mathcal{R}$ is differentiable function. Then the following relation holds true:

for all $\eta \in [0, 1],$ such that $\alpha + \eta \frac{{\beta - \alpha}}{2}$ and $\beta - \eta \frac{{\beta - \alpha}}{2}$ are in $\Gamma$ where $\hat{v} \in [\alpha + \eta \frac{{\beta - \alpha}}{2}, \beta - \eta \frac{{\beta - \alpha}}{2}] \cap \Gamma$, and $M = \mathop {\sup }\limits_{\alpha < \hat{v} < \beta} \left| {{\Psi^\Delta }(\hat{v})} \right| < \infty.$ Its sharpness is conditioned with

Here ${[\alpha, \beta]_\Gamma}$ represents a closed interval on $\Gamma$.

Xu & Fang [10,Lemma 1] investigated the following identity: Let $\alpha, \beta, \hat{u}, \hat{v} \in \Gamma, \alpha < \beta, \Psi:{[\alpha, \beta]_\Gamma} \to \mathcal{R}$ is differentiable, and $\zeta: [0, 1]\rightarrow [0, 1]$ is given, then we have

where

By making use of (1.4), they proved Ostrowski Inequality [10,Theorem 1] by using a parametric function and developed the result:

Let $\alpha, \beta, \hat{u}, \hat{v} \in \Gamma, \alpha < \beta, \Psi:{[\alpha, \beta]_\Gamma} \to \mathcal{R}$ is differentiable, and $\zeta: [0, 1] \rightarrow [0, 1]$, then

for all $\eta \in [0, 1]$ such that $\alpha_1$ and $\alpha_2$ are in $\Gamma$, and $t \in [\alpha_1, \alpha_2] \cap \Gamma$, where $M = \mathop {\sup }\limits_{\alpha < \hat{v} < \beta} \left| {{\Psi^\Delta }(\hat{v})} \right| < \infty$. Its sharpness is conditioned with

We refer ^[11,12,13] for detail textual-cum-mathematical description on the weighted Ostrowski type inequalities (wOTIs) via time scales. Such as Liu, Tuna and Jiang ^[11] developed few wOTIs by using weighted Montgomery identity on $\Gamma$. Liu and Tuna ^[13] characterized wOTIs on $\Gamma$ by utilizing the concept of combined dynamic derivatives on $\Gamma$. Several scholars investigated multivariate OTIs on $\Gamma$ in ^[14,15,16]. Few authors ^{[17,18,19,20,21,22,23,24,25,26,27,28]} utilized various methods to develop OTIs on $\Gamma$ for functions of two variables. Motivated by the mentioned work, we extend OTIs for bivariate functions, which can be considered as generalizations of OTIs proved by Liu & Ngô, Xu & Fang and by Dragomir et al. ^[29].

1.2.   Essentials on time scales

(1) Time scale: It is a closed subset of the real numbers. In present study, it is denoted by the symbol $\Gamma$. Examples of time scales include Cantor set, closed intervals, $\mathbb{Z}.$

(2) Forward jump operator: For $t \in \Gamma$, the Forward jump operator $\rho :\Gamma \to \Gamma$ is defined as

(3) $\mathop \Gamma\nolimits^k$ notation:

(4) $\mathop \Psi\nolimits^\sigma$ notation: If $\Psi:\Gamma \to \mathcal{R}$ is a function, then we define a function $\mathop \Psi\nolimits^\sigma:\Gamma \to \mathcal{R}$ by

i.e., $\mathop \Psi\nolimits^\sigma = \Psi \circ \, \, \sigma$.

(5) rd-continuous function: A function $\zeta: \Gamma \to \mathcal{R}$ is stated as rd-continuous if it is continuous and its left-sided limits exist at right-dense points and left dense points respectively in $\Gamma$. The symbol ${C_{rd}}$ stands for the family of all such functions.

(6) The delta derivative: Let $\Psi: \Gamma\to \mathcal{R}$ with $\hat{v} \in {\Gamma^k}$. The term ${\Psi^\Delta }(\hat{v})$ is said to be a number (if exists) if for any $\epsilon > 0$, $\exists$ a neighbourhood $\mathcal{U}$ of $\hat{v}$ (i.e., $\mathcal{U} = (\hat{v} - \delta, \hat{v} + \delta)\cap \Gamma$ for any $\delta > 0$) such that

The value ${\Psi^\Delta }(\hat{v})$ is known as the delta (or Hilger) derivative of $\Psi$ at $\hat{v}$. Furthermore, the function $\Psi$ is said to be delta differentiable on ${\Gamma^k}$ if ${\Psi^\Delta }(\hat{v})$ exists $\forall \hat{v} \in {\Gamma^k}$.

(7) Integration by parts: If $\alpha, \beta \in \Gamma$ and $\Psi, \zeta \in {C_{rd}}$ then

or

(8) Polynomials on time scales: The generalized polynomials are the functions ${{\zeta}_k}, {{\Omega}_k}:{\Gamma^2} \to \mathcal{R}, k \in {\mathbb{N}_0},$ defined recursively as follow: the functions ${{\Omega}_0}$ and ${{\zeta}_0}$ are ${{\zeta}_0}(\hat{v}, \hat{u}) = {{\Omega}_0}(\hat{v}, \hat{u}) = 1$ for all $\hat{u}, \hat{v} \in \Gamma$, and, for given ${{\zeta}_k}$ and ${{\Omega}_k}$ with $k \in {\mathbb{N}_0}$, the functions ${{\zeta}_{k + 1}}$ and ${{\Omega}_{k + 1}}$ are ${{\zeta}_{k + 1}}(\hat{v}, \hat{u}) = \int\limits_{\hat{u}}^{\hat{v}} {{{\zeta}_k}(\sigma (\tau), \hat{u})\Delta \tau },$ for all $\hat{u}, \hat{v} \in \Gamma$ and ${{\Omega}_{k + 1}}(\hat{v}, \hat{u}) = \int\limits_{\hat{u}}^{\hat{v}} {{{\Omega}_k}(\tau, \hat{u})\Delta \tau }$ for all $\hat{u}, \hat{v} \in \Gamma.$ If $\mathop {\Omega}\nolimits_k^\Delta \left({\hat{v}, \hat{u}} \right)$ represents the derivative of $\mathop {\Omega}\nolimits_{k} \left({\hat{v}, \hat{u}} \right)$ w.r.t. $\hat{v}$ for any $\hat{u}$, then $\mathop {\Omega}\nolimits_k^\Delta \left({\hat{v}, \hat{u}} \right) = \mathop {\Omega}\nolimits_{k - 1} \left({\hat{v}, \hat{u}} \right), \, \forall \, k \in \mathbb{N}, \, \hat{v} \in {\Gamma^k}.$ Similarly $\mathop {\zeta}\nolimits_k^\Delta \left({\hat{v}, \hat{u}} \right) = \mathop {\zeta}\nolimits_{k - 1} \left({\sigma (\hat{v})\, ,\hat{u}} \right)\, \, \forall \, k \in \mathbb{N}, \, \hat{v} \in {\Gamma^k}.$

For further study of time scale calculus, readers are referred to ^[30,31].

Note: In this article, several abbreviations are used in order to lighten the notation and shorten the proofs; we refer to the table at the end just after the section of conclusions. Moreover throughout the paper we consider $[a, b]_{\Gamma} = [a, b]\cap{{\Gamma}}.$

2.   Main results

This section presents the characterization of novel wOTIs on $\Gamma$ through the generalization of Montgomery identity with parameter functions.

2.1.   Generalized Montgomery identity for parametric function ${\zeta}(\eta)$

Lemma 2.1. Let $\alpha, \beta, \gamma, \theta, \hat{u}, \hat{v} \in\Gamma$ with $\alpha < \beta, \gamma < \theta, \Psi:I = {[\alpha, \beta]_{{\Gamma_1}}} \times {[\gamma, \theta]_{{\Gamma_2}}} \to \mathcal{R}$ is differentiable. Assume that the delta derivatives $\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u})$ exist on I and $\zeta: [0, 1]\rightarrow [0, 1].$ Then we have the following identity

where

Proof. Since

Denote

By using (1.6), we integrate ${I_2}$ to get

Similarly

By using ${I_2}$ and ${I_3}$ in (2.3), we have

Use ${I_1}$ in (2.2) to find

where ${I_4} = \int\limits_{\alpha}^{\beta} {\mathop k\nolimits_1 (\hat{x}, \hat{v})\mathop \Psi\nolimits^\Delta (\hat{v}, \hat{y})\Delta \hat{v}}$, ${I_5} = \int\limits_{\alpha}^{\beta} {\mathop k\nolimits_1 (\hat{x}, \hat{v})} \mathop \Psi\nolimits^\Delta (\hat{v}, \gamma)\Delta \hat{v}$ and ${I_6} = \int\limits_{\alpha}^{\beta} {\mathop k\nolimits_1 (\hat{x}, \hat{v})} \mathop \Psi\nolimits^\Delta (\hat{v}, \theta)\Delta \hat{v}$.

Now,

Use (1.6) to find

In similar fashion,

By adding ${I_7}$ and ${I_8}$, we have

Similar calculations for $I_5$ and $I_6$ give

and

Using ${I_4}$, ${I_5}$ and ${I_6}$ in (2.4), we have

Simplification yields

Remark 2.1. If $\Psi$ is single valued function then Eq (2.1) coincides with [10,Lemma 1].

Corollary 2.1. Let $\alpha, \beta, \gamma, \theta, \hat{u}, \hat{v} \in\Gamma$ with $\alpha < \beta, \gamma < \theta, \Psi:I = {[\alpha, \beta]_{{\Gamma_1}}} \times {[\gamma, \theta]_{{\Gamma_2}}} \to \mathcal{R}$ is differentiable. Assume that the delta derivatives $\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u})$ exist on I and $\eta \in [0, 1]$. We then have the equation

where

Proof. If we choose ${\zeta}(\eta) = \eta$ in Lemma 2.1, we get the required estimate.

Remark 2.2. If $\Psi$ is single valued function then Eq (2.6) coincides with [9,Lemma 3.2].

2.2.   Generalized Ostrowski inequality for parameter function ${\zeta}(\eta)$

Theorem 2.1. Suppose that $\alpha, \beta, \gamma, \theta, \hat{u}, \hat{v} \in\Gamma$ with $\alpha < \beta, \gamma < \theta, \Psi:I = {[\alpha, \beta]_{{\Gamma_1}}} \times {[\gamma, \theta]_{{\Gamma_2}}} \to \mathcal{R}$ is differentiable. Assume that the delta derivatives $\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u})$ exist on I and $\zeta: [0, 1]\rightarrow [0, 1]$. We then have the inequality

for all $\eta \in [0, 1]$ such that ${\alpha}_1$ and ${\alpha}_2$ are in ${\Gamma_1}$, and $\hat{x} \in [{\alpha}, {\beta}] \cap {\Gamma_1}$, $\gamma_1$ and $\gamma_2$ are in ${\Gamma_2}$, $\hat{y} \in [{\gamma}, \theta] \cap {\Gamma_2}$, where $M_1 = \mathop {Sup}\limits_{\begin{array}{*{20}{c}} {\alpha < \hat v < \beta }\\ {\gamma < \hat u < \theta } \end{array}} \left| {{\Psi^{\Delta \Delta }}\left({\hat{v}, \hat{u}} \right)} \right| < \infty$, $M_2 = \mathop {Sup}\limits_{\begin{array}{*{20}{c}} {\alpha < \hat v < \beta }\\ {\gamma < \hat u < \theta } \end{array}} \left| {{\Psi^{\Delta \sigma }}\left({\hat{v}, \hat{u}} \right)} \right| < \infty$ and $M: = Max\{M_1, M_2\}$.

Proof. By taking absolute value on both sides of (2.1), one yields

Further we have to use $\left| {\Psi + \zeta} \right| \le \left| \Psi \right| + \left| \zeta \right|$, $\left| {\int\limits_{\alpha}^{\beta} {\Psi d{\hat{x}}} } \right| \le \int\limits_{\alpha}^{\beta} {\left| \Psi \right|} d{\hat{x}}$ & $\left| {\mathop \Psi\nolimits^{\Delta \sigma } (\hat{v}, \hat{u}) } \right| \leq M; \, \left| {\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u}) } \right| \leq M; \, \left| {\Psi. \zeta} \right| = \left| \Psi \right|\left| \zeta \right|$ toestimate as following:

Simplifications give the required result.

Corollary 2.2. If all the assumptions of Corollary 2.1 hold, then we find the following Ostrowski type inequality for parameter $\eta$

Proof. The proof is similar to proof of Theorem 2.1.

Remark 2.3. The inequality (2.8) can be considered as extension of [9,Theorem 3.1]. Since if $\Psi$ is single valued in (2.8), we get [9,Theorem 3.1].

Corollary 2.3. Under the assumptions of Theorem 2.1, we have the following Ostrowski type inequality:

Proof. Take ${\zeta}(\eta) = {\eta ^2}$ in Theorem 2.1 to meet the requirement.

Remark 2.4. The following Ostrowski type inequalities are obtained by choosing $\eta = 0, \eta = \frac{1}{2}$ and $\eta = 1$ in Corollary 2.3 respectively:

$\bf{(a)}$ $\left| \begin{array}{l} \Psi(\hat{x}, \hat{y}) - \frac{1}{{\beta - \alpha}}\int\limits_{\alpha}^{\beta} {\mathop {\{ \Psi}\nolimits^\sigma (\hat{v}, \hat{y})} \\ + \mathop \Psi\nolimits^\sigma (\hat{v}, \gamma) + \mathop \Psi\nolimits^\sigma (\hat{v}, \theta)\} \Delta \hat{v} \end{array} \right| \le$ $\frac{M}{{(\beta - \alpha)(\theta - \gamma)}}\left\{ {\mathop {\Omega}\nolimits_2 (\hat{x}, \alpha) + \mathop {\Omega}\nolimits_2 (\hat{x}, \beta)} \right\}\left[ {(\theta - \gamma) + \mathop {\Omega}\nolimits_2 (\hat{y}, \gamma) + \mathop {\Omega}\nolimits_2 (\hat{y}, \theta)} \right]$.

$\bf{(b) }$ $\left| \begin{array}{l} \Psi(\hat{x}, \hat{y}) + \frac{1}{4}\{ \Psi(\alpha, \hat{y}) + \Psi(\hat{x}, \gamma)\} + \frac{3}{4}\{ \Psi(\beta, \hat{y}) + \Psi(\hat{x}, \theta)\} \\ + \frac{1}{{16}}\Psi(\alpha, \gamma) + \frac{3}{{16}}\{ \Psi(\beta, \gamma) + \Psi(\alpha, \theta)\} + \frac{9}{{16}}\Psi(\beta, \theta)\\ - \frac{4}{{\beta - \alpha}}\int\limits_{\alpha}^{\beta} {\mathop {\{ \Psi}\nolimits^\sigma (\hat{v}, \hat{y})} + \mathop \Psi\nolimits^\sigma (\hat{v}, \gamma) + \mathop \Psi\nolimits^\sigma (\hat{v}, \theta)\} \Delta \hat{v} \end{array} \right| \le \frac{{4M}}{{(\beta - \alpha)(\theta - \gamma)}}$

$\bf{(c)}$ $\left| \begin{array}{l} \Psi(\alpha, \gamma) + \Psi(\beta, \gamma) + \Psi(\alpha, \theta) + \Psi(\beta, \theta)\\ - \frac{4}{{\beta - \alpha}}\int\limits_{\alpha}^{\beta} {\mathop {\{ \Psi}\nolimits^\sigma (\hat{v}, \hat{y})} + \mathop \Psi\nolimits^\sigma (\hat{v}, \gamma) + \mathop \Psi\nolimits^\sigma (\hat{v}, \theta)\} \Delta \hat{v} \end{array} \right| \le \frac{{4M}}{{(\beta - \alpha)(\theta - \gamma)}}$

2.3.   Generalized Montgomery identity involving parametric functions ${{\zeta}_1}(\eta)$ and ${{\zeta}_2}(\mu)$

Lemma 2.2. Let $\alpha, \beta, \gamma, \theta, \hat{u}, \hat{v} \in\Gamma$ with $\alpha < \beta, \gamma < \theta, \Psi:I = {[\alpha, \beta]_{{\Gamma_1}}} \times {[\gamma, \theta]_{{\Gamma_2}}} \to \mathcal{R}$ is differentiable. Assume that the delta derivatives $\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u})$ exist on I and ${{\zeta}_1}, {{\zeta}_2}: [0, 1]\rightarrow [0, 1]$. We then have the equation

where

Proof. It can easily be proved by following the steps of Lemma 2.1.

Remark 2.5. If ${{\zeta}_1}(\eta)$ = ${{\zeta}_2}(\mu)$ in Lemma 2.2, it becomes Lemma 2.1.

2.4.   Generalized Ostrowski type inequalities involving parametric functions ${{\zeta}_1}(\eta)$ and ${{\zeta}_2}(\mu)$

Theorem 2.2. Suppose that $\alpha, \beta, \gamma, \theta, \hat{u}, \hat{v} \in\Gamma$ with $\alpha < \beta, \gamma < \theta, \Psi:I = {[\alpha, \beta]_{{\Gamma_1}}} \times {[\gamma, \theta]_{{\Gamma_2}}} \to \mathcal{R}$ is differentiable. Assume that the delta derivatives $\mathop \Psi\nolimits^{\Delta \Delta } (\hat{v}, \hat{u})$ exist on I and ${\zeta}_1, {\zeta}_2: [0, 1]\rightarrow [0, 1]$. We then have the inequality

Proof. By using Lemma 2.2 and adopting the technique of proof of Theorem 2.1, we get the desired result.

Remark 2.6. In similar fashion, remaining results of Section 2.2 can be extended for (2.11).

3.   Applications to some particular time scales

Some important examples of time scales include continuous time scale $\Gamma = \mathbb{R}$ (set of all real numbers, which gives rise to differential equations), discrete time scale $\mathbb{Z}$ (set of integers, which gives rise to difference equations) and quantum time Scale ${q^{{\mathbb{N}_0}}}, q > 1.$ In this section we have discussed Ostrowski type Inequality (2.8) for these special time scales.

Example 3.1. If we take $\Gamma_1 = \Gamma_2 = \mathcal{R}$, then the delta integral is the usual Riemann integral i.e. $\int\limits_{\alpha}^{\beta} {\mathop \Psi\nolimits^\sigma (\hat{v})\Delta \hat{v}} = \int\limits_{\alpha}^{\beta} {\Psi(\hat{v})d\hat{v}}$ as $\sigma (\hat{v}) = \hat{v}$. In this case, the generalized polynomial $\Omega_2$ is

which implies the following relations:

The Eq (2.8) takes the following form

Remark 3.1. If $\Psi$ is single valued function then assumptions and calculations made in Example 3.1 coincide with [29,Theorem 2].

Example 3.2. Using $\Gamma_1 = \Gamma_2 = \mathbb{Z}, \alpha = 0 = \gamma, \beta = n, \theta = m, s = j, t = i, \Psi(p, q) = {{\hat{x}}_p}{{\hat{y}}_q}, p = k, q = l$ and ${\Psi^\sigma }(p, q) = \sigma ({{\hat{x}}_p}{{\hat{y}}_q}) = {{\hat{x}}_{p + 1}}{{\hat{y}}_{q + 1}}$; $\int\limits_{\alpha}^{\beta} {{\Psi^\sigma }(\hat{v}, \theta)\Delta \hat{v}} = \frac{4}{n}\sum\limits_{t = 0}^{n - 1} {{{\hat{x}}_{t + 1}}{{\hat{y}}_m}}$ in Eq (2.8), with the known result

we have

Example 3.3. If we take $\Gamma_1 = \Gamma_2 = {q^{{\mathbb{N}_0}}}, q > 1, \alpha = \gamma = {q^m}, \beta = \theta = {q^n}, m < n, \eta = 1$ in Eq (2.8), we have

Remark 3.2. If $\Psi$ is single valued then Example 3.1 to Example 3.3 coincide with [9,Corollaries 3.6–3.8]. Furthermore, it is also possible to reset Eq (2.7) instead of Eq (2.8) for these particular time scales, which will be extensions of [10,Corollary 1,2] in case of continuous and discrete time scales.

4.   Conclusions

In this study, a novel approach is employed for the establishment of Ostrowski type integral inequalities for double integrals via Montgomery identity under the setting of time scales calculus. In addition, certain generalizations are made for some weighted and parameterized functions. Moreover, some particular cases, applications and examples are discussed for some specific time scales. It is also worth mentioning that the results of the paper extend the results of ^[9,10,29]. Further extensions can be sought by the expansion of this proposed study for multiple integrals.

Notations

Following notations have been used in the paper for vivid understanding of the concept:

Acknowledgments

This research received funding support from the NSRF via the Program Management Unit for Human Resources and Institutional Development, Research and Innovation (grant number B05F640088).

Conflict of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.