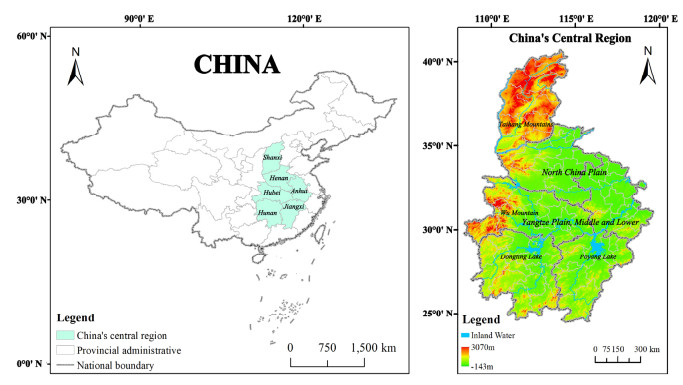
Under the influence of global climate change, the climatic conditions of China's major agricultural regions have changed significantly over the last half-century, affecting regional grain production levels. With its favorable conditions for agricultural activities, China's central region has been a strategic location for grain production since ancient times and has assumed an essential responsibility for maintaining national grain security. However, the key concerns of this study are whether the national grain security pattern is stable and whether it might be affected by global climate change (especially climate instability and increased risks in recent years). Therefore, the present study collected grain production data and used descriptive statistical and geospatial analyses to reveal the trend and spatiotemporal pattern of grain production in China's central region from 2010 to 2020. Then, a further analysis was conducted by combining meteorological data with a geographically weighted regression (GWR) model to investigate the relationship between spatial differences in the output per unit of the grain sown area (OPUGSA). The findings were as follows: (1) The overall development trend of grain production in China's central region from 2010 to 2020 revealed a positive overall trend in grain production, with notable differences in growth rates between northern and southern provinces. (2) Most regions in the southern part of the central region from 2015 to 2020 showed varying degrees of total output of grain (TOG) and OPUGSA reduction, possibly affected by the effects of the anomalies for global climate change and a strong El Niño effect in 2015. (3) Low-low (L-L) clusters of TOG and OPUGSA indicators were consistently in the northwest part (Shanxi) of the central region, and high-high (H-H) clusters of TOG were consistently in the central part (Henan and Anhui) of the central region, but H-H clusters of OPUGSA were not stably distributed. (4) The fitting results of the GWR model showed a better fit compared to the ordinary least squares (OLS) model; it was found that the annual average temperature (AAT) had the greatest impact on OPUGSA, followed by annual sunshine hours (ASH) and annual precipitation (AP) last. The spatiotemporal analysis identified distinct clusters of productivity indicators. It suggested an expanding range of climate impact possibilities, particularly in exploring climate-resilient models of grain production, emphasizing the need for targeted adaptation strategies to bolster resilience and ensure agricultural security.
1.
Introduction
Suppose B is a Banach space and ∅≠C⊆B. Now we many set an operator T:C→C. T is known as contraction if ||Tv−Tv′||≤α||v−v′||, whenever v,v′∈C and α∈(0,1). We call T a nonexpansive operator if α=1. When Tv∗=v∗ for some v∗∈C, then this element v∗ is known as a fixed point for T and in this case we denote the set {v∗∈C:Tv∗=v∗} simply by FT. However, if Gv∗=0, for an operator G:C→C, then it is called a zero of G and in this case we denote the set {v∗∈C:Gv∗=0} by S. The class of nonexpansive operators is widely considered by lot of authors in different frame of works. In particular, Browder [6] and Gohde [10] separately provided the existence of fixed point result for these operators in a uniformly convex Banach space (UCBS) setting. Precisely, they noted that if C is bounded convex and closed in a UCBS, then a nonexpansive operator T:C→C essentially admits a fixed point. In 1975, Zhang [24] noticed a new notion of nonlinear operators as follows: an operator T:C→C on a subset C is essentially called mean nonexpansive if one can find two nonnegative reals a,b satisfying a+b≤1 such that
Remark 1.1. The class of mean nonexpansive operators is one of the important class of nonlinear mappings because it includes properly the class of all nonexpansive operators, that is, if T:C→C is nonexpansive then T satisfies the requirement of a mean nonexpansive operator with a=1 and b=0. However, the converse is not valid in general as shown by the following example (see also Examples 5.1 and 5.2 in the last section of this paper).
Example 1.1. If C=[0,4], then we can set an operator T:C→C by the following formula
Here, T is discontinuous at v=4 and hence not nonexpansive. On the other hand, it is straightforward to show that T is a mean nonexpansive operator.
The existence of fixed points of mean nonexpansive operators in Banach spaces has been studied by some authors. In particular, Zhang [24] suggested a unique fixed point result for the class of mean nonexpansive operators in a Banach space endowed with a normal structure. Moreover, Wu and Zhang [23] and Zuo [25] provided some related properties and fixed point theorems for these operators in a Banach space. The first purpose of this research is to study the computation of fixed points for these maps under an appropriate algorithm. Secondly, we apply these results to solve some problems under new algorithms.
After the existence of a fixed point for a given operator, it is very natural to construct an iterative scheme, which approximate the value of this fixed point. We know that in general, that Picard iterates vk+1=Tvk converges for Banach contractions but not for nonexpansive maps. Thus to find the value of the fixed point for nonexpansive and accordingly of generalized nonexpansive maps and also to obtain a relatively better rate of convergence, many schemes are available in the literature given below.
Mann [14] provided the following algorithm:
where μk∈(0,1).
Ishikawa [11] constructed a new iterative algorithm as follows:
where μk,ηk∈(0,1).
In 2000, Noor [16] first time introduced a three-step iterative algorithm, which is more general than that of Mann and Ishikawa iterative algorithms:
where μk,ηk,θk∈(0,1).
In 2007, Agarwal et al. [4] provided the S iterative algorithm, which is independent of but better than the both the Mann and Ishikawa iterative algorithm for many nonlinear operators:
where μk,ηk∈(0,1).
In 2014, Abbas and Nazir [2] considered another three-step iterative algorithm, which gives better approximation results as compared Mann, Ishikawa, Noor and S iterative algorithm. Their algorithm reads as follows:
where μk,ηk,θk∈(0,1).
In 2016, Thakur et al. [21] (TTP) constructed a novel three-step iterative algorithm as follows:
where μk,ηk,θk∈(0,1).
By means of the iterative algorithm [21], they approximate fixed points for nonexpansive operators through weak and strong convergence on a Banach space setting. They also compared the high accuracy of this algorithm with the other well-known algorithms in the setting of nonexpansive operators. Maniu [15] proved that this algorithm is stable with respect to weak contractions. Here, we want to show that the main results of [21] can be extended to the setting of mean nonexpansive operators. We also give an example of mean nonexpansive operators which fails to hold the nonexpansiveness condition. We connect the three-step algorithm (1.6) and the other three-step algorithms with this example and show that this algorithm provide a high accuracy as compared the others three-step algorithms in the general setting of mean nonexpansive operators.
2.
Preliminaries
To obtain the required aim, we first provide some elementary facts and results.
Consider a Banach space B and ∅≠C⊆B. Select an element q0∈B and choose a bounded sequence, namely, {vk}⊆B. We may set r(q0,{vk}) as
The asymptotic radius of the sequence {vk} connected with the set V will be denoted by r(C,{vk}) and given by
The asymptotic center of the sequence {vk} connected with the set C will be denoted by A(C,{vk}) and given by
Remark 2.1. The set A(C,{vk}) some-times does not has any element. But in the setting of UCBS, it is always a singleton set. The convexity of the A(C,{vk}) is also known in the case when C is a weakly compact and convex set, (see, e.g., [3,20] and others).
If a Banach space B is given. Then it is said to be endowed with the Opial's condition [17] in the case, when each {vk} in B converges in the weak sense to v∈B enjoys the following strict inequality:
The following result is known from [25].
Lemma 2.1. Assume that C is a nonempty convex and closed subset of a reflexive Banach space (RBS) B and T:C→C a mean nonexpansive operator. If a sequence {vk} converges in the weak sense to v∗ and limk→∞||vk−Tvk||=0, then v∗∈FT provided that B has the Opial's property.
Now we take an important property of a UCBS from [18].
Lemma 2.2. If B is a UCBS such that for any two sequences {ek} and {vk} in B with lim supk→∞||ek||≤z, lim supk→∞||vk||≤z and limk→∞||μkek+(1−μk)vk||=z, for 0<c≤μk≤d<1 and some z≥0. Then limk→∞||ek−vk||=0.
3.
Convergence theorems of mean nonexpansive operators
Notice that, throughout the section, B denotes a UCBS. The main outcome of this section is begun with the following key lemma. It should be noted that this lemma extends and improves [21, Lemma 4.1] from the setting of nonexpansive operators to the setting of mean nonexpansive operators.
Lemma 3.1. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅. Then limk→∞||vk−v∗|| exists for every v∗∈FT, where {vk} is a sequence generated by (1.6).
Proof. For, v∗∈FT, we have v∗=Tv∗. Then using (1.6), we have
and
While using the above inequilities, we have
It has been observed that {||vk−v∗||} is non-increasing and bounded. It follows that limk→∞||vk−v∗|| exists for all fixed point v∗ of T.
The next theorem will be helpful in proving the main results of the sequel.
Theorem 3.1. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅ and {vk} is a sequence defined in (1.6). Then the sequence {vk} is bounded and limk→∞||vk−Tvk||=0.
Proof. If we select any element v∗∈FT, then it is clear from the Lemma 3.1, that, {vk} is bounded. We want to show that limk→∞||vk−Tvk||=0. Now, according to Lemma 3.1, limk→∞||vk−v∗|| exists. We set
Now,
Also,
Similarly,
From (3.2) and (3.4), we get
From (3.5), we have
Applying Lemma 2.2, we obtain
Now we want to establish a strong convergence theorem on a compact domain. This result includes the result if one considers a nonexpansive operator.
Theorem 3.2. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅. Then {vk} defined in (1.6) converges in the strong sense to a point of FT if C is compact.
Proof. Thanks to the convexity of C, we can say that {vk}⊆C. Also remembering the compactness of C, one can choose a strongly convergent subsequence {vkm} of {vk} such that vkm→v0. Now we show that Tv0=v0. For this
Consequently, we obtain
According to Theorem 3.1, we have limk→∞||vkm−Tvkm||=0, so applying m→∞ on (3.6), we obtain Tv0=v0. This shows that v0∈FT. By Lemma 3.1, limk→∞||vk−v0|| exists. Consequently, v0 is the strong limit of {vk} and element of FT.
If we drop the compactness assumption, we have the following result. It should be noted that this theorem extends and improves [21, Theorem 4.4] from the setting of nonexpansive operators to the setting of mean nonexpansive operators.
Theorem 3.3. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅. Then {vk} defined in (1.6) converges in the strong sense to a point of FT, if and only if lim infk→∞d(vk,FT)=0.
Proof. The necessity is straight forward.
Conversely, we may assume that lim infk→∞d(vk,FT)=0 and choose v∗∈FT. From the Lemma 3.1, limk→∞||vk−v∗|| exists. By assumption, we conclude that limk→∞d(vk,FT)=0. We want to show that {vk} form a Cauchy sequence in the set C. As we have proved that limk→∞d(vk,FT)=0, so for a given ε>0, one can choose r0∈N in such a way that for each k≥r0,
In particular, inf{||vk0−v∗||:v∗∈FT}<ε2. This suggests the existence of v∗∈FT such that
Now for r,m≥k0,
Hence, we observe that {vk} form a Cauchy sequence in the closed set V and so one can choose some v∗∈C such that limk→∞vk=v∗. Now limk→∞d(vk,FT)=0 gives that d(v∗,FT)=0. The closeness of FT follows from the mean nonexpansiveness of T. Hence v∗∈FT.
We want to show a strong convergence theorem under the following condition.
Definition 3.1. [19] On a nonempty subset C of B, an operator T:C→C is said to have a condition (I) in the case, when there is a selfmap R:[0,∞)→[0,∞) such that R(i)=0, if and only if i=0, R(i)>0 for all real constants i∈(0,∞) and ||v−Tv′||≥R(d(v,FT)) for all v∈C.
The following theorem extends and improves [21, Theorem 4.5] from the setting of nonexpansive operators to the setting of mean nonexpansive operators.
Theorem 3.4. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅. Then {vk} defined in (1.6) converges in the strong sense to a point of FT if T has a condition (I).
Proof. In the view of Theorem 3.1, we conclude the following
By combining condition (I) with (3.7), we get
Since the selfmap R is such that R(0)=0 and R(a)>0 for all i>0. It follows that
It has been observed that all the requirements of Theorem 3.3 are present, one concludes that T converges strongly to a fixed point of T.
This section we close by providing a weak convergence theorem. It should be noted that this theorem extends and improves [21, Theorem 4.3] from the setting of nonexpansive operators to the setting of mean nonexpansive operators.
Theorem 3.5. If C is a nonempty convex and closed subset of B such that T:C→C is a mean nonexpansive operator having FT≠∅. Then {vk} defined in (1.6) converges in the weak sense to a point of FT if B has the Opial's property.
Proof. We can write from Theorem 3.1 that {vk} is bounded and limk→∞||vk−Tvk||=0. It is known that B is RBS in the case when B is UCBS. Thanks to the reflexiveness of the space, the generated sequence {vk} eventually possess a subsequence which we may denote by {vks} equiped with a weak limit v1∈C. Now we may apply Lemma 2.1, and obtain v1∈FT. Next we want to show that the element v1 is also a weak limit of {vk}. If the element v1 is not the weak limit of the sequence {vk}, then we may set another weakly convergent subsequence {vkt} of {vk} equiped with a weak limit v2∈C in such a way that v2≠v1. Applying Lemma 2.1, v2∈FT. Now applying Lemma 3.1 and also the Opial condition, one has
The above observations give a contradiction. Thus, we must accept that the element v1 is the weak limit of {vk}. This finishes the proof.
4.
Some applications
If a linear or nonlinear equation has a solution then some-times it is either very hard or impossible to compute the value of such a solution under ordinary analytical approaches [1,12,22]. For instance, see the following equations,
which are not easy to solve by applying available analytical approaches of the literature. In such a case, the approximate value of such a solution is desirable. To find an approximate value of a solution, we must rearrange the given equation in the form of fixed point equation v=Tv. Notice that here the operator T should be set on a certian space B. In this case, fixed point set of T is same as the solution set of the given equation. Fixed point theorems provides the existence and uniqueness of a fixed point for T, while iterative algorithms finds the value of this fixed point by imposing some conditions (on T, the domain of T or any other). Banach Contraction Principle (BCP) [5] offers a unique fixed point for T if T is a contraction and B is a complete metric space and suggest a basic iterative algorithm due to Picard for computing its value. However, for nonexpansive operators, Picard algorithm in general fails to converge. The class of nonexpansive operators includes contractions and has important applications in many areas of applied sciences, that is, in image reconstruction and signal processing problems, the operator T is essentially nonexpansive, when the method of an averaging operators is used, (see e.g., Byrne [7] and others).
Accordingly, here we propose algorithms that are the modifications of the TTP algorithm (1.6) (which we call here TTP type algorithms) and using our main results, we show that these algorithms eventually solves SFPs and VIPs, respectively.
4.1. Split feasibility problems
If B1 and B2 are two given real Hilbert spaces. Then the concept of a SFP mathematically, a SFP [8] reads as follows:
The subset C⊆B1 as well as the subset Q⊆B2 are assumed as closed, convex and A:B1→B2 is an operator which is assumed at the same time linear and bounded. From [13], we know that, many problems arise in the research of signal processing as well as the design of any provided nonlinear synthetic discriminant filter as concerns optical pattern recognition, can be set in the form of SFPs.
We may suppose that the SFP (4.1) has a nonempty solution set, and we denote it by S. Now, from [13], we know that, v∗∈C solves (4.1) if and only if it solves the below provided fixed point equation:
The above used notations PC as well as PQ are used for the nearest point projection (NPP) onto the already choosen sets C and Q, respectively. While ξ>0 and A∗ denotes the adjoint operator of corresponding to the operator A. In [7], Byrne was the first researcher among other things, who noted that if η is a scalar that denotes a spectral radius of A∗A and suppose 0<ξ<2η, we can say that
is essentially nonexpansive and the weak convergence of the below CQ iterative algorithm
is confirm in the set S.
The improvement and extension the above weak convergence to case of strong convergence gained the attention of many authors. However to do this, one needs some more assumptions, (see e.g., [13] and others) to study a recent survey on the Halpern type algorithms.
In this research, our approach is to consider mean nonexpansive operators, which are generally not continuous on the domain on which they are defined (as shown by examples in this paper), instead of nonexpansive operators, that are essentially throughout continuous on the domain on which they are defined. In this case, we assume that a SFP has a solution, and prove that the proposed iterative algorithm converges weakly and strongly to its solution.
Theorem 4.1. Let the SFP (4.1) be consistent, that is, S≠∅, 0<ξ<2η and PC(Iid−ξA∗(Iid−PQ)A) be a mean nonexpansive operator. Then there exists μk,ηk,θk∈(0,1) in a way that the suggested iterative algorithm sequence {vk} produced as
accordingly weakly convergent to v∗ which is a solution of SFP problem (4.1).
Proof. Puti T=PC(Iid−ξA∗(Iid−PQ)A). Then T is a mean nonexpansive operator. According to Theorem 3.5, {vk} converges weakly to a point of FT. But FT=S, it follows that {vk} converges weakly to a solution v∗ of the SFP problem (4.1).
The strong convergence is the following.
Theorem 4.2. Let the SFP (4.1) be consistent, that is, S≠∅, 0<ξ<2η and PC(Iid−ξA∗(Iid−PQ)A) be a mean nonexpansive operator. Then there exists μk,ηk,θk∈(0,1) in a way that the suggested iterative algorithm sequence {vk} produced as
accordingly strongly convergent to v∗ which is a solution of SFP problem (4.1) provided that lim infk→∞d(vk,S)=0.
Proof. Puti T=PC(Iid−ξA∗(Iid−PQ)A). Then T is mean nonexpansive. According to Theorem 3.3, {vk} converges strongly to a point of FT. But FT=S, it follows that {vk} converges strongly to a solution v∗ of the SFP problem (4.1).
4.2. Variational inequality problems
Suppose a Hilbert space B and ∅≠C⊂B is closed and convex. The operator M:B→B is known as monotone if
Now we give the concept of a VIP. Mathematically, a VIP reads as follows:
In [7], the author noted that if ξ>0, then v∗∈C is always a solution for the VIP (4.2) if and only if v∗ is a solution of the below given fixed point equation:
where PC denotes the nearest point projection onto the set C.
In [7], the author noted that if Iid−ξM and PC(Iid−ξM) are nonexpansive operators, then, the sequence {vk} generated by the following iterative algorithm:
converges weakly to a solution of the VIP (4.2), provided that such solutions essentially exist.
In this research, our approach is to consider mean nonexpansive operators, which are generally not continuous on the domain on which they are defined (as shown by examples in this paper), instead of nonexpansive operators, that are essentially throughout continuous on the domain on which they are defined. In this case, we assume that a VIP has a solution, and prove that the proposed iterative algorithm converges weakly and strongly to its solution.
Theorem 4.3. Let the VIP (4.2) be consistent, that is, S≠∅, ξ>0. If PC(Iid−ξM) is a mean nonexpansive operator. Then there exists μk,ηk,θk∈(0,1) in a way that the suggested iterative algorithm sequence {vk} produced as
accordingly weakly convergent to v∗ which is a solution of VIP problem (4.2).
Proof. Puti T=PC(Iid−ξM). Then T is a mean nonexpansive operator. According to Theorem 3.5, {vk} converges weakly to a point of FT. But FT=S, it follows that {vk} converges weakly to a solution v∗ of the VIP problem (4.2).
Theorem 4.4. Let the VIP (4.2) be consistent, that is, S≠∅, ξ>0. If PC(Iid−ξM) is a mean nonexpansive operator. Then there exists μk,ηk,θk∈(0,1) in a way that the suggested iterative algorithm sequence {vk} produced as
accordingly strongly convergent to v∗ which is a solution of VIP problem (4.2) provided that lim infk→∞d(vk,S)=0.
Proof. Put T=PC(Iid−ξM). Then T is mean nonexpansive. According to Theorem 3.3, {vk} converges weakly to a point of FT. But FT=S, it follows that {vk} converges strongly to a solution v∗ of the VIP problem (4.2).
5.
Examples
We first construct an example of discontinuous mean nonexpansive maps having a unique fixed point. We show that this example does not belong to the class of nonexpansive operators as.
Example 5.1. If C=[1,5], then C is clearly close and convex. We now set T:C→C that is defined as follows:
We want to show that T is mean nonexpansive on C. We need to find some positive real constants a,b with a+b≤1, suchjthat ||Tv−Tv′||≤a||v−v′||+b||v−Tv′||, for every v,v′∈C. Choose a=12=b, then a+b≤1. We suggest the following cases.
(i) Suppose that 1≤v,v′<2. Then
(ii) Suppose that 2≤v,v′<5. Then
(iii) Suppose that 1≤v′<2 and 2<v≤5.
(iv) Suppose that 1≤v<2 and 2≤v′≤5.
It has been observed that the operator T is mean nonexpansive on the set C. Notice that T is being discontinuous and hence not nonexpansive. Precisely, if v=1.9 and v′=2, then ||Tv−Tv′||>||v−v′||. Using this example, we provide some values obtained from different iterative algorithms in the Table 1 and the behaviors of there iterates can be viewed in the Figure 1.
Now, we show some furhter high accuracy of the TTP iterative algorithm. We use Example 5.2, and set ||vk−v∗||<10−15 our stopping cretrian. Observations are provided in the Tables 2–4 and Figures 2–4.
We finish our paper with the following example that illustrates our main results.
Example 5.2. If C=[0,1], then we can set an operator T:C→C by the following formula
Here, T is discontinuous and hence not nonexpansive. On the other hand, T is a mean nonexpansive operator. Moreover, the domain of T is closed convex subset of a UCBS, so the sequence of TTP iteration (1.6) converges to its fixed point.
6.
Conclusions
The paper provided a three-step iterative approach to compute fixed points of mean nonexpansive maps in a Banach space setting. Weak and strong convergence on compact and noncompact domains are essentially established. We have showed by examples that mean nonexpansive mappings are in general discontinuous and include all nonexpansive mappings. Accordingly, we have improved the main results of Thakur et al. [21] in two ways:
(i) From nonexpansive operators to the wider setting of mean nonexpansive operators.
(ii) From continuous operators to the general setting of discontinuous operators.
As applications of the main outcome, we have suggested two new three-step TTP type projection algorithms to find a solution for SFP and VIP in the context of mean nonexpansive mappings. We have performed some numerical experiments to provide the high accuracy of the studied three-step algorithm corresponding to the other three-step algorithms in context of mean nonexpansive operators.
7.
Open problem
We now leave an intersting open problem for the readers as follows.
Open Problem. Can we extend the results of this paper to the setting of hyperbolic spaces?
Acknowledgments
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: